Introduction and related work

E-learning systems have become an integral part of modern education, providing students with flexibility and access to educational resources from anywhere in the world. However, with the increasing amount of information available to students in online environments, there is an urgent need to develop effective methods and tools for managing and classifying information objects1,2. A variety of learning materials, including textual, graphic, audio, and video resources, require automated processing and classification to ensure convenient and effective learning.

Several studies have addressed the challenges of classifying and organizing educational content in e-learning systems. For instance, machine learning approaches have been employed to categorize learning objects based on metadata and content features3. In4, the authors proposed a semantic-based classification system that uses ontologies to improve the retrieval and organization of educational resources. Additionally, deep learning techniques, such as convolutional and recurrent neural networks, have shown promising results in processing and classifying multimedia data within educational platforms5,6. Hybrid models combining natural language processing (NLP) with neural networks have also been introduced for analyzing textual resources and enhancing the adaptability of content recommendations7. Despite these advancements, many existing systems struggle with scalability, adaptability to domain-specific content, and handling ambiguous or unstructured data, which highlights the need for more robust and flexible classification approaches.

Neural networks, due to their ability to extract features and analyze data, have become a powerful tool in the fields of computer vision, word processing, and audio. In our work, we explore their potential in the context of classifying educational resources.

The main model for fuzzy inference is the Mamdani-Zadeh model8,9. Although this model is fundamental, only one fuzzy production neural network has become widespread, and that is the Wang-Mendel network10,11,12. This network was developed using the concepts of the Mamdani-Zadeh model and complementing them with innovative approaches. The Wang-Mendel network has proven to be particularly effective in solving problems where objects can belong to several classes at the same time, or where there is a complex intersection of classes. Its successful application testifies to the powerful potential of combining fuzziness and neural networks in the field of classifying of information objects.

In the study presented in13, a new multi-output modification of the Wang-Mendel network is described and analyzed in detail. In this scientific material, the concept of innovative architecture of the neural fuzzy production network, based on the basic Mamdani-Zadeh model, is put forward. Particular attention is paid to solving classification problems using the proposed fuzzy network and comparative analysis with the Wang-Mendel network with several outputs. This paper examines in detail the use of the new fuzzy network and compares it with a Wang-Mendel network with multiple outputs, particularly in the context of interpretations of fuzzy logical operations.

Neural networks based on fuzzy logic make it possible to automatically adapt to changing conditions and characteristics of educational data14,15,16,17,18,19,20,21,22. This combination of technologies provides more accurate and consistent results in classification tasks, especially when there is ambiguity in the interpretation of the content of training materials23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54.

We will look at the application of fuzzy logic in the context of neural network training, detailing methods for adapting to different levels of uncertainty.

In the article, we will present our methodology and experimental results, demonstrating the effectiveness of the proposed model. Our work contributes to the development of the field of machine learning and artificial intelligence in the field of education and is likely to be an important step in improving the quality of e-learning.

Our approach combines the power of neural networks with the flexibility of fuzzy logic, allowing us to effectively handle uncertainty and fuzziness in educational resource data. This is especially important in the context of the diverse formats and content inherent in modern learning.

The analysis of the related works above enabled us to highlight their main drawbacks, which limit their practical application and effectiveness in modern e-learning environments:

Limited adaptability to different learning contexts

Many classification systems are domain-specific and cannot be easily generalized to other educational fields or subject areas without significant reconfiguration or retraining.

Insufficient handling of heterogeneous data

Although deep learning models demonstrate high performance with structured or homogeneous data, they often struggle when dealing with diverse formats such as text, images, audio, and video in a unified classification framework.

Dependence on large labeled datasets

Most deep learning and machine learning approaches require extensive labeled training data, which is often unavailable or expensive to create in educational contexts, especially for under-resourced languages or specialized topics.

Lack of interpretability and transparency

The use of complex neural architectures makes it difficult to interpret how decisions are made, which is a critical issue in educational systems where trust and explainability are important for both learners and instructors.

Limited personalization

Although some systems attempt to tailor content to learner preferences, they often rely on static learner models and fail to adapt in real time to evolving learning needs and styles.

Semantic gaps in content understanding

Ontology-based and semantic systems, while promising, often suffer from incomplete domain knowledge and cannot fully capture the nuanced meaning of educational content, especially in multimedia formats.

These drawbacks emphasize the necessity for more adaptive, interpretable, and multimodal classification approaches that can robustly handle diverse educational content and provide personalized learning experiences.

Therefore, the aim of this paper is to develop the intelligent systems for automatically classifying the types of educational materials. To reach the aim the following objectives are formed: ….

Our work proposes a new approach to classifying information objects in e-learning systems using a combination of neural networks and fuzzy logic. This study shows the possibilities of using modern machine learning techniques to efficiently analyze and process information in sensory systems. This will allow students to find the resources they need faster and make it easier for educators to manage content in educational platforms.

To implement the proposed approach to classifying information objects in e-learning systems using a combination of neural networks and fuzzy logic, the following main tasks have been identified:

  1. 1.

    Analysis and preprocessing of educational content

  • Collect and categorize heterogeneous data types (textual, visual, audio, and video materials) commonly used in e-learning platforms.

  • Apply preprocessing techniques such as feature extraction, data normalization, and format unification to prepare the content for classification.

  1. 2.

    Development of a hybrid classification model

  • Design a neural network architecture capable of learning complex patterns and representations from diverse learning materials.

  • Integrate fuzzy logic modules to enhance interpretability and enable reasoning with imprecise, vague, or linguistic input data.

  • Ensure the hybrid model can effectively deal with uncertainty and ambiguity present in real-world educational content.

  1. 3.

    Creation of fuzzy rule base for semantic interpretation

  • Define fuzzy sets and construct a set of classification rules that reflect human-like reasoning about educational content (e.g., “highly visual”, “technical and detailed”, “introductory level”).

  • Enable dynamic adjustment or generation of rules based on training data using learning or optimization techniques (e.g., genetic algorithms or rule pruning).

  1. 4.

    Training and evaluation of the model

  • Train the neural-fuzzy system on a labeled dataset of learning resources categorized by content type, complexity, or learning objective.

  • Evaluate the system’s performance using classification metrics such as accuracy, precision, recall, F1-score, and interpretability.

  1. 5.

    Integration into e-learning platforms

  • Develop an interface or module that allows seamless integration of the classification system into existing LMS (Learning Management Systems).

  • Provide user-friendly tools for educators to upload, organize, and tag content based on the model’s recommendations.

  1. 6.

    Support for personalized learning

  • Use the classification outcomes to recommend resources to students based on their learning styles, progress, and preferences.

  • Continuously adapt recommendations as student behavior evolves, leveraging the adaptive capabilities of the neural-fuzzy model.

When solving the problems of classifying information objects, fuzzy production networks are successfully used. These networks successfully combine the capabilities of fuzzy inference systems and neural networks, which allows to solve the complex classifying tasks effectively.

Materials and methods

Let’s consider the solution of the problem of recognizing information objects using fuzzy output systems and neural networks.

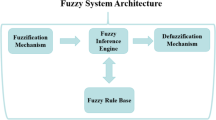
The general structure of the fuzzy inference system includes several main stages: fuzzification, a base of fuzzy inference rules, a decision-making module, and defuzzification32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48.

In the fuzzification step, the exact set of inputs

\(\:{io}_{in}=({io}_{{in}_{1}},\:i{o}_{{in}_{2}},\dots\:,{io}_{{in}_{i}})\in\:{SP}_{in}\) turns into a fuzzy set \(\:Mul\subseteq\:{SP}_{in}\) with the help of a specific affiliation function \(\:{f}_{Mul}\left(io\right)\).

Here \(\:Mul={Mul}_{1}\times\:{Mul}_{2}\times\:\dots\:\times\:{Mul}_{i}\), where \(\:i\) – number of information objects.

Fuzzification is a key step, allowing the system to efficiently process fuzzy inputs, which is often found in real-world situations where accurate measurements may be limited or inaccurate.

Defuzzification, on the other hand, transforms several fuzzy sets \(\:{FS}^{j}\),

\(\:j=\text{1,2},\dots\:,S\) or a single fuzzy set \(\:FS\) into a specific value of the source variable \(\:i{o}_{out}\in\:{SP}_{out}\). This is done on the basis of fuzzy conclusions generated by the decision-making module. The method of defuzzification is chosen depending on the specific conditions of the task.

Such a system can have different representations, illustrated, for example, in (Fig. 1)7. This shows the flexibility and adaptability of fuzzy output systems, which can be successfully applied in a variety of industries and tasks.

Fig. 1
figure 1

Scheme of operation of the system of recognition of information objects using fuzzy logic and neural networks.

Full size image

It is believed that all \(\:S\) rules are interconnected by a logical operation «OR», at the same time, the outputs of the rules \(\:{io}_{out}^{1},\:{io}_{out}^{1},\dots\:,{io}_{out}^{S}\) are considered mutually independent. Thus, it’s possible to use the following type of rules:

$$\begin{gathered} Rul{e^1}:{\text{If}}\;io_{{i{n_1}}}^{1}\;{\text{belongs}}\;Mul_{1}^{1}\;{\text{AND}}\;io_{{i{n_2}}}^{1}{\text{belongs}}\;Mul_{2}^{1}\;{\text{AND}}\cdots{\text{AND}}\;io_{{i{n_i}}}^{1}\; \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\text{belongs}}\;Mul_{i}^{1},{\text{THEN}}\;io_{{out}}^{1}\;{\text{belongs}}\;F{S^1}; \hfill \\ Rul{e^j}:{\text{If}}\;io_{{i{n_1}}}^{j}\;{\text{belong}}s\;Mul_{1}^{j}\;{\text{AND}}\;io_{{i{n_2}}}^{j}\;{\text{belongs}}\;Mul_{2}^{j}\;{\text{AND}}\cdots{\text{AND}}\;io\;_{{i{n_i}}}^{j}\; \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\text{belongs}}\;Mul_{i}^{j},{\text{THEN}}\;io_{{out}}^{j}\;{\text{belongs}}\;F{S^j}; \hfill \\ Rul{e^S}:{\text{If}}\;io_{{i{n_1}}}^{S}\;{\text{belongs}}\;Mul_{1}^{S}\;{\text{AND}}\;io_{{i{n_2}}}^{S}{\text{belongs}}\;Mul_{2}^{S}{\text{AND}}\cdots{\text{AND}}\;io_{{i{n_i}}}^{S}\; \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\text{belongs}}\;Mul_{i}^{S},{\text{THEN}}\;io_{{out}}^{S}\;{\text{belongs}}\;F{S^S}. \hfill \\ \end{gathered}$$
(1)

Variables \(\:\left({io}_{{in}_{1}}^{j},{io}_{{in}_{2}}^{j},\dots\:,{io}_{{in}_{i}}^{j}\right)\) form the \(\:i\)-dimensional input vector \(\:{io}_{in}^{j}\), which is an argument for the condition in which \(\:{Mul}_{1}^{j},{Mul}_{2}^{j},\dots\:,{Mul}_{i}^{j}\) and \(\:{FS}^{j}\) denote fuzzy sets, and \(\:{SP}_{in}^{1},{SP}_{in}^{2},\dots\:,{SP}_{in}^{i}\) and \(\:{SP}_{out}\)—distinct sets, and \(\:{Mul}_{1}^{j}\subseteq\:{SP}_{in}^{1},\:{Mul}_{2}^{j}\subseteq\:{SP}_{in}^{2},\dots\:,{Mul}_{i}^{j}\subseteq\:{SP}_{in}^{i},\) а\(\:{\:FS}^{j}\subseteq\:{SP}_{out}\).

If we denote the Cartesian product of sets \(\:{Mul}_{1}^{j},{Mul}_{2}^{j},\dots\:,{Mul}_{i}^{j}\) as

\(\:{Mul}^{j}={Mul}_{1}^{j}\times\:{Mul}_{2}^{j}\times\:\dots\:\times\:{Mul}_{i}^{j}\), then the corresponding values of the coefficients of belonging to the condition and the conclusion of the derivation rule – is \(\:{f}_{{Mul}^{j}}\left({io}_{in}^{j}\right)\) and \(\:{f}_{{FS}^{j}}\left({io}_{out}^{j}\right)\). Then the rule of type (1) can be represented as a fuzzy implication:

$$\:{Rule}^{j}:\:\:\:{Mul}^{j}\to\:{FS}^{j},\:\:\:j=\text{1,2},\dots\:,S.$$
(2)

At the same point, a rule of type (1) can be considered as a fuzzy relation defined on the set \(\:{SP}_{in}{\times\:SP}_{out}\), where \(\:{SP}_{in}\)—Cartesian product of distinct sets represented as \(\:{SP}_{in}^{1},{SP}_{in}^{2},\dots\:,{SP}_{in}^{i}\). In this case, \(\:\left({io}_{{in}_{1}}^{j},{io}_{{in}_{2}}^{j},\dots\:,{io}_{{in}_{i}}^{j}\right)\in\:{SP}_{in}\), \(\:{io}_{{in}_{1}}^{j}\in\:{SP}_{in}^{1},\:{io}_{{in}_{2}}^{j}\in\:{SP}_{in}^{2},\dots\:,{io}_{{in}_{i}}^{j}\in\:{SP}_{in}^{i},\) and \(\:{io}_{out}^{j}\in\:{SP}_{out}\), which means that \(\:{Rule}^{j}\subseteq\:{SP}_{in}{\times\:SP}_{out}\) – it is a fuzzy set with a membership function11:

$$\:{f}_{{Rule}^{j}}\left({io}_{in}^{j},{io}_{out}^{j}\right)={f}_{{Mul}^{j}\to\:{FS}^{j}}({io}_{in}^{j},{io}_{out}^{j})$$
(3)

Fuzzy inference systems, which include neural fuzzy production networks12, can be represented as multilayered neural structures with a direct signal propagation mechanism. These networks are defined by a peculiar combination of fuzzy logic and neural modeling techniques to efficiently process vaguely defined data and draw meaningful conclusions.

Neural fuzzy production networks have been widely used in a variety of fields, including control, forecasting, and decision-making systems. Gradient algorithms and the backpropagation method of error propagation are used to effectively train such networks. These techniques enable to optimize network parameters by adjusting them to best match the input data and achieve optimal results in solving fuzzy output problems.

This approach combines the advantages of neural machine learning with the flexibility and efficiency of fuzzy logic, making these systems effective tools for solving problems related to fuzzy or uncertain data.

Case study

Model description. Classical neural network model

For experimental testing, three models of CNN neural networks with different architectures were used, whith differ number of the internal layers from 2 to 4.

Let’s consider one of the variants of the developed neural network which was chosen. A neural network consists of the following layers: the input layer – 8 neurons that receive input parameters, 3 hidden layers that classify information objects, and they are fully connected, and the output layer – 4 neurons, the output of which is classified information objects, which are among one of the four classes.

With three hidden layers, this network has a certain level of depth. Deep neural networks can learn hierarchical representations of data, which can be beneficial for capturing complex patterns and relationships in e-learning systems.

As an activation function for hidden layers, the ReLU function is used, which has a special feature to solve the problem of a disappearing gradient. The ReLU activation function used in the hidden layers introduces non-linearity to the network. This enables the network to learn and represent non-linear relationships in the data, which is crucial for capturing the complexities often present in datasets with information object in e-learning systems. Also, the ReLU activation function used in the hidden layers introduces non-linearity to the network. This enables the network to learn and represent non-linear relationships in the data, which is crucial for capturing the complexities often present in e-learning datasets. The ReLU activation function helps alleviate the vanishing gradient problem, which can occur during training of deep neural networks.

The output layer uses the softmax function, which features cross-entropy learning. The softmax function used in the output layer is suitable for multi-class classification tasks like information object classification in e-learning systems. Softmax outputs probabilities for each class, making it easy to interpret the model’s confidence in its predictions. Additionally, softmax naturally handles the multi-class nature of the problem, allowing the model to assign probabilities to each class.

The use of cross-entropy loss with softmax activation is a common choice for multi-class classification problems. It is well-suited for training neural networks to output probability distributions over multiple classes. Cross-entropy loss penalizes the model based on the difference between predicted probabilities and the true distribution of class labels, encouraging the model to produce accurate and confident predictions.

Overall, this neural network model combines depth, non-linearity, and appropriate activation functions and loss functions, making it well-suited for effectively learning and classifying information objects in e-learning systems.

Neural network model based on fuzzy logic

The main idea of the approach is that a set of fuzzy rules is formed for each class of information objects.

\(\:IO=\left\{\stackrel{\sim}{{p}_{1}},\:\stackrel{\sim}{{p}_{2}},\:\dots\:,\:\stackrel{\sim}{{p}_{n}}\}\right\}\) is passed at the input of the systems, multiple classes are defined as \(\:Cl\left\{c{l}_{j}\right\}\), \(\:j=1,…,m\) as well as a set of rules (for training):

$$\begin{gathered} {\text{rule1 }}={\text{ ctrl}}.{\text{Rule}}\left( \begin{gathered} {\text{P1}}\left[ {^\prime{\text{average}}^\prime} \right]{\text{ }}\left| {{\text{ P2}}\left[ {^\prime{\text{average}}^\prime} \right]{\text{ }}} \right|{\text{ P3}}\left[ {^\prime{\text{poor}}^\prime} \right]{\text{ }}\left| {{\text{ P4}}\left[ {^\prime{\text{average}}^\prime} \right]{\text{ }}} \right|{\text{ P5}}\left[ {^\prime{\text{poor}}^\prime} \right]{\text{ }} \hfill \\ \left| {{\text{ P6}}\left[ {^\prime{\text{average}}^\prime} \right]{\text{ }}} \right|{\text{ P7}}\left[ {^\prime{\text{poor}}^\prime} \right],{\text{ Cl}}\left[ {^\prime{\text{low}}^\prime} \right] \hfill \\ \end{gathered} \right) \hfill \\ {\text{rule2 }}={\text{ ctrl}}.{\text{Rule}}\left( \begin{gathered} {\text{P1}}\left[ {^\prime{\text{average}}^\prime} \right]{\text{ }}\left| {{\text{ P2}}\left[ {^\prime{\text{good}}^\prime} \right]{\text{ }}} \right|{\text{ P3}}\left[ {^\prime{\text{poor}}^\prime} \right]{\text{ }}\left| {{\text{ P4}}\left[ {^\prime{\text{average}}^\prime} \right]{\text{ }}} \right|{\text{ P5}}\left[ {^\prime{\text{poor}}^\prime} \right]{\text{ }} \hfill \\ \left| {{\text{ P6}}\left[ {^\prime{\text{average}}^\prime} \right]{\text{ }}} \right|{\text{ P7}}\left[ {^\prime{\text{poor}}^\prime} \right],{\text{ Cl}}\left[ {^\prime{\text{medium}}^\prime} \right] \hfill \\ \end{gathered} \right) \hfill \\ {\text{rule3 }}={\text{ ctrl}}.{\text{Rule}}\left( \begin{gathered} {\text{P1}}\left[ {^\prime{\text{good}}^\prime} \right]{\text{ }}\left| {{\text{ P2}}\left[ {^\prime{\text{average}}^\prime} \right]{\text{ }}} \right|{\text{ P3}}\left[ {^\prime{\text{good}}^\prime} \right]{\text{ }}\left| {{\text{ P4}}\left[ {^\prime{\text{average}}^\prime} \right]{\text{ }}} \right|{\text{ P5}}\left[ {^\prime{\text{good}}^\prime} \right]{\text{ }} \hfill \\ \left| {{\text{ P6}}\left[ {^\prime{\text{average}}^\prime} \right]{\text{ }}} \right|{\text{ P7}}\left[ {^\prime{\text{good}}^\prime} \right],{\text{ Cl}}\left[ {^\prime{\text{high}}^\prime} \right] \hfill \\ \end{gathered} \right) \hfill \\ \end{gathered}$$
(4)

Rules in fuzzy logic are formulated for the purpose of logical derivation as a result of the use of fuzzy rules. Each rule consists of two main parts: the antecedent (the if part) and the consequent (the then part).

Antecedent (if part)

This part contains conditions or statements that describe the input parameters and objects to which the rule applies. The antecedent determines whether the rule is activated.

Consequent (then-part)

This part contains the conclusion or result that is derived from the rule as a result of its activation. A consequent defines the original class or action associated with the antecedent.

Each such rule is formed based on measurable fuzzy parameters that informationally characterize each class of objects.

It is also necessary to carry out primary data processing, that is, to remove from the training sample knowingly inaccurate or erroneous data—parameters that are oversaturated with experimental data—and to identify the main parameters for each class.

There are several types of erroneous data in the tasks of classifying information objects in e-education systems. This is due to the human factor, which leads to the introduction of deliberately incorrect values, or to an overabundance of parameters. Then it’s possible to get be rid of incorrect data with the help of an expert or based on statistical search methods.

The training sample \(\:I{O}_{train}\) is specified as a set of pairs

$$\:I{O}_{train}=\left\{\right(I{O}_{i},\:c{l}_{j}\left)\right|I{O}_{i}\in\:IOE,\:\:c{l}_{j}\in\:Cl\}$$

.

The article discusses the problem of building a basic rule based on the training sample, which would allow for the specified parameters \(\:\stackrel{\sim}{{p}_{i}}\in\:P\) to specify the class \(\:{l}_{j}\in\:Cl\). In this case, there may be uncertainty in the indication of the class, the degree of which must be evaluated. An appropriate assessment is supposed to be made based on fuzzy logic methods.

In this paper, the problem of pattern recognition is considered on the example of information objects in e-learning systems.

There are many types of materials in e-learning systems that are not structured. When receiving such an information object, it is necessary to determine its type, the discipline to which it belongs, and so on.

Let’s formulate the main stages of the proposed approach.

First, the rules for the classes of information objects are build. For each class, the rules are a set of functions that correspond to individual parameters and describe the degree of confidence in the correspondence of the parameter value to the selected object class. The primary characteristic of the integral confidence in the belonging of the analyzed information object to the class is the sum of the corresponding functions.

Based on the rules for each class and the primary characteristics of integral confidence, the degrees of confidence of the presented information object belonging to the specified classes are calculated.

When considering the classification problem, we will assume that many parameters are selected with the help of an Expert Advisor and are strictly fixed.

The universal set U for the class of an information object \(\:I{O}_{Class}\) is determined on a case-by-case basis, depending on how the numerical value of the class is calculated. In this paper, the range [0; 120] was chosen to divide it into four equal parts. Thus, the universe \(\:U=[0;120]\), and the membership functions of the corresponding terms will be defined by triangular functions with graphs of membership functions presented in (Fig. 2).

Fig. 2
figure 2

The result of experiments for the case of syllabus.

Full size image

The class membership functions of the information objects are defined as follows:

$$\:{\mu\:}_{s}\left(x\right)=\left\{\begin{array}{c}\frac{1}{15}x,\:\:for\:0<x\le\:15\\\:-\frac{1}{15}x+2,\:\:for\:15<x\le\:30\\\:0,\:\:for\:all\:other\end{array}\right.$$
(5)
$$\:{\mu\:}_{m}\left(x\right)=\left\{\begin{array}{c}\frac{1}{15}x-2,\:\:for\:30<x\le\:45\\\:-\frac{1}{15}x+4,\:\:for\:45<x\le\:60\\\:0,\:\:for\:all\:other\end{array}\right.$$
(6)
$$\:{\mu\:}_{l}\left(x\right)=\left\{\begin{array}{c}\frac{1}{15}x-4,\:\:for\:60<x\le\:75\\\:-\frac{1}{15}x+6,\:\:for\:75<x\le\:90\\\:0,\:\:for\:all\:other\end{array}\right.$$
(7)
$$\:{\mu\:}_{h}\left(x\right)=\left\{\begin{array}{c}\frac{1}{15}x-6,\:\:for\:90<x\le\:105\\\:-\frac{1}{15}x+8,\:\:for\:105<x\le\:120\\\:0,\:\:for\:all\:other\end{array}\right.$$
(8)

where \(\:{\mu\:}_{s}\left(x\right)\) – class membership function to the syllabus class, \(\:{\mu\:}_{m}\left(x\right)\) – class membership function to the manual class, \(\:{\mu\:}_{l}\left(x\right)\) – class membership function to the lecture class, \(\:{\mu\:}_{h}\left(x\right)\) – class membership function to the handbook class.

The proposed approach is universal within the context of the subject area of e-learning and can be extended to other classes of information objects. The limitation of this approach is that all initial parameters must be specified with real values. And it will not work if some of this values are set to null.

Experiments

For experimental testing of the proposed approach, an appropriate data set has been employed49. This data set consists of information objects from real e-learning systems, namely such as manuals, lectures, syllabuses, and textbooks. It is important to ensure a variety of information objects and their parameters in the sample to achieve representativeness and universality of the proposed approach.

Four parameters were chosen:

Parameter 1–number of authors,

Parameter 2–number of pages,

Parameter 3–number of tables,

parameter 4–number of figures.

Table 1 shows a fragment of the dataset that was used to train and test the neural network.

Table 1 Fragment of input data.
Full size table

During the experiment, evaluation metrics such as classification accuracy, completeness, F-measure, and others were also considered to obtain an objective assessment of the effectiveness of the proposed approach.

To conduct experimental testing, several neural networks with different numbers of layers and neurons were developed and tested to determine the optimal settings. The training took place on 1000 epochs, and the dataset was divided into training and test samples in a ratio of 8 to 2.

In addition, the sample was divided into training and test parts. The training part will be used to train machine learning models, while the test part is designed to evaluate and compare the performance of the proposed approach with other classification methods.

Table 2 Results of neural networks depending on parameters and settings.
Full size table

As can be seen from Table 2, the best result was shown by the convolutional neural network.

The average accuracy of the selected neural network model across all three data sets was 94.44%.

On the other hand, for a neural network based on fuzzy logic, as mentioned earlier, a set of fuzzy rules for each class of information objects is formed.

Let’s take a look at the four basic rules for each class:

$$\begin{gathered} {\text{rule1}}={\text{ctrl}}.{\text{Rule}}\left( {{\text{P1}}\left[ {^\prime{\text{low}}^\prime} \right]\& {\text{P2}}\left[ {^\prime{\text{low}}^\prime} \right]\& {\text{P3}}\left[ {^\prime{\text{low}}^\prime} \right]\& {\text{P4}}\left[ {^\prime{\text{low}}^\prime} \right],\;{\text{Class}}\left[ {^\prime{\text{syllabus}}^\prime} \right]} \right) \hfill \\ {\text{rule2}}={\text{ctrl}}.{\text{Rule}}\left( {{\text{P1}}\left[ {^\prime{\text{medium}}^\prime} \right]\& {\text{P2}}\left[ {^\prime{\text{low}}^\prime} \right]\& {\text{P3}}\left[ {^\prime{\text{low}}^\prime} \right]\& {\text{P4}}\left[ {^\prime{\text{low}}^\prime} \right],\;{\text{Class}}\left[ {^\prime{\text{manual}}^\prime} \right]} \right) \hfill \\ {\text{rule3}}={\text{ctrl}}.{\text{Rule}}\left( {{\text{P1}}\left[ {^\prime{\text{low}}^\prime} \right]\& {\text{P2}}\left[ {^\prime{\text{medium}}^\prime} \right]\& {\text{P3}}\left[ {^\prime{\text{high}}^\prime} \right]\& {\text{P4}}\left[ {^\prime{\text{medium}}^\prime} \right],\;{\text{Class}}\left[ {^\prime{\text{lecture}}^\prime} \right]} \right) \hfill \\ \end{gathered}$$
(9)

The proposed rules characterize four classes of information objects in e-learning systems, namely syllabus, manual, lecture, and handbook.

Based on these rules, a system for classifying information objects in e-learning systems was built and tested.

Table 3 shows input parameter intervals for a neural network based on fuzzy logic.

Table 3 Input parameter intervals for a neural network based on fuzzy logic.
Full size table

Let’s look at some examples.

For the first example, 4 parameters were fed into the system input that define the syllabus.

Based on the formed rules, as can be seen from (Fig. 3), the system determined it correctly.

Fig. 3
figure 3

The result of experiments for the case of syllabus.

Full size image

Similarly, Fig. 4 shows the result of the classification when a neural network based on fuzzy logic classifies an information object correctly as a manual.

Fig. 4
figure 4

The result of experiments for the case of manual.

Full size image

The other two examples in Figs. 5 and 6 illustrate how a fuzzy logic neural network works to classify information objects in e-learning systems such as lecture and handbook.

Fig. 5
figure 5

The result of experiments for the case of lecture.

Full size image
Fig. 6
figure 6

The result of experiments for the case of handbook.

Full size image

To summarize the results obtained, the quantity of information objects by type was determined in each dataset, the quantity of correctly and incorrectly classified information objects for each dataset, as well as the percentage of accuracy were calculated.

Table 4 shows the numerical results of the experiment on determining information objects in e-learning systems based on fuzzy logic, which were previously shown in (Figs. 4, 5, 6 and 7).

Table 4 Results of a neural network based on fuzzy logic.
Full size table

For every experiment aimed at classifying information objects in e-learning systems, an integral step involved the construction and analysis of a confusion matrix (Figs. 7, 8 and 9). This matrix provides a comprehensive breakdown of the model’s classification performance, offering insights into its accuracy and efficacy in distinguishing between different classes of information objects.

The diagonal elements of the matrix represent the number of instances where the model correctly predicted the class. For example, (Fig. 7), the value of 446 in the first row and first column indicates that there were 446 information objects where the actual class was Syllabus, and the model correctly predicted it as such.

Fig. 7
figure 7

Confusion matrix for dataset with 2400 information objects.

Full size image

Also in confusion matrix, all off-diagonal elements in a column represent false positives. For example, Fig. 8, the value of 22 in the second row and first column indicates that there were 22 information objects where Manual, but the model incorrectly predicted it as Syllabus.

Fig. 8
figure 8

Confusion matrix for dataset with 3600 information objects.

Full size image

In confusion matrix, all off-diagonal elements in a row represent false negatives. For example, Fig. 9, the value of 73 in the third row and fourth column indicates that there were 73 instances where the actual class was Lecture, but the model incorrectly predicted it as Handbook.

Fig. 9
figure 9

Confusion matrix for dataset with 4800 information objects.

Full size image

Calculating the F1 score for three datasets of information objects in e-learning is a crucial step in evaluating the performance of classification models. The F1 score is a harmonic mean of precision and recall and provides a single metric that balances both false positives and false negatives.

For data set with 2400 information objects f1-score is 0,97845, for data set with 3600 information objects f1-score is 0,97525, for data set with 4800 information objects f1-score is 0,98165.

The results of the experimental studies have revealed that when the input parameters for a certain set of fuzzy inference rules are changed, the weight coefficients change. In other words, the ratio of correctly recognized objects to incorrectly recognized objects varies depending on the input data. Thus, a neural network built based on fuzzy logic is able to classify the various information objects in e-learning systems efficiently and correctly.

The average accuracy of the neural network based on fuzzy logic across all three data sets was 97.84%, which is 3.40% better than a classical neural network.

Discussion

Based on the experimental results, we conclude that the use of fuzzy logic in neural networks allows us to cope with the uncertainty inherent more effectively in a variety of educational contexts. This is especially important in a rapidly changing educational landscape, where new formats and types of learning materials are emerging.

In addition, our work highlights the importance of considering the individual needs of students and educators when designing educational resource management systems. An approach based on fuzzy logic contributes to the adaptability and flexibility of the model, which enables to work effectively with different subject areas and learning styles.

In conclusion, our research not only contributes to the field of machine learning and artificial intelligence in education, but also provides practical recommendations for developers of educational platforms and systems. Further research should focus on extending the applicability of this approach, considering scalability for large educational platforms, as well as an in-depth analysis of the impact of diverse data on the effectiveness of the proposed model.

The proposed model does not have the ability to use it for the dataset, in which some parameters of information objects are undefined. In the future, a model for classifying information objects in e-learning systems for which some parameter values are missing will be proposed.

The paper considers the solution of the problem of classifying information objects using fuzzy output systems and neural networks.

Fuzzy inference systems make it possible to effectively model fuzzy relationships between information objects and their classification, especially in conditions where the boundaries between them can be blurred or uncertain. These systems use fuzzy logic rules to handle vaguely defined or ambiguous inputs, making them effective at recognizing complex scenarios.

Neural networks, in turn, make it possible to consider complex nonlinear relationships between different parameters of information objects, especially in conditions where some parameters are unknown. The use of deep learning using neural networks allows studying the complex relationships between information objects automatically, increasing the accuracy of recognition.

Conclusions

The article proposes the integration of neural networks based on fuzzy logic into e-learning systems in order to improve the processes of classification of information objects. The results of the study confirm that this combination of technologies can significantly increase the efficiency of educational resource management, providing accuracy and flexibility in processing data with interval-set parameters.

This approach, combining fuzzy logic and the power of neural networks, makes it possible to solve the problem of recognizing information objects with a high degree of reliability and accuracy 97,84%.

In future it’s expected to explore the field for formation of fuzzy rules for the dataset, in which some parameters of information objects are undefined.

The paper proposes the integration of neural networks based on fuzzy logic into e-learning systems in order to improve the processes of classification of information objects. The core idea is to combine the strengths of both neural networks—capable of learning complex, nonlinear patterns from data—and fuzzy logic—which excels at handling vagueness and imprecision often present in real-world educational content. This synergy enables a more intelligent and adaptive classification mechanism that can better reflect the semantic diversity of learning materials.

The results of the study confirm that this combination of technologies can significantly increase the efficiency of educational resource management, providing not only high classification accuracy but also flexibility in processing data with interval-set or uncertain parameters. Specifically, the hybrid model demonstrated a classification accuracy of 97.84%, which indicates its strong potential for practical deployment in real-world e-learning platforms. This high degree of reliability ensures that students receive accurate recommendations and educators are able to organize and retrieve learning content more effectively.

Moreover, the integration of fuzzy logic allows for better interpretability of the system’s decision-making process—an important advantage over purely black-box neural models. By incorporating human-like reasoning through fuzzy inference rules, the system can provide insights into why certain resources are categorized in specific ways, thereby enhancing transparency and trust in automated educational tools.

In future research, it is expected to expand this approach by exploring methods for automated generation and optimization of fuzzy rules based on datasets in which some parameters of information objects are undefined, missing, or partially known. Such scenarios are common in large-scale educational repositories, where metadata might be incomplete or inconsistently labeled. To address this, evolutionary algorithms, such as genetic algorithms or particle swarm optimization, may be employed to evolve and adapt rule bases dynamically. This would further enhance the model’s robustness, allowing it to handle uncertain or incomplete data with minimal performance degradation.

Additionally, further investigation will focus on the personalization aspect of the system—adapting classification outcomes based on learners’ individual profiles, preferences, and learning progress. By continuously learning from user interactions, the system could refine its classification logic and recommendation strategies, contributing to more engaging and effective learning experiences.