Introduction

Background

Accurate and effective predictions of PM2.5 concentrations are important for air quality management1. PM2.5, characterized by particles with a diameter less than 2.5 micrometers, is regarded as one of the most detrimental components of air pollution2,3. Studies have indicated that prolonged exposure to high concentrations of PM2.5 not only increases the risk of lung cancer4 but also leads to severe damage to the heart and other organs2,5,6. Due to the hazards caused by excessive PM2.5 concentrations, there has been a growing focus on predictions. However, the performance of the current methods for predicting PM2.5 concentrations is still insufficient7. Hence, achieving greater precision in forecasting PM2.5 concentrations is instrumental in shaping and executing alert decision-making procedures, which are indispensable for safeguarding public health and tackling environmental issues1,8,9.

Research status

There are three types for PM2.5 concentrations predictions, the mechanistic models, statistical models, and machine learning models. Mechanistic models primarily focused on investigating the PM2.5 formation mechanisms10, taking into account the interactions among various pollutants and employing mathematical methods to describe the diffusion and deposition processes of PM2.510,11. Prominent examples of such models include the weather research and forecasting model coupled with chemistry (WRF-Chem)12, the community multiscale air quality model (CMAQ)10, and the comprehensive air quality model with extensions (CAMx)13, among others. However, due to limited knowledge of air pollution sources and the influence such as geography and meteorology, mainstream mechanistic models14,15 exhibit significant biases in predicting PM2.5 concentration, especially during heavy pollution periods in autumn and winter, with prediction biases reaching as high as 30–50%16,17,18. Compared to mechanistic models, statistical models based on historical data are simpler and often exhibit higher prediction accuracy19,20. These models include the autoregressive integrated moving average model (ARIMA)21, the Kalman filter22, and the multiple linear regression (MLR)23, among others. Given the nonlinear and non-stationary nature of PM2.5, these statistical models often face challenges in achieving the desired level of predictive accuracy24,25.

PM2.5 concentration is predicted using machine learning models, including the extreme learning machines (ELM)26, the support vector regression (SVR)27, and other artificial neural networks (ANN)28. These models leverage neural networks and other machine learning methods to extract patterns in historical PM2.5 and predict future trends. Compared to traditional mechanistic and statistical models, machine learning models are proficient in capturing the nonlinear features of PM2.529. In recent years, recurrent neural network models, proficient in handling sequence data, have demonstrated advantages in PM2.5 prediction. For example, gated recurrent units (GRU) networks30,31,32 and long short-term memory (LSTM) networks33,34 have been used for PM2.5 concentration prediction. Despite their effectiveness, basic single recurrent neural networks (RNNs) models often struggle to comprehensively explore data variation patterns, potentially leading prediction instabilities7. Currently, researchers are actively investigating strategies to enhance the predictive performance of single models from various perspectives.

Researchers have sought to enhance the prediction performance through model improvements or the hybridization of different models. Advanced models such as directional long short-term memory (BiLSTM)35, built upon improved versions of LSTM, effectively reduce prediction errors by capturing features from both forward and backward directions. Combining different neural networks, such as convolutional and recurrent networks36,37,38, leverages their complementary advantages for improved prediction effectiveness. The attention mechanism, widely applied in various fields39,40, enhances prediction accuracy by extracting long-term dependencies and minimizing information loss through probabilistic weight allocations. Recent studies19,41,42 have demonstrated that PM2.5 prediction models that integrate attention mechanisms can enhance the precision and generalizability of predictions. The integration of attention mechanisms into PM2.5 prediction models enhances performance but requires attention weights to be computed at each time step35,42,43.

The integration of data preprocessing into machine learning models effectively enhances the PM2.5 prediction performance. By integrating data preprocessing techniques, the predictive accuracy of PM2.5 models has improved through simplifying and decomposing the original sequence data into subsequences with distinct informational content7,41. For instance, hybrid models that combine empirical mode decomposition (EMD) and its variants, or variational mode decomposition (VMD) with neural networks, have demonstrated substantial improvements in PM2.5 prediction41,42,44,45. Further refinements using hybrid data decomposition techniques and secondary decomposition methods have enabled more detailed feature extractions, boosting model performance46. In order to capture the periodicity characteristics of PM2.5 sequence data, the method of seasonal trend decomposition based on loess (STL) was attempted by researchers47,48,49,50 to separate the trend factors and periodic variation characteristics of sequence data.

Research motivation and innovation

Summary of the research status and research gap

The aforementioned studies indicate that employing various model hybridizations and integrating data preprocessing into machine learning models can effectively enhance the prediction performance of PM2.5 concentrations. Various methods for improving the performance of the PM2.5 prediction models are summarized in Table 1. According to Table 1, the following research gap can be observed:

Table 1 PM2.5 concentrations prediction models with different hybridization methods.
Full size table

(1) The data preprocessing method utilized is EMD or its variants. A certain level of effectiveness can be achieved in predicting PM2.5 concentrations when utilizing EMD and its variants within integrated data processing machine learning models. However, it is worth noting that these data preprocessing methods may neglect the periodicity of PM2.5 7,48.

(2) Conventional attention mechanisms may decrease modeling efficiency. Conventional attention mechanisms necessitate the calculation of attention weights at each time step or position. While the integration of conventional attention mechanisms with neural networks can enhance the predictive performance of the model, it also results in decreased model efficiency42,64.

(3) Predicting subsequences independently could disrupt their relationship with the raw sequence. During training, each subsequence is predicted separately, and their predictions are aggregated to determine the final result. This approach, concentrating solely on particular segments of the input sequence, overlooks intersegment relationships, potentially impeding the model’s capacity to capture complex dependencies and comprehensive information across the sequence43,65,66.

To address these issues, a novel hybrid data-driven model for predicting PM2.5 concentrations, called FSR-MSAGRU, is proposed. This model leverages feature space reconstruction and a multi-head self-attention gated recurrent unit. It not only captures the periodic characteristics of the sequence data but also effectively captures the global feature information within the data.

Contributions and innovations

The innovations and contributions of this study are summarized as follows:

  1. (1)

    Based on gated recurrent unit, a multihead self-attention gated recurrent unit (MSAGRU) model that incorporates perception global feature information is proposed. The dynamic characteristics of the sequence data are captured by the model using a GRU, and multiple key information units within the GRU is concurrently processed through a multihead self-attention mechanism, facilitating the capture of the global feature information.

  2. (2)

    By employing the STL, the periodic and trend variations within the PM2.5 sequence data can be accurately captured, mitigating noise interference in the prediction results. To determine the parameter values for the STL, Fourier transform analysis is utilized in this study to analyze the sequence data and identify the period value from the spectrum plot, reducing the influence of human factors on the decomposition results.

  3. (3)

    A feature space reconstruction method for data preprocessing is proposed. It reconstructs the feature space from the raw PM2.5 sequence data and the STL decomposition results, and encompasses the seasonal, trend, and residual components. This method retains vital raw data information while incorporating sequence change trends and periodicity features, enhancing the feature expression capacity of the sequence data.

  4. (4)

    A new PM2.5 prediction model is proposed that integrates model enhancements and data preprocessing. Compared with 13 reference models on 6 different experimental datasets, the proposed feature space reconstruction and multihead self-attention gated recurrent unit (FSR-MSAGRU) model achieves more favorable prediction performances and more robust generalizability.

Structure of the paper

The remaining sections of this paper are organized as follows. In Sect. 2, the process and results of reconstructing the feature space of PM2.5 sequence data are described. In Sect. 3, the framework and basic theoretical methods of the FSR-MSAGRU model proposed in this study are described, and the metrics used to evaluate the performance of each model are outlined. The results of the ablation and comparative experiments for the proposed model are presented in Sect. 4. In Sect. 5, the performance of the proposed model is verified through hypothesis testing and a comprehensive evaluation of the model’s prediction performance. The influence of individual model enhancements and data preprocessing on improving model performance is thoroughly discussed, as well as the advantages and limitations of the FSR-MSAGRU model. Finally, the conclusions of this study are stated, and suggestions for future research are proposed in Sect. 6.

Data and data processing

This section primarily presents PM2.5 data and describes how its feature spaces is reconstructed through data processing.

Data description

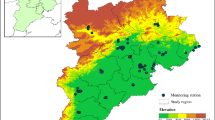
In this study, the PM2.5 data observed at the air quality monitoring stations located in different regions and altitudes were selected. The data were obtained from the “PM2.5 Historical Data Network” (https://www.aqistudy.cn/historydata/). Data from 6 cities (the cities where data were collected are shown in Fig. 1), including Lanzhou, Xi’an, Beijing, Shijiazhuang, Chengdu, and Lhasa, covering the period from January 1, 2015, to December 31, 2022, totaling eight years of daily average PM2.5 data, were chosen. The data distributions of the 6 experimental datasets is illustrated in Fig. 2.

Fig. 1
figure 1

Locations of cities for data collection.

Full size image
Fig. 2
figure 2

Distribution of the dataset samples.

Full size image

Figure 2 shows that PM2.5 exhibits substantial periodic variations across all 6 experimental datasets. This study provides empirical support for studying the seasonal/periodic patterns of PM2.5. Additionally, Fig. 2 also indicates that the amplitude of the PM2.5 fluctuations gradually decreases over time, showing an overall declining trend. This trend reflects positive strides in air quality improvement in China, and underscores the effectiveness and necessity of environmental management measures. In Fig. 2, Shijiazhuang and Lanzhou exhibited larger fluctuations in PM2.5, indicating significant variations in air quality over the different time periods in these areas. In contrast, the data from Lhasa exhibited smaller fluctuations, suggesting relatively stable air quality conditions.

The sample statistics are presented in Table 2, including the minimum value (Min), maximum value (Max), mean value, standard deviation (Std), skewness, and kurtosis.

Table 2 Statistical information for the dataset samples.
Full size table

Table 2 shows that Lanzhou and Shijiazhuang exhibit extremely high maximum PM2.5 concentrations (657.25 µg/m³ and 635.5 µg/m³, respectively), indicating very unhealthy air quality under extreme pollution conditions. Moreover, Shijiazhuang has the highest mean PM2.5 concentration (70.3859 µg/m³), suggesting generally poor air quality in the region. In contrast, Lhasa has a relatively low PM2.5 maximum concentration (104.5 µg/m³) and the lowest mean concentration (16.3143 µg/m³), indicating better air quality with fewer pollution events. The standard deviation of PM2.5 varies significantly across the 6 experimental datasets, indicating notable differences in the PM2.5 levels among the different cities. Among them, Shijiazhuang has the largest standard deviation, implying more significant fluctuations in PM2.5 compared to the other five cities. Furthermore, PM2.5 in Lanzhou exhibited very high skewness and kurtosis values (5.8781 and 93.5463, respectively), indicating a highly skewed data distribution with the presence of extreme high values. Conversely, PM2.5 in Chengdu has the lowest skewness and kurtosis values (1.8909 and 5.4761, respectively), suggesting a distribution closer to normal and fewer extreme values.

Data processing

Data processing methods

In this study, the data processing procedure follows a structured workflow to ensure the accuracy and reliability of the PM2.5 data. The detailed flowchart illustrating the steps involved in data preprocessing, feature extraction, and reconstruction is presented in Fig. 3.

Fig. 3
figure 3

Flowchart of the data processing.

Full size image

The algorithm for the data processing procedure entails the following specific steps:

Step 1

Determine the period T. Perform Fourier transforms on the PM2.5 sequence data collected from different regions, plot the frequency domain spectrum of the sequence, and identify the frequency value f corresponding to the peak frequency spectrum. Calculate the period T of the sequence using Eq. (1).

$$T=1/f$$
(1)

where f represents the peak value of the frequency spectrum of the sequence.

Step 2

Decomposition of sequence data. Using the period T determined in Step 1 as the parameter value for the STL, the raw PM2.5 sequence data Xt=[x0, x1, x2, ……, xt] are decomposed into the trend components Xt-trend=[x0-trend, x1-trend, x2-trend, ……, xt-trend], the seasonal components Xt-seasonal=[x0-seasonal, x1-seasonal, x2-seasonal, ……, xt-seasonal], and the residual components Xt-residual=[x0-residual, x1-residual, x2-residual, ……, xt-residual].

Step 3

Reconstruction of the sequence data feature space. The raw PM2.5 sequence data Xt, along with the trend components Xt-trend, seasonal components Xt-seasonal, and residual components Xt-residual obtained from the STL, are reconstructed into an elevated-dimensional feature space of the PM2.5 sequence data. The reconstructed feature space is represented as\({\mathbf{X}}_{t}^{\prime }\)

$${\mathbf{X}}_{t}^{\prime }=\left[ {{{\mathbf{X}}_t} ,\,{{\mathbf{X}}_{t - trend}} ,\,{{\mathbf{X}}_{t - seasonal}} ,\,{{\mathbf{X}}_{t - residual}}} \right]$$
(2)

where Xt, Xt-trend, Xt-seasonal, and Xt-residual respectively represent the raw PM2.5 sequence data, the trend components, the seasonal components, and the residual components.

Step 4

Feature standardization. Z score standardization is applied to eliminate the influence of the different scales and dimensions in the feature space, ensuring that all the features have the same importance and proportion during model training.

Step 5

Dataset partitioning. the standardized feature space is partitioned into training, validation, and test sets at a ratio of 8:1:1. This partitioning ensures that the model is trained under a unified standard and validated for its generalizability to unknown data.

Data processing results

Variation period T of PM2.5

As indicated in Sect. 2.1, PM2.5 exhibits significant periodic variations over time. To further investigate and quantitatively analyze the periodicity of the PM2.5 variations, Fourier transforms were employed to perform frequency domain analysis on the PM2.5 sequence data from the 6 experimental datasets. The frequency domain spectra of PM2.5 in the different experimental datasets are provided in Fig. 4.

Fig. 4
figure 4

Frequency spectrum of PM2.5 in different datasets.

Full size image

The PM2.5 variation period T on the different experimental datasets is presented in Table 3.

Table 3 Period T of PM2.5 in the different datasets.
Full size table

Figure 4 and Table 3 show that the variation period of PM2.5 varies significantly across the different experimental datasets, which is associated with the differences in the geographical location, environmental policies, and local meteorological conditions of the cities.

Reconstructed feature spaces

Based on the specific feature space reconstruction process in Sect. 2.2.1, the additive model of the STL is used to decompose the raw PM2.5 sequence data, obtaining the trend components Xt-trend, seasonal components Xt-seasonal, and residual components Xt-residual. The above decomposed data are dimensionally expanded according to Eq. (2) to reconstruct the feature space of PM2.5. The reconstructed feature spaces of the different datasets are depicted in Fig. 5.

Fig. 5
figure 5

Reconstructed feature spaces in the different datasets.

Full size image

Figure 5 shows that the reconstructed feature space, transformed from one-dimensional feature vectors to a four-dimensional feature space, integrates features such as sequence trends and periodic variations while retaining all the important information from the original data, enriching the feature representation of the sequence.

Models

This section provides a detailed introduction to the working principles and processes of the proposed model. Subsequently, a theoretical description of the proposed model is provided. Finally, the metrics utilized to evaluate the performance of the model predictions in this study are introduced.

Construction of the proposed model

This section provides a comprehensive overview of the proposed feature space reconstruction and multihead self-attention gated recurrent unit (FSR-MSAGRU) model, outlining its mathematical formulation, framework, and algorithmic steps. The FSR-MSAGRU model is designed to predict future PM2.5 concentration levels by effectively leveraging historical PM2.5 data while capturing both short-term temporal dependencies and long-range correlations. Its mathematical formulation is presented in Eq. (3), offering a formal representation of the underlying predictive mechanism. Furthermore, the overall framework of the FSR-MSAGRU model is illustrated in Fig. 6, demonstrating the key components and the flow of information within the proposed architecture.

$$\begin{gathered} {{\mathbf{H}}_t}={f_{GRU}}({\mathbf{X}}_{{t - n}}^{\prime },{\mathbf{X}}_{{t - n+1}}^{\prime }, \cdots ,{\mathbf{X}}_{{t - 1}}^{\prime }) \hfill \\ {{\mathbf{Z}}_t}={f_{MSA}}({{\mathbf{H}}_{t - m}},{{\mathbf{H}}_{t - m+1}}, \cdots ,{{\mathbf{H}}_t}) \hfill \\ {\mathbf{X}}_{{t+{\text{h}}}}^{\prime }=f({{\mathbf{Z}}_t}) \hfill \\ \end{gathered}$$
(3)

where \({\mathbf{X}}_{{t - n}}^{\prime },{\mathbf{X}}_{{t - n+1}}^{\prime }, \cdots ,{\mathbf{X}}_{{t - 1}}^{\prime }\) represent the PM2.5 data reconstructed in the feature space over the past time steps, \({{\mathbf{H}}_{t - m}},{{\mathbf{H}}_{t - m+1}}, \cdots ,{{\mathbf{H}}_t}\)denote the hidden states extracted by the GRU model, capturing short-term temporal features over time steps. \({{\mathbf{Z}}_t}\) represents the features processed by the multihead self-attention mechanism, which captures long-range dependencies. The predicted PM2.5 concentration for ℎ time steps ahead is denoted as \({\mathbf{X}}_{{t+{\text{h}}}}^{\prime }\). The functions \({f_{GRU}}\left( \cdot \right)\) and \({f_{MSA}}\left( \cdot \right)\) respectively correspond to the nonlinear mapping functions of the GRU model and the multihead self-attention mechanism, respectively, while \(f\left( \cdot \right)\) represents the final fully connected layer mapping function.

Fig. 6
figure 6

Framework of the FSR-MSAGRU model.

Full size image

The FSR-MSAGRU model comprises two primary components, feature space reconstruction and multihead self-attention GRU. During feature space reconstruction, the raw PM2.5 sequence data undergo a frequency spectrum analysis using Fourier transforms to identify periodicity, reducing the impact of human factors on the model’s parameter settings. Next, the STL is applied to extract the periodicity and trend information from the PM2.5 sequence data, mitigating the influence of noise on the prediction results. Finally, the raw PM2.5 sequence data, along with the extracted seasonal, trend, and residual components, collectively constitute a new feature space to enhance the representation of the sequence data features. During the model training and prediction process, the internal update and reset gates of the GRU are utilized to regulate the information flow, effectively capturing the dynamic characteristics of sequential data. The features extracted by the GRU are subsequently processed by the multihead self-attention mechanism, allowing multiple key information points within the GRU output to be attended to simultaneously. Different attention weights are assigned to these points, enabling the capture of long-range dependencies across time steps in the sequence data and enhancing the extraction of global correlation information. Finally, the processed features are passed through a fully connected layer, where the final output is generated.

Methodologies relevant to the proposed model

Gated recurrent unit

The gated recurrent unit (GRU) is a type of recurrent neural network that was developed as an improvement upon the LSTM network in 201467. The GRU comprises two gating units, the reset gate and the update gate. Compared to the LSTM network, it offers higher computational efficiency. The gating process of the GRU in Fig. 6(d) is as follows:

At time t, the input to the GRU is \({\mathcal{x}_t}\), and the hidden state from the previous time step is \({\mathcal{h}_{t - 1}}\). The states of the reset gate and the update gate are as follows:

$${\mathcal{r}_t}=\sigma \left( {{{\mathbf{W}}_r} \cdot \left[ {{\mathcal{h}_{t - 1}},{\mathcal{x}_t}} \right]+{{\mathbf{b}}_r}} \right)$$
(4)
$${\mathcal{z}_t}=\sigma \left( {{{\mathbf{W}}_z} \cdot \left[ {{\mathcal{h}_{t - 1}},{\mathcal{x}_t}} \right]+{{\mathbf{b}}_z}} \right)$$
(5)

where \({\mathcal{r}_t}\) represents the output of the reset gate, \({{\mathbf{W}}_r}\) is the weight matrix corresponding to the reset gate, \(\left[ {{\mathcal{h}_{t - 1}},{\mathcal{x}_t}} \right]\) is the input vector formed by concatenating \({\mathcal{h}_{t - 1}}\) and \({\mathcal{x}_t}\), \({{\mathbf{b}}_r}\) is the bias matrix of the reset gate, \({\mathcal{z}_t}\) represents the output of the update gate, \({{\mathbf{W}}_z}\) is the weight matrix corresponding to the update gate, \({{\mathbf{b}}_z}\) is the bias matrix of the update gate, and \(\sigma\) is the activation function.

The candidate hidden state \({\mathcal{h}_t}^{\prime }\) is calculated as follows:

$${\mathcal{h}_t}^{\prime }=\tanh \left( {{{\mathbf{W}}_h} \cdot \left[ {{\mathcal{r}_t} \otimes {\mathcal{h}_{t - 1}},{\mathcal{x}_t}} \right]+{{\mathbf{b}}_h}} \right)$$
(6)

where \({{\mathbf{W}}_h}\) represents the weight matrix corresponding to the candidate hidden state, \(\otimes\) denotes the Hadamard product operation, \({{\mathbf{b}}_h}\) represents the bias matrix corresponding to the hidden state, and \({\mathcal{h}_t}^{\prime }\) denotes the hyperbolic tangent activation function.

The current time step hidden layer output \({\mathcal{h}_t}\;({\mathcal{y}_t})\) is given by:

$${\mathcal{h}_t}=(1 - {\mathcal{z}_t}) \otimes {\mathcal{h}_{t - 1}}+{\mathcal{z}_t} \otimes \mathcal{h}_{t}^{\prime }$$
(7)

As indicated by Eq. (5), the update gate’s output \({\mathcal{z}_t}\) is controlled to retain the information from the previous time step until the current time step. When \({\mathcal{z}_t}\) approaches 1, the output mainly consists of the candidate hidden state \({\mathcal{h}_t}^{\prime }\) at the current time step. Conversely, when \({\mathcal{z}_t}\) approaches 0, the output mainly comprises the hidden state \({\mathcal{h}_{t - 1}}\) from the previous time step. Thus, the update gate and reset gate determine which data from the previous neuron input should be forgotten and which should be updated to the current state at this time step.

Multihead self-attention

The multihead self-attention mechanism is a variant of the self-attention mechanism developed to enhance the expressive and generalization capabilities of the model43. It utilizes multiple independent self-attention heads in parallel to capture information from different subspaces of the input sequence. Each head calculates attention weights separately, and the results are then concatenated or weight summed to obtain a richer feature representation43,68.

The attention function of the MSAGRU model in Fig. 6(e) is represented as follows:

$$Attention({\mathbf{Q,K,V}})=\operatorname{softmax} \left( {\frac{{{\mathbf{Q}}{{\mathbf{K}}^T}}}{{\sqrt {{d_k}} }}} \right){\mathbf{V}}$$
(8)

In the multihead self-attention mechanism, Q, K, and V are linearly transformed independently h times using different parameter matrices for each head. Then, the transformed Q, K, and V are input into h parallel heads to perform the attention function operation described above. Each parallel head can capture the unique feature information of the data in different representation subspaces within the sequence. Finally, the results from the h parallel heads are concatenated and linearly transformed to obtain the final output.

Model evaluation metrics

To comprehensively and objectively evaluate the performance of the model predictions, this study selected the performance metrics, root mean square error (RMSE), mean absolute error (MAE), mean bias error (MBE), symmetric mean absolute percentage error (SMAPE), Pearson correlation coefficient (PCC), and direction accuracy of the forecasting results (DA). The expressions for each metric are shown in Eq. (9) to (14) .

$$RMSE=\sqrt {\frac{1}{m}\sum\limits_{{t=1}}^{m} {{{({y_t} - y_{t}^{\prime })}^2}} }$$
(9)
$$MAE=\frac{1}{m}\sum\limits_{{t=1}}^{m} {\left| {{y_t} - y_{t}^{\prime }} \right|}$$
(10)
$$SMAPE=\frac{{100\% }}{m}\sum\limits_{{t=1}}^{m} {\frac{{\left| {{y_t} - y_{t}^{\prime }} \right|}}{{{{\left( {\left| {{y_t}} \right|+\left| {y_{t}^{\prime }} \right|} \right)} \mathord{\left/ {\vphantom {{\left( {\left| {{y_t}} \right|+\left| {y_{t}^{\prime }} \right|} \right)} 2}} \right. \kern-0pt} 2}}}}$$
(11)
$$PCC=\frac{{\sum\limits_{{t=1}}^{m} {\left( {{y_t} - \overline {y} } \right)\left( {y_{t}^{\prime } - \overline {{y_{t}^{\prime }}} } \right)} }}{{\sqrt {\sum\limits_{{t=1}}^{m} {{{\left( {{y_t} - \overline {y} } \right)}^2}\sum\limits_{{t=1}}^{m} {{{\left( {y_{t}^{\prime } - \overline {{y_{t}^{\prime }}} } \right)}^2}} } } }}$$
(12)
$$DA=\frac{1}{{m - 1}}\sum\limits_{{t=1}}^{{m - 1}} {1\left( {{\text{sign}}\left( {y_{{t+1}}^{\prime } - y_{t}^{\prime }} \right)={\text{sign}}\left( {{y_{t+1}} - {y_t}} \right)} \right)} \;$$
(13)
$$MBE=\frac{1}{m}\sum\limits_{{t=1}}^{m} {\left( {{y_t} - y_{t}^{\prime }} \right)}$$
(14)

where \({y_t}\) and \(y_{t}^{\prime }\) represent the actual observed data and the predicted result at time t, respectively; m represents the length of the test sets; \(\overline {y}\) and \(\overline {{{y^{\prime}}}}\) represent the mean values of the actual observed data and the predicted results, respectively; \({y_{t+1}}\) and \(y_{{t+1}}^{\prime }\) represent the one-dimensional observed data and predicted result at time t + 1, respectively; and “1” is the indicator function.

The RMSE, MAE, and SMAPE are used to measure the difference between the model-predicted results and the actual observed data, where smaller values indicate a higher prediction accuracy and better performance. The PCC is used to assess the linear correlation between the predicted results and the actual observed data, with values ranging from − 1 to 1. The closer the absolute value of the PCC is to 1, the stronger the linear correlation between the predicted results and the actual observed data. DA is used to evaluate the accuracy of the model in capturing the direction of data trends, which is measured by judging the consistency of the trends between the consecutive time steps, with values ranging from 0 to 1. The MBE measures the systematic bias of the model, with positive values indicating a tendency to overestimate the actual observed data and the negative values indicating underestimations. However, due to the potential cancellation of positive and negative biases, the MBE alone does not fully represent the extent of systematic bias. Therefore, in this study, the MBE is considered only as a supplementary metric for assessing model prediction bias. The numerical value of MBE and its impact on the experimental results are not discussed in this study.

Code availability

The code is available at https://github.com/zeroyi123/PM2.5-Concentrations-Prediction/tree/master.

Experimental results and analysis

In this section, the effectiveness of the proposed FSR-MSAGRU model in predicting PM2.5 is validated through ablation experiments and comparative experiments using PM2.5 from different regions.

Experimental parameter settings

The numerical experiments in this study were conducted on a computer with a 2.50 GHz Intel(R) Core(TM) i7-11700 CPU and 16.0 GB of RAM running the Windows 11 64-bit operating system. The development environment utilized was PyCharm 2022.3.2 (Community Edition), with the Python environment version 3.7.16.

In the experiments, all the neural network models were built using the Keras framework, with the main model comprising 128 neurons. The mean squared error (MSE) was employed as the loss function, and the Adam optimizer was selected. During model training, the maximum number of epochs was set to 20,000 to ensure sufficient learning of the model. To balance the memory usage and model update frequency, the batch size was set to 64. Additionally, the early stopping technique was applied to monitor the training progress and prevent overfitting. Specifically, training was stopped if the validation loss did not improve within 500 consecutive epochs. For enhanced transparency and traceability of the training process, CSV-Logger callback was used to record detailed performance metrics for each training epoch. Moreover, the model checkpoint mechanism was employed to monitor the validation loss on the validation set. Whenever an improvement in model performance was detected, the current best-performing model was saved, facilitating subsequent model evaluation, deployment, and invocation. All the other model parameters were kept at their default values. It is important to note that the final experimental results for all models are evaluated based on the average of five predictions from the best-performing model.

Experiment I: ablation experiment of the proposed model

In this section, the contributions of each component of the FSR-MSAGRU model (i.e., the multihead attention mechanism, STL data preprocessing, and feature space reconstruction) to improving the PM2.5 prediction performance are systematically evaluated through ablation experiments. Through individual comparisons of the prediction results from the baseline GRU model, the MSAGRU model, the STL data preprocessing-based GRU model (STL-GRU), the STL data preprocessing-based MSAGRU model (STL-MSAGRU), the feature space reconstruction-based GRU model (FSR-GRU), and the feature space reconstruction-based MSAGRU model (FSR-MSAGRU), the influence of the addition of each component on the prediction results is analyzed. The performance metrics of the baseline and improved models in predicting results are presented in Table 4.

Table 4 Performance metrics of ablation experiment prediction results.
Full size table

The comparative curve of the prediction results from the ablation experiments is shown in Fig. 7.

Fig. 7
figure 7

Comparison curves of the ablation experiment prediction results.

Full size image

By combining the comparison curves of the PM2.5 prediction results on different datasets and the performance metrics of the GRU, STL-GRU, MSAGRU, STL-MSAGRU, FSR-GRU and FSR-MSAGRU models in Table 4 and Fig. 7, the following conclusions can be drawn:

(1) The inclusion of the multihead self-attention mechanism can slightly enhance the prediction performance of the baseline model.

Table 4 shows that the improved MSAGRU model outperforms the baseline GRU model. Across the 6 different experimental datasets, the RMSE decreases, and the MAE decreases in all the datasets except for Shijiazhuang and Chengdu, where it increases slightly. The MSAGRU exhibits a better overall prediction accuracy than the GRU. The SMAPE shows similar values between the GRU and the MSAGRU, indicating a similar performance in terms of relative error. In terms of model fitting, except for Beijing, the PCC values of the MSAGRU model are better than those of the GRU model. However, the DA values decrease in the four datasets, indicating that the MSAGRU performs slightly worse in capturing the trend direction of the data, which may be attributed to the attention mechanism focusing on the global correlation properties, which sometimes weakens the dependency between the individual sequence steps. As shown in Table 4, among the 30 primary evaluation metrics across 6 different experimental datasets, the MSAGRU model outperformed the GRU model, achieving the best performance in 22 metrics. However, the inclusion of the multihead self-attention mechanism does not significantly improve prediction performance compared to the data decomposition and feature space reconstruction modules.

The impact of the multihead self-attention mechanism on improving model predictive performance varies with datasets complexity. For example, when using STL-MSAGRU model to predict PM2.5 concentrations, the data decomposition method effectively reduces sequence complexity, limiting the contribution of long-term dependencies captured by the multihead self-attention mechanism to performance improvement. As shown in Table 4, the performance gains from the multihead self-attention mechanism are more pronounced in the more complex Lanzhou dataset compared to lower-complexity datasets. Moreover, after feature space reconstruction, the PM2.5 sequence data undergo dimensional expansion, resulting in a more complex feature representation compared to the purely decomposed sequence. In this case, the long-term dependencies extracted by the multi-head self-attention mechanism contribute more effectively to enhancing predictive performance. As shown in Table 4, the FSR-MSAGRU model generally outperforms the FSR-GRU model.

(2) The STL preprocessing of the sequence data can significantly enhance the prediction performance of the model.

From the metrics listed in Table 4, it can be observed that the improvement in prediction results is more pronounced in datasets such as Lanzhou, Xi’an, Shijiazhuang, and Chengdu, where the performance metrics RMSE, MAE, and SMAPE are reduced by approximately half. The improvement in model fitting is even more significant, with the PCC values all exceeding 0.94, specifically 0.9475, 0.9614, 0.9493, and 0.9596; moreover, the DA values also increased by more than 0.25. In the Beijing and Lhasa experimental datasets, after preprocessing the sequence data using the STL, the RMSE, MAE, and SMAPE of the MSAGRU data decreased by 28.85%, 29.40%, and 17.75%, respectively, and by 11.79%, 18.86%, and 22.90%, respectively. The fitting metrics PCC and DA are improved by 45.23% and 18.18% and 4.25% and 58.00%, respectively. In conclusion, on all 6 of the different experimental datasets, the performance metrics of the MSAGRU model prediction results are significantly improved after preprocessing the raw PM2.5 sequence data using the STL algorithm.

(3) The predictive performance of the model can be significantly enhanced by feature space reconstruction.

Figure 7 shows that on all 6 different experimental datasets, the prediction curves of the proposed FSR-MSAGRU model are closer to the actual data curve than are those of the GRU, MSAGRU, and STL-MSAGRU models, demonstrating the excellent prediction capability of the FSR-MSAGRU model. Compared to the prediction results of the MSAGRU and STL-MSAGRU models, the FSR-MSAGRU model exhibits outstanding performance in datasets such as Lanzhou, Xi’an, Shijiazhuang, and Chengdu, with a reduction of more than 90% in the performance metrics RMSE, MAE, and SMAPE. In the Beijing and Lhasa experimental datasets, the RMSE, MAE, and SMAPE of the FSR-MSAGRU model are reduced by at least 59% compared to those of the STL-MSAGRU model and by at least 68% compared to those of the MSAGRU model. Additionally, the FSR-MSAGRU model consistently demonstrated high PCC values exceeding 0.98 across all the datasets, indicating a strong positive correlation between the prediction results and the actual data. Despite slightly lower DA metrics in the Beijing and Lhasa datasets, the FSR-MSAGRU model maintains robust performances, validating its effectiveness in PM2.5 prediction. The experimental results above validate the superiority of the proposed FSR-MSAGRU model in predicting PM2.5, fully illustrating that feature space reconstruction significantly enhances the model’s predictive performance.

Experiment II: comparative experiment of the proposed model with other models

The purpose of the experiments in this section is to verify the effectiveness of the proposed FSR-MSAGRU model in predicting PM2.5 through comparative experiments with mainstream single models and hybrid models. The selected mainstream single models include the convolutional neural network (CNN), Elman regression neural network, LSTM, and BiLSTM35. The hybrid models include the convolutional neural network and gated recurrent unit hybrid model (CNN-GRU)56, the GRU based on complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN-GRU), the LSTM hybrid model based on the STL (STL-LSTM), the LSTM hybrid model based on second-order trend decomposition with the STL (STL2-LSTM), the integrated 3D-CNN and GRU network model (3D-CNN-GRU)36, and the ensemble empirical mode decomposition, attention mechanism and long short-term memory network model (EEMD-ALSTM)69. The performance metrics of the PM2.5 prediction results on the Lanzhou dataset are presented in Table 5. The comparative curves of the PM2.5 prediction results and model fitting scatter plots for single models and hybrid models with the FSR-MSAGRU model on the Lanzhou dataset are shown in Fig. 8.

Table 5 Performance metrics of different models (Lanzhou).
Full size table
Fig. 8
figure 8

Comparison curves and scatter plots of the single models, hybrid models, and FSR-MSAGRU model prediction results (Lanzhou).

Full size image

The variations in the prediction performance metrics of the different models on various datasets are depicted in Fig. 9 through radar charts, histograms, scatter plots, etc.

Fig. 9
figure 9

Performance metrics of the different models on various datasets.

Full size image

Detailed comparisons and analyses are conducted between the PM2.5 prediction results of the aforementioned single models, hybrid models, and the FSR-MSAGRU model on 6 different datasets. The following conclusions can be drawn:

(1) The prediction results of the FSR-MSAGRU model outperform those of the mainstream single models.

By comparing the scatter plots of the prediction values versus the actual values between the single models and the FSR-MSAGRU model shown in Fig. 8, it is evident that on the Lanzhou dataset, the scatter plots between the prediction values and actual values of the FSR-MSAGRU model are more tightly clustered around the ideal line. Furthermore, from the curves of the prediction results and their locally magnified views, it is visually apparent that the consistency between the prediction curve of the FSR-MSAGRU model and the actual value curve is significantly greater than that of the single models. As demonstrated in Table 5, a comprehensive comparison of the performance metrics on the Lanzhou dataset between the single model and the FSR-MSAGRU model reveals that the FSR-MSAGRU model exhibits superior prediction accuracy and model fitting performance. The prediction results on the remaining 5 experimental datasets, as depicted in Fig. 9, similarly demonstrate that the FSR-MSAGRU model achieves the optimal predictive performance. These experimental results demonstrate that the proposed FSR-MSAGRU model outperforms mainstream single models in terms of prediction performance.

(2) The prediction performance of the FSR-MSAGRU model surpasses that of the experimental reference hybrid models.

From Fig. 8, it is evident that the scatter plots of the hybrid models demonstrate a more centralized distribution around the actual values on the Lanzhou dataset, with the prediction trajectories of most hybrid models closely aligning with the actual data. Nonetheless, in contrast to the prediction performance of the FSR-MSAGRU model, the prediction performance of hybrid models still exhibits certain shortcomings. A comprehensive analysis of the performance metrics of the prediction results between the hybrid models and the FSR-MSAGRU model, as shown in Fig. 9, indicates that the hybrid models CEEMDAN-GRU, STL-LSTM, STL2-LSTM and EEMD-ALSTM demonstrate certain prediction advantages on the 6 different experimental datasets. However, the overall prediction effectiveness of these hybrid models still falls short of that of the FSR-MSAGRU model. These experimental results demonstrate that the prediction performance of the proposed FSR-MSAGRU model for PM2.5 surpasses that of all the other experimental reference hybrid models.

Discussion of the experiments

Discussion on model performance evaluation

Diebold–Mariano test

The Diebold–Mariano test is a common nonparametric statistical test used to compare the prediction accuracy of two or more models. Its main purpose is to examine whether there is a significant difference between the prediction errors of two models, thus determining the superiority or inferiority of the models. In this study, the Diebold–Mariano test is conducted using the RMSE as the loss function. The prediction errors of the FSR-MSAGRU model versus the actual values are used as the benchmark data to evaluate the effectiveness of the FSR-MSAGRU model. The DM statistic is negative if the reference model prediction performance is superior to that of the FSR-MSAGRU model, and positive if the FSR-MSAGRU model prediction performance is superior to that of the reference model. A larger absolute value of the DM statistic indicates a more significant difference in the prediction performance between the two models. The results of the Diebold–Mariano test for the 13 reference models on the 6 different experimental datasets are presented in Table 6.

Table 6 Diebold–Mariano test results of the reference model and the proposed model on the different datasets.
Full size table

Table 6 shows that at a significance level of 0.05, the Diebold–Mariano test rejects the null Hypothesis H0: there is no significant difference between the two models being tested. Therefore, there is a significant difference in the prediction performance between the FSR-MSAGRU model proposed in this study and all the reference models, with positive values of the DM statistic indicating that the prediction performance of the FSR-MSAGRU model is superior to that of all the reference models.

A comprehensive evaluation of the prediction results of the various models

To comprehensively evaluate the prediction results of each model, the statistical metrics (standard deviation, root mean square deviation (RMSD), and the correlation coefficient) of the different model prediction results are displayed through Taylor diagrams in this section. By comparing Taylor diagrams, the matching degree between the prediction results of the different models and the actual observations can be intuitively compared, enabling the assessment of differences in prediction performances among the various models. Taylor diagrams of the prediction results for the 14 models across 6 different datasets are shown in Fig. 10. In the Taylor diagrams depicted in Fig. 10, the red dashed circular arc represents the standard deviation of the actual observations. The closer the model prediction results are to the red dashed circular arc, the closer the variation range of the model prediction results is to the actual observations, indicating an improved consistency of the model. Moreover, the closer the model prediction results are to the “Actual” point marked in the diagram, the closer the model prediction results are to the actual observations, indicating a lower RMSD and higher correlation, thus demonstrating the superior prediction performance of the model.

Fig. 10
figure 10

Taylor diagram of the prediction results of the different models on the various datasets.

Full size image

Figure 10 shows that for the Lanzhou dataset, the correlation between the prediction results of the single models and the actual observations is generally weak. On the Xi’an dataset, the weakest correlation with the actual observations is demonstrated by the 3D CNN-GRU model. On the Beijing dataset, very similar correlations with the actual observations are observed for the CEEMDAN-GRU and STL2-LSTM models, the EEMD-ALSTM model achieved the second-best predictive performance among the 14 models. On the Shijiazhuang dataset, the STL2-LSTM model prediction results exhibit the highest standard deviation, indicating a greater variation range in its prediction results. On the Chengdu dataset, the predictive performance of the STL2-LSTM and EEMD-ALSTM models is essentially comparable. On the Lhasa dataset, the prediction performance of the EEMD-ALSTM model is only slightly inferior to that of the FSR-MSAGRU model. Overall, the FSR-MSAGRU model’s performance across the 6 different experimental datasets is closest to the “Actual” point marked in the diagram. Compared to the other models, the FSR-MSAGRU model demonstrates better consistency and correlation with the actual observations, indicating that the prediction performance of the FSR-MSAGRU model is superior to that of all the other reference models across the different experimental datasets.

Discussion on single-model prediction performance and improvements

(1) None of the single models can maintain the best prediction performance.

From the performance metrics of the 5 single models depicted in Fig. 9, it is evident that none of the single models achieved an optimal performance across all the datasets. Specifically, on the Lanzhou dataset, the BiLSTM model attains the highest prediction accuracy. The LSTM and Elman models demonstrate relatively strong predictive performance on the Xi’an and Chengdu datasets. On the Beijing dataset, the Elman model outperforms the other models in terms of the RMSE and PCC. For the Shijiazhuang dataset, the GRU model outperforms the other models in terms of the RMSE, MAE, SMAPE, and PCC. The Elman model performs best on the Lhasa dataset in terms of prediction accuracy, but the LSTM model achieves the best correlation with the actual data. The above discussion illustrates that single models exhibit varied performances in PM2.5 prediction across the different regions, making it difficult to discern the strength of model generalization. Therefore, exploring methods to improve the prediction performance of single models is necessary.

(2) The improvement of single-model predictions necessitates appropriate methods.

As demonstrated in Sect. 4.3, the inclusion of the multihead self-attention mechanism can enhance the prediction performance of the GRU. By comparing the MSAGRU model with five single models—CNN, Elman, LSTM, BiLSTM, and GRU—on 6 different experimental datasets, it was found that the MSAGRU model achieved the highest performance, obtaining 10 out of 30 optimal primary evaluation metrics in Fig. 9. The LSTM model, with 9 optimal metrics, performs the next best, while the GRU model achieves only 3 optimal metrics. This comparison indicates that the prediction performance of the MSAGRU model, enhanced by the inclusion of the multihead attention mechanism, is slightly better than that of the other mainstream single models, further reinforcing the experimental conclusion in Sect. 4.3. In contrast, the CNN-GRU model, an improvement of the CNN and GRU hybrid, not only fails to improve the prediction performance of the baseline model but also performs worse than the single models. Therefore, in terms of improving the single models, it is necessary to select appropriate methods for model improvement, or to choose suitable hybrids of the single models to enhance the prediction performance; otherwise, these methods may have adverse effects.

Discussion on the impact of data preprocessing on model performance

The experimental results in Sect. 4.3 demonstrate that preprocessing the input data using the STL can lead to a significant improvement in the prediction performance of the model. To validate the influence of data preprocessing on the prediction results, the CEEMDAN data decomposition method, the EEMD data decomposition method, and the method of second-order trend decomposition with the STL, were incorporated into this study for comparison. By comparing the prediction results of models incorporating data decomposition (CEEMDAN-GRU, EEMD-ALSTM, STL-MSAGRU, STL-LSTM, and STL2-LSTM) with those of single models (CNN, Elman, LSTM, BiLSTM, GRU, and CNN-GRU), as depicted in Fig. 9, it can be observed that the prediction results of the four models incorporating data decomposition preprocessing are superior to those of any single model. Therefore, data decomposition preprocessing can effectively enhance the prediction performance of the main model.

To verify the performance of the STL method, this study preprocessed the raw sequence data using both the CEEMDAN and the STL methods on 6 different experimental datasets. The GRU model was then used to predict the preprocessed data. The performance metrics of the GRU model using the two different data decomposition methods are presented in Table 7.

Table 7 Comparison of the prediction results of the different decomposition methods.
Full size table

Table 7 shows that on the datasets of Lanzhou, Xi’an, Shijiazhuang, and Chengdu, the GRU model using the STL data decomposition method (STL-GRU) outperforms the GRU model using the CEEMDAN data decomposition method (CEEMADN-GRU). However, on the Lhasa dataset, the CEEMADN-GRU model performed better. In the Beijing dataset, except for the SMAPE indicator, the CEEMADN-GRU model outperforms the STL-GRU model in the remaining four metrics. Analyzing the principles and processes of the two decomposition methods, it can be observed that the reason for the inferior performance of the STL-GRU model compared to the CEEMADN-GRU model on the datasets of Beijing and Lhasa lies in the fact that the STL data decomposition method for these datasets is set to 8 days. During data processing, the STL method may overlook or fail to adequately capture periodic fluctuations with a period length shorter than 8 days, thereby influencing the subsequent predictive performance of the GRU model.

Conclusion

Accurate predictions of PM2.5 concentrations are vital for safeguarding public health and addressing environmental issues. However, machine learning models often overlook the periodic and global features of the sequence data when predicting PM2.5. In response to these challenges, a novel hybrid data-driven modeling approach to PM2.5 concentrations prediction, termed the FSR-MSAGRU model, which excels in improving feature representations through feature space reconstructions and capturing global features, is proposed in this study. The FSR-MSAGRU model demonstrated excellent prediction performance across 6 distinct experimental datasets. The conclusions drawn from this study are summarized as follows:

(1) The incorporation of the multihead self-attention mechanism can enhance the prediction performance of the GRU. The MSAGRU model, which incorporates perception global feature information, was proposed in this study by innovatively extending the basic gated recurrent unit through the introduction of a multihead self-attention mechanism. Through parallel processing via multiple self-attention heads, the model achieves a simultaneous focus on various crucial pieces of information within the GRU. Additionally, it learns distinct attention weights among these information points, facilitating the capture of long-range dependencies across the sequence data within the GRU.

(2) Data preprocessing, combined with the STL decomposition method, can enhance the prediction performance of the model. According to the data description analysis in, Sect. 2.1 PM2.5 sequence data exhibit pronounced periodic features, highlighting the crucial importance of accurately extracting the periodic features of the sequences during data preprocessing. Therefore, in this study, the STL data decomposition method is adopted to refine the raw sequence data into three subsequences, enabling precise capture of the periodic variations and trend directions of the PM2.5 sequence data, and effectively reducing the interference of the sequence data noise on the prediction results. Moreover, in determining the STL parameter values, Fourier transform analysis is applied to the PM2.5 sequence data to perform frequency domain analysis, providing accurate periodic parameter values for the STL based on a scientific analysis and reducing the biases introduced by manual parameter settings.

(3) The model prediction performance is significantly enhanced by feature space reconstruction. Although the method of separately predicting subsequences and then aggregating them to determine the final prediction results can yield a certain level of prediction accuracy, its limitation lies in the fact that the main model treats each subsequence as an independent entity, overlooking the correlations between the subsequences as well as between the subsequences and the raw data. Therefore, a feature space reconstruction method for data preprocessing is proposed in this study to enhance feature representation. The reconstructed feature space is expanded from one-dimensional feature vectors to four-dimensional feature vectors, enabling the model to capture more complex and hidden feature patterns and relationships.

(4) The FSR-MSAGRU model proposed in this study demonstrates promising predictive performance and generalizability. Six experimental datasets from different regions with varying levels of complexity were selected to verify the effectiveness of the proposed FSR-MSAGRU model. The SMAPE values of the results predicted by the FSR-MASGRU model are 0.63%, 0.75%, 16.33%, 0.45%, 0.53%, and 6.61%, representing reductions of 96.66%, 97.60%, 68.50%, 98.62%, 97.99%, and 70.05%, respectively, compared to those of the baseline model. The fitting performance metric PCC of the FSR-MASGRU model exceeds 0.98 for all the datasets. These results underscore the exceptional prediction performance of the proposed FSR-MSAGRU model across diverse datasets and its robust generalization capability.

The FSR-MSAGRU model proposed in this study provides an accurate and stable method for short-term PM2.5 concentrations prediction in different regions. In future research, comprehensive consideration will be given to multiple environmental factors, with an in-depth analysis of the interrelationships among the multifeature data. Effective multistep prediction methods will be explored to enhance the prediction capabilities over broader time ranges. Additionally, Fig. 9(c) shows that most neural network models exhibit a positive bias in PM2.5 prediction. This provides a direction for future research on error corrections in these models and warrants further investigation. Furthermore, fully utilizing the multi-head self-attention mechanism remains a limitation of this study and an important direction for future research.