A unified multifield formulation for analysis of a sandwich graphene origami reinforced composite curved structure

Abstract

The present paper investigates influence of the graphene origami’s characteristics and multi-load of piezoelectric materials on the frequency responses of a sandwich curved composed of a Graphene Origami (Gori) reinforced core. The Gori reinforced core is sandwiched with piezoelectric/piezomagnetic layers. A novel higher-order flexible model with thickness stretch-ability is employed for extension of the kinematic relations. The constitutive relations are derived using the important relations for effective material properties for Gori reinforced core and the multi-field equations for integrated piezoelectric/piezomagnetic layers. The natural frequency responses are presented with changes of foldability parameter and content of Gori as well as multi-field characteristics. An investigation on the geometric parameters of the sandwich curved beam and foundation’s parameters is presented. A verification with available results of literature. The proposed model in this paper can be considered as an element of intelligent and controllable systems and structures with tunable responses and reflections.

Introduction

Novel reinforcement and nanocomposite materials and structure are extensively used in the technical application and various instruments and systems. These materials can be manufactured from the new reinforcement specially in nanoscales. Carbon nanotubes, nanoplatelets, and graphene sheets are introduced as nanoreinforcements^1,2,3,4,5. Graphene origami is known as a new group of nanoreinforcement with foldability characteristic. The latest characteristic is known as a parameter for control of material properties in the various types of loading^6,7,8,9,10. Combination of these materials and structures with piezoelectric and piezomagnetic materials leads to the novel structures and systems with more tuneability and controllability for application in vibration control/feedback systems^{11,12,13,14,15}. Authors are provided a literature review regarding recent works on the higher-order kinematic models and structures as well as nanoreinforcement such as Gori, GNPs and CNTs. The novelty of this work is confirmed through regarding the recent works.

Liu et al.¹⁶ investigated effect of the distributed load on the free vibration results of a curved beam based on the state space approach. Authors provided a detailed convergence and comparative study using superposition of the results for a point moment loading. Su et al.¹⁷ extended a novel mathematical modeling for investigating impact of various boundary conditions using the methodology of Fourier format. The Voigt rule of mixture has been employed for modeling the variable material properties. Arefi and Zenkour¹⁸ extended a complete electro-magneto-elastic modeling of the sandwich curved beams in hybrid multi-field loading condition. The kinematic modeling was performed based on a shear deformable flexible model. The novel kinematic modeling of a curved beam based on an higher-order interpolation was performed by Kim and Kim¹⁹. A finite element-based formulation for analysis of the bridges with various cross sections was studied by El-Amin and Kasem²⁰. The stiffness matrix was developed using a warping functions. Transvers vibration responses of higher-order initially curved beam was studied using the Hellinger Reissner mixed variation methodology by Thurnherr et al.²¹ using the Legendre polynomial functions. The main goal of this analysis was computation of inter-laminar stresses at all surfaces. Merzouki et al.²² studied scale dependent dynamic modeling of the curved beam in nano scale based on a transverse flexible kinematic model. The solution was developed using the finite element approach. Impact of longitudinally change of different material properties in a curved beam was studied by Rajasekaran²³. In order to cover all types of cross section, a novel differential form of transformation method and shape function was employed. The application of this method was examined for different boundary conditions. Zhang and Zhuang²⁴ developed a new approach based on strong discontinuity approach for analysis of a brittle material in order to analyze fracture mode behavior. Yaylı²⁵ studied effect of elastic boundaries on the vibrational results of a nanorod using the Rayleigh method. In another work, Yaylı²⁶ studied the impact of gradation of cross section on the vibration response of the beam. Yaylı^27,28 studied the impact of various distributions of the carbon nanotube reinforcements on the longitudinal vibration responses of the beam. Maghami et al.²⁹ suggested a novel control method and genetic algorithm for investigating for displacement control of a non-rigid origami analysis. Vinh et al.³⁰ developed a novel shear deformable model for vibration analysis of plates. In another work, Duong et al.³¹ considered both effect of various boundary conditions and higher order deformability on the static analysis of cylindrical shell. Duc et al.³² investigated impact of a crack on the buckling responses of nanoplate with variable thickness. Tien et al.³³ investigated impact of small size on the stability and bending results of organic nanoplates. In order to account all terms of rotary inertia for analysis of thick, moderate and thin curved beam, a new beam model was employed. Qatu et al.³⁴ studied the bending and extension coupling effect on the responses of the model. The intelligent systems and structures can be used for vibrational analysis of the suspension system and structures based on new control analysis methods^35,36,37,38. Yaylı^39,40 studied vibration analysis of the nanorods and nanobeams with variable thickness and elastic edges. Application of the control systems and intelligent materials was illustrated in the mechanical instruments and structural elements^40,41,42,43. The effect of micro size of the beams was studied on the vibrational results of the beams with various boundary conditions by Yaylı⁴⁴.

The important relations for the derivation of the governing equations of advanced materials and intelligent structures can be observed in the references^45,46,47,48. The new solution procedure for analysis of novel structural elements are described in the recent works^{49,50,51,52,53}. Analysis of the stress distribution in a structural element with hole was studied by Lv et al.⁵⁴. The new hybrid method for measurement of the strain was developed by Luo and Dong⁵⁵. Arefi and Zenkour^56,57,58 studied transient, free vibration, tension analysis and wave propagation characteristic analysis of the nanobeams and nanorods. The analysis was performed using the higher-order sinusoidal shear deformation theory . The proposed model was applicable for a feedback and control system because of existence of piezoelectric and piezomagnetic layers as sensor and actuator layers. The structure was subjected to the initial electric and magnetic potentials using the multi-dimensional electric and magnetic field components. The impact of nonlinear strain components was studied on the static analysis of the multi-layered annular plate including the elastic core and two intelligent layers⁵⁹. Chu et al.⁶⁰ analyzed the underwater vehicles based on the control system. The proposed material in this paper is a copper matrix enriched by graphene origami reinforcement. The copper matrix can be used in the new composite materials for better material properties^61,62,63. In order to verify our formulation, a comparative study is presented using the available works in the literature. Timoshenko⁶⁴ presented a book on the vibration analysis of various structures using the analytical, semi analytical and numerical methods. Correa et al.⁶⁵ developed a novel finite element method for analysis of the curved beams. Leung and Zhu⁶⁶ presented a new method based on the Fourier p-elements for studying the vibration and bending analyses of the curved beam structures. Zhao et al.⁶⁷ studied an atomic insight about the material characteristics of the graphene origami reinforced materials. Zhao et al.⁶⁸ developed a novel work on the application genetic programming based analysis on the Gori reinforced materials. The present model is subjected to multi field loading including thermal, mechanical, electrical and mechanical loads. In order to investigate effect of these parameters, the external work is evaluated with computation of these works⁶⁹. Yang et al.⁷⁰ studied the mechanical behavior of a composite subway vehicle using the analytical method. There are some time-dependent and vibration-based analysis of the novel materials such anisotropic materials and metamaterials for application in the various conditions^{71,72,73,74,75}. The most common types of piezoelectric materials are PZT materials in the patch and layer shapes for application in the energy saving and ultrasonic applications^71,72. High frequency devices and transduces applications of the piezoelectric materials are developed by Zhu et al.⁷³ and Zhu et al.⁷⁴. Novel material productions methods and some processing procedures are explained by various researchers to arrive at more flexible and more strength materials^{76,77,78,79,80}. Bai et al.⁸¹ developed a new procedure for removal of heavy metals using the chemical process. In order to analyze the mechanical problems and investigating the responses, some analytical and numerical methods have been developed by various researchers in the literature works^82,83,84,85. Analysis of the novel materials such as graphene origami, nanocomposite and bio-composites were presented to arrive at more efficient scheme using the artificial intelligent and optimization methods^{86,87,88,89,90}. The nanocomposite materials and structures are suggested for application in various situations because of higher stiffness and lower weights. The nanocomposite materials are manufactured from the nano reinforcements such as graphene nanoplatelets and carbon nanotubes. Malikan et al.⁹¹ investigated the impact of magnetic field loading and a general small scale theory on the torsional stability responses of the composite shells in the nano scale. The effect of small scale dimensions was captured using the nonlocal strain gradient theory. Malikan⁹² presented a comprehensive multi-field analysis on the shell structures made of composite materials with piezoelasticity properties.

Authors developed a detailed literature survey regarding recent works on the higher order shear deformable models and various nanocomposite structures and reinforcement. One can conclude that there is no published work on the vibrational characteristics of graphene origami reinforced sandwich curved beam integrated with piezoelectric/piezomagnetic layers rested on Pasternak’s foundation. The governing motions equations are derived using the Hamilton’s principle. The numerical results are obtained using the Navier’s technique. The effective material properties of the Gori reinforced core is evaluated using the Halpin-Tsai micromechanical model. The natural frequency responses will be presented in terms of affective parameters such as content and foldability parameters of Gori, geometric parameters and foundation’s parameters. The proposed model in this paper can be considered as an element of intelligent and controllable systems and structures with tunable responses and reflections. The graphene origami can be used as a novel reinforcement with tunable material properties for application in various composite structures and systems. integrating the tunable structure with piezoelectric layers offers an option for application in intelligent systems and structures.

Formulation

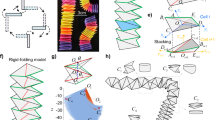
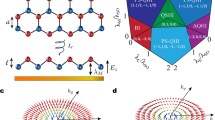
The governing motion equations are derived in this section. Our model (Fig. 1) in this paper is a sandwich curved beam composed of a Gori reinforced copper core integrated with piezoelectric/piezomagnetic layers rested on the Pasternak’s foundation. The piezoelectric/piezomagnetic layers are assumed fully attached with Gori reinforced core and therefore no discontinuities are assumed between the interfaces. The displacement field is simultaneously applied for the core and integrated layers. It is assumed that the curved beam is higher-order shear deformable. Furthermore, it is assumed that the piezoelectric layers are fully attached to the graphene origami reinforced core and no discontinuities are considered between them. The simply-supported boundary conditions are assumed for the edge conditions. The constitutive relations for the Gori reinforced core using the plane strain assumption with accounting the thermal loads are derived as follows^{56,64,65,66,93}:

Fig. 1

A multi-load subjected curved beam made of origami.

$$\:\begin{array}{c}\begin{array}{c}\left\{\begin{array}{c}{\sigma\:}_{rr}\\\:{\sigma\:}_{\theta\:\theta\:}\\\:{\sigma\:}_{r\theta\:}\end{array}\right\}=\frac{{E}_{Gori}}{\left(1-{{\nu\:}_{Gori}}^{2}\right)}\left[\begin{array}{ccc}1&\:{\nu\:}_{Gori}&\:0\\\:{\nu\:}_{Gori}&\:1&\:0\\\:0&\:0&\:\frac{1-{\nu\:}_{Gori}}{2}\end{array}\right]\left\{\begin{array}{c}{\epsilon\:}_{rr}-{\alpha\:}_{Gori}\left(T-{T}_{0}\right)\\\:{\epsilon\:}_{\theta\:\theta\:}-{\alpha\:}_{Gori}\left(T-{T}_{0}\right)\\\:{\epsilon\:}_{r\theta\:}\end{array}\right\},\end{array}\end{array}$$

(1)

In which stress and strain components are denoted with $\:{\sigma\:}_{ij},{\epsilon\:}_{ij}$, thermal loads with T and the effective material properties of Gori are obtained using the Halpin-Tsai micromechanical models and rule of mixture as follows^67,68:

$$\begin{aligned} \:E_{{Gori}} & = \frac{{1 + 2\frac{{l_{{Gr}} }}{{t_{{Gr}} }}\frac{{\frac{{E_{{Gr}} }}{{E_{{Cu}} }} - 1}}{{\frac{{E_{{Gr}} }}{{E_{{Cu}} }} + \xi \:}}\frac{{W_{{Gr}} }}{{W_{{Gr}} + \frac{{\rho \:_{{Gr}} }}{{\rho \:_{{Cu}} }}\left( {1 - W_{{Gr}} } \right)}}}}{{1 - \frac{{\frac{{E_{{Gr}} }}{{E_{{Cu}} }} - 1}}{{\frac{{E_{{Gr}} }}{{E_{{Cu}} }} + \xi \:}}\frac{{W_{{Gr}} }}{{W_{{Gr}} + \frac{{\rho \:_{{Gr}} }}{{\rho \:_{{Cu}} }}\left( {1 - W_{{Gr}} } \right)}}}}E_{{Cu}} \\ & \left\{ \begin{gathered} 1.11 - 1.22\frac{{W_{{Gr}} }}{{W_{{Gr}} + \frac{{\rho \:_{{Gr}} }}{{\rho \:_{{Cu}} }}\left( {1 - W_{{Gr}} } \right)}} - 0.134\left( {\frac{T}{{T_{0} }}} \right) \hfill \\ + 0.559\frac{{W_{{Gr}} }}{{W_{{Gr}} + \frac{{\rho \:_{{Gr}} }}{{\rho \:_{{Cu}} }}\left( {1 - W_{{Gr}} } \right)}}\left( {\frac{T}{{T_{0} }}} \right) - 5.5\frac{{W_{{Gr}} }}{{W_{{Gr}} + \frac{{\rho \:_{{Gr}} }}{{\rho \:_{{Cu}} }}\left( {1 - W_{{Gr}} } \right)}}H_{{GOFD}} \hfill \\ + 38\left( {\frac{{W_{{Gr}} }}{{W_{{Gr}} + \frac{{\rho \:_{{Gr}} }}{{\rho \:_{{Cu}} }}\left( {1 - W_{{Gr}} } \right)}}} \right)^{2} H_{{GOFD}} - 20.6\left( {\frac{{W_{{Gr}} }}{{W_{{Gr}} + \frac{{\rho \:_{{Gr}} }}{{\rho \:_{{Cu}} }}\left( {1 - W_{{Gr}} } \right)}}} \right)^{2} H_{{GOFD}}^{2} \hfill \\ \end{gathered} \right\}, \\ \end{aligned}$$

$$\begin{aligned} \:\nu \:_{{Gori}} & = \left( {\nu \:_{{Gr}} \frac{{W_{{Gr}} }}{{W_{{Gr}} + \frac{{\rho \:_{{Gr}} }}{{\rho \:_{{Cu}} }}\left( {1 - W_{{Gr}} } \right)}} + \nu \:_{{Cu}} \left( {1 - \frac{{W_{{Gr}} }}{{W_{{Gr}} + \frac{{\rho \:_{{Gr}} }}{{\rho \:_{{Cu}} }}\left( {1 - W_{{Gr}} } \right)}}} \right)} \right) \\ & \left\{ \begin{gathered} 1.01 - 1.43V_{{GOAM}} + 0.165\left( {\frac{T}{{T_{0} }}} \right) - 1.1\frac{{W_{{Gr}} }}{{W_{{Gr}} + \frac{{\rho \:_{{Gr}} }}{{\rho \:_{{Cu}} }}\left( {1 - W_{{Gr}} } \right)}}H_{{GOFD}} \left( {\frac{T}{{T_{0} }}} \right) \hfill \\ - 16.8\frac{{W_{{Gr}} }}{{W_{{Gr}} + \frac{{\rho \:_{{Gr}} }}{{\rho \:_{{Cu}} }}\left( {1 - W_{{Gr}} } \right)}}H_{{GOFD}} + 16V_{{GOAM}}^{2} H_{{GOFD}}^{2} \hfill \\ \end{gathered} \right\}, \\ \end{aligned}$$

$$\begin{aligned} \:\rho \:_{{Gori}} & = \left( {\rho \:_{{Gr}} \frac{{W_{{Gr}} }}{{W_{{Gr}} + \frac{{\rho \:_{{Gr}} }}{{\rho \:_{{Cu}} }}\left( {1 - W_{{Gr}} } \right)}} + \rho \:_{{Cu}} \left( {1 - \frac{{W_{{Gr}} }}{{W_{{Gr}} + \frac{{\rho \:_{{Gr}} }}{{\rho \:_{{Cu}} }}\left( {1 - W_{{Gr}} } \right)}}} \right)} \right) \\ & \left\{ {1.01 - 2.01\left( {\frac{{W_{{Gr}} }}{{W_{{Gr}} + \frac{{\rho \:_{{Gr}} }}{{\rho \:_{{Cu}} }}\left( {1 - W_{{Gr}} } \right)}}} \right)^{2} - 0.0131\left( {\frac{T}{{T_{0} }}} \right)} \right\}, \\ \end{aligned}$$

$$\begin{aligned} \:\alpha \:_{{Gori}} & = \left( {\alpha \:_{{Gr}} \frac{{W_{{Gr}} }}{{W_{{Gr}} + \frac{{\rho \:_{{Gr}} }}{{\rho \:_{{Cu}} }}\left( {1 - W_{{Gr}} } \right)}} + \alpha \:_{{Cu}} \left( {1 - \frac{{W_{{Gr}} }}{{W_{{Gr}} + \frac{{\rho \:_{{Gr}} }}{{\rho \:_{{Cu}} }}\left( {1 - W_{{Gr}} } \right)}}} \right)} \right) \\ & \left\{ \begin{gathered} 0.794 - 16.8\left( {\frac{{W_{{Gr}} }}{{W_{{Gr}} + \frac{{\rho \:_{{Gr}} }}{{\rho \:_{{Cu}} }}\left( {1 - W_{{Gr}} } \right)}}} \right)^{2} - 0.0279\left( {\frac{T}{{T_{0} }}} \right)^{2} \hfill \\ + 0.182\left( {1 + \frac{{W_{{Gr}} }}{{W_{{Gr}} + \frac{{\rho \:_{{Gr}} }}{{\rho \:_{{Cu}} }}\left( {1 - W_{{Gr}} } \right)}}} \right)\left( {\frac{T}{{T_{0} }}} \right) \hfill \\ \end{gathered} \right\}, \\ \end{aligned}$$

(2)

where, $\:{V}_{Gr}=\frac{{W}_{Gr}}{{W}_{Gr}+\frac{{\rho\:}_{Gr}}{{\rho\:}_{Cu}}\left(1-{W}_{Gr}\right)},{V}_{Cu}=1-{V}_{Gr}$ are content percentage of graphene origami and Cu matrix, respectively, and $\:\eta\:=\frac{\frac{{E}_{Gr}}{{E}_{Cu}}-1}{\frac{{E}_{Gr}}{{E}_{Cu}}+\xi\:},\xi\:=2\frac{{l}_{Gr}}{{t}_{Gr}}$ ($\:{l}_{Gr},{t}_{Gr}$ are leng and thickness of graphene origami).

The constitutive electro-magneto-elastic relations for curved integrated layers in the mechanical, thermal, electrical and magnetic fields are derived as follows^56,93:

$$\begin{array}{*{20}c} {\begin{array}{*{20}c} \begin{aligned} \left\{ {\begin{array}{*{20}c} {\sigma _{{\theta \theta }} } \\ {\sigma _{{rr}} } \\ {\sigma _{{r\theta }} } \\ \end{array} } \right\} & = \left[ {\begin{array}{*{20}c} {C_{{\theta \theta \theta \theta }} } & {C_{{\theta \theta rr}} } & 0 \\ {C_{{rr\theta \theta }} } & {C_{{rrrr}} } & 0 \\ 0 & 0 & {C_{{r\theta r\theta }} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon _{{\theta \theta }} - \alpha \left( {T - T_{0} } \right)} \\ {\varepsilon _{{rr}} - \alpha \left( {T - T_{0} } \right)} \\ {\varepsilon _{{r\theta }} } \\ \end{array} } \right\} \\ & - \left[ {\begin{array}{*{20}c} 0 & {e_{{\theta \theta r}} } \\ 0 & {e_{{rrr}} } \\ {e_{{r\theta \theta }} } & 0 \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {E_{\theta } } \\ {E_{r} } \\ \end{array} } \right\} - \left[ {\begin{array}{*{20}c} 0 & {f_{{\theta \theta r}} } \\ 0 & {f_{{rrr}} } \\ {f_{{r\theta \theta }} } & 0 \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {H_{\theta } } \\ {H_{r} } \\ \end{array} } \right\}, \\ \end{aligned} \\ \end{array} } \\ \end{array}$$

(3)

.

In which $\:{C}_{ijkl},{e}_{ijk},{f}_{ijk}$ are stiffness, piezoelectric and piezomagnetic coefficients, respectively. Furthermore, the electric and magnetic field components are denoted with $\:{E}_{i},{H}_{i}$. To complete electro-magneto-elastic relations, one can extend these relations in curvilinear coordinate system as follows^56,93:

$$\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} \begin{aligned} \left\{ {\begin{array}{*{20}{c}} {{D_\theta }} \\ {{D_r}} \end{array}} \right\} & =\left[ {\begin{array}{*{20}{c}} 0&0&{{e_{\theta r\theta }}} \\ {{e_{r\theta \theta }}}&{{e_{\theta \theta \theta }}}&0 \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\varepsilon _{\theta \theta }} - \alpha \left( {T - {T_0}} \right)} \\ {{\varepsilon _{rr}} - \alpha \left( {T - {T_0}} \right)} \\ {{\varepsilon _{r\theta }}} \end{array}} \right\} \\ & +\left[ {\begin{array}{*{20}{c}} {{\kappa _{\theta \theta }}}&0 \\ 0&{{\kappa _{rr}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{E_\theta }} \\ {{E_r}} \end{array}} \right\}+\left[ {\begin{array}{*{20}{c}} {{g_{\theta \theta }}}&0 \\ 0&{{g_{rr}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{H_\theta }} \\ {{H_r}} \end{array}} \right\}, \\ \end{aligned} \end{array}} \end{array}$$

(4)

and

$$\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} \begin{aligned} \left\{ {\begin{array}{*{20}{c}} {{B_\theta }} \\ {{B_r}} \end{array}} \right\} & =\left[ {\begin{array}{*{20}{c}} 0&0&{{f_{\theta r\theta }}} \\ {{f_{r\theta \theta }}}&{{f_{\theta \theta \theta }}}&0 \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\varepsilon _{\theta \theta }} - \alpha \left( {T - {T_0}} \right)} \\ {{\varepsilon _{rr}} - \alpha \left( {T - {T_0}} \right)} \\ {{\varepsilon _{r\theta }}} \end{array}} \right\} \\ & +\left[ {\begin{array}{*{20}{c}} {{g_{\theta \theta }}}&0 \\ 0&{{g_{rr}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{E_\theta }} \\ {{E_r}} \end{array}} \right\}+\left[ {\begin{array}{*{20}{c}} {{\mu _{\theta \theta }}}&0 \\ 0&{{\mu _{rr}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{H_\theta }} \\ {{H_r}} \end{array}} \right\}, \\ \end{aligned} \end{array}} \end{array}$$

(5)

Using the new coordinates measured from middle surface of tegrated face-sheets are employed as: $\:\stackrel{\sim}{z}=z\pm\:\frac{{h}_{e}}{2}\pm\:\frac{{h}_{p}}{2}$ for top and bottom face-sheets, the electromagnetic filed components are derived as follows^1,18:

$$\:\begin{array}{c}{E}_{r}=-\pi\:/{h}_{p}\psi\:\text{sin}\left(\pi\:\stackrel{\sim}{z}/{h}_{p}\right)-2{\psi\:}_{0}/{h}_{p},\:\:\:\:\:{E}_{{\uptheta\:}}={\psi\:}_{,{\uptheta\:}}/r\text{cos}\left(\pi\:\stackrel{\sim}{z}/{h}_{p}\right),\\\:{H}_{r}=-\pi\:/{h}_{p}\varphi\:\text{sin}\left(\pi\:\stackrel{\sim}{z}/{h}_{p}\right)-2{\varphi\:}_{0}/{h}_{p},\:\:\:\:\:{H}_{{\uptheta\:}}={\varphi\:}_{,{\uptheta\:}}/r\text{cos}\left(\pi\:\stackrel{\sim}{z}/{h}_{p}\right).\end{array}$$

(6)

where $\:{{\Psi\:}}_{0},\:{{\Phi\:}}_{0}$ are initial voltage and amperage. Regard to Eq. 6, it is concluded that the first terms of electric and magnetic potentials present the required boundary condition and second ones are used for applying the initial electric and magnetic potentials.

In this stage, to complete the constitutive relations, the kinematic relations should be extended in curved coordinate regarding thickness stretch ability as follows^56,93:

$$\:{u}_{\theta\:}\left(\text{z},\theta\:,\text{t}\right)=u\left(\theta\:,\text{t}\right)-\text{z}{w}_{b,\theta\:}\left(\theta\:,\text{t}\right)/r-f\left(\text{z}\right){w}_{s,\theta\:}\left(\theta\:,\text{t}\right)/r$$

$$\:{u}_{r}\left(\text{z},\theta\:,\text{t}\right)={w}_{b}\left(\theta\:,\text{t}\right)+{w}_{s}\left(\theta\:,\text{t}\right)+g\left(\text{z}\right)\chi\:\left(\theta\:,\text{t}\right)$$

(7)

,

Where, the shape function for more accurate modeling and accounting shear strain along the thickness is assumed as $\:f\left(\text{z}\right)=\text{z}-\frac{h}{\pi\:}\text{s}\text{i}\text{n}\left(\frac{\pi\:\:\mathbb{Z}}{h}\right),g\left(\text{z}\right)=\text{c}\text{o}\text{s}\left(\frac{\pi\:\:\text{z}}{h}\right)$. Based on the assumed radial deflection, the transverse deflection is assumed as bending, shearing and stretching functions, in which the last term show the changes along the thickness direction.

As first step in construction of Hamilton’s principle, the kinetic energy of the curved beam is expressed as follows^1,45,56:

$$\begin{aligned} \delta T & = \iint_{V} {\left( {\dot{u}_{\theta } \delta \dot{u}_{\theta } + \dot{u}_{r} \delta \dot{u}_{r} } \right)rdzd\theta } \\ & = \mathop {\iint {\left( \begin{gathered} \left[ {\dot{u}\left( {\theta ,t} \right) - z\dot{w}_{{b,\theta }} \left( {\theta ,t} \right)/r - f\left( z \right)\dot{w}_{{s,\theta }} \left( {\theta ,t} \right)/r} \right]\left[ {\delta \dot{u}\left( {\theta ,t} \right) - z\delta \dot{w}_{{b,\theta }} \left( {\theta ,t} \right)/r - f\left( z \right)\delta \dot{w}_{{s,\theta }} \left( {\theta ,t} \right)/r} \right] \hfill \\ + \left[ {\dot{w}_{b} \left( {\theta ,t} \right) + \dot{w}_{s} \left( {\theta ,t} \right) + g\left( z \right)\dot{\chi }\left( {\theta ,t} \right)} \right]\left[ {\delta \dot{w}_{b} \left( {\theta ,t} \right) + \delta \dot{w}_{s} \left( {\theta ,t} \right) + g\left( z \right)\delta \dot{\chi }\left( {\theta ,t} \right)} \right] \hfill \\ \end{gathered} \right)}}\limits_{{}}^{{}} rdzd\theta . \\ \end{aligned}$$

(8)

Through definition of some integration constants as presented below^1,45,56:

$$\begin{aligned} \left\{ {{\Pi _1},{\Pi _2},{\Pi _3},{\Pi _4},{\Pi _5},{\Pi _6},{\Pi _7},{\Pi _8}} \right\} & =\mathop \smallint \limits_{{ - \frac{{{h_e}}}{2} - {h_p}}}^{{ - \frac{{{h_e}}}{2}}} r{\rho ^p}\left\{ {\begin{array}{*{20}{c}} {1,z,f\left( z \right),\frac{{{z^2}}}{r},\frac{z}{r}f\left( z \right),\frac{1}{r}f{{\left( z \right)}^2},} \end{array}rg\left( z \right),rg{{\left( z \right)}^2}} \right\}dz \\ & +\mathop \smallint \limits_{{ - \frac{{{h_e}}}{2}}}^{{+\frac{{{h_e}}}{2}}} r\rho \left\{ {\begin{array}{*{20}{c}} {1,z,f\left( z \right),\frac{{{z^2}}}{r},\frac{z}{r}f\left( z \right),\frac{1}{r}f{{\left( z \right)}^2},} \end{array}rg\left( z \right),rg{{\left( z \right)}^2}} \right\}dz \\ & +~\mathop \smallint \limits_{{\frac{{{h_e}}}{2}}}^{{\frac{{{h_e}}}{2}+{h_p}}} r{\rho ^p}\left\{ {\begin{array}{*{20}{c}} {1,z,f\left( z \right),\frac{{{z^2}}}{r},\frac{z}{r}f\left( z \right),\frac{1}{r}f{{\left( z \right)}^2},} \end{array}rg\left( z \right),rg{{\left( z \right)}^2}} \right\}dz, \\ \end{aligned}$$

(9)

.

One can arrive at kinetic energy variation in arranged form as follows¹:

$$\delta T=\int {\left( \begin{gathered} \left[ { - {\Pi _1}\mathop u\limits^{{.}} +{\Pi _2}\frac{{d{{\mathop w\limits^{{.}} }_b}}}{{d\theta }} - {\Pi _3}\frac{{d\mathop {{w_s}}\limits^{.} }}{{d\theta }}} \right]\delta u \hfill \\ +\left[ { - {\Pi _2}\frac{{d\mathop u\limits^{{.}} }}{{d\theta }}+{\Pi _4}\frac{{{d^2}{{\mathop w\limits^{{.}} }_b}}}{{d{\theta ^2}}}+{\Pi _5}\frac{{{d^2}{{\mathop w\limits^{{.}} }_s}}}{{d{\theta ^2}}} - {\Pi _1}{{\mathop w\limits^{{.}} }_b} - {\Pi _1}~{{\mathop w\limits^{{.}} }_s} - {\Pi _7}\mathop \chi \limits^{{.}} } \right]\delta {w_b} \hfill \\ +\left[ { - {\Pi _3}\frac{{d\mathop u\limits^{{.}} }}{{d\theta }}+{\Pi _5}\frac{{{d^2}{{\mathop w\limits^{{.}} }_b}}}{{d{\theta ^2}}}+{\Pi _6}\frac{{{d^2}{{\mathop w\limits^{{.}} }_s}}}{{d{\theta ^2}}} - {\Pi _1}{{\mathop w\limits^{{.}} }_b} - {\Pi _1}~{{\mathop w\limits^{{.}} }_s} - {\Pi _7}\mathop \chi \limits^{{.}} ~} \right]\delta {w_s} - \left[ {{\Pi _7}{{\mathop w\limits^{{.}} }_b}+{\Pi _7}~{{\mathop w\limits^{{.}} }_s}+{\Pi _8}\mathop \chi \limits^{{.}} } \right]\delta \chi \hfill \\ \end{gathered} \right)d\theta .}$$

(10)

To constitutive the strain energy variation, one can derive the strain components as follows⁴⁷:

$$\:\begin{array}{c}{\epsilon\:}_{r}={g}_{,z}\left(\text{z}\right)\chi\:\\\:{\epsilon\:}_{{\Theta\:}}={u}_{,\theta\:}/r+{w}_{b}/r-\text{z}{w}_{b,\theta\:,\theta\:}/{r}^{2}+{w}_{s}/r-{f\left(\text{z}\right)w}_{s,\theta\:,\theta\:}/{r}^{2}+g\left(\text{z}\right)\chi\:/r\\\:{\gamma\:}_{r\theta\:}=-u/r+2z{w}_{b,\theta\:}/{r}^{2}+g\left(\text{z}\right)\left({w}_{s,\theta\:}+{\chi\:}_{,\theta\:}\right)/r\end{array}$$

(11)

The constitutive relations are extended through substitution of strain components, electric and magnetic potentials. The strain energy variation $\:\delta\:U={\sigma\:}_{ij}\delta\:{\epsilon\:}_{ij}-{D}_{i}\delta\:{E}_{i}-{B}_{i}\delta\:{H}_{i}$ including the mechanical, electrical and magnetic components is developed with substitution of the constitutive relations as follows^1,18:

$$\delta U = \iiint\limits_{V} {\left( \begin{gathered} \sigma _{{rr}} g_{{,z}} \left( z \right)\delta \chi + \sigma _{{\theta \theta }} \left[ \begin{gathered} \delta u_{{,\theta }} /r + \delta w_{b} /r - z\delta w_{{b,\theta ,\theta }} /r^{2} \hfill \\ + \delta w_{s} /r - f\left( z \right)\delta w_{{s,\theta ,\theta }} /r^{2} + g\left( z \right)\delta \chi /r \hfill \\ \end{gathered} \right] \hfill \\ + \sigma _{{r\theta }} \left[ { - \delta u/r + 2z\delta w_{{b,\theta }} /r^{2} + g\left( z \right)\left( {\delta w_{{s,\theta }} + \delta \chi _{{,\theta }} } \right)/r} \right] \hfill \\ - D_{r} \left[ { - \pi /h_{p} \delta \psi \sin \left( {\pi \tilde{z}/h_{p} } \right) - 2\delta \psi _{0} /h_{p} } \right] \hfill \\ - D_{\theta } \left[ {\delta \psi _{{,\theta }} /r\cos \left( {\pi \tilde{z}/h_{p} } \right)} \right] - B_{r} \left[ { - \pi /h_{p} \delta \phi \sin \left( {\pi \tilde{z}/h_{p} } \right) - 2\delta \phi _{0} /h_{p} } \right] \hfill \\ - B_{\theta } \left[ {\delta \phi _{{,\theta }} /r\cos \left( {\pi \tilde{z}/h_{p} } \right)} \right] \hfill \\ \end{gathered} \right)}rdzd\Theta .$$

(12)

In which following definition:

$$\:\left\{{N}_{rr}\right\}={\int\:}_{-\frac{h}{2}}^{\frac{h}{2}}\left\{{r\sigma\:}_{rr}{g}_{,z}\left(\text{z}\right)\right\}\text{d}z,\left\{{N}_{{\uptheta\:}{\uptheta\:}},{M}_{{\uptheta\:}{\uptheta\:}},{S}_{{\uptheta\:}{\uptheta\:}},{P}_{{\uptheta\:}{\uptheta\:}}\right\}={\int\:}_{-\frac{h}{2}}^{\frac{h}{2}}{\sigma\:}_{{\uptheta\:}{\uptheta\:}}\left\{1,z/r,f\left(\text{z}\right)/r,g\left(z\right)\right\}\text{d}z,$$

$$\:\left\{{N}_{r{\uptheta\:}},{M}_{r{\uptheta\:}},{P}_{r{\uptheta\:}}\right\}={\int\:}_{-\frac{h}{2}}^{\frac{h}{2}}{\tau\:}_{r{\uptheta\:}}\left\{\text{1,2}z/r,g\left(z\right)\right\}\text{d}z,$$

$$\:\left\{\stackrel{-}{{D}_{r}},\stackrel{-}{{D}_{{\uptheta\:}}}\right\}={\int\:}_{-\frac{h}{2}}^{\frac{h}{2}}{D}_{r}\left\{\pi\:/{h}_{p}\text{sin}\left(\pi\:\stackrel{\sim}{z}/{h}_{p}\right),\text{cos}\left(\pi\:\stackrel{\sim}{z}/{h}_{p}\right)\right\}\text{d}\text{z},$$

$$\:\left\{\stackrel{-}{{B}_{r}},\stackrel{-}{{B}_{{\uptheta\:}}}\right\}={\int\:}_{-\frac{h}{2}}^{\frac{h}{2}}{B}_{r}\left\{\pi\:/{h}_{p}\text{sin}\left(\pi\:\stackrel{\sim}{z}/{h}_{p}\right),\text{cos}\left(\pi\:\stackrel{\sim}{z}/{h}_{p}\right)\right\}\text{d}\text{z},$$

(13)

Simplified strain energy variation as follows:

$$\begin{aligned} \delta U & =\iiint_{V} {\left( \begin{gathered} {N_{rr}}\delta \chi +\left[ {{N_{\theta \theta }}\delta {u_{,\theta }}+{N_{\theta \theta }}\delta {w_b} - {M_{\theta \theta }}\delta {w_{b,\theta ,\theta }}+{N_{\theta \theta }}\delta {w_s} - {S_{\theta \theta }}\delta {w_{s,\theta ,\theta }}+{P_{\theta \theta }}\delta \chi } \right] \hfill \\ +\left[ { - {N_{r\theta }}\delta u+{M_{r\theta }}\delta {w_{b,\theta }}+{P_{r\theta }}\left( {\delta {w_{s,\theta }}+\delta {\chi _{,\theta }}} \right)} \right]+{D_r}\delta \psi - {D_\theta }\delta {\psi _{,\theta }}+{B_r} - {B_\theta }\delta {\phi _{,\theta }} \hfill \\ \end{gathered} \right)d\theta } \\ & =\mathop \smallint \limits_{0}^{\Theta } \left( \begin{gathered} \left[ { - {N_{\theta \theta ,\theta }} - {N_{r\theta }}} \right]\delta u+\left[ {{N_{\theta \theta }} - {M_{\theta \theta ,\theta \theta }} - {M_{r\theta ,\theta }}} \right]\delta {w_b} \hfill \\ +\left[ {{N_{\theta \theta }} - {S_{\theta \theta ,\theta \theta }} - {P_{r\theta ,\theta }}} \right]\delta {w_s}+\left[ {{N_{rr}}+{P_{\theta \theta }} - {P_{r\theta ,\theta }}} \right]\delta \chi +\left[ {{D_r}+{D_{\theta ,\theta }}} \right]\delta \psi +\left[ {{B_r}+{B_{\theta ,\theta }}} \right]\delta \phi \hfill \\ \end{gathered} \right)d\theta . \\ \end{aligned}$$

(14)

.

In which the last terms are derived using integration by part.

As final step, the virtual work due to mechanical, thermal, electrical and magnetic preloads is derived as follows⁶⁹:

$$\:\delta\:W={\int\:}_{0}^{{\Theta\:}}\left\{{K}_{1}{u}_{r}-{K}_{2}{{u}_{r}}_{,\theta\:,\theta\:}/{r}^{2}-\left({N}_{0}+{N}_{E}+{N}_{M}\right.+{N}_{T}){{u}_{r}}_{,\theta\:,\theta\:}/{r}^{2}\left(\delta\:{u}_{r}\right)\right\}\text{r}\text{d}\theta\:.$$

(15)

In which the initial mechanical, electrical, magnetic and thermal loads are denoted with $\:{N}_{0},{N}_{E},{N}_{M},{N}_{T}$ respectively. furthermore, the reaction of Pasternak’s foundation are included spring $\:{K}_{1}$ and shear $\:{K}_{2}$ parameters. The governing motion equations can be derived using $\:\delta\:{\Pi\:}=\delta\:W-\delta\:U+\delta\:T$ as follows:

$$\:\delta\:u:\:\:-{N}_{r\theta\:}-{N}_{\theta\:\theta\:,\theta\:}\:=-{{\Pi\:}}_{1}\ddot{u}+{{\Pi\:}}_{2}{\ddot{w}}_{b,\theta\:}-{{\Pi\:}}_{3}{\ddot{w}}_{s,\theta\:},$$

$\begin{gathered} \delta {w_b}:~~{N_{\theta \theta }} - {M_{\theta \theta ,\theta ,\theta }} - {N_{r\theta ,\theta }} - 2{M_{r\theta ,\theta }}+\left( {{N_0}+{N_E}+{N_M}} \right.+{N_T})\left( {{w_{b,\theta ,\theta }}+~{w_{s,\theta ,\theta }}+{\chi _{,\theta \theta }}} \right)/r \hfill \\ ={K_1}{u_r} - {K_2}{u_r}_{{,\theta ,\theta }}/{r^2} - {\Pi _2}{\mathop u\limits^{{.}} _{,\theta }}+{\Pi _4}{\mathop w\limits^{{.}} _{b,\theta ,\theta }}+{\Pi _5}{\mathop w\limits^{{.}} _{s,\theta ,\theta }} - {\Pi _1}{\mathop w\limits^{{.}} _b} - {\Pi _1}~{\mathop w\limits^{{.}} _s} - {\Pi _7}\mathop \chi \limits^{{.}} \hfill \\ \end{gathered}$

$\begin{gathered} \delta {w_s}:~~{N_{\theta \theta }} - {S_{\theta \theta ,\theta ,\theta }} - {N_{r\theta ,\theta }} - 2{S_{r\theta ,\theta }}+\left( {{N_0}+{N_E}+{N_M}} \right.+{N_T})\left( {{w_{b,\theta ,\theta }}+~{w_{s,\theta ,\theta }}+{\chi _{,\theta \theta }}} \right)/r \hfill \\ ={K_1}{u_r} - {K_2}{u_r}_{{,\theta ,\theta }}/{r^2} - {\Pi _3}{\mathop u\limits^{{.}} _{,\theta }}+{\Pi _5}{\mathop w\limits^{{.}} _{b,\theta ,\theta }}+{\Pi _6}{\mathop w\limits^{{.}} _{s,\theta ,\theta }} - {\Pi _1}{\mathop w\limits^{{.}} _b} - {\Pi _1}~{\mathop w\limits^{{.}} _s} - {\Pi _7}\mathop \chi \limits^{{.}} , \hfill \\ \end{gathered}$

$$\:\delta\:\chi\::\:{P}_{\theta\:\theta\:}-{P}_{r\theta\:,\theta\:}+\left({N}_{0}+{N}_{E}+{N}_{M}\right.+{N}_{T})\left({w}_{b,\theta\:,\theta\:}+\:{w}_{s,\theta\:,\theta\:}+{\chi\:}_{,\theta\:\theta\:}\right)/r={K}_{1}{u}_{r}-{K}_{2}{{u}_{r}}_{,\theta\:,\theta\:}/{r}^{2}-[{{\Pi\:}}_{7}{\ddot{w}}_{b}+{{\Pi\:}}_{7}\:{\ddot{w}}_{s}+{{\Pi\:}}_{8}\ddot{\vartheta\:}$$

$$\:\delta\:\psi\::\:\:-{\stackrel{-}{D}}_{r}-{\stackrel{-}{D}}_{\theta\:,\theta\:}=0,$$

$$\:\delta\:\varphi\::\:\:-{\stackrel{-}{B}}_{r}-{\stackrel{-}{B}}_{\theta\:,\theta\:}=0.$$

(16)

The governing equations in Eq. 16 are presented in terms of resultant components $\:{N}_{ij},{M}_{ij},{S}_{ij},{P}_{ij},\stackrel{-}{{D}_{i}},\stackrel{-}{{B}_{i}}$, but it is needed to arrive at the governing equations in terms of the unknown functions including $\:u,{w}_{b},{w}_{s},\chi\:,\psi\:,\varphi\:$. The solution will be applied for the unknown deformation components, electric and magnetic potential components. Substitution of strain components into stress components and then into resultant components leads to:

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} {N_{{rr}} } \\ {N_{{\theta \:\theta \:}} } \\ {M_{{\theta \:\theta \:}} } \\ {S_{{\theta \:\theta \:}} } \\ {P_{{\theta \:\theta \:}} } \\ {\mathop {D_{r} }\limits^{ - } } \\ {\mathop {B_{r} }\limits^{ - } } \\ \end{array} } \right\} = & \left[ {\begin{array}{*{20}c} {{\daleth }\:_{1} } & {{\daleth }\:_{1} } & {\begin{array}{*{20}c} { - {\daleth }\:_{2} } & {{\daleth }\:_{1} } & {\begin{array}{*{20}c} { - {\daleth }\:_{3} } & {{\daleth }\:_{4} + {\daleth }\:_{5} } & {\begin{array}{*{20}c} {{\daleth }\:_{6} } & {{\daleth }_{7} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ {{\daleth }\:_{8} } & {{\daleth }\:_{8} } & {\begin{array}{*{20}c} { - {\daleth }\:_{9} } & {{\daleth }\:_{8} } & {\begin{array}{*{20}c} { - {\daleth }\:_{{10}} } & {{\daleth }\:_{{11}} + {\daleth }\:_{{12}} } & {\begin{array}{*{20}c} {{\daleth }\:_{{13}} } & {{\daleth }_{{14}} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} {{\daleth }\:_{{15}} } \\ {{\daleth }\:_{{22}} } \\ {\begin{array}{*{20}c} {{\daleth }\:_{{29}} } \\ {{\daleth }\:_{{56}} } \\ {{\daleth }\:_{{68}} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {{\daleth }\:_{{15}} } \\ {{\daleth }\:_{{22}} } \\ {\begin{array}{*{20}c} {{\daleth }\:_{{29}} } \\ {{\daleth }\:_{{56}} } \\ {{\daleth }\:_{{68}} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - {\daleth }\:_{{16}} } & {{\daleth }\:_{{15}} } & {\begin{array}{*{20}c} { - {\daleth }\:_{{17}} } & {{\daleth }\:_{{18}} + {\daleth }\:_{{19}} } & {\begin{array}{*{20}c} {{\daleth }\:_{{20}} } & {{\daleth }_{{21}} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} { - {\daleth }\:_{{23}} } & {{\daleth }\:_{{22}} } & {\begin{array}{*{20}c} { - {\daleth }\:_{{24}} } & {\:{\daleth }\:_{{25}} + {\daleth }\:_{{26}} } & {\begin{array}{*{20}c} {{\daleth }\:_{{27}} } & {{\daleth }_{{28}} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - {\daleth }\:_{{30}} } \\ { - {\daleth }\:_{{57}} } \\ { - {\daleth }\:_{{69}} } \\ \end{array} } & {\begin{array}{*{20}c} {{\daleth }\:_{{29}} } \\ {{\daleth }\:_{{56}} } \\ {{\daleth }\:_{{68}} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - {\daleth }\:_{{31}} } \\ { - {\daleth }\:_{{58}} } \\ { - {\daleth }\:_{{70}} } \\ \end{array} } & {\begin{array}{*{20}c} {{\daleth }\:_{{32}} + {\daleth }\:_{{33}} } \\ {{\daleth }\:_{{59}} + {\daleth }\:_{{60}} } \\ {{\daleth }\:_{{71}} + {\daleth }\:_{{72}} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\daleth }\:_{{34}} } \\ { - {\daleth }\:_{{61}} } \\ { - {\daleth }\:_{{73}} } \\ \end{array} } & {\begin{array}{*{20}c} {{\daleth }_{{35}} } \\ { - {\daleth }_{{62}} } \\ { - {\daleth }_{{74}} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] \\ & \left\{ {\begin{array}{*{20}c} {u_{{,\theta \:}} } \\ {\:w_{b} } \\ {\:w_{{b,\theta \:,\theta \:}} } \\ {\:w_{s} } \\ {\:w_{{s,\theta \:,\theta \:}} } \\ {\:\chi \:} \\ {\:\psi \:} \\ {\:\varphi \:} \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} {{\mathcal{N}}_{{rr}}^{{\psi \:_{0} }} + {\mathcal{N}}_{{rr}}^{{\varphi \:_{0} }} - {\mathcal{N}}_{{rr}}^{T} } \\ {{\mathcal{N}}_{{\theta \:\theta \:}}^{{\psi \:_{0} }} + {\mathcal{N}}_{{\theta \:\theta \:}}^{{\varphi \:_{0} }} - {\mathcal{N}}_{{\theta \:\theta \:}}^{T} } \\ {{\mathcal{M}}_{{\theta \:\theta \:}}^{{\psi \:_{0} }} + {\mathcal{M}}_{{\theta \:\theta \:}}^{{\varphi \:_{0} }} - {\mathcal{M}}_{{\theta \:\theta \:}}^{T} } \\ {{\mathcal{S}}_{{\theta \:\theta \:}}^{{\psi \:_{0} }} + {\mathcal{S}}_{{\theta \:\theta \:}}^{{\varphi \:_{0} }} - {\mathcal{S}}_{{\theta \:\theta \:}}^{T} } \\ {{\mathcal{P}}_{{\theta \:\theta \:}}^{{\psi \:_{0} }} + {\mathcal{P}}_{{\theta \:\theta \:}}^{{\varphi \:_{0} }} - {\mathcal{P}}_{{\theta \:\theta \:}}^{T} } \\ { - {\mathcal{D}}_{{rr}}^{{\psi \:_{0} }} - {\mathcal{D}}_{{rr}}^{{\varphi \:_{0} }} - {\mathcal{D}}_{{rr}}^{T} } \\ { - {\mathcal{B}}_{{rr}}^{{\psi \:_{0} }} - {\mathcal{B}}_{{rr}}^{{\varphi \:_{0} }} - {\mathcal{B}}_{{rr}}^{T} } \\ \end{array} } \right\} \\ \end{aligned}$$

$$\:\left\{\begin{array}{c}{N}_{r\theta\:}\\\:{M}_{r\theta\:}\\\:{P}_{r\theta\:}\\\:\stackrel{-}{{D}_{\theta\:}}\\\:\stackrel{-}{{B}_{\theta\:}}\end{array}\right\}=\left[\begin{array}{ccc}-{\daleth\:}_{36}&\:{\daleth\:}_{37}&\:\begin{array}{ccc}{\daleth\:}_{38}&\:-{\daleth\:}_{39}&\:-{\daleth\:}_{40}\end{array}\\\:-{\daleth\:}_{41}&\:{\daleth\:}_{42}&\:\begin{array}{ccc}{\daleth\:}_{43}&\:-{\daleth\:}_{44}&\:-{\daleth\:}_{45}\end{array}\\\:\begin{array}{c}-{\daleth\:}_{46}\\\:-{\daleth\:}_{51}\\\:-{\daleth\:}_{63}\end{array}&\:\begin{array}{c}{\daleth\:}_{47}\\\:{\daleth\:}_{52}\\\:{\daleth\:}_{64}\end{array}&\:\begin{array}{c}\begin{array}{ccc}{\daleth\:}_{48}&\:-{\daleth\:}_{49}&\:-{\daleth\:}_{50}\end{array}\\\:\begin{array}{ccc}{\daleth\:}_{53}&\:{\daleth\:}_{54}&\:{\daleth\:}_{55}\end{array}\\\:\begin{array}{ccc}{\daleth\:}_{65}&\:{\daleth\:}_{66}&\:{\daleth\:}_{67}\end{array}\end{array}\end{array}\right]\left\{\begin{array}{c}u\\\:{w}_{b,\theta\:}\\\:{w}_{s,\theta\:}+{\chi\:}_{,\theta\:}\\\:{\psi\:}_{,\theta\:}\\\:{\varphi\:}_{,\theta\:}\end{array}\right\}$$

(17)

An update form of the motion governing equations can be presented using substituting the resultant components into governing equations as follows:

$$\:\begin{array}{c}\begin{array}{c}\delta\:u:\:-{\daleth\:}_{8}{u}_{,\theta\:\theta\:}+{\daleth\:}_{36}u+{\daleth\:}_{9}{w}_{b,\theta\:\theta\:\theta\:}-\left({\daleth\:}_{37}+{\daleth\:}_{8}\right){w}_{b,\theta\:}+{\daleth\:}_{10}{w}_{s,\theta\:\theta\:\theta\:}-\left({\daleth\:}_{8}+{\daleth\:}_{38}\right){w}_{s,\theta\:}-\left({\daleth\:}_{11}+{\daleth\:}_{12}+{\daleth\:}_{38}\right){\chi\:}_{,\theta\:}\\\:+\left({\daleth\:}_{39}-{\daleth\:}_{13}\right){\psi\:}_{,\theta\:}+\left({\daleth\:}_{40}-{\daleth\:}_{14}\right){\varphi\:}_{,\theta\:}-{\mathcal{N}}_{\theta\:\theta\:,\theta\:}^{{\psi\:}_{0}}-{\mathcal{N}}_{\theta\:\theta\:,\theta\:}^{{\varphi\:}_{0}}-{\mathcal{N}}_{\theta\:\theta\:,\theta\:}^{T}=-{{\Pi\:}}_{1}\ddot{u}+{{\Pi\:}}_{2}{\ddot{w}}_{b,\theta\:}-{{\Pi\:}}_{3}{\ddot{w}}_{s,\theta\:},\\\:\delta\:{w}_{b}:-{\daleth\:}_{15}{u}_{,\theta\:\theta\:\theta\:}+\:\left({\daleth\:}_{8}+{\daleth\:}_{41}\right){u}_{,\theta\:}+{\daleth\:}_{16}{w}_{b,\theta\:\theta\:\theta\:\theta\:}-\left({\daleth\:}_{9}+{\daleth\:}_{42}+{\daleth\:}_{15}\right){w}_{b,\theta\:\theta\:}+{\daleth\:}_{8}{w}_{b}+{\daleth\:}_{17}{w}_{s,\theta\:\theta\:\theta\:\theta\:}\\\:-\left({\daleth\:}_{10}+{\daleth\:}_{43}+{\daleth\:}_{15}\right){w}_{s,\theta\:\theta\:}+{\daleth\:}_{8}{w}_{s}-\left({\daleth\:}_{18}+{\daleth\:}_{19}+{\daleth\:}_{43}\right){\chi\:}_{,\theta\:\theta\:}+\left({\daleth\:}_{11}+{\daleth\:}_{12}\right)\chi\:+\left({\daleth\:}_{44}-{\daleth\:}_{20}\right){\psi\:}_{,\theta\:\theta\:}+{\daleth\:}_{13}\psi\:\\\:+\left({\daleth\:}_{45}-{\daleth\:}_{21}\right){\varphi\:}_{,\theta\:\theta\:}+{\daleth\:}_{14}\varphi\:+{\mathcal{N}}_{\theta\:\theta\:}^{{\psi\:}_{0}}+{\mathcal{N}}_{\theta\:\theta\:}^{{\varphi\:}_{0}}-{\mathcal{M}}_{\theta\:\theta\:,\theta\:\theta\:}^{{\psi\:}_{0}}-{\mathcal{M}}_{\theta\:\theta\:,\theta\:\theta\:}^{{\varphi\:}_{0}}-{\mathcal{N}}_{\theta\:\theta\:}^{T}-{\mathcal{M}}_{\theta\:\theta\:,\theta\:\theta\:}^{T}=-{K}_{1}u-{K}_{2}/{R}^{2}{u}_{,\theta\:,\theta\:}\\\:-\left({N}_{0}+{N}_{E}+{N}_{M}\right.+{N}_{T})\left({w}_{b,\theta\:,\theta\:}+\:{w}_{s,\theta\:,\theta\:}+g\left(\text{z}\right){\chi\:}_{,\theta\:\theta\:}\right)/R-{{\Pi\:}}_{2}{\ddot{u}}_{,\theta\:}+{{\Pi\:}}_{4}{\ddot{w}}_{b,\theta\:,\theta\:}+{{\Pi\:}}_{5}{\ddot{w}}_{s,\theta\:,\theta\:}-{{\Pi\:}}_{1}{\ddot{w}}_{b}-{{\Pi\:}}_{1}\:{\ddot{w}}_{s}-{{\Pi\:}}_{7}\ddot{\chi\:},\end{array}\\\:\begin{array}{c}\delta\:{w}_{s}:-{\daleth\:}_{22}{u}_{,\theta\:\theta\:\theta\:}+\left({\daleth\:}_{8}+{\daleth\:}_{46}\right){u}_{,\theta\:}+{\daleth\:}_{23}{w}_{b,\theta\:\theta\:\theta\:\theta\:}-\left({\daleth\:}_{9}+{\daleth\:}_{22}+{\daleth\:}_{47}\right){w}_{b,\theta\:\theta\:}+{\daleth\:}_{8}{w}_{b}+{\daleth\:}_{24}{w}_{s,\theta\:\theta\:\theta\:\theta\:}\\\:-\left({\daleth\:}_{10}+{\daleth\:}_{22}+{\daleth\:}_{48}\right){w}_{s,\theta\:\theta\:}+{\daleth\:}_{8}{w}_{s}-\left({\daleth\:}_{25}+{\daleth\:}_{26}-{\daleth\:}_{48}\right){\chi\:}_{,\theta\:\theta\:}+\left({\daleth\:}_{11}+{\daleth\:}_{12}\right)\chi\:+\left({\daleth\:}_{49}-{\daleth\:}_{27}\right){\psi\:}_{,\theta\:\theta\:}+{\daleth\:}_{13}\psi\:\\\:+\left({\daleth\:}_{50}-{\daleth\:}_{28}\right){\varphi\:}_{,\theta\:\theta\:}+{\daleth\:}_{14}\varphi\:+{\mathcal{N}}_{\theta\:\theta\:}^{{\psi\:}_{0}}+{\mathcal{N}}_{\theta\:\theta\:}^{{\varphi\:}_{0}}-{\mathcal{S}}_{\theta\:\theta\:,\theta\:\theta\:}^{{\psi\:}_{0}}-{\mathcal{S}}_{\theta\:\theta\:,\theta\:\theta\:}^{{\varphi\:}_{0}}-{\mathcal{N}}_{\theta\:\theta\:}^{T}-{S}_{\theta\:\theta\:,\theta\:\theta\:}^{T}=-{K}_{1}u-{K}_{2}/{R}^{2}{u}_{,\theta\:,\theta\:}\\\:-\left({N}_{0}+{N}_{E}+{N}_{M}\right.+{N}_{T})\left({w}_{b,\theta\:,\theta\:}+\:{w}_{s,\theta\:,\theta\:}+g\left(\text{z}\right){\chi\:}_{,\theta\:\theta\:}\right)/R-{{\Pi\:}}_{3}{\ddot{u}}_{,\theta\:}+{{\Pi\:}}_{5}{\ddot{w}}_{b,\theta\:,\theta\:}+{{\Pi\:}}_{6}{\ddot{w}}_{s,\theta\:,\theta\:}-{{\Pi\:}}_{1}{\ddot{w}}_{b}-{{\Pi\:}}_{1}\:{\ddot{w}}_{s}-{{\Pi\:}}_{7}\ddot{\chi\:}\\\:\delta\:\chi\::\left({\daleth\:}_{1}+{\daleth\:}_{46}+{\daleth\:}_{29}\right){u}_{,\theta\:}-\left({\daleth\:}_{2}+{\daleth\:}_{30}-{\daleth\:}_{47}\right){w}_{b,\theta\:\theta\:}+\left({\daleth\:}_{1}+{\daleth\:}_{29}\right){w}_{b}-\left({\daleth\:}_{48}+{\daleth\:}_{3}+{\daleth\:}_{31}\right){w}_{s,\theta\:\theta\:}\\\:+\left({\daleth\:}_{1}+{\daleth\:}_{29}\right){w}_{s}-{\daleth\:}_{48}{\chi\:}_{,\theta\:\theta\:}+\left({\daleth\:}_{32}+{\daleth\:}_{33}+{\daleth\:}_{4}+{\daleth\:}_{5}\right)\chi\:\\\:+{\daleth\:}_{49}{\psi\:}_{,\theta\:\theta\:}+\left({\daleth\:}_{6}+{\daleth\:}_{34}\right)\psi\:+{\daleth\:}_{50}{\varphi\:}_{,\theta\:\theta\:}+\left({\daleth\:}_{35}+{\daleth\:}_{7}\right)\varphi\:+{\mathcal{N}}_{rr}^{{\psi\:}_{0}}+{\mathcal{N}}_{rr}^{{\varphi\:}_{0}}+{\mathcal{P}}_{\theta\:\theta\:}^{{\psi\:}_{0}}+{\mathcal{P}}_{\theta\:\theta\:}^{{\varphi\:}_{0}}-{\mathcal{N}}_{rr}^{T}-{P}_{rr}^{T}=-{K}_{1}u-{K}_{2}/{R}^{2}{u}_{,\theta\:,\theta\:}\\\:-\left({N}_{0}+{N}_{E}+{N}_{M}\right.+{N}_{T})\left({w}_{b,\theta\:,\theta\:}+\:{w}_{s,\theta\:,\theta\:}+g\left(\text{z}\right){\chi\:}_{,\theta\:\theta\:}\right)/R+{K}_{1}u-{K}_{2}/{r}^{2}{u}_{,\theta\:,\theta\:}-[{{\Pi\:}}_{7}{\ddot{w}}_{b}+{{\Pi\:}}_{7}\:{\ddot{w}}_{s}+{{\Pi\:}}_{8}\ddot{\vartheta\:}]\\\:\delta\:\psi\::\left({\daleth\:}_{56}-{\daleth\:}_{51}\right){u}_{,\theta\:}+\left({\daleth\:}_{52}-{\daleth\:}_{57}\right){w}_{b,\theta\:\theta\:}+{\daleth\:}_{56}{w}_{b}+\left({\daleth\:}_{53}-{\daleth\:}_{58}\right){w}_{s,\theta\:\theta\:}+{\daleth\:}_{56}{w}_{s}\\\:+{\daleth\:}_{53}{\chi\:}_{,\theta\:\theta\:}+\left({\daleth\:}_{59}+{\daleth\:}_{60}\right)\chi\:+{\daleth\:}_{54}{\psi\:}_{,\theta\:\theta\:}-{\daleth\:}_{61}\psi\:+{\daleth\:}_{55}{\varphi\:}_{,\theta\:\theta\:}-{\daleth\:}_{62}\varphi\:-{\mathcal{D}}_{rr}^{{\psi\:}_{0}}-{\mathcal{D}}_{rr}^{{\varphi\:}_{0}}-{\mathcal{D}}_{rr}^{T}=0\\\:\delta\:\varphi\::\left({\daleth\:}_{68}-{\daleth\:}_{63}\right){u}_{,\theta\:}+\left({\daleth\:}_{64}-{\daleth\:}_{69}\right){w}_{b,\theta\:\theta\:}+{\daleth\:}_{68}{w}_{b}+\left({\daleth\:}_{65}-{\daleth\:}_{70}\right){w}_{s,\theta\:\theta\:}+{\daleth\:}_{68}{w}_{s}\\\:+{\daleth\:}_{65}{\chi\:}_{,\theta\:\theta\:}+\left({\daleth\:}_{71}+{\daleth\:}_{72}\right)\chi\:+{\daleth\:}_{66}{\psi\:}_{,\theta\:\theta\:}-{\daleth\:}_{73}\psi\:+{\daleth\:}_{67}{\varphi\:}_{,\theta\:\theta\:}-{\daleth\:}_{74}\varphi\:-{\mathcal{B}}_{rr}^{{\psi\:}_{0}}-{\mathcal{B}}_{rr}^{{\varphi\:}_{0}}-{\mathcal{B}}_{rr}^{T}=0\end{array}\end{array}$$

(18)

For example, the first governing equation of motion is derived using the substitution of resultant components into governing equations. The governing equation and the components are presented as follows:

$$\:\delta\:u:\:\:-{N}_{r\theta\:}-\frac{d{N}_{\theta\:\theta\:,\theta\:}}{d\theta\:}\:=-{{\Pi\:}}_{1}\ddot{u}+{{\Pi\:}}_{2}{\ddot{w}}_{b,\theta\:}-{{\Pi\:}}_{3}{\ddot{w}}_{s,\theta\:},$$

$$\:{N}_{r\theta\:}=-{\daleth\:}_{36}\:u+{\daleth\:}_{37}{w}_{b,\theta\:}+{\daleth\:}_{38}\left({w}_{s,\theta\:}+{\chi\:}_{,\theta\:}\right)-{\daleth\:}_{39}{\psi\:}_{,\theta\:}-{\daleth\:}_{40}{\varphi\:}_{,\theta\:},$$

$$\:{N}_{\theta\:\theta\:}={\daleth\:}_{8}{u}_{,\theta\:}+{\daleth\:}_{8}{w}_{b}-{\daleth\:}_{9}{w}_{b,\theta\:,\theta\:}+{\daleth\:}_{8}{w}_{s}-{\daleth\:}_{10}{w}_{s,\theta\:,\theta\:}+\left({\daleth\:}_{11}+{\daleth\:}_{12}\right)\chi\:+{\daleth\:}_{13}\psi\:+{\daleth\:}_{14}\varphi\:+{\mathcal{N}}_{\theta\:\theta\:}^{{\psi\:}_{0}}+{\mathcal{N}}_{\theta\:\theta\:}^{{\varphi\:}_{0}}-{\mathcal{N}}_{\theta\:\theta\:}^{T}$$

(19)

Substitution of the resultant into governing equation leads to:

$$\:\delta\:u:\:\:-\left(-{\daleth\:}_{36}\:u+{\daleth\:}_{37}{w}_{b,\theta\:}+{\daleth\:}_{38}\left({w}_{s,\theta\:}+{\chi\:}_{,\theta\:}\right)-{\daleth\:}_{39}{\psi\:}_{,\theta\:}-{\daleth\:}_{40}{\varphi\:}_{,\theta\:}\right)-$$

$$\begin{aligned} \:\frac{d}{{d\theta \:}} & \left( \begin{gathered} {\daleth }\:_{8} u_{{,\theta \:}} + {\daleth }\:_{8} w_{b} - {\daleth }\:_{9} w_{{b,\theta \:,\theta \:}} + {\daleth }\:_{8} w_{s} - {\daleth }\:_{{10}} w_{{s,\theta \:,\theta \:}} \hfill \\ + \left( {{\daleth }\:_{{11}} + {\daleth }\:_{{12}} } \right)\chi \: + {\daleth }\:_{{13}} \psi \: + {\daleth }\:_{{14}} \varphi \: + {\mathcal{N}}_{{\theta \:\theta \:}}^{{\psi \:_{0} }} + {\mathcal{N}}_{{\theta \:\theta \:}}^{{\varphi \:_{0} }} - {\mathcal{N}}_{{\theta \:\theta \:}}^{T} \hfill \\ \end{gathered} \right) \\ & = {\daleth }\:_{{36}} \:u - {\daleth }\:_{{37}} w_{{b,\theta \:}} - {\daleth }\:_{{38}} \left( {w_{{s,\theta \:}} + \chi \:_{{,\theta \:}} } \right) + {\daleth }\:_{{39}} \psi \:_{{,\theta \:}} + {\daleth }\:_{{40}} \varphi \:_{{,\theta \:}} , \\ \end{aligned}$$

$$\begin{gathered} \: - {\daleth }\:_{8} u_{{,\theta \:\theta \:}} - {\daleth }\:_{8} w_{{b,\theta \:}} + {\daleth }\:_{9} w_{{b,\theta \:\theta \:\theta \:}} - {\daleth }\:_{8} w_{{s,\theta \:}} + {\daleth }\:_{{10}} w_{{s,\theta \:\theta \:\theta \:}} \hfill \\ - \left( {{\daleth }\:_{{11}} + {\daleth }\:_{{12}} } \right)\chi \:_{{,\theta \:}} - {\daleth }\:_{{13}} \psi \:_{{,\theta \:}} + {\daleth }\:_{{14}} \varphi \:_{{,\theta \:}} + {\mathcal{N}}_{{\theta \:\theta \:,\theta \:}}^{{\psi \:_{0} }} + {\mathcal{N}}_{{\theta \:\theta \:,\theta \:}}^{{\varphi \:_{0} }} - {\mathcal{N}}_{{\theta \:\theta \:,\theta \:}}^{T} \hfill \\ = - {\daleth }\:_{8} u_{{,\theta \:\theta \:}} + {\daleth }\:_{{36}} u + {\daleth }\:_{9} w_{{b,\theta \:\theta \:\theta \:}} - \left( {{\daleth }\:_{{37}} + {\daleth }\:_{8} } \right)w_{{b,\theta \:}} + {\daleth }\:_{{10}} w_{{s,\theta \:\theta \:\theta \:}} \hfill \\ - \left( {{\daleth }\:_{8} + {\daleth }\:_{{38}} } \right)w_{{s,\theta \:}} - \left( {{\daleth }\:_{{11}} + {\daleth }\:_{{12}} + {\daleth }\:_{{38}} } \right)\chi \:_{{,\theta \:}} \: + \left( {{\daleth }\:_{{39}} - {\daleth }\:_{{13}} } \right)\psi \:_{{,\theta \:}} + \left( {{\daleth }\:_{{40}} - {\daleth }\:_{{14}} } \right)\varphi \:_{{,\theta \:}} \hfill \\ - {\mathcal{N}}_{{\theta \:\theta \:,\theta \:}}^{{\psi \:_{0} }} - {\mathcal{N}}_{{\theta \:\theta \:,\theta \:}}^{{\varphi \:_{0} }} - {\mathcal{N}}_{{\theta \:\theta \:,\theta \:}}^{T} = - \Pi \:_{1} \ddot{u} + \Pi \:_{2} \ddot{w}_{{b,\theta \:}} - \Pi \:_{3} \ddot{w}_{{s,\theta \:}} , \hfill \\ \end{gathered}$$

(20)

The same procedure can be performed to arrive at final governing equations of motions.

Analytical solution

The procure of numerical results derivation is developed in this section. The results are derived for simply-supported boundary conditions, where short-circuited electromagnetic boundary conditions are applied. For the mentioned boundary conditions, one can arrive at the following solution for circumferential displacement $\:u$, bending $\:{w}_{b}$, shear $\:{w}_{s}$ and stretch $\:\chi\:$ functions, maximum electric $\:\psi\:$ and magnetic $\:\varphi\:$ potentials with maximum unknown values $\:{U}_{m},{W}_{m}^{b},{W}_{m}^{s},{{\Psi\:}}_{m},{{\Phi\:}}_{m}$ as follows:

$$\:\left\{\begin{array}{c}u\\\:{w}_{b}\\\:{w}_{s}\\\:\chi\:\\\:\psi\:\\\:\varphi\:\end{array}\right\}=\sum\:_{m=1}^{\infty\:}{e}^{i\omega\:t}\left\{\begin{array}{c}{U}_{m}cos\frac{m\pi\:\theta\:}{{\Theta\:}}\\\:{W}_{m}^{b}sin\frac{m\pi\:\theta\:}{{\Theta\:}}\\\:{W}_{m}^{s}sin\frac{m\pi\:\theta\:}{{\Theta\:}}\\\:{\text{X}}_{m}sin\frac{m\pi\:\theta\:}{{\Theta\:}}\\\:{{\Psi\:}}_{m}sin\frac{m\pi\:\theta\:}{{\Theta\:}}\\\:{{\Phi\:}}_{m}sin\frac{m\pi\:\theta\:}{{\Theta\:}}\end{array}\right\}$$

(21)

where $\:{\Theta\:}$ is span angle. It is observed that the radial deflection components are zero at both ends, while the circumferential deflection is not vanished at same points. In addition, the electric and magnetic potential distributions are zero at both ends. Substitution of the solution into governing equations of motion yields the characteristic equation for finding natural frequencies as follows:

$$\:{\left[K\right]}_{6\times\:6}{\left\{X\right\}}_{6\times\:1}\:={\omega\:}^{2}{\left[M\right]}_{6\times\:6}{\left\{X\right\}}_{6\times\:1}$$

(22)

In which $\:{\left[\varvec{K}\right]}_{6\times\:6}$ and $\:{\left[\varvec{M}\right]}_{6\times\:6}$ are known as stiffness and mass matrices. These matrices are computed as follows:

$$\:\begin{array}{c}\begin{array}{c}{\mathcal{K}}_{11}={\daleth\:}_{8}{\beta\:}_{m}^{2}+{\daleth\:}_{36},{\mathcal{K}}_{12}=-{\daleth\:}_{9}{\beta\:}_{m}^{3}-\left({\daleth\:}_{37}+{\daleth\:}_{8}\right){\beta\:}_{m},{\mathcal{K}}_{13}=-{\daleth\:}_{10}{\beta\:}_{m}^{3}-\left({\daleth\:}_{8}+{\daleth\:}_{38}\right){\beta\:}_{m},\\\:{\mathcal{K}}_{14}=-\left({\daleth\:}_{11}+{\daleth\:}_{12}+{\daleth\:}_{38}\right){\beta\:}_{m},{\mathcal{K}}_{15}=+\left({\daleth\:}_{39}-{\daleth\:}_{13}\right){\beta\:}_{m},{\mathcal{K}}_{16}=+\left({\daleth\:}_{40}-{\daleth\:}_{14}\right){\beta\:}_{m}\\\:{\mathcal{M}}_{11}=-{{\Pi\:}}_{1},{\mathcal{M}}_{12}={{\Pi\:}}_{2}{\beta\:}_{m},{\mathcal{M}}_{13}=-{{\Pi\:}}_{3}{\beta\:}_{m},\\\:{\mathcal{K}}_{21}=-{\daleth\:}_{15}{\beta\:}_{m}^{3}-\:\left({\daleth\:}_{8}+{\daleth\:}_{41}\right){\beta\:}_{m},\\\:{\mathcal{K}}_{22}={\daleth\:}_{16}{\beta\:}_{m}^{4}+\left({\daleth\:}_{9}+{\daleth\:}_{42}+{\daleth\:}_{15}\right){\beta\:}_{m}^{2}+{\daleth\:}_{8}+{K}_{1}{\beta\:}_{m}^{2}+{K}_{2}{\beta\:}_{m}^{2}/{R}^{2}+\left({N}_{0}+{N}_{E}+{N}_{M}\right.+{N}_{T}){\beta\:}_{m}^{2}/R,\\\:{\mathcal{K}}_{23}={\daleth\:}_{17}{\beta\:}_{m}^{4}+\left({\daleth\:}_{10}+{\daleth\:}_{43}+{\daleth\:}_{15}\right){\beta\:}_{m}^{2}+{\daleth\:}_{8}+{K}_{1}{\beta\:}_{m}^{2}+{K}_{2}{\beta\:}_{m}^{2}/{R}^{2}+\left({N}_{0}+{N}_{E}+{N}_{M}\right.+{N}_{T}){\beta\:}_{m}^{2}/R\\\:,{\mathcal{K}}_{24}=\left({\daleth\:}_{18}+{\daleth\:}_{19}+{\daleth\:}_{43}\right){\beta\:}_{m}^{2}+\left({\daleth\:}_{11}+{\daleth\:}_{12}\right)+{K}_{1}{\beta\:}_{m}^{2}+{K}_{2}{\beta\:}_{m}^{2}/{R}^{2}+\left({N}_{0}+{N}_{E}+{N}_{M}\right.+{N}_{T}){\beta\:}_{m}^{2}/R\\\:,{\mathcal{K}}_{25}=-\left({\daleth\:}_{44}-{\daleth\:}_{20}\right){\beta\:}_{m}^{2}+{\daleth\:}_{13},{\mathcal{K}}_{26}=+\left({\daleth\:}_{45}-{\daleth\:}_{21}\right){\beta\:}_{m}^{2}+{\daleth\:}_{14}\varphi\:,\\\:{\mathcal{M}}_{21}=-{{\Pi\:}}_{2}{\beta\:}_{m},{\mathcal{M}}_{22}=-{{\Pi\:}}_{4}{\beta\:}_{m}^{2}-{{\Pi\:}}_{1},{\mathcal{M}}_{23}=-{{\Pi\:}}_{5}{\beta\:}_{m}^{2}-{{\Pi\:}}_{1}\:,{\mathcal{M}}_{24}=-{{\Pi\:}}_{7},\\\:{\mathcal{K}}_{31}=-{\daleth\:}_{22}{\beta\:}_{m}^{3}-\left({\daleth\:}_{8}+{\daleth\:}_{46}\right){\beta\:}_{m},\\\:{\mathcal{K}}_{32}={\daleth\:}_{23}{\beta\:}_{m}^{4}+\left({\daleth\:}_{9}+{\daleth\:}_{22}+{\daleth\:}_{47}\right){\beta\:}_{m}^{2}+{\daleth\:}_{8}+{K}_{1}{\beta\:}_{m}^{2}+{K}_{2}{\beta\:}_{m}^{2}/{R}^{2}+\left({N}_{0}+{N}_{E}+{N}_{M}\right.+{N}_{T}){\beta\:}_{m}^{2}/R,\end{array}\\\:\begin{array}{c}{\mathcal{K}}_{33}={\daleth\:}_{24}{\beta\:}_{m}^{4}+\left({\daleth\:}_{10}+{\daleth\:}_{22}+{\daleth\:}_{48}\right){\beta\:}_{m}^{2}+{\daleth\:}_{8}+{K}_{1}{\beta\:}_{m}^{2}+{K}_{2}{\beta\:}_{m}^{2}/{R}^{2}+\left({N}_{0}+{N}_{E}+{N}_{M}\right.+{N}_{T}){\beta\:}_{m}^{2}/R,\\\:{\mathcal{K}}_{34}=\left({\daleth\:}_{25}+{\daleth\:}_{26}-{\daleth\:}_{48}\right){\beta\:}_{m}^{2}+\left({\daleth\:}_{11}+{\daleth\:}_{12}\right)\chi\:+{K}_{1}{\beta\:}_{m}^{2}+{K}_{2}{\beta\:}_{m}^{2}/{R}^{2}+\left({N}_{0}+{N}_{E}+{N}_{M}\right.+{N}_{T}){\beta\:}_{m}^{2}/R,\\\:{\mathcal{K}}_{35}=-\left({\daleth\:}_{49}-{\daleth\:}_{27}\right){\beta\:}_{m}^{2}+{\daleth\:}_{13},{\mathcal{K}}_{36}=-\left({\daleth\:}_{50}-{\daleth\:}_{28}\right){\beta\:}_{m}^{2}+{\daleth\:}_{14}\\\:{\mathcal{M}}_{31}={{\Pi\:}}_{3}{\beta\:}_{m},{\mathcal{M}}_{32}=-{{\Pi\:}}_{5}{\beta\:}_{m}^{2}-{{\Pi\:}}_{1},{\mathcal{M}}_{33}=-{{\Pi\:}}_{6}{\beta\:}_{m}^{2}-{{\Pi\:}}_{1}\:,{\mathcal{M}}_{34}=-{{\Pi\:}}_{7}\ddot{\chi\:}\\\:{\mathcal{K}}_{41}=-\left({\daleth\:}_{1}+{\daleth\:}_{46}+{\daleth\:}_{29}\right){\beta\:}_{m}\\\:{\mathcal{K}}_{42}=\left({\daleth\:}_{2}+{\daleth\:}_{30}-{\daleth\:}_{47}\right){\beta\:}_{m}^{2}+\left({\daleth\:}_{1}+{\daleth\:}_{29}\right)+{K}_{1}{\beta\:}_{m}^{2}+{K}_{2}{\beta\:}_{m}^{2}/{R}^{2}+\left({N}_{0}+{N}_{E}+{N}_{M}\right.+{N}_{T}){\beta\:}_{m}^{2}/R,\\\:{\mathcal{K}}_{43}=\left({\daleth\:}_{48}+{\daleth\:}_{3}+{\daleth\:}_{31}\right){\beta\:}_{m}^{2}+\left({\daleth\:}_{1}+{\daleth\:}_{29}\right)+{K}_{1}{\beta\:}_{m}^{2}+{K}_{2}{\beta\:}_{m}^{2}/{R}^{2}+\left({N}_{0}+{N}_{E}+{N}_{M}\right.+{N}_{T}){\beta\:}_{m}^{2}/R,\\\:{\mathcal{K}}_{44}={\daleth\:}_{48}{\beta\:}_{m}^{2}+\left({\daleth\:}_{32}+{\daleth\:}_{33}+{\daleth\:}_{4}+{\daleth\:}_{5}\right)+{K}_{1}{\beta\:}_{m}^{2}+{K}_{2}{\beta\:}_{m}^{2}/{R}^{2}+\left({N}_{0}+{N}_{E}+{N}_{M}\right.+{N}_{T}){\beta\:}_{m}^{2}/R,\\\:{\mathcal{K}}_{45}=-{\daleth\:}_{49}{\beta\:}_{m}^{2}+\left({\daleth\:}_{6}+{\daleth\:}_{34}\right),{\mathcal{K}}_{46}=-{\daleth\:}_{50}{\beta\:}_{m}^{2}+\left({\daleth\:}_{35}+{\daleth\:}_{7}\right),\\\:{\mathcal{M}}_{41}=-{{\Pi\:}}_{7},{\mathcal{M}}_{42}=-{{\Pi\:}}_{7},{\mathcal{M}}_{43}=-{{\Pi\:}}_{7}\\\:{\mathcal{K}}_{51}=-\left({\daleth\:}_{56}-{\daleth\:}_{51}\right){\beta\:}_{m},{\mathcal{K}}_{52}=-\left({\daleth\:}_{52}-{\daleth\:}_{57}\right){\beta\:}_{m}^{2}+{\daleth\:}_{56},{\mathcal{K}}_{53}=-\left({\daleth\:}_{53}-{\daleth\:}_{58}\right){\beta\:}_{m}^{2}+{\daleth\:}_{56},\\\:{\mathcal{K}}_{54}=-{\daleth\:}_{53}{\beta\:}_{m}^{2}+\left({\daleth\:}_{59}+{\daleth\:}_{60}\right),{\mathcal{K}}_{55}=-{\daleth\:}_{54}{\beta\:}_{m}^{2}-{\daleth\:}_{61},{\mathcal{K}}_{56}=-{\daleth\:}_{55}{\beta\:}_{m}^{2}-{\daleth\:}_{62},\\\:{\mathcal{K}}_{61}=-\left({\daleth\:}_{68}-{\daleth\:}_{63}\right){\beta\:}_{m},{\mathcal{K}}_{62}=-\left({\daleth\:}_{64}-{\daleth\:}_{69}\right){\beta\:}_{m}^{2}+{\daleth\:}_{68},{\mathcal{K}}_{63}=-\left({\daleth\:}_{65}-{\daleth\:}_{70}\right){\beta\:}_{m}^{2}+{\daleth\:}_{68}\\\:{\mathcal{K}}_{64}=-{\daleth\:}_{65}{\beta\:}_{m}^{2}+\left({\daleth\:}_{71}+{\daleth\:}_{72}\right),{\mathcal{K}}_{65}=-{\daleth\:}_{66}{\beta\:}_{m}^{2}-{\daleth\:}_{73},{\mathcal{K}}_{66}=-{\daleth\:}_{67}{\beta\:}_{m}^{2}-{\daleth\:}_{74},\end{array}\end{array}$$

(23)

In which $\:{\beta\:}_{m}=m\pi\:/{\Theta\:}$. The natural frequencies are obtained using determinant of the characteristics equation as follows:

$$\:Det\left\{{\left[K\right]}_{6\times\:6}-\:{\omega\:}^{2}{\left[M\right]}_{6\times\:6}\right\}=0$$

(24)

Parametric results and discussion

The parametric numerical results are presented in this section. The results are presented in tabular form to investigate impact of multi-field loading characteristics, Gori content and foldability parameters, geometric parameters and foundation’s characteristics on the natural frequency responses of the sandwich curved beam.

In order to verify formulation procedure and numerical results, Table 1 is presented. Listed in Table 1 is comparison of the numerical results with available results of the literature in terms of various mode number.

Table 1 Comparison of the natural frequency responses with available results in the literature.

In continuation, the complete numerical results are presented with changes of significant parameters with accounting the input parameters $\begin{gathered} \:E_{{Cu}} = 65.79GPa,E_{{Gr}} = 929.57GPa, \hfill \\ \vartheta \:_{{Cu}} = 0.387,\vartheta \:_{{Gr}} = 0.22,\:\alpha \:_{{Cu}} = 16.51 \times \:10^{{ - 6}} \frac{1}{K},\vartheta \:_{{Gr}} \hfill \\ = - 3.98 \times \:10^{{ - 6}} \frac{1}{K},\:l_{{Gr}} = 83.76 \times \:10^{{ - 10}} m,t_{{Gr}} \hfill \\ = 3.4 \times \:10^{{ - 10}} m \hfill \\ \end{gathered}$.

The input geometric parameters are assumed as:

$$R = 1m,\Theta = 1Rad,h_{e} = 0.01m,h_{p} = 0.001m,$$

Provided in Table 2 is an investigation on the effect of volume fraction of Gori $\:\%{V}_{GO}$ as well as thermal loads on the variation of the frequencies of the sandwich curved beam. The results show an increase in natural frequencies of the sandwich curved beam due to an enhancement in Gori content. Furthermore, a decrease in frequencies is deduced because of an enhancement in thermal loads. The latest phenomenon is occurred because of a decrease in stiffness.

Table 2 Effect of volume fraction of Gori $\:\mathbf{\%}{\mathbf{V}}_{\mathbf{G}\mathbf{O}}$ on the changes of frequencies of the sandwich curved beam with changes of thermal loads.

Table 3 list an interesting investigation in order to study the impact of foldability parameter of Gori $\:\%{H}_{GO}$ and thermal enhancement on the variation of the frequencies of the sandwich curved beam. It is observed a decrease in natural frequencies of sandwich curved beam with an enhancement in foldability parameter of Gori $\:\%{H}_{GO}$ and thermal load. One can conclude that an increase in foldability parameter of Gori $\:\%{H}_{GO}$ yields a softer folded structure with lower frequencies.

An enhancement in the foldability parameter leads to concurrent decrease in structural stiffness (Young’s modulus) and density of the constituent materials. An analysis is needed to investigate on the impact of folding parameter on the variation in the frequencies. The present numerical results indicate that an enhancement in the folding parameter leads to mode decrease of density that stiffness that leads to a decrease in frequencies.

Table 3 Effect of foldability parameter of Gori $\:\varvec{\%}{\varvec{H}}_{\varvec{G}\varvec{O}}$ on the changes of frequencies of the sandwich curved beam with changes of thermal loads.

In continuation, the characteristics of piezoelectric/piezomagnetic layers are investigated on the natural frequency responses. Table 4 highlights impact of initial voltage $\:{{\Psi\:}}_{0}$ as well as thermal load on the natural frequency variation of the sandwich curved beam. The results show an enhancement in natural frequencies with an increase in initial voltage $\:{{\Psi\:}}_{0}$.

Table 4 Effect of initial voltage $\:{\varvec{\Psi\:}}_{0}$ of the integrated layers on the changes of frequencies of the sandwich curved beam with changes of thermal loads.

Table 5 highlights impact of initial amperage $\:{{\Phi\:}}_{0}$ as well as thermal load on the natural frequency variation of the sandwich curved beam. An enhancement in frequencies is observed with an enhancement in initial amperage $\:{{\Phi\:}}_{0}$. Furthermore, a decrease in frequencies is observed with an enhancement in thermal loads of the sandwich curved beam. One can conclude that the stiffness of the curved beam is decreased with an enhancement in the thermal load.

Table 5 Effect of initial amperage $\:{\varvec{\Phi\:}}_{0}$ of the integrated layers on the changes of frequencies of the sandwich curved beam with changes of thermal loads.

Table 6 provides an investigation on the effect of mode shape number on the variation infrequencies of sandwich curved beam. One can arrive an enhancement in natural frequencies of sandwich curved beam with an increase in mode shape number. As an interesting output, an enhancement in natural frequencies is observed with an increase in thermal loads for higher order mode shapes.

Table 6 Effect of mode shape number $\:\varvec{m}$ of the integrated layers on the changes of frequencies of the sandwich curved beam with changes of thermal loads.

Tables 7 and 8 are provided to investigate impact of geometric parameters of sandwich curved beam on the frequencies distribution with changes of thermal loads. Table 7 plots variation in natural frequencies with changes of opening angle $\:\theta\:=L/R$. A decrease in natural frequencies of sandwich curved beam is observed with an increase in opening angle $\:\theta\:=L/R$ because of more flexibility.

Table 7 Effect of opening angle $\:\varvec{\theta\:}=\varvec{L}/\varvec{R}$ of the integrated layers on the changes of frequencies of the sandwich curved beam with changes of thermal loads.

Table 8 highlights impact of piezoelectric to Gori thickness ratio $\:{h}_{p}/{h}_{e}$ on the changes of natural frequencies of the sandwich curved beam with changes of thermal loads. The results show an enhancement in natural frequencies of sandwich curved beam with an increase in piezoelectric to Gori thickness ratio $\:{h}_{p}/{h}_{e}$ for this constraint that total thickness should be constant.

Table 8 Effect of piezoelectric to Gori thickness ratio $\:{\varvec{h}}_{\varvec{p}}/{\varvec{h}}_{\varvec{e}}$ on the changes of frequencies of the sandwich curved beam with changes of thermal loads.

Tables 9 and 10 investigates impact of parameters of foundation $\:{K}_{1},{K}_{2}$ on the variation of the frequencies of the sandwich curved beam. The results show an enhancement in natural frequencies with an enhancement in two parameters $\:{K}_{1},{K}_{2}$.

Table 9 Effect of parameter $\:{\varvec{K}}_{1}$ on the changes of frequencies of the sandwich curved beam with changes of thermal loads.

Table 10 Effect of parameter $\:{\varvec{K}}_{2}$ on the changes of frequencies of the sandwich curved beam with changes of thermal loads.

In order to arrive at a visual understanding and presentation of a physical interpretation on the results, some graphical results are presented in Figure form. Shown in Figs. 2 and 3 are variation in natural frequencies (Hz) with changes of thermal loads with changes of volume fraction and folding parameter, respectively.

Fig. 2

The effcet of thermal load and volume fraction of Gori $\:\text{\%}{\text{V}}_{\text{G}\text{O}}$on the variation in the natural frequency.

Fig. 3

The effcet of thermal load and foldability parameter of Gori $\:\%{H}_{GO}$ on the variation in the natural frequency.

Shown in Figs. 4 and 5 are variation in the frequencies with changes of parameters of Pasternak’s foundation.

Fig. 4

The effcet of spring parameter $\:{\text{K}}_{1}$ of foundation and thermal loads on the variation in the natural frequency.

Fig. 5

The effcet of shear parameter $\:{\text{K}}_{2}$ of foundation and thermal loads on the variation in the natural frequency.

In order to investigate the impact of multi-field loading on the natural frequency responses, Figs. 6 and 7 represent variation in the natural frequencies with changes of $\:{{\Psi\:}}_{0},{{\Phi\:}}_{0}$ in terms of thermal loads. An enhancement in the natural frequencies is observed with an enhancement in the multi field loading parameters.

Fig. 6

The effcet of intial electric potential $\:{{\Psi\:}}_{0}$ and thermal loads on the variation in the natural frequency.

Fig. 7

The effcet of initial magnetic potential $\:{{\Phi\:}}_{0}$ and thermal loads on the variation in the natural frequency.

To account the impact of thickness stretchable model as defined in Eq. 7, some comparative results are presented based on stretchable and not stretchable models. Listed in Tables 11, 12 are variation in the natural frequencies with changes of thermal loads and volume fraction based on stretchable and not stretchable models. The results show that the natural frequencies based on not stretchable model are more than stretchable model results. A stiffer model through the not stretchable model is obtained than the stretchable one. Actually based on the model without stretching, the structure’ deformation is restricted and therefore a stiffer model is represented. The results are obtained for the thick beam $\:{h}_{e}/\left(R{\Theta\:}\right)=0.1$.

Table 11 Variation in the natural frequencies with changes of thermal loads T and volume fraction $\:\%{V}_{GO}$ based on the stretchable and not stretchable models.

Table 12 Variation in the natural frequencies with changes of thermal loads and foldability parameter $\:\%{H}_{GO}$ based on the stretchable and not stretchable models.

Conclusions

Authors provided a detailed procedure for derivation of the frequencies of the sandwich curved beam composed of Gori reinforced core integrated with piezoelectric/piezomagnetic layers subjected to thermal, electrical and magnetic loading. The governing equations of motion have been derived using Hamilton’s principle with accounting the kinetic and strain energies as well as external work. The constitutive relations have been derived for the reinforced core based on the experimental effective material properties available in literature and the multi-field relations for piezoelectric/piezomagnetic layers. The structure was subjected to thermal, electrical and magnetic loads and its effect has been investigated on the vibrational characteristics of the sandwich curved beam. The numerical results show that characteristics of Gori such as content amount and foldability parameter as well as multi-field loading have significant effect on the natural frequency responses. One can arrive at following main conclusions as follows:

The natural frequency was evaluated with changes of foldability parameter of the Gori as a folded reinforcement, where a decrease in natural frequency was detected with an enhancement in the foldability parameter. It is accordance with experimental results that an enhancement in foldability parameter leads to a decrease in structural stiffness of the composite structure. An enhancement in the foldability parameter leads to concurrent decrease in structural stiffness (Young’s modulus) and density of the constituent materials. An analysis is needed to investigate on the impact of folding parameter on the variation in the natural frequencies. The present numerical results indicate that an enhancement in the folding parameter leads to mode decrease of density that stiffness that leads to a decrease in natural frequencies.

Content amount of Gori in the copper matrix has an enhancement effect on the stiffness property of the composite structure that lead to an enhancement in natural frequencies of the structures.

Effect of multi-field loading on the vibrational characteristics of sandwich curved beam indicates an enhancement in frequencies with an increase in initial voltage and amperage as well as a decrease in thermal loads because of a decrease in structural stiffness.

An investigation on the effect of piezoelectric/piezomagnetic thickness to Gori thickness ratio on the natural frequency variation reflects an enhancement because of an increase in structural stiffness.

Accounting effect of two parameters of Pasternak’s foundation on the natural frequency responses show an enhancement on the responses because of an enhancement in foundation stiffness.