A comparative study of shear crack growth mechanisms in concrete through acoustic emission analysis

Abstract

The shear failure of concrete is a sudden brittle failure, which is difficult to be forewarned. To investigate the shear crack mechanisms in concrete, this study first systematic compared acoustic emission (AE) behavior during direct shear tests, compression shear tests (Z-shaped specimens), and three point bending shear tests. AE parameters (amplitude, cumulative count and energy), average frequency (AF)-rise time/amplitude (RA) analysis, K-means clustering, and b-value analysis were integrated to classify cracks and characterize damage progression. The correlation between the shear crack propagation mechanism of concrete and AE parameters was revealed. The AE activity during concrete shear failure was successfully characterized, providing valuable insights into the damage development and evolution processes. The research findings establish a quantitative framework for using AE technology to detect shear cracks and monitor real-time damage evolution in concrete structures.

Introduction

The mechanical properties and damage evolution of quasi-brittle materials, such as concrete under stress, have received widespread attention. In particular, crack propagation is a crucial factor in studying the failure of concrete structures. Acoustic emission (AE) refers to the phenomenon in which strain energy is released in the form of elastic waves during material deformation under external forces, from crack initiation and propagation to rupture. By analysing AE signals, the internal damage evolution of concrete can be successfully obtained^1,2.

Currently, the AE characteristics of the failure process in concrete materials have been established. It is widely accepted that during the initial loading stage, microcracks gradually form due to stress, but AE activity remains relatively low. As microcracks propagate and the material approaches failure, the AE activity intensifies, releasing more energy, which is influenced by factors such as material strength and aggregate composition^3,4,5. For instance, Ji et al.³ analyzed the AE signals during the compressive failure of high-strength concrete and observed that larger fractures are often accompanied by high-amplitude, low-frequency signals. When the frequencies within the dominant frequency band disperse, concrete rupture typically follows. Moreover, they found that higher concrete strength correlates with greater AE energy release during large fractures. Geng et al.⁴ recorded changes in AE energy and counts during the compressive process of concrete, determined the three-dimensional evolution of AE source locations during dynamic damage and failure process of concrete, and conducted that concrete damage variables follow a Weibull distribution. Carnì et al.⁵ identified the AE signals of critical damage through uniaxial compressive tests on concrete, applied b-value analysis to these signals, and established a relationship between AE signals and the stress level of the specimen. AE parameter analysis is commonly used to study the AE characteristics of damaged concrete materials. However, different AE parameters often exhibit distinct behaviors under varying damage and stress mechanisms. To assess the crack state of concrete structures composed of composite materials using AE technology, relying solely on single-parameter analysis is traditionally insufficient. Instead, a comparative analysis of multiple parameters is necessary to improve the accuracy of AE technology in evaluating damage to engineering structures. This represents an inevitable development trend in AE parameter analysis methods.

AE technology has been extensively developed and utilized to determine concrete fracture types. Since 2003, the Japan Concrete Institute has correlated the parameters of average frequency (AF) and rise time/amplitude (RA) to evaluate the crack failure mechanisms of concrete materials⁶. Previous studies suggest that shear cracks are generally associated with higher RA values and lower average frequencies, while tensile cracks are accompanied by lower RA values and higher average frequencies⁷. This has led to the development of a crack identification and classification method based on RA-AF parameters. The core principle of this method involves obtaining AE signals with known crack patterns by loading specimens with predetermined failure mechanisms and then comparing the actual crack patterns with the results of RA-AF analysis. For example, Ohno et al.⁷ conducted four-point bending tests on concrete beams and obtained actual crack patterns based on the failure mechanism, which aligned with the results of RA-AF analysis. They found that when the ratio of RA value (ms/V) to AF (kHz) is set to 1 ~ 200, the ratio of shear cracks identified by simplified Green’s functions for moment tensor analysis (SIGMA) closely matches that identified by parameter analysis. Prem et al.⁸ performed four-point bending tests on beams with three different reinforcement ratios and derived a separation line with a slope of 0.004 from their RA-AF (µs/V-kHz) analysis. Aggelis et al.⁹ also validated the accuracy of RA-AF (µs/V-kHz) analysis on four-point bending concrete beams but obtained a separation line with a slope of 0.03 and an intercept of 200. Das et al.¹⁰ conducted four-point bending tests on steel fibre-reinforced concrete beams and obtained four different separation lines due to variations in the concrete mix ratios.

In summary, the principle of the RA-AF analysis method for crack classification is sound, but the key separation line distinguishing the two crack patterns cannot be determined using a unified approach. This limitation restricts its application in practical engineering and research on new structures with unknown failure mechanisms. Given that each AE signal contains multiple features, determining the separation line in the RA-AF scatter plot can be transformed as a clustering problem for unclassified data¹¹. Researchers have also found that clustering learning algorithms can address the challenges in crack pattern recognition faced by traditional RA-AF methods. For instance, Ma et al.¹² effectively revealed the evolution of crack types in basalt fibre-reinforced polymer (BFRP)-repaired pre-damaged cylinders through axial compression tests using both traditional RA-AF analysis and Gaussian mixture model (GMM) analysis. Their work validated the effectiveness of RA-AF analysis via GMM and provided more accurate crack type classification than conventional RA-AF analysis of diagonal method. Chen et al.¹³ adopted GMM method to process the data from corroded reinforced concrete columns for crack type identification. Wang et al.¹⁴ also used clustering learning algorithms related to GMM to classify RA-AF data from the direct shear AE monitoring test of granite. Prem et al.¹⁵ studied the AE characteristics of bending beams made of ordinary and fibre-reinforced ultra-high-performance concrete (UHPC) and employed the K-means method to identify crack types under different loading rates. Radhika and Kishen² applying K-means clustering to AE data collected from twelve beam specimens under three-point bending, four distinct damage mechanisms in plain concrete were identified. These studies demonstrate that traditional clustering analysis algorithms can effectively classify concrete cracks. Therefore, this paper adopts an RA-AF analysis method based on the K-means algorithm for identifying concrete crack patterns.

Moreover, in general engineering structures, concrete materials are primarily designed for compressive state, and extensive research has been conducted on the compressive performance of concrete using AE technology^3,4,5. The study of the AE characteristics of the bending performance of concrete has also been the focus of researchers^7,8,9,10,15. However, the shear performance of concrete is another critical factor affecting the state of concrete structures, yet few studies have investigated the AE characteristics of concrete under shear damage. Typically, the shear performance of concrete specimens is obtained through shear tests, which commonly use Z-shaped specimens^16,17,18. To explore the time-varying damage and failure mechanism of concrete materials under shear, in this work, Z-shaped specimens are selected to study the AE characteristics of concrete under shear conditions.

Therefore, direct shear tests and compression shear tests through Z-shaped specimens are designed to comprehensively understand the AE mechanism of concrete shear cracks. Bending-shear cracks are also common in practical engineering. To better investigate the AE characteristics of shear cracks, bending shear test through three-point loaded beams are added to facilitate a more comprehensive comparison and analysis of the AE features under different stress conditions. This is the first time to systematic comparison of AE characteristics across direct shear, compression shear, and bending shear tests. Through laboratory experiments, the AE characteristics under shear are explored to provide a foundation for applying AE technology in real bridge inspections and refining tensile-shear crack early warning methods for in-service bridges.

The structure of this study is as follows: Fist, the AE parameter analysis method is introduced, and multiple AE characteristic parameters, including the distribution of cumulative energy, amplitude, and cumulative count with loading time, as well as amplitude-count, RA-AF and b-value analyses, are used to evaluate the AE activity during the shear loading process of concrete. Second, a detailed description of three experiments is provided, including direct shear, compression shear and bending shear test, along with observations of experimental phenomena. Furthermore, characteristic signals of crack development in test specimens under shear are extracted, and the crack types are classified automatically using the K-means method. Finally, to describe the shear damage evolution in concrete, instantaneous b-values during the loading process are calculated based on monitoring data. The aim of this study is to provide a reference for identifying shear cracks in load tests of existing concrete structures using AE technology for detection and characterization.

AE parameter analysis methods

At present, the AE parameter analysis method is widely used for damage monitoring and research on concrete structures. Typical AE signal characteristics, including amplitude, count, duration time, rise time, threshold, etc., are shown in Fig. 1.

Fig. 1

Characteristic diagram of a typical AE signal.

The parametric analysis method is frequently employed in AE monitoring of concrete materials and structural damage. Existing research has demonstrated that AE counts and energy parameters are closely related to damage in concrete materials⁴. Maximum amplitudes have been used to estimate the degree of damage to the concrete structure¹⁹. A log-linear relationship between AE parameters (such as hits, amplitude, count and energy) and fatigue crack growth in concrete was identified through three-point bending tests²⁰. Additionally, a quantitative relationship between AE events and stress levels has been established, enabling the quantitative assessment of damage in concrete beams²¹. The abrupt points on the cumulative energy curve correspond to the stage characteristics of the stress process in concrete specimens, and the energy distribution shifts from low frequency to high frequency as the load increases²². However, while the energy parameter analysis method can assess changes in AE source activity, it cannot promptly detect the emergence of defects such as microcracks or the frequency characteristics of material failure²³. Furthermore, single-parameter analysis often fails to fully capture the characteristics of damage, necessitating multiparameter analysis for a comprehensive characterization. Therefore, this paper combines various AE parameter analysis methods, including cumulative energy, amplitude, count, and cumulative count, to conduct a thorough investigation of concrete shear cracks.

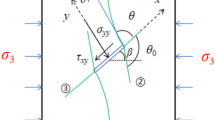
RA-AF analysis is another effective method for evaluating the crack failure mechanism of concrete materials⁶. Research indicates that when shear cracks occur, AE signals generally exhibit higher RA values and lower average frequencies, whereas tensile cracks are associated with lower RA values and higher average frequencies⁷. As shown in Fig. 2, data points above the dividing line represent tensile cracks, whereas those below the line correspond to shear cracks.

Fig. 2

JCMS-IIIB 5706 method crack classification⁶.

The b-value analysis method was initially developed to evaluate the distribution relationship between the frequency and amplitude of seismic signals²⁴. Previous studies have demonstrated that this method can be applied to the analysis of AE signals²⁵. In the early stage of loading, as microcracks develop, the b-value gradually increases. However, when microcracks propagate into larger cracks, the b-value decreases. The b-value is calculated using the following formula from a related investigation²⁶:

$$b = \frac{{20\log _{{10}} {\text{e}}}}{{\overline{a} - a_{0} }}$$

(1)

where $\overline{a}$ is the arithmetic mean amplitude, and a₀ is the threshold amplitude.

Test overview

To investigate the AE characteristics of shear cracks, this study employs Z-shaped specimens and prestressed concrete (PC) box girder specimens at the specimen and structural component levels, respectively, to study the dynamic development of concrete shear cracks under direct shear, compression shear, and bending shear conditions. This subsection provides a detailed introduction to the experimental setup. It is worth mentioning that the same set of AE system was used for data acquisition of all specimens during the experiment, and the data processing method was the same.

Materials

The concrete mix proportions, given as weight ratios, are as follows: admixtures: water: cement : fly ash : mineral powder : sand : stone = 0.0352 : 0.3916 : 1 : 0.1190 : 0.2910 : 1.8333 : 2.7937. The compressive strengths of the three cubic specimens were measured as 51.5 MPa, 49.8 MPa and 54.1 MPa, with an average value of 51.8 MPa.

Direct shear and compression shear tests

Drawing on the design of commonly used Z-shaped specimens^16,17,18, steel plates were incorporated to maximize the principal tensile stress on the shear plane, ensuring that cracking and failure occur first on the shear plane²⁶. These steel plates were bonded to the concrete using a structural adhesive. The Z-shaped specimen has a thickness of 100 mm and overall dimensions of 360 mm × 440 mm × 100 mm. The two notches are 180 mm long and 20 mm wide. The dimensions of steel plates A, B, and C are 180 mm × 3 mm × 100 mm, 270 mm × 3 mm × 100 mm, and 360 mm × 3 mm × 100 mm, respectively. The specific dimensions are illustrated in Fig. 3(f).

Fig. 3

Test process: (a) direct shear specimen; (b) compression shear specimen; c direct shear specimen failure; (d) compression shear specimen failure; (e) host machine of AE acquisition system; (f) Specimen dimensions (unit: mm).

Since cracks primarily develop on the shear plane of the Z-shaped specimen, this test focuses on monitoring AE signals from this plane. A special coupling agent is applied near the shear plane on both the front and back sides of the specimen, and sensors are attached using adhesive tape. The specific sensor locations are shown in Fig. 3(f), and the sensor type used is R6I. For compression shear specimens, due to the constraints imposed by the steel rod used to fix the horizontal jack, the sensor positions are slightly shifted upwards but remain near the shear plane.

The tests are conducted using a servo-hydraulic testing machine (PMW800-2000) in force control mode, starting starts at 0 kN and increases in increments of 5 kN until the specimen fails. Due to the limitation of test equipment and conditions, the loading method is manually controlled, so the influence of loading rate is not considered. Simultaneously, AE monitoring is performed using a Micro-II Samos digital AE instrument from the Physical Acoustics Corporation (PAC), with AEwin^™ software employed for data analysis and processing. AE signals are recorded when the amplitude exceeds threshold level of 40 dB to minimize the influence of noise^4,26. The host machine of AE acquisition system is shown in Fig. 3(e). To ensure test repeatability, more than three specimens are tested under each loading conditions. For direct shear specimens, only a vertical force is applied. For compression shear specimens, a horizontal force is applied first, and after it stabilizes, a vertical force is applied. The test process is shown in Fig. 3.

For compression-shear specimens, in order to adopt a compression-shear stress ratio that conforms to actual engineering conditions, based on the time-history analysis results of principal tensile stress at the main beams of three different medium- and small-span conventional continuous girder bridges presented in Reference²⁷, it was found that the peak value of the ratio between normal stress and shear stress at the location of maximum principal tensile stress was approximately 0.3. Therefore, at the peak of vertical loading, the average normal stress on the shear plane is taken as 0.3 times the average shear stress. That is, when the static load strength tested reaches the failure point of the specimen, the horizontal force value is exactly 0.3 times the vertical force value. After multiple iterative trials, the horizontal force was ultimately determined to be 31 kN. In the compression shear test, horizontal pressure is applied and controlled using a jack and a pressure sensor, A horizontal force of 31 kN is applied, followed by a vertical force after the load stabilizes. Both the direct shear and compression shear failure processes involve the initiation and propagation of microcracks. The appearance of macroscopic cracks indicates specimen failure, suggesting that the shear failure of the Z-shaped concrete specimen is brittle. For the compression shear specimen, due to the restraining effect of the horizontal force, the specimen retains some load-bearing capacity after cracking. However, since the shear plane has already cracked, the test is terminated. To ensure data reliability, each set of experiments includes at least three specimens.

Bending shear tests

To study bending-induced shear cracks, a test beam subjected to three-point loading was selected for experimental test. The prestressed concrete (PC) box girder has a clear span of 2.5 m, a height of 0.5 m, a top plate width of 1.22 m, and a bottom plate width of 0.7 m. The concrete material used is the same as that for the Z-shaped specimen. After curing for 28 days, the prestressed tendons were tensioned using the post-tensioning method and subsequently grouted. Grouting was completed once the material met the design requirements. The dimensions and reinforcement configuration of the box girder are shown in Fig. 4. The ordinary reinforcement consists of R235 and HRB400 steel bars. The longitudinal prestressed tendon are 15.2 mm (1 × 7) steel strands with a cross-sectional area of 280 mm², positioned 50 mm from the bottom of the box girder. These tendons were tensioned and anchored in one operation, with an effective prestressing stress of 1116 MPa. The vertical prestressed tendons are 20 mm diameter precision-rolled threaded bars with a standard tensile strength of 540 MPa. The top and bottom plate reinforcement meshes, as well as the transverse diaphragm reinforcement mesh, use 6 mm diameter R235 steel bars. The top plate is reinforced with 14 HRB400 steel bars of 8 mm diameter, the web longitudinal reinforcement consists of 16 HRB400 steel bars of 6 mm diameter, and the bottom plate is reinforced with 10 HRB400 steel bars of 12 mm diameter. The structural reinforcement employs 6 mm diameter R345 steel bars.

Fig. 4

Box girder dimensions and reinforcement configuration (unit: mm): (a) side elevation; (b) cross-section view.

During the test, an SW-LW-201 surface crack width tester was used for measurement. The loading was applied using the MTS hydraulic servo system in a transverse mid-span loading configuration, strictly adhering to the “Standard for Test Methods of Concrete Structures” (GB/T50152-2012)²⁸. Before formal loading, a preload of 50 kN is applied to minimize the gaps between the components and ensure the proper functioning of all instruments, thereby reducing data errors. The test employs a graded loading method, starting with increments of 50 kN, with loading rate of 4 Hz. Initial loading continued until cracking occurred in the normal section, with a loading force of approximately 250 kN (0.22P_u, where P_u is the ultimate failure load). Loading was then increased until cracking occurred in the oblique section near the support, with a loading force of approximately 360 kN (0.32P_u). Subsequently, loads was increased in increments of 100 kN until failure, which occurred at a load of 1140 kN. After each loading increment, the specimen was allowed to rest for 10 min. AE data were recorded continuously during the loading process, and crack development in the web was documented after each load increment. A total of 8 sensors were installed for this test, and their layout is shown in Fig. 4. In order to better observe the distribution of web cracks, the sensors were not directly placed on the web, but it was found during the test that all the sensors could still receive AE signals well, especially the 4^# and 5^# sensors near the mid-span area. Therefore, this sensor arrangement form can provide good data assurance. The AE data acquisition system was the same as that used for the Z-shaped specimens. Photographs of the test loading diagram is shown in Fig. 5, and the final crack distribution in the web of the PC box girder is illustrated in Fig. 6.

Fig. 5

Test loading diagram.

Fig. 6

Final crack distribution diagram of the test beam.

Test results and discussion

Experimental phenomena and single-parameter analysis

The AE parameters of shear cracks in different specimens under various experimental conditions were analyzed, focusing on the characteristics of cumulative energy, cumulative count and amplitude with time.

Direct shear and compression shear tests

During the test, under vertical loading, two main cracks appeared in the shear plane region of the direct shear specimen. In contrast, an almost vertical crack formed in the shear plane during the final failure of the compression shear specimen due to the clamping effect of the horizontal load. Both specimens exhibited a brittle failure mode, as shown in Fig. 3(c) and (d).

The curves of the cumulative energy, cumulative count and load over time, as well as the amplitude distribution, are shown in Fig. 7. Analysis of the test results reveals that during the initial loading stage, the cumulative energy remains relatively low and stable, with no visible cracks observed on the specimen surface. However, when the load reaches 0.8 to 0.9 times the failure load, the cumulative energy increases sharply. As the load continues to rise, the specimen undergoes brittle failure, accompanied by a loud “bang”, the detachment of mortar and fine particles, and cracks penetrating he shear plane. This indicates that while the AE energy analysis method can asses changes in AE source activity, it cannot promptly detect the emergence of defects such as microcracks.

Fig. 7

Distributions of AE parameter and load over time of Z-shaped specimen.

For the direct shear specimens, as Fig. 7(a) shows, throughout the entire process, the cumulative energy and cumulative count change almost synchronously over time. At the beginning of loading, no AE events or high-amplitude signals were detected, and the cumulative energy was less than 300 mV·ms. Once the stress level exceeded 15% (approximately 150 s, with a load of approximately 9.1 kN), AE counts began to accumulate, but the increase in cumulative energy was very slow, with amplitudes less than 60 dB. The few events recorded during the initial loading stage can be attributed to microcracks and defects formed during the specimen manufacturing process. When the stress level exceeded 30% (400 s, with a load of approximately 17.6 kN), the cumulative energy showed a slight increase, accompanied by a relatively large number of signals with a denser amplitude distribution, indicating the emergence of initial cracks on the concrete shear plane. As the load continued to increase (with the stress level remaining below 80%), the cumulative energy increased slowly. During this period, the amplitude distribution over time was relatively sparse, reflecting stable crack propagation and gradual damage accumulation. In the final 200 s of loading, as the load level increased from 80% to failure (from 42.6 kN to 53.0 kN), the cumulative energy underwent a sudden change, with amplitudes exceeding 80 dB. The amplitude distribution became more concentrated, indicating highly active AE signals during the final failure stage. Simultaneously, the specimen failed due to crack penetration, as shown in Fig. 4. The failure exhibited clear characteristics of brittle failure.

For the compression shear specimens, as the loading process progressed, concrete damage accumulated continuously, and the cumulative energy and the cumulative count increased over time. During the vertical force loading process, as shown in Fig. 7(b), the variation in cumulative energy and cumulative count over time was similar to that of the direct shear specimens. In the initial loading stage, AE signals were not active, with amplitudes below 80 dB. However, after the load level exceeded 80% (150 s before failure, with a load of approximately 87.7 kN), AE signals with amplitudes exceeding 80 dB appeared. The AE activity increased sharply, and the cumulative energy and count rose rapidly. Compared to the direct shear specimens, the clamping effect of the vertical force enhanced the overall AE signals, resulting in greater cumulative energy and count, indicating more severe concrete damage and degradation.

In summary, the shear damage process of concrete can be characterized by the variation in cumulative energy, amplitude, and cumulative count over time. Crack propagation is accompanied by energy release, and the amplitude reflects the intensity of concrete damage. The AE signals in the direct shear test exhibit a two-stage pattern. Initial stage (0 ~ 80% relative stress level): AE signals are inactive, and the cumulative energy and count increase slowly; Final stage (> 80% relative stress level): cumulative energy and count increase sharply, accompanied by the expansion of internal cracks to an unstable state and the appearance of two distinct cracks on the shear plane. This differs from the typical three-stage failure process of concrete structures²⁹, as stress concentration on the shear plane at lower levels does not stimulate sufficient AE activity. Once the stress exceeds the concrete’s threshold, brittle failure occurs with the sudden appearance of two main cracks. The compressed shear specimen exhibits a similar pattern during vertical force loading, albeit with less pronounced brittle failure characteristics due to clamping effect of the horizontal force.

Bending shear test

During the static loading process, the first flexural crack appeared at the mid-span position when the load reached 250 kN. This crack had a length of 5 ~ 15 cm and a width of less than 0.04 mm. Overall, all cracks extended from the mid-span towards both ends of the support, exhibiting a roughly symmetrical distribution pattern. The final crack distribution of the test beam is shown in Fig. 6. Since the bending shear test data for the PC box girder were collected in stages, with a total of 14 loading stages, the AE instrument recorded the data at each loading increment. Although the test data were not continuous in time, this approach allowed for a better comparison of AE characteristics at different loading stages. For ease of analysis, data from sensor 4^#, which received the most signals, were selected for detailed examination. The state of the test beam under different loading levels is summarized in Table 1, where P_u represents the failure load, and the count data was collected from 4^# sensor.

Table 1 Test beam state under different loading levels.

The cumulative energy, cumulative count, and amplitude distribution for each loading segment are shown in Fig. 8. Since the data for each loading segment were recorded anew, the cumulative energy and cumulative count for each stage start from zero. As the loading segment progresses, both the cumulative energy and cumulative count increase during the loading process. The distribution of the cumulative count for each loading segment is generally consistent, showing a linear distribution characteristic. As the loading level increases, the data points become denser, and amplitude signals exceeding 75 dB are continuously collected. This behavior significantly differs from that observed in the direct shear and compression shear specimens, primarily due to the larger size and more complex reinforcement of the bending shear specimens, which generate more damage source signals.

Fig. 8

AE parameter distribution of the bending shear test results under different loading processes.

Because the data were collected in stages, it is not possible to obtain the overall loading distribution pattern as in the case of Z-shaped specimens. Therefore, further analysis is required using other parameter characteristics.

Count-amplitude correlation analysis

Change statistics of the count and its proportion with the amplitude are shown in Fig. 9. The count ratio is the proportion of counts within different amplitude ranges to the total counts.

Fig. 9

Change statistics of the count and its proportion with the amplitude.

For the compression shear and direct shear specimen, as shown in Fig. 9(a), the variation law of count ratio with amplitude under two different stress states is basically the same. The AE signals are predominantly low- to medium-amplitude, with recorded signals concentrated between 40 ~ 75 dB, accounting for over 90% of the total counts. For compression shear specimen under horizontal loading, the counts under each load are relatively small, approximately one order of magnitude lower than those under vertical force loading. Therefore, AE data for this part of the loading process are not discussed. Notably, high-amplitude AE signals above 80 dB represent approximately 4% of the total counts. Combined with the observations in Fig. 7, these signals occur when data point increase dramatically before failure, which may be attributed to the increased AE signals from slip friction between the steel plate and the concrete during the final failure stage of vertical force loading.

The distribution of counts with amplitude during the loading process of the direct shear specimen is similar to that of the compression shear specimen during vertical force loading. During vertical force loading, the amplitude range with the highest count proportion is 50 ~ 55 dB, accounting for more than 20% of the total counts. However, the total counts for the direct shear specimen is lower than that during the vertical force loading of the compression shear specimen. The difference is primarily due to the application of a horizontal force, which exacerbates the damage and deterioration of the concrete.

For the bending shear specimen, the count ratio curves for different amplitude ranges at various loading levels are generally similar, with the count ratio decreasing as the amplitude increases, as shown in Fig. 9(b). Compared with the Z-shaped specimen, the PC box girder exhibits the highest count proportion in the low- to medium-amplitude range across all loading levels. Specifically, the count proportion exceeds 90% in the amplitude range of 40 ~ 70 dB. The amplitude range with the highest count ratio is 40 ~ 50 dB. This behavior can be attributed to the larger size of the PC box girder and the addition of steel reinforcement and prestressing, which introduce more complex damage mechanisms. As a result, there is an increased proportion of medium- to high-amplitude signals. However, concrete cracking remains the primary source of AE, as evidenced by the count proportions of 40 ~ 45 dB and 45 ~ 50 dB both exceeding 20%. Overall, owing to its size and structural complexity, the AE signal data of the PC box girder, including counts and total energy, far exceed those of the Z-shaped specimen.

RA-AF analysis

The RA-AF analysis method is widely used to classify cracks into shear cracks and tensile cracks. When shear cracks occur, AE signals typically exhibit higher RA values and lower average frequencies, whereas tensile cracks are often accompanied by lower RA values and higher average frequencies³⁰. However, the diagonal method used for crack classification has certain limitations, as different RA and AF ratio settings can influence the results. These setting are often determined empirically, and there is currently no unified method for determining the specific boundary between tensile and shear cracks. To further investigate the impact of RA-AF parameter correlation analysis on concrete crack classification, clustering algorithms such as the K-means method are introduced to perform clustering analysis on the experimental data.

K-means method

The K-means algorithm is a widely used unsupervised pattern recognition algorithm for solving clustering problems³¹. The clustering criterion for this method is based on minimizing the sum of the squares of the squares of the distances from each data point in a subset to the centre of the subset to which it is assigned. This minimization criterion and the detailed calculation procedure can be seen in Ref.³².

Although the K-means algorithm is computationally efficient, its result is highly sensitive to the initial assumption of the cluster centers. To mitigate this limitation, the algorithm was repeated at least 12 times with different initial guess values selected randomly. The final result with the minimum error criterion was accepted. It is worth mentioning that the RA-AF data in this study is only two-dimensional, and there are only two types of data for clustering analysis. By running the algorithm multiple times through iteration, the clustering results obtained are reliable³².

In this study, the clustering analysis method divides dataset into two subsets, corresponding to tensile cracks and shear cracks. The results of the K-means analysis of the AE dataset recorded during the entire loading process for the direct shear and compression shear specimen are shown in Fig. 10. The results of the RA-AF analysis of the bending shear test based on the K-means method are presented in Fig. 12. Based on the crack classification results for each loading segment, a percentage stacked bar chart is constructed, as shown in Fig. 13.

Fig. 10

Results of the RA-AF analysis via the K-means method.

According to the results of the RA-AF analysis using the K-means method, as shown in Figs. 10 and 11, two distinct clustering results can be observed. The total number of units with shear cracks is significantly greater than that of units with tensile cracks for each sample. The proportions of shear cracks in the direct shear and compression shear specimen are 84.8% and 92.5%, respectively. This indicates that the cracks generated in each specimen are primarily shear cracks, which align with the stress patterns of the specimens. The K-means method systematically divides the dataset into two groups without requiring manually specifying of a partition line. Since the the minimization principle is based on the sum of the squares of the distances to the cluster center, the magnitude of the two eigenvalues (AF and RA values) play a crucial role. Determining the ranges of the AF and RA values for the shear clustering center can provide early warnings for detecting and characterizing shear cracks in existing concrete bridge structures using AE technology.

Fig. 11

Results of the RA-AF analysis of the bending shear test results using the K-means method.

For the bending shear test, as shown in Figs. 11 and 12, the proportion of shear cracks in each loading segment exceeds 68%, indicating that the dominant failure mode throughout the loading process is shear cracking. The proportion of shear cracks exceeds 68% and tends to increase overall. Further analysis reveals that the proportion of shear cracks increases slowly during the initial loading stage. As loading progressed, at the 0.36P_u stage, the proportion of shear fracture events sharply increases to 83%. This is likely due to the appearance of inclined cracks in the specimen during this stage. Notably, when the first bending crack appears, tensile fracture events are not dominant, which may be related to the force application method and the large size of the specimen.

Fig. 12

Crack classification results with RA-AF analysis of the bending shear test results.

b-value analysis

The b-value analysis method, also referred to as AE amplitude distribution analysis, is defined as the negative gradient of the log-linear plot between the frequency and magnitude of an earthquake^33,34. To describe the shear damage evolution in concrete, the instantaneous b-value during the loading process is calculated based on the monitoring data, and the b-value at each point determined for every 100 signals.

Direct shear and compression shear tests

Figure 13 shows the loading history curves and b-values of the Z-shaped specimens under different stress states.

Fig. 13

Variation in b-value versus loading history of Z-shaped specimen: (a) direct shear specimen; (b) compression-shear specimen.

For the direct shear specimen, as Fig. 13(a) shown, during the first 1300 s, the b-value fluctuates around 1.6. At approximately 1400 s (crack point), the b-value occurs sharply decline in a short period of time, which is different from the previous oscillation change, indicating the emergence of cracks in the specimen. In the subsequent 100 s, the AE signals intensify significantly, and the b-value data points increase. High-amplitude signals exceeding 80 dB appear, and the specimen subsequently fails, demonstrating clear characteristics of brittle failure. Notably, there is a short period (less than 20 s) between crack emergence and specimen failure, during which the b-value fluctuates strongly around 1.4. This represents the stable crack propagation stage. Due to its short duration, this period can be classified as part of the failure stage. Thus, the direct shear specimen exhibits a two-stage stress process, consistent with the earlier analysis conclusion of single-parameter analysis above. The brittle failure characteristics of the direct shear specimens are more obvious.

For compression shear specimens under vertical force loading process, as illustrated in Fig. 13(b), the b-value gradually increases with load during the initial stage of loading. This indicates that microcracks have developed, but their overall development process is relatively slow. Moreover, the AE signal have high b-value and low amplitude, generally below 70 dB. No visible cracks are observed during this stage, and the signals are primarily caused by the compaction of defects such as voids and fissures in the material. No signal with amplitudes exceeding 75 dB are collected during the low-stress loading process. After 575 s (crack point), the b-value experiences its first continuous decline, indicating the formation of microcracks within the concrete material. The b-value then increases sharply and then experiences another continuous decline. Subsequently, the b-value data points become dense, and the values stabilize around 1.4, indicating a relatively stable stage of damage propagation. Finally, in the b-value decreases rapidly and accompanied by a significant increase in high-amplitude signals exceeding 80 dB, suggesting that microcracks within the specimen have developed into macroscopic cracks, ultimately leading to shear failure of the specimen.

Overall, the process of loading vertical loads on the compression shear specimen until failure exhibits three distinct stages of failure characteristics. In the initial stage, the b-value is high, and the amplitude is low. This stage corresponds to the compaction of internal voids and fissures within the material. Subsequently, a continuous decline in the b-value occurs, indicating the emergence of internal cracks in the material. This is followed by a stage of stable damage propagation, where the b-value data points become dense, and the values stabilize, fluctuating around 1.4. This stage represents a period of relatively stable crack propagation. In the final failure stage, the b-value decreases sharply and continuously, accompanied by a significant increase in high-amplitude signals exceeding 80 dB, ultimately leading to failure of the specimen.

Bending shear test

The analysis results of the b-value for the bending shear specimens under different loading levels are shown in Fig. 14. Notably, the AE data were collected in stages, but the data were continuous across each loading segment.

Fig. 14

Results of the b-value analysis of the bending shear test.

Before 0.18P_u, there were few data points for the b-value, indicating a slightly fluctuating trend. At 0.25P_u, the b-value curve reached a minimum of 0.37, corresponding to the emergence of macroscopic cracks in the test beam. This aligns with the experimental observations in Table 1, where the first bending crack was identified at this stage. Similarly, at 0.31P_u, the b-value also reached a minimum of 0.37. Although no new cracks were observed at this stage, the first diagonal crack appeared at the next stage (0.36P_u). This suggests that b-value analysis can provide early warning of the formation of oblique shear cracks. Similar to the shear failure of the Z-shaped specimen, when the bending shear test specimen experiences initial cracking in both the normal and oblique sections, the b-value decreases sharply. This continuous decrease in the b-value often indicates the emergence of new rupture points, with the minimum value typically below 0.40. After the 0.36P_u stage, the number of data points in the b-value curve increases significantly, indicating an oscillating distribution. Moreover, as the load level increases, the oscillation amplitude of the b-value becomes more intense, indicating that after the emergence of cracks, with increasing load level, crack development becomes denser, and many microcracks coalesce to form macroscopic cracks that then continue to propagate stably. At the stages of 0.42P_u, 0.57P_u, and 0.73P_u, the b-value exhibited a significant continuous decrease, with minimum values of 0.71, 0.48, and 0.41, respectively, all above 0.40. Experimental observations revealed that during these loading stages, the macroscopic cracks in the web of the test beam continued to propagate. In the final failure stage, the b-value also decreased sharply, reaching the minimum value of 0.45. This suggests that a continuous oscillating decrease in the b-value, with the minimum value remaining above 0.40, is associated with the stable and continuous propagation of macroscopic cracks. These findings demonstrate that the b-value analysis method can identify the bending-shear cracking points during the failure process of PC box beams. However, during the loading process of the test beam, the phenomenon of a continuous decrease in the b-value occurred multiple times, which differs from direct shear and compression shear tests. This difference may be attributed to the segment data acquisition method used in bending shear test. Therefore, it is necessary to combine other parameter analysis methods to provide early warning of structural failure. It is evident that combining multi-parameter analysis can effectively characterize the damage process of concrete, whereas single-parameter analysis often excels only in specific aspects. Utilizing artificial intelligence methods to develop an AE analysis factor that integrates multiple parameters and quantifies concrete damage will be a key future direction for AE parameter analysis methods.

Conclusion

The AE parameters of shear crack were first systematically analyzed in detail through direct shear, compression shear and bending shear tests. The AE parameters include cumulative energy, cumulative count, amplitude, average frequency (AF) and rise time/amplitude (RA) and b-value. The major conclusions of this experimental study are summarized as follows:

• 1. AE technology can effectively study the shear damage process in concrete through parametric analysis. The variation in the cumulative energy, amplitude, and cumulative count over time can characterize the shear damage process of concrete. Crack propagation is accompanied by energy release, and the amplitude and counts can be used to assess the intensity of concrete damage.

• 2. During the shear failure process, most AE signals in the microcrack initiation stage have amplitudes below 80 dB. In contrast, the formation and stable propagation of cracks, as well as the emergence of macroscopic large cracks, are often accompanied by signals with amplitudes above 80 dB. This characteristic is independent of the stress form. Compared with direct shear specimens, the compression shear specimens under the processes of vertical force loading and failure exhibit a gradual increase in high-amplitude signals exceeding 80 dB. A larger number of AE signals were received due to the constraint of the horizontal force, which increases the bearing capacity and the degree of concrete damage and deterioration, resulting in more active AE signals. The more complex the force acting on the concrete, the greater the degree of damage and degradation, leading to enhanced AE signal, particularly in terms of energy magnitude and count. Therefore, the activity of these two parameters can determine the complexity of structural forces to a certain extent.

• 3. The RA-AF analysis combined with the K-means method can automatically identify concrete crack as shear or tensile. Due to the influence of the loading mode, the final failure mode of all the specimens was shear failure, consistent with the crack classification results.

• 4. The b-value analysis method is useful for exploring shear crack formation and propagation in concrete. A continuously sharp decrease in the b-value is often related to initial occurrence of crack or the rapture of large cracks. For the compression shear specimen, the b-value oscillates around 1.4 during the stable propagation stage of concrete shear cracks. Similarly, for the bending shear specimen, after the emergence of bending cracks, the b-value also oscillates around 1.4 in each loading segment. For the bending shear specimens, the b-values calculated from the segmented AE data are beneficial for identifying bending or shear cracking points, but they may interfere with the early warning of specimen failure. Additionally, when the b-value sharply continuous decreases, it often indicates the initial formation of cracks or the acceleration of their propagation.

Since this study is mainly based on laboratory tests, the influence of environmental factors such as temperature, humidity, bridge traffic vibration, and wind environment on acoustic emission parameters will be considered in the later stage. Combined with actual engineering data, the method of early warning for bending and shear cracks in bridges during service based on AE technology will be verified and further improved based on artificial intelligence methods.