Introduction

The development of dense observation networks has enabled us to discover and investigate various seismic phenomena along plate interfaces, including slow earthquakes, which have longer relaxation times than regular earthquakes1,2,3,4,5. Because slow earthquakes may be a trigger of devastating earthquakes5,6,7 as well as a mechanism of the release of strain energy along megathrusts8, understanding how the two types of fault slip are related presents a major scientific and disaster-mitigation challenge4,5. The spatial dependency of such seismic activity, which is exhibited both at the plate interface depth and along the strike of the subduction interface4,7,9,10, suggests that elucidation of the physical properties around plate interfaces is important for improving understanding of fault rupture processes. One major factor causing varying fault behavior may be a heterogeneous pore-water distribution11,12,13,14, because the presence of pore water reduces rock strength15. Subducted seamounts and ridges can also play an important role because they affect the water supply to the plate interface as well as its shape10,16,17.

Electrical resistivity measurement is an essential tool for assessing the fluid distribution at plate interfaces because saline pore fluids significantly affect the bulk rock resistivity17,18,19,20,21,22,23. For example, along the Hikurangi subduction margin in New Zealand, regions of low electrical resistivity, which imply the presence of fluids released from the subducting slab or subducted sediments, are associated with tremor and the occurrence of slow slip events (SSEs)20,21. Additionally, the heterogeneous resistivity distribution along the plate interface is related to inter-plate coupling and the areal strain rate21,22,23. However, the existing resistivity models are mostly based on onshore observations and do not cover the marine region where many plate interface phenomena occur. One study in a marine area across the Hikurangi margin has demonstrated the effect of fluid-filled porous regions in seamounts on seismic activities by two-dimensional resistivity modeling17, but the deep structure and along-strike heterogeneity have not been characterized.

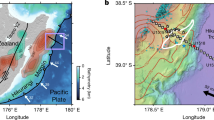
The Hyuga-nada region, which is situated at the western end of the Nankai Trough where the Philippine Sea Plate is subducting under the Eurasian Plate at a convergence rate of 63–68 mm/year toward N55W24, is well suited for studying the role of structural heterogeneity in fault ruptures. Various types of slow earthquakes and regular earthquakes have been reported in this region (Fig. 1). Regular earthquakes occurring here include frequent M7 class earthquakes, such as the 1968 Hyuga-nada earthquake (M7.5)25 and the 2024 Hyuga-nada earthquake (M7.1), which prompted Japanese government to issue a massive earthquake warning. Slow earthquakes, including shallow tremor26 and SSEs1,27, have been detected around the regular earthquake (Fig. 1). In addition, the Kyushu–Palau Ridge (KPR), a group of seamounts on the Philippine Sea Plate, is subducting beneath the southwestern part of Hyuga-nada28. The slow earthquakes occur near to the subducting seamounts. Areas of low seismic velocity found in the subducted KPR and the overriding plate above the KPR may imply the existence of fluid-filled porous regions that affect the shallow tremors occurring nearby10,29. However, because the electrical resistivity distribution in the Hyuga-nada area has not been investigated, direct evidence of the pore-fluid distribution around the plate interface and the subducting KPR has been lacking. The major reason that the resistivity distribution has not been elucidated is the complex oceanic topography, which severely distorts magnetotelluric (MT) impedances and renders conventional 2D analyses impractical30,31,32,33. For this reason, there have been no previous studies on three-dimensional resistivity structures offshore regions in subduction zone. Recently, however, the analysis of marine MT data using a 3D inversion code based on the finite difference method34,35 has enabled us to evaluate the subsurface resistivity structure while taking account of the seafloor topography. Therefore, in this study, to elucidated the fluid distribution in the Hyuga-nada area, we conducted marine MT investigations at 15 sites with ocean bottom electro-magnetometers (OBEMs) (Fig. 1). We carefully analyzed MT impedances in the observed marine MT data and obtained the optimum model of electrical resistivity distribution by utilizing 3D forward and inversion procedures. We then assessed the reliability and resolution of optimum model based on sensitivitys test and a hypothetical inversion test (see Methods).

Fig. 1
figure 1

Study location and bathymetry of the Hyuga-nada region. (a) Regional bathymetry. The orange star denotes the Kakioka Geomagnetic Observatory Station of the Japan Meteorological Agency. (b) Observation array and fault rupture areas. Red circles denote marine ocean bottom electro-magnetometer observation sites. Sky-blue dotted lines are the depth contours of the plate boundary interface66. The turquoise bold dotted line denotes where the Kyushu–Palau Ridge is subducting29. Granite areas known from terrestrial geological surveys are shown in magenta67. Solid blue lines indicate the slip areas of the 1946 Nankai68 and the 1968 Hyuga-nada25 earthquakes. Blue stars denote regular earthquakes (> M7.0) determined by the Japan Meteorological Agency. The orange contours show the total cumulative slip of long-term SSEs (contour interval 20 cm) from 1996 to 201727. The yellow crosses denote the shallow tremors generated from May to July 201326. The purple solid arrow indicates a convergence direction of the Philippine Sea Plate toward the Amurian Plate.

Full size image

Result

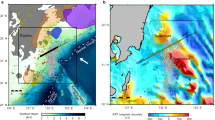
The optimum model of 3D resistivity distribution reveals a conductive region (C1) and resistive region (R1) along the plate interface (Fig. 2). The C1 is located mainly within the subducting plate, where subducting seamounts are estimated to be situated28. We validated the C1 anomalies based on sensitivity tests which create replaced models in which the anomaly was filled with the resistivity value of the surrounding area (see Methods). The sensitivity test results indicated that the resistivity in C1 anomaly was less than 20 Ωm, with a deep limit extending beyond 70 km (Fig. 3a,b). On the other hand, heterogeneities within C1 are difficult to detected due to the resolution limitation of natural source marine MT data36. The R1 is mainly within the overriding Eurasian Plate at depths between 5 and 40 km (Fig. 2). Sensitivity test results indicated a resistivity greater than 430 Ωm in R1 (Fig. 3c). The hypothetical inversion test successfully reconstructs both the resistive and conductive anomalies in the expected locations (Supplementary Figs. S1, S2) (see Methods). However, the model shows poor recovery in the deep part of the conductive anomaly and obscured boundaries of both the anomalies due to the smoothness constraint and low sensitivity at greater depths, as demonstrated in the sensitivity test for the depth of C1 (Fig. 3b).

Fig. 2
figure 2

3D Resistivity model. Red diamonds indicate OBEM observation sites, and red and blue dashed lines enclose the areas used for the sensitivity tests of the C1 (19.03 Ωm) and R1 (430.6 Ωm) anomalies, respectively. (a) Resistivity section along the plate interface. (b) Vertical cross sections along lines A–A’, B–B’, C–C’, and D–D’ in (a). On each section, the black dotted line indicates the plate boundary interface66. Blue and pink solid lines denote the slip areas of regular earthquakes25,68 and long-term SSEs27, respectively. Blue stars represent regular earthquakes (M > 7.0) as determined by the Japan Meteorological Agency. Note that the vertical positions of the regular earthquakes in (b) are assumed to be on the plate interface due to the low accuracy of vertical location determination.

Full size image
Fig. 3
figure 3

RMS misfits of the sensitivity test models of the C1 and R1 anomalies. The solid and dashed purple lines indicate the RMS misfit of the optimum model and the 95% confidence limit (one-sided F-test), respectively.

Full size image

Discussion

Hydrous subducting seamounts

We interpreted the main cause of C1 to be a high amount of saline fluid in interconnected pores that significantly reduced the bulk resistivity of the rock, as reported in other subduction zones17,21. In this area, the seismic tomographic surveys also show low seismic velocity anomalies, which are interpreted as pore fluids37,38. Around the plate interface in C1, a serpentinized area is implied by a high Poisson’s ratio, detected by a seismic tomographic survey38. Serpentine is formed by the hydration of mantle material; thus, it requires a supply of aqueous fluid from a deeper area in the subducting slab. Its presence, therefore, supports the presence of aqueous fluid in the C1 area. Fluid-filled serpentine areas, in which bulk resistivity is reduced, are a known cause of conductive anomalies39,40.

Other factors that can decrease resistivity include the presence of conductive ores or partial melting. However, conductive ores (such as clay minerals, graphite, sulfides, and magnetite) are unlikely to be stable in the lower oceanic crust and mantle at this depth41. Moreover, the estimated temperature in the C1 area, between 200 and 600 ℃42, does not exceed the solidus temperature of igneous rocks such as granite, basalt43, gabbro44, and peridotite45, even under water-saturated conditions.

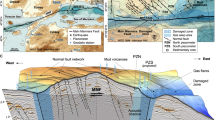
Seismic investigations have captured the shape of the subducting KPR, which includes several seamounts, within the Philippine Sea Plate on the southwest side of Hyuga-nada28,29. Since this low-velocity region is approximately located within the fluid-rich conductive region (C1) (Fig. 4b)29, the subducting KPR is inferred to contain large amounts of pore fluid. The presence of hydrous subducting seamount could be a general feature, as a similar interpretation is made based on low Vs and high Poisson’s ratio anomalies around the subducting Joban seamount chain in the NE Japan arc46. In addition, the precise seismic velocity image near line C–C’ implies the migration of aqueous fluid into the overriding plate from the subducting KPR10. The hydrous C1 area above the plate interface supports the existence of migrated fluid in the overriding plate (Fig. 4).

Fig. 4
figure 4

(a) Resistivity section along the plate interface. (b) Resistivity section along a surface 10.5 km below the plate interface. Note that this surface corresponds to the region where KPR range was estimated based on low-velocity anomaly29. (c) Vertical section along line B–B’. (d) Interpretation of the section shown in (c). Red diamonds are OBEM observation sites. Other symbols are same as Fig. 2.

Full size image

A marine MT study of the Philippine Sea Plate has shown the presence of a conductive region at 40–80 km depth that is consistent with the position of the incoming KPR36; thus, the KPR may capture fluid before it is subducted beneath the Eurasian plate. Along the Hikurangi subduction margin, large amounts of aqueous fluid are trapped within seamounts on the incoming plate17. Therefore, seamounts can incorporate fluids such as seawater before subduction more easily than ordinary oceanic crust. Because the many seamounts, including subducting seamounts, observed along the KPR collectively have a large volume, a huge amount of aqueous fluid is likely transported into the Earth’s interior in the western Hyuga-nada area. On the other hand, the low Vp anomaly at depths greater than 80 km around the subducting KPR is interpreted as hot mantle material rising through a slab window in the subducting Philippine Sea plate47. Therefore, the deep region of C1 may be attributed to a high-temperature anomaly.

Dry plate interface

The main factors causing resistive anomalies (R1) at this depth are a lack of fluid, and a lack of fluid interconnections. On islands near the study area, the presence of exposed Tertiary granites, which are generally dry and show high resistivity48 (Fig. 1), suggests that such plutonic rocks in the overriding plate are responsible for a lack of pore fluid, or a lack of interconnections around R1 (Fig. 4). The results of seismic studies49,50 showing a high P-wave velocity zone in the overriding plate are consistent with the presence of dense plutonic rocks with low fluid content in R1, because the P-wave velocity in granite is generally larger than that in accretionary sedimentary rocks. Therefore, the most feasible interpretation of R1 is a lack of pore fluid or its interconnections due to the distribution of plutonic rock, although direct evidence is still needed to confirm the presence of plutonic rock in the R1 region.

Relationship between resistivity and earthquake distributions

Areas of long-term SSEs27 are located around the upper part of the C1 conductive anomaly, which is interpreted as having a high amount of fluid derived from the subducting seamounts (see previous sub-section). Trapped pore fluid, which increases pore fluid pressure, has recently been discussed as a potential trigger to promote slow earthquakes7,13. In the south of C–C’ profile, fluid migrated from the subducting KPR to the overriding plate is thought to enhance low-frequency tremors10. Off the Kii Peninsula in the Nankai Trough, structural change due to fluid migration are considered to precede very low-frequency earthquakes51. Although studies on the relationship between pore fluid and slow slip events are limited, fluid pressure fluctuations within the subducting oceanic crust are suggested to influence the timing of SSEs in the Hikurangi subduction zone14. Therefore, pore fluids derived from subducting seamounts likely enhance slow earthquakes activities, including SSEs, in the Hyuga-nada area. On the other hand, SSE has not been detected in the area of lowest resistivity within C1. Additionally, C1 has not been validated under the Bungo Channel, where the largest slip is estimated in the SSE region, although the model shows a slightly low resistivity anomaly (Fig. 2d).

Conversely, the R1 resistive region around the plate boundary interface, which indicates an area depleted of pore fluids, corresponds to the slip area of the largest Hyuga-nada earthquake in 1968 (M7.5)25 (Fig. 4). Dry conditions along the plate interface can cause stick–slip behavior15 and may have contributed to the fast fault slip during the 1968 event. The epicenters (rupture initiate points) of other large earthquakes (M7.1–7.2) are located in the transition zone between “dry” and “wet” areas (Fig. 4). The slip area of the 1968 earthquake is also in contact with the transition zone. For the M7-class earthquake regions in the intra-plate earthquake, epicenters area also located around the edge of the fluid rich area estimated based on resistivity, b-value and high Poisson’s ratio52,53,54.They may imply an effect of fluids initiating fast fault rupture.

Based on the above discussion, this study demonstrates a correlation between heterogeneous pore-fluid distribution and fault slip behavior in the Hyuga-nada region: SSEs occur in wet areas, whereas fast earthquakes originate in the transition zone to dry areas. A similar contrast in fluid distribution between slow and fast earthquakes has also been found in the Hikurangi margin21, suggesting that this may be a general phenomenon. Because slow earthquakes have been suggested to contribute to strain transfer to adjacent fast earthquake zones4,5, further investigations for detailed resistivity distribution and monitoring of resistivity changes are crucial. However, the hypothetical inversion test shows that the resolution of resistivity distribution is limited. To address these challenges, improving data quality is essential, particularly by increasing the density of observation points. In particular, for C1, which lies outside the observation network, integrating marine and land-based data is crucial. Additionally, it is important to incorporate seismologically and geologically verified plate boundaries into the resistivity inversion, allowing for resistivity discontinuities. Furthermore, establishing a probabilistic approach to quantify the reliability of model parameters55 is necessary. These methodologies are not yet well established in three-dimensional resistivity structure analysis, making future advancements in these areas crucial challenges.

Methods

Marine magnetotelluric investigation

Magnetotelluric (MT) sounding, a passive exploration technique that employs natural electromagnetic variations, is used to identify deep resistivity heterogeneity. In this study, electromagnetic data were acquired at 15 observation sites on the seabed in the Hyuga-nada area (Fig. 1, Supplementary Table S1). The observations were conducted as a joint research project of Nagoya University, Kobe University, Kyoto University, University of Hyogo, and the Japan Agency for Marine-Earth Science and Technology (JAMSTEC). We deployed and recovered ocean bottom electro-magnetometers (OBEMs) during several research cruises conducted between March 2017 and September 2020 by training ship Fukae-maru (Kobe University) and research vessel Kairei (JAMSTEC). The OBEMs were deployed by free fall from the ship onto the seabed and were recovered via a self-pop-up system, in which the anchors are released by an acoustic signal from the ship. Observations were conducted by each OBEM for 5–12 months (Supplementary Table S1). For most of the observation period, measurements were made with a 60 s sampling interval to save power consumptions; for each OBEM, time series of electromagnetic field variations were obtained using a 0.125 s sampling interval over an approximately three-week period to estimate short-period MT impedances (less than several hundreds of seconds). Three orthogonal components of the magnetic field were measured with fluxgate magnetometers, two horizontal components of the electric field were measured with Ag–AgCl electrodes, and two components of tilt were measured for posture correction. Newly developed OBEMs equipped with an absolute pressure gauge were deployed at sites EMP1, EMP2, and NU9. At the other sites, conventional OBEM systems were deployed56.

Estimation of magnetotelluric impedance

Magnetotelluric impedance (Z), which reflects the resistivity structure of the Earth, is obtained from the equation E = ZH, where E and H are the horizontal components of the electric and magnetic fields, respectively. At each site, Z was estimated from the observed electromagnetic field data as follows. First, the observed tilt data, the magnetic field data, and the IGRF-13 declination value57 were used to apply posture corrections. The Bound Influence Remote Reference Processing code (BIRRP)58 was then used to estimate MT impedances from the posture-corrected time series. To reduce the influence of local noise, magnetic field data at Kakioka Magnetic Observatory was used as a remote reference site59,60. Short-period (less than several hundreds of seconds) and long-period (more than several hundreds of seconds) MT impedances were estimated using the 1 s and 60 s sampled data, respectively. MT responses at NU2 and NU8, where magnetic field data were not available, were calculated using the electric field data at the site and the magnetic field data for NU3 and NU12, respectively.

High-quality MT impedances were estimated in a period range between 11 and 30,720 s (Fig. 5). The apparent resistivity and impedance phase obtained from the estimated short-period MT impedances indicate that the subsurface resistivity structure can be regarded as a 1D structure, because off-diagonal components of the impedance tensor were approximately equal and about one digit larger than diagonal components at most sites. The relatively low apparent resistivity in the short period range (less than 100 s) at most observation sites indicates the presence of a homogeneous conductive layer beneath the seafloor. The responses may exhibit distortions such as cusps of apparent resistivity, which are thought to be due to the effects of coastline and ocean topography30,31 (e.g., around 300–3000 s at NU8, Fig. 5).

Fig. 5
figure 5

Apparent resistivity and impedance phases of the observed and computed response functions for the optimum model.

Full size image

Construction of the initial resistivity model for inversion

Because derivation of the resistivity distribution from MT impedances is a nonlinear problem, resistivity models obtained by an inversion procedure depend on the initial model. This dependency is pronounced in the case of marine MT analyses, especially in coastal regions, because the observed response functions are strongly influenced by the bathymetry and the shape of the coastline30. Hence, we first used 3D forward modeling procedures to construct an appropriate initial model close to the actual structure. For the 3D forward and subsequent inversion analyses, we used a WSINV3DMT-based61 3D modeling code developed for marine MT impedance modeling that utilizes a staggered grid finite-difference method35 to incorporate submarine topography. The mesh used for this analysis consisted of 79 × 79 × 61 (+ 9 air layers) blocks; it extended about 2200 km vertically and 4200 km × 4200 km horizontally (Supplementary Fig. S3). The horizontal mesh size was 5–8 km within the observation area and larger outside the observation area. The vertical mesh size was 100 m immediately beneath the sea surface and gradually increased with depth. The maximum size ratio of adjacent meshes was kept to 1.32 and 1.67 in the horizontal and vertical directions, respectively.

For the forward modeling, we constructed resistivity models consisting of seawater (0.3 Ωm), a conductive sediment layer beneath the seabed with uniform resistivity and uniform thickness, and an underlying background area with uniform resistivity. The bathymetry incorporated into these models was based on the ETOPO1 1-arc-minute global relief model62 (Supplementary Fig. S3). The resistivity of the conductive layer was set to 1 Ωm by referring to the results of excavations in the Nankai trough off the Kii Peninsula63. The resistivity value of each block on the seafloor boundary was calculated by taking the volumetric average of the conductivity35 based on the bathymetry. Because the conductive layer thickness and background resistivity were unknown, we varied these parameters between 0.1–8 km and 1–500 Ωm, respectively, and then determined the optimum model for each observation site by a grid search. For this modeling, we used 20 periods between 11 and 7,680 s to compute the impedance tensor. As an indicator of agreement between the data and the model response, we adopted the model with the minimum root mean square misfit (RMSm), which we calculated as follows:

$$RMSm\left( {\mathbf{m}} \right) = { }\sqrt {\frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \frac{{\left( {d_{i} - f_{i} \left( {\mathbf{m}} \right)} \right)^{2} }}{{\sigma_{i}^{2} }}} ,$$

where \({d}_{i}\) and \({f}_{i}\left(\mathbf{m}\right)\) are impedance components, observed and computed using model m, respectively; \({\sigma }_{i}\) is the estimated error of the observed impedance components; and N is the number of data (total of the real and imaginary parts of all impedance components at all sites). In this forward modeling and in the subsequent inversion procedures, the error floor was set to 3% of the sum of the squared impedance64. The RMSm distribution obtained by grid search indicates that the best-fit model differed among the observation sites (Supplementary Figs. S4, S5). First, the thickness of the 1 Ωm conductive subseafloor layer was greater in the south than in the north throughout the survey area (Supplementary Fig. S5a). This result implies that sediments just below the seabed were thicker on the south side. Second, the background resistivity with the lowest RMSm varied among the sites, and no spatial trend was apparent (Supplementary Fig. S5b). Third, the RMSm values of the models were small on the east side, but were large in the middle area (Supplementary Fig. S5c).

Using the forward modeling results, we constructed four three-layer models by using different background resistivities (50, 100, 200, and 500 Ωm) but otherwise the same parameter values (Supplementary Fig. S6). All of the models had a sub-seabed conductive layer with a thickness of 0.7 km in the north (around NU1, NU2, NU5, and EM4), 1 km in the middle north (NU3, NU7, NU8, NU11, NU12, and EM3), 2 km in the middle south (around EMP1, EMP2, and NU6), and 3 km in the south (around NU9 and NU10). The thickness of the conductive layer beneath shallow-water areas (water depth < 0.5 km) was set to 0.5 km because the sediment layer beneath the seafloor thins as it approaches land. Here, and also in the inversion analysis, we used impedances of 32–30,720 s. In total, N = 2178 data points were used for the calculations. MT responses computed from the forward models roughly matched the observed responses at the east and north stations; RMSm of the model with the minimum RMSm was 6.52 (background resistivity, 50 Ωm, Supplementary Fig. S7). However, improved models based on inversion analysis results are essential for explaining the observed responses, especially with regard to the following two points. First, the diagonal components of the forward model responses are about one order smaller than those of the observation data. Second, the model responses at around 100–1,000 s at sites NU1, EM3, EM4, and NU5 do not explain the cusps of apparent resistivity in the observed responses.

3D Inversion Analysis

Three-dimensional inversion analyses were performed using the four three-layer models described in the previous section as initial models. The inversion algorithm35 estimates the optimum resistivity model by minimizing the following constrained objective function61:

$$W_{\lambda } \left( {\mathbf{m}} \right) = \left( {{\mathbf{m}} - {\mathbf{m}}_{p} } \right)^{{\text{T}}} {\mathbf{C}}_{m}^{ - 1} \left( {{\mathbf{m}} - {\mathbf{m}}_{p} } \right) + \lambda^{ - 1} \left\{ {\left( {{\mathbf{d}} - f\left[ {\mathbf{m}} \right]} \right)^{{\text{T}}} {\mathbf{C}}_{d}^{ - 1} \left( {{\mathbf{d}} - f\left[ {\mathbf{m}} \right]} \right)} \right\},$$

where mp is the prior model vectors; d is a data parameter vector consisting of the observed MT impedances; and Cm is the model covariance matrix, which characterizes the expected magnitude and smoothness of the resistivity variations relative to mp. Cd is a data covariance matrix representing the observation errors, and the superscript T represents the transpose. The term λ is a hyperparameter that balances the data misfit and model misfit terms, including model roughness; in the inversion procedure, it is determined by Occam’s inversion approach65.

The analyzed impedances (d) were the same as the those used for the second stage of forward modeling. The calculation range and mesh size were the same as in the forward modeling. We attempted inversion procedures starting from the four initial models adopted in the second stage of forward modeling (background resistivity: 50, 100, 200, and 500 Ωm). The resistivity value for seawater was fixed at 0.3 Ωm during each iteration of the inversion analysis. In the first stage of inversion, the prior model (mp) was set to the same model as the initial one at the beginning of the inversion. The inversion procedure was iterated seven times. In the second stage of inversion, we adopted the initial and prior models from the best-fit model of the first stage inversion result and iterated the inversion procedures five times.

The resulting minimum RMSm model, which we adopted as the optimum model in this study, was derived from the initial model with a 200 Ωm background resistivity (RMSm = 2.23, Supplementary Fig. S8). Most model-predicted responses (\(f\left[\mathbf{m}\right]\)) matched the observed responses (d), including those for the southwest stations and the diagonal components (Fig. 5), which were not adequately explained by the initial models. Additionally, cusps in apparent resistivity in the model responses at around 100–1000 s at sites NU1, EM3, EM4, and NU5, which were not explained in the forward modeling, were successfully reproduced in the inverted model. Because a large resistivity contrast between seawater and underground resistivity is required to explain coast effect31, the resistive anomaly R1, situated near these OBEM sites, is essential to explain the observed cusp in apparent resistivity.

Sensitivity tests of resistivity anomalies

We validated the conductive anomaly C1 of the optimum model by creating replaced models in which the anomaly was filled with the resistivity value of the surrounding area; specifically, the area around C1 with resistivity higher than a threshold value was changed to that value. Forward analyses were performed by varying the threshold resistivity value between 4 and 128 Ωm. We then compared the RMSm of the optimum and replaced models (Fig. 3a). For quantitative evaluation, we adopted a one-sided F-test to determine whether the optimum and the replaced models were statistically different. The 95% confidence level of the RMSm obtained by F-test was 2.32 based on the optimum model RMSm (2.23) and the data quantity (2178). The obtained RMSm exceeded the criterion value (2.32) when the C1 was replaced with 19.03 Ωm. This result indicates that C1 had a resistivity of less than 20 Ωm.

The deep extension of C1 was also examined by filling the deeper region of C1, where resistivity was lower than 100 Ωm, with a resistivity value of 100 Ωm. Threshold depths were varied between 20 and 140 km. The calculated RMSm for the models indicated that if the lower boundary of the C1 anomaly was at a depth of less than approximately 70 km, the F-test criterion value was exceeded (Fig. 3b). Therefore, the C1 anomaly should extend to a depth greater than 70 km.

We also validated the resistive anomaly R1. Specifically, the resistive region around R1 with resistivity lower than a threshold value was replaced with that value. We varied the threshold value between 128 and 1024 Ωm. The calculated RMSm of the model showed that if the resistivity of the R1 anomaly was less than 430.6 Ωm, the F-test criterion value was exceeded (Fig. 3c). Therefore, the resistivity of the R1 anomaly was greater than 430 Ωm.

Hypothetical inversion test

We further assessed the reliability and resolution of the inverted resistivity model using a hypothetical inversion test, which inverts synthetic data generated from hypothetical resistivity model. The hypothetical model is based on the initial model of inversion (background resistivity: 200 Ωm) (Supplementary Fig. S6) but includes resistive (3000 Ωm) and conductive (1 Ωm) anomalies at locations corresponding to the R1 and C1 anomalies, respectively (Supplementary Fig. S1). We then calculated the model-predicted MT impedances (synthetic data) for this hypothetical model at the same locations and periods using the same forward modeling code35 employed in the real data analyses. They synthetic data were assigned the same errors levels as those used in the inversion analyses. The same procedure applied to the real data was used for the hypothetical inversion test; however, to save computational costs, the inversion procedure was iterated four times in the first stage and two times in second stage. The RMSm (2.52 in the initial model) was reduced to 0.49 and 0.39 in the first second stages, respectively.

The hypothetical inversion successfully recovers both the resistive and conductive anomalies at the expected locations (Supplementary Fig. S2). The minimum resistivity in the conductive anomaly region is reduced to 7 Ωm (1 Ωm in the hypothetical model) from 200 Ωm in the initial model, despite the conductive anomaly being located out of the observation array. On the other hand, the model exhibits low recovery in the deep part in the conductive anomaly, consistent with the sensitivity test result for the depth of C1 (Fig. 3b), where RMSm changes are significantly reduced when lower depth limit of C1 is extended. The maximum resistivity in the resistive anomaly is increased to 1600 Ωm from 200 Ωm in the initial model, whereases the hypothetical value is 3000 Ωm.