Cross perspective AFF-CNN-HTransformer target recognition matching of satellite and UAV aerial images

Abstract

To improve the matching accuracy of cross view object recognition between unmanned aerial vehicle aerial images and satellite images, an object recognition matching algorithm based on attention mechanism and feature fusion of convolutional neural network and Transformer (AFF-CNN-HTransformer) is proposed. Firstly, to address the issue of large-scale differences and unclear image features between drone aerial images and satellite images, a preprocessing algorithm is proposed that uses satellite images as a reference and registers the direction and scale of aerial images based on the attitude angle information of the aerial camera. Secondly, in response to the low accuracy and efficiency of existing image matching methods in matching drone aerial images with satellite images, a two-step matching process is designed. The target matching area of the satellite image is reduced through a rough matching process, and fine matching is performed through an AFF-CNN-HTransformer feature fusion recognition process. The findings from the experiments indicate that, when juxtaposed against currently available image object recognition and matching techniques, the algorithm presented in this study exhibits superior accuracy in the matching process, while simultaneously reducing Match recognition time.

Introduction

Over the past few years, advancements in drone flight technology coupled with the widespread commercial availability of related equipment have led to the extensive utilization of aerial imagery across diverse domains, including target detection¹ and tracking applications². The precise matching between drone aerial images and satellite images can assist in the localization of drones through image assistance³, achieve the fusion of aerial images and satellite images to create high-definition maps, or detect large unknown environmental conditions, which has certain application value. In the field of drone target tracking, there have been many successful solutions, such as Xue et al.⁴ have put forth the Smalltrack algorithm, which utilizes wavelet pooling and classification methods enhanced by graph-based techniques to enhance the tracking of small objects in drone imagery. Xue et al.⁵ presented a novel approach for unmanned aerial vehicle visual tracking, which includes a frequency attention mechanism based on templates and a loss function that adapts the cross-entropy approach. Xue et al.⁶ has put forward a technique for mining consistent representations tailored for multi-drone single target tracking. The research avenue explored in this article diverges from previous directions, with a primary emphasis on addressing the matching challenges between aerial images captured by drones and satellite imagery, which involves two different resolutions of images, as well as seasonal interference and other issues. Overall, it has two difficulties:

• (1) Difficulty 1: The scale difference between these two images is extremely large. Satellite imagery is a large-scale, wide field of view image typically collected by remote sensing satellites and produced through methods such as color enhancement, stitching, and annotation. The actual ground area covered by a single pixel is relatively large. Relatively speaking, drone aerial images are small-scale, narrow field of view images. Due to the limitation of drone flight altitude, the actual ground area covered by their aerial images is limited, and the area covered by a single pixel is relatively small⁷. The scale difference between these two images makes it impossible to perform effective object recognition matching.

Traditional Solution: The multi-scale analysis method can be employed to construct an image pyramid, so as to meet the feature matching requirements of images with different resolutions. The advantages and disadvantages of this solution are as follows: (1) Advantages. Firstly, by extracting features at different scales, stable feature points that persist across scales can be identified. Secondly, during the process of constructing the image pyramid, spatial structural information of the image can be effectively preserved, enabling the matching results to better reflect the spatial relationships between images. (2) Disadvantages. Firstly, it requires multiple downsampling and feature extraction operations on the image, resulting in a large computational load. Secondly, under conditions of substantial scale variation, the description of features may become ambiguous.

• (2) Difficulty 2: The manifestation of features varies considerably across diverse environments. The resolution of satellite imagery is usually low, and the image update time is relatively long. While drone-captured aerial images offer the advantages of ease of acquisition and improved timeliness, they may exhibit substantial discrepancies when compared to satellite images. These differences can stem from projection effects, variations in lighting conditions, momentary changes to the ground surface caused by moving objects or rainwater, as well as long-term changes like the erection of new structures or the development of roads. The existence of these differences makes it difficult to match images based on these features, even if the feature points extracted at the same location have significant differences in feature performance⁸. Traditional template matching, correlation matching, and other methods mostly require the matching image to be at the same scale as the search image, with minimal changes in lighting and no occlusion of the template, in order to achieve good matching. Therefore, ideal matching results cannot be achieved in large-scale image matching scenarios such as drone aerial images and satellite images. Therefore, achieving the matching of aerial and satellite images poses significant challenges.

Traditional Solution: Develop robust feature extraction algorithms. The advantages and disadvantages of this solution are as follows: (1) Advantages. Firstly, it can extract features that are insensitive to illumination changes, occlusions, etc., enabling the extracted feature points to have good stability in different environments. Secondly, the algorithm principle is relatively simple, and the requirements for computing resources are also relatively low. (2) Disadvantages. Firstly, it has limited feature representation capability. Secondly, in complex scenes with a large number of occlusions, similar textures, etc., it may extract a relatively large number of incorrect feature points.

Based on the above analysis, the purpose of this study is to achieve precise matching between Unmanned Aerial Vehicle (UAV) aerial images and satellite images. In response to the aforementioned two issues, the following solutions are proposed: (1) To address the problem of inability to match due to the large scale difference and inconspicuous image features between UAV aerial images and satellite images, a preprocessing algorithm is proposed that uses satellite images as a reference and registers the orientation and scale of aerial images according to the attitude angle information of the aerial camera. (2) To tackle the issue of low accuracy and efficiency of existing image matching methods when matching UAV aerial images with satellite images, a two-step matching process is designed. The target matching area in the satellite image is narrowed down through a coarse matching process, and fine matching is conducted through an AFF-CNN-Transformer feature fusion recognition process.

Related research

The technology of image matching⁹ stands as a pivotal component within the realm of computer vision, finding extensive applications in tasks such as image stitching, visual localization, and the retrieval of images. At present, according to the different matching methods and application scenarios adopted by image matching technology, image matching technology can be divided into two categories: feature-based image matching technology and template based image matching technology. The development status of these two types of image matching technology will be analyzed in detail below.

• (1) Feature based image matching. It is mainly divided into three parts¹⁰: feature detection, descriptor construction, and similarity matching. Early feature detection mainly focused on corner detection, such as Hais corner detection, FAST corner detection, etc.¹¹, but both algorithms do not involve the description of feature corners, do not have scale invariance and direction invariance, are sensitive to noise, and have low detection accuracy. In response, Stacchiotti et al.¹² proposed the SFT algorithm (Scale Invariant Feature Transform) to extract feature points with scale and direction invariant characteristics, but its feature dimensionality is high, resulting in high time complexity. Zhang et al.¹³ proposed the Principle Component Analysis, SIFT (PCA-SFT) algorithm, which introduces principal component analysis techniques to compress SFT features and reduce matching time overhead.

In addition, to address the issues of time-consuming construction of Gaussian difference image pyramids and slow feature point detection, Bay et al.¹⁴ proposed the Speed Up Robust Feature (SURF) algorithm, which replaces the stable extremum point detection process in the SFT algorithm with the image pyramid by integrating the image and Hessian matrix, resulting in significant improvements in feature detection speed and matching efficiency. Vobruba et al.¹⁵ proposed the Temporarily Invariant Learned Detector (TLDE) detection algorithm, which selects key points that can be repeatedly detected by the SFT algorithm as the training dataset to detect more robust feature points. Xu et al.¹⁶ proposed a Super Point key point detector, which is trained based on a self-supervised network framework. The detector’s multi angle and scale adaptability is improved by transforming the image with multiple inputs after viewpoint transformation. Liu et al.¹⁷ proposed a Super Blue neural network based on Super Point, which achieves accurate feature matching results by jointly searching for corresponding points and rejecting unmatched points to match two sets of Super Point feature points.

The advantages and disadvantages of the feature-based image matching scheme are as follows: (1) Advantages. Firstly, by extracting feature points with scale and rotation invariance, it has strong adaptability to geometric transformations (rotation, scaling) of images. Secondly, it has good tolerance to interference such as illumination changes and partial occlusions. Thirdly, the feature descriptors contain rich local information, enabling precise matching through similarity measures (such as Euclidean distance). Fourthly, it is widely used in scenarios such as image stitching, 3D reconstruction, and visual localization, especially when there are significant scale differences or deformations between targets. (2) Disadvantages. Firstly, the process of feature extraction and descriptor construction is time-consuming (for example, SIFT requires constructing a difference-of-Gaussian pyramid), making it difficult to meet real-time requirements. Secondly, the distribution of feature points is uneven, which may lead to the loss of image information (for example, feature points are sparse in low-texture regions). Thirdly, the parameters (such as the Hessian threshold) of feature detection algorithms (such as SURF) need to be manually adjusted, affecting the stability of matching.

• (2) Template based image matching. No longer focusing on local feature points of the image, but matching images by measuring the correlation between matching images. The classic template matching methods include Sum of Squared Differences (SSD), Sum of Absolute Differences (SAD), and Normalized Cross Correlation (NCC). This matching method requires the template image and the search image to be in the same scale space, and has no adaptability to the deformation of the image¹⁸. In response to this, Kormanv et al.¹⁹ proposed the Fast Affine Template Matching (FAST Match) matching algorithm, which can adapt to any affine transformation of images. It can better match the optimal matching position in the search image, but its accuracy in matching uneven lighting changes is relatively low. Jia et al.²⁰ proposed the CFAST Match (Color FAST Match) template matching algorithm based on FAST Match, which can adapt to color image matching. This method extends the SAD of image grayscale space to the RGB space of image color to obtain the CSAD (Color SAD) similarity measurement factor. This method has good matching results when matching images with obvious color differences, but some parameter settings are completely determined based on experience and are not very adaptable to large-sized images. Valdez-Flores et al.²¹ proposed a template matching algorithm based on score maps. This approach employs the Sampling Vector NCC (SV-NCC) algorithm to assess the local consistency between a pair of images intended for matching. It leverages the multi-channel characteristics of color images, like RGB, to mitigate the impact of factors such as illumination and noise on the matching outcomes.

The advantages and disadvantages of the template-based image matching scheme are as follows: (1) Advantages. Firstly, it is based on pixel-level similarity measurement, which is simple to implement, has low computational overhead, and is suitable for real-time applications (such as object tracking). Secondly, template matching directly compares image regions without the need for feature extraction, preserving the global structural information of the image. Thirdly, the algorithm logic is simple, with fewer parameters, making it easy to deploy. (2) Disadvantages. Firstly, template matching relies on the consistency of image scale and rotation and has poor robustness to affine transformations (such as scaling and rotation). Secondly, it is still not applicable to illumination changes and nonlinear deformations. Thirdly, pixel-level comparisons are susceptible to uneven illumination and noise, leading to matching failures. Fourthly, the template size needs to be predetermined, with oversized templates increasing computational load and undersized templates losing key information.

This research designs a two-step matching process to address the precise matching problem between UAV aerial images and satellite images: The first step is a coarse matching process to narrow down the target matching area in the satellite image, which is essentially a template-based image matching method. It fully utilizes the simplicity of its algorithm logic to achieve rapid localization of the matching area. The second step involves a fine matching process through the AFF-CNN-Transformer feature fusion recognition process, which is essentially a feature-based image matching method. It fully leverages its advantages of high matching accuracy and good robustness to achieve precise matching between UAV aerial images and satellite images.

Cross view target recognition matching between satellite and drone images

Target recognition matching algorithm framework

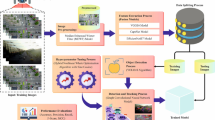
This article introduces a matching approach that accommodates the substantial discrepancies in scale and features between these two types of images, utilizing prior information such as the pose of the drone-captured images and the latitude and longitude of the satellite images. Furthermore, it investigates the application of the matching relationship between aerial and satellite images for target localization within aerial imagery. The technical framework for the proposed matching method between drone aerial images and satellite images is illustrated in Fig. 1.

Fig. 1

Algorithm framework of this article.

Figure 1 outlines the structure of this article’s research on pairing drone-captured aerial images with satellite imagery, which is primarily organized into two key components: the registration of aerial images and the process of image matching. (1) Within the aerial image registration component, the drone-captured aerial image is ascertained by acquiring the attitude angle of the onboard camera at the moment of imaging, which is then used to establish its relative rotational angle in comparison to the satellite image. Then, the drone aerial image is rotated and transformed in the opposite direction of the attitude angle to achieve the same correction registration of the aerial image. Then, by adjusting the pixel scale of aerial images to the pixel scale of satellite images through image sampling, the registration of the two types of image scale spaces can be achieved. (2) In the image matching module, the satellite images are first roughly matched. Due to the fact that satellite imagery is a large-scale image, aerial images have a relatively small coverage area. Because the camera’s latitude, longitude, and other positional information have been recorded during the aerial photography process, the coverage area corresponding to the aerial image can be roughly determined based on this positional information. Then, the satellite image subgraph and the registered aerial image are input into the feature extraction network to extract corresponding feature vectors, and the vector similarity score is calculated based on the cosine multiplication result. Ultimately, the region exhibiting the highest similarity score is chosen as the optimal match between the drone-captured aerial image and the satellite image, thereby concluding the matching procedure.

Direction registration method for aerial images

This paper focuses on the alignment of nadir aerial images with satellite imagery, where the aerial camera is configured with an elevation angle of − 90°, pointing vertically downwards towards the ground, and a roll angle of 0°. The aerial images captured by the airborne aerial camera in the local geographic coordinate system O_gX_gY_gZ have consistent directionality with satellite images. However, due to the rotation of the camera yaw angle during aerial photography, the rotation of the camera attitude angle results in a rotational relationship between the captured aerial images and satellite images, as shown in Fig. 2. The existence of rotation relationship will affect the matching results between aerial images and satellite images, so it is necessary to register the rotation direction of aerial images.

Fig. 2

Schematic diagram of aerial image rotation.

The directional registration of aerial images can be achieved through geometric transformation relationships²², including image translation, scaling, rotation, and other operations. Specific mathematical transformation models are used to change the pixel spatial position of the image, and interpolation is used to estimate the pixel values at the new pixel spatial position after transformation. The formula for the geometric transformation’s mathematical model is presented below:

$$\left[ {\begin{array}{*{20}l} x \hfill \\ y \hfill \\ z \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {a_{1} } \hfill & {a_{2} } \hfill & {t_{x} } \hfill \\ {a_{3} } \hfill & {a_{4} } \hfill & {t_{y} } \hfill \\ {v_{1} } \hfill & {v_{2} } \hfill & s \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{0} } \\ {y_{0} } \\ 1 \\ \end{array} } \right]$$

(1)

where$t_{x}$ and $t_{y}$ represent the translational changes, $a_{1} \sim a_{4}$ controls the rotation, scaling, and cropping of the image, $v_{1} \sim v_{2}$ controls the intersection position transformation after image transformation, and s is a scaling factor related to $v_{1} \sim v_{2}$.

The direction registration of aerial images is actually the process of solving the geometric transformation matrix of the image in Eq. (1). In the process of capturing aerial images, the resulting image is represented in the coordinate system of the onboard camera, while the image intended for registration is expressed in the local geographic coordinate system. Below is an outline of the series of transformations required to convert coordinates from the local geographic coordinate system to the airborne camera coordinate system, which takes into account the yaw angle, pitch angle, and roll angle.

Step 1: Rotate the yaw angle around the Z-axis, assuming the rotation angle is α, the rotation matrix is calculated as follows:

$$R_{z} (\alpha ) = \left[ {\begin{array}{*{20}c} {\cos \alpha } & { - \sin \alpha } & 0 \\ {\sin \alpha } & {\cos \alpha } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]$$

(2)

Step 2: Rotate the pitch angle around the Y-axis, assuming the rotation angle is β, the rotation matrix is calculated as follows:

$$R_{y} (\beta ) = \left[ {\begin{array}{*{20}c} {\cos \beta } & 0 & {\sin \beta } \\ 0 & 1 & 0 \\ { - \sin \beta } & 0 & {\cos \beta } \\ \end{array} } \right]$$

(3)

Step 3: Rotate the roll angle around the X-axis coordinate. Assuming the rotation angle is γ, the rotation matrix is calculated as follows:

$$R_{x} (\gamma ) = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {\cos \gamma } & { - \sin \gamma } \\ 0 & {\sin \gamma } & {\cos \gamma } \\ \end{array} } \right]$$

(4)

Utilizing the aforementioned rotation transformation procedure, the ultimate rotation transformation matrix, the transformation that shifts coordinates from the local geographic coordinate system to the coordinate system of the onboard camera can be determined using the following computation:

$$R(\alpha ,\beta ,\gamma ) = R_{z} (\gamma )R_{y} (\beta )R_{x} (\alpha )$$

(5)

Perform inverse operation on the obtained coordinate rotation transformation matrix, and the inverse matrix obtained is the transformation matrix for achieving directional registration of aerial images. Then, use the registration transformation matrix to register the aerial images.

Due to the fact that the pixel coordinates of the image are positive integers, rounding the pixel coordinates of the image after registration transformation may result in some pixels having no grayscale values and causing pixel dispersion. To overcome this drawback, this article uses reverse mapping (Fig. 3a) and bilinear interpolation (Fig. 3b) to process the transformed image. The reverse mapping transformation starts from the transformed image. Assuming that the transformed pixel coordinates are $\left( {x,y} \right)$, which corresponds to the pixel coordinate position $\left( {x^{\prime},y^{\prime}} \right)$ in the original image, the pixel grayscale value of the transformed coordinate $\left( {x,y} \right)$ is obtained by bilinear interpolation of the grayscale values of the four pixels around the point $\left( {x^{\prime},y^{\prime}} \right)$ in the original image.

Fig. 3

Direction registration process of aerial images.

Bilinear interpolation operation, first perform two linear interpolation operations on the four pixels around point P in the x-axis direction to obtain the pixel grayscale values of points $R_{1}$ and $R_{2}$, and then perform linear interpolation on points $R_{1}$ and $R_{2}$ in the y-axis to obtain the pixel grayscale value of point P. Assuming that the grayscale value of point P is represented as $f\left( P \right)$, and the grayscale values of other points are defined similarly, the grayscale values of points $R_{1}$ and $R_{2}$ can be calculated as follows:

$$\left\{ \begin{gathered} f\left( {R_{1} } \right) = \frac{{\left( {x_{2} - x^{\prime}} \right)}}{{\left( {x_{2} - x_{1} } \right)}}f\left( {P_{11} } \right) + \frac{{\left( {x^{\prime} - x_{1} } \right)}}{{\left( {x_{2} - x_{1} } \right)}}f\left( {P_{21} } \right) \hfill \\ f\left( {R_{2} } \right) = \frac{{\left( {x_{2} - x^{\prime}} \right)}}{{\left( {x_{2} - x_{1} } \right)}}f\left( {P_{12} } \right) + \frac{{\left( {x^{\prime} - x_{1} } \right)}}{{\left( {x_{2} - x_{1} } \right)}}f\left( {P_{22} } \right) \hfill \\ \end{gathered} \right.$$

(6)

The calculation method for obtaining the pixel grayscale value of point P by linearly interpolating points $R_{1}$ and $R_{2}$ on the axis based on the values of $f\left( {R_{1} } \right)$ and $f\left( {R_{2} } \right)$ is as follows:

$$\begin{gathered} f(P) = \frac{{\left( {y_{2} - y^{\prime}} \right)\left( {x_{2} - x^{\prime}} \right)}}{{\left( {y_{2} - y_{1} } \right)\left( {x_{2} - x_{1} } \right)}}f\left( {P_{11} } \right) + \frac{{\left( {y_{2} - y^{\prime}} \right)\left( {x^{\prime} - x_{1} } \right)}}{{\left( {y_{2} - y_{1} } \right)\left( {x_{2} - x_{1} } \right)}}f\left( {P_{21} } \right) \hfill \\ \, + \frac{{\left( {y^{\prime} - y_{1} } \right)\left( {x_{2} - x^{\prime}} \right)}}{{\left( {y_{2} - y_{1} } \right)\left( {x_{2} - x_{1} } \right)}}f\left( {P_{12} } \right) + \frac{{\left( {y^{\prime} - y_{1} } \right)\left( {x^{\prime} - x_{1} } \right)}}{{\left( {y_{2} - y_{1} } \right)\left( {x_{2} - x_{1} } \right)}}f\left( {P_{22} } \right) \hfill \\ \end{gathered}$$

(7)

Ground coverage distance of satellite imagery

In satellite image data, given that the upper left corner, designated as point A, has latitude and longitude coordinates of (lomA, latA), and the lower right corner, designated as point B, has coordinates of (lomB, latB), since the size of the ground coverage area of the satellite imagery is relatively small compared to the Earth, the influence of the Earth’s sphere can be ignored, and the ground area covered by the satellite imagery can be considered as a planar area to calculate its actual distance.

To calculate the ground distance covered by satellite images with known latitude and longitude coordinates, it is necessary to first calculate the average ground distance corresponding to each degree of latitude and longitude. In the calculation of this article, the geographical range of the Northern Hemisphere is mainly considered. According to reference²³, in the WGS-84 coordinate system, when the latitude is constant, the distance corresponding to one degree of longitude interval can be calculated as follows:

$$S = \frac{\cos (B) \times (R - lat \times (R - r)/90) \times \pi }{{180}}$$

(8)

where B is the latitude size, measured in degrees. R = 6378137 m is the radius of the Earth’s equator, and r = 6,356,752.314 m is the radius of the Earth’s polar axis. According to the satellite image coordinate position and Eq. (8), the ground coverage distance of the satellite image in the horizontal direction can be calculated as follows:

$$L_{x} = \left| {{\text{lon}}B - {\text{lonA}}} \right|{\mkern 1mu} \cdot \frac{\cos (lat) \times (R - lat \times (R - r)/90) \times \pi }{{180}}$$

(9)

where lat is the average latitude of points A and B, taken to minimize the impact of the Earth’s curvature on the calculation of the actual distance between the ground. Similarly, the vertical ground coverage distance of satellite imagery can be calculated as follows:

$$L_{y} = \left| {{\text{lon}}B - {\text{lonA}}} \right| \cdot \frac{(R - lat \times (R - r)/90) \times \pi }{{180}}$$

(10)

Rough matching of location information

When matching drone-captured aerial images with satellite imagery, it is often the case that the ground coverage area depicted in satellite images is relatively extensive, while the coverage area of aerial images is relatively small, if the aerial images are directly matched with the entire satellite image, the calculation of feature extraction and feature matching is very large, and this is also unnecessary matching. After calculating the ground coverage distance between the drone aerial image and the satellite image using the above method, a coarse matching area based on location information can be used to select the camera’s latitude and longitude position information (lomT, latT) recorded at the imaging time of the drone aerial image as the latitude and longitude position of the center point of the aerial image. Then, a threshold Rt is set based on the camera positioning accuracy, and a satellite sub image is extracted from the global satellite image with the latitude and longitude of the aerial image as the center and the threshold Rt as the radius as the coarse matching result.

The specific selection of satellite image subgraphs is shown in Fig. 4, where the red dashed box area is the satellite image subgraph area selected based on the distance calculation of the ground coverage area and the threshold Rt size.

Fig. 4

Schematic diagram of satellite image sub image extraction.

The specific steps are as follows:

Step 1: Calculate the ground coverage distance $L_{x}$ and $L_{y}$ of the satellite image based on its latitude and longitude coordinates.

Step 2: Calculate the ground coverage distance per unit pixel of the satellite image based on its pixel size.

Step 3: Calculate the pixel coordinates of the center of the coarse matching area on the satellite image based on the latitude and longitude of the unmanned aerial image and the unit pixel size of the satellite image.

Step 4: Determine the pixel coordinate range of the coarse matching area in the satellite image based on the unit pixel size of the satellite image and the clipping threshold Rt, and clip it.

Dual stream feature fusion extraction based on AF-CNN-Transformer

CNN feature branch

The CNN feature branch is based on the residual dense module Residual Dense Module(RDB)²⁴ as the core module, Fig. 5 presents a comprehensive breakdown of the implementation for every RDB module. Essentially, an RDB module is a type of residual module that features dense internal linkages. Each core block involved in these dense connections is made up of two functional units: 3 × 3 spatial convolutions and ReLU operation.

Fig. 5

Implementation example of RDB.

Within the fundamental block of the current level, the output feature map originating from the earlier basic blocks is combined with the input feature map of the residual module on a per-pixel basis, with channels aligned, to form the input feature map for the present basic block. This process embodies the dense connectivity between the current basic block and its preceding counterparts. Ultimately, the output feature maps from all levels of basic blocks within the same residual block, along with the input feature map of the residual block, are concatenated across channels. The fusion of the feature maps at all levels is achieved through channel compression using a 1 × 1 convolution method, and rich local feature information about the input feature map of the RDB module is effectively embedded at the output end using the residual connection method.

As illustrated in Fig. 5, the unique dense connection methodology employed among the fundamental blocks within the RDB block guarantees that the input for each stage of the basic block is a fusion of the output feature maps from the prior stages of basic blocks and the original input feature maps of the RDB block. By leveraging this incremental dense linkage and processing framework, the initial input feature maps of the RDB block acquire a more varied and comprehensive range of local feature extractions, spanning multiple levels and implying multi-scale receptive field influences.

HTransformer feature branch

Yin et al.²⁵ attempted to apply Transformer to computer vision tasks and proposed the Vision Transformer (ViT) module. ViT consists of Multi Head Self Attention (MHSA), Layer Normalization (LN), and Multi-Layer Perceptron (MLP). The ViT model initially carries out a spatial division of the input feature map, resulting in a series of sub-blocks. It then applies a linear transformation directly to these sub-blocks via patch embedding, generating initial feature vectors for each. This process enables the encoding of features within the input feature map by utilizing self-attention layers, following normalization in the succeeding layers, obtaining contextual feature vector representations of these sub block sequences and better capturing remote dependencies in the sub block sequences.

Replace the MHSA layer in ViT with a Hierarchical Multi Head Self Attention Layer (HMHSA) to obtain the HTransformer shown in Fig. 6. HMHSA calculates self-attention in a hierarchical manner, with each HMHSA layer consisting of several MHSA sub layers connected in series. The HMHSA layer presented in Fig. 6 consists of three MHSA sub-layers organized in a bottom-up order, as shown in the second column of the figure. In the context of using a recursive quadtree with a depth of three for spatial segmentation of the input feature map, the bottom-most MHSA sub-layer within the HMHSA structure gives primary attention to computing multi-head self-attention for each specific molecular block located in the region of the leaf nodes. This approach underscores the modeling of spatial interdependencies among distinct fine-grained molecular blocks within a confined local area. The self-attention calculation of the corresponding spatial regions in the subsequent MHSA sub layers is based on the self-attention calculation of its child nodes, which encode all its child nodes to form a token sequence for multi head self-attention calculation in higher sub layers. Therefore, the focus is on modeling the spatial dependency relationship between the corresponding spatial regions of its child nodes.

Fig. 6

HTransformer structure.

For the convenience of subsequent dual path feature fusion, the Transformer feature branch, like the CNN feature branch, contains four feature extraction layers. The output feature maps located at the same level of feature extraction layers in both branches have the same number of rows, columns, and feature channels.

Dual stream feature fusion based on AFF module

In order to efficiently integrate the encoded features originating from the two feature extraction pathways of CNN and Transformer, this paper presents the Attention Feature Fusion (AFF) module, as outlined by Zhang et al.²⁶ and depicted in Fig. 7. This module is incorporated at every feature extraction layer of the encoder.

Fig. 7

CNN-Transformer dual stream feature fusion based on AFF module.

As shown in Fig. 7, taking the information fusion of the i-th feature layer of the encoder’s dual branch as an example, the multi-channel feature map tⁱ from the i-th feature layer of the Transformer branch and the multi-channel feature map gⁱ from the i-th feature layer of the CNN branch are simultaneously sent to the AFF module; To enhance the global information from the Transformer branch, channel attention enhancement is applied to tⁱ to obtain $\tilde{t}^{i}$. To effectively enhance the spatial local structural information from the CNN branch, spatial attention enhancement is applied to gⁱ to obtain $\tilde{g}^{i}$; At the same time, with the help of Hadamard product and subsequent 3 × 3 spatial convolution, fine-grained cross path interaction is performed on the two sets of multi-channel feature maps tⁱ and gⁱ. The final processing results were connected through channels and convolved in a 3 × 3 space to generate the output of the AFF module.

Analysis of computational complexity

To assess the viability of the presented approach for aligning drone aerial images with satellite imagery, and to provide a fair evaluation of the proposed matching method’s performance, this section delves into the algorithmic implementation complexity and presents the simulation experiment matching outcomes of the introduced matching algorithm, and compare and analyze the advantages and disadvantages of the proposed matching algorithm with widely used image matching algorithms such as NCC²⁷, Best Buddies Similarity (BBS) ²⁸, and Deformable Diversity Similarity (DDIS) ²⁹. The main considerations are the computational complexity and memory overhead of the algorithm.

In the method proposed in this article, rough matching based on location information is an operation with limited steps, and its time complexity and memory usage complexity are both O(1). In the CNN based feature fine matching, assuming that the registered drone aerial image size is $T_{w} \times T_{h} \triangleq l$, the satellite image size is $S_{w} \times S_{h} \triangleq L$, and the satellite image sub image size obtained through coarse matching method is $S_{{w^{\prime}}} \times S_{{h^{\prime}}} \triangleq L^{\prime}$, the feature dimension size of the image is d. According to the matching algorithm process, the image feature vectors are first cosine multiplied, and the dimension of the resulting storage matrix D is $L^{\prime} \times l$, resulting in a memory complexity of $O\left( {L^{\prime}l} \right)$. The feature vectors are cosine operated on pairwise and stored in matrix D, with a computation time complexity of $O\left( {L^{\prime}ld} \right)$. Then calculate the feature matching quality score function $Q\left( {s,t} \right)$, and the storage matrix Q of $Q\left( {s,t} \right)$ is also $L^{\prime} \times l$ dimensional, with a memory complexity of $O\left( {L^{\prime}l} \right)$.

According to the definitions of $P\left( {t\left| s \right.} \right)$ and $P\left( {s\left| t \right.} \right)$, calculating $Q\left( {s,t} \right)$ requires summing up the l terms $L^{\prime}$ times and the l terms $L^{\prime}$ times in the cosine multiplication result storage matrix D, and then performing operations according to the definitions, with a computation time complexity of $O\left( {2L^{\prime}l} \right)$. Finally, based on the search for the best matching area in $Q\left( {s,t} \right)$, first find the maximum value of each row in the feature matching quality score matrix Q to obtain an $L^{\prime} \times 1$ dimensional vector, then adjust the vector to an $S_{{w^{\prime}}} \times S_{{h^{\prime}}}$ dimensional score probability matrix, and use $T_{w} \times T_{h}$ as the sliding window size to find the area with the highest score probability in the score probability matrix as the best matching area output. The calculation time complexity is $O\left( {L^{\prime}l} \right)$, and the memory usage complexity is $O\left( {L^{\prime}} \right)$.

After consolidating the aforementioned complexities and eliminating lesser order variables along with constant terms, the overall time complexity of the matching algorithm proposed in this work is denoted as $O\left( {L^{\prime } ld} \right)$, while the memory complexity is represented as $O\left( {L^{\prime}l} \right)$. The comparative analysis results of algorithm complexity in this article are shown in Table 1.

Table 1 Comparison of algorithm complexity.

In Table 1, $d^{\prime}$ represents the feature dimension size of the image feature vector d after dimensionality reduction using principal component analysis algorithm. Due to the rough matching process $L^{\prime} \ll L$, the matching algorithm proposed in this paper has significant advantages in terms of time complexity and memory usage complexity compared to BBS and DDIS algorithms. For the NCC matching algorithm, this method has a significant advantage in memory complexity, and the time cost difference in time complexity depends on the size of the feature vector dimension d used for matching.

Experimental analysis

To assess the effectiveness of the methodology introduced in this article, experiments will be carried out using aerial images captured by unmanned aerial vehicles (UAVs) during summer and winter seasons. The outcomes will be compared and analyzed against those of other image matching algorithms, including Scale invariant feature transform (SIFT)³⁰, Single Shot MultiBox Detector (SSD)³¹, Normalized Cross-Correlation (NCC)³², Sum of absolute differences (SAD)³³, MatchNet (Unifying feature and metric learning for patch-based matching)³⁴, and 2chDCNN (2-channel deep convolution neural network)³⁵. Experimental hardware configuration: CPU i7-4700 K, Memory 16 GB DDR4-2400 GHz, testing platform Matlab2020b, operating system Win10 LTSC.

Experimental data

In winter, especially when the ground is covered with snow, the ground features contained in satellite images are greatly reduced, and the images lack rich textures. Therefore, satellite images in winter are generally not suitable as reference libraries for drone visual positioning. And the ground information features of summer satellite images are obvious, making them more suitable as a benchmark image library. Therefore, summer satellite images are selected as the benchmark image library for matching in the article. The aerial images of unmanned aerial vehicles in summer and winter are shown in Fig. 8.

Fig. 8

Drone aerial image.

The summer drone aerial images used in the experiment were taken by DJI drone, with a resolution of 2000 × 2000. The satellite image to be matched is a level 17 satellite map downloaded from open-source map downloader. If you choose a level 15 satellite map, afterproportional preprocessing, the ground resolution is higher and the drone aerial images are smaller, so you choose a level 17 satellite map. The winter droneaerial images used were taken by DJI drones in the Shenbei area of Shenyang City, Liaoning Province, with flight heights of 200 meters and 300 meters,and an image resolution of 4000 × 3000. The satellite image to be matched is a level 15 satellite map downloaded by open-source map downloader.

Result analysis

In order to confirm the efficacy of the matching approach presented in the article, the intersection-over-union ratio ($R_{{{\text{Iou}}}}$) was employed as an objective assessment metric to gauge the matching outcomes. When evaluating image matching results, $R_{{{\text{Iou}}}}$ mainly refers to the overlap rate between the ground truth position and the predicted position of the template image, that is, the ratio of the intersection and union of two rectangular boxes:

$$R_{{{\text{IoU}}}} = \frac{{B_{{\text{e}}} \cap B_{{\text{t}}} }}{{B_{{\text{e}}} \cup B_{{\text{t}}} }}$$

(11)

where $B_{{\text{e}}}$ represents the predicted rectangular box area;$B_{{\text{t}}}$ represents the actual rectangular area of the ground. The larger the $R_{{{\text{Iou}}}}$ value, the closer the true value is to the test value, resulting in better image matching performance.

It should be noted that the reason for selecting square segmentation here is that square segmentation, as a basic and common segmentation method, can evenly divide the image into multiple small blocks, which is convenient for subsequent processing and analysis. Meanwhile, the implementation of square segmentation is relatively simple and computationally efficient, making it suitable for large-scale image processing tasks. When choosing segmentation methods, we also considered circular segmentation, but compared to square segmentation, circular segmentation presents some challenges in practical applications. On the one hand, circle segmentation requires more complex algorithms and computational resources to accurately identify circular regions in images, which may increase processing complexity and time costs. On the other hand, square segmentation has shown good performance in many practical application scenarios and is easier to combine with other image processing techniques. Through simulation experiments, it was found that using circular segmentation method on the selected dataset of the summer drone aerial imagesincreased the time required by more than 15% compared to square segmentation. Therefore, we chose square segmentation as the starting point for this study to demonstrate the resolution performance of Transformers under square segmentation. Of course, we do not rule out further exploring the combination of circle segmentation and other segmentation methods with Transformers in future research.

Figure 9 shows examples of image matching between the method proposed in the article and six other methods. From left to right are UAV image, SIFT, SSD, NCC, SAD, 2chDCNN, MatchNet, and the method described in the article.

Fig. 9

Matching outcomes of unmanned aerial vehicle (UAV) aerial images.

The red rectangle depicts the forecasted position for each technique, whereas the blue rectangle signifies the genuine ground position. Upon examining the rectangular boxes, it becomes evident that the matching outcomes of the method discussed in the article exhibit the closest proximity to the actual ground position, demonstrating a clear advantage over other approaches.

In addition, the receiver operating characteristic curve (ROC curve) is used in the article to further evaluate the quality of the matching results. The ROC curve illustrates the percentage of images that exceed the specified overlap threshold, with the horizontal axis depicting the overlap threshold and the vertical axis representing the success rate. The larger the overlap threshold, the stricter the criteria for successful matching, that is, the matching success rate decreases with the increase of the overlap threshold.

The ROC curves of the method proposed in the article compared to six other methods on winter and summer datasets are shown in Fig. 10.

Fig. 10

Comparison of ROC curve experimental results.

The area $S_{{{\text{AUG}}}}$ below the curve quantifies the overall accuracy, with larger $S_{{{\text{AUG}}}}$ representing better performance. The $S_{{{\text{AUG}}}}$ index results of different matching algorithms are shown in Table 2.

Table 2 Comparison of experimental results of different methods.

It can be observed that the method described in the article has higher $S_{{{\text{AUG}}}}$ scores than other matching methods on both summer and winter datasets. Although there is no snow cover in summer images, UAV aerial images and satellite images are usually obtained at different times, different sensors, different observation point angles, and different meteorological conditions, resulting in large differences in the visual characteristics of the same scene between the two images, which has an impact on image matching. The article utilizes the ability of fuzzy information granules to describe imprecise and uncertain events and phenomena to extract ground image features, and matches similar but not completely consistent features to overcome the impact of differences on matching and improve the accuracy of image matching. At the same time, fuzzy information granules can achieve image feature extraction through simple calculations, which is efficient. In addition, all methods perform better on summer datasets than on winter datasets, indicating that snow has a significant impact on drone aerial image matching. The $S_{{{\text{AUG}}}}$ results of the method in the article on the summer dataset are higher than those on the winter dataset. This is because summer can display the details and features of images more clearly compared to winter images, which has a certain promoting effect on the accuracy of image matching.

The selected algorithms mentioned above are all classic algorithms. In order to better verify the performance advantages of the proposed method, Swin Transformer (SWTR)³⁶, Detection Transformer (DETR)³⁷ and hybrid CNN-transformer (HC-transformer)³⁸ are selected for comparison; Due to limited winter image materials, only summer images were selected for testing. Four sets of test sets were formed by selecting 50, 150, 500, and 1500 images from the summer drone aerial images to verify their testing performance on datasets of different scales; Supplement algorithm running time as a comparative indicator. The experimental results are shown in Table 3.

Table 3 Experimental comparison of detection accuracy and calculation efficiency.

According to the experimental results in Table 3, compared to the selected SWTR, DETR and HC-transformer comparison algorithms, our algorithm outperforms the selected comparison algorithm in terms of S_AUG, R_IoU, and computation time. From the perspective of S_AUG indicators, as the size of the dataset increases, the S_AUG indicators of all four algorithms show a decreasing trend, which is related to the increase in interference images caused by the increase in dataset size. However, the decrease in values is not severe and can be ignored. From the R_IoU metric, as the dataset size increases, the S_AUG metrics of the three algorithms also show a decreasing trend, which is similar to the S_AUG metric, but the decrease is not significant and can be ignored. In terms of computational time metrics, the algorithm presented in this paper requires less time than the chosen comparison algorithms, thereby suggesting that the computational efficiency of our proposed algorithm is comparatively higher.

To further substantiate the efficacy of the enhanced algorithm proposed in this article, ablation experiments were conducted focusing on the improvements made to the Transformer series. The ablation experiment decomposes the AFF-CNN-HTransformer algorithm into Transformer HMHSA + Transformer (HTransformer), AFF + CNN + HTransformer。 Because the function of the AFF module is to integrate CNN and HTransformer features and cannot be used separately, it was not considered separately in the ablation experiment. Here, summer images are still selected for testing, with 50, 150, 500, and 1500 images selected form four sets of test sets. The experimental results are shown in Table 4.

Table 4 Ablation experiment.

Based on the ablation experiment results presented in Fig. 4, it is evident that the incorporation of the multi-head attention mechanism and the CNN feature analysis method in the refinement of the Transformer in this paper significantly enhances the algorithm’s target matching accuracy. On the four test sets consisting of 50, 150, 500, and 1500 selected images, the AFF + CNN + HTransformer algorithm has higher recognition accuracy than HMHSA + Transformer and Transformer. At the same time, in terms of computation time, the algorithm proposed in this article has increased its computation time due to the addition of more computation processes. However, from the perspective of the magnitude of the increase, it does not reflect a significant increase in computation time. That is to say, although the algorithm proposed in this article has added computation processes compared to the Transformer algorithm, its computational complexity has not increased by an order of magnitude. In addition, similar performance characteristics are also observed in the comparison between HMHSA + Transformer and Transformer.

Conclusion

This paper primarily investigates the technique for matching unmanned aerial vehicle (UAV) aerial images with satellite imagery, examines the challenges associated with this task, and introduces a scale registration-based approach for matching UAV aerial images with satellite images, taking into account these challenges and the shortcomings of existing matching techniques.

This article effectively solves the two difficult problems of matching drone aerial images with satellite images raised in the introduction section, as follows: (1) To address the issue of significant scale differences between drone aerial images and satellite images, a preprocessing algorithm is proposed that uses satellite images as a reference and registers the direction and scale of aerial images based on the attitude angle information of the aerial camera. This step aims to adjust the scale and orientation of aerial images to make them closer to satellite imagery, thereby reducing the impact of scale differences on the subsequent matching process. (2) A two-step matching process was designed to address the issue of significant differences in feature performance in different environments. Firstly, the target matching area of the satellite image is narrowed down through a rough matching process, which aims to quickly locate possible matching areas and reduce search space. Secondly, fine matching is performed through the AFF-CNN Transformer feature fusion recognition process, which leverages the strengths of deep learning to extract and integrate more distinctive features, thereby enhancing the precision and robustness of the matching process.

The problem is that the image registration method based on camera pose parameters proposed in this article needs to ensure the accuracy of the camera’s pose angle in order to achieve correct registration of image direction. However, during the flight of unmanned aerial vehicles, due to factors such as wind and body shaking, as well as the delay in updating camera parameters, there may be some errors between the attitude angle recorded by the camera and the true attitude angle, resulting in the inability to achieve true alignment of the image direction and affecting the accuracy of image matching³⁹. Therefore, in future research work, the primary focus of this paper will be on developing strategies to accommodate attitude angle error registration in images and enhancing the resilience of the image matching technique proposed herein against image rotation.

In addition, residual dense models require more computational resources to support training due to their complex structure. When faced with large datasets, the computational and memory consumption required during the training process will significantly increase, which may result in slower training speed or even inability to complete the training⁴⁰. Therefore, in the next step of work, further improvements need to be made in the following aspects: (1) optimizing the model structure. Considering the attributes of extensive datasets, the architecture of residual dense models can be refined by decreasing the number of layers or nodes within the network, thereby mitigating computational complexity. Meanwhile, it is also possible to consider using more efficient network structures or modules to replace some residual dense connections. (2) Adjust the training strategy. Adjust training strategies based on the characteristics of big datasets and the requirements of residual dense models, such as using distributed training, using larger batch sizes, optimizing learning rate scheduling strategies, etc., to improve training efficiency and model performance. (3) Utilize regularization techniques. To prevent overfitting, regularization techniques such as L1 regularization, L2 regularization, Dropout, etc. can be used during the training process to limit the complexity of the model and improve its generalization ability. (4) One potential avenue for enhancing model performance and training efficiency is to integrate residual dense models with other methodologies, such as transfer learning and knowledge distillation. This area will be explored and refined in future research endeavors.