Data-driven robust outpatient physician scheduling with medical visiting information

Abstract

Over the last decades, hospitals have faced shortages of medical personnel due to increasing demand. As one of the busiest divisions, the outpatient department plays a vital role in delivering public healthcare services, leading to a significant focus on physician work schedules. In this study, we develop a data-driven optimization framework for a mid-term period spanning several weeks within the outpatient department of a dermatology hospital. This framework integrates patient visit clustering and physician work scheduling sequentially, thereby ensuring its scalability for application in many other hospitals. We first employ a hybrid clustering model that classifies patient visits based on a joint distribution of physician-patient characteristics. This clustering model inherently captures patient preferences for physicians so that patient demand is stratified to each physician. Then, we propose a robust physician scheduling model based on a novel risk measure called Likelihood Robust Value at Risk (LRCVaR). In particular, the proposed LRCVaR considers the worst-case demand in an ambiguity set of possible distributions, leading to mitigated tail risks of service capacity shortages. Therefore, this scheduling model mitigates tail risks of service capacity shortages. A tractable reformulation of the proposed robust physician scheduling model is newly derived, and we show their equivalence using strong duality theory. An iterated algorithm for the reformulation is also delicately designed, and we demonstrate its applicability to off-the-shelf solvers. The case study demonstrates that our LRCVaR is less conservative while controlling for the risk level. Such a result indicates that our proposed approach can satisfy patient demand with a smaller number of physicians at the same level of risk. Dermatologists and venereologists serving as chief physicians in our studied hospital are more prone to reaching their service capacity limits. Thus, our framework outperforms existing robust approaches in reducing tail risks of capacity shortages and identifying the bottleneck of service provision.

Introduction

The scheduling of outpatient physicians is crucial for hospital operational management, as hospital outpatient departments serve as frontline clinical units. The service capacity provided by outpatient physicians must meet patient demand to avoid the risk of capacity shortages, while also adhering to mandatory requirements related to the protection of physicians’ rights, stipulated by labor laws and hospital management regulations. A reasonable workload and a supportive working environment can effectively prevent potential medical incidents¹. Additionally, a scheduling plan that prioritizes humanization and fairness can improve job satisfaction among medical staff, thereby enhancing their energy and creativity, which ultimately elevates the quality of healthcare services^2,3,4. However, over the past decades, hospitals have been facing significant shortages of medical personnel due to increasing demand, making the primary challenge in outpatient physician scheduling how to effectively utilize limited physician resources to meet growing needs.

A central challenge arises from the inherent variability in physician-patient characteristics, which standard personnel scheduling methods fail to address. For instance, patients with different disease categories (e.g., allergic dermatitis vs. skin tumors) often require varying consultation times, while physicians at different ranks (e.g., chief physicians vs. residents) experience distinct workloads. To illustrate these disparities, we collected outpatient visiting records from the Dermatology Hospital of Southern Medical University, which is the largest specialist hospital and the tertiary care center for dermatology in Guangzhou, China. As shown in Fig. 1a, patients with allergic dermatitis exhibit the highest average daily demand (206.9), whereas patients with skin tumors have the lowest (19.3). Meanwhile, Fig. 1b indicates that chief physicians handle an average of 52.2 consultations per day, compared with only 38.9 for resident physicians. These stark disparities underscore the necessity of distinguishing the varying service demands and supply capacities shaped by disease categories and physician expertise levels. Ignoring such differences can result in mismatches between patient demand and service capacity. Moreover, as the dimensionality of these physician and patient attributes grows, the data in each subgroup become sparser-known as the “curse of dimensionality”-which poses additional challenges when the historical sample is small. In other words, the analysis of actual data from the hospital shown in the Fig. 1 demonstrates that failing to effectively account for different patients’ preferences for different physicians can lead to resource misallocation and unmet demand.

Fig. 1

Probability density distribution of daily outpatient visits at the dermatology department. (a) Probability density distribution of daily outpatient visits by disease type. (b) Probability density distribution of daily outpatient visits by physician title. Data Source: outpatient database from dermatology hospital of southern medical university in Guangzhou, China, 2019

Literature review

Physician scheduling, as part of broader scheduling models, is distinct due to the heterogeneity of both physicians and patients. Healthcare services inherently involve partial standardization due to the diverse health conditions, available information, and treatment responses of patients^1,5. This results in varying patient demand for different physicians, influenced by factors such as education, experience, and specialty. Additionally, outpatient demand is highly uncertain, often linked to unforeseen events. Mid-term scheduling models, spanning several weeks, face even greater uncertainty than short-term ones. Insufficient scheduling can lead to service capacity shortages, reducing quality⁶ and increasing wait times⁷, while excess capacity wastes resources and raises costs. Thus, accounting for heterogeneity and modeling uncertain demand is essential for robust outpatient scheduling.

Most studies about physician scheduling do not take these individual characteristics of physicians and patients into account, with only a few works involving different types of physicians or patients.⁸ considered outpatient, emergency, and ICU (Intensive Care Unit) physician scheduling issues but did not delve into disease-specific patient demands.⁹ differentiated physicians by technical levels to accommodate various types of emergency patients, while¹⁰ classified physicians into junior, senior, and medical student categories based on their qualifications. However, they merely required a certain ratio combination of these categories rather than aligning specific physician types with particular patient needs. As a result, the significant differences among individuals- both physicians and patients- are often overlooked, potentially leading to suboptimal scheduling outcomes. In addition, some studies consider individual preferences during scheduling^11,12,13. These articles primarily focus on physician preferences, as doctors are valuable resources for hospitals, especially those with high qualifications and experience who have a certain degree of autonomy. However, research that focuses on patient preferences to meet the needs of different patient categories, thereby optimizing the allocation of medical resources (physicians) for more efficient utilization, is still limited and warrants further exploration.

Research on demand modeling methods generally falls into two categories: physician scheduling decisions based on deterministic demand and those based on stochastic demand. The majority of research on physician scheduling utilizes deterministic demand, such as average demand¹⁴, maximum demand⁴, and specified demand levels^15,16. However, deterministic demand simplifies mathematical programming models but overlooks the challenges posed by the fluctuations in real-world demand on healthcare systems. A smaller segment of the literature examines stochastic demand, with a particular focus on emergency departments.¹⁷ provided a decision support system for scheduling physicians in the emergency department of a public hospital in Kuwait, aiming to maximize patient throughput and minimize waiting times. After analyzing the reception, examination, laboratory, and treatment processes, they established a stochastic optimization model and derived heuristic solutions through stochastic simulation.⁹ considered stochastic demands at different emergency levels and devised scheduling plans based on physicians’ technical skills, using chance inequalities to ensure that the service capacity at each level exceeded the stochastic demands. Assuming a normal distribution for the stochastic demands, these chance inequalities could be resolved using their inverse distributions.¹⁸ described the emergency room process as several stages, including assessment, examination, and treatment stages, and developed a stochastic optimization model to optimize physician scheduling. The decision objective was to minimize the sum of expected waiting times for each stage. Due to the complex nature of the queuing system studied, deriving analytical expressions for expected waiting times was challenging, so they estimated expected waiting times using stochastic simulation.¹⁹ employed a two-stage planning model to address the emergency room physician scheduling problem, where the first stage involved determining the number of physicians and shifts without knowing specific demands, and the second stage optimized queue lengths and idle service capacities once demands were known. The objective was to minimize the sum of expected queue lengths. Although similar to¹⁸, they used stochastic simulation to estimate expected queue lengths, but unlike them, they considered physicians’ preferences in their model.²⁰ introduced the concept of extending shifts and used it to model scheduling for physicians. Considering the high randomness in demands typical of emergency or operating rooms, physicians could extend their shifts beyond the planned schedule based on a certain probability. They employed the Dantzig-Wolfe decomposition to break the model into master and sub-problems, enabling effective solving of large-scale problems. Overall, the research primarily employs stochastic optimization models. When the distribution of stochastic demand is unknown, service capacity is typically determined using random simulation or expected demand. Although stochastic optimization models account for demand variability, their reliance on predefined stochastic demand distributions can lead to suboptimal decisions when these distributions deviate from real-world patterns. Therefore, further exploration of more robust, data-driven decision frameworks and risk control methods is necessary to ensure that, even with small sample sizes, the decisions provide probabilistic guarantees against service capacity shortages.

In summary, existing research on physician scheduling has addressed physician-patient differences and demand uncertainty to some extent but still faces several limitations. Studies on patient preferences are limited, especially in terms of utilizing personal characteristics to categorize patient demand and optimize physician resource allocation. Moreover, most research relies on deterministic demand models, which simplify the problem but overlook the challenges posed by real-world demand fluctuations. While some studies have introduced stochastic demand models, they depend on predefined demand distributions, which fail to effectively manage the risk of service shortages. To address these gaps, this study proposes a data-driven robust optimization framework for mid-term outpatient scheduling, considering physician-patient heterogeneity and demand uncertainty.

Goals and contributions

This study provides a novel optimization framework for a mid-term period spanning several weeks within the outpatient department of a dermatology hospital. Based on the critical aspects of personal preferences and service capacity, we investigate the following research questions: (1) How can we estimate patients’ personal preferences for physicians to achieve demand stratification? (2) How can we optimize physicians’ service capacity for patients to enhance supply provision? (3) How are the estimation and optimization procedures coordinated in a data-driven manner? To answer these questions, we first employ a hybrid clustering model that classifies patient visits into several groups. The clustering model employs the joint distribution of physician-patient characteristics, such as gender, educational degree, and medical specialty. For each physician, we exploit a service capacity ratio that calculates the probability of a patient visit group being served by that physician. Inherently, such a ratio captures patient preferences for physicians reflected in historical data. Given the calculated service capacity ratios, we then propose a robust physician scheduling model that determines physician rosters to satisfy grouped demand. Specifically, we introduce a novel risk measure called Likelihood Robust Value at Risk (LRCVaR), which particularly mitigates tail risks of service capacity shortages for each demand group. We demonstrate that LRCVaR possesses a desired property of large samples, which facilitates the selection of the robust control parameter.

The major contributions of this study are summarized as follows:

• We develop a data-driven optimization framework to concomitantly address physician scheduling and patient preferences. The developed framework has scalable extensions for many applications.

• We propose a novel risk measure LRCVaR that addresses tail risks of service capacity shortages: it possesses an asymptotic distribution for the robust control parameter.

• An equivalent tractable reformulation and an iterated algorithm are derived for solution methods.

• Case studies demonstrate that our framework outperforms existing robust approaches in reducing tail risks of capacity shortages and identifying the bottleneck of service provision.

Outline

The structure of this paper is outlined as follows: The “Introduction“ section introduces the background and motivation of this study, with the “Literature review“ section providing a review of relevant works as part of the introduction. The “Methods“ section consists of two parts: the first part, the “Hybrid clustering model“ section, outlines the method for clustering patient visits based on patient-physician characteristics; the second part, the “Robust outpatient physician scheduling model“ section, proposes the method for scheduling physicians using LRCVaR. The “Results and discussion“ section presents the results of case studies and discusses the comparative performance evaluation with other robust approaches. Finally, the “Conclusions“ section concludes the paper and highlights its limitations.

Methods

This section aims to describe the approach and techniques employed in this study, which are divided into two main parts: the “Hybrid clustering model” for grouping patient visits based on patient-physician characteristics, and the “Robust outpatient physician scheduling model” for scheduling physicians using LRCVaR. Next, we will provide a detailed introduction to these methods.

Hybrid clustering model

This paper uses a clustering model to group outpatient data, enabling a more precise understanding of patient demand while mitigating the curse of dimensionality. The underlying principle is founded on the assumption that the joint distribution of physician and patient characteristics consists of a mixture of several unknown distributions, which allows for the classification of samples by identifying the distribution that generates them. In this section, we provide a brief overview of the outpatient physician scheduling decision-making process, followed by a detailed discussion of the clustering model that takes into account the patient-physician characteristics.

Problem setup and parameters

We assume that the department requiring scheduling operates on a decision-making of W weeks, denoted as ${\mathscr {W}} = \{1, 2, \ldots , W\},$ with each week consisting of 7 days, represented as ${\mathscr {D}} = \{1, 2, \ldots , 7\}.$ There are a total of $I$ physicians in this department, denoted as ${\mathscr {J}} = \{1, 2, \ldots , I\}.$ Patients can be categorized into $K$ classes, represented as ${\mathscr {K}} = \{1, 2, \ldots , K\}.$ The service capacity ratio of the $k$-th patient class for physician $i$ can be expressed as a value between 0 and 1, denoted as $a_{i,k},$ where $\sum _{k \in {\mathscr {K}}} a_{i,k} = 1$ for $\forall i \in {\mathscr {J}}.$ A larger service capacity ratio $a_{i,k}$ indicates a greater proportion of the $k$-th patient class among those treated by physician $i.$

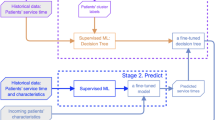
Figure 2 illustrates the decision-making process for outpatient physician scheduling. First, the joint distribution of patient-physician characteristics is established using historical outpatient records that include these features. And a clustering model is utilized to classify patients into different groups. Thus, we can estimate the service capacity ratio $a_{i,k}$ based on the results of clustering for any physician $i \in {\mathscr {J}}.$ Then, we create a robust distribution ambiguity set for each patient class and establish the corresponding service capacity constraints, based on the clustering model. Finally, we minimize the number of physicians scheduled according to these constraints and other scheduling requirements to develop a mid-term outpatient scheduling plan.

Fig. 2

Outpatient physician scheduling decision-making process.

Note that, for any given day $d \in {\mathscr {D}},$ the model considers assigning physicians to a specific day rather than to specific morning or afternoon shifts, because assignments can be adjusted based on specific circumstances in practice. And to set the scope of this paper, we make the following assumption.

Assumption 1

The joint distribution of patient-physician characteristics is a mixture of several unknown distributions, and the samples are assumed to be independently and identically distributed (i.i.d.).

The relevant symbols and definitions used in this paper are shown in Table 1, where the script uppercase letters represent sets (e.g., ${\mathscr {D}}$), bold lowercase letters represent vectors (e.g., $\varvec{y}$), and tilde denotes random variables (vectors) (e.g., $\tilde{\varvec{y}}$). $[S]$ represents the index set $\{1, 2, \ldots , S\}.$ The function $(x)^+$ denotes $\max (x, 0).$

Table 1 Symbols and definitions.

Gaussian mixture distribution-based clustering model

Assume that outpatient records consist of $p$-dimensional samples $\varvec{x}_j,$ $j \in {\mathscr {N}},$ where ${\mathscr {N}}=\{1, 2, \ldots , N\}$ and $N$ represents the number of samples. Each sample $\varvec{x}_j$ is composed of two parts, $\varvec{x}_j = [ \varvec{x}_j^{(1)}, \varvec{x}_j^{(2)}],$ where $\varvec{x}^{(1)}$ and $\varvec{x}^{(2)}$ represent the personal characteristics of physicians and patients respectively. Thus, $\varvec{x}_j$ can also be referred to as a patient-physician characteristic vector. Let ${\mathscr {N}}_i$ denote the set of sample indices for the $i$-th physician, with ${\mathscr {N}} = \bigcup _{i \in {\mathscr {J}}} {\mathscr {N}}_i.$

Under Assumption 1, the joint distribution of patient-physician characteristic vector $p( \varvec{x} | \varvec{\alpha }, \varvec{\theta })$ is mixed from unknown $K$ distributions, expressed as:

$$\begin{aligned} p( \varvec{x} | \varvec{\alpha }, \varvec{\theta }) = \sum _{k \in {\mathscr {K}}} \alpha _k \cdot \phi ( \varvec{x} | \varvec{\theta }_k), \end{aligned}$$

(1)

where $\varvec{\alpha } = [\alpha _1, \alpha _2, \ldots , \alpha _K]$ is a vector of weights, $\alpha _k \ge 0,$ and $\sum _{k \in {\mathscr {K}}} \alpha _k = 1;$ $\varvec{\theta }_k$ denotes the parameters of the $k$-th distribution. In practice, we rarely have full knowledge on the probability distribution $\phi ( {\varvec{x}} | \varvec{\theta }_k),$ but can instead infer it ambiguously using Gaussian distributions based on available data. Thus, let $\varvec{\theta }_k = ( \varvec{\mu }_k, \varvec{\Sigma }_k),$ where $\varvec{\mu }_k$ represents the mean vector, $\varvec{\Sigma }_k$ is the covariance matrix, and $\phi ( {\varvec{x}} | \varvec{\theta }_k)$ is the probability density of the Gaussian distribution. The probability density function is given by^21,22:

$$\begin{aligned} \phi ( {\varvec{x}} | \varvec{\theta }_k) = \frac{1}{\sqrt{(2\pi )^p | \varvec{\Sigma }_k|}} \exp \left( -\frac{1}{2} ( {\varvec{x}} - \varvec{\mu }_k)^T \varvec{\Sigma }_k^{-1} ( {\varvec{x}} - \varvec{\mu }_k)\right) , \end{aligned}$$

where $| \varvec{\Sigma }_k|$ denotes the determinant of the covariance matrix $\varvec{\Sigma }_k.$

Given a sample ${\varvec{x}}_j,$ $j \in {\mathscr {N}},$ the generation process can be described as follows: (a) The sample ${\varvec{x}}_j$ is selected from the $k$-th distribution with probability $\alpha _k.$ Since it is not possible to record whether the sample originates from the $k$-th distribution, a binary latent variable $r_{j,k}$ is used to represent this. If $r_{j,k}=1,$ it indicates that the sample ${\varvec{x}}_j$ comes from the $k$-th distribution; otherwise, $r_{j,k}=0.$ (2) The sample ${\varvec{x}}_j$ is generated according to the probability density $\phi ({\varvec{x}} | \varvec{\theta }_k)$. The log-likelihood function with latent variables ${\varvec{r}} = [r_{1,1}, \ldots , r_{j,k}, \ldots , r_{N,K}]$ is:

$$\begin{aligned} \ln p({\varvec{x}}, {\varvec{r}} | \varvec{\alpha }, \varvec{\theta })&= \ln \prod _{k \in {\mathscr {K}}} \left( \prod _{j \in {\mathscr {N}}} \left[ \alpha _k \cdot \phi ({\varvec{x}}_j | \varvec{\theta }_k) \right] ^{r_{j,k}} \right) = \ln \prod _{k \in {\mathscr {K}}} \left( \alpha _k^{n_k} \prod _{j \in {\mathscr {N}}} \left[ \phi ({\varvec{x}}_j | \varvec{\theta }_k) \right] ^{r_{j,k}} \right) \\&= \sum _{k \in {\mathscr {K}}} \left( n_k \ln \alpha _k + \sum _{j \in {\mathscr {N}}} r_{j,k} \ln \phi ({\varvec{x}}_j | \varvec{\theta }_k) \right) , \end{aligned}$$

where $n_k = \sum _{j \in {\mathscr {N}}} r_{j,k}.$ The maximum likelihood estimation of the hybrid clustering model (1) can be obtained using the EM algorithm^23,24.

Assume that $\hat{r}_{j,k}$ is the maximum likelihood estimator of the latent variable $r_{j,k},$ where $\hat{r}_{j,k} \in [0,1]$ represents the estimated probability that sample j belongs to class k. Therefore, the service capacity ratio $a_{i,k}$ for patient class k with physician i can be estimated by

$$\begin{aligned} \hat{a}_{i,k} = \frac{\sum _{j \in {\mathscr {N}}_i} \hat{r}_{j,k}}{|{\mathscr {N}}_i|}, \end{aligned}$$

(2)

where $\sum _{k \in {\mathscr {K}}} \hat{a}_{i,k} = 1,$ $\forall i \in {\mathscr {J}}.$

Note that choosing the number of distributions $K$ is a common practical challenge in clustering models. Since it is not feasible to determine $K$ based on the expertise of outpatient specialists and the true class labels of samples are unavailable, this paper employs two classic model evaluation methods based on the clustering data itself, as proposed in the literature, for parameter selection in completely unlabeled clustering models.

Calinski-Harabasz²⁵. The index essentially measures clustering quality by calculating the ratio of between-group variance to within-group variance. A higher index value indicates greater differences between groups and smaller differences within groups, thus reflecting better clustering performance. Let the column vector $\textbf{c}_k$ represent the centroid of class $k,$ the column vector $\textbf{c}$ represent the centroid of all samples, and ${\mathscr {N}}_k$ denote the set of indices for samples in class $k .$ The Calinski-Harabasz index is defined as:

$$\text {Calinski} = \frac{\text {tr}(B)}{\text {tr}(W)} \times \frac{|{\mathscr {N}}| - K}{K - 1},$$

where

$$B = \sum _{k \in {\mathscr {K}}} n_k \cdot ({\varvec{c}}_k - {\varvec{c}})({\varvec{c}}_k - {\varvec{c}})^T,$$

$$W = \sum _{k \in {\mathscr {K}}} \sum _{j \in {\mathscr {N}}_k} ({\varvec{x}}_j - {\varvec{c}}_k)({\varvec{x}}_j - {\varvec{c}}_k)^T,$$

$\text {tr}(B)$ and $\text {tr}(W)$ represent the trace of the between-group and the within-group variance matrix respectively.

Davies-Bouldin²⁶. The index fundamentally measures the ratio of within-group similarity to between-group distance to characterize clustering performance. A lower index value indicates smaller similarity within groups and larger distances between groups, thus suggesting better clustering performance. Let $s_k$ denote the average distance from the samples in class $k$ to their class centroid ${\varvec{c}}_k,$ and $d_{i,k}$ represent the distance between centroids ${\varvec{c}}_i$ and ${\varvec{c}}_k .$ The Davies-Bouldin index is defined as:

$$\text {Davies} = \frac{1}{K} \sum _{k \in {\mathscr {K}}} \max _{i \ne k, i \in {\mathscr {K}}} R_{i,k},$$

where

$$R_{i,k} = \frac{s_i + s_k}{d_{i,k}}.$$

Overall, the proposed hybrid clustering method effectively classifies patient demand preferences by fully leveraging the individual characteristics of both physicians and patients. Unlike previous approaches, it differs in three significant ways: it simultaneously incorporates both patient and physician characteristics, rather than solely focusing on physician preferences during scheduling, enabling more accurate resource allocation; it employs a data-driven approach to directly learn patient preference patterns from data, providing stronger generalizability; and it is particularly well-suited for small-sample scenarios, effectively addressing the issue of data sparsity caused by high-dimensional features.

Robust outpatient physician scheduling model

Typically, a hospital operates multiple outpatient departments, each staffed with a designated number of physicians specializing in similar patient groups. Due to the relative independence of each department, hospital administrative units generally formulate outpatient physician scheduling plans by department. Generally, the long-term scheduling model of outpatient physician has predetermined the level of physician allocation for each department. The mid-term outpatient physician scheduling model primarily focuses on formulating executable scheduling plans. In section, we first provide a mid-term deterministic outpatient physician scheduling model. To mitigate the risk of outpatient service capacity shortages, we further propose a robust outpatient physician scheduling model based on distribution ambiguity set, along with its solution method.

A deterministic outpatient physician scheduling model

Assume that for any physician $i \in {\mathscr {J}}$ and day $d \in D ,$ the expected outpatient demand $E[\tilde{y}_{k,d}]$ is known. Given the estimated service capacity ratio $\hat{a}_{i,k}$ for the $k$-th patient group with physician $i ,$ $\forall i \in {\mathscr {J}}, k \in {\mathscr {K}},$ we establish the Deterministic Outpatient Physician Scheduling Model (DOPSM) as follows:

$$\begin{aligned} \text {(DOPSM)} \quad&\min \sum _{i \in {\mathscr {J}}} \sum _{w \in {\mathscr {W}}} \sum _{d \in {\mathscr {D}}} \chi _{i,w,d} \end{aligned}$$

(3a)

$$\begin{aligned} \text {s.t. }&\sum _{i \in {\mathscr {J}}} \hat{a}_{i,k} \cdot c_i \cdot \chi _{i,w,d} \ge E[\tilde{y}_{k,d}], \quad \forall k \in {\mathscr {K}}, w \in {\mathscr {W}}, d \in {\mathscr {D}},\end{aligned}$$

(3b)

$$\begin{aligned}&\sum _{w \in {\mathscr {W}}} \sum _{d \in {\mathscr {D}}^w} \chi _{i,w,d} \le W \cdot T^{\max }, \quad \forall i \in {\mathscr {J}},\end{aligned}$$

(3c)

$$\begin{aligned}&\sum _{w \in {\mathscr {W}}} \sum _{d \in {\mathscr {D}}^w} \chi _{i,w,d} \ge W \cdot T^{\min }, \quad \forall i \in {\mathscr {J}},\end{aligned}$$

(3d)

$$\begin{aligned}&\sum _{w \in {\mathscr {W}}} \sum _{d \in {\mathscr {D}}} \chi _{i,w,d} \le W \cdot H^{\max }, \quad \forall i \in {\mathscr {J}},\end{aligned}$$

(3e)

$$\begin{aligned}&\sum _{w \in {\mathscr {W}}} \sum _{d \in {\mathscr {D}}} \chi _{i,w,d} \ge W \cdot H^{\min }, \quad \forall i \in {\mathscr {J}},\end{aligned}$$

(3f)

$$\begin{aligned}&\chi _{i,w,d} \in \{0, 1, 2\}, \quad \forall i \in {\mathscr {J}}, w \in {\mathscr {W}}, d \in {\mathscr {D}}. \end{aligned}$$

(3g)

The (3a) minimizes the number of outpatient shifts. The (3b) ensures that the outpatient service capacity allocated for each patient category per day exceeds $E[\tilde{y}_{k,d}],$ where $\hat{a}_{i,k} \cdot c_i$ represents the average outpatient service capacity for category $k$ patients per shift by physician $i$. The (3c)–(3f) consider the limits on the number of outpatient shifts. The (3c) and (3d) limit the number of holiday outpatient shifts for each physician within the range $[W \cdot T^{\min }, W \cdot T^{\max }];$ The (3e) and (3f) limit the total number of outpatient shifts for each physician within the range $[W \cdot H^{\min }, W \cdot H^{\max }].$ The (3g) specifies the decision variable constraints, indicating the number of outpatient shifts assigned to physician $i$ on day $d$ of week $w.$ Since a physician can have a maximum of two outpatient shifts per day, i.e., morning and afternoon shifts, the decision variable is less than or equal to 2.

However, outpatient physician scheduling based on $E[\tilde{y}_{k,d}]$ may still face significant risks of outpatient service capacity shortages. This is primarily because the true distribution of outpatient demand is generally difficult to obtain. Additionally, in the case of small samples, the sample average is likely to deviate significantly from the $E[\tilde{y}_{k,d}],$ resulting in actual demand constraints not being met. To address this, this section further constructs a likelihood-robust distribution ambiguity set based on the expected demand $E[\tilde{y}_{k,d}]$ and introduces the LRCVaR measure, which considers tail risks to control the probability of outpatient service capacity shortages.

Robust outpatient service capacity constraints

Let $\varvec{\delta } \in Q \subseteq \mathbb {R}^m$ be the outpatient service capacity decision vector, and let the outpatient demand $\tilde{{\varvec{y}}}:\Xi \rightarrow \Omega \subseteq \mathbb {R}^m$be a random vector defined on a measurable space $(\Xi , {\mathscr {F}}).$ The function $h(\varvec{\delta }, \tilde{{\varvec{y}}}): Q \times \Xi \rightarrow \mathbb {R}$ represents the outpatient service capacity shortfall function. Assume that the support of $\tilde{{\varvec{y}}},$ $\Xi = \{{\varvec{y}}_1, {\varvec{y}}_2, \dots , {\varvec{y}}_S\},$ is a finite discrete set, where ${\varvec{y}}_i$ is observed with $N_i$ independent samples, hence $N = \sum _{i \in [S]} N_i$ is the total number of samples. Let ${\mathscr {P}}(\Xi )$ denote all probability measures on the support $\Xi ,$ and let $\hat{{\mathbb {P}}} \in {\mathscr {P}}(\Xi )$ represent the empirical distribution of the outpatient demand $\tilde{{\varvec{y}}}.$ The empirical outpatient service capacity constraint (4) can replace the expected outpatient service capacity constraint (3b) as follows:

$$\begin{aligned} \sum _{i \in [S]} \left[ \frac{N_i}{N} \cdot h(\varvec{\delta }, {\varvec{y}}_i)\right] \le 0. \end{aligned}$$

(4)

Although according to the law of large numbers, for any given decision variable $\varvec{\delta },$ the sample average of outpatient service capacity shortages converges to the true expectation^27,28. However, as mentioned earlier, the estimation error generated by the sample, especially in the case of small samples, can lead to shortage risks and decision failures^29,30. Thus, we introduce a data-driven robust optimization decision-making framework, which is constructed based on a distribution ambiguity set, denoted as ${\mathscr {B}}(r),$ of outpatient demand $\tilde{{\varvec{y}}}$³¹. Due to the desirable statistical properties of the likelihood function for the discrete random vector $\tilde{{\varvec{y}}},$³² proposed constructing the distribution ambiguity set ${\mathscr {B}}(r)$ using the distribution likelihood function, defined as:

Definition 1

Given $r \ge 0,$ a likelihood robust distribution ambiguity set is defined as:

$$\begin{aligned} {\mathscr {B}}(r) = \left\{ {\varvec{p}} \in \mathbb {R}^S \mid {\mathscr {L}}({\mathbb {P}}, \hat{{\mathbb {P}}}) \le r, \sum _{i \in [S]} p_i = 1, p_i \ge 0, \forall i \in [S] \right\} , \end{aligned}$$

(5)

where ${\mathscr {L}}({\mathbb {P}}, \hat{{\mathbb {P}}}) = -\sum _{i \in [S]} N_i \cdot \ln p_i$ is the negative log-likelihood function.

It is evident that ${\mathscr {B}}(r)$ includes all the distributions from ${\mathscr {P}}(\Xi )$ whose likelihood functions are greater than $e^{-r}.$ The larger the value of $r,$ the more distributions $B(r)$ includes. Due to the statistical properties of the distribution likelihood function, the relevant properties of ${\mathscr {B}}(r)$ are shown as follows.

Proposition 1

Assuming the prior distribution of ${\varvec{p}}$ follows a Dirichlet distribution with parameter $\varvec{\alpha },$ denoted as $Dir(\varvec{\alpha }),$ and ${\varvec{N}} = [N_1, N_2, \dots , N_S]$ are the observed historical data. Given ${\varvec{N}}$ and $\varvec{\alpha },$ the posterior probability that ${\varvec{p}}\in {\mathscr {B}}(r)$ satisfies:

$$\begin{aligned} {\mathbb {P}}_{{\varvec{N}}} \{{\varvec{p}} \in {\mathscr {B}}(r)\} \propto \int _{{\varvec{p}} \in {\mathscr {P}}(\Xi )} \prod _{i \in [S]} p_i^{N_i + \alpha _i - 1} \cdot {\mathbb {I}}\left( \sum _{i \in [S]} -N_i \cdot \ln p_i \le r\right) d{\varvec{p}}, \end{aligned}$$

(6)

where ${\mathbb {I}}(x)$ is the indicator function, ${\mathbb {I}}(x) = 1$ if condition $x$ holds, otherwise ${\mathbb {I}}(x) = 0.$ $x \propto y$ indicates that $x$ is proportional to $y$.

Proposition 2

Given the observed historical data ${\varvec{N}} = [N_1, N_2, \dots , N_S]$ and a significance level $\alpha \in (0, 1),$ define $r_{{\varvec{N}}}$ as the solution that satisfies the posterior probability ${\mathbb {P}}_{{\varvec{N}}} \{{\varvec{p}} \in {\mathscr {B}}(r_{{\varvec{N}}})\} = 1 - \alpha.$ Here, $r_{{\varvec{N}}}$ is a random variable relative to the observed data ${\varvec{N}},$ and as the total sample size $N = \sum _{i \in [S]} N_i \rightarrow +\infty,$

$$\begin{aligned} r_{{\varvec{N}}} + \sum _{i \in [S]} \left( N_i \cdot \log \frac{N_i}{N}\right) \xrightarrow {\text {p}} \frac{1}{2} \chi _{S-1, 1-\alpha }^2. \end{aligned}$$

(7)

Here, $\chi _{S-1, 1-\alpha }^2$ denotes the $1-\alpha$ quantile of the chi-squared distribution with $S-1$ degrees of freedom.

Proposition 1 presents the posterior probability of ${\varvec{p}} \in {\mathscr {B}}(r)$ from a Bayesian statistical perspective. When there is no prior knowledge of the distribution of ${\varvec{p}},$ the Dirichlet distribution is typically used, making the posterior probability $f({\varvec{p}}|{\varvec{N}})$ also follow a Dirichlet distribution. For general prior distributions, however, the specific form of the posterior probability $f({\varvec{p}}|{\varvec{N}})$ is often difficult to derive directly. Proposition 2 provides an asymptotic distribution for the robust control parameter $r_{{\varvec{N}}},$ based on the posterior probability of ${\varvec{p}} \in {\mathscr {B}}(r),$ offering theoretical support for the selection of the robust control parameter. Given the sample size $N$ and significance level $\alpha,$ the robust control parameter can be set as

$$\begin{aligned} r^* = \frac{1}{2} \chi _{S-1, 1-\alpha }^2 - \sum _{i \in [S]} \left( N_i \cdot \ln \frac{N_i}{N}\right) , \end{aligned}$$

(8)

which ensures that ${\mathbb {P}}_{{\varvec{N}}} \{{\varvec{p}} \in {\mathscr {B}}(r^*)\} = 1 - \alpha$ holds. In our proposed likelihood robust outpatient physician scheduling model, the required service capacity $\sup _{{\mathbb {P}} \in {\mathscr {B}}(r)} {\mathbb {E}}_{{\mathbb {P}}} [\tilde{y}_{k,d}]$ increases in the parameter r. Thus, increasing the value of r can improve the model’s robustness. However, an excessively high value of the parameter r may require unnecessary service capacity, leading to the over protection of robustness. In Proposition 2, we showed that the parameter r has an asymptotic distribution as the number of data increases to $+\infty.$ This asymptotic property implies choosing $r^*$ in Eq. (8). The underlying rationale is that the constructed likelihood robust distribution ambiguity set ${\mathscr {B}}(r^*)$ contains the true probability distribution ${\mathbb {P}}$ with a high confidence level of $1-\alpha$ in the asymptotic property.

According to Definition 1, the Likelihood Robust (LR) outpatient service capacity constraint can be expressed as

$$\begin{aligned} \sup _{{\mathbb {P}} \in {\mathscr {B}}(r^*)} {\mathbb {E}}_{{\mathbb {P}}} [h(\varvec{\delta }, \tilde{{\varvec{y}}})] \le 0. \end{aligned}$$

(9)

Compared to the empirical outpatient service capacity constraint (4), the likelihood robust outpatient service capacity constraint (9) considers all distributions in ${\mathscr {B}}(r)$ and selects the worst distribution, which maximizes the expected service capacity shortage, to optimize capacity allocation. This constraint requires decision-making for worst-case scenarios regarding capacity shortages.

Overall, we assumed that the true probability distribution ${\mathbb {P}}$ is unknown but its distance from the empirical probability distribution $\hat{{\mathbb {P}}}$ is less than a delicately designed parameter r. This assumption is intrinsic in robust optimization³¹. In the context of outpatient scheduling, we constructed a likelihood robust distribution ambiguity set in terms of outpatient demand $\tilde{{\varvec{y}}}$. The underlying rationale is that outpatient demand is randomly distributed and its empirical probability distribution $\hat{{\mathbb {P}}}$ usually does not represent the true one. The constructed likelihood robust distribution ambiguity set contains the true probability distribution ${\mathbb {P}}$ with a high confidence level of $1-\alpha,$ as proved in Proposition 2. Then, our proposed likelihood robust outpatient physician scheduling model (LROPSM), which will be mentioned later, considered the worst-case probability distribution in the constructed likelihood robust distribution ambiguity set. With this, our optimized physician schedules remain valid for the true probability distribution ${\mathbb {P}}.$

In addition, although the likelihood robust outpatient service capacity constraint significantly reduces the risk associated with sample estimation errors, there remains a substantial risk of capacity shortages. To prevent congestion during peak times, we further propose LRCVaR measure based on our likelihood robust distribution ambiguity set ${\mathscr {B}}(r).$ The literature often employs conditional value-at-risk (CVaR;³³) to quantify average losses in the tail, defined as

$$\text {CVaR}_{1-\alpha }(\tilde{y}) = \inf _{t \in \mathbb {R}} \left\{ \frac{1}{\alpha } {\mathbb {E}}_{{\mathbb {P}}} [(\tilde{y} + t)^+] - t \right\} .$$

Then, the CVaR outpatient service capacity constraint can be expressed as:

$$\begin{aligned} \inf _{t \in \mathbb {R}} \left\{ \frac{1}{\alpha } {\mathbb {E}}_{{\mathbb {P}}} [(h(\varvec{\delta }, \tilde{{\varvec{y}}}) + t)^+] - t \right\} \le 0. \end{aligned}$$

(10)

This paper proposes the LRCVaR measure, and the LRCVaR outpatient service capacity constraint can be defined as:

$$\begin{aligned} \text {LRCVaR}_{1-\alpha }(h(\varvec{\delta }, \tilde{{\varvec{y}}})) = \inf _{t \in \mathbb {R}} \left\{ \frac{1}{\alpha } \sup _{{\mathbb {P}} \in {\mathscr {B}}(r^*)} {\mathbb {E}}_{{\mathbb {P}}} [(h(\varvec{\delta }, \tilde{{\varvec{y}}}) + t)^+] - t \right\} \le 0. \end{aligned}$$

(11)

Note that³⁴ proposed the RCVaR (Robust CVaR) with moment-based robust distribution ambiguity set, and the RCVaR outpatient service capacity constraint can be expressed as

$$\begin{aligned} \text {RCVaR}_{1-\alpha }(h(\varvec{\delta }, \tilde{{\varvec{y}}})) = \bar{{\varvec{y}}}^T \varvec{\delta } + \sqrt{\frac{1-\alpha }{\alpha }} \sqrt{\varvec{\delta }^T \Sigma \varvec{\delta }}\le 0. \end{aligned}$$

(12)

Here, $h(\varvec{\delta }, \tilde{{\varvec{y}}}) = \bar{{\varvec{y}}}^T \varvec{\delta } + \tilde{{\varvec{z}}}^T \varvec{\delta }$ is a linear function, where $\bar{{\varvec{y}}}$ is the mean vector of $\tilde{{\varvec{y}}},$ $\tilde{{\varvec{z}}} = \tilde{{\varvec{y}}} - \bar{{\varvec{y}}},$ and $\Sigma$ is the covariance matrix of $\tilde{{\varvec{z}}}.$ Since both LRCVaR and RCVaR estimate CVaR within a robust optimization framework, the outpatient service capacity constraints based on LRCVaR and RCVaR ensure a certain level of robustness in decision-making. Compared to the LRCVaR, the RCVaR is also an upper bound of CVaR, but it only utilizes the first and second moments of the sample, whereas the LRCVaR uses all available information from the sample.

The likelihood robust outpatient physician scheduling model (LROPSM)

The robust outpatient physician scheduling models constructed based on the constraints (9), (11), and (12) are denoted as LR-OPSM, LRCVaR-OPSM and RCVaR-OPSM, respectively. We introduce them as follows.

$$\begin{aligned} & \text {(LR-OPSM)} \quad \min \sum _{i \in {\mathscr {J}}} \sum _{w \in {\mathscr {W}}} \sum _{d \in {\mathscr {D}}} \chi _{i,w,d} \nonumber \\ & \text {s.t. }\sum _{i \in {\mathscr {J}}} \hat{a}_{i,k} \cdot c_i \cdot \chi _{i,w,d} \ge \sup _{{\mathbb {P}} \in {\mathscr {B}}(r^*)} {\mathbb {E}}_{{\mathbb {P}}} [\tilde{y}_{k,d}], \quad \forall k \in {\mathscr {K}}, w \in {\mathscr {W}}, d \in {\mathscr {D}},\nonumber \\ & (3c)-(3g). \end{aligned}$$

(13a)

$$\begin{aligned} & \text {(LRCVaR-OPSM)} \quad \min \sum _{i \in {\mathscr {J}}} \sum _{w \in {\mathscr {W}}} \sum _{d \in {\mathscr {D}}} \chi _{i,w,d} \nonumber \\ & \text {s.t. }\sum _{i \in {\mathscr {J}}} \hat{a}_{i,k} \cdot c_i \cdot \chi _{i,w,d} \ge \inf _{t \in \mathbb {R}} \left\{ \frac{1}{\alpha } \sup _{{\mathbb {P}} \in {\mathscr {B}}(r^*)} {\mathbb {E}}_{{\mathbb {P}}}[(\tilde{y}_{k,d} + t)^+] - t \right\} , \forall k \in {\mathscr {K}}, w \in {\mathscr {W}}, d \in {\mathscr {D}},\nonumber \\ & (3c)-(3g). \end{aligned}$$

(14a)

$$\begin{aligned} & \text {(RCVaR-OPSM)} \quad \min \sum _{i \in {\mathscr {J}}} \sum _{w \in {\mathscr {W}}} \sum _{d \in {\mathscr {D}}} \chi _{i,w,d} \nonumber \\ & \text {s.t. }\sum _{i \in {\mathscr {J}}} \hat{a}_{i,k} \cdot c_i \cdot \chi _{i,w,d} \ge \bar{y}_{k,d}+\sqrt{\frac{1-\alpha }{\alpha }}* \sigma _{d,k}, \forall k \in {\mathscr {K}}, w \in {\mathscr {W}}, d \in {\mathscr {D}}, \nonumber \\ & (3c)-(3g). \end{aligned}$$

(15a)

Solution methods to LROPSM

This section presents the solution methods for the LR-OPSM and LRCVaR-OPSM models. Assuming the support $\Xi _{k,d} = \{y_{k,d}^{(1)}, y_{k,d}^{(2)}, \ldots , y_{k,d}^{(S)}\}$ of $\tilde{y}_{k,d}$ is a finite discrete set, where the number of observed independent samples for $y_{k,d}^{(i)}$ is $N_{k,d}^{(i)},$ the total sample size is given by $N_{k,d} = \sum _{i \in [S]} N_{k,d}^{(i)}.$

Note that the original problem $\sup _{{\mathbb {P}} \in {\mathscr {B}}(r)} {\mathbb {E}}_{{\mathbb {P}}} [\tilde{y}_{k,d}]$ in LR-OPSM is equivalent to

$$\begin{aligned} \begin{aligned}&\max \sum _{i \in [S]} y_{k,d}^{(i)} \cdot p_i \quad \text {s.t.}-\sum _{i \in [S]} N_{k,d}^{(i)} \cdot \ln p_i \le r^*, \sum _{i \in [S]} p_i = 1, p_i \ge 0, \forall i \in [S]. \end{aligned} \end{aligned}$$

(16)

Its dual problem is:

$$\begin{aligned} \begin{aligned}&\min \lambda *\left( r^* - N + \sum _{i \in [S]} N_i \cdot \ln N_i \right) + \mu + \sum _{i \in [S]} N_i \cdot \lambda \cdot \ln \frac{\lambda }{h^{(i)}}\\ \text {s.t.}&~~~~~~~~h^{(i)} = \mu - y_{k,d}^{(i)}, \quad h^{(i)} \ge 0, \quad \forall i \in [S], \quad \lambda \ge 0. \end{aligned} \end{aligned}$$

(17)

Given that the primal problem (16) constraints satisfy Slater’s conditions, the primal and dual problems are equivalent by strong duality in convex programming. Let $\delta _{k,d}^*$ be the optimal solution for the dual problem (17), then the (13a) in LR-OPSM can be reformulated as:

$$\sum _{i \in {\mathscr {J}}} \hat{a}_{i,k} \cdot c_i \cdot \chi _{i,w,d} \ge \delta _{k,d}^*, \quad \forall k \in {\mathscr {K}}, w \in {\mathscr {W}}, d \in {\mathscr {D}}.$$

Similarly, given $t \in \mathbb {R},$ the primal problem $\sup _{{\mathbb {P}} \in {\mathscr {B}}(r)} {\mathbb {E}}_{{\mathbb {P}}}[(\tilde{y}_{k,d} + t)^+]$ in LRCVaR-OPSM is equivalent to:

$$\max \sum _{i \in [S]} (y_{k,d}^{(i)} + t)^+ \cdot p_i$$

subject to the same constraints as in (16). Its dual problem is also formulated with the same objective function as (17), except that the constraints are replaced by

$$h^{(i)} = \mu - (y_{k,d}^{(i)} + t)^+, \quad h^{(i)} \ge 0, \quad \forall i \in [S], \quad \lambda \ge 0.$$

The original problem in LRCVaR-OPSM and its dual are also equivalent, by strong duality theory of convex programming. Let $\delta _{(k,d)}^{(t)}$ denote the optimal solution of the dual problem for a given $t \in \mathbb {R}$. Although $t$ can take any real value, we consider $\tilde{y}_{k,d} \ge 0.$ When $t > 0,$ the expression $\alpha ^{-1} {\mathbb {E}}_{{\mathbb {P}}}[(\tilde{y}_{k,d} + t)^+] - t$ is a monotonically increasing function of $t.$ Conversely, when $t < -\max \{ y_{k,d}^{(1)}, y_{k,d}^{(2)}, \ldots , y_{k,d}^{(S)} \},$ the expression becomes a monotonically decreasing function of $t .$ Therefore, the optimal value of $t$ must satisfy the inequality $-\max \{ y_{k,d}^{(1)}, y_{k,d}^{(2)}, \ldots , y_{k,d}^{(S)} \} \le t \le 0.$

Assume ${\mathscr {T}} _{k,d}$ is a set of discrete value on the continuous interval $[-\max \{ y_{k,d}^{(1)}, y_{k,d}^{(2)}, \ldots , y_{k,d}^{(S)} \}, 0].$ For example, we can discretize this interval with a step size of 1. Consequently, the (14a) in LRCVaR-OPSM can be reformulated as:

$$\begin{aligned} \sum _{i \in {\mathscr {J}}} \hat{a}_{i,k} \cdot c_i \cdot \chi _{i,w,d} \ge \min _{t \in {\mathscr {T}}_{k,d}} \left\{ \frac{1}{\alpha } \delta _{k,d}^{(t)} - t \right\} , \quad \forall k \in {\mathscr {K}}, w \in {\mathscr {W}}, d \in {\mathscr {D}}. \end{aligned}$$

(18)

Thus, solving the LRCVaR-OPSM can be transformed into solving several deterministic convex programming problems, which ensures the solvability of LRCVaR-OPSM.

Finally, we present the complete solution method for the LRCVaR-OPSM model based on a hybrid clustering of patient-physician characteristics. The process is outlined in Table 2 as follows:

Table 2 The solution of LRCVaR-OPSM based on a hybrid clustering of patient-physician characteristics.

In summary, the proposed LROPSM is a data-driven robust optimization framework designed to address challenges arising from stochastic demand. Unlike deterministic demand models, it explicitly considers the impact of demand variability. Compared to approaches that rely on random simulation or empirical distributions to describe demand fluctuations, our method emphasizes a robust optimization paradigm. Specifically, we construct a likelihood robust ambiguity set to account for decision-making under worst-case service shortages and introduce LRCVaR to provide probabilistic guarantees against tail risks. Moreover, the ambiguity set is more precise, as it incorporates the likelihood function of the samples, ensuring favorable convergence to the true demand distribution as the sample size increases.

Our proposed method adopted a separated estimation and optimization, also known as “predict-then-optimize”. This method first classifies patients into groups and then optimizes physician schedules to satisfy the demand for each patient group. Because the two steps are separate, the overall solution might not be the best possible. If the classification isn’t tailored to the optimization’s objective, the combined result isn’t optimal. To address this suboptimality issue, we may resort to the joint estimation and optimization method in the future.

Results and discussion

The experimental dataset was sourced from the outpatient database of the dermatology department at a specialized hospital for skin diseases in Guangzhou City in 2019. Data were accessed on December 18, 2022 for this study. The authors did not have access to information that could identify individual participants. Only de-identified patient information was used in this study. This department recorded 217,000 outpatient visits throughout the year with a staff of 24 physicians. As illustrated in Fig. 1, there exists a variation in the distribution of outpatient visits based on different characteristics such as patient disease types or physician titles. After performing the Kruskal-Wallis test, the significance level (p-values) were all less than 0.01, indicating significant differences in patient demands under the associated physician and patient characteristics.

Clustering model analysis

The experiment selected 196,000 samples from January to November 2019 as the training set for the clustering model.

According to literature review and data analysis, as shown in Table 3, eight common physician and patient characteristics were selected. Among the outpatient physicians, the majority are female, accounting for 58.3%; those with a master’s degree are the most prevalent, also representing 58.3%; most hold the position of attending physician, accounting for 54.2%; and the largest specialty is dermatology and venereology, accounting for 66.6%. Among outpatient patients, females predominate, comprising 53.2%; patients with allergic dermatitis are the most numerous, at 33.9%; the average age of patients is 34 years, and the average cost per visit is 409.6 RMB. For our experimental data, Pearson correlation analysis indicates that at the 0.01 significance level, the absolute values of the correlation coefficients among all variables are less than 0.1, suggesting no significant linear correlation exists between the variables.

Table 3 Physician and patient characteristics.

Furthermore, the experiment employed the Calinski-Harabasz and Davies-Bouldin as model evaluation criteria to determine the number of clusters. The horizontal axis of Fig. 3 represents the number of clusters, the left vertical axis shows the Calinski-Harabasz index, and the right vertical axis shows the Davies-Bouldin index. The results indicate that the metrics stabilize when the number of clusters exceeds 21 and show a reversal trend beyond 29. To prevent overfitting, an initial cluster count of 21 is chosen. Additionally, due to five categories having sample sizes below 1000, to avoid sparsity, these categories are merged, leading to a final cluster count of 17.

Fig. 3

Model performance on different evaluation criteria.

Finally, the service capacity ratio $\hat{a}_{i,k}$ for each patient category with each physician is estimated, based on the clustering results. In Fig. 4, the horizontal axis represents individual physician $i ,$ and the vertical axis represents cluster categories $k.$ Darker colors indicate larger values of $\hat{a}_{i,k}.$ The results show that 11 physicians have a maximum service capacity ratio exceeding 0.8, and 21 doctors exceed 0.5, with the highest $\hat{a}_{22,16}$ being 0.921, indicating that physician 22 primarily serves patients in category 16. This demonstrates that the clustering effectively distinguishes different patient-physician groups, which directly addresses Research Question (1)-stratifying patient preferences using clustering methods.

Fig. 4

Service capacity ratio of each patient category for the physicians.

Service capacity analysis

This section compares demand estimation methods under different parameter settings, where the demand $\tilde{y}$ is randomly generated in the experiment. For different distributions and sample sizes, the expected values ${\mathbb {E}}_{{\mathbb {P}}} [\tilde{y}]$ estimated by LR, LRCVaR, and RCVaR are used as the outpatient service capacity $\delta ^*.$ The experiment randomly generates demand samples following normal, Poisson, uniform, and exponential distributions, with the normal distribution having a mean of 50 and a standard deviation of 15, while the other distributions have a mean of 50. These distributions exhibit notable differences in tail heaviness, with the exponential distribution being the heaviest, followed by uniform and normal distributions, and the Poisson distribution being the lightest. To minimize the risk of service capacity shortages, the significance level $\alpha$ is set at 0.05. Since the likelihood robust distribution ambiguity set is applicable only to discrete distributions, the following data preprocessing steps are undertaken: (1) Truncate the data to ensure it falls within the range of 0–100. (2) Discretize the data with a bin length of 10 to facilitate frequency calculation, replacing each group’s value with the bin center.

First, the experiment compares the outpatient service capacity $\delta ^*$ allocated by LR, LRCVaR, and RCVaR. Given the demand estimation method, sample distribution, and sample size, the experiment randomly generates 10 datasets, calculates the corresponding $\delta ^*$ for each, and takes the average as the final $\delta ^*.$ In Fig. 5, the horizontal axis represents the sample size, while the vertical axis represents the service capacity $\delta ^* .$ The results show that with small sample sizes, the service capacity allocated by LR is higher and deviates significantly from the sample average. As the sample size increases, the service capacity allocated by LR gradually declines, and the difference from the sample average diminishes, stabilizing over time. According to Proposition 2, as the sample size $N$ approaches infinity, the maximum likelihood estimate of the demand distribution converges to the true distribution, ensuring that the likelihood robust distribution ambiguity set ${\mathscr {B}}(r^*)$ includes the true distribution with a probability of $1 - \alpha.$ Therefore, the conservativeness of the decision decreases with increasing sample size $N$ and eventually stabilizes.

Fig. 5

Comparison of outpatient service capacity $\delta.$

Compared to RCVaR, LRCVaR allocates less service capacity with greater precision. For example, with the exponential distribution, the 95th percentile of the sample is 100 due to its tail heaviness. LRCVaR allocates a service capacity of exactly 100, while RCVaR allocates approximately 188.2. This is because RCVaR only utilizes the first and second moments of the sample, leading to greater conservativeness in decision-making. Finally, as the tail heaviness of the distribution decreases, the gap between RCVaR and LRCVaR also narrows. For exponential, uniform, normal, and Poisson distributions, the differences are approximately 88.2, 76.2, 22.1, and 13.6, respectively. Thus, the greater the tail heaviness of the distribution, the more pronounced the advantage of LRCVaR.

Additionally, the experiment compares the probabilities of service capacity shortages under LR, LRCVaR, and RCVaR. Given the allocated service capacity $\delta ^*,$ 5000 demand samples are randomly generated, and the proportion of samples exceeding $\delta ^*$ is calculated as the probability of service capacity shortage. In Fig. 6, the horizontal axis represents the sample size, and the vertical axis represents the probability of service capacity shortage, with the grey dashed line indicating a significance level $\alpha$ of 0.05. The results show that with increasing sample size, the probability of service capacity shortages under LR significantly increases and eventually stabilizes. At low sample sizes, LR allocates higher service capacities to guard against uncertainty, reducing as sample sizes increase and thereby stabilizing, reflecting corresponding changes in the probability of shortages. Both LRCVaR and RCVaR have service capacity shortage probabilities below the significance level $\alpha,$ with LRCVaR’s slightly higher than RCVaR’s. Taking the normal distribution as an example, the shortage probability under LRCVaR is about 0.24%, higher than RCVaR’s 0%. Overall, both LRCVaR and RCVaR exhibit strong capabilities in mitigating tail risks, adapting to both large and small sample scenarios, but LRCVaR’s conservatism is superior to RCVaR’s.

It is important to note that this part of the analysis is based on synthetic sample data generated from a stochastic distribution function, focusing on the intuitive performance of different methods in a low-noise setting. This corresponds to Research Question (2)-optimizing the allocation of physician service capacity.

Fig. 6

Comparison of the probability of outpatient service capacity shortage.

Scheduling model analysis

This section compares the outpatient doctor scheduling plans under different parametric backgrounds. Samples from January to November 2019, spanning 48 weeks, were used as the model’s training set for the clustering model and to generate random demands $\tilde{y}_{k,d}.$ Samples from December 2019, totaling 4 weeks, were used as the test set to evaluate the performance of the scheduling plan in terms of outpatient service capacity shortages and surplus. Initially, the service capacity ratio $\hat{a}_{i,k}$ was calculated based on the results of clustering model. For the random demand $\tilde{y}_{k,d}$ of class $k$ patients on day $d,$ samples from the training set were used as historical data. If there is no outpatient data for patient class $k$ on day $d,$ the historical data for that day are set to zero, thus each patient class has a total of 48 samples. Lastly, as the likelihood robust distribution set is only applicable to discrete distributions, each piece of historical data was discretized into intervals of 10 for ease of calculating frequency counts for each group, with each group’s value represented by the midpoint of the interval.

Table 4 Comparison of service capacity shortage and excess for different estimation methods.

First, the experiment compares the monthly scheduling plan’s performance on outpatient service capacity. Data from December 2019, covering 4 weeks, are used as the test set to evaluate service capacity shortages and surpluses. The Mean reports the average daily service capacity shortage (or surplus) for each patient category; the Max reports the daily maximum shortage (or surplus); and the Prob(%) reports the likelihood of daily shortages (or surpluses). Based on the 95th, 98th percentiles, and maximum values of historical data, the capacity per outpatient shift $c_i$ is set at 60, 70, and 80, with a significance level $\alpha$ of 0.1. To illustrate the demand estimation method’s impact on the number of physicians, scheduling constraints (3c)–(3f) are temporarily ignored.

As shown in Table 4, LR outperforms the Sample Average in service capacity shortage metrics. For instance, at $c_i = 70 ,$ LR’s average and maximum service capacity shortages were 4.3 and 104.0 respectively, representing reductions of 51.1% and 0.7% compared to the Sample Average. However, LR still exhibits a significant shortage probability, reaching 21.0% even when $c_i$ is at the maximum of 80. In comparison, LRCVaR outperforms RCVaR in surplus metrics while ensuring the probability of service capacity shortages remains below the significance level of 0.1. For $c_i = 70 ,$ LRCVaR’s average and maximum service capacity surpluses are 57.2 and 333.4, respectively, decreasing by 10.3% and 2.6% compared to RCVaR. Thus, at the same significance level, LRCVaR generates fewer outpatient shifts and exhibits lower decision conservativeness

Table 5 Comparison of computational accuracy of the LRCVaR-OPSM.

Next, the experiment compares the computational accuracy of the LRCVaR-OPSM model at different scales. The maximum service capacity per outpatient shift $c_i$ is set at 80, with a significance level $\alpha$ of 0.1. The minimum and maximum number of outpatient shifts on holidays per week are set at $T^{\min } = 1$ and $T^{\max } = 3 ,$ respectively, while the minimum and maximum total outpatient shifts per week are $H^{\min } = 3$ and $H^{\max } = 12 .$ To assess the model’s accuracy at various scales, the decision periods $W$ are set to 2, 3, and 4, and the number of clusters $K$ is set to 5, 12, and 17. The branch-and-price algorithm from Gurobi 9.1 is used to solve the model, reporting the optimal objective upper bound obtained within a given time and the gap between the upper and lower bounds. A gap of 0.0 indicates that the optimal solution has been found. To avoid solving large-scale integer programming models, a rolling scheduling approach was employed, where short-term schedules are created and repeated to form long-term plans. Thus, the rolling schedule provides an upper bound for the optimal solution. The experiment generates a schedule for one week as the short cycle and repeats it for several weeks. As shown in Table 5, the solving time for branch-and-price increases with the model scale. When the number of clusters is 5, the algorithm can quickly obtain optimal solutions for schedules within 4 weeks. However, when the number of clusters exceeds 5, while the algorithm may not find optimal solutions within the allotted time, the gap between the optimal bounds remains under 2%, indicating that quality feasible solutions are found. Although rolling scheduling can quickly yield feasible solutions, its optimal objective is higher than the upper bound of the branch-and-price method. As the decision period increases, the gap between the two approaches widens. Finally, as the number of clusters increases, so does the number of outpatient shifts. For example, with a 2-week decision period, increasing the number of clusters from 5 to 17 by 240.0% raises the number of outpatient shifts from 202 to 294, an increase of 45.5%. While more clusters enhance demand management precision, they also necessitate greater outpatient service capacity to mitigate uncertainty in patient demand, leading to an increase in the number of outpatient shifts.

Finally, the experiment analyzes the service capacity constraints for each patient category. For the $k$-th category of patients, the tension in outpatient service capacity can be measured by the ratio of estimated demand to maximum service capacity. Let $E_k = \max _{d \in {\mathscr {D}}} \text {LRCVaR}_{(1 - \alpha )}(\tilde{y}_{k,d})$ represent the estimated demand using LRCVaR, and $C_k = \sum _{i \in {\mathscr {J}}} 2 \cdot \hat{a}_{i,k} \cdot c_i$ denote the maximum service capacity without considering the scheduling constraints (3c)–(3f). Thus, the tension in outpatient service capacity for the $k$-th category can be assessed using $\frac{E_k}{C_k}.$ The maximum service capacity per outpatient shift $c_i$ is set at 80, with a significance level $\alpha$ of 0.1.

As shown in Fig. 7, five patient categories have $\frac{E_k}{C_k}$ values exceeding 0.5, with the $12$-th category having the highest ratio of approximately 0.6. Figure 4 indicates that the $12$-th category tends to choose physicians 14 and 5, with service capacity proportions of 0.4 and 0.8, respectively, indicating limited overall service capacity for this group. Additionally, the $12$-th category accounts for the seventh-highest visit volume among all patient types, comprising 8.0% of the total demand. Since over 67.9% of patients in the $12$-th category are diagnosed with allergic dermatitis and skin infections, and are treated by chief physicians specializing in dermatology and venereology, it is evident that the demand from these patients represents a significant bottleneck in outpatient service capacity management.

This part of the experimental results relates to Research Question (2) and (3)- integrating a data-driven approach. This section employs real-world data to evaluate the effectiveness of our data-driven method and demonstrates the robustness and computational accuracy advantages of the proposed approach.

Fig. 7

Service capacity saturation level under different patient categories.

Conclusions

The key findings of this study directly align with its research objectives: (1) Demand Stratification via Hybrid Clustering–The proposed hybrid clustering model effectively classifies patient demand based on physician-patient characteristics, capturing patient preferences without requiring labeled data. (2) Tail Risk Management with LRCVaR–The LRCVaR measure provides a more effective approach to mitigating tail risks of service shortages compared to traditional methods, ensuring a balance between risk control and decision conservativeness. (3) Robustness in Scheduling under Uncertainty–The likelihood robust optimization framework enhances scheduling reliability, particularly in small-sample scenarios, by ensuring that decision conservativeness decreases as sample size increases. These findings validate the effectiveness of the proposed framework in improving outpatient scheduling efficiency, optimizing physician-patient matching, and ensuring stable service capacity under uncertain demand conditions.

The practical significance of the proposed method lies in addressing critical challenges faced by hospitals, including medical personnel shortages and rising patient demand, particularly in outpatient departments, which play a vital role in public healthcare services. Inefficient scheduling often leads to service capacity shortages, compromising care quality and increasing patient wait times, while over-scheduling results in resource wastage and higher operational costs. By accounting for physician-patient heterogeneity and modeling uncertain demand, the proposed framework ensures reliable patient demand satisfaction, optimizes resource allocation, and enhances scheduling efficiency, offering a robust and scalable solution for real-world healthcare operations.

It is important to note that data is key to our proposed method, as it is a data-driven model. Accurate data, including patient and physician characteristics and preferences, should be collected and integrated into the scheduling system, allowing for better alignment of resources with patient needs. Additionally, continuous monitoring of system performance, such as patient wait times, physician workload, and patient satisfaction, is essential. And the model should be regularly updated to respond to real-time data and changing conditions. Because this study assumes that key parameters (such as patient preferences and arrival patterns) remain relatively stable over time, it may not fully capture the dynamic nature of real-world healthcare settings. Future work could address this by developing adaptive scheduling approaches that update parameters in a timely manner, thereby enhancing the model’s responsiveness to fluctuating conditions.

Future research could focus on extending the model to general hospitals, where more complex patient classifications and cross-department coordination present significant challenges, requiring substantial adaptations beyond direct application. Additionally, beyond addressing service capacity shortages, further evaluating the impact of optimized physician scheduling on key healthcare performance indicators, such as patient satisfaction, treatment efficiency, and cost-effectiveness, would provide valuable insights for hospital administrators and further validate the model’s practical benefits.

Technical details

Proof of Proposition 1

Similar conclusions can be found in³², and this paper provides a complete derivation. Given the observed data ${\varvec{N}},$ the likelihood function of ${\varvec{p}}$ is defined as $f({\varvec{N}} | {\varvec{p}}) = \prod _{i \in [S]} p_i^{N_i}.$ According to Bayes’ theorem, the posterior probability is given by

$$f({\varvec{p}} | {\varvec{N}}) = \frac{f({\varvec{N}} | {\varvec{p}}) f({\varvec{p}})}{f({\varvec{N}})}.$$

Although the specific form of $f({\varvec{N}})$ is unknown, it can be treated as a constant. The posterior distribution $f({\varvec{p}} | {\varvec{N}})$ formed by the Dirichlet distribution $\text {Dir}(\varvec{\alpha })$ and the likelihood function $f({\varvec{N}} | {\varvec{p}})$ is a $\text {Dir}(\varvec{\alpha } + {\varvec{N}})$ distribution:

$$f({\varvec{p}} | {\varvec{N}}) \propto \prod _{i \in [S]} p_i^{N_i + \alpha _i - 1}.$$

Thus, by the definition of probability, Eq. (6) holds. This completes the proof of Proposition 1. $\square$

Proof of Proposition 2

The relevant conclusions and proofs can be found in^32,35. The proof is complete. $\square$