A cutter contacting point trajectory prediction method combining harmonic functions and dimensionality reduction for improving machining precision in flat-end milling

Abstract

In five-axis machining, deviations between actual and theoretical cutter contacting (CC) point trajectories lead to nonlinear errors, adversely affecting machining precision. This paper presents a novel method aimed at reducing nonlinear errors at CC points, enhancing overall accuracy in machining processes. We establish that interpolated CC points within a machining segment lie on the same plane, which provides a foundational insight into the geometric behavior of the machining system. To simplify the calculation process, we apply a geometric method to reduce the dimensionality of CC points, making the subsequent analysis more efficient. A harmonic function is then utilized to predict CC point trajectories, enabling effective compensation for identified errors. Our approach is integrated into five-axis linear trajectory interpolation, where it quantitatively addresses nonlinear errors that exceed tolerance limits. Comprehensive simulation and experimental validation demonstrate that this method not only maintains CC point errors within allowable limits but also significantly reduces tool center point errors. The results confirm the effectiveness of our method in enhancing machining precision, paving the way for improved performance in five-axis machining applications.

Introduction

Five-axis computer numerical control (CNC) machine tools, as advanced manufacturing equipment, play an increasingly important role in industries such as aerospace, automotive, and mold processing^1,2. A five-axis CNC machine tool comprises three translational and two rotational axes, enabling coordinated motion control of the tool in five axes and facilitating efficient and precise machining of complex curved surfaces and parts³. However, five-axis CNC machines, which extend traditional three-axis systems with two additional rotational axes, introduce more uncertainty in tool path control⁴. This uncertainty may cause nonlinear positional errors in the machining trajectory, potentially reducing the machining accuracy and quality of complex curved surfaces.

Nonlinear errors in machining trajectories are inherent and cannot be completely eliminated, but they can be mitigated through compensation techniques. To address this challenge, scholars worldwide have conducted extensive research and proposed various methods to improve machining accuracy from different perspectives. Specifically, some researchers have focused on tool orientation optimization to minimize nonlinear trajectory errors. For example, Ma⁵ introduced a solution for tool orientation within a feasible region under nonlinear error constraints, enhancing accuracy and preventing tool interference. However, this method involves iterative computations with high complexity, resulting in slower convergence and complicated implementation processes. Xiao⁶ proposed an adaptive contour error pre-compensation method for five-axis CNC machines. This method uses model reference adaptive control (MRAC) and model predictive control (MPC), accurately predicting tool tip and orientation errors. Despite its accuracy, the method heavily depends on precise modeling, causing robustness issues when machining parameters vary dynamically.

In addition to tool orientation optimization, another important research direction involves geometric error modeling and interpolation strategies to improve trajectory accuracy. For instance, Wang⁷ and Fu⁸ proposed geometric error identification and optimization models, providing theoretical foundations for improving machining accuracy. Yet, these models faced difficulties in practical applications due to challenges in comprehensive geometric error measurement and high computational complexity. Li⁹ and Xu¹⁰ developed interpolation strategies enhancing geometric path accuracy of CC points. However, these methods did not fully address nonlinear errors continuously occurring between adjacent CC points, reducing their overall effectiveness. Wu¹¹ employed non-uniform rational B-splines (NURBS) curve fitting techniques to preprocess the cutter location points, effectively improving machining efficiency. Nevertheless, NURBS-based methods introduced complex calculations and lacked flexibility for diverse machining scenarios.

Beyond geometric modeling and fitting, certain researchers have investigated real-time interpolation adjustment and dynamic error compensation to handle complex and rapidly varying tool paths. Shi¹² and Kang¹³ explored real-time interpolation adjustments and geometric error modeling, effectively addressing certain dynamic machining errors. However, their methods provided limited flexibility and had difficulties adapting to highly complex or rapidly varying toolpath trajectories. Moreover, several methods focused on improving CC point distribution or local interpolation accuracy to enhance trajectory smoothness and uniformity. Liu¹⁴ approximated the tool envelope surface using discrete bottom circles, improving CC point distribution uniformity. Yet, the method required repeated and detailed error analysis at individual points, limiting its scalability to large-scale machining applications. Zhang¹⁵ and Dong¹⁶ introduced spherical angle linear interpolation and constant chord error approaches, showing promising error reductions. However, these techniques lacked generalizability, exhibiting significant performance degradation when machining tasks became complex or involved highly variable curvatures. Lin¹⁷ emphasized singularity avoidance during tool path planning to ensure smoother axis movements. Although effective in reducing singularities, it did not incorporate explicit models to continuously predict and compensate nonlinear errors.

Furthermore, node-based error allocation and motion control methods have been proposed to improve machining accuracy. For example, Song¹⁸ and Wang¹⁹ focused on error allocation and motion control within node space, significantly improving machining accuracy. However, their node-based approaches lacked continuous error compensation strategies between interpolation nodes, potentially causing residual errors in actual machining trajectories. Chen²⁰ proposed a five-axis Tri-NURBS interpolation method that synchronizes the tool center point, tool axis, and CC point splines to significantly reduce machining errors. Despite its effectiveness, this method required complicated and computationally demanding spline synchronizations, making accurate error prediction difficult and reducing the robustness of compensation under changing machining conditions. Therefore, there is still a strong need for simpler yet effective methods capable of systematically predicting and compensating nonlinear trajectory errors under practical machining conditions.

In contrast to the existing research, which predominantly focuses on tool orientation optimization, geometric error modeling, and interpolation strategies, the prediction of cutter contacting (CC) points—specifically for flat end mills between two adjacent cutter locations—has received relatively limited attention. Precise prediction of the interpolated cutter location points between adjacent CC points is crucial for accurately assessing nonlinear errors along the machining trajectory. This gap in the current literature has hindered the ability to fully address continuous nonlinear error compensation between CC points.

This paper introduces a novel cutter contacting point trajectory prediction method that integrates harmonic functions and geometric dimensionality reduction. By focusing on accurate prediction of the interpolation points between adjacent CC points, our approach improves the accuracy of nonlinear error prediction and compensation within each interpolation cycle. Furthermore, we have validated the effectiveness of our proposed method through actual machining experiments, demonstrating its ability to reduce nonlinear errors while ensuring real-time performance. This experimental verification underscores the practical applicability and superiority of our approach compared to existing methods, offering significant improvements in machining precision and efficiency.

Determination of actual tool center point and actual CC point

When calculating the nonlinear errors of the tool center point and CC point trajectories in five-axis CNC machining, it is necessary to determine the actual positions of both the tool center point and CC point. To this end, mathematical models for both the forward and inverse motion transformations of an A-C type double-rotary table five-axis CNC machine are established in this paper, using this type of CNC machine as an example. Based on the data sampling and interpolation principles, the positions of the actual tool center point and CC point during the five-axis linear interpolation process are determined.

Mathematical model of machine tool motion transformation

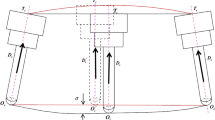
As shown in Fig. 1, the A-C type double-rotary table five-axis CNC machine features two rotational axes. The axis fixed to the machine bed is the A-axis (tilted axis), while the other axis, whose orientation changes with the A-axis, is the C-axis (moving axis).

Fig. 1

Schematic diagram of the A-C type double-rotary table five-axis CNC machine tool.

Separate coordinate systems are established for this type of five-axis CNC machine: machine coordinate system O_MX_MY_MZ_M, workpiece coordinate system O_WX_WY_WZ_W, tool coordinate system O_TX_TY_TZ_T (with the origin at the tool center point), A-axis coordinate system O_AX_AY_AZ_A, and C-axis coordinate system O_CX_CY_CZ_C, as shown in Fig. 2.

Fig. 2

The coordinate system and change relationship of A-C double turntable CNC machine tool.

Within the coordinate framework of a five-axis CNC machining tool, the five motion control coordinates govern the tool’s forward movement relative to the workpiece. Based on the principle of coordinate transformation, the expressions for the tool center point and the tool axis unit vector in the workpiece coordinate system are derived as follows:

$$\left\{ \begin{gathered} x=X\cos \theta _{\varvec{C}}^{\varvec{M}} - Y\cos \theta _{\varvec{A}}^{\varvec{M}}\sin \theta _{\varvec{C}}^{\varvec{M}}+Z\sin \theta _{\varvec{A}}^{\varvec{M}}\sin \theta _{\varvec{C}}^{\varvec{M}} \hfill \\ y=X\sin \theta _{\varvec{C}}^{\varvec{M}}+Y\cos \theta _{\varvec{A}}^{\varvec{M}}\cos \theta _{\varvec{C}}^{\varvec{M}} - Z\sin \theta _{\varvec{A}}^{\varvec{M}}\cos \theta _{\varvec{C}}^{\varvec{M}} \hfill \\ z=Y\sin \theta _{\varvec{A}}^{\varvec{M}}+Z\cos \theta _{\varvec{A}}^{\varvec{M}} \hfill \\ \end{gathered} \right.$$

(1)

and

$$\left\{ \begin{gathered} {I^{W}}=\sin \theta _{\varvec{A}}^{\varvec{M}}\sin \theta _{\varvec{C}}^{\varvec{M}} \hfill \\ {J^W}= - \sin \theta _{\varvec{A}}^{\varvec{M}}\cos \theta _{\varvec{C}}^{\varvec{M}} \hfill \\ {K^{W}}=\cos \theta _{\varvec{A}}^{\varvec{M}} \hfill \\ \end{gathered} \right.$$

(2)

In the above equations, (x,y,z) represents the coordinates of the tool center point in the workpiece coordinate system, (I^W,J^W,K^W) denotes the tool axis unit vector in the workpiece coordinate system, (X,Y,Z) represents the translational coordinates of the tool center point in the machine coordinate system, and $\left( {\theta _{\varvec{A}}^{\varvec{M}},\theta _{\varvec{C}}^{\varvec{M}}} \right)$indicates the rotational motion coordinates of the tool in the machine coordinate system.

From Eqs. (1) and (2), the mathematical model for the inverse motion coordinate transformation from the workpiece coordinate system to the machine coordinate system is derived as follows²¹:

$$\left\{ \begin{gathered} \theta _{\varvec{A}}^{\varvec{M}}=\arccos {K^{W}} \hfill \\ \theta _{\varvec{C}}^{\varvec{M}}=\left\{ \begin{gathered} \frac{\pi }{2} - \arctan \frac{{{J^{W}}}}{{{I^{W}}}}\left( {{I^{W}}>0,{J^{W}}<0} \right) \hfill \\ \frac{\pi }{2}+\arctan \frac{{{J^{W}}}}{{{I^{W}}}}\left( {{I^{W}}>0,{J^{W}}>0} \right) \hfill \\ \frac{{3\pi }}{2}+\arctan \frac{{{J^{W}}}}{{{I^{W}}}}\left( {{I^{W}}<0,{J^{W}}<0} \right) \hfill \\ \frac{{3\pi }}{2} - \arctan \frac{{{J^{W}}}}{{{I^{W}}}}\left( {{I^{W}}<0,{J^{W}}>0} \right) \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \right.$$

(3)

and

$$\left\{ \begin{gathered} X=x\cos \theta _{\varvec{C}}^{\varvec{M}}+y\sin \theta _{\varvec{C}}^{\varvec{M}} \hfill \\ Y= - x\cos \theta _{\varvec{A}}^{\varvec{M}}\sin \theta _{\varvec{C}}^{\varvec{M}}+z\sin \theta _{\varvec{A}}^{\varvec{M}}+y\cos \theta _{\varvec{A}}^{\varvec{M}}\cos \theta _{\varvec{C}}^{\varvec{M}} \hfill \\ Z=x\sin \theta _{\varvec{A}}^{\varvec{M}}\sin \theta _{\varvec{C}}^{\varvec{M}}+z\cos \theta _{\varvec{A}}^{\varvec{M}} - y\cos \theta _{\varvec{C}}^{\varvec{M}}\sin \theta _{\varvec{A}}^{\varvec{M}} \hfill \\ \end{gathered} \right.$$

(4)

Determination of the actual tool center point

As illustrated in Fig. 3, in the cutter location data files generated by computer-aided manufacturing (CAM)software, each linear interpolation path segment includes the coordinates of the starting tool center point ($O_{s}^{\text{W}}$) and the tool axis unit vector (${{\text{T}}_s}$), as well as the coordinates of the ending tool center point ($O_{e}^{\text{W}}$) and the tool axis unit vector (${{\text{T}}_e}$) in the workpiece coordinate system, represented as $\left( {{x_s},{y_s},{z_s},I_{s}^{\varvec{W}},J_{s}^{\varvec{W}},K_{s}^{\varvec{W}}} \right)$$\left( {{x_e},{y_e},{z_e},I_{e}^{\varvec{W}},J_{e}^{\varvec{W}},K_{e}^{\varvec{W}}} \right)$ respectively. After substituting these into Eqs. (3) and (4), the machine motion control translational coordinates $\left( {{X_s},{Y_s},{Z_s}} \right)$,$\left( {{X_e},{Y_e},{Z_e}} \right)$and rotational motion coordinates $\left( {\theta _{{\varvec{A}s}}^{\varvec{M}},\theta _{{\varvec{C}s}}^{\varvec{M}}} \right)$, $\left( {\theta _{{\varvec{A}e}}^{\varvec{M}},\theta _{{\varvec{C}e}}^{\varvec{M}}} \right)$ are obtained through the inverse motion transformation. Assuming the cutting feed rate for this segment is f and the interpolation time is t, the subsequent five-axis linear interpolation procedure follows the data sampling interpolation methodology.

First, the length G of the interpolation path segment and the number n of interpolation time required to complete this segment are calculated as follows:

$$G=\sqrt {{{\left( {{X_e} - {X_S}} \right)}^2}+{{\left( {{Y_e} - {Y_S}} \right)}^2}+{{\left( {{Z_e} - {Z_S}} \right)}^2}}$$

(5)

and

$$n=\left\{ {\frac{G}{{ft}}} \right\}$$

(6)

In Eq. (6), the operator $\left\{ \odot \right\}$ denotes the rounding down of $\odot$ to the nearest integer.

Fig. 3

Five-axis interpolation path segment.

In the five-axis linear interpolation cycle, the rotational motion control coordinates for the i-th cycle can be computed as follows:

$$\left\{ \begin{gathered} \theta _{{\varvec{A}i}}^{\varvec{M}}=i\left[ {\left( {\theta _{{\varvec{A}e}}^{\varvec{M}} - \theta _{{\varvec{A}s}}^{\varvec{M}}} \right)/n} \right]+\theta _{{\varvec{A}s}}^{\varvec{M}} \hfill \\ \theta _{{\varvec{C}i}}^{\varvec{M}}=i\left[ {\left( {\theta _{{\varvec{C}e}}^{\varvec{M}} - \theta _{{\varvec{C}s}}^{\varvec{M}}} \right)/n} \right]+\theta _{{\varvec{C}s}}^{\varvec{M}} \hfill \\ \end{gathered} \right. (i=1,2, \cdots ,n)$$

(7)

By substituting Eq. (7) into Eq. (2), the corresponding tool axis unit vector associated with these rotational motion control coordinates is obtained, as shown in Fig. 3.

$${\varvec{T}_i}=\left( {I_{i}^{\varvec{W}},J_{i}^{\varvec{W}},K_{i}^{\varvec{W}}} \right)$$

In Fig. 3, points$Q_{s}^{\text{W}}$ and $Q_{e}^{\text{W}}$ respectively represent the tool rotation center points at the start and end of the interpolation, respectively. In this paper, these are defined as tool axis points. Thus, the tool axis points $Q_{s}^{\text{W}}$ and $Q_{e}^{\text{W}}$ at the beginning and conclusion of the interpolation, the respective formulations are as follows:

$$\varvec{Q}_{\varvec{s}}^{\mathcal{W}}=\left( {{x_s},{y_s},{z_s}} \right)+L * \left( {I_{s}^{\mathcal{W}},J_{s}^{\mathcal{W}},K_{s}^{\mathcal{W}}} \right)$$

and

$$\varvec{Q}_{e}^{\mathcal{W}}=\left( {{x_e},{y_e},{z_e}} \right)+L * \left( {I_{e}^{\mathcal{W}},J_{e}^{\mathcal{W}},K_{e}^{\mathcal{W}}} \right)$$

Here, L represents the distance between the tool center point and the tool axis point (the length of tool swing). Using the concept of linear interpolation, the formula for computing the tool axis point in the i-th interpolation cycle is as follows.

$$\varvec{Q}_{i}^{\mathcal{W}}=i\left[ {\left( {\varvec{Q}_{e}^{\mathcal{W}} - \varvec{Q}_{s}^{\mathcal{W}}} \right)/n} \right]+\varvec{Q}_{s}^{\mathcal{W}}$$

(8)

In Fig. 3, $\varvec{O}_{i}^{\mathcal{W}}$ represents the actual tool center point during the i-th interpolation cycle. At this point, the position coordinates of the tool axis point in the workpiece coordinate system are as follows:

$$\varvec{Q}_{i}^{\text{W}}=\varvec{O}_{i}^{\mathcal{W}}+L * {\varvec{T}_i}$$

(9)

By combining Eqs. (8) and (9), the actual coordinates of the tool center point in the workpiece coordinate system are obtained as follows:

$$\left\{ \begin{gathered} {x_i}=i\left[ {\left( {{x_e}+L * I_{e}^{\varvec{W}} - {x_s} - L * I_{s}^{\varvec{W}}} \right)/n} \right]+{x_s}+L*I_{s}^{\varvec{W}} - L * I_{i}^{\varvec{W}} \hfill \\ {y_i}=i\left[ {\left( {{y_e}+L * J_{e}^{\varvec{W}} - {y_s} - L * J_{s}^{\varvec{W}}} \right)/n} \right]+{y_s}+L*J_{s}^{\varvec{W}} - L * J_{i}^{\varvec{W}} \hfill \\ {z_i}=i\left[ {\left( {{z_e}+L * K_{e}^{\varvec{W}} - {z_s} - L * K_{s}^{\varvec{W}}} \right)/n} \right]+{z_s}+L*Z_{s}^{\varvec{W}} - L * K_{i}^{\varvec{W}} \hfill \\ \end{gathered} \right.$$

(10)

By substituting Eqs. (7) and (10) into Eq. (4), the translational coordinates $\left( {{X_i},{Y_i},{Z_i}} \right)$ of the tool center point in the machine coordinate system for the i-th interpolation cycle are obtained. These coordinates represent the actual position of the tool center point in the machine coordinate system.

Determination of the actual CC point

Equations (1) and (4) represent the forward and inverse coordinate transformation models from the machine coordinate system to the workpiece coordinate system, respectively, and are equally applicable to the CC point. Assuming (U, V, W) are the coordinates of the CC point in the machine coordinate system, and (u, v, w) are the coordinates in the workpiece coordinate system, the transformation relationship between (U, V, W) and (u, v, w) based on Eqs. (1) and (4), is expressed as follows:

$$\left\{ \begin{gathered} u=U\cos \theta _{\varvec{C}}^{\varvec{M}} - Vos\theta _{\varvec{A}}^{\varvec{M}}\sin \theta _{\varvec{C}}^{\varvec{M}}+W\sin \theta _{\varvec{A}}^{\varvec{M}}\sin \theta _{\varvec{C}}^{\varvec{M}} \hfill \\ v=U\sin \theta _{\varvec{C}}^{\varvec{M}}+V\cos \theta _{\varvec{A}}^{\varvec{M}}\cos \theta _{\varvec{C}}^{\varvec{M}} - W\sin \theta _{\varvec{A}}^{\varvec{M}}\cos \theta _{\varvec{C}}^{\varvec{M}} \hfill \\ w=U\sin \theta _{\varvec{A}}^{\varvec{M}}+W\cos \theta _{\varvec{A}}^{\varvec{M}} \hfill \\ \end{gathered} \right.$$

(11)

and

$$\left\{ \begin{gathered} U=u\cos \theta _{\varvec{C}}^{\varvec{M}}+v\sin \theta _{\varvec{C}}^{\varvec{M}} \hfill \\ V= - u\cos \theta _{\varvec{A}}^{\varvec{M}}\sin \theta _{\varvec{C}}^{\varvec{M}}+w\sin \theta _{\varvec{A}}^{\varvec{M}}+v\cos \theta _{\varvec{A}}^{\varvec{M}}\cos \theta _{\varvec{C}}^{\varvec{M}} \hfill \\ W=u\sin \theta _{\varvec{A}}^{\varvec{M}}\sin \theta _{\varvec{C}}^{\varvec{M}}+w\cos \theta _{\varvec{A}}^{\varvec{M}} - v\cos \theta _{\varvec{C}}^{\varvec{M}}\sin \theta _{\varvec{A}}^{\varvec{M}} \hfill \\ \end{gathered} \right.$$

(12)

In theory, the interaction between the tool and the workpiece should occur at a singular contact point, specifically at the CC point. However, real machining scenarios often deviate due to cutting forces, causing more extensive contact along a line between the tool’s cutting edge and the workpiece surface. This complicates the precise identification of the correct interpolation CC point. To mitigate this, the point on the tool’s cutting edge nearest to the theoretical CC point typically contacts and begins cutting the workpiece first, thus acting as the actual CC point. As illustrated in Fig. 4, if we project the theoretical CC point onto the plane of the tool’s cutting edge circle to locate point F, the actual CC point determined by the intersection of the line from the real tool center to point F with the tool’s cutting surface.

Fig. 4

Determination of actual cutter contact (CC) point.

Based on the cutter location data files generated by CAM software, the starting and ending interpolation CC points of each linear interpolation path segment in the workpiece coordinate system, (u_s,v_s,w_s) and (u_e,v_e,w_e), can be obtained, respectively. Similarly, in the context of five-axis linear interpolation, the theoretical CC point, denoted as C_i, for any given interpolation i is determined by the following calculation:

$$\left\{ \begin{gathered} {u_i}=i\left[ {\left( {{u_e} - {u_s}} \right)/n} \right]+{u_s} \hfill \\ {v_i}=i\left[ {\left( {{v_e} - {v_s}} \right)/n} \right]+{v_s} \hfill \\ {w_i}=i\left[ {\left( {{w_e} - {w_s}} \right)/n} \right]+{w_s} \hfill \\ \end{gathered} \right. (i=1,2, \cdots ,n)$$

(13)

In Eq. (13), (u_i,v_i,w_i) represent the position coordinates of the theoretical CC point C_i.

It should be noted that the unit vector d_i is not simply the vector directly connecting the actual tool center point $\varvec{O}_{i}^{\mathcal{W}}$ and the actual CC point ${\varvec{C^{\prime}}_i}$. Instead, it represents the direction of the shortest distance from $\varvec{O}_{i}^{\mathcal{W}}$​ to the cutting edge of the tool, where the actual CC point ${\varvec{C^{\prime}}_i}$is located.

In five-axis machining, the actual CC point often lies on the cutting edge circle of the tool due to tool radius and cutting conditions. Therefore, the vector d_i is determined by projecting the line from the theoretical CC point C_i​ to the tool center point $\varvec{O}_{i}^{\mathcal{W}}$​ onto the plane perpendicular to the tool axis vector T_i, ensuring that d_i​ is perpendicular to the tool axis and points from $\varvec{O}_{i}^{\mathcal{W}}$​ towards the tool cutting surface.

The specific formulation of d_i ​is given in Eq. (14) as follows:

$${\varvec{d}_i}=\frac{{\left[ {{\varvec{T}_i} \times \left( {{\varvec{C}_i} - \varvec{O}_{i}^{\mathcal{W}}} \right)} \right] \times {\varvec{T}_i}}}{{\left\| {\left[ {{\varvec{T}_i} \times \left( {{\varvec{C}_i} - \varvec{O}_{i}^{\mathcal{W}}} \right)} \right] \times {\varvec{T}_i}} \right\|}}=\left[ \begin{gathered} {d_{xi}} \hfill \\ {d_{yi}} \hfill \\ {d_{zi}} \hfill \\ \end{gathered} \right]$$

(14)

In Eq. (14), $\left\| \cdot \right\|$ represent the operation of taking the modulus of the vector.

The relationship between the actual tool center point and the actual CC point coordinates in the workpiece coordinate system is expressed as follows:

$${\varvec{C^{\prime}}_i}=\varvec{O}_{i}^{\mathcal{W}}+R * {\varvec{d}_i}$$

(15)

In Eq. (15), R represents the tool radius.

By substituting $\varvec{O}_{i}^{\mathcal{W}}$ and ${\varvec{d}_i}$ into Eq. (15), the actual CC point ${\varvec{C^{\prime}}_i}$ in the workpiece coordinate system for the i-th interpolation cycle during the interpolation process can be obtained as follows:

$$\left\{ \begin{gathered} {{u^{\prime}}_i}=\mathcal{i}\left[ {\left( {{x_e}+L * I_{e}^{\varvec{W}} - {x_s} - L * I_{s}^{\varvec{W}}} \right)/n} \right]+{x_s}+L*I_{s}^{\varvec{W}} - L * I_{i}^{\varvec{W}}+R * {d_{xi}} \hfill \\ {{v^{\prime}}_i}=\mathcal{i}\left[ {\left( {{y_e}+L * J_{e}^{\varvec{W}} - {y_s} - L * J_{s}^{\varvec{W}}} \right)/n} \right]+{y_s}+L*J_{s}^{\varvec{W}} - L * J_{i}^{\varvec{W}}+R * {d_{yi}} \hfill \\ {{w^{\prime}}_i}=\mathcal{i}\left[ {\left( {{z_e}+L * K_{e}^{\varvec{W}} - {z_s} - L * K_{s}^{\varvec{W}}} \right)/n} \right]+{z_s}+L*K_{s}^{\varvec{W}} - L * K_{i}^{\varvec{W}}+R * {d_{zi}} \hfill \\ \end{gathered} \right.$$

(16)

In Eq. (16), $\left( {{{u^{\prime}}_i},{{v^{\prime}}_i},{{w^{\prime}}_i}} \right)$ represents the position coordinates of the actual CC point ${\varvec{C^{\prime}}_i}$ in the workpiece coordinate system. Similarly, by substituting Eq. (16) into Eq. (12), the position coordinates of the actual CC point $\varvec{C}_{i}^{\mathcal{M}}$ in the machine coordinate system can be obtained as follows:

$$\left\{ \begin{gathered} {{U^{\prime}}_i}={{u^{\prime}}_i}\cos \theta _{\varvec{C}}^{\varvec{M}}+{{v^{\prime}}_i}\sin \theta _{\varvec{C}}^{\varvec{M}} \hfill \\ {{V^{\prime}}_i}= - {{u^{\prime}}_i}\cos \theta _{\varvec{A}}^{\varvec{M}}\sin \theta _{\varvec{C}}^{\varvec{M}}+{{w^{\prime}}_i}\sin \theta _{\varvec{A}}^{\varvec{M}}+{{v^{\prime}}_i}\cos \theta _{\varvec{A}}^{\varvec{M}}\cos \theta _{\varvec{C}}^{\varvec{M}} \hfill \\ {{W^{\prime}}_i}={{u^{\prime}}_i}\sin \theta _{\varvec{A}}^{\varvec{M}}\sin \theta _{\varvec{C}}^{\varvec{M}}+{{w^{\prime}}_i}\cos \theta _{\varvec{A}}^{\varvec{M}} - {{v^{\prime}}_i}\cos \theta _{\varvec{C}}^{\varvec{M}}\sin \theta _{\varvec{A}}^{\varvec{M}} \hfill \\ \end{gathered} \right.$$

(17)

Establishment of the mathematical model for the CC point plane

Proof of the coplanar relationship of CC points

A set of interpolation CC points for a given machining program segment forms a group of discrete CC points. Since the calculation of the actual CC points uses the interpolation tool axis vector, which is computed using Eq. (2), the expression for the actual CC points includes trigonometric functions. The interpolation tool axis vector T_i has a nonlinear relationship with the angles of the A and C axes. Verifying whether this group of discrete CC points lies on a single plane makes it difficult to derive a definitive plane equation through specific expressions. Therefore, a numerical method will be employed to verify that all interpolation CC points of the same machining program segment lie on a single plane.

The coordinates of three actual interpolation CC points C_s, ${\varvec{C^{\prime}}_i}$, and C_e in a given machining program segment can determine a plane equation, denoted as Ax + By + Cz + D = 0. With these three points, two vectors can be calculated: ${\varvec{M}_1}=\left( {{m_1},{m_2},{m_3}} \right)$ and ${\varvec{M}_2}=\left( {{m_4},{m_5},{m_6}} \right)$. M₁ and M₂ are determined by the following equations:

$${\varvec{M}_1}={\varvec{C}_e} - {\varvec{C^{\prime}}_i}=\left( {{u_e} - {{u^{\prime}}_i},{v_e} - {{v^{\prime}}_i},{w_e} - {{w^{\prime}}_i}} \right) \;{\varvec{M}_2}={\varvec{C^{\prime}}_i} - {\varvec{C}_s}=\left( {{{u^{\prime}}_i} - {u_s},{{v^{\prime}}_i} - {v_s},{{w^{\prime}}_i} - {w_s}} \right)$$

(18)

By substituting Eq. (16) into Eq. (18), the following can be obtained:

$$\left\{ \begin{gathered} {m_1}={x_e}+R{d_{xe}} - \left\{ {i\left[ {\left( {{x_e}+L * I_{e}^{\varvec{W}} - {x_s} - L * I_{s}^{\varvec{W}}} \right)/n} \right]+{x_s}+L*I_{s}^{\varvec{W}} - L * I_{i}^{\varvec{W}}+R * {d_{xi}}} \right\} \hfill \\ {m_2}={y_e}+R{d_{ye}} - \left\{ {i\left[ {\left( {{y_e}+L * J_{e}^{\varvec{W}} - {y_s} - L * J_{s}^{\varvec{W}}} \right)/n} \right]+{y_s}+L*J_{s}^{\varvec{W}} - L * J_{i}^{\varvec{W}}+R * {d_{yi}}} \right\} \hfill \\ {m_3}={z_e}+R{d_{ze}} - \left\{ {i\left[ {\left( {{z_e}+L * K_{e}^{\varvec{W}} - {z_s} - L * K_{s}^{\varvec{W}}} \right)/n} \right]+{z_s}+L*K_{s}^{\varvec{W}} - L * K_{i}^{\varvec{W}}+R * {d_{zi}}} \right\} \hfill \\ \end{gathered} \right.$$

(19)

and

$$\left\{ \begin{gathered} {m_4}=\left\{ {i\left[ {\left( {{x_e}+L * I_{e}^{\varvec{W}} - {x_s} - L * I_{s}^{\varvec{W}}} \right)/n} \right]+{x_s}+L*I_{s}^{\varvec{W}} - L * I_{i}^{\varvec{W}}+R * {d_{xi}}} \right\} - {x_s} - R{d_{xs}} \hfill \\ {m_5}=\left\{ {i\left[ {\left( {{y_e}+L * J_{e}^{\varvec{W}} - {y_s} - L * J_{s}^{\varvec{W}}} \right)/n} \right]+{y_s}+L*J_{s}^{\varvec{W}} - L * J_{i}^{\varvec{W}}+R * {d_{yi}}} \right\} - {y_s} - R{d_{ys}} \hfill \\ {m_6}=\left\{ {i\left[ {\left( {{z_e}+L * K_{e}^{\varvec{W}} - {z_s} - L * K_{s}^{\varvec{W}}} \right)/n} \right]+{z_s}+L*K_{s}^{\varvec{W}} - L * K_{i}^{\varvec{W}}+R * {d_{zi}}} \right\} - {z_s} - R{d_{zs}} \hfill \\ \end{gathered} \right.$$

(20)

Consequently, the normal vector of this plane can be calculated using Eqs. (19) and (20) as follows:

${\varvec{M}_3}={\varvec{M}_1} \times {\varvec{M}_2}=\left( {{m_2}{m_6} - {m_3}{m_5},{m_3}{m_4} - {m_1}{m_6},{m_1}{m_5} - {m_2}{m_4}} \right)$

By substituting C_s into the plane equation Ax + By + Cz + D = 0, the coefficients of the plane equation can be obtained as follows:

$$\left\{ \begin{gathered} A={m_2}{m_6} - {m_3}{m_5} \hfill \\ B={m_3}{m_4} - {m_1}{m_6} \hfill \\ C={m_1}{m_5} - {m_2}{m_4} \hfill \\ D= - A{u_s} - B{v_s} - C{z_s} \hfill \\ \end{gathered} \right.$$

(21)

In practical calculations, by substituting ${\varvec{C^{\prime}}_i}$ into Eq. (21), the expression for the plane equation Ax + By + Cz + D = 0 can be obtained. Then, using the formula for the distance of a point to a plane, the distance $\varvec{\varvec{\Omega}}$from the next interpolation CC point ${\varvec{C^{\prime}}_{i+1}}$ to this plane can be calculated as follows:

$$\varvec{\varvec{\Omega}}=\frac{{\left| {Ax+By+Cz+D} \right|}}{{\sqrt {{A^2}+{B^2}+{C^2}} }}$$

(22a)

Let [ε] = 10⁻⁵·N (where N is the distance between the starting and ending CC points), and then based on the size relationship between $\varvec{\varvec{\Omega}}$and [ε].

$$\left\{ \begin{gathered} \varvec{\varvec{\Omega}}>\left[ \varepsilon \right],\operatorname{Do} not \;lie\; on \;the\; same\; plane \hfill \\ \varvec{\varvec{\Omega}}<\left[ \varepsilon \right],\operatorname{Do} lie\; on\; the\; same\; plane \hfill \\ \end{gathered} \right.$$

(22b)

Determine whether the interpolation CC point ${\varvec{C^{\prime}}_{i+1}}$ lies on that plane.

It should be noted that the data used in this section are not directly assumed or manually defined. These data are extracted from the cutter location file of a machining program, which includes the theoretical tool center point coordinates, theoretical tool axis vectors, and theoretical CC points. Specifically, the theoretical data corresponding to Data 1 in Sect."Nonlinear error compensation example calculation"are substituted into Eq. (10) to calculate the actual interpolation tool center points, considering the kinematic error model. Then, these actual tool center points are further substituted into Eq. (16) to calculate the corresponding actual interpolation CC points.

Therefore, the data used for verification in this section are practical simulation data generated from a real machining program, rather than hypothetical or arbitrarily defined points.

Below, a set of machining program segment cutter location points and CC point data, exported from a machining file of a free-form surface part, is used to verify whether the next interpolation CC point ${\varvec{C^{\prime}}_{i+1}}$ lies on the plane determined above. The cutter location points and CC point data are as follows:

$\varvec{O}_{s}^{\mathcal{W}}=(81.5026,40.1848, - 9.7426)$$\varvec{O}_{e}^{\mathcal{W}}=(81.5145,39.9593, - 9.3645)$

$\varvec{I}_{s}^{\mathcal{W}}=(0.0919958,0.7525291,0.6521018)$$\varvec{I}_{e}^{\mathcal{W}}=(0.0926868,0.7684483,0.6331638)$

${\varvec{C}_s}=(83.3026,37.7224, - 7.1548)$${\varvec{C}_e}=(83.3137,37.5608, - 6.7169)$

Based on Eq. (6), n is calculated to be 7. Taking L = 75 mm and R = 4 mm, and by substituting the cutter location points and CC point data into Eq. (16), the actual interpolation CC point coordinates in the workpiece coordinate system are obtained, as shown in Table 1.

Table 1 Actual interpolation CC point coordinates for the machining program segment to be interpolated.

When taking i = 4, substituting a into Eq. (21) yields A = 18.79528207, B=−1.4187133, C=−0.9999999, D=−1519.3334092. By substituting ${\varvec{C^{\prime}}_5}$ into Eq. (22a), the distance of the fifth interpolation CC point from the CC point plane calculated to be $2.2804485 \times {10^{ - 6}}$, is obtained. In this machining program segment, [ε] equals 10⁻⁵·N, and [ε] equals $4.6686847 \times {10^{ - 6}}$. Based on Eq. (22b), it can be determined that the interpolation CC points of a machining program segment lie on the same plane.

Fig. 5

Distance from the interpolation CC point to the CC point plane.

By performing the above calculation process for all interpolation CC points and plotting the obtained distance data, a data curve is produced, as shown in Fig. 5. As shown in Fig. 5, all interpolation CC points lie on the CC point plane, unlike previous approaches that considered the interpolation CC point trajectories only in three-dimensional space, which led to more complex mathematical models for calculating CC point trajectories.

By proving that the interpolation CC points lie on the same plane, the three-dimensional interpolation CC point trajectories can be reduced to two-dimensional plane studies, simplifying the mathematical model for calculating actual CC point trajectories.

Conversion of two-dimensional and three-dimensional actual interpolation CC points

After demonstrating that the interpolated CC points of the same machining program segment lie on the same plane, a two-dimensional coordinate system can be established within the three-dimensional coordinate system to simplify the mathematical model of the CC point trajectory curve, as shown in Fig. 6. The origin of this coordinate system is located at the starting interpolation CC point C_s. The horizontal axis${u^{\mathcal{II}}}$is the line connecting the starting interpolation CC point C_s and the ending interpolation CC point C_e with the positive direction from C_s to C_e. A perpendicular line is drawn from the interpolated CC point${\varvec{C^{\prime}}_i}$ to the line C_s C_e, with the foot of the perpendicular line denoted as P_i. The vertical axis${v^{\mathcal{II}}}$ is a line passing through the starting interpolation CC point C_s and parallel to the perpendicular line, with its positive direction extending from P_i to the interpolated CC point ${\varvec{C^{\prime}}_i}$.

Next, the three-dimensional coordinates of the interpolated CC points are converted to two-dimensional coordinates. The vertical coordinate$v_{i}^{{II}}$represents the perpendicular distance from the interpolated CC point to the line C_s C_e in space. The distance between the interpolated CC point${\varvec{C^{\prime}}_i}$and the starting interpolation CC point C_s, along with the vertical coordinate$v_{i}^{{II}}$and the horizontal coordinate$u_{i}^{{II}}$forms a right triangle. Therefore, the horizontal coordinate$u_{i}^{{II}}$can be calculated using the Pythagorean theorem. Finally, the mathematical expression for the two-dimensional coordinates$\varvec{C}_{i}^{{II}}=(u_{i}^{{II}},v_{i}^{{II}})$ of the interpolated CC point is:

$$\left\{ \begin{gathered} u_{i}^{{II}}={\left( {{{u^{\prime}}_i} - {u_s}} \right)^2}+{\left( {{{v^{\prime}}_i} - {v_s}} \right)^2}+{\left( {{{w^{\prime}}_i} - {w_s}} \right)^2} - {\left( {v_{i}^{{II}}} \right)^2} \hfill \\ v_{i}^{{II}}=\frac{{\left\| {\begin{array}{*{20}{c}} \varvec{i}&\varvec{j}&\varvec{k} \\ {{{u^{\prime}}_i} - {u_s}}&{{{v^{\prime}}_i} - {v_s}}&{{{w^{\prime}}_i} - {w_s}} \\ \mathcal{\alpha }&\mathcal{\beta }&\mathcal{\gamma } \end{array}} \right\|}}{{\sqrt {{\alpha ^2}+{\beta ^2}+{\mathcal{\gamma }^2}} }} \hfill \\ \end{gathered} \right.$$

(23)

In Eq. (23), $\left( {\mathcal{\alpha },\mathcal{\beta },\mathcal{\gamma }} \right)$ represents the directional vector of the linear path of the cutter contact points C_s, C_e, $\left( {\varvec{i},\varvec{j},\varvec{k}} \right)$ is the unit vector.

Fig. 6

The conversion between three-dimensional coordinates and two-dimensional coordinate system of the CC point.

Nonlinear error prediction model

Once the CC point plane coordinate system has been set up, the three-dimensional coordinates of all actual interpolation CC points within the machining path segment can be calculated using Eq. (16). Together with the three-dimensional coordinates of the starting and ending CC points C_s and C_e of the path segment, these three-dimensional CC point coordinates can be dimensionally reduced to two-dimensional coordinates using Eq. (24). This process ultimately forms a two-dimensional CC point set for that machining path segment.

$${\varvec{M}}=\left\{ {\left( {u_{s}^{{II}},v_{s}^{{II}}} \right), \cdots ,\left( {u_{i}^{{II}},v_{i}^{{II}}} \right), \cdots ,\left( {u_{e}^{{II}},v_{e}^{{II}}} \right)} \right\} (i=1,2, \cdots ,n - 1)$$

This section describes two different methods for fitting and predicting the nonlinear error of interpolation CC points: the traditional second-order polynomial fitting model and the proposed harmonic function fitting model. A comparative analysis is conducted to verify the accuracy and computational efficiency of the proposed method.

Second-order polynomial fitting model

The second-order polynomial fitting method is a commonly used approach for modeling nonlinear error distributions. In this method, the trajectory of the CC points in the tool contact plane coordinate system is fitted using a second-order polynomial curve${\varvec{C}}({u^{II}})$ is set as follows:

$${v^{II}}={{a}_0}+{{a}_1}{u^{II}}+{{a}_2}{({u^{II}})^2}$$

(24a)

Since the starting point of the quadratic polynomial curve is always the starting CC point C_s, which is the coordinate origin (0,0) of the CC point plane coordinate system, substituting into Eq. (24a) reveals that ${{a}_0}=0$ in Eq. (24a). Thus, Eq. (24a) can be rewritten as follows:

$${v^{II}}=0+{{a}_1}{u^{II}}+{{a}_2}{({u^{II}})^2}$$

(24b)

Then, based on the principle of least squares, the following system of equations in matrix form for a₁ and a₂ can be obtained:

$$\left[ {\begin{array}{*{20}{c}} \begin{gathered} \sum\limits_{{i=0}}^{n} {u_{i}^{{II}}} \hfill \\ \sum\limits_{{i=0}}^{n} {{{\left( {u_{i}^{{II}}} \right)}^2}} \hfill \\ \end{gathered} &\begin{gathered} \sum\limits_{{i=0}}^{n} {{{\left( {u_{i}^{{II}}} \right)}^2}} \hfill \\ \sum\limits_{{i=0}}^{n} {{{\left( {u_{i}^{{II}}} \right)}^3}} \hfill \\ \end{gathered} &\begin{gathered} \sum\limits_{{i=0}}^{n} {{{\left( {u_{i}^{{II}}} \right)}^3}} \hfill \\ \sum\limits_{{i=0}}^{n} {{{\left( {u_{i}^{{II}}} \right)}^4}} \hfill \\ \end{gathered} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 0 \\ {{a_1}} \\ {{a_2}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {\sum\limits_{{i=0}}^{n} {u_{i}^{{II}}v_{i}^{{II}}} } \\ {\sum\limits_{{i=0}}^{n} {{{\left( {u_{i}^{{II}}} \right)}^2}v_{i}^{{II}}} } \end{array}} \right]$$

(25)

By substituting all two-dimensional CC points from the point set M into Eq. (25), a₁ and a₂ can be solved for. Then, by substituting a₁ and a₂ into Eq. (24b), the equation for the two-dimensional actual CC point trajectory in the CC point plane coordinate system can be obtained.

Proposed harmonic function fitting model

Based on the characteristics of the nonlinear error distribution of the CC points, the error variation shows a typical oscillating and periodic pattern along the machining trajectory due to the kinematic characteristics of five-axis motion and tool orientation changes.

Based on the characteristics of the nonlinear error distribution of the CC points, predictions are made using a harmonic function as the basis.

$$L\left( {{u^{II}}} \right)=\sum\limits_{1}^{m} {{{\rm A}_j}\sin } \left( {\frac{{2\pi }}{\sigma }{u^{II}}} \right)+{{\rm B}_j}\cos \left( {\frac{{2\pi }}{\sigma }{u^{II}}} \right)\left( {m=1,2, \cdots ,n} \right)$$

(26)

In the equation: A_j ​and B_j are the amplitudes of the harmonic function, m is the order of the polynomial, and $\sigma$ represents the length of one oscillation period.

In this paper, to simplify the calculation, a first-order polynomial is used to approximate the nonlinear error. The errors at the first and last points are zero, and the difference in their horizontal positions, ${u^{II}}$is half a period. The initial value is

B_j=0, m = 1,$\sigma =2\left( {u_{e}^{{II}} - u_{s}^{{II}}} \right)$

Thus, Eq. (26) can be simplified to

$$L\left( {{u^{II}}} \right)={{\rm A}_j}\sin \left( {\frac{\pi }{{\left( {u_{e}^{{II}} - u_{s}^{{II}}} \right)}}{u^{II}}} \right)\left( {{{\rm A}_j}=\mathop {\text{m}\text{a}\text{x}}\limits_{{0 \leqslant {u^{II}} \leqslant u_{e}^{{II}}}} \left\{ {v_{s}^{{II}} \cdots v_{i}^{{II}} \cdots v_{e}^{{II}}} \right\}} \right)$$

(27)

By substituting the horizontal coordinate$u_{i}^{{II}}$ into Eq. (27), the predicted two-dimensional CC point coordinates L_i$\left( {u_{i}^{{II}},v{{_{i}^{{II}}}^\prime }} \right)$can be obtained.

Case study and comparison of fitting results

In this section, a case study is carried out to verify the effectiveness and efficiency of the proposed harmonic function fitting method. The data used in this case are the two-dimensional actual interpolation CC points obtained from the dimensionality reduction of the CC point set in Table 1, as shown in Table 2.

Table 2 Two-dimensional interpolated CC point trajectory.

First, the traditional second-order polynomial fitting method is employed to fit the trajectory of the two-dimensional actual interpolated CC points. The fitted curve expression is shown in Fig. 7a. The calculated coefficient of determination R² reaches 0.9995, indicating excellent fitting accuracy.

Then, the proposed harmonic function fitting method is applied to the same data set. The fitted curve expression is shown in Fig. 7b. The calculated R² value is 0.9947, which is slightly lower than that of the polynomial fitting method, but still sufficient to accurately reflect the nonlinear variation trend of the CC point trajectory.

In addition, the computation time of both methods is compared, as shown in Fig. 7. The polynomial fitting method requires solving linear equations based on the least squares method, resulting in a computation time of 1.131 ms. In contrast, the proposed harmonic function fitting method only involves a simple function calculation without solving any equations, taking only 0.110 ms.

These results demonstrate that although the polynomial fitting method achieves better fitting accuracy, the proposed harmonic function fitting method significantly reduces the computation time and provides a simple and explicit expression. Therefore, considering the balance between fitting accuracy, computational efficiency, and model simplicity, the harmonic function fitting method is finally adopted in this study for CC point trajectory modeling and error prediction.

Fig. 7

Comparison of fitting results for the two-dimensional actual interpolated CC point trajectory using second-order polynomial and harmonic functions.

Nonlinear error evaluation method

As shown in Fig. 8, ${\text{M}}({u^{II}})$ represents the two-dimensional actual interpolation CC point trajectory calculated by Eq. (23). The line segment ${\text{R}}({u^{II}})$, connecting the starting and ending CC points C_s and C_e, represents the theoretical CC point trajectory lying above the horizontal axis ${u^{\mathcal{II}}}$of the CC point plane coordinate system. Noticeably, there is a distance deviation between the actual and theoretical CC point trajectories. This paper defines the maximum value of this distance deviation as the nonlinear error $\delta$ within the machining path segment. As seen in Fig. 8, since ${\text{R}}({u^{II}})$ lies above the horizontal axis ${u^{\mathcal{II}}}$ of the CC point plane coordinate system, the vertical coordinate of the theoretical CC point trajectory ${\text{R}}({u^{II}})$ should be 0, i.e., ${v^{II}}=0$. Therefore, the distance deviation between the actual and theoretical CC point trajectories is the absolute value of the vertical coordinate of the CC point calculated by Eq. (28). Based on the definition of nonlinear error, this error $\delta$ can be calculated as follows:

$$\delta =\mathop {\text{m}\text{a}\text{x}}\limits_{{0 \leqslant {u^{II}} \leqslant u_{e}^{{II}}}} \left\{ {v_{i}^{{II}}} \right\}$$

(28)

Fig. 8

CC points error model.

Nonlinear error compensation mechanism

In Sect. 3 of this paper, a nonlinear error model for the actual interpolation CC point trajectory was established based on the CC point plane. For the optimization of the CC point trajectory and compensation of its nonlinear error, it is still necessary to operate within the CC point plane, ensuring that the optimized CC point trajectory after error compensation remains on the CC point plane. As shown in Fig. 8, this paper proposes compensating for nonlinear errors by adjusting the difference between the actual interpolated CC point trajectory and the predicted interpolated CC point trajectory. The specific implementation method involves predefining a maximum allowable adjustment error, $[\delta ]$, and optimizing the CC point trajectory and compensating for nonlinear errors for the machining path segments where the nonlinear error exceeds$[\delta ]$.

Assuming the optimized CC point trajectory is ${\text{C}}\left( {u_{i}^{{II}}} \right)$, and the compensation function is$L\left( {u_{i}^{{II}}} \right)$, nonlinear error compensation is performed based on the distribution of CC point errors predicted by the CC point error prediction model. The analytical expression is:

$${\text{C}}\left( {u_{i}^{{II}}} \right)={\text{M}}\left( {u_{i}^{{II}}} \right) - {\text{L}}\left( {u_{i}^{{II}}} \right)$$

(29)

In the equation, $M\left( {u_{i}^{{II}}} \right)$ represents the actual CC point trajectories, composed of a set of two-dimensional CC points M.

By substituting the interpolation CC point $u_{i}^{{II}}$ value calculated from Eq. (25) into Eq. (27), the adjusted value of $v_{i}^{II^\prime}$ can be obtained, and thereby the two-dimensional coordinates $(u_{i}^{{II}},v{_{i}^{{II^\prime}}})$ of the actual interpolation CC point after adjustment can be acquired. In this paper, the horizontal coordinates are kept unchanged. The compensated vertical coordinate $v{_{i}^{{II^{\prime \prime}}}}$ (compensated nonlinear error of the CC point) is obtained by subtracting the predicted two-dimensional vertical coordinate $v{_{i}^{{II^\prime }}}$ of the CC point from the original two-dimensional vertical coordinate $v_{i}^{{II}}$ of the CC point. If this error is still greater than the set maximum allowable adjustment error $[\delta ]$, repeat the above process of optimizing and adjusting the CC point trajectory until the nonlinear error of the CC point trajectory is no longer greater than the predefined maximum allowable adjustment error $[\delta ]$. This completes the compensation for the nonlinear error of the CC point trajectory. Since the CNC system ultimately recognizes the three-dimensional interpolated tool center point coordinates, which are obtained by back-calculating from the three-dimensional actual interpolated CC point coordinates described in Eq. (15), it is necessary to convert the compensated two-dimensional interpolated CC point coordinates into three-dimensional actual interpolated CC point coordinates. Since the adjustments in this study keep the horizontal coordinate unchanged, only the compensated vertical coordinate needs to be calculated. The compensated vertical coordinate$v{_{i}^{{II^{\prime \prime }}}}$ is determined by substituting the horizontal coordinate into Eq. (30). The compensated CC point coordinate ${\varvec{C^{\prime\prime}}_i}$ is equal to the foot point P_i plus the product of $v{_{i}^{{II^{\prime \prime }}}}$and the directional vector S_i of the vertical coordinate. The expression for this is:

$${\varvec{C^{\prime\prime}}_i}={\varvec{P}_i}+v{_{i}^{{II^{\prime \prime }}}} * {\varvec{S}_i}$$

(30)

The calculation method for the foot of the perpendicular point P_i is to add the product of the starting CC point and the horizontal coordinate value to the directional vector of the linear path C_s C_e of the CC point. The expression is:

$${\varvec{P}_i}={\varvec{C}_s}+u_{i}^{{II}} * \left( {\mathcal{\alpha ,\beta ,\gamma }} \right)$$

(31)

Meanwhile, the directional vector S_i of the vertical coordinate pointing from the foot of the perpendicular P_i to the CC point before compensation${\varvec{C^{\prime}}_i}$.

$${\varvec{S}_i}\varvec{=}\frac{{{{\varvec{C^{\prime}}}_i} - {\varvec{P}_i}}}{{\left\| {{{\varvec{C^{\prime}}}_i} - {\varvec{P}_i}} \right\|}}$$

(32)

By substituting the two-dimensional actual interpolation CC point coordinates $(u_{i}^{{II}},v_{i}^{{II}})$, which have been optimized and compensated for nonlinear error, into Eqs. (30–32), the corresponding three-dimensional compensated interpolation CC point coordinates${\varvec{C^{\prime\prime}}_i}$ can be calculated. Then, using Eq. (15), the compensated three-dimensional actual interpolation tool center point coordinates are obtained as follows:

$${\varvec{O^{\prime}}_i}={\varvec{C^{\prime\prime}}_i} - R * {\varvec{d}_\mathcal{i}}$$

(33)

In Eq. (33), ${\varvec{O^{\prime}}_i}$ represents the compensated three-dimensional actual interpolation tool center point coordinates, R is the tool radius, and d_i can be obtained by calculating Eq. (14).

Nonlinear error compensation process

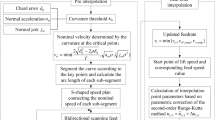
The process for compensating nonlinear error through trajectory optimization of the CC point, as proposed in this document, is illustrated in Fig. 9. In the cutter location data files produced by CAM software, the coordinates of the starting and ending tool center points, tool axis vectors, and CC point locations are included as $\left( {{x_s},{y_s},{z_s},I_{s}^{\varvec{W}},J_{s}^{\varvec{W}},K_{s}^{\varvec{W}}} \right)$, $\left( {{x_e},{y_e},{z_e},I_{e}^{\varvec{W}},J_{e}^{\varvec{W}},K_{e}^{\varvec{W}}} \right)$, $\left( {{u_s},{v_s},{w_s}} \right)$, and $\left( {{u_e},{v_e},{w_e}} \right)$. By reading adjacent cutter location data and using Eq. (10), the actual tool center points are determined, followed by the locations of the actual interpolation CC point coordinates in the workpiece and machine coordinate systems using Eqs. (16) and (17). It is demonstrated that the interpolation CC points of a machining program segment lie on a single plane. The two-dimensional actual interpolation CC point coordinates are then obtained through Eq. (23).

Fig. 9

Flowchart of the nonlinear error prediction and compensation method for CC point trajectories.

Next, a harmonic function is used to predict the trajectory of the two-dimensional interpolation CC points, and the actual interpolation CC point nonlinear error of a machining program segment is calculated using Eq. (28), thus establishing a nonlinear error model. If the calculated nonlinear error exceeds the maximum allowable adjustment error $\left[ \delta \right]$, error compensation is performed. The compensated two-dimensional actual interpolation CC point coordinates are obtained through Eq. (29), and the compensated actual interpolation tool center point coordinates are obtained through Eq. (33). Following this process, the compensated nonlinear error is calculated and compared with the maximum allowable adjustment error $\left[ \delta \right]$. If the compensated nonlinear error still exceeds $\left[ \delta \right]$, compensation is repeated. If the calculated nonlinear error is less than $\left[ \delta \right]$, the compensated actual interpolation tool center point coordinates are sent to the servo controllers of the five motion axes.

Nonlinear error compensation example calculation

Selection of tool center Point/CC point trajectories

To validate the effectiveness of the nonlinear error compensation method proposed in Sect. 5, a spatial free-form surface is selected as an example, and a validation of the method is conducted in a MATLAB environment. Initially, a model of the spatial free-form surface is formed in Unigraphics software, as shown in Fig. 10. This model serves as the basis for the toolpath planning of the surface part. Utilizing UG’s five-axis variable contour milling module, the toolpath is designed and planned using a 4 mm radius flat-end mill, resulting in a cutter location file with the ‘.cls’ extension. The five-axis simulation allows for continuous changes in the A and C axes, which can be directly observed in the toolpath data, reflecting the dynamics of five-axis machining. This file contains all necessary tool position information for subsequent nonlinear error analysis and compensation. Next, this cutter location file is imported into MATLAB for a detailed analysis of the planned toolpath.

The tool path information containing CC points was extracted from the tool position data to validate the nonlinear error control method. For a more intuitive analysis of the nonlinear error control method for tool center points and CC points in the machining program segments, four groups of CC point machining program segments were selected from the chosen tool path information according to the point-line-surface principle (the blue points in Fig. 10 represent these four groups of CC point machining segments). Subsequently, a machining path segment containing these four groups of CC point machining segments was analyzed, and the surface was then subjected to simulation machining.

Fig. 10

Selection of interpolation CC points.

The cutter position information data for the four selected machining program segments, which were extracted from the cutter location file, are shown in Table 3.

Table 3 Cutter location data for four machining program segments in the workpiece coordinate system.

The machine coordinate system data for the four adjacent machining program segments, calculated using Eqs. (4) and (16), are presented in Table 4.

Table 4 Cutter location data for four machining program segments in the machine coordinate system.

The coplanarity of the CC points within a machining program segment was verified, as illustrated in Fig. 11. It is evident from the figure that the actual CC points of each machining program segment are located on the same plane.

Fig. 11

CC points data with fitted plane.

Comparison of nonlinear errors in tool center points/cc points

To perform linear interpolation, this study employs a uniform linear interpolation method with an interpolation time set to 4 ms and a cutting feed rate of 1500 mm/min. By conducting linear interpolation calculations on the data listed in Table 3, the actual CC point trajectory was obtained. Simultaneously, a harmonic function was applied to the data in Table 3 for prediction and compensation, resulting in the predicted and adjusted CC point trajectories. Figure 12 illustrates the CC point trajectories obtained by three different methods: the hollow circle line represents the trajectory obtained using the conventional interpolation method. Due to the combined motion of the two rotational axes, this trajectory forms a single arc-shaped path between the start and end points of the interpolated linear segment. As seen in the figure, there is a significant height deviation between this arc-shaped trajectory and the ideal CC point trajectory.

In contrast, the hollow square line in Fig. 12 shows the predicted three-dimensional CC point trajectory using the harmonic function, which aligns closely with the actual CC point trajectory, reflecting strong prediction accuracy. The hollow diamond line depicts the optimized CC point trajectory obtained through the method presented in this study, demonstrating an even closer alignment with the ideal CC point trajectory. Therefore, when compared to the traditional linear interpolation method, the proposed approach significantly reduces the deviation between the CC point trajectory and the ideal trajectory by predicting and compensating for the CC point trajectory.

It should be noted that the “actual CC point trajectory” shown in Fig. 12 is not directly measured from real machining but is calculated based on the established actual CC point model using the cutter location file data generated from the machining program. In real machining processes, the actual CC point trajectory is influenced by many factors, such as thermal errors, cutting force errors, and dynamic load errors, which are difficult to model and directly measure. As discussed in the literature [Reference²³, these factors lead to deviations between the theoretical trajectory and the real machining trajectory. In this study, we conducted real machining experiments and verified the reliability of the proposed model by measuring the surface error of the machined workpiece, which indirectly reflects the modeling accuracy of the CC point trajectory.

Fig. 12

Trajectory analysis of CC points: actual, predicted, and optimized paths.

When establishing a nonlinear error model to meet high-precision and high-quality machining requirements, the maximum allowable adjustment error is set to 3 μm. To ensure computational feasibility and the practical application of the model, all machining program segments with nonlinear errors exceeding this limit require compensation. As shown in the error distribution of the four datasets in Fig. 13, the CC point errors before compensation exceed the maximum allowable adjustment error, indicating that compensation is necessary for all datasets. In this study, harmonic functions are used to predict the errors during the machining process. By comparing the CC point errors before compensation, after compensation, and the predicted errors, it can be observed that the compensation strategy significantly reduces the error values in each dataset. Before compensation, the errors in all datasets peaked at the central position, far exceeding the 3 μm error threshold. After applying the prediction and compensation mechanisms described in this paper, the errors in all datasets were significantly reduced, and the compensated error values were all below the 3 μm threshold, achieving the desired accuracy. This result validates that the adopted harmonic function can accurately predict error distribution and that the compensation mechanism effectively reduces machining errors and improves accuracy. Therefore, the error model and compensation method demonstrate good potential for application in high-precision machining.

Fig. 13

Comparison of CC point errors before and after compensation.

In Fig. 14, it is clear that in areas where the pre-compensation error discrepancy between the tool center point (red curve) and the CC point (black curve) is relatively small, the errors for both the tool center point (blue curve) and the CC point (green curve) are significantly reduced after compensation. This indicates a strong compensation effect. However, in regions where the error difference before compensation is more significant, particularly around interpolation point 175, the compensation strategy, while still effective in reducing errors, shows a less pronounced impact on the tool center point. This highlights the necessity of evaluating both tool center point and CC point errors, as their characteristics differ. The CC point, being the point in direct contact with the workpiece, has errors that directly influence machining quality. Therefore, in nonlinear error compensation, it is crucial to address the trajectory errors of the CC point as well as tool center point errors, ensuring overall machining precision and workpiece quality. After compensation, the maximum error of the CC point was reduced from 19.49 μm to 2.81 μm, and this improvement extended beyond the maximum error points, with most CC point errors successfully reduced to below 1 μm. Similarly, the maximum error of the tool center point decreased from 19.0 μm to 4.88 μm after compensation. This demonstrates the approach’s effectiveness in enhancing machining precision, especially for high-accuracy applications.

Fig. 14

Errors at the tool center point and CC point before and after compensation for a machining path.

Figure 15 illustrates the error distribution across the surface before and after the application of error compensation techniques. Specifically, panels Fig. 15a and c depict the error distribution of the CC point and the tool center point prior to compensation, whereas Fig. 15b and d show the corresponding distributions following compensation.

Analysis of Fig. 15a and c reveals a non-uniform distribution of errors for both the tool contact and center points across the surface before compensation. Notably, significant error accumulation is observed in localized regions, particularly near the edges and in areas of pronounced curvature changes, where the maximum errors can reach 35 μm. These findings suggest substantial deviations between the actual tool path and the ideal path in these regions.

Following the implementation of the error compensation strategy, a marked reduction in error is evident, as shown in Fig. 15b and d. The post-compensation error distribution for the tool contact point Fig. 15b is significantly improved, with most errors reduced to below 2.5 μm, indicating a highly effective overall reduction in tool path deviation. Similarly, the tool center point errors Fig. 15d are substantially minimized, with most regions showing errors reduced to within 12 μm. Although some residual errors remain, the overall error range is greatly diminished. These results demonstrate the efficacy of the applied error compensation strategy in mitigating tool path deviations during surface machining, particularly in areas initially characterized by higher error levels, where the compensation effect is most pronounced.

Based on the comprehensive analysis from point to line and finally to surface, these results clearly demonstrate the effectiveness of the nonlinear error compensation theory proposed in this paper in practical applications. This approach provides a robust method for reducing machining defects caused by nonlinear errors, thereby improving overall machining efficiency and quality. Furthermore, minimizing nonlinear errors is crucial for precision machining and high-quality manufacturing, especially in applications that require high accuracy. Consequently, this compensation method is not only of theoretical significance but also holds substantial practical value, particularly in the fields of high-precision CNC machining and advanced manufacturing technologies.

Fig. 15

Errors at the tool center point and CC point before and after compensation for a surface.

In CNC machining, after compensating for system errors, real-time performance is a critical indicator of interpolation algorithm performance. Real-time performance is crucial for CNC machining; the system must complete interpolation calculations and motion control within strict time constraints to ensure machining accuracy and efficiency.

Fig. 16

Comparison of interpolation time between the proposed method and reference 22 across interpolation points.

This paper utilizes harmonic functions to predict interpolation points, significantly reducing interpolation calculation time. Experimental results show that the average calculation time for interpolation points is 2.64618 ms, and the maximum calculation time does not exceed 3.42240 ms, both within the real-time threshold (i.e., interpolation cycle T = 4 ms). As shown in the Fig. 16, the calculation time for interpolation points without error compensation is shorter than that for points with error compensation. In contrast, the method in Reference²² uses a covariance matrix and fitting functions for interpolation prediction, which, while improving accuracy, significantly increases calculation time, exceeding the real-time threshold of the interpolation cycle. Therefore, the method proposed in this paper not only ensures interpolation accuracy but also greatly reduces calculation time, better meeting the stringent requirements for real-time performance and efficiency in CNC machining.

Experiment results

In this experiment, an HS-500 T five-axis CNC machine equipped with a 0i-MF Plus control system was used (as shown in Fig. 17a). The aluminum 6061 workpiece, with initial dimensions of 120 mm × 50 mm × 35 mm, was secured to the rotary table using the fixture shown in Fig. 17b, ensuring stability and precise positioning during the multi-axis machining process. In the roughing processing stage (Fig. 17c), a 5 mm radius tungsten carbide flat-end mill was used, employing a dynamic machining strategy to quickly remove excess material and roughly shape the workpiece. The roughing processing parameters were as follows: cutting feed rate of 6000 mm/min, spindle speed of 11,500 rpm, axial depth of cut of 0.5 mm, and an interpolation cycle of 6 ms. This strategy optimized the tool path and significantly improved machining efficiency. The finishing processing stage (Fig. 17d) was carried out using 4 mm radius tungsten carbide flat-end mill with a conventional profile milling strategy to enhance the surface quality and dimensional accuracy of the workpiece. During the finishing process, the tool oscillated at a slight angle along the curved surface of the workpiece, ensuring smoother transitions and finer surface finish. The proposed compensation method was applied in this stage. The finishing processing parameters were: cutting feed rate of 1500 mm/min, spindle speed of 10,000 rpm, and an interpolation cycle of 4 ms. Figure 17e shows the workpiece after the machining process, with good surface quality and precise contours, meeting the desired machining expectations.

Fig. 17

Free-form surface machining process (a) HS-500 T five-axis CNC machine (b) Fixture and blank(c) Roughing stage (d) Finishing processing (e) After processing.

The process of measuring machining error on the workpiece surface using the Tianzhun VME222 optical image measuring instrument is illustrated in Fig. 18a. First, the workpiece was securely fixed on the measuring platform and focused. Then, the reference coordinate system was located using the measurement software. The camera was manually adjusted to select the start and end points of the machining path. Using the crosshair tool in the software, the actual machining points were manually marked, and their three-dimensional coordinates were recorded. Subsequently, the machining error at each interpolation point was calculated based on the Euclidean distance between these actual coordinates and the corresponding theoretical points.

The average machining error calculated was 20.35 μm, with a maximum machining error of 40.26 μm, which shows significant deviation from the theoretical expectations. In contrast, after compensation, the average machining error was reduced to 4.127 μm, and the maximum machining error to 8.546 μm, demonstrating substantial improvement in machining precision, as shown in Table 5. Figure 18b presents a comparison of machining errors before and after compensation for the first set of data. It is evident that the machining error before compensation is larger, with a maximum value of approximately 8 μm in the middle of the path. After compensation, the error is significantly reduced, and the overall error curve becomes smoother.

However, when compared with the simulation results in Fig. 13a, a noticeable discrepancy remains. Although the compensated error trends in both the simulation and the actual results are consistent, the pre-compensation error predicted by the simulation is smaller than the actual observed error. This difference suggests that the actual machining error may not be solely influenced by CC point error, but could also be affected by other factors, such as inter-axis coupling error and cutting forces.

In actual machining, inter-axis coupling errors reduce the synchronization and accuracy of each axis, which in turn affects the accuracy of the machining path. Furthermore, cutting forces induce slight tool deformation during the cutting process, particularly in the middle region where cutting forces are the greatest, resulting in a peak in the observed error. These factors were not fully accounted for in the simulation model, which likely explains the observed discrepancy between Fig. 13a and the actual error data.

To further improve compensation accuracy, future work should incorporate inter-axis coupling and cutting force effects into the simulation and compensation models for more precise optimization.

Fig. 18

Measurement and comparison of machining errors before and after compensation using an optical image measuring instrument.

The roughness of the machined surfaces was measured using a roughness tester, benchtop model SRA-1 (as shown in Fig. 19). The results of machining without compensation, as detailed in this study, are shown on the left side of Fig. 20b, yielding an average surface roughness of 9.356 μm. Employing the nonlinear error compensation technique proposed herein, the machined part shown on the right side of Fig. 19b exhibited a significantly reduced average surface roughness of 1.521 μm (as shown in Table 5).

Fig. 19

Assessing the roughness of machined components using the SRA-1 benchtop surface roughness tester.

Table 5 Comparison of machined part roughness pre- and post-compensation.

Using a high-definition CCD microscope, a more detailed surface analysis was conducted after measuring machining errors and surface roughness. Figure 20a presents a magnified view of the machined surface, allowing a closer inspection of the finish at a microscopic level. Figure 20b compares two aluminum 6061 workpieces. On the left, the workpiece machined without the proposed compensation method displays visible irregularities, including scratches and a rough texture. On the right, after applying the compensation technique, the workpiece reveals a much smoother surface with fewer defects. The difference is clearly visible, with the right side showing a finer and more uniform finish. This improvement demonstrates the success of the compensation method in reducing nonlinear machining errors, which enhances both surface quality and overall machining precision. The results confirm that the proposed method significantly improves the machining process, as well as the workpiece’s functional performance and aesthetic quality.

Fig. 20

Free-form surface machining results before and after compensation.

Results and discussion

To validate the effectiveness of the proposed error compensation method, a free-form surface machining experiment was conducted on an aluminum 6061 workpiece, a material commonly used in precision part manufacturing. The experiment was carried out on a five-axis CNC machine tool. The surface roughness was measured using a SRA-1 stylus roughness analyzer (SRA-1), and the machining error was measured with an optical measurement system, both of which are widely used for accurate surface quality and dimensional assessments.

The results, as shown in Table 5; Fig. 20, demonstrate that the proposed method effectively reduced the maximum machining error from 40.26 μm to 8.546 μm, and the average machining error from 20.35 μm to 4.127 μm. Moreover, surface roughness measurements indicated a significant improvement, with the average surface roughness decreasing from 9.356 μm (pre-compensation) to 1.521 μm (post-compensation). These results confirm the effectiveness of the proposed method in improving both machining accuracy and surface quality.

It is important to note that some discrepancies still exist between the predicted and actual machining results. These discrepancies arise because the actual CC point trajectory during five-axis machining is influenced by multiple complex factors that are not considered in the current model. These factors include thermal errors, cutting force-induced deformation, dynamic load errors, and inter-axis coupling effects, as discussed in recent literature^23,24. The comparison between the actual machining error shown in Fig. 18(b) and the predicted error in Fig. 13(a) further reveals that the actual CC point trajectory is affected by these additional factors, leading to deviations from the theoretical predictions.

In addition to its high accuracy, the proposed method demonstrates good computational efficiency. As shown in Fig. 16, the average calculation time for each interpolation point is 2.64618 ms, which meets the real-time requirement of CNC machining systems with a typical interpolation period of 4 ms. Compared to other methods based on complex optimization algorithms²², the proposed method offers significant advantages in computational simplicity and real-time performance.

Overall, the proposed method is particularly suitable for offline trajectory optimization and high-precision free-form surface machining using five-axis CNC machine tools, where trajectory error control and surface quality are critical. This method can be effectively applied to industrial applications such as aerospace component manufacturing, precision mold machining, and the production of other high-value parts.

Although the proposed method is characterized by a simple model structure and fast computation, offering promising potential for real-time error prediction and compensation, this study focuses on offline error compensation scenarios for experimental validation. This is mainly because offline implementation provides greater stability, controllability, and reliability for high-precision machining tasks in practical industrial applications. Future work will focus on extending the proposed method to online real-time compensation, incorporating sensor-based monitoring techniques and adaptive control strategies to dynamically mitigate errors during machining processes. This research direction is highly consistent with recent advances in CNC machine tool error modeling and adaptive control technologies^23,24.

Conclusions

This paper presents an error compensation method based on the optimization of CC point trajectories, aiming to reduce the nonlinear errors resulting from deviations in actual CC point trajectories. Through the development of a mathematical model for A-C double rotary table CNC machines’ bidirectional motion, leveraging data sampling interpolation, the method effectively calculates the actual positions of the tool center and CC points in five-axis linear interpolation, improving the accuracy of the machining process.

We also introduced a CC point plane model, which is based on the hypothesis that CC points in the same machining program segment interpolate on a single plane. This model simplifies the conversion between three-dimensional and two-dimensional CC point coordinates. Furthermore, we proposed a nonlinear error modeling algorithm for the CC points and a compensation model to address errors caused by the rotation axis swing, improving the overall error correction performance.

The effectiveness of the proposed method was validated through both simulations and actual machining experiments. In the simulations, the maximum error at the CC points was reduced by approximately 85.58%, from 19.49 μm to 2.81 μm, with most errors falling below 1 μm. Tool center point errors also showed significant improvement, with a reduction of 75.13%. In the actual machining experiments conducted on an aluminum 6061 workpiece, the maximum machining error decreased by 78.74%, from 40.26 μm to 8.546 μm, while the average machining error was reduced by 79.7%, from 20.35 μm to 4.127 μm. Furthermore, surface roughness improved significantly, decreasing from 17.62 μm (pre-compensation) to 2.440 μm (post-compensation). These results confirm that the proposed method enhances both machining precision and surface quality.

However, the study is focused on modeling, calculating, and compensating for CC point nonlinear errors. It addresses a limited range of error sources, and other significant factors such as inter-axis coupling, cutting force errors, and nonlinear characteristics caused by simplifying CC points to two-dimensional coordinates also influence machine accuracy. The simplification process neglects complex rotational movements and orientation errors, especially when two rotational axes are active simultaneously. This limitation makes it challenging to capture the full nonlinear behavior of the system. Additionally, errors like eccentricity and oscillation effects during C-axis rotation, as well as dynamic changes in motion errors due to factors like tool path and thermal deformation, are not fully accounted for. Therefore, future research should consider integrating these additional error sources into the model to further enhance its accuracy and applicability in complex machining environments.