Optimizing coverage in wireless sensor networks using deep reinforcement learning with graph neural networks

Abstract

In Wireless Sensor Networks (WSNs), achieving optimal coverage in dynamic environments remains a significant challenge. Traditional optimization techniques, such as genetic algorithms, particle swarm optimization, and ant colony optimization, have demonstrated adaptability in node placement but struggle with real-time self-learning capabilities, requiring frequent retraining to handle continuously changing conditions. To address these limitations, this research introduces a novel hybrid model that integrates Deep Reinforcement Learning (DRL) with Graph Neural Networks (GNN). The DRL component enables adaptive decision-making, allowing real-time sensor node adjustments based on network performance feedback. Simultaneously, the GNN model enhances spatial awareness by capturing relational dependencies among sensor nodes, optimizing coverage efficiency. This integration significantly improves network adaptability and operational efficiency. Extensive simulations demonstrate that the proposed DRL-GNN model achieves a coverage ratio of up to 96.4%, energy efficiency of 95.8%, and minimizes overlap to 5.2%, outperforming traditional methods. These results validate the effectiveness of the proposed approach in enhancing WSN coverage while maintaining energy efficiency and minimal redundancy.

Introduction

Wireless sensor networks (WSN) are used in numerous applications from environmental monitoring to defense and industrial automation¹. However, the performance of the network is presents in its ability to cover the geographic areas. Effective coverage defines that the network is monitored without gaps. By providing optimal coverage accurate and reliable data acquisition can be made in WSN. However, attaining optimal coverage in WSN faces challenges like limited range of individual sensor, battery constraints, environment factors which block signals, etc., Moreover the dynamic nature of WSN and the deployment of sensors in complicated areas increases the coverage issues². Networks must be flexible and adapt to the changes quickly to provide effective services. Attaining such adaptability not only requires proper initial deployment but also it needs reconfiguration of nodes to maintain coverage.

Traditional coverage optimization strategies mainly focus on static node deployment, employing methods such as Voronoi diagrams, genetic algorithms, particle swarm optimization, and ant colony optimization, aiming to identify optimal sensor locations prior to network deployment³. However, these traditional methods struggle with real-time adaptability due to their inability to dynamically adjust node positions once initially set⁴. Although approaches involving genetic algorithms, particle swarm optimization, and other nature-inspired methods have demonstrated improved adaptability by enabling mobile nodes to reposition in response to network changes, these techniques often require extensive computational resources⁵. Additionally, they typically need retraining or recalibration whenever the environmental conditions or network parameters change significantly, limiting their efficiency and practicality in highly dynamic scenarios^6,7,8. Recognizing these limitations, our proposed DRL-GNN model integrates adaptive decision-making capabilities through Deep Reinforcement Learning (DRL) and structural awareness⁹ provided by Graph Neural Networks (GNN), ensuring robust real-time adaptation and enhanced operational efficiency in dynamic WSN environments^10,11,12.

Traditional coverage optimization strategies focused on static deployment in which identifying optimal location is essential before network creation. Subsequent changes in the node position are not possible after employing static deployment. Techniques like Voronoi diagrams and optimization algorithms are used for static deployment³. However, for a dynamic WSN environment there is a need to reposition the nodes physically or reconfigured virtually⁴. Thus, recent approaches adapt mobile sensor nodes so that the node position can be changed in response to the environmental changes or the network requirement. Optimization algorithms like genetic algorithm⁵, particle swarm optimization⁶ and other nature inspired, evolutionary algorithms^7,8 are employed to obtain optimal solution for dynamic node placement⁹. Though these methods increased the adaptability but often require high computational resources which limits the network features^10,11,12.

The recent advancement in machine learning offers solutions for this coverage optimization. The network behavior can be predicted through the machine learning models by learning the data patterns¹³. Optimal coverage can be attained by learning the network data however the ML approaches require larger datasets for training¹⁴. Moreover, the techniques are not generalized to adapt to different network environments. ML approaches can produce better results only after retraining based on the new network environment. Thus, the motivation of this research is obtained by observing the essential need to enhance the adaptability and efficiency of Wireless Sensor Networks (WSNs) in dynamic environments. Traditional methods which depend on static deployments are not ready to handle changes in network conditions and environmental dynamics. This leads to suboptimal coverage and inefficient resource utilization. Considering these limitations in the existing approaches, this research work presents a novel model that utilizes the features of deep learning algorithm Deep Reinforcement Learning with Graph Neural Network. The dynamic challenges and complex topologies of modern WSN and its requirements are considered and developed an optimal coverage model using DRL and GNN. The proposed DRL-GNN model provides an adaptive learning to refine the sensor deployment based on the real time feedback from the network. The policy driven adjustments reduce human interventions and refines the node deployment where the network conditions are continuously changing. The utilization of GNN in the model is to manage network changes. GNN can interpret and capture the relationship between the nodes and network to optimize the coverage more effectively compared to traditional methods. The integration of DRL with GNN allows the network to learn from its topology and dynamically adjust the location based on the operational parameters. The resulting network will provide enhanced optimal coverage with high efficiency which improves the overall performance of WSNs.

The novelty lies in the structured integration of DRL’s adaptive, real-time decision-making capabilities with GNN’s capacity to effectively model complex spatial relationships among nodes. This combination enables dynamic adjustment of sensor node positions based on real-time feedback, significantly improving coverage optimization, energy efficiency, and reducing overlap. Moreover, the integration approach allows DRL to leverage the spatial insights provided by GNN to make more informed decisions compared to traditional DRL or GNN methods alone. Consequently, our proposed DRL-GNN framework uniquely addresses the dynamic environmental changes and structural complexities in WSNs, thereby providing a substantial performance improvement over conventional approaches.

The research work contributes to the following.

• Presented a novel hybrid model that combines Deep Reinforcement Learning (DRL) with Graph Neural Network (GNN) to provide optimal coverage for a dynamic wireless sensor network. By dynamically optimizing sensor node placements based on the network performance feedback, the proposed model provides significant improvements in coverage, energy efficiency, and overall network robustness. The integration of DRL allows for adaptive decision-making, while GNN captures and processes spatial relationships between nodes which enhances the system response to environmental changes.

• Presented an intense simulation analysis of proposed model and evaluated the performances through metrics like coverage ratio, energy efficiency, overlap ratio, throughput, latency, average hop count and network lifetime.

• Evaluated the network performances with different node count and analyzed the performance of proposed hybrid model in attaining optimal coverage to WSN.

The remaining discussions are presented in the following order. Sect “Related works” presents a brief literature review; Sect “Proposed work” provides the proposed hybrid model for optimal coverage of WSN. Sect “Results and discussion” presents the simulation results and discussion, and Sect “Conclusion” concludes the research work.

Related works

A brief literature of recent research works on coverage optimization is considered for analysis. The discussion brief discusses the methodology and its feature merits and demerits. Traditional optimization algorithms, nature-inspired hybrid optimization algorithms, and machine learning-based methods. Subsequently, we elaborated each category individually, providing relevant studies that highlight the strengths, limitations, and specific contexts of their application. This structured approach enhances readability and clearly delineates our research’s positioning relative to prior work. The revised manuscript now reflects this organizational improvement, offering readers a logical progression through existing research methods toward the justification of our proposed DRL-GNN model.

The optimization model presented in¹⁵ incorporated the Honey badger algorithm to attain enhanced coverage of WSN. The presented model introduces an optimization factor in addition to traditional honey badger algorithm so that a better balance between exploration and exploitation is obtained while finding the optimal solution. The experimental validation of the presented model confirms that parameter optimized Honey badger algorithm attained improved coverage performance over existing grey wolf optimization and particle swarm optimization algorithms. The optimal coverage algorithm for sensor network presented in¹⁶ improves the efficiency and coverage of WSN by utilizing sensor cloud systems. The presented model integrates genetic algorithm for optimizing the clustering and node path planning. The mutation parameter of genetic algorithm and its threshold parameters improves the clustering uniformity and reduces the energy consumption. Simulation results demonstrate the better coverage performance of the presented model over existing methods. Considering network coverage, network lifetime and energy overhead, the presented model attains better performances compared to traditional methods.

An improved ant lion optimization model is presented in¹⁷ to enhance the service quality of WSN. The presented model focuses on network coverage and minimizes the sensor node movement to improve the network performance. To attain this, fast nondominated sorting and elite strategies from NSGA-II are combined with ant lion optimization algorithm. Due to this, the presented avoids local optima and attains improved solution accuracy. Simulation results of presented model validate the better performance in terms of increased coverage over traditional methods. A minimum exposure path searching algorithm is presented in¹⁸ to provide improved coverage for WSN. The presented model simplifies the traditional minimum exposure path problem using grid discretization and constructs a weighted graph. Then using particle swarm optimization optimal sensor deployment locations are identified to obtain improved coverage during deployment. The experimental result of the presented model validates that the better coverage performance through its minimum exposure value compared to traditional method.

To address the complexities in 3D wireless sensor, network a coverage optimization procedure is presented in¹⁹ using an improved sparrow search algorithm. The presented model overcomes the limitation of traditional sparrow search algorithm by introducing a safety threshold attenuation function and stagnation update procedure. Due to this the optimization model avoids local optimal and improves the convergence performance. The optimal threshold minimizes the network energy consumption by optimizing the node movement distance. simulation analysis of presented model confirms the improvements in terms of enhanced connectivity and reduced moving distances.

The multi-objective optimization-based network coverage and lifetime enhancement model presented in²⁰ introduces an improved army ant search optimizer algorithm. The optimization algorithm considers four key enhancements for army ant search optimizer for multi-objective transformation, initial population diversity, avoid local optima and boost optimization abilities. The multi-objective transformation is obtained through fast-nondominated sorting NSGA-II, and the initial population diversity is attained by employing chaotic mapping. The local optimal is avoided by incorporating average fitness value adaptor and the optimization abilities are enhanced by integrating competitive swarm optimizer. Experimental results show that the performance of the presented model is better than existing methods, however incorporation of multiple optimization algorithm increases the computational complexity.

The coverage optimization model presented in²¹ includes Harris Hawk optimization algorithm to improve the WSN performance. The presented utilize the optimal solution of HHO to optimize the mesh router placement to attain maximum network connectivity and client coverage. The experimental results provide a comparative analysis with traditional optimization algorithms like gray wolf optimization, sine cosine algorithm and particle swarm optimization to demonstrate the better coverage performances. A self-adaptive artificial bee colony optimization algorithm is presented in²² to address the node deployment issue in WSN. The presented model utilizes the optimization features of artificial bee colony algorithm. Additionally, the presented model includes a strategic pool and an adaptive selection mechanism to improve the optimization model performance. Due to this, the presented model attained improved performance and effectively avoids local optima. Thus, robust node placement enhances the overall performance and reliability of WSN.

An advanced optimization procedure to improve the coverage of WSN is presented in²³. Evolutionary optimization algorithm NSGA-III is incorporated in the presented work to solve the multi-objective optimization problem. The optimal solutions of NSGA-III are utilized to maximize connectivity and coverage with minimized energy consumption. The experimental results confirm that the presented model improves network coverage and network lifetime over traditional methods. The hybrid model presented in²⁴ utilizes an enhanced cuckoo search algorithm (CSA) and non-uniform clustering algorithm to improve the performance of WSN. The presented model incorporates Cauchy distribution to optimize CSA. The distribution improves the convergence speed and accuracy of optimization algorithm. Also, the presented model includes a dynamic cluster radius optimization to fine tune the non-uniform clustering process. Due to this, the hybrid model provides better balance between network stability and energy consumption.

The whale optimization-based coverage optimization model presented in²⁵ for WSN overcomes the poor and inconsistent exploration problem of traditional optimization algorithms. The whale optimization is combined with levy flight to update the current search of location to place the sensor nodes. Due to combined process, the whale optimization exploration ability is enhanced and avoids local optimal solution. Experimental results present the better performance of hybrid whale optimization over traditional optimization algorithms in terms of enhanced coverage efficiency.

The hybrid optimization model presented in²⁶ combines Voronoi-Glowworm Swarm Optimization-K-means algorithm to enhance the coverage area of WSN. The presented model provides better sensor deployment by optimizing the sensing radius calculation. Also, it enhances the network lifetime by deploying the sensor nodes optimally. By using multi-hop transmission and effective sleep wake procedure the energy consumption is reduced further. Experimental results present the model better coverage performance over traditional methods. The hybrid optimization presented in²⁷ incorporates PSO and chaos optimization for coverage optimization in WSN. The hybrid approach encodes the node as particle position and allows the node to move towards optimal location. Further the chaos optimization optimizes the PSO parameters to enhance the coverage performances compared to existing optimization algorithms.

The coverage enhancement procedure presented in²⁸ employs a bipartite graph model to optimize the moving distance of node during redeployment. The presented model incorporates vampire bat algorithm with bipartite graph model to improve the effectiveness of redeployment. Further to refine the coverage virtual force-based optimization is incorporated which reduces the node movement during redeployment. Experimental results show that the performance of the presented model is better than traditional optimization algorithms. The multi-objective Dingo optimization algorithm presented in²⁹ for optimal network coverage of WSN analyzes the node sensing capabilities and supply energy over time. The dynamic sensing model analyze the interaction between the nodes and optimizes the sensing coverage rate over traditional optimization algorithms like vulture optimization, particle swarm optimization algorithms. The findings from the analysis are summarized in Table 1.

Table 1 Summary of literature review.

Research gap

From the summary of the above research works, providing optimal coverage or attaining enhanced coverage, energy efficiency and network lifetime are identified as key challenges in traditional WSN. Many studies employed different optimization algorithms like artificial bee colony, ant lion optimization, and non-dominated sorting genetic algorithms. However, the existing methods focus on energy consumption and coverage and do not address multi-objectives simultaneously. The optimization algorithms incorporate additional methods to overcome the local optimal and enhance the coverage but do not consider the dynamic network conditions. The major research gap identified from the study is to address the complex relationship between node mobility and energy decomposition. Moreover, traditional optimization algorithms computational complexity increases when it is modified as a hybrid model by combining with other optimization algorithms. optimization algorithms like sparrow search and bat algorithms show reduced energy consumption and lack in scalability when the environment id varying. Thus, there is a need for developing an adaptive multi-objective model that should integrate coverage, energy efficiency and network lifetime to manage dynamic WSN environment.

Proposed work

The proposed work introduces a novel optimal coverage model for Wireless Sensor Networks (WSNs) by integrating Deep Reinforcement Learning (DRL) and Graph Neural Networks (GNN). The primary objective is to dynamically optimize sensor node positions to maximize coverage, minimize overlap, and enhance energy efficiency. DRL provides adaptive, real-time decision-making by adjusting node positions based on network performance feedback, crucial in dynamically changing environments. Simultaneously, GNN effectively captures spatial dependencies among nodes, modeling their interactions to inform DRL decisions. Detailed discussions on the network model, mathematical formulations, and optimization strategies involving DRL and GNN are elaborated in the subsequent subsections.

Network model

The network model of the proposed system deploys $\:N$ sensor nodes within the monitoring area $\:A\subset\:{R}^{2}$ to provide optimal coverage and connectivity. The monitoring area of the network is a two-dimensional region rectangular area with dimensions $\:(L\:\times\:W)$ in which sensors are deployed randomly. Each sensor node $\:i$ is placed at a position $\:{p}_{i}=\left({x}_{i},{y}_{i}\right)$ within the area $\:A$. The position of the nodes can be represented as $\:P=\{{p}_{1},{p}_{2},\dots\:,{p}_{N}\}$ where $\:{x}_{i}\in\:\left[0,L\right]$ and $\:{y}_{i}\in\:\left[0,W\right]$. The sensor node position is randomly determined using uniform distributions for $\:x$ and $\:y$ coordinates which is modelled as $\:{x}_{i}\sim\:\mathcal{U}\left(0,L\right)\hspace{1em}\text{and}\hspace{1em}{y}_{i}\sim\:\mathcal{U}\left(0,W\right)$. where $\:\mathcal{U}\left(a,b\right)$ indicates uniform distribution between $\:a$ and $\:b$, $\:N$ indicates the total number of sensor nodes, $\:L$ indicates the length of the monitoring area, $\:W$ indicates the width of the monitoring area, $\:{p}_{i}$ indicates the position of sensor node $\:i$, $\:({x}_{i},{y}_{i})$ indicates the coordinates of sensor node $\:i$.

For modelling the coverage area $\:{C}_{i}$ of the sensor node, each node sensing radius $\:{r}_{i}$ is defined. The coverage area of sensor node $\:i$ is circle centered at $\:{p}_{i}$ with radius $\:{r}_{i}$. Mathematically if is expressed as

$$\:{C}_{i}=\{p\in\:{R}^{2}\mid\:|p-{p}_{i}|\le\:{r}_{i}\}$$

(1)

where $\:\left(\right|\cdot\:\left|\right)$ denotes the Euclidean distance. The total coverage area of the sensor network is defined by taking union of the all the sensor nodes coverage area which is formulated as

$$\:C={\bigcup\:}_{i=1}^{N}{C}_{i}$$

(2)

The major objective is to attain maximize the total coverage area $\:C$ to ensure entire monitoring $\:A$ are covered. The coverage ratio of the monitoring area is defined by fraction of monitoring area $\:A$ that is covered by the sensor nodes. Mathematically it is expressed as

$$\:Coverage\:Ratio=\frac{\left|{C}_{covered}\cap\:{A}_{monitoring}\right|}{\left|{A}_{monitoring}\right|}$$

(3)

where $\:\left(\right|\cdot\:\left|\right)$ denotes the area of the set. When the coverage area of two or more sensor nodes intersects there will be an overlap in the coverage area which is defined as follows.

$$\:{C}_{\text{overlap}}={\bigcup\:}_{i\ne\:j}\left({A}_{i}\cap\:{A}_{j}\right)$$

(4)

where $\:{r}_{i}$ indicates the sensing radius of sensor node $\:\left(i\right)$, $\:{A}_{i}$ indicates the coverage area of sensor node $\:\left(i\right)$, $\:C$ indicates the total coverage area of the WSN, $\:{C}_{\text{overlap}}$ indicates the overlap area.

Fig. 1

Wireless sensor network model.

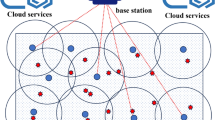
Figure 1 illustrates the wireless sensor network model which is used in the proposed work where the nodes are randomly placed with coverage overlap. The random deployment of sensor nodes ensures that the nodes spread across the entire monitoring area, however some regions are under covered or over covered. The coverage model defines the effectiveness of the deployment considering the total coverage area and coverage ratio. By minimizing the coverage overlap and maximizing the coverage ratio an efficient sensor deployment can be achieved so that entire area can be monitored with minimal redundancy and energy consumption.

Objective function

The main objective of this research work is to maximize the sensor node coverage while minimizing the coverage overlap between coverage area and energy consumed. The objective is formulated as a multi-objective optimization model. The first objective is to maximize the total coverage area and the second objective is to minimize redundant coverage. The third objective is to minimize the energy consumption of nodes. Combining all the three objectives using weighting factors $\:\left({\upalpha\:}\right)$ and $\:\left({\upbeta\:}\right)$ the multi-objective function is formulated as follows.

$$\:\underset{P}{{max}}Coverage\left(P\right)$$

(5)

$$\:\underset{P}{{min}}Overlap\left(P\right)=\underset{P}{{min}}{\sum\:}_{i\ne\:j}\left|{C}_{i}\cap\:{C}_{j}\right|$$

(6)

$$\:\underset{P}{{min}}Energy\left(P\right)=\underset{P}{{min}}{\sum\:}_{i=1}^{N}{E}_{i}$$

(7)

$$\:\underset{P}{{max}}\left(Coverage\left(P\right)-\alpha\:\cdot\:Overlap\left(P\right)-\beta\:\cdot\:Energy\left(P\right)\right)$$

(8)

where $\:P=\{{p}_{1},{p}_{2},\dots\:,{p}_{N}\}$ denotes the sensor node positions, $\:{E}_{i}$ is the energy consumed by sensor node $\:i$, node position is indicated as $\:P$, node coverage is indicated as $\:{C}_{i}$, coverage overlap is indicated as $\:{C}_{overlap}$, node energy consumption is indicated as $\:{E}_{i}$ and $\:({\upalpha\:},\:{\upbeta\:})$ indicates the weighting factors for overlap and energy consumption.

Constraints

To solve the optimization problem, the sensor network constraints are identified and formulated. The major constraints considered in this research work are coverage, energy, and connectivity. The coverage constraint ensures that the entire monitoring area is covered by the sensor nodes. The energy constraint defines that total energy consumed by the sensor node should not exceed its actual energy. The connectivity constraint ensures that the sensor nodes must relate to each other so that they can communicate with each other or with base station. Mathematically the network constraints are formulated as follows.

$${\text{Coverage~Constraint}}:{\text{~}}\mathop \cup \limits_{{i = 1}}^{N} C_{i} \supseteq A$$

(9)

$${\text{Energy~Constraint}}:{\text{~}}\mathop \sum \limits_{{t = 1}}^{T} e_{{i,t}} \le E_{{max}} \quad {\text{for~all~}}i \in \left\{ {1,2, \ldots ,N} \right\}$$

(10)

$${\text{Connectivity~Constraint}}:{\text{~}}G = \left( {V,E} \right)$$

(11)

where $\:\left({e}_{i,t}\right)$ is the energy consumed by sensor node $\:\left(i\right)$ at time $\:\left(t\right)$, connectivity graph is indicated as $\:G$, the set of sensor nodes is indicated as $\:V$ and $\:E$ indicates the set of communication links, $\:A$ indicates the monitoring area, $\:T$ indicates the total time period of operation, $\:{E}_{max}$ indicates the maximum available energy for each sensor node. Addressing these constraints is essential to ensure efficient deployment of WSN.

Deep reinforcement learning (DRL) with graph neural networks (GNNs)

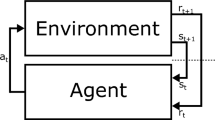
To solve the above defined multi-objective problem, the proposed model incorporates DRL with GNN to optimize the WSN coverage. To dynamically optimize the sensor node positions for maximum coverage, minimized overlap, and minimized energy consumption over time, DRL is used in the proposed work. The mathematical model of DRL defines the state, action, reward, and Q-functions as follows.

The sensor nodes current position and their residual energy levels are used to represent the state $\:{s}_{t}$ of the DRL which is formulated as follows.

$$\:{s}_{t}=\{\left({p}_{i},{E}_{i}\right)\mid\:i=\text{1,2},\dots\:,N\}$$

(12)

where $\:{p}_{i}$ indicates the position of sensor node $\:i$, $\:{E}_{i}$ indicates the residual energy of sensor node $\:i$.

The sensor node movement is represented by the action $\:{a}_{t}$ which is formulated as follows.

$$\:{a}_{t}=\{\varDelta\:{p}_{i}\mid\:i=\text{1,2},\dots\:,N\}$$

(13)

where $\:\varDelta\:{p}_{i}=\left(\varDelta\:{x}_{i},\varDelta\:{y}_{i}\right)$ is the sensor node movement vector. The reward function $\:{r}_{t}$ is designed to guide the learning process by providing feedback on the quality of the actions taken. Mathematically the reward function is formulated as

$$\:{r}_{t}=Coverage\left({P}_{t+1}\right)-\alpha\:\cdot\:Overlap\left({P}_{t+1}\right)-\beta\:\cdot\:Energy\left({P}_{t+1}\right)$$

(14)

where $\:{P}_{t+1}$ indicates the positions of sensor nodes at time $\:(t+1)$. $\:{\upalpha\:}$ and $\:{\upbeta\:}$ indicates the weighting factors for overlap and energy consumption, respectively. Finally, the Q-function of the DRL estimates the expected cumulative reward for acting $\:{a}_{t}$ in state $\:{s}_{t}$. Mathematically the Q-function is formulated as follows.

$$\:Q\left({s}_{t},{a}_{t};\theta\:\right)={r}_{t}+\gamma\:\underset{{a}_{t+1}}{{max}}Q\left({s}_{t+1},{a}_{t+1};{\theta\:}^{{\prime\:}}\right)$$

(15)

where $\:{\upgamma\:}$ indicates the discount factor, $\:\theta\:$ and $\:{\theta\:}^{{\prime\:}}$ are the weights of the Q-network and the target network, respectively. DRL allows adaptive optimization of sensor nodes position by learning the environment. By integrating the coverage, overlap and energy considerations, the reward function ensures a balanced optimization. The process flow of proposed model is given in Fig. 2.

Fig. 2

Proposed model process flow.

Graph neural networks (GNNs)

In the proposed work GNN is utilized to model the relationship and interactions between sensor nodes. The network graph structure is utilized to optimize coverage and communication. In the mathematical model, the sensor network is represented as graph $\:G=\left(V,E\right)$ in which $\:V\:$indicates is the set of sensor node vertices $\:V=\{{v}_{1},{v}_{2},\dots\:,{v}_{N}\}$, $\:E\:$indicates is the set of communication link edges $\:E=\{{e}_{ij}\mid\:\text{sensor\:node\:}i\text{\:is\:connected\:to\:sensor\:node\:}j\}$. After representing the network as graph, the node features are defined. Each node $\:{v}_{i}$ has features $\:{h}_{i}$ representing its position and energy which is formulated as follows.

$$\:{h}_{i}=\left({p}_{i},{E}_{i}\right)$$

(16)

where $\:{p}_{i}$ indicates the sensor node position $\:\left({x}_{i},{y}_{i}\right)$, $\:{E}_{i}$ indicates the sensor node remaining energy. The nodes features define the node position and energy, and the nodes update their states by aggregating information from neighbors. The node update rule at iteration $\:k+1$ is formulated as follows.

$$\:{h}_{i}^{\left(k+1\right)}=\sigma\:\left({W}_{1}{h}_{i}^{\left(k\right)}+{\sum\:}_{j\in\:N\left(i\right)}{W}_{2}{h}_{j}^{\left(k\right)}\right)$$

(17)

where $\:\mathcal{N}\left(i\right)$ is the set of neighbors of node $\:\left(i\right)$, $\:{W}_{1}$ and $\:{W}_{2}$ are weight matrices, $\:\sigma\:$ is a non-linear activation function. A graph-level output can be derived after several iterations of message passing to make decisions about the overall network configuration which is formulated as follows.

$$h_{G} = R\left( {\{ h_{i}^{{\left( K \right)}} i \in V\} } \right)$$

(18)

where $\:R$ indicates a function that aggregates node features to produce a graph-level representation. $\:{h}_{G}$ indicates the graph-level output, $\:{h}_{i}$ indicates the features of node $\:i$. The network inherent graph structure of GNN effectively models the interactions between sensor nodes. The message passing mechanism in the GNN allows nodes to share information between nodes and make coordinated decisions. This improves the communication efficiency between nodes and enhances the network coverage. By deploying the combined algorithm optimal coverage is attained so that maximum coverage and minimal overlap, energy consumption can be obtained.

The summarized pseudocode for the proposed model is presented as follows.

• Step.1: Initialize the network parameters: monitoring area $\:\text{A}$, number of sensor nodes $\:\text{N}$, initial energy $\:{\text{E}}_{0}$, sensing radius $\:{\text{r}}_{\text{i}}$.

• Step.2: Randomly place the sensor nodes $\:\text{N}$ within the defined monitoring area $\:\text{A}$.

• Step.3: At each time step.

  • a. Define the state of the network $\:{\text{s}}_{\text{t}}$ which includes positions and energies of all nodes as per Eq. (12).

  • b. Define actions $\:{\text{a}}_{\text{t}}\:$for each node as movements based on the current state as per Eq. (13).

  • c. Calculate the reward $\:{\text{r}}_{\text{t}}$ based on changes in coverage, overlap, and energy following the reward function as per Eq. (14).

  • d. Update the Q-network $\:\text{Q}\left({\text{s}}_{\text{t}},{\text{a}}_{\text{t}};{\uptheta\:}\right)$ using the experiences stored in the replay buffer as per Eq. (15).

  • e. Update the target network parameters $\:{{\uptheta\:}}^{{\prime\:}}$ to match the current Q-network parameters $\:{\uptheta\:}$.

  • f. Use the policy to select actions based on Q-values.

  • g. Move the sensor nodes according to the selected actions.

  • h. Compute the energy consumed by each node for transmission and movement.

  • i. Update the residual energy for each node.

• Step.4: Repeat from step 3 until termination conditions are reached (maximum number of iterations or stable network coverage).

Results and discussion

The proposed optimal coverage model performance for WSN which utilizes DRL with GNN is verified through simulation analysis performed using MATLAB. Essential library functions and toolboxes to implement the DRL and GNN models. The system environment includes an Intel Core i5 processor with 16GB RAM running on windows 11. MATLAB simulation environment allows seamless integration and visualization of network models. Various parameters can be used to evaluate the network parameters. The proposed model performance is evaluated through parameters like coverage ratio, energy efficiency, coverage overlap, throughput, latency, energy consumption, transmission delay and network lifetime. The detailed simulation network parameters are presented in Table 2.

Table 2 Simulation network.

The simulation hyperparameters for implementing the proposed Deep Reinforcement Learning (DRL) with Graph Neural Networks (GNNs) is presented in Table 3. The learning rate is defined as 0.001 for the batch size of 64. Adam optimizer is selected for the proposed model due to its ability in handling of sparse gradients, which are common in Graph Neural Networks (GNNs). Also, Adam optimizer enhances efficiency by adjusting learning rates for each parameter based on estimates of the gradients’ first and second moments which leads to faster and more stable convergence. Specifically, Adam optimizer is beneficial in the dynamic environments Wireless Sensor Networks (WSNs) where network topologies and conditions frequently change necessitating effective model adaptability. Moreover, Adam’s robustness to various hyperparameter settings especially initial learning rates make it an ideal choice for complex models ensuring optimal performance without the need for extensive hyperparameter tuning.

Table 3 Simulation hyperparameters.

Fig. 3

Results of optimal WSN coverage using proposed DRL-GNN.

Figure 3 presents the results of optimal WSN model that utilizes DRL-GNN to enhance the network coverage. The top left figure step 1 defines the state in which initial position of sensor nodes are indicated as blue dots. The nodes are distributed randomly across the monitoring area and the figure clearly depicts the node distribution and coverage gaps. The top right figure step 2 defines the results of action in which the black arrow indicates the sensor nodes movements defined by the DRL agent. The red dots in the figure indicate that as the new positions. The action results effectively visualize the agent decision making process in enhancing the network coverage. The bottom left figure step 3 defines the results of reward function that integrates reward mechanism, coverage area achieved by each node movement. The circles over the nodes represent its sensing range and the overlapping areas indicate the improved coverage and efficient node positioning. The effectiveness of the DRL agent action and decision is evaluated from the results obtained in this step. The policy execution step which is provided in step 4 depicts the outcome of policy to the network. The black arrows indicate the node’s movement direction, and it demonstrates the agent ability in redeploying the nodes to enhance the coverage. After redeployment, the nodes are strategically positioned to minimize the coverage holes and enhance the overall network performance. The message passing in the optimization process is depicted in step 5 in which the communication between sensor nodes is indicated using green lines. The node in the center which is marked in red color facilitates data aggregation and distribution over the network. based on the data received from the neighbors the node states are updated. The interconnected structure indicates the extensive communication and coordination of nodes in optimizing the network coverage and connectivity. Using GNN, the spatial relationship and dependencies among the nodes are modeled so that more informed decision making is made in the network which further improves the overall network performances.

The performance of the proposed model is evaluated through metrics like coverage ratio, energy efficiency and coverage overlap ratio. The network is experimented with different learning rates and discount factors to observe the changes in the network in optimizing the coverage. A combination of (LR, DR) such as (0.001, 0.99), (0.001, 0.95), (0.001, 0.9), (0.0005, 0.99), (0.0005, 0.99), (0.0005, 0.9), (0.0001, 0.9), (0.0001, 0.99), and (0.0001, 0.9) are considered for the network model. Figure 4 depicts the proposed model convergence ratio performance for different LR and DF parameters. The coverage ratio is observed for 1000 iterations, and it is observed that the proposed model exhibits its maximum coverage for the combination (0.001, 0.99) over other (LR, DF) combinations. The combination of effective learning provided by DRL-GNN makes the network perform well. Whereas the other combinations (0.001, 0.95) and (0.001, 0.9) also exhibit better coverage ratio than other combinations but it is not high as the (0.001, 0.99) combination. The low learning rates (0.0005) and (0.0001) with lower discount factors exhibit their slow improvement and reaches coverage ratio of about 0.65 to 0.7. The higher discount factors result in better coverage ratios and indicate the importance of long-term rewards in providing optimal coverage. The coverage ratio improvements observed in Fig. 4 highlights the adaptive learning capabilities of the DRL component which optimizes node placements dynamically based on real-time feedback. The DRL effectively learns to reduce coverage gaps by adjusting node positions over iterations and highlights its significant improvement especially with the optimal learning rate (LR) and discount factor (DF) settings.

Fig. 4

Coverage ratio analysis.

The energy efficiency of the network over 1000 iterations for different LR and DF combinations are presented in Fig. 5. From the results it can be observed that the combination (0.001, 0.99) achieves maximum energy efficiency over other combinations. The maximum performance indicates that the presented model effectively balances the energy consumption and network performance. The combinations of LR 0.0005 and 0.0001 with lower DF exhibits minimum improvement and reaches lesser energy efficiency compared to (0.001, 0.99) combination. The least energy efficiency is exhibited for the (0.0005, 0.0001) combination which is approximately 0.5 which is much lesser than (0.001, 0.99). Higher discount factors result in better energy efficiency and maximize the overall network performances. Results reflects the model’s ability in enhancing network energy efficiency through optimal node positioning and minimized operational redundancy. The DRL component’s policy optimizes the energy usage by reducing unnecessary node movements. Also, it ensures that nodes operate within their optimal sensing ranges thus conserves energy. The results indicates that optimal tuning of the learning rate and discount factor leads to the most energy-efficient network operations correlating higher efficiency with optimal parameter settings.

Fig. 5

Energy efficiency analysis.

Fig. 6

Overlap analysis.

The overlap ratio analysis given in Fig. 6 depicts the proposed model performance for different LR and DR combinations for 1000 iterations. The results clearly depict that the proposed model exhibits minimum overlap ratio for the combination (0.001, 0.99) which reaches minimum overlap ratio. The better indicates that model effectively minimizes the overlap and maximizes the coverage efficiency. The results of LR = 0.001 with 0.95 and 0.90 DF also perform well when compared to other combinations, however it is lesser than that of (0.001, 0.99). The least performance is exhibited by the combinations with LR = 0.0005 and LR = 0.0001 exhibits its slow improvement in overlap ratio but attained less performance than (0.001, 0.99) combination. Specifically, the results exhibit the reduction in overlap ratio which clearly demonstrates the GNN ability in managing and optimizing the spatial relationships between nodes. By effectively learning the topological dependencies the GNN component guides the DRL to place nodes in positions that maximize coverage also minimize sensing overlap which enhances the overall network efficiency and sensor utility.

The results given in Figs. 3, 4, 5 and 6 highlight that the combination (0.001, 0.99) exhibit better performance over other combinations for coverage ratio, energy efficiency and overlap ratio. Thus, further experimentation is conducted with LR of 0.001 and DF of 0.99. The coverage performance is then evaluated with different node counts with the above-mentioned LR and DF. Figure 7 depicts the proposed model performance in terms of coverage ratio for different node counts. For the node count like 20, 30, 40, 50 the performance is measured for different iterations. The results depict that the proposed model exhibits better coverage ratio when the number of increases. The higher node densities lead to better coverage and provide balanced load distribution among nodes. As the number of nodes increases, the DRL-GNN model efficiently utilizes the resources to close coverage gaps which further improves the overall coverage ratio. This result validates the model’s effectiveness in handling the network and clearly exhibits the direct correlation between the number of nodes and the coverage capability, which is essential for practical deployments in wide environments.

Fig. 7

Coverage ratio analysis with different number of sensor nodes.

The energy efficiency of proposed model with different number of nodes for LR = 0.001 and DF = 0.99 is presented in Fig. 8. The results indicate that increasing the number of nodes significantly enhances energy efficiency. The configuration with 50 nodes achieves the highest energy efficiency, reaching approximately 0.92 for 1000th iteration. This demonstrates the better energy management attained by the proposed model. From the results optimizing node count enhances the energy efficiency of the wireless sensor network. The increasing number of sensor nodes enhances the energy efficiency of the network. Larger number of nodes allows for better distribution of monitoring tasks which reduces the energy consumption of individual nodes and optimizes the overall energy usage. The highest efficiency is observed with 50 nodes demonstrating that the model effectively utilizes the increased node density to minimize energy consumption while maintaining coverage.

Fig. 8

Energy efficiency analysis with different number of sensor nodes.

Fig. 9

Coverage overlap analysis with different number of sensor nodes.

The overlap ratio analysis for different node count is presented in Fig. 9. The proposed model with LR of 0.001 and DF of 0.99 with node count of 50 attains minimum overlap ratio and reaches zero for 1000th iteration. The lowest overlap ratio attained for 50 node counts indicates minimal redundancy and efficient coverage. Though the overlap ratio for node count 40 and 30 shows substantial improvement but exhibit lesser performance than the overlap ratio of 50 nodes. The results indicate that high node densities provide better spatial distribution and reduce redundant coverage area. Thus, the increasing node count minimizes the overlap and maximizes the coverage efficiency of the wireless sensor network. The decrease in overlap ratio with increasing node counts reflects the proposed model ability in optimizing node placement more effectively as more nodes are available. The DRL-GNN model dynamically adjusts node positions to minimize redundant coverage which is more efficiently achieved with a higher node density. The final result highlights the model ability in enhancing coverage efficiency by reducing overlaps and maximizing the utility of each sensor in the network.

Further the network performance is evaluated for latency metric with LR of 0.001 and DF of 0.99 for 1000th iteration. Latency is defined as the average time taken for a packet to travel from the sender node to the receiver node over the network:

$$\:{L}_{avg}=\:\frac{1}{{P}_{success}}\sum\:_{k=1}^{{P}_{success}}({T}_{rk}-{T}_{sk})$$

(19)

In Eq. (19), $\:{T}_{rk}$ denotes the reception time of packet k, while $\:{T}_{sk}$ denotes the transmission time of packet k. $\:{P}_{success}$ denotes the number of successfully transmitted packets

The results given in Fig. 10 indicate that there is a significant reduction in latency when the node count increases. The configuration with 50 nodes exhibits the lowest latency of approximately 2ms for 1000th iteration. This indicates the improved network performance of the proposed model. The lowest performance is exhibited for 20 nodes reaching a latency of about 5ms. The findings suggest that higher node densities improve network efficiency by reducing the communication delay. Result demonstrates the impact of node density on network latency. When more nodes available, the DRL-GNN model can reduce the distance that data travel from any given point to the nearest node. Also, it significantly reduces communication delay across the network. This improvement in latency is crucial for real-time data processing applications illustrating the proposed model effectiveness in enhancing network responsiveness.

Fig. 10

Latency analysis with different number of sensor nodes.

The average hop count analysis given in Fig. 11 with LR of 0.001 and DF of 0.99 for different node count indicates that the configuration with 50 nodes achieves lowest average hop count nearly to 1 for 1000th iteration. The efficient routing with fewer hops provides better performance whereas for 20 nodes, the proposed model exhibits an average hop count of 2.5 which is higher compared to the performance of 50 nodes. The results confirm that higher node densities improve the routing efficiency and reduces the number of hops required for data transmission. The average hop count decreases as the number of nodes increases and a higher density of nodes creates more direct routes for data transmission which reduces the number of hops required. This efficient routing is critical in minimizing transmission delays and reducing the energy consumed during data relays further underscoring the proposed model ability in optimizing network communication paths.

Fig. 11

Average Hop count with different number of sensor nodes.

Fig. 12

Throughput analysis with different number of sensor nodes.

The throughput analysis of proposed model for different node count is presented in Fig. 12 with LR of 0.001 and DF of 0.99. Throughput is defined as the total number of successfully delivered packets $\:{P}_{delivered}$over the total simulation time $\:{T}_{sim}$:

$$\:Throughput\:(packets/s)=\:\frac{{P}_{success}}{{T}_{simulation}}$$

(20)

In Eq. (20), $\:{P}_{success}$ denotes the number of successfully transmitted packets and $\:{T}_{sim}\:$indicates the total simulation duration.

The proposed model exhibit improves the network throughput when the network has 50 nodes. The proposed model achieves the highest throughout of 1400 packets per second for 1000th iteration. For 40 and 30 nodes, the network attains 1200 and 1000 packets per second as throughput. Results highlights that network throughput improves with an increased number of nodes. As the node count increases the network capacity to handle data traffic enhances which allows more data packets per second to be processed. This is particularly evident with 50 nodes where the model reaches peak throughput showcasing the DRL-GNN model ability to scale effectively while maintaining high performance.

The performance evaluation of proposed model for transmission delay metric with different node count is presented in Fig. 13. With a learning rate of 0.001 and discount factor of 0.99, the network with 50 nodes significantly reduces the transmission delay. Approximately 10 ms is observed as delay with the network has 50 nodes for 1000th iteration. The performance is about 15 ms and 20 ms for the network configured with 40 and 30 nodes. When the node count is less is about 20, the transmission delay increases. Thus, utilizing optimal node count to reduce the transmission delay is essential for attaining maximum performance. From the results the reduction in transmission delay with a higher node count is observed. With more nodes data can be routed more efficiently decreasing the time it takes for data to travel across the network. This results important for applications requiring timely data updates.

Fig. 13

Data transmission delay analysis with different number of sensor nodes.

The energy consumption distribution of the proposed model is analyzed in Fig. 14 with different node counts. Energy consumption is calculated as the total energy used by all nodes during sensing, transmission, and reception operations, defined as follows:

$$\:{E}_{total}=\:\sum\:_{i=1}^{N}({E}_{sense,\:\:i}+{E}_{tx,i}+{E}_{rx,i})$$

(21)

In Eq. (21), $\:{E}_{sense,\:\:i}$ is the Energy consumed by node i for sensing, $\:{E}_{tx,i}$ is the Energy consumed by node i for transmission. $\:{E}_{rx,i}$ is the Energy consumed by node i for receiving data. N denotes the Total number of sensor nodes.

With LR of 0.001 and DF of 0.99 the proposed model exhibits higher total energy consumption due to active nodes when the network is configured with 50 nodes. The findings suggest that the network coverage and performance increases when node count increases, however it results in greater energy consumption. Thus, optimizing the node count is essential to balance the performance and energy consumption of wireless sensor networks. Results in Fig. 13 clearly highlights the total energy consumption of the network as node density increases. While more nodes lead to greater total energy use and this is balanced by the enhanced performance in coverage and throughput. This highlights the model effectiveness in balancing energy consumption with operational benefits.

The network lifetime analysis of the proposed model is presented in Fig. 15. Network lifetime is defined as the duration from network initialization to the time when the first node depletes its available energy.

$$\:{T}_{lifetime}=\underset{i\in\:N}{\text{min}}({T}_{depletion},\:i)$$

(22)

In Eq. (22), $\:{T}_{depletion}$ is the time duration until node i exhausts its energy.

The analysis considered different node count, and the responses observed for LR of 0.001 and DF of 0.09. The increased node count significantly enhances the network lifetime. For 50 nodes the proposed model achieves a maximum network lifetime of approximately 2500 h. The network lifetime when the network has 30 and 40 nodes is about 1500 and 2000 h which is lesser when the network has 50 nodes. The lowest network lifetime is about 1000 h attained when the network has 20 nodes. The higher node count evenly distributes the energy consumption across the nodes in the network thus it increases the network lifetime. Results exhibits that network lifetime extends as the number of nodes increases. With more nodes distributing the workload individual node energy depletion reduces prolonging the overall operational period of the network. This improvement in network lifetime with increased node density confirms the DRL-GNN model effectiveness in utilizing additional resources to extend the lifetime of the network.

Fig. 14

Energy consumption distribution with different number of sensor nodes.

Fig. 15

Network lifetime analysis with different number of sensor nodes.

Considering the best performance of proposed model for LR as 0.001 and DF as 0.99, the results are compared with existing learning and optimization algorithms. The comparative analysis utilizes deep learning models like convolutional Neural Network (CNN), DenseNet50, and optimization models like particle swarm optimization, whale optimization algorithms. The network model of the proposed approach is used to obtain the performance of existing models. The performances are measured for each algorithm and compared with proposed model. For experimentation the specific simulation hyperparameters are used for each model. For the deep learning models like CNN and DenseNet50 the learning rate is used as 0.001, trained over 50 epochs using a batch size of 32. The Adam optimizer is employed due to its effectiveness in handling sparse gradients, with a dropout rate of 0.5 applied to prevent overfitting. DenseNet50 additionally utilize pretrained weights applying fine-tuning at a minimized learning rate to adapt to the specifics of the sensor network data. For the optimization algorithms, PSO is initialized with 50 particles and runs for 100 iterations, employing linearly decreasing inertia weight from 0.9 to 0.4 and cognitive and social coefficients both set at 2.05. WOA operates with 50 agents for 100 iterations, with parameter $\:a$ decreasing from 2 to 0 to modulate between exploration and exploitation phases effectively. These settings aim to provide a fair basis for comparing performance metrics across all models under similar operational conditions.

The energy efficiency for the proposed DRL-GNN model and existing models are comparatively presented in Fig. 16. Starting from around 85% and peaking at 95.8% the proposed model outperformed existing methods. In contrast, CNN achieves a maximum of 85%, DenseNet50 goes up to 87%, PSO reaches 80%, and WOA climbs to 82%. The proposed model efficiency illustrates its ability in managing the power consumption effectively which is essential in enhancing the network lifetime.

Fig. 16

Energy efficiency comparative analysis.

The comparative analysis given in Fig. 17 highlights the proposed DRL-GNN model significant performance in reduction of overlap ratio from 20% to as low as 0.5. This is substantially better than the existing methods where CNN reduces overlap to only 15%, DenseNet50 to 12%, PSO to 12%, and WOA to 10%. The rapid decrease in overlap by the proposed model highlights the model effectiveness in avoiding redundant coverage. Also the results ensures the efficient utilization of network resources compared to the slower rates of reduction by other models.

Fig. 17

Overlap ratio comparative analysis.

Fig. 18

Latency comparative analysis.

The comparative analysis given in Fig. 18 exhibits the latency over iterations highlights the proposed DRL-GNN model lower latency and efficiency in network communications. Starting at an initial latency of approximately 10 ms the proposed model exhibits reduced latency and reach approximately 0.85ms by 1000 iterations. This performance is slightly better than the CNN and DenseNet50 models which end around 1.4 ms and 1.25 ms, respectively. The PSO and WOA models show the least efficiency with final latencies closer to 1.6 ms and 1.8 ms, respectively. This analysis highlights the proposed DRL-GNN model effectiveness in optimizing network latency compared to existing models particularly in scenarios with higher node counts.

Fig. 19

Coverage ratio comparative analysis.

Figure 19 exhibits the proposed DRL-GNN model superior performance in coverage ratio which is an increasing performance ranges from 85 to 96.4% over 1000 iterations. The performance of proposed model coverage ratio is higher than the other models specifically CNN reaches at about 88%, DenseNet50 at 90%, PSO at 85%, and WOA at 87%. The increased performance of the proposed model highlights its robustness in optimizing sensor placement dynamically and outperforming other models.

From the experimental analysis of proposed model, it is observed that the coverage ratio significantly increases while increasing the number of nodes specifically, when the network utilizes LR as 0.001 and DF of 0.99. In the case of energy efficiency, the higher node count provides better energy efficiency of 95% and prolongs the network lifetime of wireless sensor networks. When increasing the node density, the overlap ratio is reduced and enhances the coverage efficiency. Similarly, when using higher node count, the latency reduces and improves the network responses. Fast data transmission can be attained when the latency is low which is essential for real time wireless sensor networks. Moreover, the increased node count increases the network lifetime by distributing the energy consumption evenly. Additionally increased node count increases the data transmission efficiency and reduces the delay in communication. Thus, the proposed DRL-GNN optimally enhances the network coverage thereby it enhances the overall network performances.

The performance of the proposed DRL-GNN model was evaluated experimentally across varying sensor node densities (20, 30, 40, and 50 nodes). Each scenario was simulated under identical environmental conditions using standardized hyperparameters (Learning Rate = 0.001, Discount Factor = 0.99). Key metrics such as coverage ratio, energy efficiency, overlap ratio, latency, throughput, average hop count, and network lifetime were measured to assess comprehensive network performance.

Table 4 Performance analysis of proposed DRL-GNN model under varying node counts.

As shown in Table 4, increasing the sensor node count consistently improved all evaluated performance metrics. Specifically, the configuration with 50 nodes achieved optimal results, yielding the highest coverage ratio (96.4%), maximum energy efficiency (95.8%), lowest overlap ratio (5.2%), minimal latency (2 ms), highest throughput (1400 packets/sec), shortest average hop count (1.0), and longest network lifetime (2500 h). This comprehensive analysis indicates that a sensor network with 50 nodes provides the best-balanced performance, optimizing coverage, energy usage, and overall operational efficiency.

To rigorously assess the effectiveness of the proposed DRL-GNN method, extensive comparative evaluations were conducted against established optimization and deep learning-based approaches, including CNN-based models, DenseNet50, Particle Swarm Optimization (PSO), and Whale Optimization Algorithm (WOA). Each method was evaluated under identical conditions, considering metrics such as coverage ratio, energy efficiency, overlap ratio, and latency, ensuring fairness and consistency in comparative analysis.

Table 5 Comparative analysis of proposed DRL-GNN with existing methods.

The comparative results summarized in Table 5 clearly illustrate the superior performance of the proposed DRL-GNN model across all evaluated metrics. Notably, the DRL-GNN approach achieved the highest coverage ratio (96.4%), the greatest energy efficiency (95.8%), the lowest overlap ratio (5.2%), and the smallest latency (0.85 ms). These results confirm the superior capability of DRL-GNN to simultaneously optimize multiple critical performance indicators. By effectively integrating spatial relationships captured through GNN and adaptive learning facilitated by DRL, the proposed method demonstrates a significant advancement over existing techniques in dynamically optimizing sensor deployments within WSNs.

To validate the robustness and reliability of the proposed DRL-GNN model, we performed extensive experimentation involving multiple trials. Specifically, the experiments were repeated five times, each initialized with a different random distribution of 50 sensor nodes. For every trial, key performance metrics—including coverage ratio, energy efficiency, overlap ratio, latency, throughput, average hop count, and network lifetime—were systematically recorded. The mean values, standard deviations, and 95% confidence intervals for each metric were then computed to perform rigorous statistical analysis, ensuring the reliability and reproducibility of the experimental outcomes.

Table 6 Statistical analysis of proposed DRL-GNN model across five experimental runs (50 Nodes).

Table 6 presents the statistical summary across the five experimental trials. The consistent and narrow ranges in the 95% confidence intervals, along with minimal standard deviations observed for all metrics, strongly demonstrate the stability and robustness of the proposed DRL-GNN algorithm. For instance, the coverage ratio averaged at 96.06% with a minimal standard deviation (± 0.23%), while throughput remained consistently high at approximately 1395 packets/sec. These results confirm that the proposed method consistently achieves superior performance, highlighting its reliability and effectiveness even with varied and random sensor deployments.

Conclusion

This research presents an optimal coverage solution for wireless sensor network using Deep Reinforcement Learning (DRL) with Graph Neural Network (GNN). The presented model utilizes DRL to dynamically optimize the sensor node positions and the spatial dependencies of the network are captured through GNN. By integrating the adaptive decision-making features of DRL with the structural data processing power of GNN the proposed model has shown significant improvements in coverage ratio, energy efficiency, and overlap reduction which is better than traditional techniques in dynamic environments. The proposed model ability to adjust node positions in response to environmental changes has enhanced the adaptability and operational efficiency of WSNs achieving a coverage ratio of up to 96.4% and an energy efficiency of 95.8% in optimal conditions. Though the model has better performances it faces certain limitations particularly concerning the computational demands of integrating DRL and GNN as it slightly introduces the computational complexity on large-scale networks. Additionally, the model performs well in controlled simulations its performance in real-world scenarios with unpredictable environmental variables remains to be thoroughly tested. The future research will focus on fine tuning the model to reduce computational complexity and enhance scalability. Algorithms can be developed to reduce the computational complexity without compromising the learning and adaptive capabilities of the model. Further, real-world testing will be prioritized to validate the model for better generalization across various WSN applications.