Investigation of flow-induced noise reduction in high-specific-speed centrifugal pumps using bionic blades

Abstract

To reduce the flow-induced noise of centrifugal pumps and reveal the noise source characteristics inside the pumps, this paper designs a bionic blade based on the “tubercle effect” of humpback whales. The noise reduction effect of the improved structure is verified through numerical simulations of the flow and acoustic fields of the prototype pump and bionic pump. Using the Ffowcs Williams–Hawkings equation and Powell vortex sound equation, the reasons for the noise reduction are explained from the perspective of pressure pulsation and sound source. The results indicate that the bionic blade has little impact on the hydraulic performance of the centrifugal pump but can achieve a maximum noise reduction of 2.53 dB. The main sources of centrifugal pump noise are the severe pressure pulsation caused by rotor–stator interaction and the sound source generated by the influence of velocity on vortices. The reduction in pressure pulsation intensity, sound source, sound source intensity, and sound source standard deviation are the main reasons the bionic pump has lower noise than the prototype pump. However, the relationship between the magnitude of pressure pulsation intensity and dipole noise amplitude is not simply linear. The total sound pressure level reduction effect caused by suppressing the pressure pulsation whose main frequency is the blade passing frequency is significantly larger than that caused by suppressing the pressure pulsation whose main frequency is the shaft frequency.

Introduction

As an important fluid transportation equipment, centrifugal pumps have stability and performance closely related to the operation noise. Centrifugal pump noise includes mechanical noise and flow noise¹. Flow noise is the main source in centrifugal pumps, which can be categorized into monopole, dipole, and quadrupole sound sources according to the occurrence mechanism². Exploring the flow-induced noise of centrifugal pump operation from the sound source is the basic guarantee for centrifugal pump noise mechanism research, low-noise design, and verification of noise reduction measures. At present, the research results of many scholars illustrate that the dipole sound source generated by rotor–stator interaction between the impeller and the volute is the main source of hydrodynamic noise in centrifugal pumps^3,4,5. Among them, optimizing the geometry and parameters of pump overflow components to attenuate rotor–stator interaction to reduce noise is the focus of the study. Tan et al.⁶ used a combination of experiments and numerical simulations to investigate the effect of different basal diameter of the volute on the performance of the pump’s flow and acoustic field, and the results show that the basal diameter of the volute has a significant effect on the flow of fluid in the volute, and that there exists an optimum value that makes the pump’s performance optimal in terms of flow and acoustic field. The results of Srivastav et al.⁷ showed that the noise decreases with the increase in the gap between the impeller and the volute tongue. Luan et al.⁸ explored the effect of different impeller outlet widths on noise with the boundary element method. Dai et al.⁹ showed that reasonably inclined blade outlets can reduce the noise of centrifugal pumps. Li et al.¹⁰ showed the results of noise characterization of double-suction centrifugal pumps that the appropriate number of blades and radial clearance distribution can significantly reduce the dimensionless pressure fluctuation and sound pressure level at the blade passing frequency.

In recent years, with the vigorous development of bionic, using unique body surface features of organisms to achieve noise reduction has become a hot research topic. Wu et al.¹¹ were inspired by the leading edge of an owl wing to design a bionic volute tongue in order to improve the interaction between the impeller and the volute and to reduce the noise. Liu et al.¹² reduced the total sound pressure level of a centrifugal pump by 4.96 dB by arranging pit-shaped bionic structures on the blades based on the body surface characteristics of dung beetles. Dai et al.¹³ set up concave and serrated bionic structures on the surface of centrifugal pump blades, and the results showed that both bionic structures have noise reduction effects compared with smooth blades. Among them, for studying the bionic serrated trailing edge, Howe¹⁴ published his theoretical analysis results of noise reduction based on owl wings for the first time as early as 1991 and summarized the corresponding prediction model of noise reduction. Since then, numerous studies have confirmed the noise reduction effect of the serrated trailing edge. The results of the experimental study by Gruber et al.¹⁵ showed that the serrated trailing edge reduces the low-frequency noise by about 5 dB. Oerlemans et al.¹⁶ applied a bionic serrated trailing edge to reduce the noise of the turbine by about 3.2 dB. Liu et al.¹⁷ investigated the effect of serrated trailing edge on the noise of centrifugal fan by numerical simulation, and the results showed that the serrated trailing edge reduces the disturbance of vortex and trailing edge to the pressure pulsation on the blade surface, which results in a maximum noise reduction of 9.8 dB. Furthermore, research has found that large mammals such as sharks and dolphins exhibit remarkable agility and maneuverability underwater, mainly due to the nodules on their fins. These nodules create small vortices at the V-shaped notches, generating disturbances in the flow field. This disruptive effect, known as the “tubercle effect” is a major reason for its excellent noise reduction performance. Specifically, according to the research results of Howe, Gruber, Oerlemans, Liu, and others, the bionic serrated trailing edge design of the blades can better reduce and control the scale and distribution range of the vortex structure in the flow field, and reduce the intensity of the pressure pulsation, turbulence pulsation intensity and vortex intensity in the centrifugal pumps, etc., while vortex, turbulence, and pressure pulsation are exactly one of the main reasons for causing the flow-induced noise in the centrifugal pumps. So this bionic design method usually plays a good role in the noise reduction of centrifugal pumps. However, the difficulty of this bionic method lies in the determination of the bionic design parameters, such as the arrangement position of the bionic nodule, the size, the distribution range, and so on. In other words, how to reduce the noise of centrifugal pumps on the premise of ensuring the performance of the external characteristics of centrifugal pumps. Given this, Custodio et al.¹⁸ conducted a study on these nodules and found that the height of the nodule is a constant fraction of the local chord length of the fin (L), measured as 0.025 L, 0.05 L, 0.12 L, etc.

In summary, optimizing geometric structures and parameters has been widely applied in centrifugal pump noise reduction. However, most traditional research on centrifugal pump noise reduction has only verified the effect of pump optimization and briefly explored the causes of noise induction and noise reduction. At the same time, most scholars only analyze the noise generated by blades or volutes when analyzing noise, without delving into the noise generated by the combined effect of the two. Given this, this article conducts numerical calculations on the noise generated by the combination of impellers and volutes. Based on the influence of the aforementioned bionic structures on flow fields and research progress in flow-induced noise control for other types of fluid machinery. The integration of bio-inspired structures into impeller systems offers a promising approach to mitigating flow-induced noise. Based on the biomimetic research of the “tubercle effect” of humpback whales, a biomimetic serrated trailing edge is designed at the outlet of the blade, attempting to explain the reason for noise reduction from the perspective of the flow field, identify indicators for predicting and judging the noise reduction effect, and provide useful references for the optimization design of centrifugal pumps for noise reduction.

Physical model and experiment setup

Overview of the original model and experiment

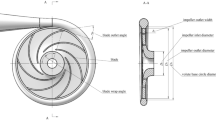
This paper takes the high specific speed (n_s = 186) single-stage single-suction centrifugal pump as the research object. The performance test verification was completed in the Key Laboratory of the Ministry of Education of Fluid and Power Machinery. The test bench is arranged under the level-2 precision required in the GB/T3216-2016 standard, as shown in Fig. 1, and the test medium is clear water. The test bench mainly comprises a piping system and a test system. The piping system includes import and export piping, centrifugal pumps, motors, water channels, valves, and so on, and the test system includes inlet and outlet pressure gauge, thermometer, torque meters, electromagnetic flow meters, data acquisition systems, etc. Table 1 lists the measurement characteristics of relevant instrument.

Fig. 1

Experimental measurements schematic diagram.

Table 1 Measurement characteristic of instruments.

The main design parameters of the centrifugal pump are shown in Table 2. To improve the realism of the numerical simulation, the impeller inlet and volute outlet are extended to 5 times the pipe diameter length, respectively. The computational domain consists of four parts: the inlet section, the impeller, the volute, and the outlet section, as shown in Fig. 2.

Table 2 Main design parameters of centrifugal pump.

Fig. 2

3D calculation domain of Centrifugal pump.

Biomimetic model

The Humpback whale flipper’s leading edge bulge is shown in Fig. 3a. From the results of Li¹⁹, Lin ²⁰, and others, it can be seen that the performance of the bionic blade is closely related to the bionic design, and there are two key parameters of the bionic design, which are the amplitude of the nodule and the wavelength of the nodule, and the different amplitudes of the nodule and the wavelength of the nodule will have different effects on the performance of the bionic blade, but it will not have a significant impact on the performance of the centrifugal pump’s external characteristics. Combining the results of Custodio D et al.¹⁸ with the arrangement of the bionic nodule on the high-efficiency turbine blades and airfoils of Whalepower (Fig. 3b) and considering that the raised structure of centrifugal pump blade outlet is too large, it can affect its hydraulic performance, the amplitude A and wavelength L of the biomimetic nodule arrangement are both 0.08b₂, as shown in Fig. 3c. (The symbol O in the diagram represents the original blade, while B represents the biomimetic blade. The same notation applies throughout).

Fig. 3

Bionic model: (a) Schematic diagram of the humpback whale leading edge bulge; (b) Whalepower’s high-efficiency turbine blades; (c) Schematic diagram of a bionic blade.

It is worth noting that: although different design parameters of the bionic blade on the centrifugal pump noise effect are different, the purpose of this paper is to explore from the perspective of the flow field of the bionic blade to reduce the noise of the centrifugal pump of the specific reasons, in other words, it is to find out the bionic blade on the centrifugal pump of the physical mechanism of noise reduction, not to analyze the impact of the different bionic blade on the noise of the centrifugal pump, so due to space constraints, this paper did not do a variety of design options, but we believe that reasonably designed bionic blades can play a good noise reduction effect on centrifugal pumps.

Numerical calculation mothed

Flow field calculation method

The basic governing equation of fluid motion is the Navier–Stokes equation. The continuity equation and momentum equation are expressed as follows:

$$\frac{\partial \rho }{{\partial t}}{ + }\frac{{\partial \left( {\rho u_{i} } \right)}}{{\partial x_{i} }}{ = 0}$$

(1)

$$\frac{{\partial \left( {\rho u_{i} } \right)}}{\partial t} + \frac{{\partial \left( {\rho u_{i} u_{j} } \right)}}{{\partial x_{j} }} = - \frac{\partial p}{{\partial x_{i} }} + \frac{\partial }{{\partial x_{j} }}\left[ {\mu \left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right) - \frac{2}{3}\frac{{\partial u_{k} }}{{\partial x_{k} }}\delta_{ij} } \right]$$

(2)

where: i, j, k is the spatial axis component; ρ is the medium density, kg/m³; p is the pressure, Pa; t is the time, s; $u_{i} ,u_{j} ,u_{k}$ is the velocity component, m/s; μ is the coefficient of dynamic viscosity, Pa s; $\delta_{ij}$ is the Kronecker coefficient.

This paper adopts the SST-SAS turbulent model for unsteady computations, and its detailed expression can be found in reference²¹. Below, only the expression of the source term Q_SAS in equation ω is presented:

$$Q_{SAS} = \max \left[ {\rho \zeta_{2} \kappa S^{2} \left( {\frac{L}{{L_{vk} }}} \right)^{2} - C \cdot \frac{2\rho k}{{\sigma_{\varphi } }}\max \left( {\frac{{\left| {\nabla \omega } \right|}}{{\omega^{2} }},\frac{{\left| {\nabla k} \right|}}{{k^{2} }},0} \right)} \right]$$

(3)

$$L_{vk} = \frac{{\kappa \sqrt {2S_{ij} S_{ij} } }}{{\sqrt {\left( {\nabla^{2} u} \right)^{2} + \left( {\nabla^{2} v} \right)^{2} + \left( {\nabla^{2} \omega } \right)^{2} } }}$$

(4)

$$L = \sqrt {k/} \left( {c_{\mu }^{1/4} \cdot \omega } \right)$$

(5)

where: k is the turbulent kinetic energy, m²s⁻²; ω is the specific dissipation rate, m²s⁻³; $S_{ij}$ is the strain rate tensor; $S$ is the mode of the strain rate tensor.$S_{ij} \left( {S = \sqrt {2S_{ij} S_{ij} } } \right)$; κ = 0.41, ζ₂ = 3.51,c_μ = 0.09, C = 2.0, σ_φ = 2/3.

The full flow field computational domain is meshed using ANSYS ICEM, as shown in Fig. 4. The whole domain of the original blade model adopts structured mesh, and the impeller of the bionic blade model adopts unstructured tetrahedral mesh with a high degree of automation due to its complex structure. The overall mesh quality of both the original model and the bionic model is controlled to be more than 0.37. The Y⁺ value of the grid in the near-wall surface is less than 60, which meets the requirements of the SST-SAS turbulence model. The Y⁺ values at the blades of the two model pumps are shown in Fig. 5.

Fig. 4

Structured grid of the prototype pump.

Fig. 5

Y + values at blades of two model pumps.

The irrelevance of the grid is verified, and the results are shown in Table 3. Under the premise of ensuring the credibility of the simulation results and reducing the computation time, the number of mesh of the original model is finally determined to be 6.5 × 10⁶, and the number of mesh of the bionic model is 5.5 × 10⁶. Steady-state and transient calculations are carried out in ANSYS CFX software, and each calculated condition is taken as a mass flow outlet and pressure inlet. The interfaces associated with the impeller were modeled using the Transient Frozen Rotor approach during transient simulations, while the General Grid Interface (GGI) method was applied to the remaining interfaces. To obtain relatively stable and reliable data from the transient calculations, the whole process is calculated for a total of 11 cycles, T_sum = 0.4552 s, time step Δt = 1.67 × 10⁻⁴ s, 20 iterations for each time step, and the convergence accuracy of the calculations is set to 1 × 10⁻⁵ (O₁ denotes the first set of grids of the original model pump, B₁ denotes the first set of grids of the bionic model pump, and the rest of the definitions of O₂, O₃, B₂, B₃, etc. are the same.)

Table 3 Grid independence verification.

Sound field calculation method

The hydrodynamic acoustic computational equation (FW–H equation) derived by Ffowcs-Williams and Hawkings² is expressed as:

$$\frac{1}{{c_{0}^{2} }}\frac{{\partial^{2} p^\prime }}{{\partial t^{2} }} - \frac{{\partial^{2} p^\prime }}{{\partial x_{i}^{2} }} = \frac{{\partial^{2} T_{ij} }}{{\partial x_{i} x_{j} }} - \frac{\partial }{{\partial x_{i} }}\left( {p_{ij} n_{j} \delta \left( f \right)} \right) + \frac{\partial }{\partial t}\left( {p_{0} v_{j} n_{j} \delta \left( f \right)} \right)$$

(6)

where: $p^\prime = p - p_{0}$ is the fluctuating pressure, Pa; $p_{0}$ is the mean pressure, Pa; $c_{0}$ is the speed of sound, m/s; $x_{i} ,x_{j}$ is the spatial coordinate, m; $v_{j}$ is the velocity, m/s; $n_{j}$ is the unit normal vector component; $T_{ij}$ is the Lighthill turbulence stress tensor; $\delta \left( f \right)$ is the Dirac function, which describes the real-time position of the object; $p_{ij}$ is the fluid stress tensor.

The three terms at the right end of the formula (6) represent quadrupole sound sources, dipole sound sources, and monopole sound sources in that order. Monopole and dipole sound sources are surface sound sources (determined by the Dirac function), and quadrupole sound sources are body sound sources (determined by the Heaviside function). As the pump medium is regarded as an incompressible fluid, the volume density is constant. Hence, the normal volume pulsation is almost zero, and the monopole sound source is negligible. Because the ratio between the quadrupole and dipole sound source intensities is proportional to the square of the Mach number, and the centrifugal pump is in the Mach number of small low-speed and subsonic flow state, the quadrupole noise is also negligible. It can be seen that the dipole source noise is the main source of flow noise inside the centrifugal pump.

The Helmholtz equation in the frequency domain can be obtained by performing a fast Fourier transform of formula (6):

$$\left( {\nabla^{2} + k^{2} } \right)p^\prime = \frac{\partial }{{\partial x_{i} }}\left( {p^\prime n_{j} \delta \left( f \right)} \right)$$

(7)

When only a dipole sound source in a stationary volute is considered, the radiated sound pressure can be obtained by using the Green function, and its expression is:

$$p^\prime_{inc} \left( {{\varvec{r}}_{0} } \right) = \iint\limits_{s} {P\left( {{\varvec{r}}_{s} } \right)}\frac{{\partial G\left( {{\varvec{r}}_{0} ,{\varvec{r}}_{s} } \right)}}{\partial n}dS\left( {{\varvec{r}}_{s} } \right)$$

(8)

where: r_S is the position vector of the source point; $P\left( {{\varvec{r}}_{{s}} } \right) = p_{0} - p$ is the fluid pressure at the boundary, Pa; $G\left( {{\varvec{r}}_{0} ,{\varvec{r}}_{s} } \right)$ is the Green’s function; subscript inc is the abbreviation of the radiation; S is the area of integration.

When only the dipole sound source with blade motion is considered, the time domain solution of the FW–H equation is:

$$p{^\prime }_{{{inc}}} \left( {{\varvec{r}}_{0} ,t} \right) = - \frac{{1}}{{{4\pi }}}\iint\limits_{s} {\frac{{r_{i} }}{{c_{{0}} Dr^{{2}} }}}\frac{{\partial }}{{{\partial }{\varvec{\tau}}}}\left( {\frac{{F_{i} }}{D}} \right){d}S$$

(9)

where: ${\varvec{r}}_{0}$ is the position vector of the field point, $r = |{\varvec{r}}_{0} - {\varvec{r}}_{{s}} |$; $F_{i} = p_{ij} n_{j}$, refers to the normal force per unit area of the object acting on the fluid, N/m²; $D = |1 - M_{r} |$ is the Doppler amplification factor, M_r which represents the Mach number of the moving sound source in the direction of the observer, τ is the viscous stress tensor.

The Powell vortex acoustic equation is expressed as²²:

$$\frac{{\partial^{2} \rho {^\prime }}}{{\partial t^{2} }}{ - }c_{{0}}^{{2}} {\nabla }^{{2}} \rho {^\prime } = {\nabla \cdot }\left( {\rho {(}\mathop \omega \limits^{{ \to }} { \times }\mathop u\limits^{{ \to }} {)} + {\nabla }\left( {\rho \frac{{u^{2} }}{2}} \right) - \mathop u\limits^{{ \to }} \frac{\partial \rho }{{\partial t}} - \frac{{u^{2} }}{2}{\nabla }\rho } \right)$$

(10)

where: $\rho {^\prime } = \rho - \rho_{0}$. is the density perturbation quantity, which can be expressed as a parameter of acoustic amplitude, kg/m³; $\rho_{0}$ is the density of incompressible fluid, kg/m³; and $\omega$ is the vorticity, s⁻¹. The terms in the equations from left to right represent the temporal, spatial, and source terms. Under low Mach number conditions and neglecting higher order minima, formula (10) can be simplified to:

$$\frac{{\partial^{2} \rho {^\prime }}}{{\partial t^{2} }}{ - }c_{{0}}^{{2}} {\nabla }^{{2}} \rho {^\prime } = {\nabla \cdot }\left( {\rho_{{0}} {(}\mathop \omega \limits^{{ \to }} { \times }\mathop u\limits^{{ \to }} {)} + {\nabla }\left( {\rho_{{0}} \frac{{u^{2} }}{2}} \right)} \right)$$

(11)

The sound propagation process can be considered as an adiabatic isentropic process. Under adiabatic isentropic conditions, the density perturbation is closely related to the pressure perturbation:

$${\nabla }p{^\prime \approx }c_{{0}}^{{2}} {\nabla }^{{2}} \rho {^\prime }$$

(12)

From this, formula (10) can be further expressed in terms of the amount of sound pressure perturbation:

$$\frac{1}{{c_{{0}}^{{2}} }}\frac{{\partial^{2} p{^\prime }}}{{\partial t^{2} }}{ - \nabla }^{{2}} p{^\prime } = {\nabla \cdot }\left( {\rho_{{0}} {(}\mathop \omega \limits^{{ \to }} { \times }\mathop u\limits^{{ \to }} {)} + {\nabla }\left( {\rho_{{0}} \frac{{u^{2} }}{2}} \right)} \right)$$

(13)

Comparing the FW–H equation of formula (6), it can be seen that the Powell vortex acoustic equation of formula (13) further reveals the relationship between the acoustic pressure perturbation quantity and the vortex and velocity vectors from the perspective of mechanism.

In this paper, the LMS Virtual Lab (LMS) software with acoustic finite element module (FEM) is utilized for the noise calculation for the model pumps and bionic pumps. The acoustic finite element internal sound field and the external sound field mesh division when the minimum division of grid cells meets the formula (10).

$$L \le \frac{{c_{0} }}{{6f_{\max } }}$$

(14)

where: $f_{{{max}}}$ is the highest frequency sought, Hz.

To satisfy the desired maximum frequency requirement, the acoustic time step setting needs to satisfy the formula (15).

$$\Delta t = \frac{{1}}{{{2}f_{{{max}}} }}$$

(15)

As the rotor–stator interaction is the main source of centrifugal pump flow noise, its main frequency is dominated by the blade passing frequency $f_{{\text{bpf}}} = {145}\;\text{ Hz}$ and the low magnification blade passing frequency, belongs to the discrete noise. So, the highest frequency $\left( {f_{{{max}}} } \right)$ is set to be 3000 Hz to meet the requirements of extracting the required features. In addition, the conveying medium is water at room temperature, and sound propagation speed in water and air is 1500 m/s and 340 m/s, respectively. Using the formula (14) and combined with the structural characteristics of the pump set itself and due to time cost considerations, the final size of the internal and external sound field grid is set to 10 mm. As shown in Fig. 6, the dipole sound source on the surface of the blade and the volute is taken as the boundary condition when solving the sound field, and the sound-absorbing flat plate is set at the inlet and outlet to be defined as a fully-absorbing property to serve as the sound-absorbing boundary. The other surfaces of the overflow components are considered completely rigid, meaning that the other surfaces are fully reflective wall surfaces with no sound transmission, and the sound is only propagated along the water to the upstream and downstream.

Fig. 6

Impeller and Volute dipole radiation sound field boundary.

Monitor point set up

Twelve monitor points were uniformly arranged on the circumference of the X–Y plane with a radius of 200 mm to investigate the radiation of centrifugal pump flow noise in the circumferential direction. Monitor points were set up at the worm case tongue and flow channel to investigate the pressure pulsation and the change in sound pressure level. The distribution of its monitor points is shown in Fig. 7, where VT₁ denotes the monitor points at the volute tongue, and CH₁ to CH₄ denote the monitor points at the flow channel.

Fig. 7

Monitor point.

Calculation results and analysis

Hydraulic performance verification

The external characteristic curve obtained from the test and simulation is shown in Fig. 8. The flow field and sound field calculations were completed based on the rated working conditions. In the figure, Q_d is the design flow rate, m³/h; H_d is the design head, m; where Q is the flow rate, m³/h; H is the head, m; d is the abbreviation of design; Sim and Exp represent the simulated and experimental values of the hydraulic performance of the centrifugal pumps of high specific rotational speed, respectively.

Fig. 8

Curves of external characteristics.

From Fig. 8, it can be seen that the efficiency and the head of the numerical simulation of the Prototype and Bionic Pumps under rated operating conditions are 80.59%, 80.72%, 38.14, and 38.55 m, respectively. At this time, the corresponding experimental efficiency and head of the prototype pump are 76.40% and 36.21 m, respectively. The numerical simulation of the trend of the external characteristic curve, indicating that the credibility of the simulation data is high. The maximum deviation of efficiency and head from the test is 7.30% and 6.63%, mainly due to the simplification of the centrifugal pump geometrical model and the lack of consideration of volume and friction losses in the simulation process.

Sound field analysis

To understand the optimization effect of the bionic blade on the noise of the prototype pump, the LMS software was used to calculate the noise of the two model pumps, and the noise frequency response curves shown in Fig. 9 were obtained, to be closer to the practice and to reduce the error, it is necessary to superimpose the various types of sound pressure levels (SPL) to obtain the total sound pressure level (TSPL). The definition of sound pressure level is shown below.

$${SPL = 20log}_{{{10}}} \left( {\frac{{P_{{e}} }}{{P_{{{ref}}} }}} \right)$$

(16)

where: ${SPL}$ is the sound pressure level, dB; $P_{{{ref}}}$ is the reference sound pressure, 1 × 10⁻⁶ Pa in the water and 2 × 10^–5 Pa in the air; $P_{{e}}$ is the effective sound pressure value, Pa; which is defined as:

$$P_{{e}} = \sqrt{\frac{1}{T}} \int_{0}^{T} {p{^\prime }^{{2}} {d}t}$$

(17)

where: $T$ is time, s; $p{^\prime }$ is instantaneous sound pressure Pa.

$${\text{TSPL}} = 10 \log_{{{10}}} \left( {\sum\limits_{{i{ = 1}}}^{n} {{10}^{{{0}{.1SPL}_{i} }} } } \right)$$

(18)

where: ${TSPL}$ is the total sound pressure level, dB; ${SPL}_{i}$ is the sound pressure level in each frequency domain, dB. At the same time, to evaluate the overall noise level inside the centrifugal pump, the total sound pressure levels of different monitor points are superimposed to obtain the average total sound pressure level $({TSPL}_{{{AVE}}}),$ which is defined as:

$${\text{TSPL}}_{{\text{AVE}}} = 10log_{{{10}}} \left( {\frac{1}{n}\sum\limits_{{i = 1}}^{n} {{10}^{{{0}{.1}\,{TSPL}_{i} }} } } \right)$$

(19)

where: ${TSPL}_{{{AVE}}}$ is the average total sound pressure level, dB; ${TSPL}_{i}$ is the total sound pressure level under each position, dB.

Fig. 9

Sound pressure level curves of two model pumps under different monitor points.

As shown in Fig. 9, it can be seen that the high sound pressure level of the centrifugal pump is mainly concentrated at the blade passing frequency and low times the blade passing frequency, which is consistent with the distribution characteristics of the broadband discrete noise in the frequency band, and the maximum eigenvalue appears at the blade passing frequency. This shows that the internal flow noise of the centrifugal pump is mainly related to the rotor–stator interaction between the impeller and the volute tongue. In addition, compared with the original model, the bionic blade is ineffective in suppressing the sound pressure level at low frequencies. The reduction of the sound pressure level is mainly concentrated at high frequencies, and the overall reduction of the total sound pressure level is realized. Among them, the most obvious is the suppression of high-frequency sound pressure levels by the volute tongue and its nearby monitor points (VT₁, CH₄).

The noise at the volute tongue and its vicinity mainly comes from the violent pressure pulsation triggered by the interaction between the impeller and the volute, and the noise in the flow channel mainly comes from the vortex and turbulence. The bionic blade primarily suppresses discrete noise caused by impeller-volute tongue interaction, resulting in better noise reduction near the volute tongue than in the flow channel. To investigate the specific suppression effect of the bionic blade on the total sound pressure level, formula (18) was used to derive the total sound pressure level of the two model pumps at each monitor point location, and the results are shown in Table 4. From Table 4, it can be seen that the bionic blade plays a noise reduction role at each monitor point, in which the maximum total sound pressure level reduction of 2.53 dB is realized at VT₁, and the overall noise reduction rate is about 0.36% to 1.49%.

Table 4 Total sound pressure level at each monitor point of two model pumps.

To explore the directional characteristics of the centrifugal pump noise, the distribution of the total sound pressure level on the circumference of the X–Y plane is shown in Fig. 10. It can be seen that the noise in the internal sound field of a centrifugal pump shows a roughly dipole-symmetric distribution and has an azimuthal character in Fig. 10, which shows that different positions have different sound pressure levels. In addition, the noise value is larger at 0°, which is mainly because the rotor–stator interaction effect is the main source of noise. The monitor position is located between the blade outlet and the tongue, where is more affected by the rotor–stator interaction effect. The bionic blades reduced the radiated noise of the prototype pump throughout the X–Y plane, with the best noise reduction at 120° position, where the noise reduction value and rate were 1.52 dB and 0.86%, respectively. According to formula (19), the average total sound pressure levels of the prototype and the bionic pumps are 176.61 dB and 175.34 dB, respectively, which means that the application of the bionic serrated trailing edge results in an average total radiated noise reduction of 1.27 dB for the centrifugal pump.

Fig. 10

Direction diagram of sound field.

Sound power is independent of the measurement position, distance, and environment and is commonly used to calculate the noise level of equipment. This paper introduces the power spectral density (PSD) through the fast Fourier transform to establish the relationship between the sound energy and the frequency distribution to explore the noise reduction effect of the bionic blade on the centrifugal pump. The results are shown in Fig. 11. The pressure coefficient, ${C}p$, is shown in Fig. 11, which was calculated following the equation below.

$${{C}_p} = \frac{{p - {p_{ave}}}}{{{0}{.5}\rho u_{{2}}^{{2}} }}$$

(20)

where: p is the static pressure value of the monitor point, Pa; p_ave is the average pressure value of the monitor point in a cycle, Pa; u₂ is the circumferential velocity at the impeller outlet, m/s.

Fig. 11

Power spectral density curves of two model pumps.

The acoustic energy of model pumps are mainly concentrated in the low-frequency band, and the acoustic energy is the strongest in the volute tongue and its nearby monitor points in Fig. 11. There are obvious characteristic peaks at the blade passing frequency and the low magnification blade passing frequency, which caused by the rotor–stator interaction effect between the impeller and the volute tongue. On the contrary, the monitor point in the flow channel is farther away from the volute tongue. The interaction between the impeller and the volute tongue has less influence on it, and it is only related to the rotation of the blade. Hence, its main frequency is the shaft frequency. In addition, comparing the PSD curves of each monitor point, it can be seen that the bionic blade reduces the PSD value at the main frequency of each monitor position. The maximum reduction rate of PSD value at the main frequency of the monitor point in the volute tongue and its vicinity and the monitor point in the flow channel are 37.13% and 55.28%, respectively. This also explains, to some extent, the lower total sound pressure level of the bionic blade pump compared to the total sound pressure level of the prototype pump.

Flow field analysis

The phenomena such as cavitation, jet, wake, vortex, and turbulence generated by the flow inside the impeller are directly related to the noise²³. To understand the internal flow state, the transient time-averaged distribution of the velocity-streamline in the impeller cross-section is shown in Fig. 12.

Fig. 12

Velocity-streamline distribution of cross-section in the impeller of two model pumps.

The velocities of both model pumps are symmetrically distributed at the blade inlet pressure surface. There is a large vortex area in the prototype pump in Fig. 12, which is mainly due to the inlet angle of the blades being greater than the relative flow angle (the relative flow angle is the positive angle of attack), making backflow phenomena on the back of the blades. The bionic blade disrupts the vortex structure, causing the large vortex to break up into smaller vortices, which means that the application of the bionic blade reduces the size of the vortex structure. In addition, near the blade outlet, the bionic blade pumps all exhibit high speeds compared to the prototype pumps, which suggests that the bionic structure improves the jet trailing phenomenon at the impeller blade outlet.

To further investigate the flow in the wake region at the blade exit, the vortex structure at the blade exit near the volute tongue was extracted using the Q-criterion (Q_cri = 73,059), and its distribution is shown in Fig. 13. Meanwhile, it can be seen that there is a difference in the distribution of vortex nuclei in the trailing edge region of the two model pumps. Prototype pump outlet trailing area, high-speed fluid from the blade outlet trailing edge of the shedding, the formation of a large group of band shedding vortex with high turbulence kinetic energy. On the wall of the volute and the flow field within the worm shell to produce a huge impact and a strong pressure pulsation. In contrast, the distribution of vortex nuclei in the wake region of the bionic blade pump is greatly reduced, and the wide shedding vortex is separated into several small shedding vortices by the V-shaped nodule trailing edge, which reduces the area and energy occupied by the vortex nuclei, and the rotor–stator interaction effects are weakened.

Fig. 13

Distribution of vortex nuclei at the blade outlet for two model pumps.

Analysis of noise induced by rotor–stator interaction

Combined with the results of the previous study, in addition to the interaction between the impeller and the volute tongue, which is the main source of flow-induced noise in centrifugal pumps, the effect of the vortex on noise is equally important. Thus, this subsection will explain the reasons for the noise reduction of centrifugal pumps by bionic blades from the point of view of rotor–stator interaction.

To investigate the noise reduction mechanism of the bionic blade in the prototype pump, the pressure coefficient $C_p$ is introduced to calculate the static pressure distribution curve for the blade and the pressure pulsation frequency curve, as shown in Figs. 14 and 15, respectively.

Fig. 14

Blade static pressure distribution curve.

Fig. 15

Pressure pulsation curves of two model pumps under different monitor points.

It can be seen that the distribution trend of the static pressure curves of the blades of model pumps is the same shown in Fig. 14. Due to the gradual increase of the flow channel area and the overall pressure on the blade surface gradually increases from the leading edge to the trailing edge, and the pressure pulsation is strongest at the working face near L_i/L = 0.9. The change in relative velocity direction causes a crowding effect near the trailing edge’s pressure surface, leading to a pressure drop. As the fluid exits the blade passage and enters the volute, the sudden expansion of the flow path increases pressure from the pressure face to the back²⁴. In addition, the static pressure coefficient of the bionic pump blades is significantly lower than that of the prototype pump, indicating that the bionic blades effectively suppress the strong pressure pulsation of the original blades.

Figure 15 shows that the main frequency of pressure pulsation of the two model pumps at the monitor point of the volute tongue is the blade passing frequency, and the main frequency of pressure pulsation at the monitor points of CH₁, CH₂, CH₃, and CH₄ in the flow channel is the shaft frequency, and blade passing frequency, respectively. Among them, the main frequency of pressure pulsation at the CH₄ monitor point is not consistent with the CH₁, CH₂, and CH₃ because it is located on the inlet circumference of the volute and is very close to the volute tongue, which is greatly influenced by the interaction between the impeller and the volute tongue. In addition, the bionic blades suppressed the pressure pulsation at the main frequency. Its suppression of the pressure pulsation at the main frequency of the monitor points in the volute tongue and its vicinity and the monitor points in the flow channel can be quantitatively seen in Table 5 up to a maximum of 20.71% and 33.12%.

Table 5 Pressure coefficients at the main frequency of the two model pumps.

There are certain shortcomings in the processing ability of using Fast Fourier Transform (FFT) to feedback frequency domain features to the time domain. To accurately count the relationship between time and frequency, a one-dimensional continuous wavelet transform (CWT) was used to analyze the pressure pulsation signals at the selected VT₁ monitor points, as shown in Fig. 16. The CWT transform formula is as follows:

$${C}({scale},{position}) = \int_{ - \infty }^{ + \infty } {f(t)\psi ({scale},{position},t){d}t}$$

(21)

where: C(scale, position) is the wavelet basis function; f(t) is the signal function; ψ is the mother wavelet.

Fig. 16

Time–frequency diagram of pressure pulsation signal for centrifugal pump.

Figure 16 is the characterizes the time–frequency characteristics of the pressure pulsation after CWT, which respond to the intensity of the pressure pulsation signal. The main frequency of pressure pulsation in a centrifugal pump at the volute tongue 145 Hz. This is mainly related to the monitor position, the monitor point at the volute tongue is more affected by the effect of rotor–stator interaction, the main frequency is blade pass frequency and the low magnification blade pass frequency. In addition, it can be seen that the pressure pulsation intensity of the bionic pump is significantly lower than the prototype pump, which indicates that the bionic blade plays a positive inhibitory effect on the pressure pulsation of the centrifugal pump throughout the transient motion process, and thus proves the validity of the bionic blade on the noise suppression of the centrifugal pump.

To analyze the suppression of pressure pulsation in the centrifugal pump by the bionic blade, the middle cross-section of the impeller and the volute is selected as the study surface, and the standard deviation is introduced to define the pressure pulsation intensity coefficient (${PFIC}$) to reveal the main pulsation region in the pump. The expression of ${PFIC}$ and the corresponding distribution cloud diagram are shown below.

$$PFIC = \frac{{\sqrt {\frac{{1}}{N}\sum\limits_{{i = 1}}^{N} {{(}p{ - }p_{ave)}^{{2}} } } }}{{{0}{.5}\rho u_{{2}}^{{2}} }}$$

(22)

where: N is the number of sample points in the statistical period. p is the pressure at each time step, Pa; p_ave is the average pressure value in the statistical period, Pa.

Figure 17 shows the centrifugal pump pressure pulsation in the most intense location is mainly distributed in the volute and impeller. This phenomenon is mainly caused by the rotor–stator interaction between the impeller outlet and the volute tongue. In addition, when the fluid flows out of the impeller outlet due to centrifugal force and is about to enter the volute, the sudden expansion of the flow channel will lead to a sudden change of pressure, especially the volute tongue due to the special structural design will lead to a greater change in the pressure gradient here. However, the trend of the pressure gradient change will decrease along the direction of fluid flow with the increase of the flow channel area in the volute. The pressure pulsation in the impeller channel gradually increases from the inlet to the outlet. It reaches the maximum at the working surface of the blade outlet, which is consistent with the distribution of the blade static pressure curve shown in Fig. 14. Although the pulsation range of the bionic pump at the volute tongue is slightly increased compared with the prototype pump, the pulsation intensities of the bionic pump at the pressure surface of the blade outlet and the inlet of the impeller are significantly lower than that of the prototype pump, which suggests that the bionic blade reduces the pressure pulsation intensity of the centrifugal pump as a whole. From a flow dynamics perspective, this phenomenon occurs because the bionic blade increases the flow area at both the blade outlet and the volute tongue. This expansion improves the unstable flow state of the fluid passing through the volute tongue, thereby reducing the pressure gradient.

Fig. 17

Pressure pulsation intensity distribution.

The relationship between the suppression of pressure pulsation and the reduction of total sound pressure level, their intensity coefficients at the volute tongue and each flow channel monitor point were plotted as shown in Fig. 18. Combined with the location of the monitor points set up in Fig. 7, it can be seen from Fig. 18 that the intensity coefficient of the pressure pulsation of the two model pumps increases gradually from the impeller inlet to the impeller outlet and reaches the maximum at the blade outlet near the volute tongue. Applying the bionic blades reduced both the pressure pulsation intensity factor and the total sound pressure level at each monitor point, proving the practicality of this bionic design. To explore the specific correspondence between pressure pulsation intensity and noise, the pressure pulsation intensity suppression rate and the total sound pressure level reduction rate were statistically determined at each monitor point, as shown in Table 6. Comparative analysis of the suppression rate of pressure pulsation intensity and the rate of decrease of total sound pressure level at each monitor point shows that the total sound pressure level decreases with the decrease of pressure pulsation intensity. However, there is no positive relationship between the two. The total sound pressure level reduction effect caused by suppressing the pressure pulsation, and the main frequency is significantly larger than that caused by suppressing the pressure pulsation. This is mainly because of the nonlinear relationship between the dipole noise amplitude in the FW–H acoustic equation and the magnitude of the pressure pulsation.

Fig. 18

Relationship between pressure fluctuation intensity coefficient and total sound pressure level.

Table 6 PFIC suppression rate and TSPL suppression rate at the main frequency of two model pumps.

Analysis of noise induced by sound sources

The previous section has explained the causes of noise reduction from the perspective of pressure pulsation based on the dipole source term in the FW–H equation, and the specific noise reduction mechanism will be further elaborated from the sound source perspective using the Powell vortex acoustic equation in the next section.

The flow noise of a centrifugal pump is closely related to the non-constant flow in the pump, so exploring the spatial and temporal distribution characteristics of the flow field, the formation mechanism, and the evolution of the rule is a prerequisite for analyzing the noise. From formula (13), it can be seen that the two components of the sound source, ${\nabla \cdot (}\rho_{{0}} {(}\mathop \omega \limits^{{ \to }} { \times }\mathop u\limits^{{ \to }} {))}$, and ${\nabla }^{{2}} {(}\rho_{{0}} u^{2} { / }2{)}$, are related to the stretching of the vortex beam caused by the effect of velocity, and the inhomogeneity of the kinetic energy of the fluid, where the radiated noise generated by the ${\nabla \cdot (}\rho_{{0}} {(}\mathop \omega \limits^{{ \to }} { \times }\mathop u\limits^{{ \to }} {))}$ sound source term presents dipole characteristics. Since it was suggested that the dipole sound source is the main hydraulic noise in a centrifugal pump, this paper only considers the dipole sound source term. By considering the correlation between the sound source, velocity, and vortex, this subsection investigates the spatio-temporal distribution and the evolution of the velocity and vorticity fields in the centrifugal pump.

The velocity and vorticity distributions on the study surface at different moments are shown below to reveal the spatio-temporal distributions of the velocity and vorticity fields in the pump and their evolution. In addition, the centrifugal pump studied in this paper contains six identical blades, the development and evolution patterns of the velocity and vorticity during the rotation cycle of one blade were sampled during the entire impeller rotation cycle.

Figure 19 and 20 show the cloud diagrams of the absolute velocity distribution characteristics of the study surface of the worm shell and impeller at different moments. (Time step = 15 when the blade passes over the volute tongue; Time step = 30 after the blade passes over the volute tongue; Time step = 45 when the other blade is close to the volute tongue) A region of high flow velocity always exists near the volute tongue during a blade rotation cycle. The absolute velocity of the fluid in this region varies with the spatial position of the blade relative to the volute tongue. The blade tail skims the volute tongue, the absolute fluid velocity is maximized at volute tongue. As the blade swept past the volute tongue, the flow channel area gradually widened, and the absolute fluid velocity near the blade tail and volute tongue decreased until the other blade approached the volute tongue. In addition, compared with the prototype pump, the bionic blade has little effect on the distribution characteristics of the absolute velocity of the fluid in the volute. The average flow velocities of the prototype and bionic pumps are 8.96 m/s and 8.98 m/s, with a slight increase in the range of the high-velocity flow at the volute tongue only. Contrary to the situation in the volute, the bionic blade has a greater effect on the absolute velocity of the fluid in the impeller. The range of high-velocity flow at the suction surface of the bionic pump blade outlet is significantly less than that of the prototype pump, suggesting that the bionic blade improves fluid flow in the impeller.

Fig. 19

Velocity changes in the volute of the two model pumps.

Fig. 20

Velocity changes in the impeller of the two model pumps.

Figures 21 and 22 show the cloud diagrams of the vorticity distribution characteristics of volute and impeller at different moments. As can be seen from the figure, the pump vorticity larger values mainly appear in the flow is more complex, the vorticity near the volute tongue of the septum is much larger than the vorticity in other regions. In a fluid motion, during a blade rotation cycle, the vortex is concentrated near the tongue of the spacer as the blade skims the tongue, and the vorticity reaches its maximum value at this location. The vortex at the trailing edge of the blade and the volute tongue decreases as the blade pass over the volute tongue, and the region of vorticity maximum migrates slightly downstream with the movement of the blade. As the blade move, the vorticity at the tail of the blade gradually decreases. In addition, there is a slight increase in the vorticity in the volute of the bionic pump compared to the prototype pump. Unlike the case in the volute, the vorticities at the blade outlet, blade suction surface, and impeller inlet of the bionic pump are significantly smaller than those in the prototype pump, suggesting that the bionic blades will reduce the vortex intensity within the impeller.

Fig. 21

Vorticity changes in the volute of the two model pumps.

Fig. 22

Vorticity changes in the impeller of the two model pumps.

In the previous contents, the non-constant flow in the pump has been described from the point of view of vorticity field and velocity field, which is the most important basic work for the study of the sound source in the pump. It also lays the foundation for the revelation of the size and distribution characteristics of the sound source of the flow-induced noise, as well as the coupling relationship between the flow field and the acoustic field. Next, to reveal the spatial and temporal distribution characteristics of the sound source in the pump and the evolution law, the distribution of the sound source in the study surface at different moments is shown in Fig. 23 and 24.

Fig. 23

Sound source changes in the volute of the two model pumps.

Fig. 24

Sound source changes in the impeller of the two model pumps.

As shown in Figs. 23 and 24, the development of the sound source in the pump when the blade swept over the tongue (Time step = 15), after the blade swept over the tongue (Time step = 30) and when the other blade was close to the tongue (Time step = 45), combined with the sound source term $\left( {{\nabla \cdot (}\rho_{{0}} {(}\mathop \omega \limits^{{ \to }} { \times }\mathop u\limits^{{ \to }} {))}} \right)$, it can be seen that the time-domain sound sources in the pump obtained from the velocity and vortex reforming are mainly concentrated in the volute tongue, impeller inlet, volute inlet, blade outlet, and blade suction surface. Among them, the maximum value of the sound source appeared at the volute tongue and its vicinity, which is consistent with the findings of Guo et al.²². Comparing the distribution characteristics of the sound source at different moments, it can be seen that in the region farther away from the volute tongue. The movement of the blades has no significant effect on the overall distribution characteristics of the sound source, while the area of the maximum region of the sound source near the volute tongue changes significantly. Specifically, during a blade rotation cycle, influenced by the fluid velocity and vorticity distribution characteristics and the evolution rule, the region of sound source maximum is concentrated at the volute tongue when the blade is swept over the volute tongue. As the blade sweeps slightly downstream of the volute tongue, the region of the sound source maximum that was previously clustered at the tongue breaks up. Due to the narrow area of the flow channel in the volute, the tail of the blade is close to the wall of the volute, and the fluid flow state is not good, resulting in the region of the maximum value of the sound source migrating slightly downstream with the movement of the blade. As this blade continues to move, the distance between the tail of the blade and the volute becomes farther away due to the increase in the area of the flow channel in the volute, resulting in a gradual reduction of the sound source near the tail of the blade. As the flow path narrows again in the vicinity of the volute tongue, the region of the sound source maximum is again clustered in the vicinity of the volute tongue. Compared to the original blades, the bionic blades resulted in a significant reduction of the time domain sound sources, which explains the lower total sound pressure level of the bionic pump compared to the prototype pump.

To reveal the specific suppression of the sound source by the bionic blade, the frequency response curves of the sound source of the two model pumps at the volute tongue monitor point are made using the fast Fourier transform, as shown in Fig. 25.

Fig. 25

Sound source frequency response curves of the two model pumps at the volute tongue.

It can be seen that the sound source frequency response curves of the bionic and prototype pumps show the maximum characteristic peak at the blade passing frequency, which reveals that the main frequency of pulsation in the frequency domain of the two model pumps is the blade passing frequency. In addition, the amplitude of sound source pulsation at the main frequency is 8.90 × 10⁹ kg/m³s² and 7.04 × 10⁹ kg/m³s² for the bionic pump and the prototype pump, respectively. The calculation shows that the pulsation amplitude of the bionic pump at the main frequency is 20.92% lower than that of the prototype pump. This phenomenon indicates that the application of bionic blades plays a positive role in suppressing the noise source and is the main reason for reducing the sound pressure level of the prototype centrifugal pump.

To explain the process of sound perturbation generation and to explore its relationship with vorticity, velocity, and time-domain sound source, the distribution of sound pressure perturbation quantity at different moments on the study surface is shown in Figs. 26 and 27 (Sound pressure perturbation quantity expressed as SPPQ).

Fig. 26

Sound pressure perturbation quantity changes in the volute of the two model pumps.

Fig. 27

Sound pressure perturbation quantity changes in the impeller of the two model pumps.

Figures 26 and 27 illustrate the evolution of sound pressure perturbation levels within the pump. It can be seen that the sound pressure perturbation in the pump, and the maximum value appears in the volute tongue and its vicinity. Comparing the quantity of sound pressure perturbation in the volute at different moments. In the region farther away from the position of the tongue, the distribution characteristics of sound pressure perturbation are almost unaffected by the movement of the blades. However, the movement of the blades changes the location of the maximum sound pressure perturbation in the vicinity of the tongue. Specifically, combined the previous study of the vorticity field and velocity field. During the cyclic movement of the impeller, the flow channel area changes. This change alters the non-constant flow characteristics within the centrifugal pump. As a result, time-domain sound source pulsations are generated. These pulsations cause the perturbation of the sound pressure. That is, affected by the fluid velocity and vorticity with the blade movement rule of change, the maximum value of the time domain sound source at the location of the volute tongue in the pump region appeared to be aggregated. And slightly migrated downstream and the phenomenon of re-aggregation, resulting in sound pressure perturbation appeared to be a similar evolution of the characteristics. This pattern of evolution is shown by the fact that the sound pressure perturbation reaches its maximum at the tongue position when the blade sweeps over the tongue. After that, the region of the maximum amount of sound pressure perturbation migrated slightly downstream with the movement of the blade as it swept over the tongue of the volute tongue. As the other blade approaches the volute tongue, the region of maximum sound pressure perturbation quantity once again converges towards the vicinity of the volute tongue. In addition, the sound pressure perturbation quantity of the bionic blade pump at the volute tongue, impeller inlet, blade outlet, blade suction surface, and blade pressure surface is significantly lower than that of the original model pump, which reveals the reason why the noise of the bionic blade pump is lower than that of the original model pump.

The sound source standard deviation (SSSD) is introduced to evaluate pulsation intensity in the time domain and locate primary acoustic source regions, with larger values corresponding to greater pulsation. In addition, to obtain the correspondence between sound sources and noise in different frequency domains, the sound source intensity (SSI) and the total sound source intensity (TSSI) are defined based on time-domain sound sources using the same method used for noise calculations. The definitions of sound source standard deviation, sound source intensity, and total sound source intensity are shown below.

$$SSSD = \sqrt {\frac{{1}}{N}\sum\limits_{{i = 1}}^{N} {{(}S{ - }S_{ave)}^{{2}} } }$$

(23)

where: N is the number of sample points in the statistical period, S is the sound source value at each time step, kg/m³s²; S_ave is the average time-domain sound source value in the statistical period, kg/m³s².

$${SSI = 20log}_{{{10}}} \left( {\frac{{S_{{e}} }}{{S_{{{ref}}} }}} \right)$$

(24)

where: SSI is the sound source intensity, dB; S_ref is the reference sound source, 1 × 10^–6 kg/m³s² in the water and 2 × 10^–5 kg/m³s² in the air; and S_e represents the time-domain sound source effective value, kg/m³s².

$$TSSI = 10 \log_{{{10}}} \left( {\sum\limits_{{i = 1}}^{n} {{10}^{{{0}{.1}\,{SSI}_{i} }} } } \right)$$

(25)

where: TSSI is the total sound source intensity, dB; SSI_i is the sound source intensity in each time domain, dB.

Based on the time-domain sources, the standard deviation of the sound sources was utilized to reveal the main source regions within the centrifugal pump, as shown in Fig. 28.

Fig. 28

Cloud map of sound source standard deviation distribution of two model pumps.

From Fig. 28, it can be seen that the standard deviation of the sound source of the time-domain sound source in the impeller is mainly concentrated in the impeller inlet, blade outlet, and blade suction surface. The maximum value of the standard deviation of the sound source is located near the suction surface of the blade outlet. It decreases gradually along the circumference of the impeller outlet, which is related to the trailing effect of the impeller outlet jet. Inside the volute, the source standard deviation maximum of the time-domain source is located at the volute tongue. It extends downstream along the direction of impeller rotation and is greater than the source standard deviation maximum inside the impeller. The results show that the main sound source area in the centrifugal pump is concentrated in the volute tongue and the part of the volute tongue that extends slightly downstream along the impeller rotation direction. Comparing the standard deviations of sound sources in two model pumps, the pulsation range of the bionic pump at the volute tongue is slightly increased compared with that of the prototype pump, and the corresponding standard deviation of sound sources here is reduced by 14.04%. The standard deviation of the sound sources of the prototype pump and the bionic pump can be calculated following formula (23) to be 1.07 × 10¹⁰ kg/m³s² and 9.23 × 10⁹ kg/m³s². In addition, the sound source pulsation intensity of the bionic pump is significantly lower at the blade outlet, impeller inlet, and blade suction surface compared to the prototype pump.

To find out the correlation between the flow field and the sound field, the sound source intensities from the two model pumps at the volute tongue are plotted in Fig. 29.

Fig. 29

Sound source intensity curves of the two model pumps at the volute tongue.

The sound source intensity curves of the prototype pump and the bionic pump show typical discrete distribution characteristics shown in Fig. 29. There are obvious characteristic peaks at the blade pass frequency and the low magnification blade pass frequency, and the values of the sound source intensity of 298.99 dB and 296.95 dB at the blade pass frequency. Comparing this curve with the sound pressure level curve at the volute tongue monitor point in Fig. 9, the frequency response of the sound source intensity is similar to the sound pressure level, with peak values appearing at the characteristic frequencies. This indicated that the generation of the frequency domain response of the sound source intensity is the direct cause of the formation of the frequency domain response of the noise sound pressure level. In addition, the sound source intensity of the bionic pump is significantly lower than that of the prototype pump. The total sound source intensity of the bionic pump is 1.33 dB lower than that of the prototype pump as calculated following formula (25), in which the total sound source intensities of the prototype pump and the bionic pump are 303.67 dB and 302.34 dB. These findings provide conclusive evidence that the bio-inspired configurations exhibit remarkable flow-noise suppression capabilities in centrifugal pump applications. The proposed bionic structures are applicable for noise suppression in wide-flow-path turbomachinery, such as high-specific-speed centrifugal, mixed-flow, and axial-flow pumps²⁵.

Conclusions

This paper is based on the humpback whale’s “tubercle effect” on the centrifugal pump blade outlet bionic modification through numerical simulation to study the effect of bionic blade on the centrifugal pump flow field and acoustic field, the following conclusions:

• 1. The bionic blade has no significant effect on the hydraulic performance of the pump. The maximum deviation of efficiency and head compared with the test is 7.30% and 6.63%, respectively.

• 2. The strong pressure pulsation between the impeller and the volute tongue due to rotor–stator interaction is one of the main reasons for the flow noise inside the centrifugal pump. However, the pressure pulsation intensity and the dipole noise amplitude are not linearly related. The total sound pressure level reduction effect caused by suppressing the pressure pulsation, whose main frequency is the blade passing frequency, is significantly larger than that caused by suppressing the pressure pulsation, whose main frequency is the shaft frequency.

• 3. Pressure pulsation intensity, sound source, sound source intensity, and the reduction of the standard deviation of the sound source is the main reason why the bionic pump noise is lower than the prototype pump and the formation of the noise sound pressure level frequency domain response characteristics originated from the frequency domain response characteristics of the sound source intensity.

• 4. Bionic blades provide noise reduction at all monitor points. Among them, the maximum noise reduction at VT₁ is 2.53 dB, and the overall noise reduction rate is in the range of 0.36–1.49%.

• 5. The introduction of bionic structures did not compromise the centrifugal pump’s performance while significantly altering the internal load distribution of the impeller. Concurrently, it substantially reduced pressure pulsations and turbulent kinetic energy intensity, demonstrating remarkable suppression effects on flow-induced noise.