Introduction

Shaft sinking by drilling methods is a widely applied technique for constructing mine vertical shafts in deep and loose strata. It has been successfully adopted in the western region of China for the construction of deep, large vertical shafts in water-bearing, weakly cemented rock formations owing to its high degree of mechanical automation, absence of downhole drilling, and inherent safety1,2,3. However, engineering practice has revealed that western Jurassic weakly cemented rock exhibits characteristics such as mudding, sanding, and strength reduction upon water exposure. Additionally, the drilling process in these formations faces significant issues, including severe tool wear and low rock-breaking efficiency of the rolling cutter, which require urgent investigation and resolution4,5. A milled-tooth rolling cutter plays a crucial role as a primary rock fragmentation tool for shaft sinking using the drilling method. Investigating the rock fragmentation process, rock-breaking mechanism, and relevant parameters is essential for designing the effective cutting tools, optimizing cutterhead layouts, and addressing the challenges of tool abrasion and low drilling efficiency in western Jurassic strata.

Researchers, both domestically and internationally, have focused their studies on rolling cutter mechanical rock breaking in three main areas: (1) rock-breaking mechanisms of polycrystalline diamond compact (PDC) and roller bits used in oil drilling rigs, (2) rock-breaking mechanisms of TBM disc cutters, and (3) rock-breaking mechanisms of inserted-tooth rolling cutters in anti-well drills or mine shaft excavators. These studies have yielded significant findings. For PDC and roller cone bits, Guo et al.6 reported that the volume and shape of single-tooth crushing pits in roller cone bits are significantly affected by the angle of internal friction. Cutting tests have indicated that conical PDC cutters can exert lower cutting forces than traditional PDC cutters7,8,9. Chen et al.10 suggested that double PDC cutters can increase the cutting area and improve cutting efficiency. Su and Akcin11 developed a single-tooth cutting force prediction model through numerical simulations. Liu et al.12 explored the optimal spacing of cloth teeth for the special-shaped PDC bits using numerical simulation. Additionally, numerous studies have demonstrated that the rock fragmentation efficiency of roller-PDC composite bits can significantly surpass that of either roller bits or PDC bits alone13,14.

Linear cutting tests have been established as reliables method for analyzing the rock-breaking mechanisms of disc cutters. These tests have enabled scholars to explore various aspects, including rock fragmentation efficiency, factors influencing rock-breaking force, stress distribution, and optimal spacing of double-rolling cutters15,16,17,18,19,20. The rock fragmentation region of a disc cutter is typically categorized into three zones: Rock powder zone, fracture zone, and primary rock zone21,22. Numerical simulations can also be extensively utilized for investigating disc cutter rock breaking. Gong et al23,24,25 highlighted that joint spacing, rolling cutter spacing, and rock brittleness significantly affect rock crack development, as indicated by the UDEC simulation results. Additionally, Li et al.26 demonstrated through numerical simulations that the efficiency of rock breaking by rolling cutters was significantly influenced by wedge angle and confining pressure.

Regarding the research of the rock-breaking mechanism of inserted-tooth rolling cutters, Tan et al.27,28 examined the optimal drilling pressure for these cutters in anti-well drills using the theory of characteristic grain size. Wu et al.29 identified that the rock-breaking with the inserted-tooth rolling cutters in rotary cutting tests followed a “progressive” breaking pattern. Numerous researchers have investigated the factors affecting the rock fragmentation force of these cutters using numerical simulations and experiments30,31,32,33. Additionally, researchers have studied rock crack lengths using indentation tests34,35,36.

Researchers worldwide have extensively studied the rock-breaking processes, mechanisms, and efficiencies of various rolling cutters. However, significant differences exist between milled-tooth rolling cutters and other types, such as PDC bits, roller cone bits, disc cutters, and inserted-tooth rolling cutters, in terms of rock-breaking methods, cutter shapes and sizes, and rock-breaking environments. Despite these differences, there has been limited research on the rock fragmentation mechanisms and efficiencies of milled-tooth rolling cutters used for shaft sinking by drilling methods in weakly cemented Jurassic strata in western China. Therefore, within the context of the shaft sinking project for the north return air shaft of the Taohutu Coal Mine, rotary cutting tests were conducted on specimens of weakly cemented sandy mudstone-like materials from the western Jurassic period. This study examined the effects of penetration and rotational speeds on the rock fragmentation process, rock-breaking force, cutting coefficient, drillability index, and rock-breaking efficiency of milled-tooth rolling cutters. This study aimed to optimize the operational parameters for shaft sinking using the drilling method and improve the drilling efficiency in weakly cemented Jurassic formations in western China.

Project background

Project description

The Taohutu Coal Mine in Ordos, Inner Mongolia, was designed with an annual production capacity of 8 million tons and features three vertical shafts: main shaft, auxiliary shaft, and north return air shaft. The main and auxiliary shafts were constructed using the freezing method of the shaft sinking, and the north return air shaft was constructed using the shaft sinking by the drilling method. The north return air shaft had a designed depth of 738 m and a clear diameter of 6.5 m, formed through a “one-drilling, one-expansion” approach. The geological data for the north return air shaft are presented in Table 1.

Table 1 Geological information of strata intersecting during shaft sinking using the drilling method.
Full size table

Introduction of shaft drilling rig

The north return air shaft of the Taohutu Coal Mine utilized a ZMD120/1200 shaft drilling rig, which employed a ϕ5.0 m drill bit for advanced drilling and a ϕ9.4 m drill bit for reaming (Fig. 1). This drilling rig has a maximum drilling depth of 800 m, maximum drilling diameter of 12.0 m, power torque of 1200 kN·m, and maximum rotational speed of 16 rpm. Figure 2 illustrates the ZMD120/1200 shaft drilling rig and the layout of the ϕ5.0 m cutterhead. The cutterhead of ϕ5.0 m drill bit was equipped with 29 rolling cutters, primarily using 12-inch 3° milled-tooth rolling cutters during field construction. The installation parameters of these rolling cutters are detailed in Table 2, including 6 side cutters (numbered a), 19 inner cutters (numbered b–m), and 1 central cutter (numbered n).

Fig. 1
figure 1

Sectional diagram of graded drilling.

Full size image
Fig. 2
figure 2

Shaft drilling rig and cutterhead layout.

Full size image
Table 2 Installation parameters of rolling cutters for ϕ5.0 m drill bit.
Full size table

Rotary cutting test of milled-tooth rolling cutters

Introduction of test equipment

The rotary cutting test of the milled-tooth rolling cutter was conducted using a multifunctional mechanical rock-breaking test platform (Fig. 3), which consisted of a mechanical system, a hydraulic system, an automatic control system, and a data acquisition system. The mechanical system, including the top frame, vertical column, reinforced steel plate, and equipment frame, ensured stability of the test platform. The hydraulic system comprising the hydraulic station and cylinder provided power to the test platform. The automatic control system adjusted the penetration and rotational speeds of the rolling cutter. The data acquisition system consists of a load sensor, signal transmission cables, and a computer terminal. The load electrical signals collected by the load sensor were transmitted to a computer terminal via signal transmission cables. The sample box accommodated specimens with dimensions of 1000 mm × 1000 mm × 660 mm, secured with high-strength screws. In addition, the equipment can be installed with two rolling cutters simultaneously, allowing for synergistic rock fragmentation and tests with different cutting tools.

Fig. 3
figure 3

Mechanical rock-breaking test platform.

Full size image

Sample preparation

The rock specimens for the rock-breaking experiments with the milled-tooth rolling cutter were poured using Jurassic sandy mudstone-like materials consisting of cement, gypsum, river sand, clay, and other components. The mix ratio for the sandy mudstone-like materials was sand: Cement: Gypsum: Kaolin: Water: Water reducer = 1:1.25:0.75:0.15:0.6:0.02, and the mineral composition of the material is shown in Fig. 4. These materials replicated the conditions of weakly cemented sandy mudstone from the western Jurassic Yan’an Formation37,38. The strength curves for sandy mudstone-like materials and rocks are shown in Figs. 5 and 6, respectively. Each rock sample measures 1.0 m × 1.0 m × 0.66 m, was poured and cured for 28 d before polishing. The compressive strength was measured using a concrete rebound tester. The pouring process of the specimens is illustrated in Fig. 7. In addition to the rock specimens, cubic test samples were cast and tested for their physical and mechanical properties. The mechanical properties of Jurassic sandy mudstone and sandy mudstone-like materials are listed in Table 3.

Fig. 4
figure 4

Mineral composition diagram of material.

Full size image
Fig. 5
figure 5

Compressive strength stress – strain curve.

Full size image
Fig. 6
figure 6

Tensile strength stress – strain curve.

Full size image
Fig. 7
figure 7

Sample preparation process.

Full size image
Table 3 Physical and mechanical parameters of sandy mudstone and sandy mudstone-like materials.
Full size table

Test scheme

The experiment employed rotary cutting for rock-breaking using a 12-inch 3° milled-tooth rolling cutter (Fig. 8). This rolling cutter featured three rings and 17 rows of cutter teeth, with a cutter body inclination angle of 3° and a cone diameter of 330 mm at the large end. The rotation radius of the milled-tooth rolling cutter in the rotary cutting test was 360 mm. It approximately simulates the rotary cutting rock-breaking process of the m# inner cutter on the ϕ5 m cutterhead. The rotary cutting test was conducted with the penetration and rotational speeds of the rolling cutter as influencing factors. The rotational speed of the rolling cutter was calculated based on the rotational speed of the cutterhead and installation parameters of the rolling cutter. The parameters of the 12-inch 3° milled-tooth rolling cutter are listed in Table 4, and the test scheme is presented in Table 5.

Fig. 8.
figure 8

12-inch 3° milled-tooth rolling cutter and its dimensions.

Full size image
Table 4 Parameters of 12 inch 3° milled-tooth rolling cutter.
Full size table
Table 5 Scheme of rotary cutting test.
Full size table

Test procedures

According to the experimental design, 8–10 layers of rotary cutting were performed at each penetration level until the rock-breaking force data stabilized, and a consistent pattern emerged, after which the test was stopped. Data on the three-directional rock-breaking force at different penetration levels were collected. When adjusting the penetration or rotational speeds of the rolling cutter, the data from the first 1–2 layers affected by these changes were discarded, and more stable data from subsequent layers were analyzed. After each layer of the rotary cutting test, the rock debris generated by the rolling cutter was collected, screened, and weighed.

Rock fragmentation mechanism and data processing of milled-tooth rolling cutters

Description of rock fragmentation phenomenon

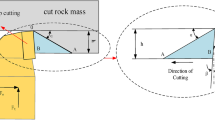
When the milled-tooth rolling cutter contacts the rock, the cutter teeth penetrate the rock under the action of normal force, creating a crushing pit and fracturing the rock once the pressure exceeds its compressive strength. The rock debris beneath the cutter teeth was compacted into a dense nucleus, which transmitted the normal force to the surrounding rock, leading to the formation of numerous cracks, including middle, radial, and lateral cracks (Fig. 9). The expansion of the middle and radial cracks caused deeper rock fragmentation, whereas lateral cracks extended within the crushing pit to form rock sheets. During the rock fragmentation process, the instantaneous rock-breaking force fluctuates regularly, peaks, and then abruptly decreases. The instantaneous rock-breaking force curves were acquired in real time using the data acquisition system of the mechanical rock-breaking platform, as shown in Figs. 10 and 11. This fluctuation occurred because the cutter teeth continuously cycle through an “invade-climb out” process as the cutter rotated, with each penetration forming a new crushing pit and contributing to the leaping destruction. Moreover, only three cutter teeth (from one row) were in contact with the rock, and the total rock-breaking force was the sum of the forces exerted by these three cutter teeth.

Fig. 9
figure 9

Schematic diagram of crack propagation.

Full size image
Fig. 10
figure 10

Instantaneous normal force curve.

Full size image
Fig. 11
figure 11

Instantaneous rolling force curve.

Full size image

When the rotational speed is held constant and penetration is small, the penetration depth of the cutter teeth of the milled-tooth rolling cutter into the rock is shallow, resulting in low resistance from the rock specimen to the cutter teeth. Consequently, this results in a smaller rock-breaking force. During this phase, the rock debris particles were predominantly smaller than 20 mm, and the debris mainly consisted of thin rock slices with relatively small thickness-to-width ratios (Fig. 12). As the penetration depth increased, the rock resistance to the cutter teeth also increased, leading to a higher rock-breaking force and a more pronounced peak force. This increase was due to the larger area of rock damaged by compression in the crushing pit, which required more normal force to break the rock. When the penetration exceeded 2 mm, the rock debris produced by the milled-tooth rolling cutter was larger, with most particles classified as “rock blocks” greater than 20 mm in size and having a high thickness-to-width ratio (Fig. 13). Thus, the maximum particle size of the “rock blocks” increased with greater penetration.

Fig. 12
figure 12

Rock-breaking effect of 1 mm and 2 mm penetration.

Full size image
Fig. 13
figure 13

Rock-breaking effect of 3 mm and 4 mm penetration.

Full size image

At the same penetration level, low rotational speeds (0.11–0.15 rps) had a minimal effect on the rock-breaking process. Owing to the low rotational speed, the cutter teeth exerted less force on the rock, resulting in a smaller rock-breaking force and a reduced slip shear effect. The cutter teeth are pressed into the rock slowly after contacting the rock sample, and there is only a small amount of rock debris splashing during the pressing process of the cutter teeth. This is because the kinetic energy obtained by the rock debris in the crushing pit was minimal during slow pressing. When the rotational speed of the milled-tooth rolling cutter exceeded 0.17 rps, the impact on the rock-breaking process became significant. As the rotational speed of the rolling cutter increased, the impact and slip shear effects of the cutter teeth on the rock intensified, with greater kinetic energy being transferred to the rock debris in the crushing pit, causing significant debris to scatter around the pit. The peak rock-breaking force of the milled-tooth rolling cutter increased at higher rotational speeds, as evidenced by the more intense vibration of the roller cutter during the rotary rock-breaking test.

Analysis of rock fragmentation modes induced by the milled-tooth rolling cutter

The rock fragmentation effect of the milled-tooth rolling cutter depends on both the penetration and rotational speeds and the tooth spacing between the two rings of the cutter teeth. The larger spacing between cutter teeth increased the difficulty of connecting lateral cracks between adjacent cutter teeth, thereby increasing the difficulty of the formation of “rock blocks”. Based on whether the lateral cracks between adjacent cutter teeth were connected, the rock fragmentation modes of the milled-tooth rolling cutters could be categorized as either cooperative or non-cooperative modes of the cutter teeth. According to Tan et al.39, the length of lateral cracks produced by the cutter can be linearly related to penetration. The test results indicated that when the penetration was less than 3 mm, the milled-tooth rolling cutter could operate in a non-cooperative rock-breaking mode of the cutter teeth. In this mode, the rock below the cutter teeth was fractured under compression once it reached its strength limit, but the lateral cracks between the crushing pits of the adjacent cutter teeth did not connect. The rock on either side of the cutter teeth was compressed and subjected to shear failure. At this stage, the rock between two adjacent rings of teeth was not entirely destroyed, resulting in a “ring direction rock ridge” left behind by the rolling cutter (Fig. 14). When the penetration reached or exceeded 3 mm, the milled-tooth rolling cutter entered the cooperative rock-breaking mode of the cutter teeth. As the cutter teeth penetrated deeper into the rock, the rock on either side simultaneously experienced shear and tensile failures. The lateral cracks of the adjacent cutter teeth’s crushing pits were connected, causing the “ring directions rock ridge” to first undergo the elastic deformation under compression and tension. Subsequently, the rock ridge released energy, leading to plastic deformation and tensile cracks. The “ring directions rock ridge” was then either completely or partially removed (Fig. 15). Figure 16 depicts both the cooperative and non-cooperative rock fragmentation modes of the cutter teeth.

Fig. 14
figure 14

Rock fragmentation surfaces with 1 and 2 mm penetration.

Full size image
Fig. 15
figure 15

Rock fragmentation surfaces with 3 and 4 mm penetration.

Full size image
Fig. 16
figure 16

Rock fragmentation modes of two cutter teeth.

Full size image

The rock-breaking process of a single-ring cutter tooth on a milled-tooth rolling cutter is as follows. Under a normal load, the cutter teeth penetrated the rock to form a crushing pit. As the milled-tooth rolling cutter continued to roll, the subsequent cutter tooth penetrated the rock again, creating another crushing pit. Simultaneously, the tangential rolling force threw the cuttings from the crushing pit, with a “radial rock ridge” generated between the two pits. This rock ridge was broken into rock slices through the sliding shear action of the milled-tooth rolling cutter, achieving the “progressive” collaborative rock-breaking between the front- and rear- row cutter teeth. When the penetration was less than 3 mm, the sliding shear action could completely destroy the “radial rock ridge”, resulting in a relatively flat rock-breaking surface (Fig. 14). However, when the penetration reached or exceeded 3 mm, the volume or area of the “radial rock ridge” was too large for the sliding shear effect to entirely remove it, leading to the retention of part of the ridge on the rock surface cut by the milled-tooth rolling cutter.

In summary, during the rotary cutting process of a milled-tooth rolling cutter, only the three cutter teeth in contact with the rock consistently experienced a rock-breaking force. The rock fragmentation process of the milled-tooth rolling cutter was primarily governed by the normal force, with the rolling force and sliding shear providing supplementary support. The rock fragmentation process of the milled-tooth rolling cutter was the “progressive” rock fragmentation of the front- and rear-row cutter teeth. The milled-tooth rolling cutters exhibited two rock fragmentation modes: Cooperative and non-cooperative of the cutter teeth.

Test data processing

  • (1) Rock-breaking force

The values for \(F_{N}\) and \(F_{R}\) were derived by calculating the average of the rock-breaking force data collected by the test platform, with the lateral rock-breaking force considered negligible and thus excluded. When calculating the average rock-breaking force, the data from the first one to two layers collected after the changes in penetration or rotational speeds of rolling cutters were excluded.

  • (2) Cutting coefficient \(C_{{\text{C}}}\)

The cutting coefficient is an index to evaluate the rolling force required for each unit of normal force in the rotary cutting test, reflecting the extent to which rolling force (torque) contributes to rock-breaking40. The calculation method is detailed in Eq. (1):

$$C_{{\text{C}}} = \frac{{F_{R} }}{{F_{N} }} \times 100\%$$
(1)

  • (3) Rock drillability index DI

The rock drillability index (DI) represents the normal force required for each 1 mm of penetration by the milled-tooth rolling cutter and serves as a key indicator of the rock-breaking difficulty of the cutter41. A lower DI indicates that the rolling cutter can break the rock more easily, leading to higher rock drillability and reduced drilling pressure per millimeter of cutterhead penetration. Conversely, a higher DI signifies that more drilling pressure is required for each 1 mm cutterhead penetration. The calculation formula is as follows:

$$DI = \frac{{F_{N} }}{P}$$
(2)

where DI is the drillability index \({\text{(kN mm}}^{ - 1} )\), and P is the penetration (mm).

  • (4) Rock-breaking specific energy SE

The SE of the milled-tooth rolling cutter was calculated as follows42:

$$SE = \frac{{F_{N} P + 2\pi nT}}{V}$$
(3)

where SE is the rock-breaking specific energy \(\left( {{\text{MJ m}}^{ - 3} } \right)\) FN is the average normal force (kN), T is the torque (kN m), and V is the rock-breaking volume of the milled-tooth rolling cutter (m3).

  • (5) Coarseness index \(C_{{\text{I}}}\)

The coarseness index \(C_{{\text{I}}}\) was proposed by Roxborough43, and the coarseness index \(C_{{\text{I}}}\) was derived from the cumulative sieve residue rate of various particle size cuttings. The calculation method for the coarseness index \(C_{{\text{I}}}\) is as follows:

$$X_{i} = \frac{{{\text{W}}_{i} }}{{\text{W}}} \times 100\%$$
(4)
$$C_{{\text{I}}} = \sum\limits_{i}^{n} {X_{i} }$$
(5)

where \({\text{W}}_{i}\) is the total weight of rock debris greater than or equal to a certain particle size (g); i is the mesh aperture; W is the total weight of cutting in each group of rock breaking test (g); and \(X_{i}\) is the cumulative sieve residue rate of rock debris greater than or equal to a certain particle size.

The processed test data are presented in Tables 6, 7, and 8.

Table 6 Average rock-breaking force.
Full size table
Table 7 Calculation results of cutting coefficient and drillability index.
Full size table
Table 8 Calculation results of rock-breaking specific energy and roughness index.
Full size table

Test result analysis

Rock-breaking force

Effect of penetration on rock-breaking force

Figures 17 and 18 illustrate the correlation between the average rock-breaking force and penetration of the milled-tooth rolling cutter. According to the analysis, under the condition of different rotational speeds of the rolling cutter, the average normal force \(F_{N}\) (referred to as \(F_{N}\)) and average rolling force \(F_{R}\) (referred to as \(F_{R}\)) exhibited the approximately linear positive correlation with penetration, and the maximum increase of \(F_{N}\) was 142% (n = 0.21rps), and the maximum increase of \(F_{R}\) was 783% (n = 0.11rps). When the normal force was small, the penetration was also small, resulting in inadequate crack propagation beneath the cutter teeth. Consequently, the lateral cracks in the “ring direction rock ridge” region between the adjacent cutter teeth were difficult to connect, making rock slice formation challenging. As the normal force of the rolling cutter increased, the penetration also increased, causing the milled-tooth rolling cutter to gradually shift to the cooperative rock-breaking mode of the cutter teeth. The area of rock compression in the crushing pit increased, and the “ring direction rock ridge” between the adjacent cutter teeth experienced extrusion, shear, and tension. This process connected the lateral cracks within the rock and formed and detached rock sheets, which effectively improved the rotary cutting efficiency. Therefore, to achieve greater penetration, the drilling pressure of the cutterhead should be increased during shaft sinking by the drilling method. \(F_{R}\) was influenced by both \(F_{N}\) and the contact area between the cutter teeth and rock. As the penetration increased during rock fragmentation, a larger \(F_{N}\) resulted in increased friction between the debris and the cutter teeth. Moreover, a larger value of \(F_{R}\) is required to expel rock debris from the crushing pit as the volume of rock fragmentation increases.

Fig. 17
figure 17

Relationship between \(F_{N}\) and penetration.

Full size image
Fig. 18
figure 18

Relationship between \(F_{R}\) and penetration.

Full size image

Figure 19 illustrates the curve of \(C_{{\text{C}}}\) versus penetration. The analysis demonstrated that \(C_{{\text{C}}}\) increased nonlinearly with the penetration at varying rotational speeds of the rolling cutter. With a penetration of 1.5 mm as the dividing line, \(C_{{\text{C}}}\) could be categorized into the intrusive zone and the cutting zone. In both intervals, \(C_{{\text{C}}}\) was linearly and positively correlated with penetration. In the intrusive zone, the cutting force was primarily \(F_{N}\), and \(F_{R}\) contributed little to rock-breaking. In the cutting zone, although the contribution of \(F_{R}\) to rock fragmentation increased, the rock fragmentation force was still predominantly governed by \(F_{N}\). In summary, during the rotary cutting test with a milled-tooth rolling cutter, \(F_{N}\) was significantly larger than \(F_{R}\), indicating that the rock fragmentation process was primarily dominated by \(F_{N}\), with \(F_{R}\) playing a secondary role. However, during shaft sinking using the drilling method, the cutterhead torque should be increased in tandem with the drilling pressure, particularly for the penetrations over 1.5 mm, where a significant increase in cutterhead torque was necessary to ensure smooth rock-breaking.

Fig. 19
figure 19

Relationship between \(C_{{\text{C}}}\) and penetration.

Full size image

Influence of rotational speeds of the rolling cutter on rock fragmentation force

Figures 20 and 21 illustrate the relationship between \(F_{N}\) and \(F_{R}\) for the milled-tooth rolling cutter versus its rotational speed. The analysis revealed that under varying penetration conditions, both \(F_{N}\) and \(F_{R}\) increased with higher rotational speeds of the rolling cutter. However, the increases in \(F_{N}\) and \(F_{R}\) varied across different rotational speed ranges. Specifically, the relationship curves could be categorized into three zones: low rotational speed (0.11 ≤ n ≤ 0.13 rps), middle rotational speed (0.13 < n ≤ 0.19 rps), and high rotational speed (0.19 < n ≤ 0.23 rps). In the low rotational speed zone, the rock-breaking force is relatively small, with the maximum increases of 16% for \(F_{N}\) (P = 3.0 mm) and 22% for \(F_{R}\) (P = 0.5 mm). In the middle rotational speed zone, the rock-breaking force increased significantly, with the maximum increases of 76% for \(F_{N}\) (P = 2.5 mm) and 68% for \(F_{R}\) (P = 2.5 mm). In the high rotational speed zone, the increase in the rock-breaking force slowed and stabilized, with the maximum increases of 13% for \(F_{N}\) (P = 3.0 mm) and 15% for \(F_{R}\) (P = 3.0 mm). This behavior can be explained by the fact that at low rotational speeds, the milled-tooth rolling cutter could have less kinetic energy, with a weaker impact on the rock and a smaller increase in the rock-breaking force. As the rotational speed increases, the cutter’s kinetic energy and impact on the rock intensify, leading to a substantial increase in the rock-breaking force in the middle-speed zone. At a rotational speed of 0.19 rps for the milled-tooth rolling cutter, the energy and force of the cutter teeth were sufficient for instant rock breaking. Hence, in the high rotational speed zone, although the kinetic energy of the milled-tooth rolling cutter increased with the rotational speed, the impact on the rock-breaking force was minimal.

Fig. 20
figure 20

Relationship between \(F_{N}\) and rotational speeds of the rolling cutter.

Full size image
Fig. 21
figure 21

Relationship between \(F_{R}\) and rotational speeds of the rolling cutter.

Full size image

Analysis of drillability index DI

Figure 22 presents the relationship between the drillability index (DI) and penetration. The analysis indicated that DI decreased nonlinearly with increasing penetration under various rotational speeds of the rolling cutter, with a maximum decrease of 75% (n = 0.15 rps). The relationship between DI and penetration can be described by a power function. Both the coefficient and exponent of the power function increase with the rotational speeds of the rolling cutter. An increase in the coefficient indicates that the cutter’s kinetic energy increases as the rotational speed of the rolling cutter increases, whereas a higher exponent suggests more pronounced rock deformation induced by the cutter’s rock-breaking action. Moreover, the coefficient and exponent of the power function exhibit a positive correlation. The DI versus penetration curves were divided into three intervals: low drillability (0.5 ≤ P < 1.5 mm), high drillability (1.5 ≤ P ≤ 3.0 mm), and extremely high drillability (3.0 < P ≤ 4.0 mm). Within each interval, DI and penetration were approximately linearly negatively correlated. When the penetration was less than 1.5 mm, DI was higher, indicating greater difficulty in breaking rock and lower rock drillability. When the penetration ranged from 1.5 to 3.0 mm, DI was lower, reflecting the reduced rock-breaking difficulty and high drillability. For penetration greater than 3.0 mm, DI became small and stabilized, signifying that the milled-tooth rolling cutter easily broke the rock, resulting in extremely high drillability.

Fig. 22
figure 22

Relationship between DI and penetration.

Full size image

Figure 23 illustrates the variation in DI with rotational speeds of the rolling cutter. The analysis indicated that DI increased as the rotational speed of the rolling cutter increased under different penetration conditions. Moreover, DI followed a trend similar to the normal force \(F_{N}\) as rotational speeds increased and can be categorized into three zones: low rotational speed (0.11 ≤ n ≤ 0.13 rps), middle rotational speed (0.13 < n ≤ 0.19 rps), and high rotational speed (0.19 < n ≤ 0.23 rps). In the low rotational speed zone, DI was very small, indicating extremely high drillability. In the middle rotational speed zone, the DI was small, corresponding to high drillability. In the high-rotational-speed zone, the DI was large, reflecting low drillability.

Fig. 23
figure 23

Relationship between DI and rotational speeds of the rolling cutter.

Full size image

In summary, when the penetration exceeded 1.5 mm and the rotational speed of the rolling cutter was less than 0.19 rps, the rock drillability was higher. To enhance rock drillability, the shaft drilling rig should operate under high drilling pressure (with a greater normal force leading to greater penetration) and a low rotational speed during shaft sinking using the drilling method in Jurassic strata in western China.

Rock-breaking efficiency

Analysis of SE

Figure 24 illustrates the relationship between SE and penetration. The analysis indicated that SE initially decreased and then increased with increasing penetration under varying rotational speeds of the rolling cutter. The SE curves were categorized into three zones: low-efficiency rock-breaking (0.5 ≤ P < 2.0 mm), high-efficiency rock-breaking (2.0 ≤ P ≤ 3.0 mm), and overcrushing (3.0 < P ≤ 4.0 mm). In the low-efficiency rock-breaking zone, SE decreased sharply with penetration, with a maximum reduction of 36% (n = 0.17 rps). Although the rock-breaking efficiency was low in this zone, it improved as penetration increased. In the high-efficiency rock-breaking zone, SE demonstrated the minimal variation with the minimum value in this zone, resulting in the highest rock-breaking efficiency. In the overcrushing zone, SE increased with increasing penetration, exhibiting a maximum increase of 27% (n = 0.11 rps). This indicated that when penetration exceeded 3.0 mm, further increases in penetration could reduce the rock-breaking efficiency. The reasons for this phenomenon are as follows. Initially, at low penetration, the milled-tooth rolling cutter operated in a non-cooperative rock fragmentation mode of the cutter teeth, making it difficult to connect the lateral cracks between adjacent cutter teeth. Consequently, the rock-breaking volume was small and the rock-breaking efficiency was low. As the penetration increased, these cracks interconnected, leading to broken “ring direction rock ridge”. This enhanced the rock-breaking volume and energy utilization, thereby improving the efficiency of the high-efficiency rock-breaking zone. However, at high penetration, although the “ring direction rock ridge” was fully broken, excessive rock fragmentation in the crushing pit significantly increased the \(F_{N}\) required for rock breaking, whereas the increase in the rock-breaking volume was minimal, leading to a reduced efficiency in the overcrushing zone.

Fig. 24
figure 24

Relationship between SE and penetration.

Full size image

Figure 25 shows the relationship between SE and the rotational speeds of the rolling cutter. The analysis demonstrated that SE was linearly positively correlated with the rotational speeds under different penetration conditions, with a maximum increase of 143% (P = 2.5 mm) and a minimum increase of 102% (P = 1.5 mm). This indicated that reducing the rotational speeds of the rolling cutter could decrease SE and improve the rock-breaking efficiency of the milled-tooth rolling cutter. In shaft sinking by drilling method engineering, assuming that other factors were constant, lower cutterhead rotational speeds could result in a higher rock-breaking efficiency. Additionally, under all penetration conditions, the SE reached its minimum at a cutterhead speed of 0.11 rps, corresponding to the maximum rock-breaking efficiency. It was observed that lower rotational speeds of both the cutter and cutterhead led to a higher drilling efficiency, which is consistent with the low rotational speed requirements of shaft drilling rigs used in shaft sinking by drilling methods.

Fig. 25
figure 25

Relationship between SE and rotational speeds of the rolling cutter.

Full size image

Analysis of coarseness index \(C_{{\text{I}}}\)

Figure 26 shows the relationship between \(C_{{\text{I}}}\) and penetration. The analysis indicated that under varying rotational speeds of the rolling cutter, \(C_{{\text{I}}}\) first increased and then decreased with increasing penetration, in contrast to the trend observed for SE. The relationship curve between \(C_{{\text{I}}}\) and penetration can be divided into three intervals: low-efficiency rock-breaking zone (0.5 ≤ P < 2.0 mm), high-efficiency rock-breaking zone (2.0 ≤ P ≤ 3.0 mm), and overcrushing zone (3.0 < P ≤ 4.0 mm). In the low-efficiency zone, \(C_{{\text{I}}}\) increased with penetration, with a maximum increase of 33% (n = 0.23 rps), whereas the rock-breaking efficiency remained low but gradually improved. In the high-efficiency zone, the \(C_{{\text{I}}}\) variation was minimal, with the peak \(C_{{\text{I}}}\) identified in this zone, corresponding to the maximum rock-breaking efficiency. In the overcrushing zone, the \(C_{{\text{I}}}\) decreased with increasing penetration, and there was a reduced rock-breaking efficiency.

Fig. 26
figure 26

Relationship between \(C_{{\text{I}}}\) and penetration.

Full size image

Figure 27 illustrates the relationship between \(C_{{\text{I}}}\) and the rotational speeds of the rolling cutter. The analysis indicated that under different penetration conditions, \(C_{{\text{I}}}\) decreased as the rotational speeds of the rolling cutter increased, with a maximum reduction of 22% (P = 0.5 mm). This demonstrated that higher rotational speeds reduced both the \(C_{{\text{I}}}\) and rock-breaking efficiency.

Fig. 27
figure 27

Relationship between \(C_{{\text{I}}}\) and rotational speeds of the rolling cutter.

Full size image

In summary, the evaluation of rock-breaking efficiency using both \(C_{{\text{I}}}\) and SE for milled-tooth rolling cutters exhibited consistent results. When the penetration was below 2.0 mm, the rock-breaking efficiency increased with increasing penetration. The efficiency peaked when the penetration ranged from 2.0 to 3.0 mm, and declined as the penetration exceeded 3.0 mm. Additionally, the rock-breaking efficiency decreased with an increase in the rotational speeds of the rolling cutter. Furthermore, when the penetration rate ranged between 2.0 and 3.0 mm, and the rolling cutter’s rotational speed was 0.11 rps, the rock-breaking efficiency of the milled-tooth rolling cutter reached its peak. These conditions represent the optimal drilling parameters for shaft sinking using drilling methods in the Jurassic strata of western China.

Discussion

  1. (1)

    Although the mechanical properties of the rock samples used in the rock-breaking experiments were consistent with those encountered under engineering field conditions, geological features such as joint dip angle and joint spacing were not considered. Moreover, the rotational cutting tests conducted with the milled-tooth rolling cutter in this study were relatively simplified and did not fully capture the complexity of the real-world scenarios. To further address the issue of low rock-breaking efficiency during shaft sinking by drilling methods through weakly cemented Jurassic strata in western China, it is essential to conduct rotational cutting experiments using rock samples that incorporate representative geological features such as joints. This will facilitate a deeper understanding of the rock-breaking mechanisms of the milled-tooth rolling cutter under varying geological conditions and enable the optimization of its structural parameters, thereby significantly improving its rock-breaking efficiency.

  2. (2)

    The rock-breaking experiments in this study considered only the rotational speed of the cutterhead in the shaft drilling rigs used for shaft sinking by drilling methods. However, mechanical parameters such as weight on bit and torque also have a minor influence on the rock-breaking efficiency. Future research should incorporate these additional parameters and employ corresponding model experiments or numerical simulations to optimize the operational parameters of both the cutterhead and the rolling cutter.

  3. (3)

    Owing to experimental limitations, this study did not consider the effect of drilling mud properties on the rock-breaking performance of a milled-tooth rolling cutter. However, the mud used in the cutting removal system also has a minor effect on drilling efficiency44. Future research should focus on conducting rock-breaking experiments with milled-tooth rolling cutters in a mud environment to evaluate the effects of parameters such as mud viscosity and density on the rock-breaking efficiency of the milled-tooth rolling cutter and to identify the optimal operational parameters for shaft sinking using this method.

Conclusion

In this study, a rotary cutting test of Jurassic weakly cemented sandy mudstone-like materials was conducted using a mechanical rock-breaking test platform and a milled-tooth rolling cutter. The effects of penetration and rotational speeds on the rock-breaking force and related parameters were analyzed, drawing the following conclusions:

  1. (1)

    Greater penetration increased the rock-breaking force, while the higher rotational speeds of the rolling cutter enhanced the impact of the cutter teeth. The rock fragmentation modes of the milled-tooth rolling cutter were classified into cooperative and non-cooperative modes of the cutter teeth. In the cooperative mode, the rock between the adjacent cutter teeth experienced both shear and tensile failure simultaneously. In the non-cooperative mode, only shear failure occurred. The rock fragmentation process of the milled-tooth rolling cutter was the “progressive” rock fragmentation of the front- and rear-row cutter teeth.

  2. (2)

    The average normal force and average rolling force exhibited a linear positive correlation with both the penetration and rotational speeds of the rolling cutter. The cutting coefficient increased nonlinearly with penetration. With a penetration of 1.5 mm as the dividing line, the cutting coefficient could be divided into two zones: the intrusive zone and cutting zone. In both intervals, the rock-breaking force was primarily due to the normal force.

  3. (3)

    The drillability index decreased nonlinearly with increasing penetration, and the relationship curve was categorized into three intervals, including low drillability, high drillability, and extremely high drillability. In each interval, the drillability index was linearly and negatively correlated with penetration. In addition, the drillability index increased with higher rotational speeds of the rolling cutter, with the relationship curve divided into low, middle, and high rotational speed zones. Drillability was extremely high in the low rotational speed zone, high in the middle rotational speed zone, and low in the high rotational speed zone.

  4. (4)

    The specific energy and coarseness index exhibited opposite trends. The specific energy initially decreased and then increased with penetration, whereas it increased at higher rotational speeds of the rolling cutter. Conversely, the coarseness index first increased and then decreased with penetration and declined at higher rotational speeds. When the penetration ranged between 2.0 and 3.0 mm, and the rolling cutter’s rotational speed was 0.11 rps, the rock-breaking efficiency of the milled-tooth rolling cutter reached its maximum. These conditions represent the optimal drilling parameters for shaft sinking using drilling methods in the Jurassic strata of western China.