Introduction

The water-force coupling characteristics of rock is a critical focus in geotechnical engineering research1,2. The interaction between the stress and seepage fields significantly influences both the mechanical and hydraulic properties of rock formations3,4. Determining effective stress is crucial for stability analysis, serving as a pivotal link between the stress and seepage fields. This determination holds substantial importance for geotechnical engineering, groundwater management, geophysics, and petroleum extraction5, 6.

The effective stress coefficient quantifies the influence of pore pressure on effective stress, defined as the ratio of the fluid-affected area to the total cross-sectional area7,8. In granular soils, the particle contact area is minimal, with the cross-section predominantly filled by fluid. Conversely, in cemented geotechnical bodies, the particle contact area is substantial, resulting in a smaller fluid-occupied cross-section and an effective stress coefficient of less than one7,8,9,11.

Initially proposed by Terzaghi12, he concept primarily described the relationship among total stress, inter-mineral skeleton stress, and pore fluid pressure in porous elastic media13. While it was predominantly applied to porous homogeneous saturated soils, its accuracy diminished when applied to rocky media. In 1941, M.A. Biot14 refined the classical effective stress principle by incorporating the influence of pore water pressure on rock deformation and introduced the effective stress coefficient, elucidating the impact of solid pore water pressure on effective stress. Subsequently, numerous scholars have extensively researched the effective stress coefficient, leading to a more comprehensive analysis of the effective stress law in geotechnical contexts14,15,17.

Dassanayake et al.18 employed the Modified Failure Envelope Method (MFEM) to determine the effective stress coefficients for both the peak and residual strengths of Kimachi sandstone. Lv et al.11 conducted triaxial tests by applying gas to a coal body without drainage, revealing that the effective stress coefficient of coal rock exhibits a bilinear relationship with volumetric stress and pore water pressure. Cheng19 et al. proposed a method for calculating the equivalent effective stress coefficient of single-fracture rocks, grounded in the principle of effective stress in porous media. This approach enables the analysis of the influence of fracture-filling-area ratio, circumferential stress, and pore pressure on the effective stress coefficient. Li20 et al. demonstrated that the effective stress coefficient provides a more precise calculation than traditional criteria. Yu21 et al. identified the effective stress coefficient αij as crucial for quantifying pore pressure effects on effective stress, noting its anisotropic nature and its close ties to permeability, damage evolution, and fissure extension, through true triaxial testing. Chen7 et al. argued that the conventional Terzaghi or Biot effective stress laws are unsuitable for fractured rocks and proposed the bulk modulus and equivalent strain methods to determine the effective stress coefficient for such rocks. Zhao et al.22 constructed a discrete fracture network for fractured rocks and analyzed it using the equivalent strain method. The study revealed that the effective stress coefficients of fractured rocks decrease with increasing normal and shear stiffness of the fractures, while they increase with the elastic modulus and Poisson’s ratio.

Under the combined influence of external stress and pore water pressure, rock deformation frequently transitions beyond the elastic stage, resulting in significant deviations in the effective stress coefficient when calculated using traditional pore elasticity theory, particularly for predicting peak rock strength. To address this limitation, we introduce a novel methodology for determining the effective stress coefficient, grounded in the established effective stress principle and the Mohr–Coulomb failure criterion. This approach integrates the mechanical behavior of rock under complex stress conditions, providing a more accurate representation of rock strength and deformation. The proposed method is rigorously validated through a series of water-force coupling experiments conducted on sandstone specimens under triaxial compression, which simulate realistic subsurface conditions. Furthermore, we conduct a comprehensive analysis of the effective stress coefficient, examining its relationship with the deformation and strength characteristics of rock across various stress states. The findings demonstrate that the effective stress coefficient is not a constant but varies with the stress path and the degree of rock deformation. This refined understanding offers critical insights for optimizing the design and implementation of well drilling and grouting programs, ensuring greater stability and efficiency in engineering applications. By bridging the gap between theoretical models and experimental observations, this study advances the field of rock mechanics and provides a robust framework for addressing challenges in geotechnical engineering.

Tests and methods

Rock samples preparation

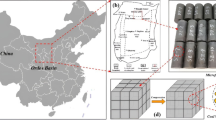
This study examines rock samples extracted from fine sandstone at a depth of 636.1 to 789.5 m in the skip main well of Hunan Baoshan Nonferrous Metals Mining Co. The sandstone in this region has remained naturally water-saturated over an extended period. To ensure specimen uniformity and test result reliability, all samples were extracted from the same rock slab and processed into standard cylindrical specimens measuring Ф50 mm × 100 mm (Fig. 1). Specimens exhibiting visible joints or fissures were excluded, and anomalous samples were further eliminated based on wave velocity tests to ensure consistency23, 24. Tests were conducted on three groups of specimens under varying pore water pressure conditions. The boiling method was employed to achieve water saturation, with specimens weighed every 2 h until the weight difference between consecutive measurements was less than 0.01 g, indicating saturation. The sandstone specimens exhibited a saturated water absorption rate of approximately 5.60%.

Fig. 1
figure 1

Specimen sampling points and rock specimens.

Full size image

The porosity of sandstone specimens was assessed using the AniMR-150 nuclear magnetic resonance (NMR) test system, yielding T2 spectral distributions for three representative samples. Based on the NMR relaxation mechanism, fluids within rock pores exhibit varying relaxation times, appearing at distinct positions on the T2 spectrum. By applying the conversion relationship between T2 values and sandstone pore sizes15,25,26, these T2 spectrum curves can be translated into pore size distribution curves, as shown in Fig. 2.

Fig. 2
figure 2

AniMR-150 nuclear magnetic resonance test system.

Full size image

As can be seen from Fig. 2, the pore size distribution of the sandstone is bimodal, corresponding to micropores and macropores, respectively. The contribution of large pores accounts for about 52.8%, while small and medium pores account for about 18.5% and 28.7%, respectively. The NMR test system found that the pore type of this sandstone specimen is tubular, with an average porosity of 9.17%. This indicates that: the sandstone used in this test is a highly porous rock with a well-developed large pore structure, and the basic information of the specimen is shown in Table 1.

Table 1 Basic physical and mechanical parameters of specimens.
Full size table

Test device and procedure

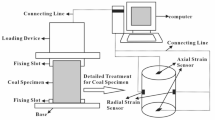
The triaxial compression test under hydraulic coupling was conducted using the MTS-815 rock mechanics test system at the Southern Coal Mining Key Laboratory, Hunan University of Science and Technology. This system is equipped with independent servo control systems for axial, peripheral and pore water pressures. The entire test envelope pressure was divided into three levels, 10, 20 and 30 MPa, respectively. In order to study the attenuation law of water pressure on the peak strength of rock, the water pressure was designed as 0%, 20%, 40%, 60% and 80% of the envelope pressure27. The specific steps of the test are as follows: (1) Install the rock specimens according to the requirements of the triaxial testing machine, and install the testing devices such as water pipe, circumferential strain transducer and axial strain transducer. (2) The loading rate was managed to achieve specific pressure values: axial stress was initially preloaded to 2 MPa at 0.05 MPa/s. Subsequently, perimeter and water pressures were sequentially applied to predetermined values at the same rate and held constant for 20 min. (3) After the circumferential pressure and the water pressure are constant, load the specimens in axial direction at a loading rate of 0.005 mm/s until the specimens are damaged and enter the residual stage.

Effective stress coefficients based on the Mohr–Coulomb criterion

The Mohr–Coulomb criterion showed that the peak strength of rock under a conventional triaxial stress state satisfied a linear relationship with confining pressure22:

$$\sigma_{P0} = \frac{1 + \sin \varphi }{{1 - \sin \varphi }}\sigma_{3} + \frac{{2c\,{\kern 1pt} \cos }}{1 - \sin \varphi }$$
(1)

where σ3 was the confining pressure; σp0 was the peak strength of rock when the pore water pressure was zero; c was cohesion; φ was the internal friction angle27. Order:

$$\frac{1 + \sin \varphi }{{1 - \sin \varphi }} = k$$
(2)
$$\frac{2c\cos \varphi }{{1 - \sin \varphi }} = d$$
(3)

The principal stress relationship of the Mohr–Coulomb criterion was shown in Fig. 4. When pore water pressure is zero, the expression of peak strength and confining pressure was as follows28:

$$\sigma_{p0} = k\sigma_{3} + d$$
(4)

where k and d were the slope and intercept of the curve in Fig. 3, respectively.

Fig. 3
figure 3

Principal stress relation of Mohr–Coulomb criterion.

Full size image

Cohesion c and internal friction angle φ can be expressed as29:

$$c = \frac{{d\left( {1 - \sin \varphi } \right)}}{2\cos \varphi }$$
(5)
$$\varphi = \arcsin \frac{k - 1}{{k + 1}}$$
(6)

When calculating the effective stress coefficient of the specimen by the Mohr–Coulomb criterion, the failure envelope was first constructed on the effective stress confining pressure plane without pore water pressure, and then the effective stress coefficient was solved on the failure envelope by the variable parameter of pore water pressure. Figure 4 shows the calculation diagram of the effective stress coefficient based on the Mohr–Coulomb criterion. Point A and point B (in Fig. 4) indicated the peak strength of the specimen under different confining pressures when the pore water pressure was zero. The effective confining pressure equaled the total confining pressure when the pore water pressure was zero. The effective confining pressure of points A and B could be stated as30:

$$\left\{ \begin{gathered} \sigma^{\prime}_{A3} = \sigma_{A3} \hfill \\ \sigma^{\prime}_{B3} = \sigma_{B3} \hfill \\ \end{gathered} \right.$$
(7)
Fig. 4
figure 4

Effective stress coefficient calculation diagram based on the Mohr–Coulomb criterion.

Full size image

When the pore water pressure was p, the peak strength of the specimen could be plotted on the principal stress-effective confining pressure plane. Moving p from right to left, α was increased from 0 (point C in Fig. 4) to 1 (point D in Fig. 4), and the crossing point E (as shown in Fig. 4) was generated on the failure envelope. And the effective stress coefficient α of the rock was shown by point E.

The effective stress coefficient could thus be written as30:

$$\sigma^{\prime}_{3} { = }\sigma_{3} - \alpha p$$
(8)

where σ3’was the effective confining pressure.

Therefore, the expression of peak strength and confining pressure of rock based on the Mohr–Coulomb criterion under hydraulic coupling was as follows:

$$\sigma_{p} = k(\sigma_{3} - \alpha p) + d$$
(9)

where σp was the peak strength of rock under hydraulic coupling.

Then the effective stress coefficient of rock could be derived by combining Eq. (4) and Eq. (9).

$$\alpha = \frac{{(1 - \frac{{\sigma_{P} }}{{\sigma_{P0} }})(k\sigma_{3} + d)}}{kp}$$
(10)

In particular, solving the effective stress coefficient based on the Mohr–Coulomb criterion requires that the test samples are all taken from the same parent rock. The same rock samples were taken from the same matrix with the same lithology, otherwise similar conclusions may not be reached.

The test data were organized, and the mechanical parameters of sandstone under hydraulic coupling were shown in Table 2. And the cohesive force of sandstone c = 19.00 MPa and the angle of internal friction φ = 17.22°. The curve in Fig. 3 has a slope k = 1.841 and an intercept d = 51.573.

Table 2 Mechanical parameters of sandstone under hydraulic coupling effect.
Full size table

Strength characteristic analysis of effective stress coefficient

The relationship between effective stress coefficient and peak strength attenuation coefficient

The stress–strain curve of a typical sandstone specimen under water-force coupling is schematically shown in Fig. 5. The stress–strain curves for the triaxial compression test progressed through five stages28,30: pore fracture compaction (OA), linear elastic (AB), stable crack development (BC), unstable crack development (CD), and post-peak (OA). The stress–strain curves of the samples were essentially the same under different confining pressures and pore water pressures. With the increase of axial displacement, the axial stress of the specimen increased to the peak value, and then rapidly dropped, demonstrating the characteristics of brittle failure31, 32.

Fig. 5
figure 5

Stress–strain curves of typical sandstone specimens under water—force coupling effect diagrams.

Full size image

Gaining the peak strength of sandstone under water-force coupling based on the stress–strain curves in Fig. 6 is shown in Table 2. Both confining pressure and pore water pressure had an impact on the peak strength of rock. The peak strength of rock under constant confining pressure decreases with pore water pressure.

Fig. 6
figure 6

Stress–strain curve of sandstone specimen under hydraulic coupling.

Full size image

Zhao et al.22,27 derived a strength decay equation normalized to the peak strength of rocks under hydraulic coupling. This was achieved by dividing the peak strength of sandstones under hydraulic coupling by their peak strength under peripheral pressure alone, utilizing the pore-perimeter ratio p/σ3 as a characteristic parameter.

$$\eta \,_{{\text{s}}} = \frac{\sigma \,p}{{\sigma \,p{\kern 1pt} 0}} = 1 - \omega_{s} \frac{p}{{\sigma_{3} }}$$
(11)

where ηs was the normalized peak strength of rock under hydraulic coupling, and ωs was the attenuation coefficient of peak strength.

Note that the attenuation coefficient of rock peak strength under hydraulic coupling was affected by confining pressure and pore water pressure. Table 2 showed the peak strength attenuation coefficient of sandstone under hydraulic coupling calculated by Eq. (11) with the obtained experimental data. The peak strength attenuation plot of sandstone specimens under hydraulic coupling was shown in Fig. 7.

Fig. 7
figure 7

Peak strength attenuation diagram of sandstone specimens under hydraulic coupling.

Full size image

The normalized peak strength ηs of rock under hydraulic coupling can be represented as19:

$$\eta_{s} { = }\frac{{\sigma_{P} }}{{\sigma_{P0} }} = \frac{{k(\sigma_{3} - \alpha p) + d}}{{k\sigma_{3} + d}} = 1 - \frac{\alpha kp}{{k\sigma_{3} + d}}$$
(12)

Combining with Eq. (10) and Eq. (11), the relationship between peak strength attenuation coefficient ωs and effective stress coefficient α was expressed as follows:

$$\alpha = \frac{{\omega_{s} (k\sigma_{3} + d)}}{{k\sigma_{3} }} = \frac{{\omega_{s} \sigma_{p0} }}{{k\sigma_{3} }}$$
(13)

The relationship between the peak strength attenuation coefficient and effective stress coefficient of sandstone samples was depicted in Fig. 8. The figure indicates a positive linear correlation between the peak strength attenuation coefficient of sandstone and the effective stress coefficient, with a fitting coefficient of 0.82. Consequently, the peak strength attenuation coefficient can reliably estimate the effective stress coefficient under hydraulic coupling.

Fig. 8
figure 8

Relationship between peak strength attenuation coefficient and effective stress coefficient of sandstone.

Full size image

Analysis of strength results

Table 2 listed the effective stress coefficient of saturated sandstone under pore water pressure, confining pressure, and axial pressure33. Multiple linear regression analysis utilizing the least square approach was used to descript the relationship. The fitting correlation coefficient was 0.986 and the regression equation was obtained and publicized as follows:

$$\alpha = a_{1} + a_{2} \Theta + a_{3} \Theta p + a_{4} p$$
(14)

where a1, a2, a3 and a4 were fitting parameters. a1 = 1.430, a2 = −0.007, a3 = −8.661 × 10–5 and a4 = 0.004.

The volume stress Θ in Eq. (14) was calculated as follows:

$$\Theta = \sigma_{1} + 2\sigma_{3}$$
(15)

Comparison of the fitting coefficients in Eq. (14) reveals that coefficients a2 and a4 differ by two orders of magnitude from a3. The analysis indicates that a3 minimally influences the effective stress coefficient α. When a3 is omitted, α can be modeled as a bilinear function of pore water pressure p and volumetric stress Θ. The signs of a2, and a4 suggest that α is positively correlated with p and negatively correlated with Θ.

Fig. 9 shows the relationship between pore water pressure and effective stress coefficient. The figure shows that the effective stress coefficient of sandstone increases with pore water pressure under constant confining pressure. Under different confining pressures, the increasing amplitude and rate of the effective stress coefficient with pore water pressure were different. At confining pressures of 10 MPa, 20 MPa, and 30 MPa, the slopes α-p were 0.030, 0.007 and 0.010, respectively. The maximum increasing rate of the effective stress coefficient occurred at low confining pressure (10 MPa), and as confining pressure increased, the increasing rate of effective stress coefficient decreases. The test revealed that pore water pressure intensified the expansion and deformation of pores and cracks in saturated sandstone, increasing porosity and the pore water pressure area while decreasing effective stress. However, once pore water pressure reached a certain threshold, neither the degree of rock fracture opening nor the effective stress coefficient showed significant improvement.

Fig. 9
figure 9

Relationship between pore water pressure and effective stress coefficient.

Full size image

Fig. 10 shows the relationship between volume stress and effective stress coefficient. The effective stress coefficient of sandstone diminishes with increasing volumetric stress, with its amplitude and rate of decrease varying according to confining pressures. As volumetric stress rises, fracture opening, pore compaction, and fracture closure areas in sandstone all decrease. Consequently, the closure of cracks reduces sandstone permeability, thereby diminishing the influence of pore water pressure and the effective stress coefficient.

Fig. 10
figure 10

Relationship between volume stress and effective stress coefficient.

Full size image

Deformation characteristics of effective stress coefficient

The relationship between effective stress coefficient, elastic modulus, and Poisson’s ratio

To study the deformation features of rock under hydraulic coupling, the elastic modulus E50 and Poisson’s ratio μ of sandstone samples at 50% peak strength were calculated27,34:

$$E_{50} = \frac{{\sigma_{50} - 2\mu \sigma_{3} }}{{\varepsilon_{1} }}$$
(16)
$$\mu = \frac{{B\sigma_{50} - \sigma_{3} }}{{\left( {2B - 1} \right)\sigma_{3} - \sigma_{50} }}$$
(17)
$$B = \frac{{\varepsilon_{3} }}{{\varepsilon_{1} }}$$
(18)

where σ50 was the axial stress at 50% peak strength; σ3 was the confining pressure at 50% peak strength; ε1 was the axial strain at 50% peak strength, and ε3 was the circumferential strain at 50% peak strength.

The elastic modulus and Poisson’s ratio of sandstone samples were shown in Table 2. Figure 11 explored the relationship between the effective stress coefficient and elastic modulus and Poisson’s ratio. Generally, the elastic modulus of sandstone under hydraulic coupling is inversely related to the effective stress coefficient, while Poisson’s ratio shows a positive correlation.

Fig. 11
figure 11

The relationship between effective stress coefficient and elastic modulus and Poisson’s ratio.

Full size image

The relationship between effective stress coefficient and porosity

The porosity of rock changed with confining pressure and pore water pressure under hydraulic-mechanical coupling. The porosity under effective stress could be calculated by the following formula15,35:

$$n = n_{o} e^{{[ - B(\sigma_{3}^{\prime } - P_{0} )]}}$$
(19)

where n0 was the initial porosity of sandstone, n was the porosity of sandstone under effective stress, and P0 was the standard atmospheric pressure, B was the rock compression coefficient of sandstone.

$$B = \frac{3 - (1 - 2u)}{{E_{50} }}$$
(20)

The following formula for porosity and effective stress coefficient was obtained by combining Eq. (7) and (18)36:

$$n = n_{o} e^{{\left[ { - B\left( {\sigma_{3} - \alpha p - P_{0} } \right)} \right]}}$$
(21)

Equation (19) illustrates that the porosity of rock under hydro-mechanical coupling was positively correlated with the effective stress coefficient. Additional investigation was required to explore how porosity affected the effective stress coefficient under hydraulic coupling37,38.

The effective stress analysis diagram for rock particles was shown in Fig. 12. During compression under water-force coupling, the pores within the solid skeletons experienced the combined effects of axial stress, confining pressure, and pore water pressure, leading to deformation of rock and soil particles. Two deformation mechanisms were identified under hydraulic coupling. The first, known as body deformation, involved the elastic and recoverable deformation of solid skeleton particles. The second was an irreversible plastic deformation, termed structural deformation39. A schematic representation of particle deformation of rock and soil under hydraulic coupling was shown in Fig. 13. The deformation of sandstone specimens under the action of hydraulic coupling was primarily driven by the deformation of particle structure, resulting in the change of porosity.

Fig. 12
figure 12

Effective stress analysis diagram of rock particles.

Full size image
Fig. 13
figure 13

Schematic diagram of particle deformation of rock and soil under hydraulic coupling.

Full size image

Discussion

Analysis of the applicability of the effective stress factor

The effective stress coefficient is traditionally calculated using poroelastic theory and volumetric strain14. However, natural rocks are anisotropic and heterogeneous, with rough pore boundaries. Only under ideal conditions, when a material is isotropic and homogeneous, does the coefficient from volumetric strain match the actual effective stress coefficient40,41. Research on the coefficient at peak strength is limited. We propose a novel method to determine the effective stress coefficient, relying on the effective stress principle and the Mohr–Coulomb failure criterion, deriving the coefficient from strength rather than strain theory. When applying the Mohr–Coulomb criterion, all test samples must originate from the same parent rock and rock type to ensure consistency. The fitting parameters of the effective stress coefficient differ across rock types and petrological characteristics. Unlike previous methods requiring high-precision instruments for strain measurement, our approach based on Mohr–Coulomb strength theory is simpler7,8, more convenient, and less reliant on specialized equipment.

Model validation

The effective stress coefficient of volumetric strain, denoted as αBiot, is a critical parameter in verifying the feasibility of the proposed model. The calculation formula for αBiot is as follows7:

$$\alpha_{{{\text{Biot}}}} = 1 - \frac{{K_{0} }}{{K_{S} }}$$
(22)

where K0 represents the equivalent bulk modulus of the porous medium, and KS denotes the bulk modulus of the solid grains. This formulation allows for a comparative analysis to assess the validity of the classical volumetric strain approach within the context of the model.

Figure 14 illustrates the correlation between effective confining pressure and the α value, where αBiot represents the effective stress coefficient derived in this study using the effective stress principle and the Mohr–Coulomb failure criterion.

Fig. 14
figure 14

Relationship between effective surrounding pressure and α-value.

Full size image

Figure 14 illustrates that, with few exceptions, αBiot consistently exceeds αMC. αBiot assumes a smooth interface, while in rough fractured rock masses, α is comparatively lower, highlighting a more pronounced weakening effect of pore-water pressure on rock mass strength. This finding aligns with Chen et al.’s7 conclusions, suggesting that αMC better represents the actual stress state of rocks. The high fitting coefficient of σ’3—α underscores the model’s strong applicability.

Conclusions

This paper introduces a novel calculation method for the effective stress coefficient, grounded in the effective stress principle and the Mohr–Coulomb criterion. Utilizing triaxial compression tests under hydro-mechanical coupling, the study verifies the correlation between the calculated effective stress coefficient and the strength and deformation characteristics of rock masses. The primary conclusions are as follows:

(1) The peak strength and volumetric stress of sandstone rise with increasing confining pressure. For instance, when the confining pressure increases from 10 to 30 MPa at p = 0, the peak strength and volumetric strain increase from 68.71 MPa and 88.71 MPa to 105.54 MPa and 165.54 MPa, respectively, representing increases of 53.61% and 86.6%. Conversely, under a constant confining pressure of σ3 = 20 MPa, both parameters decrease with rising pore water pressure, dropping from 90.96 MPa and 130.96 MPa to 69.15 MPa and 109.15 MPa, corresponding to decreases of 23.98% and 16.65%.

(2) The relationship between the strength characteristics of sandstone and the effective stress coefficient was determined using a water-force coupling test. The peak strength attenuation coefficient of sandstone exhibits a positive linear correlation with the effective stress coefficient, with a correlation coefficient of 0.82. In contrast, the relationship between pore water pressure, volumetric stress, and the effective stress coefficient is bilinear. It is positively correlated with pore water pressure and negatively correlated with volumetric stress, achieving a correlation coefficient of 0.986 in the analysis.

(3) The study of sandstone’s deformation characteristics and effective stress coefficient reveals an exponential positive correlation between porosity and the effective stress coefficient under hydraulic coupling. At constant circumferential pressure, the effective stress coefficient shows a positive linear correlation with Poisson’s ratio and a negative linear correlation with the deformation modulus.

This test was based on the ideal indoor condition, while the coupled field conditions faced by the aquifer rock body in the real engineering are more complicated, and the loads suffered during the excavation construction process change dynamically. For this reason, in the future research, it is necessary to consider multi-field coupling, different loading paths, dynamic loading conditions and microscopic observation means to study the change characteristics of the effective stress coefficient of the rock.