A hybrid security protocol based on honey encryption and hyperchaotic systems for improving security in internet of things

Abstract

Communication security in the internet of things (IoT) is essential to prevent devices and data from being vulnerable to cyber-attacks and possible abuses. In IoT systems, some sensors transmit critical data, so maintaining the security of these data and preventing their unauthorized interpretation is of great importance. For this reason, it is necessary to use advanced and complex encryption methods. The proposed research method consists of two phases: in the first phase, we use a hyperchaotic system to generate a complex sequence of pseudo-random numbers, and then by applying this system, we covertly replace the data. After that, we use the honey encryption technique to increase the security and obfuscation of the information, which helps us to improve the security of the data and prevent unauthorized interpretation. The proposed method has several key advantages, including the enhanced security that results from the combination of honey cryptography and chaotic systems, and this combination provides higher security than previous methods. In addition, the flexibility of the proposed protocol ensures its adaptability in various IoT applications, especially in cases where data security is required. These advantages help us to improve the security and efficiency of IoT systems in various situations. The proposed method is able to reduce the energy consumption caused by calculations and reduce the delay to the values of 21.8 and 0.34, respectively. Also, in terms of security, this method has been able to improve the security of information, which has achieved values of 1.041 and 0.49, respectively, using the Mean Squared Error and Bit Error Ratio criteria.

Introduction

The internet of things (IoT) has been a prominent topic in research and practical application in recent years. The IoT is a framework that encompasses commonplace items equipped to perceive and connect with other devices over the Internet¹. With the widespread availability of broadband Internet and decreased connectivity costs, an increasing number of devices and sensors are being connected². Such factors are fostering the development of IoT. The IoT entails significant complications, as we aim to access everything from any location globally³. The advanced electronics and sensors are integrated into the physical objects around us, each relaying significant data. The process of transmitting substantial data commences with the devices, which must establish secure communication with the IoT platform. This platform consolidates data from numerous devices and using analytics to disseminate the most valuable information to the apps. The IoT is advancing traditional internet, sensor networks, and mobile networks by ensuring that all devices are interconnected via the internet. It is essential to evaluate the challenges pertaining to confidentiality, data integrity, and authenticity that may arise due to security and privacy concerns⁴. Security, which includes freshness, availability, authentication, data integrity, and data confidentiality is one of the most difficult problems in IoT, much like in earlier network structures. Critical restrictions like scalability, dynamicity, and dependability must be taken into consideration in any changed structure of the internet of things and its fundamental protocols. Furthermore, before being transmitted, the data has to be encrypted using the proper security protocols among connected gadgets and the cloud⁵.

Over time, several cryptographic techniques have been employed to guarantee the security of data while it is being transmitted. The methods used to organize, create, and disseminate the secret keys dictated the cryptographic algorithms’ effectiveness. Even though the cryptographic procedure is both theoretically and practically optimal, poorly handled secret keys render it unusable^6,7. Asymmetric and symmetrical methods are two categories into which the different cryptographic algorithms suggested for IoT can be divided. Symmetric methods employ the same key for both encoding and decoding. In fact, the security of the key interchange among the sender and the recipient determines how strong the symmetric algorithms are. The public and private keys are two distinct keys that are provided by the asymmetric methods. A private key will therefore be safe because it is never transmitted over the network. The recipient receives the public key over a computer network. The sender will use the recipient’s public key to encode the plaintext and then transmit the ciphertext to the recipient across the network. The attacker cannot read the hashed or scrambled data even if he knows the public key since he is unaware of the secret key. The recipient will decrypt the encrypted content using his private key. Compared to symmetric algorithms, asymmetric algorithms use more resources and are more complicated to set up^8,9.

IoT applications are finding greater importance in daily life, including healthcare, smart grids, smart homes, and smart cities. In addition, these platforms do require very strong security measures for protecting user data against hackers, attacks, and vulnerabilities. The previous methods in the field of cryptography are faced with shortcomings, including limitations in flexibility and generality of application. These models usually focus on the encryption of one type of data, which reduces their generality. Also, the use of complex techniques makes the algorithms not applicable on systems with limited computing resources. Our proposed method, by combining hyperchaotic permutations and honey encryption, aims to overcome these limitations and has several innovative aspects. Our key contributions are the novel combination of a spatiotemporal chaotic system with Honey Encryption for enhanced security and efficiency in IoT environments, the optimized implementation of this hybrid approach for resource-constrained devices, and the thorough evaluation of its performance and security properties. Unlike previous approaches that use simpler chaotic maps, our system offers a larger key space and more complex dynamics, making it more resistant to cryptanalysis. Furthermore, our optimized Honey Encryption scheme reduces computational overhead compared to traditional implementations. This paper’s main contributions are:

• In this paper, a new approach to increase security in the IoT is discussed.

• A theoretical framework for understanding the proposed protocol and its basic principles is presented, which is designed based on the modeling of a new hyperchaotic system.

• Combining hyperchaotic with honey encryption can improve the performance of encryption algorithms in the IoT.

The rest of this paper is arranged as follows: "Related works" section analyses works similar to the present one. "Proposed research" section presents the proposed approach, while "Results and discussion" section depicts the results of the study and "Conclusion" section outlines the conclusions.

Related works

This section reviews the papers published in recent years in this field. Mhaibes et al.¹⁰ reported that the Tiny Encryption Algorithm (TEA) is fast and efficient but suffers from severe key attacks. In this respect, a variant of TEA was proposed; it included an extra key generation part based on Linear Feedback Shift Registers that outperformed simple TEA in three sets of tests: key sensitivity analysis, avalanche effect, and completeness.

Masadeh¹¹ proposed a novel cryptographic algorithm for the security of IoT devices, which includes an embedded key cryptosystem. This algorithm segments messages in blocks, encrypts and decrypts them using a key. It utilizes two tables for character set generation and key element generation.

Yasmin and Gupta¹² proposed an energy-efficient file encryption scheme over IoT applications by utilizing a modified lightweight block cipher, called GIFT, to improve the trust and security of e-commerce.

Hedayati and Mostafavi¹³ proposed one lightweight algorithm for data compression in order to encrypt images on IoT devices; this algorithm reduced computational complexity and volume of data, power consumption, and packet rate compared with previous algorithms.

Jammula et al.¹⁴ proposed Lightweight Cryptography-Attribute-based Encryption (LWC-ABE), representing a lightweight cryptography scheme to enhance security in IoT devices. In the scheme considered here, many aspects are involved: a trusted authority, a reduced time for encryption and decryption, high expressiveness, updates of an access policy, and large domains of an attribute.

Tiwari et al.¹⁵ have presented a secure encryption algorithm that uses permutation and diffusion structures, pseudo-random sequences, a key stream for sensitive communication and transmission of data.

In order to provide limited memory consumption, quick encryption, and resilience against various types of assaults. Kifouche et al.¹⁶ suggested a lightweight and effective chaos-based encryption system for safe IoT exchanges of information. This system merged the advantages of a chaos-based arbitrarily generator with confusion and diffusion blocks.

Lekha et al.¹⁷ proposed the Modified Optimal Advanced Encryption Standard-Chaotic Map (MOAES-CM) as the security solution for IoT-cloud environments related to healthcare applications. It provides all the features that are necessary for data storage and retrieval operations with low computational complexity and high performance.

Pamarthi and Narmadha¹⁸ proposed a chaotic cryptography-based model for preserving MANET IoT application privacy with the SA-SFO algorithm for optimizing key generation. With Self-Adaptive Sailfish Optimization, it will ensure efficient performance in various analyses.

developed an efficient scheduling mechanism by incorporating the logistic map algorithm with a 3-dimensional substitution-box to enhance security on IoT devices such as smart home appliances, using key generation delay.

Trujillo-Toledo et al.¹⁹ proposed a new chaotic map-based medical cryptosystem which ensures security and secrecy of transmitted medical images from IoT devices in healthcare by resisting attacks and suitability for edge computing devices.

Clemente-Lopez et al.²⁰ proposed a chaos-based lightweight encryption scheme for IoT healthcare systems focused on wearable devices, with the purpose of increasing security while guaranteeing real-time data flow in spite of such necessary lightweight encryption methods.

Rahman et al.²¹ developed an efficient scheduling mechanism by incorporating the logistic map algorithm with a 3-dimensional substitution-box to enhance security on IoT devices such as smart home appliances, using key generation delay.

Zhang and Lei Zhang²² proposed a chaotic gene fusion-based multi-image encryption algorithm for big data, aiming at enhancing the security and efficiency. Chaotic sequences for pixel position and chaotic images for pixel cyclic shifts were used in the algorithm, then integrated into gene fusion for final encryption.

Alexan et al.²³ presented a color image encryption algorithm that utilized Shannon’s security principles by combining KAA maps with chaotic maps. The algorithm employed bit confusion and diffusion, utilizing two encryption keys from different maps, and was robust, efficient, and passed all NIST SP 800 suite tests.

Hosny et al.²⁴ proposed a color image encryption with block scrambling and chaos, where the plain image decomposed into three channels and blocks was finally transformed into a nonrecognizable image without losing the information obtained from the experimental results.

Wen et al.²⁵ researched the Color Image Encryption Algorithm based on bit-level and Improved One-dimensional Chaotic Map (CIEA-IOCM) color image encryption algorithm and pointed out that, though claimed to be secure against some conventional attacks, it had the defect that it could be breached under a chosen plaintext attack since there existed equivalent keys for the bitwise permutation and diffusion operations. Table 1 summarizes the reviewed literature.

Table 1 Summary of the studied works.

Multiple research gaps exist within existing IoT security solutions according to the reviewed literature. The current security solutions operate with different levels of protection and speed but they concentrate their efforts on particular data categories (such as medical or image data) and particular application domains (for instance e-commerce or healthcare). The specialized nature of these methods makes them ineffective for the multiplying communication formats which occur in common IoT platforms. The utilization of chaotic systems in certain methods fails to maximize the security benefits of high-dimensional or spatiotemporal chaotic maps because these maps provide larger key spaces and complex dynamics that could potentially create weaker security. The security of systems suffers due to insufficient attention paid to key generation and management processes which represent essential components of total security. Some research investigations focus on weightless cryptography yet fail to achieve proper balance between processing speeds for attacks and effective adversarial defense.

The proposed hybrid security protocol bridges these security gaps through its flexible and efficient approach to protecting IoT data at a general level. Our method generates a larger key space with complex dynamic behavior when spatiotemporal hyperchaotic systems and honey encryption are combined into a single framework thus creating better resilience against cryptanalytic attacks compared to chaotic map-based methodologies. Honey encryption creates an additional covering of secrecy which prevents attackers from separating actual information from simulated data. The designed security protocol considers IoT device limitations and uses simple computational operations for common IoT hardware. Our proposed design provides an advanced security solution for IoT environments because its emphasis on performance speed and its improved security protective measures generate an essential addition to the IoT security domain.

Proposed research

In this section, a new hybrid protocol for secure data encryption in the IoT network will be presented, combining chaotic permutation and encryption. The proposed method utilizes chaotic permutation for shuffling and hashing the data, employs honey encryption for altering values and encoding information, and uses a symmetric key as input for the honey encryption algorithm. Following this, after presenting the assumptions and the system model considered for this research, we will introduce the proposed method.

Assumptions and system model

In this section, we will detail the specifications of the system model on which the proposed compression method is based. We consider a network structured around the IoT, consisting of several wireless nodes. In this network, all wireless nodes can act as sources or data senders. Each piece of data generated by a wireless node is encrypted using the proposed algorithm and sent to the intended destination.

In this network, the wireless nodes are distributed at the network level within a limited area. The deployment of network nodes at the network level is unrestricted, and the position of each node in the coverage area is considered random. Due to the use of uniform random distribution for the deployment of nodes, it is assumed that the density of nodes is consistent across different points in the network.

Each node at the network level has a buffer memory with a capacity of at least one data packet. In the assumed network, all wireless nodes are assumed to have the same initial energy and maximum radio range.

In the proposed method, the model presented in²⁶ will be used to calculate the energy consumption for data exchange. This model was selected because it is a widely used and well-established model specifically designed for wireless sensor networks, which are a representative component of IoT systems. This model considers both the energy consumed by the radio electronics and the energy required for signal amplification, providing a realistic estimate of energy consumption in wireless communication. While more complex models exist, this simplified model provides a reasonable approximation for our analysis and allows us to focus on the relative energy consumption of different encryption methods. According to this model, sending N bits of information among two nodes requires the following amount of energy:

$$E_{TX} \left( {N,d} \right) = \left\{ {\begin{array}{*{20}l} {N \times \left( {E_{elec} + E_{amp} .d^{2} } \right)} & { if\;d \le \sqrt {\frac{{E_{fs} }}{{E_{amp} }}} } \\ {N \times \left( {E_{elec} + E_{amp} .d^{4} } \right)} & {otherwise} \\ \end{array} } \right.$$

(1)

${E}_{elec}$ is the amount of energy use per bit in both the transmitting and reception circuits, ${E}_{amp}$ represents the power usage per bit in the RF amplifiers, and $d$ is the total distance among the two terminals in the equation above. Additionally, the transmitter gain variable in free space is represented by ${E}_{fs}$. The following formula is used to determine how much energy is needed to get N bits of data:

$${E}_{RX}\left(N,d\right)=N\times {E}_{elec}$$

(2)

According to this energy model, ${E}_{elec}=50\frac{nJ}{bit}$ and ${E}_{amp}=100\frac{pJ}{bit\times {m}^{2}}$.

Chaotic permutation used in the proposed algorithm

A hyperchaotic mechanism is one that exhibits chaotic behavior and is characterized by a minimum of two positive Lyapunov exponents. This mechanism indicated sensitivity yo initial conditions along multiple dimensions. The least amount of dimensions needed for a continuous hyperchaotic structure is four, taking into account both a null (zero) negative exponent across the flow and at least one negative exponent to guarantee the system’s boundedness (preventing trajectories from escaping to infinity). One of the most well-studied and canonical models of discontinuous chaotic dynamics is the 2D Henon’s map, which converts a data point like $\left({x}_{n},{y}_{n}\right)$ to a new data point:

$$\left\{\begin{array}{l}{x}_{n+1}=1-\alpha {x}_{n}^{2}+{y}_{n}\\ {y}_{n+1}=\beta {x}_{n}\end{array}\right.$$

(3)

The two control variables $\alpha$ and $\beta$ determine the hyperchaotic pattern and dynamic behavior of this map. The literature of chaos theory demonstrates that the Henon map produces chaotic results when specific parameter ranges are used particularly when α equals 1.4 and β equals 0.3. The system contains multiple extensive areas which display chaotic behavior. The system produces chaotic or complex dynamics such as periodic orbits and quasi-periodic behavior when the values of these two variables are adjusted. Our study aims to develop hyperchaotic-like behavior which can be used for cryptographic applications. In Fig. 1, the phase space portrait illustrating the attractor of the chaos map resulting from Eq. (3) is depicted according to the value ranges of the two variables $\alpha$ and $\beta$, explored in this study. This figure assumes a starting value of ${x}_{0}=0.1$ and considers the range of modifications of the two variables, α and β, as $1\le \alpha \le 2$ and $1.5\le \beta \le 2$.

Fig. 1

Structure of the chaotic map attractor derived from Eq. (3) based on the values of the keys $\alpha$ and $\beta$.

Figure 1 together with numerous studies in the literature confirms that the mapping defined through Eq. (3) demonstrates chaotic behavior in certain parameter domains, exhibiting complex, chaotic dynamics within specific parameter regions. The parameter combination of [1.55, 2.0] for the variables α and β produces highly sensitive dynamic behavior suitable for cryptographic applications based on visual observations in Fig. 1 and empirical verification in Fig. 4. The chosen parameter range exists to produce robust chaotic behavior with initial condition and parameter sensitivity properties needed for encryption pseudorandom sequence generation.

The direct application of conventional Henon map encounters two main restrictions in encryption usage: It possesses a restricted key parameter domain controlled by α and β values. The system shows sensitivity but some particular parameter values with specific initial settings can produce brief periodic patterns along with less intricate system responses. The key sensitivity setting to ${10}^{-10}$ does not eliminate the possibility of two keys producing equivalent sequences during limited periods of time.

The limitations of the Henon map can be overcome through space–time-based solutions which maintain its beneficial chaotic properties. We chose the Henon map for base local mapping because it demonstrates well-known chaos while requiring basic arithmetic operations and serves commonly as a benchmark in chaos-based cryptography research. The Henon map maintains both a simple implementation for resource-limited IoT systems and strong sensitivity to initial states and parameter alterations (Fig. 4 shows this later).

The Coupled Map Lattice (CML) serves as our method to boost complexity while expanding available key choices. CML is frequently employed as a powerful theoretical framework for examining dynamics in space and time chaotic structures because it simulates a system that changes with discrete space and positions that has sequential states where neighboring sites influence each other. The following formula can be used to represent a bidirectional CML network²⁷:

$$\left\{\begin{array}{l}{x}_{n+1}=\left(1-\varepsilon \right)f\left({x}_{n}\left(i\right)\right)+\frac{\varepsilon }{2}\left\{f\left({x}_{n}\left(i-1\right)\right)+f\left({x}_{n}\left(i+1\right)\right)\right\}\\ f\left(x\right)=\mu x\left(1-x\right) \end{array}\right.$$

(4)

where, i is the space index, n is the time index, and $\varepsilon$ is a coupling constant that lies within the range (0,1) and based on that, we can determine the influence between neighbors. Additionally, $3.57\le \mu \le 4, 0<x<1 , 0<f\left(x\right)<1$ specifies the range of feasible values in Eq. (4). Instead of the logistic map, Eq. (3) can be employed as the local chaotic map in Eq. (4) in order to profit from its inherent two-dimensional dynamics and specific chaotic properties. Therefore, a combined space and time hyperchaotic model is obtained in the following equation:

$${x}_{n+1}=\left(1-\varepsilon \right)f\left({x}_{n}\left(i\right)\right)+\frac{\varepsilon }{2}\left\{f\left({x}_{n}\left(i-1\right)\right)+f\left({x}_{n}\left(i+1\right)\right)\right\},$$

(5)

$$f\left({x}_{n}\right)=1-\alpha {x}_{n}^{2}+{y}_{n}$$

$${y}_{n}=\beta {x}_{n-1}$$

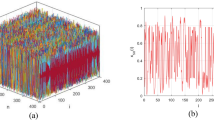
The nonlinear chaos function is represented by $f(x)$ in the formula given above. The proposed spatiotemporal chaotic system (Eq. 5) offers several theoretical and practical advantages over the basic Henon map. The system achieves substantial effective dimensionality growth through the combination of spatial coupling parameter ($\epsilon$) with state observations across different lattice sites (i). The theoretical connection between lattice sites through spatial coupling enables advanced spatiotemporal behavior with hyperchaos potential (multiple positive Lyapunov exponents) that shields information from analysis approaches. The system enlarges its key space beyond what traditional 2D maps can provide which results in better security. The coupled map lattice structure generates complex unpredictable dynamics that enhances security against brute-force attacks, which become computationally infeasible. The expanded key space resists brute-force attacks because they become impractical for computers to execute. Figure 2 illustrates the rich variety of spatiotemporal patterns arising from the bidirectional chaotic interactions in the system that are employed in the suggested technique for encrypting sensitive data.

Fig. 2

variety of bidirectional chaotic changes in the introduced CML-Henon model.

As shown in Fig. 2, the proposed chaotic system can exhibit chaotic behavior in both spatial and temporal dimensions. The CML structure with its implemented Henon map inside the selected parameter range resolves key space and predictability weaknesses to deliver stronger encryption capabilities. In Fig. 3a and b, the range of variations of the nonlinear chaotic sequence for changes in the keys $\alpha$ and $\beta$ is displayed, respectively, demonstrating that the system maintains complex dynamics across the selected parameter ranges.

Fig. 3

Range of variations of the nonlinear chaotic sequence for changes in (a) key $\alpha$ and (b) key $\beta$.

As shown in Fig. 3a and b, with variations in any of the keys of the nonlinear chaotic sequence, the entire range from zero to one is well covered by the output values. This behavior suggests the strong mixing properties of the CML-Henon model. These figures illustrate that these sequences exhibit chaotic behavior for all of their key values, making them suitable options for use in permutation and data scrambling. In addition to the range of variations, a suitable chaotic permutation should be sensitive to the input key. This means that changes in the key should produce different sequences. This feature for the nonlinear chaotic sequence is displayed in Fig. 4.

Fig. 4

Different sequences generated for various key values in the nonlinear chaotic sequence.

In Fig. 4, the key values for each sequence are displayed above the graph. In all these graphs, the first 100 terms of the sequence are shown for the selected key values. To test the sensitivity of the keys in the nonlinear chaotic sequence, the key value in Fig. 4c is set to $\alpha =1.56$. Then, in Fig. 4d, the key value is changed to $\alpha =1.560000000001$. As can be seen, the two generated sequences are different, and consequently, the proposed nonlinear chaotic sequence can be suitable for permutation and scrambling of confidential data due to its high sensitivity.

Honey encryption algorithm in the proposed method

In the proposed method, we use a honey encryption-based algorithm²⁸ to enhance the security of data encryption. In this algorithm, we consider the message space as the set M = {0,1,…,X}. The set M can include all possible values for a message exchanged over the IoT network. The input to the proposed honey encryption algorithm is the data scrambled by the chaotic sequence. At the beginning, we map all the values of set M to a space S. The space S includes the set of all binary permutations of n bits, such that each member of space M can have multiple values in space S. In other words, each member of M is assigned a range from within the space S. To this end, the number of bits in set S must be large enough. The proposed method considers $n>{2}^{X}$, so for each member of M, we will have at least one member in space S and at most ${\text{log}}_{2}\left|M\right|$ members. To determine the number of members to be assigned in S to each member of M, we use the probability of the presence of members of M in the content of the exchanged data. Therefore, if the value m_i exists in the content of exchanged messages in the network with probability ${p}_{i}=\frac{n}{\left|M\right|}$ where n is the number of occurrences of value m_i in the messages, a certain number $\left\lceil {n \times \frac{{\left| S \right|}}{{\left| M \right|}}} \right\rceil$ of members of S can be assigned to the value m_i. This condition is illustrated in Fig. 5.

Fig. 5

Assigning space S to members of M in honey encryption.

According to Fig. 5, a number of members of S have been assigned to each member of set M. To encrypt each data value, we first search for the value in space M and then randomly select one of the members of S assigned to the current value. The extracted value in S is then XORed with a pre-distributed symmetric key. The resulting value is the modified data obtained using honey encryption and the symmetric key. It is worth noting that the key used in the honey encryption algorithm is the same size as the elements of space S (equal to n). Symmetric key algorithms are a class of algorithms for encryption that use similar cryptographic keys for both encrypting plaintext and decrypting the ciphertext. The keys may be identical or there may be a simple relationship between the two keys. The key, in practice, represents a shared secret among two or more parties that can be used to safeguard private information. In symmetric key encryption, either stream or block ciphers can be used. In stream cipher encryption, one digit (usually a bit) of a message is encrypted at a time. In block cipher encryption, a number of bits are encrypted as a single unit. The algorithm approved by NIST in December 2001 was confirmed by the Advanced Encryption Standard (AES), using 128-bit blocks. The proposed method also utilizes block encryption with AES using blocks of length 128.

AES acts on a 4 × 4 matrix of bytes, called the state; versions of Rijndael with a block size greater than 128 bits have more columns in the state. Most of the transformations in AES are done in a specific finite field. The size of the key used in AES defines the number of rounds of transformations, which involves changing the input, known as plaintext into the final output or ciphertext. The number of rounds is defined as follows:

• 10 rounds for 128-bit keys.

• 12 rounds for 192-bit keys.

• 14 rounds for 256-bit keys.

The encryption key determines one of the multiple processing steps in every cycle. The same encryption key is employed to convert the ciphertext again to the plaintext through a series of inverted cycles. The following are the steps in this algorithm.

The mentioned algorithm is produced in 3 structures and the minimum string length for the key of this algorithm is 128 bits. In the first stage, there is an XOR operation. After this stage, there are 10 additional stages, and finally, the ciphertext is produced. But how is the key state structured in this layer? The key is entered into the round at the very beginning and generates new keys for each of the stages using the Sub Key generation module. After the first XOR operation, the plaintext enters 10 stages of operations as described below:

In each stage, 4 operations are performed. First stage is Substitution. In the second stage, Transposition is performed. In the third stage, Substitution is performed again, and lastly, an XOR operation is carried out on the 128-bit string. It can be observed that the Sub Key developed for every stage was fed into the cycle in the fourth stage. Assuming the assumptions and notions, the next paragraphs will describe the different stages of encryption for information based on the proposed approach.

Data encryption steps in the proposed algorithm

The proposed algorithm consists of two main operations: scrambling and diffusion. In the scrambling stage, the sequence of confidential data values is mixed using a chaotic permutation sequence generated by the permutation. In the next step, the diffusion operation is performed using honey encryption, and the scrambled data values are altered. After completing these steps, the encrypted data for transmission will be obtained. We will explain these steps further. Without reducing the generality of the proposed method, we assume that the data to be encrypted consists of ASCII characters. The following steps describe the necessary stages for encrypting a given message using the proposed method:

Step 1: Convert the content of the message into a one-dimensional array denoted as $P=\left\{{p}_{1},{p}_{2},\dots ,{p}_{X}\right\}$. In this vector, X indicates the length of the message, and p_i is the ASCII code corresponding to the i-th character in the message.

Step 2: Perform the initial diffusion operation using Eq. (6):

$$q_{i} = \left\{ {\begin{array}{*{20}l} {p_{1} \oplus p_{X} ,} & {if\;i = 1} \\ {p_{{i - 1}} \oplus q_{{i - 1}} ,} & {if\;i \in \left\{ {{\text{2,3}}, \ldots ,X - 1} \right\}} \\ \end{array} } \right.$$

(6)

In the above equation, X is the length of the message, and the operator $\oplus$ indicates the bitwise XOR operation. The result of this operation will be the set $Q=\left\{{{q}^{\prime}}_{1},{{q}^{\prime}}_{2},\dots ,{{q}^{\prime}}_{X}\right\}$.

Step 3: Calculate the sum of the values in the vector Q and, by performing successive divisions of that number by 10, transfer it to the range of zero to one. For example, we convert the sum 126,133,514 to 0.126133514. The resulting number is used as the initial value x₁ in Eq. (5) to generate the chaotic sequence. To avoid the detrimental effects of the transfer, we select a specific term in the chaotic sequence (such as the 100th term: M = 100) and extend it to term $M+X$, defining that sequence as $CH=\left\{{a}_{1},{a}_{2},\dots ,{a}_{X}\right\}$.

Step 4: Sort the sequence CH in descending order to produce the permutation sequence Prm. The permutation sequence Prm indicates the order in which each element of CH has been arranged and, in other words, defines the positions of the elements of CH in the newly sorted sequence. For example, Prm(i) specifies the position where the i-th element in the sorted sequence was located in the original sequence CH. By applying the order used in the permutation sequence Prm to the sequence Q, we obtain the scrambled sequence R as $R=\left\{{r}_{Prm\left(1\right)},{r}_{Prm\left(2\right)},\dots ,{r}_{Prm\left(X\right)}\right\}$.

Step 5: Map the sequence CH obtained from Step 3 to the range [0, N] using the following equation:

$$y_{i} = \left( {CH\left( i \right) \times 10^{20} } \right)modN$$

(7)

In the above equation, N is the number of unique characters in the ASCII table. It is clear that $y_{i} \in \left[ {0,N} \right]$ is always the case. The vector y has the same dimensions as the scrambled vector CH.

Step 6: With the vectors y and CH of the same size, we perform the diffusion operation on the vector CH:

$${F}_{x}={y}_{x} \oplus C{H}_{x}$$

(8)

Step 7: In the next step, using the honey encoding algorithm, we convert the vector F obtained through the previous step and obtain the final vector C according to the process described in Sect. 3.3. For this purpose:

Step 1–7: Using the AES128 algorithm, a symmetric key of the same size as the data block being encrypted, such as A, is generated.

Step 7–2: A set of distinct members in the message space, denoted as M, is generated. To every member of the set M, a number of members from S are assigned. Since space S constitutes all permutations of binary n bits, there may be more than one value in space S for every member of space M. For any given value of data, it will look for the value in space M, and one of the members of S assigned to the current value is randomly picked. The value extracted from S is combined with the pre-distributed symmetric key A via the XOR operator. The result of this operation will be the encrypted message C.

Figure 6 presents the steps of the proposed encryption algorithm as a diagram.

Fig. 6

Steps of the proposed encryption algorithm.

Complexity analysis

The proposed protocol’s implementation within resource-limited IoT systems needs both memory evaluation and computational runtime assessment. The evaluation of this hybrid security system examines its computational complexity by using performance values regarding the message quantity (n) alongside suitability criteria for constrained IoT devices. The main computational operations which affect the total cost analysis operate based on message length. The key stages are:

• 1. The second step of initial diffusion uses successive bitwise XOR operations that traverse the message once. Its complexity is linear, $O(n)$.

• 2. The generation of an n-length chaotic sequence CH through the spatiotemporal CML system occurs in Steps 3 and 5 using the mathematical expression (Eq. 5). The generation of n-length chaotic sequence CH through n iterations starts after the initial setup. The mapping process from the sequence to y requires application of (Eq. 7) also takes n steps. Each step in the mapping process and each iteration in the phase takes a constant amount of time which results in $O(n)$ complexity.

• 3. The fourth step known as Chaotic Permutation stands as the essential part of the process. The process requires sorting the n-element chaotic sequence CH to produce the permutation sequence $Prm$. Standard efficient sorting algorithms (Merge Sort, Heap Sort and Quick Sort in the average case) require $O(n.logn)$ time complexity for execution. The application of permutation $Prm$ to sequence $Q$ for generating scrambled sequence $R$ requires $O(n)$ time. The sorting operation controls this stage of the algorithm.

• 4. The n bitwise XOR operations between elements of y and CH in Step 6 result in $O(n)$ complexity.

• 5. The Honey Encryption process under Step 7 applies AES Encryption to sequence $F$ of length $n$ through mapping each element to value in space $S$ (Step 7–2). The process requires either distribution-based lookups or calculations which can be estimated as $O(n)$ for the complete sequence. AES encryption forms the essential part of this step. AES-128 functions by processing 128-bit (16-byte) blocks with a standardized method. A message with n bytes needs approximately n/16 block encryption operations to become encrypted. The AES encryption section requires a time complexity of $O(n)$ because each block operation runs at a constant duration that depends on hardware implementation but not on $n$. The implementation of Honey Encryption together with AES encryption results in $O(n)$ time complexity.

The time complexity of the proposed protocol stems from its most resource-intensive step. The sorting operation for chaotic permutation ($O(n.logn)$) consumes more computational resources than the linear ($O(n)$) time required by initial diffusion, chaotic sequence generation, second diffusion, Honey Encryption mapping and AES encryption combined. The proposed protocol demonstrates $O(n.logn)$ as its final time complexity evaluation.

Encryption duration grows at a speed that exceeds linear growth by a small margin according to message length measurements yielding an $O(n.logn)$ complexity value. The computational requirements of this approach exceed those of lightweight block ciphers PRESENT²⁹ and CLEFIA³⁰ which operate at $O(n)$ complexity but the logarithmic factor logn grows gradually. The system enables processing of larger messages within reasonable time periods. The algorithm demands a computation time that exceeds the original value by approximately 2 when message size increases by a factor of 2 (in contrast to $O(n)$ which doubles precisely).

Memory usage (RAM) proves to be a fundamental limitation for typical IoT devices along with time complexity. The following section demonstrates the main memory usage needed by the protocol:

• Data Buffers: The algorithm needs memory space to store plaintext message (P) and intermediate sequences (Q,R,F) and final ciphertext (C) and generated chaotic sequence (CH) and mapped sequence (y). The data structures need memory space that matches the length of the message n. All data buffers require memory space that grows proportionally to n.

• Permutation Index: The permutation sequence $Prm$ that stores sorting indices after sorting needs $O(n)$ storage space.

• Keys and Parameters: The chaotic system parameters $(\alpha ,\beta ,\epsilon )$ together with the AES symmetric key (128, 192, or 256 bits) and the message sum initial condition require storage space along with potential Honey Encryption mapping parameters (distribution information ${p}_{i}$ and $M$ and $S$ definitions). The storage requirements for these elements are either constant or smaller than the message data which leads to $O(1)$ (constant) space complexity in relation to $n$.

• AES State and Round Keys: AES encryption uses a fixed amount of memory for its internal state matrix which measures 128 bits for AES-128 and also includes the derived round keys that depend on key size and number of rounds but remain constant for specific configurations. This also contributes $O(1)$ space.

• Temporary Variables: The sorting process needs additional temporary storage space for its execution. Heap Sort demonstrates an efficient sorting method that operates within $O(1)$ auxiliary space while Merge Sort typically requires $O(n)$ auxiliary space. The selected sorting algorithm affects this process yet $O(n)$ auxiliary space remains manageable in most cases.

Overall Memory Usage: Memory usage depends primarily on the storage requirements for various data buffers (plaintext, intermediate sequences, ciphertext, chaotic sequence, mapped sequence) and permutation index which scale proportionally to message size n. The total space requirements of this protocol amount to $O(n)$. The implementation of multiple n-sized arrays requires attention to the constant memory factor because linear complexity remains desirable. The $O(n)$ memory requirement is suitable for IoT messages that measure between a few bytes and several kilobytes since most IoT devices contain RAM between kilobytes and low megabytes.

The proposed protocol delivers suitable characteristics for resource-limited devices because it accounts for time and memory usage through multiple reasons:

• Manageable Scalability: The proposed protocol maintains predictable scalability through its $O(n.logn)$ time complexity and its $O(n)$ space complexity which grows proportionally to message size $n$. The logarithmic time factor grows at a steady pace while standard linear memory consumption applies to variable-length data processing.

• Efficient Algorithms: The sorting operation and AES encryption process benefits from specialized algorithms which include Heap Sort for $O(1)$ auxiliary space requirements and highly optimized AES libraries that function well on embedded devices with limited memory capacity. Different researchers have investigated these algorithms to maximize their optimization potential.

• Security-Efficiency Balance: The $O(n.logn)$ time complexity establishes an equilibrium between security enhancement from the hybrid security method (chaotic permutation + Honey Encryption + AES) and the available resources of minimal devices. Security effectiveness remains our primary focus instead of achieving the lowest possible computational cost in our method while keeping operations simple.

• Practical Performance: The typical small message sizes ($n$) found in IoT applications show that the performance gap between $O(n)$ and $O(n.logn)$ will be unnoticeable while $O(n)$ memory requirements fit comfortably within IoT devices’ capabilities. The execution time and feasibility of a system depend on both the constant factors hidden within Big-O notation and the actual processing power of the target device. The importance of conducting future hardware-based empirical tests on actual devices becomes clear because the study acknowledges this limitation.

This thorough analysis of computational time and memory usage supports the theoretical effectiveness of the protocol for resource-limited environments even though testing on various IoT devices still needs to be done in the future.

Results and discussion

The proposed method was implemented using the MATLAB 2020a software. The proposed method was evaluated in two phases. In the first phase of the experiments, the performance of this approach was evaluated at the network level and in addition to required processing time, its effect on the delay and energy consumption (caused by computational operations of encryption steps) was examined. Then, in the second phase of the experiments the security of our algorithm was evaluated. These analyses, examine the robustness of the proposed algorithm against various security treats. The remainder of this section presents and discusses the obtained results.

Performance analysis at the network level

At the network level, we considered a hypothetical network consisting of 300 nodes with heterogeneous characteristics in a simulated environment with dimensions of 500 m × 500 m. These nodes are different in terms of processing power, initial energy and buffer memory capacity. The nodes are assumed to be fixed and each one encrypts the generated information through the proposed method or the compared methods and sends it to the data center. In this experiment, we investigate the effect of message size on the performance of the encryption algorithm and checked the network performance based on three parameters: average transmission delay, energy consumption and average processing time. All of these metrics consider the resources used by the encryption algorithm.

In Fig. 7a, the average transmission delay is displayed. The sum of computation and transmission time shows how much time each node spent on average to encrypt a packet and send it to the data center. The computing time is calculated based on the processing power of the node and the sending delay is also determined according to parameters such as the network traffic rate and the status of the nodes in the network. This experiment shows that our proposed method in terms of performance improvement with packet size changes has been able to achieve lower delay than other investigated methods. In general, as the packet size increases, the transmission delay also increases; because in this case, the number of calculations required for packet encryption as well as the number of packets sent in a stream for data delivery increases, and this increases the delay in the network. However, a significant part of the delay is caused by the computational delay that our proposed method has been able to reduce compared to the compared methods through the efficient and lightweight algorithm it uses.

Fig. 7

The effect of message size on (a) transmission delay and (b) consumed energy.

Figure 7b shows the amount of energy consumed. This computing energy has been compared in different ways solely based on the number of operations performed at the bit level for data encryption. With the increase of the packet size, the number of calculations also increases, and therefore it is natural that energy consumption also increases. However, the lower energy consumption of the proposed method compared to the two compared methods of Clemente-Lopez et al.²⁰ and Rahman et al.²¹ indicates that this method requires fewer computational operations for information encryption. This issue demonstrates the high computational efficiency of the proposed method and shows that this model can be used more effectively for nodes with limited energy and computing resources.

Figure 8 shows the average processing time and indicates how much time each node, on average, spends encrypting data of a specified size. This experiment also demonstrates that as the packet size increases, the number of calculations increases, and therefore more time is spent encrypting the information. Clearly, our proposed method has managed to spend less time on packet encryption in all cases. This reduction in processing time is due to the decrease in the number of fundamental computational operations required by the proposed method. Thus, it can be concluded that this method has succeeded in reducing the computational load on the system. Our experiments indicate that this improvement can lead to increased network performance; meaning that we can perform encryption with a lower computational load and reduced latency. To ensure that this algorithm provides sufficient security and can improve network performance compared to other methods, we introduced a second phase that examines the security of information encryption at the packet level.

Fig. 8

Evaluation of average processing time.

The design of our proposed protocol system determines these performance metrics. The protocol achieves computational efficiency through its implementation of the computationally efficient Henon map with chaotic permutations and Honey Encryption optimization to minimize encryption-related computational delays and energy usage. The faster encryption speed achieved by nodes due to reduced computational requirements results in decreased overall transmission delay. The encryption algorithm influences transmission delay but this delay also depends on network traffic and node status. The reduction of computational requirements in our protocol helps achieve better overall delay performance than alternative encryption methods. The amount of energy that a system consumes depends directly on the number of calculations needed to encrypt data. The protocol design requires fewer bit-level operations than other methods which leads to reduced power consumption for each transmitted packet. The total energy consumption decreases when our protocol performs operations because each operation costs less than other methods despite their growing operational counts. The energy efficiency of IoT nodes requires this approach because they operate under limited resources. The duration of data encryption at each node depends directly on the reduced processing complexity built into our protocol. The quick encryption process achieved through our chaotic permutation and Honey Encryption steps becomes possible because of their lightweight nature. The design of our protocol leads to faster processing which constitutes a main element for better network performance.

Security analysis at the message level

In this phase, the security of information encryption is examined at the message level. The assessment method includes evaluations of both chaos-based image encryption schemes^22,23,24 and established lightweight cryptographic primitives PRESENT²⁹, CLEFIA³⁰ and ASCON³¹ to provide a comprehensive evaluation framework. In this experiment, various analytical tests were conducted on the encryption of information to assess the efficiency and safety of this method. The performance of the proposed method was evaluated using image data, and both color image data and grayscale systems were analyzed to determine the effectiveness of this model in encrypting these types of data.

Figure 9a shows the histogram of the original image and Fig. 9b the histogram of the encoded image. Figures 10, 11, 12, 13, 14, 15, 16 and 17 analyze the histogram for various images. In each of these figures, the top row (from left to right) demonstrates the original image, the encrypted image, and the decrypted image. Also, the second row of each figure show the histogram of each image below it. These results demonstrate that our proposed method has successfully eliminated extractable information from the histograms of images and transformed this information in such a way that it cannot be extracted. This effectiveness has been achieved through hyperchaotic systems that manage the pixel values. By using the honey encryption algorithm, we can further enhance these changes and obtain a nearly smooth histogram based on these algorithms. The proposed method is designed to remove or alter extractable information from histograms for both color images and grayscale images, preventing the extraction of useful information from histogram analysis. Consequently, this method is resistant to statistical attacks. The standard deviation analysis of histogram distributions from images encrypted through this method is performed against several reference benchmarks. A lower standard deviation value produces a histogram with flat distribution which impedes frequency analysis attacks in statistical cryptanalysis. Comparing the standard deviation values of the histogram vectors of the encryption algorithms proves the effectiveness of the proposed algorithm against statistical attacks. The average standard deviation in the histogram of the images encrypted by the proposed method is 36.51. This is while these results for methods^22,23, and²⁴ are 84.91, 48.23, and 65.52, respectively. Standard lightweight ciphers including PRESENT²⁹, CLEFIA³⁰ and ASCON³¹ produce very flat histograms because of their strong pseudo-random output properties which causes low standard deviation values. The test results obtained under equivalent conditions show PRESENT with 37.03 and CLEFIA with 35.89 and ASCON with 35.58. Our chaos-based method shows equivalent uniformity achievement because the standard cryptographic diffusion and confusion principles lead to identical distribution outcomes.

Fig. 9

Image histogram of the (a) original image and (b) the encrypted image.

Fig. 10

Image histogram analysis of the bird image (source of initial image: https://commons.wikimedia.org/wiki/File:Hummingbird.jpg, other subplots obtained through experiments).

Fig. 11

Image histogram analysis of the baboon image (source of initial image: https://commons.wikimedia.org/wiki/File:Olive_baboon_animal_papio_anubis.jpg, other subplots obtained through experiments).

Fig. 12

Image histogram analysis of the boats image (source of initial image: https://www.flickr.com/photos/36637817@N05/3379298128/, other subplots obtained through experiments).

Fig. 13

Image histogram analysis of the camera image (source of initial image: https://commons.wikimedia.org/wiki/File:Camera-man(byJenniferTrovato).jpg, other subplots obtained through experiments).

Fig. 14

Image histogram analysis of the chilies image (source of initial image: https://commons.wikimedia.org/wiki/File:Chillies_chili_peppers_garlic_parsley.jpg, other subplots obtained through experiments).

Fig. 15

Image histogram analysis of the houses image (source of initial image: https://www.hlevkin.com/hlevkin/TestImages/houses.bmp, other subplots obtained through experiments).

Fig. 16

Image histogram analysis of the mandrill image (source of initial image: https://www.flickr.com/photos/36637817@N05/3379300004/, other subplots obtained through experiments).

Fig. 17

Image histogram analysis of the peppers image (source of initial image: https://www.hlevkin.com/hlevkin/TestImages/pepper.bmp, other subplots obtained through experiments).

Figures 18 and 19 illustrate on the correlation between adjacent pixels before and after encryption for the camera and peppers images, respectively. To analyze the correlation between adjacent pixels, a thousand random pixels were selected, and the correlation of these pixels based on horizontal, vertical, and diagonal adjacency was analyzed. The results of the correlation analysis are clear. Each of the two diagrams contains six shapes; the upper row displays the correlation values for vertical, horizontal, and diagonal relationships of the original image, while the lower row presents these values for the encrypted image. In an image with meaningful textures, there is a high correlation between pixels, meaning that neighboring pixels are much alike, hence increased correlation. This can be seen from the top row in the diagrams. The encryption reduces the correlation to the extent that it may reach a level where information about the original image cannot be extracted by using correlation analysis. The results show that the level of horizontal, vertical and diagonal correlation of the proposed method compared to the compared methods has a significant reduction in terms of the average correlation.

Fig. 18

Correlation coefficient diagram of the original (top row) and encrypted (bottom row) of the camera image. Left: vertical, middle: horizontal, and right: diagonal correlation.

Fig. 19

Correlation coefficient diagram of the original (top row) and encrypted (bottom row) of the peppers image. Left: vertical, middle: horizontal, and right: diagonal correlation.

Table 2 shows the results against PRESENT²⁹, CLEFIA³⁰, and ASCON³¹ as well as the obtained results from methods^22,23,24. Standard cryptographic primitives eliminate statistical patterns through their design approach that results in very low correlation among adjacent data elements (bits or bytes). The minimal pixel-level correlation demonstrates that the method shows strong diffusion properties when used on image data.

Table 2 The average values obtained by the correlation analysis.

The proposed method demonstrates correlation results that match or surpass the values recorded by referenced chaos-based methods^22,23,24 in Table 2. The proposed method demonstrates correlation reduction capabilities that match or exceed those of PRESENT, CLEFIA, and ASCON lightweight ciphers because their design principles already produce outputs with minimal correlation.

The metrics of BER and MSE appear in Fig. 20a and b. The rate of bit difference between original and encrypted images is shown by BER. A secure encryption system should alter around 50% of its bits compared to plaintext to achieve a BER value close to 0.5. The proposed method yielded BER results that amounted to 0.4937. The proposed value stands in comparison to related works and standard lightweight ciphers as shown in Fig. 20a. The BER value in^22,23,24 shows a smaller result. Standard lightweight ciphers including PRESENT, CLEFIA, and ASCON fulfill their avalanche criteria well and reach BER values near the theoretical 0.5 value with 0.4945 for PRESENT, 0.4977 for CLEFIA, and 0.4981 for ASCON.

Fig. 20

Evaluation of BER and MSE criteria.

The proposed methodology demonstrates excellent capabilities in altering image data and reduces information interpretability to a high extent while achieving BER performance that matches theoretical limits and matches standard cryptographic primitives. The evaluation of this metric also utilized MSE which represents the average value of squared pixel value differences between original and encrypted images. The encryption effect based on pixel difference becomes stronger when MSE values increase because this indicates greater deviation between encrypted and original images. The pixel comparison for MSE and BER calculations occurred between original and permuted pixels in both figures. The calculated MSE value from the proposed technique reaches a high level (Fig. 20b) which shows dramatic pixel value modifications. The proposed technique achieves high security performance based on MSE criterion when compared to standard ciphers (PRESENT, CLEFIA, ASCON) and methods^22,23,24 which demonstrates its effectiveness in distorting original image data.

Resilience against data-driven cryptanalysis

The speed of machine learning and deep learning technique advancement creates new cryptanalysis opportunities through the field known as Data-Driven Cryptanalysis (DDC). Recent security threats include deep neural network and generative model frameworks where the Denoising Diffusion Cryptanalytic Model (DDCM) stands as an example for cracking anonymized facial images according to³². Such methods represent new security risks that modern encryption protocols must address. The DDCM model uses diffusion models to reverse engineer original images from weakly encrypted or visually degraded versions through the analysis of leaked visual information and learning the inverse transformation. The data-driven model principle behind DDCM demands attention for any cryptographic protocol including the one presented in this work because it targets specific anonymization methods.

The proposed hybrid security protocol contains built-in qualities which make it resistant to data-driven cryptanalytic methods. The cryptographic operations used in multiple layers demonstrate effective security through the security analyses presented in "Security analysis at the message level" section.  which supports the creation of a secure complex transformation. Several factors work together to make the proposed hybrid security protocol resilient.:

• A. Hyperchaotic Permutation for Statistical Obfuscation and Pattern Disruption: The first fundamental stage of our protocol applies hyperchaotic permutation to data elements through sequences produced by complex hyperchaotic systems (Eq. 5) because these systems exhibit sensitivity and pseudo-random properties (Figures 3, 4). The main purpose of this permutation phase (Step 4 in Section 3.4) is to break statistical connections and data position relationships found in original plaintext information. Data-driven models require exact identification of statistical patterns which connect plaintext to ciphertext between which they establish structural associations. The chaotic permutation effectively scatters data sequences based on keys to create substantial pattern obscuration. "Security analysis at the message level" section demonstrates the effectiveness of statistical obfuscation through encrypted images that show uniform histograms in Figures 9, 10, 11, 12, 13, 14, 15, 16 and 17 and achieve an average histogram standard deviation of 36.51 which matches lightweight ciphers such as CLEFIA (35.89) and ASCON (35.58). The consistent distribution of data points in the cipher makes frequency analysis attacks which are part of DDC much harder to execute. The strong diffusion properties of the cipher match those of CLEFIA and ASCON because the local structure disruption produces negligible correlation coefficients between adjacent pixels (Table 2 shows 0.0015 horizontal and 0.0008 vertical). The combination of a large key space and sensitive chaotic system makes it difficult for attackers to discover the permutation function.

• B. Honey Encryption for Ambiguity and Plausible Deniability: The protocol applies honey encryption through Step 7 of Section 3.4 after the permutation stage (Section 3.3 presents details about this technique). The protocol uses honey encryption to make plaintext values from space M correspond to multiple possible valid ciphertext values in space S through distribution-based mapping. The attacker who tries DDC cannot identify the original plaintext element using the correct key because observing a specific ciphertext block remains ambiguous. Multiple possible plaintext values would match the same ciphertext during decryption which leads to the production of confusing and unclear data points. Supervised learning-based cryptanalysis faces a core obstacle from the built-in ambiguity because it demands consistent and unambiguous input-output (ciphertext-plaintext) pairs for successful training. Honey encryption contaminates the possible training data collection of attackers thus making it difficult for the model to establish an effective decryption mechanism.

• C. AES Encryption and Overall Transformation Strength: The implementation of honey encryption uses AES-128 encryption (Section 3.3 and Step 7–2) to finalize the symmetric key encryption process. AES stands as a fully examined standardized block cipher which delivers secure encryption through multiple examination-resistant attack types including statistical attacks. The combination of AES encryption with the chaotic permutation and honey encryption mapping produces an intricate non-linear and sensitive transformation which converts plaintext into ciphertext. The Bit Error Rate (BER) analysis in "Security analysis at the message level" section (Fig 20a) demonstrates an overall strength through its calculated value of 0.4937. The BER value of 0.4937 demonstrates strong cryptographic strength by closely approaching the expected 0.5 threshold for secure ciphers which exhibit a strong avalanche effect and matches the performance of standard ciphers PRESENT (0.4945) and ASCON (0.4981). The high Mean Squared Error (MSE) values shown in Fig 20b demonstrate a significant statistical difference between plaintext and ciphertext which makes the transformation difficult to predict through DDC predictive modeling.

Contrast with Visual Anonymization Targeted by DDCM: Our cryptographic operations stand apart from visual anonymization methods such as blurring or pixelation which DDCM³² targets. The anonymization methods focus on hiding visual identification yet they maintain crucial structural information and statistical properties which DDC models can potentially detect. The cryptographic layers in our protocol work together to remove statistical relationships (verified through histogram and correlation tests) and create semantic confusion (through honey encryption) while using AES and chaos for computational difficulty based on Sect. 4.2 metric results.

The operational link between plaintext and ciphertext becomes highly complex because of the combination between a hyperchaotic permutation which breaks statistical and pattern relationships (tested in Sect. 4.2 through correlation analysis and histogram tests) together with a honey encryption method (Sect. 4.2 proves its strength through its deniability properties) and the AES cryptographic core (Sect. 4.2 exhibits ideal BER metrics). The multi-level defense system demonstrates competitive security properties against statistical and structural attacks according to Sect. 4.2 yet it does not contain the predictable patterns which data-driven cryptanalysis methods normally seek. The analyzed hybrid protocol provides better protection against data-driven cryptanalytic threats than basic encryption approaches and plain data obfuscation methods. Future work on data encryption requires sustained research together with specific framework evaluations since improvement efforts in DDC tools matter fundamentally.

Conclusion

Research on communication security in the IoT is of paramount importance, especially in the face of cyber threats and the protection of sensitive information. The proposed method in this study, combining hyperchaotic systems and honey encryption, not only significantly enhances the security of data but also improves efficiency and reduces energy consumption. The obtained results ensure an impressive delay and energy consumption reduction with values of 21.8 and 0.34, respectively, as well as improvement in the security metrics such as MSE and BER with values of 1.041 and 0.49, respectively. The proposed method is well adapted for different IoT applications and can be advocated as an effective solution to enhance security and efficiency attributes for IoT systems from existing threats. With the increasing needs of security in the digital age, this may well be a significant approach or methodology in the design and development of IoT systems. Despite the impressive outcomes obtained by the proposed algorithm, the are several limitations that need to be addressed in future works:

• In general, the first limitation that can be pointed out is that although the proposed method has fewer computational operations and imposes less load on the system, this protocol still has additional computational overhead that may be too high for resource-intensive IoT devices.

• The second limitation is related to key management; Secure key management is one of the inherent challenges of cryptographic systems that should be considered in future research and efforts should be made to manage this properly.

• The next limitation is the robustness analysis of the proposed method against timed attacks and side attacks. The proposed protocol may be vulnerable to this kind of attack; thus, future research should try to improve this vulnerability.

• Future research about the proposed protocol will examine its performance against various modern IoT security solutions beyond established benchmarks for general-purpose IoT deployments. New algorithms targeted at application fields like industrial IoT and healthcare will be tested to determine how the protocol handles different IoT environments. Extending the evaluation methodology will result in a more complete analysis of protocol capabilities and shortcomings so researchers gain better understanding of its IoT security position.

• The final limitation is the applicability and reliability of the proposed protocol in real IoT environments. This, of course, still needs to be assessed, since field implementation of the proposed method on real networks has not been done yet.