A modified TOPSIS algorithm for the assessment of sports quality in higher education using circular pythagorean fuzzy information

Abstract

Higher education institutions experience difficulties in sports quality assessment because multiple qualitative and quantitative factors, including sports facilities and coaching abilities, combine with student participation and institutional backing. Standard assessment systems encounter challenges when measuring subjective phenomena found in quality assessment evaluations. This research introduces an improved version of the technique for order of preference by similarity to ideal solution (TOPSIS) based multi-criteria decision-making (MCDM) model that utilizes circular Pythagorean fuzzy sets (CPyFS) to effectively process imprecise expert judgments. The proposed model implements redesigned weight assignment and distance computation techniques for optimizing decision reliability. A practical investigation analyzes different key evaluation criteria for sports programs, including basketball, soccer, volleyball, tennis, and swimming, through consultation with a sports director, senior coach, and a student representative. According to the results, the swimming program leads all other programs in sports quality assessment. The proposed model performs better than conventional fuzzy MCDM methods through robust ranking results, precise findings, and rapid computational speed. The evaluation system delivers a dependable method that enables sports policymakers and administrators to maximize investment while increasing student involvement within higher educational settings.

Introduction

In higher education learning institutions¹, the quality of the sporting activities is crucial for the students and the institution. They focus on enhancing human health in terms of physical fitness² and integrating into academics to develop teamwork, discipline, and community spirit. However, assessing the quality of such programs seems to pose some challenges because of the underlying factors such as the status of facilities, talent and quality coaching, students, and institutional receptiveness.

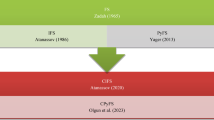
For comparing so many criteria where the criteria are conflicting in nature, MCDM methods such as TOPSIS³ are instrumental. However, they have inherent weaknesses in areas involving risk and assessment of values. Fuzzy sets (FS), developed by Zadeh⁴ in 1965, overcome the above limitation of classical sets by admitting partial membership to quantify fuzziness in decision-making. Circular fuzzy sets (CFS)⁵ can be considered to develop the basic fuzzy set theory to better cater to circular data, which has a cyclic or periodic nature, e.g., repetitions, seasonality, etc., combining the development of intuitionistic fuzzy sets (IFS), Atanassov⁶ extended FS by introducing the non-membership and hesitation margins. Carrying forward this, circular intuitionistic fuzzy sets (CIFS)⁷ are obtained by merging CFS’s circular features and the further uncertainty measure in IFS. CIFS includes the notions of degrees of membership, non-membership, and hesitation. However, these are located within a circular structure, which is useful particularly when applied to cyclic systems and systems with a high degree of uncertainty. This combination is essential in such situations, where a judgment is likely to differ in different seasons, for example, in ordinary sports programs. Still, it is also valuable in other cases when the judgment cannot be very accurate. The IFS is generalized by Yager⁸ as Pythagorean fuzzy sets (PyFS) with much more freedom to represent the uncertainty. The concept of CPyFS⁹ generalizes PyFS for circular or periodic uncertainty, where CPyFS are appropriate for sports performance analysis. Previously used assessment methodologies rely on simple quantitative outcomes instead of the more complex quality, resulting in an inconsistent approach to assessing sports-related programs.

To counteract this difficulty, the present study includes a new framework that employs the CPyFS-MCDM model¹⁰. It intends to incorporate the uncertainty of the experts’ judgments through the circular Pythagorean fuzzy (CPyF) approach and the TOPSIS algorithm better to assess the quality of sports in higher learning institutions. The proposed research focuses on developing a comprehensive framework for evaluation that policymakers and administrators can use to improve existing sports programs and raise students’ interest in physical activity and other co-curricular activities for the balanced development of the institution. Expectedly, the findings feature the promise of usefulness in enhancing sports quality in higher educational institutions. In this paper, we contribute an assessment of sports quality in higher education using the CPyFS in the environment of the TOPSIS method. For several sports activities¹¹, we evaluate the quality of a sports program based on the availability of facilities, the quality of coaches, and the participation levels of students. The evaluation includes alternative sports programs, such as basketball, soccer, volleyball, tennis, and swimming, as proposed by three decision-makers. The uncertainty is again tackled by adopting CPyFS with TOPSIS and implementing the circular Pythagorean fuzzy weighted averaging (CPyFWA) operator to decide between more precise and accurate options. It not only improves the accuracy of the assessment but also offers a framework for developing sports programs in higher education institutions.

Novelty of CPyF-TOPSIS approach

Higher education sports assessment is a complicated MCDM challenge because it combines numerical and non-numerical elements, including sports infrastructure, coaching quality student participation, and institutional backing. The conventional decision-making methods encounter difficulties in managing expert assessment uncertainties together with their hesitance behavior. This study develops a CPyF-TOPSIS-based method that solves evaluation difficulties occurring when handling imprecise and shared assessments in sports quality assessments. The main contribution of this system comes from its capability to merge CPyFS together with TOPSIS to create a more detailed decision evaluation method. The CPyFS model introduces three important fuzzy parameters, including MD, NMD, and radius terms, which serve to enhance expert uncertainty handling. The research implements CPyFWA operator to consolidate expert assessments throughout a process that maintains intact fuzzy information consistency. The research utilizes a normalized Euclidean distance measure as a ranking method to deliver accurate sports program evaluation. The proposed framework that integrates these methodological improvements produces a reliable and structured system to analyze higher education sports quality which delivers beneficial information for decision-makers to strengthen their sports initiatives and maximize their resources. Further, we will follow the explanation of the objectives, the contribution of the research, the gap existing in literature, and the motivation of this study as follows:

Research gap and motivation

Although there are studies on assessing sports quality in higher education that have been researched in the past, there are some gaps that have not been filled. Many standard assessment techniques can easily involve deterministic methods, while sports program evaluations involve most probably stochastic methods in their broadest sense. Moreover, many previous studies often rely on fewer numbers of factors. At the same time, other elements should also be considered, including community involvement and athletes’ health and safety are some of them. Additionally, there are no adequate resource paradigms that contain guidelines implemented with the principles of fuzzy logic for effective uncertainty management. This research will use the circular Pythagorean fuzzy MCDM model to analyze the given sports quality and address these gaps comprehensively.

This research is driven by rising awareness of the need for quality sports about the tag and quality of higher learning institutions regarding student commitment and health. Due to increasing competition among universities, universities must improve sports activities for student attraction and retention. As such, this research attempts to apply a sophisticated assessment paradigm to come up with insights that can be helpful to decision-makers in defining the suitable approaches that need to be taken and where resources may need to be directed. In addition, fuzzy logic in this context is intended to reduce uncertainties in the judgment of human beings, thus increasing reliability in the evaluation process. Finally, this study aims to help build and enhance effective patterns of developing students and institutions through sports programs.

Objectives and contribution

The objectives of this study are as follows:

• To develop the systematic evaluation of the quality of sports programs offered in higher education institutions using an innovative model based on the circular Pythagorean fuzzy MCDM model integrated with the TOPSIS algorithm.

• To set up objectives to enhance the quality of sports initiatives with excellence, such as sports facilities, the quality of coaches, students, and institutional support must be documented and distinguished based on the prism of criticality.

• To depict an honest and transparent system that choice makers can use more effectively for advancement and asset designation.

• To deal with the unstructured aspects of the evaluation process, use CPyFS.

• To build a comprehensive practical approach to evaluating the quality of sports programs in the context of higher education, thereby developing an effective evaluation plan for adoption in different higher education settings.

There are many contributions of this study organized as follows:

• The present research proposes a new circular Pythagorean fuzzy MCDM model incorporating the TOPSIS method, thus providing a complicated technique for assessing the quality of sports in higher educational institutions.

• Thus, the present study may offer a more encompassing vision of sports quality than the usual measurement approaches.

• The paper can be valuable for improving higher education institutions because it shows the lecturer’s angling strategies, strengths and weaknesses of respective universities’ sports programs, and other valuable impulses for further improvement.

• CPyFS helps overcome the difficulties associated with applying the concept of uncertainty in evaluating human judgment and increases the reliability of the assessment.

• The study presents the basis for future research by underlining the importance of constant evaluation and modifications of sports programs and contributing to future research regarding other possible factors influencing the quality of sports.

Organization of study

The study is divided into specific parts to assess the sport’s quality in higher education using the CPyF TOPSIS approach. Section 2, the literature review, will examine the relevant theories, such as the TOPSIS approach and the use of the model to evaluate sports quality. Section 3 preliminaries define the general concepts of CPyFS and their operational laws. Section 4 of the CPyF TOPSIS approach presents the method used in this study. Section 5 describes the evaluation of sports in higher education using the CPyF TOPSIS approach process. Then, the results are discussed, which gives an understanding. Section 6, sensitivity analysis, examines the findings’ stability and reliability where the study’s advantages display significant offerings. Section 7 briefly reiterates the research results and consequences, restating the importance of conducting an adequate assessment of sports quality in higher education institutions, and also discusses limitations and future research related to this study. It also improves the clear comprehension of presented data and helps readers move through the findings in a highly organized manner.

Literature review

This section will briefly analyze the TOPSIS method of MCDM¹² and its usefulness in solving decision-making issues. Further, this study will consider how MCDM models can be applied to determine the quality of sports in higher education based on criteria affecting the efficiency of sports programs.

Studies employing the TOPSIS approach

TOPSIS is one of the specific and reliable techniques of MCDM, which compares the solutions and the degree of their closeness to the so-called ideal and anti-ideal solution. The method is also commonly used in different fields, for example, to assess sustainable cities with the use of the ANP-TOPSIS hybrid method¹³, in material selection problems¹⁴, and in supply chain management¹⁵. TOPSIS has been identified as flexible working with other MCDM techniques like COPRAS¹⁶, DEA¹⁷, and fuzzy methods that improve decision-making processes even in complicated and uncertain situations. The integration of TOPSIS with other methods, such as fuzzy ANP¹⁸, DEMATEL¹⁹, and BWM²⁰, has been used in green supplier selection and the evaluation of cloud services. In addition, fuzzy AHP-TOPSIS models have also been used in selecting industrial robots, where efficient decision-making models in a technological environment have been established²¹. TOPSIS comparative research integrating VIKOR²², MOORA²³, and Entropy Weight Methods has featured the applicability of these approaches in vendor selection in the manufacturing industry²⁴. In addition, recent developments of new MCDM models, which combine fuzzy rough sets with TOPSIS, have been proposed to deal with decision-making uncertainties²⁵. These adaptations demonstrate that TOPSIS offers more tremendous success in the MCDM than the other methods when ranking the alternatives for multiple circumstances^26,27,28. The TOPSIS method receives widespread application across different domains, but CPyFS remains absent from existing studies that evaluate higher education sports quality through this method. The research fills a recognized gap by merging CPyFS with TOPSIS to create an advanced sports quality assessment methodology system.

Sports quality in higher education using the MCDM model

The assessment of sports quality in higher education states that using MCDM models involves adopting qualitative and quantitative data to enhance decision-making. The following have been used to evaluate different aspects, including teachers’ involvement in recreational sports²⁹, the quality of teaching and learning in physical education using fuzzy TOPSIS³⁰, and the performance of sports centers using fuzzy³¹. In higher education, fuzzy MCDM methods provide elaborate findings, such as those applied to rank the universities regarding service quality³² and assess the sustainable sports tourism criterion³³. These studies add to the increasing awareness of MCDM methods in improving sports technology³⁴ and professional sports³⁵ and aligning with strategies for universities’ purposes³⁶ using powerful picture fuzzy³⁵ and other MCDM approaches. Intuitionistic Fuzzy and SWARA-AROMAN models have been used to enhance decision-making strategies applied to the management of sports events, analyzing planning and operational strategy from a perspective that has not yet been the subject of extensive academic studies³⁷. These models improve an essential extent of overall resource management, risk minimization, and event success by incorporating fuzzy logic for different combinations of uncertain and imprecise data. Furthermore, the linguistic neutrosophic MCDM models developed here help assess sustainable sports tourism, contributing to an advanced comprehension of sports management from the environmental and social sustainability lens. Such methodologies remain relevant to analyzing and developing sports quality within educational settings. Table 1 compares existing studies on sports quality using the MCDM model.

Table 1 Comparison of existing studies on sports quality in higher education using MCDM models.

Preliminaries

Yager⁸ introduced the concept of PyFS as an expansion of regular IFS. This section provides a comprehensive literature assessment of existing concepts important to PyFS, CPyFS, and other related ideas.

Definition 1

⁸ A PyFS, denoted as$\:\:\text{F}$ on universal set$\:\:\text{X}$, is characterized by$\:\:\text{F}=\left\{\left(\text{x},\mathfrak{M}\left(\text{x}\right),\mathfrak{N}\left(\text{x}\right)\right):\text{x}\in\:\text{X}\right\}$, where $\:\mathfrak{M}\left(\text{x}\right)$ and $\:\mathfrak{N}\left(\text{x}\right)$ denotes the membership degree (MD) and non-membership degree (NMD) of the element $\:\text{x}\in\:\text{X}$ to $\:\text{F},$ respectively. These functions operate within the range$\:\:\left[\text{0,1}\right]$, and satisfy the condition:

$$\:0\le\:{\left(\mathfrak{M}\left(\text{x}\right)\right)}^{2}+{\left(\mathfrak{N}\left(\text{x}\right)\right)}^{2}\le\:1$$

(1)

Further, the hesitancy degree (HD) is defined by:

$$\:\text{h}\left(\text{x}\right)=1-\mathfrak{M}\left(\text{x}\right)-\mathfrak{N}\left(\text{x}\right)$$

.

Definition 2

⁹ A CPyFS, denoted as$\:\:\text{F}$ on universal set$\:\:\text{X}$, is characterized by$\:\:\text{F}=\left\{\left(\text{x},\mathfrak{M}\left(\text{x}\right),\mathfrak{N}\left(\text{x}\right),\mathfrak{r}\left(\text{x}\right)\right):\text{x}\in\:\text{X}\right\}$, where $\:\mathfrak{M}\left(\text{x}\right)$ and $\:\mathfrak{N}\left(\text{x}\right)$ denotes the MD and NMD of the element $\:\text{x}\in\:\text{X}$ to $\:\text{F},$ respectively. These functions operate within the range$\:\:\left[\text{0,1}\right]$, and satisfy the condition:

$$\:0\le\:{\left(\mathfrak{M}\left(\text{x}\right)\right)}^{2}+{\left(\mathfrak{N}\left(\text{x}\right)\right)}^{2}\le\:1$$

(2)

Also, the HD is determined by:

$$\:\text{h}\left(\text{x}\right)=1-\mathfrak{M}\left(\text{x}\right)-\mathfrak{N}\left(\text{x}\right)$$

And$\:\mathfrak{\:}\mathfrak{r}\in\:[0,\:1]$ be the radius of the circle. Figure 1 shows the graphical representation of CPyFS.

Fig. 1

Graphical representation of CPyFS.

Definition 3

⁹ For any two circular Pythagorean fuzzy values (CPyFVs), We discussed various algebraic laws, such as:

$$\:{\text{F}}_{1}{\oplus\:}_{\text{T}\text{N}}{\text{F}}_{2}=\left(\begin{array}{c}\sqrt{{\left({\mathfrak{M}}_{1}\left(\text{x}\right)\right)}^{2}+{\left({\mathfrak{M}}_{2}\left(\text{x}\right)\right)}^{2}-{\left({\mathfrak{M}}_{1}\left(\text{x}\right)\right)}^{2}{\left({\mathfrak{M}}_{2}\left(\text{x}\right)\right)}^{2}},\\\:{\mathfrak{N}}_{1}\left(\text{x}\right){\mathfrak{N}}_{2}\left(\text{x}\right),\\\:\sqrt{{\left({\mathfrak{r}}_{1}\left(\text{x}\right)\right)}^{2}+{\left({\mathfrak{r}}_{2}\left(\text{x}\right)\right)}^{2}-{\left({\mathfrak{r}}_{1}\left(\text{x}\right)\right)}^{2}{\left({\mathfrak{r}}_{2}\left(\text{x}\right)\right)}^{2}}\end{array}\right)$$

•

$$\:{\text{F}}_{1}{\oplus\:}_{\text{T}\text{C}\text{N}}{\text{F}}_{2}=\left(\begin{array}{c}\sqrt{{\left({\mathfrak{M}}_{1}\left(\text{x}\right)\right)}^{2}+{\left({\mathfrak{M}}_{2}\left(\text{x}\right)\right)}^{2}-{\left({\mathfrak{M}}_{1}\left(\text{x}\right)\right)}^{2}{\left({\mathfrak{M}}_{2}\left(\text{x}\right)\right)}^{2}},\\\:{\mathfrak{N}}_{1}\left(\text{x}\right){\mathfrak{N}}_{2}\left(\text{x}\right),\\\:{\mathfrak{r}}_{1}\left(\text{x}\right){\mathfrak{r}}_{2}\left(\text{x}\right)\end{array}\right)$$

•

$$\:{\text{F}}_{1}{\otimes\:}_{\text{T}\text{N}}{\text{F}}_{2}=\left(\begin{array}{c}{\mathfrak{M}}_{1}\left(\text{x}\right){\mathfrak{M}}_{2}\left(\text{x}\right),\\\:\sqrt{{\left({\mathfrak{N}}_{1}\left(\text{x}\right)\right)}^{2}+{\left({\mathfrak{N}}_{2}\left(\text{x}\right)\right)}^{2}-{\left({\mathfrak{N}}_{1}\left(\text{x}\right)\right)}^{2}{\left({\mathfrak{N}}_{2}\left(\text{x}\right)\right)}^{2}},\\\:{\mathfrak{r}}_{1}\left(\text{x}\right){\mathfrak{r}}_{2}\left(\text{x}\right)\end{array}\right)$$

•

$$\:{\text{F}}_{1}{\otimes\:}_{\text{T}\text{C}\text{N}}{\text{F}}_{2}=\left(\begin{array}{c}{\mathfrak{M}}_{1}\left(\text{x}\right){\mathfrak{M}}_{2}\left(\text{x}\right),\\\:\sqrt{{\left({\mathfrak{N}}_{1}\left(\text{x}\right)\right)}^{2}+{\left({\mathfrak{N}}_{2}\left(\text{x}\right)\right)}^{2}-{\left({\mathfrak{N}}_{1}\left(\text{x}\right)\right)}^{2}{\left({\mathfrak{N}}_{2}\left(\text{x}\right)\right)}^{2}},\\\:\sqrt{{\left({\mathfrak{r}}_{1}\left(\text{x}\right)\right)}^{2}+{\left({\mathfrak{r}}_{2}\left(\text{x}\right)\right)}^{2}-{\left({\mathfrak{r}}_{1}\left(\text{x}\right)\right)}^{2}{\left({\mathfrak{r}}_{2}\left(\text{x}\right)\right)}^{2}}\end{array}\right)$$

•

$$\:{\upeta\:}{\text{F}}_{\text{T}\text{N}}=\left(\sqrt{1-{\left(1-{\left(\mathfrak{M}\left(\text{x}\right)\right)}^{2}\right)}^{{\upeta\:}}},{\left(\mathfrak{N}\left(\text{x}\right)\right)}^{{\upeta\:}},\sqrt{1-{\left(1-{\left(\mathfrak{r}\left(\text{x}\right)\right)}^{2}\right)}^{{\upeta\:}}}\right)$$

•

$$\:{\upeta\:}{\text{F}}_{\text{T}\text{C}\text{N}}=\left(\sqrt{1-{\left(1-{\left(\mathfrak{M}\left(\text{x}\right)\right)}^{2}\right)}^{{\upeta\:}}},{\left(\mathfrak{N}\left(\text{x}\right)\right)}^{{\upeta\:}},{\left(\mathfrak{r}\left(\text{x}\right)\right)}^{{\upeta\:}}\right)$$

•

$$\:{\text{F}}_{\text{T}\text{N}}^{{\upeta\:}}=\left({\left(\mathfrak{M}\left(\text{x}\right)\right)}^{{\upeta\:}},\sqrt{1-{\left(1-{\left(\mathfrak{N}\left(\text{x}\right)\right)}^{2}\right)}^{{\upeta\:}}},{\left(\mathfrak{r}\left(\text{x}\right)\right)}^{{\upeta\:}}\right)$$

•

$$\:{\text{F}}_{\text{T}\text{C}\text{N}}^{{\upeta\:}}=\left({\left(\mathfrak{M}\left(\text{x}\right)\right)}^{{\upeta\:}},\sqrt{1-{\left(1-{\left(\mathfrak{N}\left(\text{x}\right)\right)}^{2}\right)}^{{\upeta\:}}},\sqrt{1-{\left(1-{\left(\mathfrak{r}\left(\text{x}\right)\right)}^{2}\right)}^{{\upeta\:}}}\right)$$

•

Furthermore, to simplify any two CPyFVs, we compute the following strategies, such as the score value.

Definition 4

⁹ For any CPyFV, we stated the technique of score value as follows:

$$\:\text{S}\text{c}\left(\text{F}\right)=\left({\left(\mathfrak{M}\left(\text{x}\right)\right)}^{2}-{\left(\mathfrak{N}\left(\text{x}\right)\right)}^{2}\right)\text{*}\left(\mathfrak{r}\left(\text{x}\right)\right)\in\:\left[-\text{1,1}\right]$$

(3)

Circular pythagorean fuzzy TOPSIS approach

The proposed CPyF-TOPSIS solution extends the original TOPSIS functionality through CPyFS model implementation, effectively addressing ambiguous decision-making conditions and criterion dependencies. CPyFS delivers the main advantage of implementing an additional radius parameter that provides enhanced flexibility for depicting uncertain data beyond basic MD and NMD measurement methods. This study developed CPyF-TOPSIS through systematic organization to boost accuracy in MCDM solutions. Through CPyFWA, expert opinions receive integration, which enables the proper combination of assessments while maintaining the natural fuzziness of evaluation data. The separation measures between alternatives and the ideal solution are calculated through normalized Euclidean distance because this method effectively tracks modifications in MD, NMD, and radius parameter measurements. The integration of the CPyFWA operator together with distance computation enhances the ranking system to offer better performance under evaluation data variations and uncertainties. The implementation of CPyFS within TOPSIS leads to an enhanced solution since it handles the uncertainties found in traditional fuzzy MCDM models for evaluation cases with multiple subjective assessment criteria and vague ratings. The proposal demonstrates effectiveness especially in sports quality assessment at educational levels. The subsequent subsection will present a systematic explanation of the CPyF-TOPSIS algorithm, showing how data collection transforms into normalized rankings to produce a complete assessment of alternatives.

Algorithms

Step 1: Define the decision matrix and compute the decision-maker weights: Construct a decision matrix for the following problem using the alternatives$\:\:\{{\text{A}}_{1},{\text{A}}_{2},\dots\:,{\text{A}}_{\mathfrak{M}}\}$ and the criteria$\{ {\text{C}}_{1} ,{\text{~C}}_{2} , \ldots ,{\text{~C}}_{{\mathfrak{N}}} \}$. Express decision matrix elements as CPyFS, including MD, NMD, and radius. Calculate the decision-maker weights$\varphi$ using the formula below.

Step 2: Aggregate the decision matrix and calculate weights:Consider a set of Then, the CPyFWA operators are described as follows:Where$\varphi _{t}$be the set of weights vector and

Step 3: Calculate the weighted aggregated decision matrix:To get the weighted aggregated decision matrix, multiply each of the aggregated CPyFVs (m_j^((k) ),n_j^((k) ),r_j^((k) )) with the weights specified in the previous step.$\:{\text{F}}_{\text{i}}{\otimes\:}_{\text{T}\text{N}}{\text{F}}_{\text{j}}=\left(\begin{array}{c}{\mathfrak{M}}_{\text{i}}\left(\text{x}\right){\mathfrak{M}}_{\text{j}}\left(\text{x}\right),\\\:\sqrt{{\left({\mathfrak{N}}_{\text{i}}\left(\text{x}\right)\right)}^{2}+{\left({\mathfrak{N}}_{\text{j}}\left(\text{x}\right)\right)}^{2}-{\left({\mathfrak{N}}_{\text{i}}\left(\text{x}\right)\right)}^{2}{\left({\mathfrak{N}}_{\text{j}}\left(\text{x}\right)\right)}^{2}},\\\:{\mathfrak{r}}_{\text{i}}\left(\text{x}\right){\mathfrak{r}}_{\text{j}}\left(\text{x}\right)\end{array}\right) \quad\quad\quad(6)$ As a result, the weighted aggregated decision matrix has a form of $\:\:({\mathfrak{M}}_{{\text{F}}_{\text{w}}}\left(\text{x}\right),{\mathfrak{N}}_{{\text{F}}_{\text{w}}}\left(\text{x}\right),{\mathfrak{r}}_{{\text{F}}_{\text{w}}}\left(\text{x}\right))$

Step 4: Determine the CPyF-positive ideal solution (CPyFPIS) A+ and CPyF-negative ideal solution $\left( {CPyFNIS} \right)\,\left( {A^{ - } } \right)$Assuming B and C are the sets of benefit and cost criteria, A+ and A- are calculated as follows $\:{\mathfrak{M}}_{{\text{F}}_{\text{w}}^{+}}\left({\text{x}}_{\text{j}}\right)=\left(\begin{array}{c}\left(\underset{\text{i}}{\text{max}}{\mathfrak{M}}_{{\text{F}}_{\text{w}}^{\text{i}}}\left({\text{x}}_{\text{j}}\right):\text{j}\in\:\text{B}\right),\\\:\left(\underset{\text{I}}{\text{min}}{\mathfrak{M}}_{{\text{F}}_{\text{w}}^{\text{i}}}\left({\text{x}}_{\text{j}}\right):\text{j}\in\:\text{C}\right)\end{array}\right),\quad\quad\quad(7)$ $\:{\mathfrak{N}}_{{\text{F}}_{\text{w}}^{+}}\left({\text{x}}_{\text{j}}\right)=\left(\begin{array}{c}\left(\underset{\text{i}}{\text{max}}{\mathfrak{N}}_{{\text{F}}_{\text{w}}^{\text{i}}}\left({\text{x}}_{\text{j}}\right):\text{j}\in\:\text{B}\right),\\\:\left(\underset{\text{i}}{\text{min}}{\mathfrak{N}}_{{\text{F}}_{\text{w}}^{\text{i}}}\left({\text{x}}_{\text{j}}\right):\text{j}\in\:\text{C}\right)\end{array}\right),\quad\quad\quad(8)$ $\:{\mathfrak{r}}_{{\text{F}}_{\text{w}}^{+}}\left({\text{x}}_{\text{j}}\right)=\left(\begin{array}{c}\left(\underset{\text{i}}{\mathfrak{M}\text{i}\mathfrak{N}}{\mathfrak{r}}_{{\text{F}}_{\text{w}}^{\text{i}}}\left({\text{x}}_{\text{j}}\right):\text{j}\in\:\text{B}\right),\\\:\left(\underset{\text{i}}{\mathfrak{M}\text{ax}}{\mathfrak{r}}_{{\text{F}}_{\text{w}}^{\text{i}}}\left({\text{x}}_{\text{j}}\right):\text{j}\in\:\text{C}\right)\end{array}\right)\quad\quad\quad((9)$ $\:{\mathfrak{M}}_{{\text{F}}_{\text{w}}^{-}}\left({\text{x}}_{\text{j}}\right)=\left(\begin{array}{c}\left(\underset{\text{i}}{\text{min}}{\mathfrak{M}}_{{\text{F}}_{\text{w}}^{\text{i}}}\left({\text{x}}_{\text{j}}\right):\text{j}\in\:\text{B}\right),\\\:\left(\underset{\text{I}}{\text{max}}{\mathfrak{M}}_{{\text{F}}_{\text{w}}^{\text{i}}}\left({\text{x}}_{\text{j}}\right):\text{j}\in\:\text{C}\right)\end{array}\right),\quad\quad\quad(10)$ $\:{\mathfrak{N}}_{{\text{F}}_{\text{w}}^{-}}\left({\text{x}}_{\text{j}}\right)=\left(\begin{array}{c}\left(\underset{\text{i}}{\text{min}}{\mathfrak{N}}_{{\text{F}}_{\text{w}}^{\text{i}}}\left({\text{x}}_{\text{j}}\right):\text{j}\in\:\text{B}\right),\\\:\left(\underset{\text{i}}{\text{max}}{\mathfrak{N}}_{{\text{F}}_{\text{w}}^{\text{i}}}\left({\text{x}}_{\text{j}}\right):\text{j}\in\:\text{C}\right)\end{array}\right),\quad\quad\quad(11)$ $\:{\text{r}}_{{\text{F}}_{\text{w}}^{-}}\left({\text{x}}_{\text{j}}\right)=\left(\begin{array}{c}\left(\underset{\text{i}}{\text{max}}{\text{r}}_{{\text{F}}_{\text{w}}^{\text{i}}}\left({\text{x}}_{\text{j}}\right):\text{j}\in\:\text{B}\right),\\\:\left(\underset{\text{i}}{\text{min}}{\text{r}}_{{\text{F}}_{\text{w}}^{\text{i}}}\left({\text{x}}_{\text{j}}\right):\text{j}\in\:\text{C}\right)\end{array}\right)\quad\quad\quad(12)$

Step 5: Calculate the distance of each alternative from CPyFPIS and CPyFNIS: The decision-making measures$A_{i}^{ * }$ and Aiare defined for each alternative using the specified CPyFPIS and CPyFNIS. The normalized Euclidean distance is employed because it efficiently manages membership, non-membership, and the radius degree in CPyFVs. The two separation values for each alternative system can be calculated as follows: $\:{\text{S}}^{+}=\sqrt{\frac{1}{2\text{n}}\sum\:_{\text{j}=1}^{\text{n}}\left[\begin{array}{c}{\left({\mathfrak{M}}_{{\text{F}}_{\text{i}}}\text{w}\left({\text{x}}_{\text{j}}\right)-{\mathfrak{M}}_{\text{F}}\text{w}\left({\text{x}}_{\text{j}}\right)\right)}^{2}\\\:+{\left({\mathfrak{N}}_{{\text{F}}_{\text{i}}}\text{w}\left({\text{x}}_{\text{j}}\right)-{\mathfrak{N}}_{\text{F}}\text{w}\left({\text{x}}_{\text{j}}\right)\right)}^{2}\\\:+{\left({\text{r}}_{{\text{A}}_{\text{i}}}\text{w}\left({\text{x}}_{\text{j}}\right)-{\text{r}}_{{\text{A}}^{\text{*}}}\text{w}\left({\text{x}}_{\text{j}}\right)\right)}^{2}\end{array}\right]}\quad\quad\quad(13)$ $\:{\text{S}}^{+}=\sqrt{\frac{1}{2\text{n}}\sum\:_{\text{j}=1}^{\text{n}}\left[\begin{array}{c}{\left({\mathfrak{M}}_{{\text{F}}_{\text{i}}}\text{w}\left({\text{x}}_{\text{j}}\right)-{\mathfrak{M}}_{\text{F}}\text{w}\left({\text{x}}_{\text{j}}\right)\right)}^{2}\\\:+{\left({\mathfrak{N}}_{{\text{F}}_{\text{i}}}\text{w}\left({\text{x}}_{\text{j}}\right)-{\mathfrak{N}}_{\text{F}}\text{w}\left({\text{x}}_{\text{j}}\right)\right)}^{2}\\\:+{\left({\text{r}}_{{\text{A}}_{\text{i}}}\text{w}\left({\text{x}}_{\text{j}}\right)-{\text{r}}_{{\text{A}}^{\text{*}}}\text{w}\left({\text{x}}_{\text{j}}\right)\right)}^{2}\end{array}\right]}\quad\quad\quad(13)$ $\:{\text{S}}^{-}=\sqrt{\frac{1}{2\text{n}}\sum\:_{\text{j}=1}^{\text{n}}\left[\begin{array}{c}{\left({\mathfrak{M}}_{{\text{F}}_{\text{i}}}\text{w}\left({\text{x}}_{\text{j}}\right)-{\mathfrak{M}}_{{\text{F}}^{-}}\text{w}\left({\text{x}}_{\text{j}}\right)\right)}^{2}\\\:+{\left({\mathfrak{N}}_{{\text{F}}_{\text{i}}}\text{w}\left({\text{x}}_{\text{j}}\right)-{\mathfrak{N}}_{{\text{F}}^{-}}\text{w}\left({\text{x}}_{\text{j}}\right)\right)}^{2}\\\:+{\left({\text{r}}_{{\text{F}}_{\text{i}}}\text{w}\left({\text{x}}_{\text{j}}\right)-{\text{r}}_{{\text{F}}^{-}}\text{w}\left({\text{x}}_{\text{j}}\right)\right)}^{2}\end{array}\right]}\quad\quad\quad(14)$

Step 6: Use the formula below to get the closeness coefficient (CC) of each alternative to the ideal solution: $\:\text{C}\text{C}=\frac{{\text{S}}^{-}}{{\text{S}}^{-}+{\text{S}}^{+}}\quad\quad\quad(15)$ The value of the CC will be between 0 and 1; the greater the value of CC, the closer the solution is to the ideal solution.

Step 7: Rank the Alternatives: Rank the alternatives based on CC.

Evaluation of sports quality in higher education

Sports quality in higher education could be defined as the quality of sports performance in an educational facility. It includes aspects of sports facilities, including their accessibility and physical state, human resources represented by the coaching staff, students’ activity level, and poll results indicating their achievements in competitions. Further, sports quality comprises the chances offered for students’ development, satisfaction with the equipment and resources, and the extent to which the programs avail health-related facilities to students. A quality program in sports improves physical education and students’ health and brings complete, overall growth to the students.

Assessing the quality of sports in higher education is crucial to determining the effectiveness of programs in physical education and sports in the development of the learners. In this case, quality assessment assists in identifying how suitable training programs, coaching strategies, facilities, equipment, and other matters concerning sports activities are. Through evaluating the quality of sports, institutions can formulate the right decisions on what to invest in to improve the programs, participation, and satisfaction of the students. Typically, evaluation systems pay much attention to authorities’ decisions and personal preferences, which causes unpredictable inconsistencies and other biases. That is why MCDM methods like the TOPSIS are helpful at this stage. TOPSIS is a technique that measures the distance and chooses the best suitable solution among many options by considering multiple factors. The main improvement proposed here is to include the CPyFS into TOPSIS, which makes it possible to provide for the vagueness of the assessments more effectively, thereby generating more accurate decisions.

Suppose a university would like to conduct a quality assessment of its sports program based on seven criteria. The evaluation would involve five options in alternative sports programs and three decision-makers. The criteria and alternatives would be modelled employing CPyFS, and the TOPSIS method would be used to assess both.

Evaluation of criteria:

• $\:{\mathbf{C}}_{1}$: The general availability and accessibility of sports facilities.

• $\:{\mathbf{C}}_{2}$: Quality of coaching staff.

• $\:{\mathbf{C}}_{3}$: Student participation rate.

• $\:{\mathbf{C}}_{4}$: Promotion schemes and development prospects.

• $\:{\mathbf{C}}_{5}$: Performance in competitions.

• $\:{\mathbf{C}}_{6}$: Customer satisfaction with the available equipment and resources.

• $\:{\mathbf{C}}_{7}$: Health and wellness benefits.

Evaluation of alternatives (Sports programs):

• $\:{\mathbf{A}}_{1}$: Basketball program.

• $\:{\mathbf{A}}_{2}$: Soccer program.

• $\:{\mathbf{A}}_{3}$: Volleyball program.

• $\:{\mathbf{A}}_{4}$: Tennis program.

• $\:{\mathbf{A}}_{5}$: Swimming program.

Decision-Makers:

• $\:{\mathbf{D}}_{1}$: Sports director.

• $\:{\mathbf{D}}_{2}$: Senior coach.

• $\:{\mathbf{D}}_{3}$: Student representative.

Figure 2 shows the flowchart of the methodology.

Fig. 2

Flowchart of the methodology.

As mentioned in the method section, the linguistic evaluations given by the decision-makers, in addition to criteria, CPyFVs, are used as shown in Table 2.

Table 2 Linguistic values for decision-makers and criteria.

Table 3 below reveals the linguistic terms used in assessing the performance levels of the different alternatives under the CPyFS framework. The CPyFVs of the dimensions based on MD, NMD, and radius, respectively, bring the uncertainty and vagueness about the options in decision-making into a clear framework.

Table 3 Linguistic values of alternatives.

Table 4 shows the importance scores of seven sports quality criteria in higher education encompassed by the three decision-makers ($\:\mathbf{D}₁,\:\mathbf{D}₂,\:\mathbf{D}₃$). These values are described using language oriented to linguistics, where each decision-maker assigns importance coefficients to those criteria.

Table 4 Values of the criteria.

Equation 4 was also applied to the decision-makers’ weights, which means that the weights can be arrived at depending on the inputs from the decision-makers. Table 5 below shows the weightage determined for each of the decision-makers. These weights are also useful because they determine the level of influence that the assessment by the various decision-makers has on the final decision.

Table 5 Decision-makers weights.

From Eq. 5 to the respective CPyFWA operator, weights of different criteria have been assessed and proposed, which are shown in Table 6. The weights of each criterion are given below in terms of MD, NMD, and radius, as shown in the following table. These values underline the role of each criterion in making a decision and give a broader perspective on the lesser importance of the other criteria in the assessment.

Table 6 Weights of the criteria.

The evaluation of the different alternatives ($\:\mathbf{A}₁$ to $\:\mathbf{A}₅$) Table 7 shows proposals according to pertinent criteria linked to sports quality in higher education. Three decision-maker ratings are presented in linguistic terms.

Table 7 Assessment of alternatives.

Table 8 shows the overall CPyF decision matrix using the CPyFWA operator by which the linguistic evaluations in Table 7 are transformed.

Table 8 Circular pythagorean fuzzy aggregated decision matrix.

Table 9 displays the weighted aggregated CPyF decision matrix for CPyFS, which was computed by the multiplication operator described. In this step, the value obtained in each criterion from Table 8 is multiplied by the weight of that criterion from Table 6, as per the rules of the CPyF methodology.

Table 9 Weighted-aggregated circular pythagorean fuzzy decision matrix.

The values of the CPyFPIS and the CPyFNIS define the CPyF-TOPSIS and are presented in Table 10. The following table is developed employment of the positive and negative ideal solution derived from the total weighted CPyF decision matrix.

Table 10 Circular pythagorean fuzzy positive ideal solution and negative ideal solution.

The separation measures and CC are presented in Table 11 for each of the mentioned alternatives. The closer an alternative is to the ideal solution while being further away from the negative solution, the higher the CC.

Table 11 Separation and closeness coefficient of each alternative.

Result discussion

The results of this study deliver essential information regarding sports program quality assessment in higher education through the implementation of CPyF-TOPSIS. The A₅ Swimming Program stood out as the most effective choice from the evaluated programs because it showed extensive affinity to the ideal solution depicted in Fig. 3. The system achieves top scores in essential assessment elements concerning facility inventory, coaching quality, student involvement, and program effectiveness. Both programs, A₂ (Soccer Program) and A₁ (Basketball Program), scored well in performance-based evaluations since they successfully addressed institutional requirements and student needs but required additional development. The rankings for A₃ (Volleyball Program) and A₄ (Tennis Program) were lower, indicating that improvements need to be made in student participation and facilities as well as promotional scheme development. The evaluation measures serve to clearly establish differences between alternatives by generating an accurate evaluation that researches their closeness to both ideal and negative-ideal solutions. Decision-making authorities utilize this process to recognize the sports programs that need further strategic and financial enhancement. The CPyF-TOPSIS methodology generates results that corroborate its capacity to deal with uncertainty and imprecision within multi-criteria environments containing both qualitative and quantitative criteria. The evaluation process combines CPyFWA data fusion techniques with a normalized Euclidean distance calculation, leading to both reliable and balanced quality assessment of programs. This methodology enables educational institutions to make decisions that improve their sports programs while maximizing student involvement and resource allocation. This research demonstrates the need for formal decision frameworks in institutional planning because they maintain consistency between student desires and institutional progress objectives in sports programs. The study strengthens the need for iterative evaluation criterion improvement and advanced computational modeling to construct evidence-based educational sports management policies. This analysis confirms that CPyF-TOPSIS allows decision-makers to better distinguish their alternatives and handle uncertainty in multi-criteria evaluation while generating practical insights for sports program enhancement.

Fig. 3

Ranking of alternatives.

Sensitivity analysis

In this case, the sensitivity analysis looks at the influence of changing the decision-makers weights on the overall ranking of the alternatives. This example is made of three deciders with weights depending on the CPyFVs of the linguistic terms used. By modifying these linguistic terms, the weights of the decision-makers are changed, and thus, the criteria weights are changed. This change in criteria weights directly impacts the ranking of alternatives where the TOPSIS method depends on separation measures and closeness coefficients. Figure 4 shows the sensitivity analysis by displaying how changes in decision-makers weights bring shifts in corresponding separation measures of each alternative. The figure illustrates the change of trends in decisions between alternatives and shows how small changes in the decision makers’ weights lead to large differences in the positioning of the various alternatives. This shows the capability of the model to adapt and deal with different requests for decisions and how powerful is a model like this one. However, Fig. 5 brings out the effects on rankings, demonstrating how the variations in decision-makers weights and the criteria weights alter the actual rank of the various options. This is done in the visualization to show how the combinations of criteria and decision-maker weights inarguably alter the evaluations’ results and provide a profound perspective of the relationship between criteria importance and decision-maker preferences. All the above analyses offer useful information on how whichever turns depending on the input signal is sensitive, improving the model’s flexibility in practical conditions.

Fig. 4

Sensitivity analysis by changing the decision-makers weights.

Fig. 5

Effect on ranking by changing decision-makers weights.

Comparison analysis

The proposed CPyF-TOPSIS method shows better outcomes than VIKOR⁴², EDAS⁴³, and DEMATEL⁴⁴, along with WASPAS⁴⁵ and SWARA⁴⁶ as established MCDM techniques, according to Table 12. The traditional decision-making methods operate with moderate or low levels of performance in uncertainty management and weighting flexibilities, while CPyF-TOPSIS maintains maximum operational effectiveness for all vital decision-making conditions. The system presents an effective equilibrium between maintaining decision reliability and computational speed and also performance adaptability that creates a powerful solution for handling advanced decision-making challenges. The ability to handle large problems is compromised for DEMATEL and SWARA because they do not operate with efficient computational capabilities. Both VIKOR and WASPAS demonstrate effective use, but their performance is restricted by their features for dealing with uncertain conditions and flexible weight settings. By uniting CPyFS with TOPSIS through the proposed CPyF-TOPSIS method decision-makers achieve both flexibility as well as precise outcomes. CPyF-TOPSIS functions as a superior process to make stable and adaptable decisions for complex multi-criteria situations.

Table 12 Comparison analysis with existing MCDM method.

The different FS frameworks are evaluated in Table 13 through their property assessments, which include MD, NMD, HD, radius, weighting, and parameter independence. The absence of NMD, as well as hesitancy along with weight functions, makes traditional FS inadequate for uncertainty model representation. CFS adds radius functionality to its structure, although it does not contain NMD or hesitancy features. The IFS and CIFS systems increase FS capabilities through the inclusion of NMD and hesitancy properties, while CIFS enhances this improvement by using circular representation formats. The flexibility of PyFS increases because it supports a wider selection of MD. The proposed CPyFS excels above all other models because it provides optimal flexibility and autonomous parameter behavior with its fully formed structure that integrates MD, NMD, hesitancy, radius, and weighting elements.

Table 13 Comparison analysis of FS models based on key properties.

Advantages of study

The advantages of this study are represented as follows:

• The study can employ CPyFS to overcome uncertainty, vagueness, and hesitation in decision-makers subjective evaluations. This makes the review more credible, enabling meaningful and accurate results.

• The advantage of employing the TOPSIS method is the possibility of evaluating multiple criteria at once, including facilities, quality of coaches, and students’ participation. The assessment carried out in this manner enables a broad appreciation of the quality of sports programs in higher education institutions.

• The MCDM framework ensures that all upcoming solutions (sports programs) are evaluated based on their proximity to the ideal solution. This helps eliminate some bias inherent in other, more conventional assessment approaches and enables fair benchmarking of all candidates.

• Using participants from varied sporting positions (sports directors, coaches, students) guarantees that the evaluation is inclusive. This enhances the evaluation by capturing aspects of the different stakeholders, a function that is paramount when developing effective and appropriate sports programs.

• This study helped identify operational strengths and weaknesses in each sports program so that there is evidence of ways to increase the quality of sports. Such insights may help institutions distribute resources better, review the effectiveness of coaching approaches, and boost student engagement.

• The evaluation process enables university administrators to make rational decisions about developing and sustaining sports programs. The findings can help formulate policies and make strategic decisions about physical education programs in an institution.

• The CPyF TOPSIS model could be applied in any other educational or organizational environment where using more than one criterion is necessary when making decisions. It is also general enough to allow for different parameters and options in quality evaluation.

• To some extent, this work presents criteria such as student participation, satisfaction with equipment, and, more importantly, enhancements of their health status as factors that directly relate to students. This fosters a compelling call for creating sports programs that enhance the positive impact on people’s physical and mental health.

Conclusions

The application of CPyF MCDM and TOPSIS creates an organized system to analyze sports quality levels in educational institutions at various levels. The CPyFS framework supports the model to efficiently assess sports programs while dealing with uncertain or imprecise decision-making processes to achieve more complete evaluation results. To deliver a comprehensive sports program assessment, the evaluation method considers multiple assessment factors, including sports facilities, coaching quality, student participation, competition results, and institutional backing. The evaluation shows that individual programs demonstrate peak performance in area-specific factors such as coaching competence and facility setup, although it needs better student involvement and program creation. Through the CPyF-TOPSIS approach, decision-makers obtain structured performances among alternatives that drive them to optimize resource distributions and improve sports quality. Using advanced fuzzy-based decision models proves vital in educational sports management systems while highlighting the value of data-driven evaluation procedures. Administrators and policymakers can use this model as a valuable instrument to enhance and perfect sports initiatives in higher education institutions. The examination establishes a transparent evaluation procedure which leads to better systematic and effective sports programs.

Limitations

There are certain limitations inherent in this study. The weighting given to the criterion is subjective and can influence the evaluation of results. That is because uncertainty raises the likelihood of making erroneous judgments concerning the quality and availability of data. Some of the ideas presented in this paper may be somewhat complex to comprehend, especially by individuals with limited fuzzy logic knowledge, especially since the study presents CPyFS. Also, some of the factors that may be evaluated may not comprehensively address issues related to the quality of sporting disciplines, the community’s involvement, and the well-being of the athletes. The work presented here suggests that sports quality is dynamic, and therefore, evaluations may degenerate within a short period due to alterations in funding or leadership.

Future research

• Future studies should expand the assessment criteria to include factors such as community involvement, mental health, and athletes’ wellbeing.

• Incorporating inputs from diverse stakeholders can enhance the weighting process, leading to more objective results.

• Integrating machine learning into the model could improve predictive capabilities and decision-making efficiency.

• Collecting data from different settings and time periods will enhance external validity and provide a broader perspective.

• Experimental designs can be employed to track changes in sports quality measures after implementing selected interventions.

• Combining qualitative and quantitative research instruments, such as medical diagnosis⁴⁷, electric cars⁴⁸, financial risk⁴⁹, martial arts teaching skills⁵⁰, and applying interval-valued t-spherical fuzzy sets⁵¹ when supplementing assessment results will give a better understanding of factors that impact the quality of sports. These efforts will improve the knowledge and impact of sports programs in higher education institutions.