Introduction

Forests are the largest terrestrial ecosystems and play a crucial role in the global carbon cycle1,2,3,4. In 2020, China announced its goal to peak carbon emissions by 2030 and achieve carbon neutrality by 2060 for the first time5,6. Accurately estimating forest aboveground carbon stock (ACS) is essential for carbon budgeting and trading carbon sinks, making it a critical component of global climate change and carbon cycle research7,8. Forest ACS refers to the process by which forest plants absorb CO₂ from the atmosphere and store it in vegetation or soil, thereby reducing atmospheric CO₂ concentration6. It is a key parameter for analyzing carbon cycle processes, assessing carbon sink capacity, and understanding carbon distribution within forest ecosystems. It also serves as an essential indicator of ecosystem integrity and community structure9,10. Therefore, access to accurate forest carbon stock data is critical for developing effective carbon emission strategies11,12. Additionally, National Forest Continuous Inventory and Forest Management Inventory data are widely used to estimate large-scale forest biomass and ACS13.

Stratified sampling is the most commonly used method in forest resource surveys14. The Forest Management Inventory data includes a large number of samples, which may introduce errors in carbon stock estimation. Remote sensing images provides macro-level forest information and is not constrained by terrain or other conditions, whereas Forest Management Inventory data includes detailed field survey information. The integration of both can facilitate complementary information, offering more accurate foundational data for stratified sampling. Research results indicate that this approach can significantly enhance the accuracy of forest ACS estimates15,16,17.While this method is well-established in remote sensing, its implementation remains crucial for the specific sample selection and analysis process in our study.

The MLR model is a widely used tool for describing existing data and serves as an essential predictive model18. Its intuitive nature, combined with low technical requirements when processing remote sensing data, makes it suitable for a variety of forest types19,20. In practical applications, the MLR model demonstrates high computational efficiency. Zhang21 used a regression residual model combined with a stepwise multiple regression model to build an estimation model, improving accuracy and reducing estimation errors. However, the MLR model is sensitive to outliers and prone to overfitting, which can result in discrepancies between the model’s predictions and the measured values22. Interpolating the residuals of the MLR model and constructing a Multiple Linear Regression Residual Kriging (MLRRK) model can effectively reduce errors and improve the estimation accuracy of the model. Li, et al.23 interpolated the residuals to reduce the prediction error.

In recent years, Random Forest (RF) has been widely used in research on estimating forest ACS using remote sensing7,24. RF is an effective method for addressing unique ecological problems in various scenarios. It can also be used for classification, regression, and evaluating the importance of variables25,26. Comparisons between RF and other machine learning techniques, as well as traditional statistical regression, have shown that RF offers higher prediction accuracy due to its lower sensitivity to noise in training samples27. Zimbres, et al.28 found that optical data contributed more to predictive models than radar data, with the RF model demonstrating slightly higher accuracy compared to the Classification and Regression Tree (CART) model. An Thi Ngoc, et al.29 showed that combining Sentinel-2 images with RF regression algorithms can effectively predict the spatial distribution of aboveground biomass (AGB) in forests. However, it is important to note that prediction errors can occur when the distance between observations is either too large or too small.

The above studies have overlooked the spatiotemporal heterogeneity of AGB and other forest parameters, as well as the ambiguity in the geographical spatial information of AGB and the physical modeling mechanisms. Geostatistical methods can effectively capture spatial heterogeneity and correlations, and construct spatial prediction models for precise estimation. Sekulic, et al.30 introduced a new spatial interpolation method, Random Forest Spatial Interpolation (RFSI), which selects the optimal combination of spatial proximity observations for making predictions at unknown locations, thereby increasing prediction accuracy. The combination of Random Forest and Kriging to build the Random Forest Kriging model effectively addresses the deficiencies mentioned above31,32. The Kriging method is based on the variable itself, accounting for its spatial variability, and provides a theoretical estimation of interpolation errors. In the random forest residual kriging (RFRK) model, Kriging interpolation is applied to model the residuals predicted by the RF model. Since the residuals contain components reflecting spatial autocorrelation, the RFRK model isolates these components and incorporates them into the RF model’s predictions. As a result, mapping accuracy is improved. This approach is widely used for estimating ACS33. Several studies have utilized the random forest/kriging framework for forest ACS mapping, leading to improved accuracy34,35,36. Du, et al.13 used kriging interpolation to study forest ACS at a small-scale county level and produced a thematic map at this fine scale. Zhou, et al.31 employed the RFCK model and included elevation data as a covariate. Demonstrating that the RFCK model significantly improved the performance of AGB prediction. However, the accuracy improvement was limited, as only elevation was considered as a covariate. Currently, the majority of studies primarily focus on predicting ACS using models such as machine learning, while neglecting the impact of spatial autocorrelation. Therefore, utilizing model residuals for kriging interpolation to enhance the accuracy of ACS estimation has become a critical task37.

As one of the dominant tree species in the region, Pinus densata holds significant research value. Most studies on forest ACS in Shangri-La focus on the impact of terrain factors, using terrain factors for modeling and estimation38. Since most of the estimations of the ACS of Pinus densata in Shangri-La City do not take into account the impacts of precipitation and temperature, this paper combines the residuals of non-parametric models with these two factors for research. This study uses the MLRRK and RFRK models to model and map the ACS of Pinus densata. We evaluated the models using the coefficient of determination (R2), relative Root Mean Square Error (rRMSE), Root Mean Squared Error (RMSE), prediction accuracy (P), and Relative Improvement (RI) to identify the most accurate models. The study’s specific objectives were to (1) utilize stratified sampling to draw representative samples and increase precision. (2) Analyze and compare the interpolation results of RFRK and MLLRK. (3) Study and analyze the interpolation results of the ordinary Kriging interpolation method and cokriging interpolation method. (4) Produce thematic maps of carbon stock. (5) Present the shortcomings of this study as well as future opportunities and challenges.

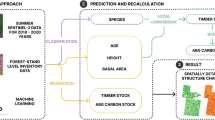
The Landsat 8 OLI remote sensing images dataset for the study area was preprocessed using ENVI 5.6 and ArcGIS 10.8 software. Based on the Forest Management Inventory data, a stratified sampling method was employed, categorizing the samples by forest age to ensure that the selected samples were representative and accurately reflected the ACS in the study area. During the remote sensing image processing, the optimal set of features strongly correlated with ACS was extracted. These features were selected using the Recursive Feature Elimination (RFE) method, which removed the less important features and retained only the most critical variables for model construction. In the predictive modeling phase, both MLR and RF models were applied to derive the predicted ACS values and calculate the corresponding residuals. Subsequently, the MLRRK and RFRK models were used to construct more accurate ACS prediction models. Finally, the optimal model was selected by comparing the predictive accuracy of the different models. The flow of this study is illustrated in Fig. 1.

Fig. 1
figure 1

Overall flow chart of this study.

Full size image

Results

Stratified sampling

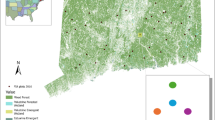
As shown in Fig. 2, the sampling base is concentrated in the third stratum, with a smaller proportion in the first and second strata, but it is ensured that each age group is sampled so that the samples are evenly distributed and representative.

Fig. 2
figure 2

Schematic diagram of stratified sampling results. The distribution map of Pinus densata was created by the author using ArcGIS 10.8 (https://www.arcgis.com/) based on Forest Management Inventory data.

Full size image

Remote sensing features selection

The 'Random Forest Regressor’ algorithm used in this study is available in the ‘Sklearn’ package of Python39. To ensure the comprehensive representation of each variable, the RFE method was employed. The RFE was applied using Random Forest to iteratively remove the least important variables. After several iterations, the top 15 variables were selected based on their contribution to model accuracy. This method selected the top 15 most important the optimal set of features in determining the regional forest ACS estimates.

The top 15 variables deemed most influential were identified. Among the selected optimal set of features, there are 9 textural features and 4 vegetation indices, and the remaining 2 are terrain factors. This indicates that the optimal set of features is highly correlated with ACS. These key factors are visualized in Fig. 3 to illustrate their significance in our analysis.

Fig. 3
figure 3

Importance ranking of the optimal set of features for remote sensing. As in R03B6HO, R03 stands for a window size of 3 × 3 and B6 stands for the 7th band of Landsat.

Full size image

Using the aforementioned 15 modeling parameters, an RF model was constructed and trained with the training set. The R2 between the predicted ACS and the measured ACS based on the training set was 0.871, and the RMSE was 3.948 t/hm2, indicating excellent model fitting performance. As shown in Table 1.

Table 1 Comparison of random forest regression evaluations modeled by multiple combinations of characteristic variables.
Full size table

Comparative analysis of MLRRK and RFRK interpolation

From Tables 2 and 3, we found that the Nugget effect and sum of squared residuals (SSR) of the Exponential model are smaller than the Spherical and Gaussian models. Additionally, the R2 value of the Exponential model surpasses that of the Spherical and Gaussian models, indicating superior fitting performance. Consequently, the Exponential model chosen in this study is adopted as the final model for residual interpolation.

Table 2 MLR residual kriging variational function fitting model and its parameters.
Full size table
Table 3 RF residual kriging variance function fitting model and its parameters.
Full size table

The performance of the MLRCK and RFCK Exponential models in Co-Kriging interpolation, using various covariates (slope, elevation, temperature, and precipitation), was assessed. The results indicate that the RFCK Exponential model consistently achieves higher fitting accuracy than the MLRCK Exponential model. Notably, when temperature and precipitation are included, the R2 value of the RFCK Exponential model increases, and the SSR value decreases, indicating enhanced precision and predictive capability. When slope and elevation were incorporated as covariates in interpolation, accuracy improved; however, the enhancement was less pronounced than when temperature and precipitation were included. The study suggests that incorporating mean annual temperature and precipitation into residual kriging interpolation helps reduce the occurrence probability of extreme values and, to some extent, mitigates the tendency to underestimate low values and overestimate high values.

Comparison of model accuracy

Figure 4b exhibited an RI value of 0.06, with an increase in R2 from 0.53 to 0.55 and a decrease in RMSE from 12 to 11.3 t/hm2. Figure 4c exhibited an RI value of 0.13, an increase in R2 from 0.53 to 0.58, and a decrease in RMSE from 12 to 10.4 t/hm2. Similarly, Fig. 4d exhibited an RI value of 0.23, with an increase in R2 from 0.53 to 0.63 and a decrease in RMSE from 12 to 9.3 t/hm2. Overall, all three models exhibited improved accuracy compared to Fig. 4a, with Fig. 4b demonstrating the most significant improvement.

Fig. 4
figure 4

Model fitting effect.

Full size image

Residual kriging interpolation

From the residual kriging interpolation results, it is evident that the RFCK model (Fig. 5b,c) exhibits a broader residual predictive range compared to the RFOK model (Fig. 5a). Specifically, the RFCKpre (Fig. 5c), which demonstrates a larger residual predictive range than the RFCKtem (Fig. 5b). The residual prediction ranges are as follows: the residual range value of the RFOK model is from − 53.65 to 38.32 t/hm2, the RFCKtem model is from − 53.48 to 38.63 t/hm2, and the RFCKpre model is from − 54.96 to 39.9 t/hm2.

Fig. 5
figure 5

Residual Kriging interpolation. The map was created by the author using ArcGIS 10.8 (https://www.arcgis.com/).

Full size image

Mapping of ACS

Figure 6 presents maps that detail the distribution of ACS in Pinus densata based on Forest Management Inventory data. Figure 6a shows the measured values of Pinus densata from the Forest Management Inventory data. Figure 6b shows the results of the RFOK model. Figure 6c,d illustrate the results of the RFCK model, with annual mean temperature and precipitation as covariates, respectively.

Fig. 6
figure 6

Map of forest ACS. The map was created by the author using ArcGIS 10.8 (https://www.arcgis.com/).

Full size image

Figure 6 shows that incorporating Kriging interpolation into ACS estimation is feasible, with results closely aligning with the measured ACS values. The range for the RFOK model is 5.38 to 104.57 t/hm2, for the RFCKtem model is 5.27 to 104.54 t/hm2, and for the RFCKpre model is 4.78 to 121.55 t/hm2.

After correcting the ACS residuals using kriging interpolation, the resulting forest ACS map accurately reflects both lower and higher AGB values, effectively alleviating issues of overestimating low values and underestimating high values, thus improving the accuracy of forest ACS estimation. Among them, the RFCKpre model exhibits a result range that is closest to the measured values.

Discussion

Influence of sampling method selection on mapping accuracy

The choice of sampling method could significantly impact the accuracy of ACS thematic maps. Scholars found that stratified sampling offers higher accuracy with smaller sample sizes compared to systematic sampling methods40,41. This underscores the critical importance of selecting appropriate sampling strategies for ensuring accurate mapping of ACS.

Research has indicated that an optimal age group structure supports sustainable forest management and ongoing utilization42. Large-scale afforestation is impractical because of space constraints, which advocates instead for near-natural regeneration principles to enhance forest quality through age group adjustments43.

In this study, we employed age groups as the primary stratification criterion for sampling Pinus densata in Shangri-La. The stratified sampling approach focused solely on age groups without incorporating other stratification factors such as origin, geomorphology, or dominant tree species. Future studies could enhance sampling precision by incorporating additional stratification criteria into the sampling framework.

Impact of temperature and precipitation on model accuracy

Most studies on carbon storage in Shangri-La focus primarily on the influence of terrain factors44,45, with limited consideration given to the impact of climate factors. Additionally, existing research suggests that changes in topographical factors are relatively small over longer time scales46.

The spatial distribution and dynamics of ACS are significantly influenced by climatic factors, particularly temperature and precipitation47. Climate change has a significant impact on forest ecosystems. Therefore, this study considers mean annual precipitation and temperature as covariates to explore the accurate estimation of ACS in Pinus densata forests. The results show that this approach provides relatively accurate estimates. Furthermore, the study indicates that including elevation and slope as covariates improves the accuracy of ACS estimation, although the precision is not optimal. This result is consistent with the findings of Luo Kai’s study48, further demonstrating that mean annual temperature and precipitation in the region play a positive role in enhancing the accuracy of forest ACS estimation.

Determination of the RFRK model for mapping

In this study, the RF model was constructed using 15 selected optimal feature sets through the RF-RFE method, achieving an RMSE of 3.948 t/hm2, an R2 of 0.871, and a P of 90.4%. These metrics indicate a strong model fit, high predictive accuracy, and good performance24. The RF model is known for its ability to handle high-dimensional data, manage outliers effectively, and mitigate overfitting issues49. However, the RF model may overlook the effects of spatial autocorrelation. To address this limitation, Kriging interpolation was employed, enhancing overall estimation accuracy by incorporating spatial autocorrelation patterns50.

Combining the RF model with the Kriging method achieves higher mapping accuracy than using the RF model alone. Specifically, the RFCK model outperforms the RFOK and MLRRK models in terms of precision. Moreover, compared with the RFOK, the RFCK demonstrated superior accuracy. This outcome highlights the mitigation of the overestimation of low values and underestimation of high values in ACS estimation to some extent. This approach underscores the effectiveness of integrating machine learning models, such as RF, with spatial interpolation techniques, such as Kriging, to enhance predictive accuracy in ACS mapping studies. This study used the RFRK model to achieve regional ACS mapping with a relatively small dataset, whereas other non-parametric models may require larger datasets for accurate ACS estimation.

Furthermore, the RFRK method can correct model errors and improve estimation accuracy. Several researchers have employed random forest kriging/co-kriging methods along with ICESat-2/ATLAS data or Landsat data for AGB mapping and biomass estimation32,34,36. Their findings consistently show that the method can effectively mitigate the underestimation of high values and the overestimation of low values, highlighting its significant potential in ACS estimation and mapping. This is consistent with the outcomes observed in the present study. In the future, additional models could be considered in combination with Kriging for ACS estimation.

In this study, the RF model achieved an R2 = 0.871 and a P of 90.4%. The RFCKpre exponential model demonstrated the highest fitting accuracy, with R2 = 0.63. In a similar study51 conducted in Shangri-La City, the RF model achieved a P of 88.3%, with the optimal model being the spherical model, which exhibited a fitting accuracy of R2 = 0.65. These results are highly consistent with those of the present study, indicating that the method for estimating the ACS of Pinus densata is feasible. However, since only a single data source was used in this study, the improvement in accuracy was somewhat limited. Future work will explore the use of multi-source remote sensing data for estimating the ACS of Pinus densata.

Conclusions

This study is based on Landsat 8 OLI data and Forest Management Inventory Data, incorporating elevation, slope, precipitation, and temperature as covariates. The residual kriging interpolation was performed using an exponential model, and the accuracies of the MLRRK and RFRK models were compared. The results indicate that (1) Residual interpolation incorporating annual precipitation and temperature as covariates produces more favorable results than interpolation using elevation and slope; (2) the accuracy of the RFRK model outperforms that of the MLRRK model. These findings provide valuable insights into the impact of climatic factors on ACS in Shangri-La. Furthermore, future studies will consider incorporating additional climatic factors to further improve estimation accuracy.

Methods

Study area

Shangri-La is situated in northwestern Yunnan Province (99° 20′ ~ 100° 19′ E, 26° 52′ ~ 28° 52′ N), covering an area of 11,613 km252. Due to its location in a high-altitude, low-latitude zone, the climate varies with increasing altitude. The region experiences distinct wet and dry seasons, characterized by wet summers and autumns and dry winters and springs. The average annual temperature is 5.4 °C, with annual rainfall ranging from 268 to 945 mm. The frost-free period spans from 129 to 197 days. According to the "Vegetation of Yunnan Province" classification standard, Shangri-La hosts ten vegetation types. Dominant forest types include Pinus densata, Quercus aquifolioides, and Abies ferreana53,54. The target species for this study is the Pinus densata, which includes young, middle-aged, near-mature, mature, and over-mature stands forest, including natural and artificial forests distributed within the study area. The location and climate information map of the study area is shown in Fig. 7.

Fig. 7
figure 7

Study area (a) Location of Yunnan; (b) Shangri-La in Yunnan; (c) Sample location in Shangri-La; (d) Distribution of Temperature; (e) Distribution of Precipitation. The map was created by the author using ArcGIS 10.8 (https://www.arcgis.com/).

Full size image

Collection and processing of remote sensing images

The data utilized in this study contains Landsat 8 OLI images obtained from the Geospatial Data Cloud (https://www.gscloud.cn/). Three scenes with minimal cloud cover from 2016 were selected, as shown in Table 4, and preprocessing was carried out using ENVI 5.6 (https://envi.geoscene.cn/) and ArcGIS 10.8 (https://www.arcgis.com/) software. Radiometric calibration and atmospheric correction were applied to mitigate the effects of terrain and aerosols on the surface reflectance55. Images composites were generated to fill cloud gaps and reduce the data volume required for periodic forest cover monitoring56.

Table 4 Provides essential details about the remote sensing images used in this study.
Full size table

Collection and processing of forest management inventory data

The field data employed in this study is the Forest Management Inventory. The dataset employed in this study is tree stand-based, focusing on the general characteristics of forest stands. This dataset includes key attributes such as tree height (H), diameter at breast height (DBH), stocking density, stand tree count, small group size, age classes, and topographic characteristics. These data were collected from various forest regions using standardized survey techniques, offering a comprehensive perspective for forest management and ecological research57.

The forest biomass expansion factor (BEF) method was employed in this study to convert stand stock to biomass, using the formula shown in Eq. (1). Specifically, a BEF of 1.650 was applied for Pinus densata, with a specific volume density (SVD) of 0.41358. Forest ACS is typically calculated by multiplying biomass by the carbon content (CC) factor59. Different forest types have varying carbon conversion coefficients, which are often difficult to obtain. Internationally, a carbon conversion coefficient of 0.5 is commonly used60. Therefore, in this study, we also adopt a carbon conversion coefficient of 0.5 to calculate the carbon stock of the Pinus densata forests in Shangri-La City. As shown in Eq. (2).

$$B = V \times SVD \times BEF$$
(1)
$$\begin{array}{*{20}c} {C = B \times C_{C} } \\ \end{array}$$
(2)

where61 B is forest aboveground biomass, V is tand stock, SVD is wood density, BEF is forest biomass conversion factor, C is Pinus densata ACS, CC is carbon conversion factor.

Collection and processing of digital elevation model data

The Digital Elevation Model (DEM) data based on ASTER utilized in this study were sourced from the Geospatial Data Cloud (https://www.gscloud.cn/). This dataset was employed to extract elevation, slope, and aspect parameters essential for the research. The DEM images underwent necessary preprocessing, with a spatial resolution of 30 m.

Collection and processing of annual average temperature and precipitation data

The annual mean temperature and precipitation data used in this study were acquired from the National Tibetan Plateau Scientific Data Center (https://data.tpdc.ac.cn). These datasets are comprehensive, providing month-by-month information at a 1-km resolution across China.

Stratified sampling

Existing studies have clearly demonstrated that forests ACS increases with the continuous growth of stand age. Accordingly, the present study adopts stand age as the sole criterion for implementing stratified sampling62. The age of Pinus densata stands was categorized into three strata based on its correlation with ACS values obtained by stratified sampling, enabling targeted data collection across different age groups, which are shown in Table 5. With a 95% confidence level, the sampling accuracy was set to 95%, and the sampling unit size was 30 × 30 m, which is consistent with the resolution of Landsat 8 OLI remote sensing images. A total of 210 sample units were selected, as shown in Eq. (3)61.

$$\begin{array}{*{20}c} {n_{0} = \frac{{t^{2} \left( {\sum {W_{i} \sigma_{i} } } \right)^{2} }}{{E^{2} \left( {\sum {W_{i} \overline{y}_{i} } } \right)^{2} }}} \\ \end{array}$$
(3)

where n0 is the total number of sample units, Wi is the proportion of overall units in layer i, \({\sigma }_{i}\) is the standard deviation of layer i, \({\overline{y} }_{i}\) is the mean value of layer i, t is a reliability indicator, E is the relative error.

Table 5 Distribution of ACS in the sample.
Full size table

Remote sensing variable extraction

Previous studies21 have demonstrated a strong correlation between forest ACS and the optimal set of remote sensing features. In this study, a total of 527 optimal features were extracted, including 524 remote sensing factors and 3 environmental factors. Correlation analysis using SPSS 27 (https://www.ibm.com/cn-zh/products/spss-statistics) software identified 271 optimal features that exhibited significant correlations with ACS, as detailed in Table 6.

Table 6 Remote Sensing Variables. The windows for the textural features in the table are 3 × 3, 5 × 5, 7 × 7, 9 × 9, 11 × 11, 13 × 13, 15 × 15, 17 × 17, 19 × 19.
Full size table

Kriging

In this study, mean annual temperature and mean annual precipitation were used as covariates. Exponential, Spherical, and Gaussian63 functions were employed to fit models for ordinary residual Kriging interpolation and residual co-Kriging interpolation. The nugget effect, R2, and the SSR were used as evaluation metrics. The nugget effect represents the ratio of the nugget value to the sill value, which describes the strength of spatial autocorrelation. The smaller the nugget effect, the stronger the spatial autocorrelation64. SSR represents the sum of the squared differences between the measured values and the predicted values. A higher R2 and lower SSR indicate better fitting performance, allowing for the selection of the best-fitting model36.

$$y\left( h \right)\left( {Exponential} \right) = \left\{ {\begin{array}{*{20}c} {0,} & {h = 0} \\ {C_{0} + C\left( {1 - e^{{\frac{ - h}{a}}} } \right)} & {h > 0} \\ \end{array} } \right.$$
(4)
$$y\left( h \right)\left( {Spherical} \right) = \left\{ {\begin{array}{*{20}c} {0,} & 0 \\ {C_{0} + C\left( {\frac{3h}{{2a}} - \frac{{h^{3} }}{{2a^{3} }}} \right),} & {0 < h \le a} \\ {C_{0} + C} & {h > 0} \\ \end{array} } \right.$$
(5)
$$y\left( h \right)\left( {Gaussian} \right) = \left\{ {\begin{array}{*{20}c} {0,} & {h = 0} \\ {C_{0} + C\left( {1 - e^{{\frac{{ - h^{2} }}{{a^{2} }}}} } \right)} & {h > 0} \\ \end{array} } \right.$$
(6)

where C₀ is the nugget constant, a is the range, C is the peak height, C₀ + C is the sill value, and h is the distance between any two points.

$$\begin{array}{*{20}c} {SSR = \mathop \sum \limits_{i = 1}^{n} \left( {y_{i} - \widehat{{y_{i} }}} \right)^{2} } \\ \end{array}$$
(7)

where \({y}_{i}\) represents the measured values,\(\widehat{{y}_{i}}\) represents the predicted values, and \(n\) is the sample size.

Residual values

The residual is the difference between the measured values and the predicted values. Both Fig. 8a,b illustrate that these residuals approximate a normal distribution. This conformity indicates that the residual values of ACS, as derived from both MLR and RF models, meet the necessary assumptions for kriging interpolation.

Fig. 8
figure 8

Histogram of residual distribution.

Full size image

Establishment of MLRRK model

MLR analyzes correlations between multiple independent variables and a dependent variable to develop a predictive model. The MLR equation is expressed as follows65:

$$\begin{array}{*{20}c} {Y = \alpha_{0} + \alpha_{1} X_{1} + \alpha_{2} X_{2} + \cdots + \alpha_{n} X_{n} } \\ \end{array}$$
(8)

where Y represents the ACS at the sample site, \(\alpha_{0}\) represents constant, \(\alpha_{1}\), \(\alpha_{2}\), \(\alpha_{n}\) are the regression coefficients, and \({\text{X}}_{1}\), \({\text{X}}_{2}\), \({\text{X}}_{\text{n}}\) are the independent variables (Selected in this paper are R03B6HO, R05B4ME).

Given the stochastic nature of the data, the MLR model may not fully capture all information, which leaves residual information in the data. Therefore, this study developed MLR residual Kriging models aimed at correcting model errors and improving estimation accuracy.

Using SPSS 27 software, the characteristics of the 15 selected optimal features identified by Random Forest were analyzed using MLR equations. The entry and removal probabilities were set to 0.05 and 0.10, respectively. This process yielded the regression equations for the model, along with R2, F-statistic, and significance values, as detailed in Table 7.

Table 7 Regression model and their associated parameters.
Full size table

The steps for constructing the MLRRK model are the same as those for the RFRK model, as described in the next section.

Establishment of RFRK model

RF generates numerous random classification trees, which can select the final result based on the most frequently occurring tree66,67. When constructing these trees, RF randomly samples n observations from the original dataset using the Bootstrap method, where n represents the number of observations for the dependent variable Y and i denotes its independent variables68.

Random Forest, as noted by35, is a non-spatial approach. However, it may struggle to account for spatial autocorrelation, leading to issues such as underestimating high values and overestimating low values of ACS. To address this, spatial prediction models are necessary. In this study, we employed both ordinary kriging and co-kriging for interpolation.

The steps are as follows:

  1. (1)

    RF Modeling: Random Forest (RF) modeling was initially employed to obtain the predicted value of ACS.

  2. (2)

    Residual Calculation: The residuals were calculated by comparing the measured values with the predicted ACS values, as shown in Eq. (6).

$$\begin{array}{*{20}c} {R\left( {Xi} \right) = ACS_{measured} - ACS_{predicted} } \\ \end{array}$$
(9)

where R(Xi) is the residual value.

  1. (3)

    Normal Distribution Test: The residuals were tested for normal distribution, and the raw data of these residuals followed a normal distribution (Fig. 8b). The residuals of the RF model were subsequently interpolated using kriging.

  2. (4)

    Final Adjustment: The residuals were added to the predicted ACS values to adjust the estimation, as shown in Eq. (7). The adjusted results were then compared with the measured values to identify the optimal model.

$$\begin{array}{*{20}c} {C_{i} = ACS_{predicted} + R\left( {Xi} \right)} \\ \end{array}$$
(10)

where \({\text{C}}_{i}\) is the ACS value, and R(Xi) is the residual value.

  1. (5)

    Mapping ACS: ACS maps were generated for each model and compared with the measured values from the Forest Management Inventory data to identify the model that most closely approximates the true values.

Accuracy assessment

To evaluate model performance, 80% of the data was allocated for training, while the remaining 20% was used for validation. Several evaluation indexes were used in this study to evaluate the predictive accuracy of the ACS model and compare the predicted values with the measured values. These indexes include the coefficient of determination (R2), Relative Improvement (RI), relative Root Mean Square Error (rRMSE), prediction accuracy (P), and Root Mean Squared Error (RMSE). The RI is used to evaluate the improvement of the RFOK and RFCK models compared to the RF model; a higher RI value indicates a more significant improvement in the model. The P reflects the average predictive ability of the model, with higher values indicating better predictive performance. These metrics assess both the prediction accuracy and validation accuracy of the ACS model. The specific evaluation indexes and their formulas are as follows:

$$\begin{array}{*{20}c} {R^{2} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {y_{i} - \hat{y}_{i} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {y_{i} - \overline{y}} \right)}}} \\ \end{array}$$
(11)
$$\begin{array}{*{20}c} {{\text{rRMSE}} = \frac{{\sqrt {{ }\frac{1}{{\text{n}}}\mathop \sum \nolimits_{{{\text{i}} = 1}}^{{\text{n}}} \left( {{\text{y}}_{{\text{i}}} - {\hat{\text{y}}}_{{\text{i}}} } \right)^{2} } }}{{\mathop \sum \nolimits_{{{\text{i}} = 1}}^{{\text{n}}} \left( {{\text{y}}_{{\text{i}}} - \overline{y}} \right)}}} \\ \end{array}$$
(12)
$$\begin{array}{*{20}c} {RMSE = \sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {y_{i} - \hat{y}_{i} } \right)^{2} }}{n}} } \\ \end{array}$$
(13)
$$\begin{array}{*{20}c} {P = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {1 - \left| {\frac{{y_{i} - \hat{y}_{i} }}{{\hat{y}_{i} }}} \right|} \right) \times 100\% } \\ \end{array}$$
(14)
$$\begin{array}{*{20}c} {RI = \frac{{RF_{RMSE} - RFOK/RFCK_{RMSE} }}{{RF_{RMSE} }}} \\ \end{array}$$
(15)

Implementation

In this study, Landsat images were pre-processed and remote sensing factors were extracted using ArcGIS 10.8 (https://www.arcgis.com/) and ENVI 5.6 (https://envi.geoscene.cn/). SPSS 27 (https://www.ibm.com/cn-zh/products/spss-statistics) was used for Pearson analysis of remote sensing factors. Furthermore, in order to establish the RF model, Anaconda3 (https://www.anaconda.com/) was used to build a Python 3.7 environment.