Enhancing Los Angeles’ resilient energy systems amid wildfires

Abstract

Wildfires pose a significant threat to urban regions, with cities like Los Angeles facing increasing challenges due to their vulnerability to frequent and severe wildfire events. This study proposes a novel framework for optimizing fire rescue vehicle scheduling and energy system operations during wildfire disasters. By integrating predictive wildfire modeling with microgrid-based energy systems, the framework dynamically allocates energy resources to critical demands such as emergency shelters, hospitals, and rescue operations when grid supply is disrupted. The wildfire model simulates fire growth, wind-driven spread, and infrastructure impact, ensuring that the framework adapts to real-time conditions. A case study focusing on Los Angeles demonstrates the practical application of the proposed methodology, showcasing improved emergency response, minimized infrastructure losses, and enhanced operational efficiency during wildfires. This research highlights the importance of combining energy systems and disaster management strategies to build resilience in wildfire-prone urban areas, offering valuable insights for emergency planners and policymakers.

Introduction

Wildfires represent one of the most devastating and persistent natural disasters, impacting ecosystems, economies, and human lives across the globe. In recent years, climate change and human activities have exacerbated the frequency and intensity of wildfires, particularly in regions like California, which witnessed catastrophic incidents in 2024 and 2025^1,2. The Los Angeles region, characterized by its extensive urbanization and proximity to wildfire-prone zones, has emerged as a focal point for understanding the interplay between wildfires and critical infrastructure resilience³. The increasing prevalence of wildfires necessitates the development of robust, scalable, and adaptive strategies to manage their impacts on essential systems, including energy networks and emergency rescue operations⁴. Energy systems in wildfire-prone regions face dual challenges: maintaining reliable power supply and supporting emergency operations during extreme events^5,6. Microgrids, as decentralized energy systems, play a crucial role in enhancing the resilience of energy supply under such conditions⁷. Comprising renewable energy sources, energy storage, and advanced control mechanisms, microgrids offer flexible solutions for maintaining critical loads, such as hospitals, shelters, and evacuation centers⁸. However, the dynamic and unpredictable nature of wildfires introduces significant operational uncertainties, such as infrastructure damage, fluctuating energy demands, and constrained rescue efforts due to road closures. These complexities demand innovative modeling and optimization frameworks capable of addressing multi-dimensional challenges in real time⁹.

Emergency rescue operations, integral to wildfire response, are similarly affected by these uncertainties. The deployment of rescue vehicles to high-risk zones, often hindered by fire-induced road closures and unpredictable fire spread, demands precise decision-making to minimize response time and maximize the efficiency of resource allocation. Traditional optimization methods struggle to capture the interdependencies between energy systems and rescue logistics under the influence of dynamic wildfire scenarios^5,10. Bridging this gap requires the integration of advanced methodologies, such as Distributionally Robust Optimization (DRO), to enhance decision-making under uncertainty¹¹. This paper presents a novel, integrated framework to address the dual challenges of energy system resilience and rescue operation optimization during wildfires. The proposed framework combines Differentiable DRO with dynamic fire modeling to capture the complexities of fire-induced uncertainties and their cascading impacts on critical infrastructure. DRO provides a robust approach to optimizing decisions under worst-case distributions of uncertain parameters, ensuring adaptability to dynamic and stochastic wildfire scenarios. Unlike conventional models, this framework introduces differentiable DRO layers, enabling seamless integration with predictive models for fire spread, wind influence, and energy demand dynamics. At the core of this research is a hierarchical optimization model that prioritizes key objectives: minimizing fire damage to energy infrastructure, reducing unmet energy demand, ensuring timely rescue operations, and maximizing system robustness. The fire modeling component leverages advanced simulation techniques, including anisotropic heat equations, to predict fire intensity and spread under varying wind conditions. This predictive capability is integrated with real-time data on wind speed, fire intensity, and suppression resources, creating a dynamic feedback loop that informs both energy allocation and rescue strategies.

The Los Angeles region serves as the case study for this research, offering a realistic and challenging testbed for the proposed framework. This region’s energy infrastructure, comprising over 1,450 microgrids with varying renewable energy penetration levels, faces significant risks from wildfires. The case study incorporates detailed data on fire spread, wind dynamics, and energy demands, enabling the validation of the proposed framework under real-world conditions. By simulating critical scenarios, such as high wind speeds and intense fire conditions, the case study demonstrates the effectiveness of the framework in minimizing fire damage, ensuring energy supply reliability, and optimizing rescue operations. This paper makes four key contributions:

• 1. Development of a Differentiable DRO-Based Framework: The paper introduces a novel optimization framework that integrates DRO with predictive fire modeling. This approach enhances decision-making under uncertainty by capturing the dynamic interactions between fire spread, wind influence, and energy system operations.

• 2. Dynamic Fire Modeling and Its Integration with Energy Systems: A sophisticated fire modeling component is developed, incorporating anisotropic heat equations and real-time wind data. This model quantifies the impact of fire dynamics on energy infrastructure reliability and rescue logistics.

• 3. Optimization of Interdependent Systems: The framework addresses the interdependencies between energy systems and rescue operations, providing a unified solution to minimize fire damage, reduce unmet energy demand, and ensure timely rescue efforts.

• 4. Validation Through a Realistic Case Study: The Los Angeles region is used as a testbed to validate the framework, with detailed simulations demonstrating its effectiveness in addressing diverse wildfire scenarios. The case study highlights the scalability and adaptability of the proposed approach, offering actionable insights for decision-makers. To further clarify the role of microgrids within wildfire scenarios, it is essential to emphasize that the objective of the proposed framework is not to restore disrupted microgrid components via rescue operations. Instead, microgrids function as foundational enablers of emergency response during wildfire-induced grid disruptions. Their ability to operate autonomously ensures the uninterrupted operation of critical emergency services, including regional coordination centers, mobile command posts, hospitals, and traffic signal control systems. This functionality is especially vital in areas where centralized grid infrastructure has been compromised due to fire damage or safety shutoffs. The presence of decentralized energy resources thus directly contributes to the reliability and reach of rescue operations, providing real-time support to first responders and ensuring continuity of life-supporting infrastructure.

Fig. 1

Wildfire-Resilient Energy and Rescue Optimization Framework.

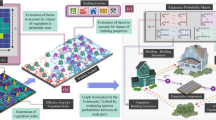
Figure 1 illustrates the proposed wildfire-resilient energy and rescue optimization framework, which integrates fire risk assessment, microgrid dispatch, and emergency vehicle coordination into a unified decision-making structure. The framework begins with multi-source data inputs, including wildfire risk zonation, critical infrastructure locations, and energy-road network topology (Figure 1a). These inputs feed into an integrated system modeling layer that captures both energy dynamics and fire propagation effects on infrastructure (Figure 1b). A real-time coordination module (Figure 1c) utilizes wildfire progression maps to guide adaptive microgrid operation and dynamic rescue routing. Finally, the decision process is governed by a differentiable distributionally robust optimization engine that balances multiple objectives, including rescue response time and energy resilience (Figure 1d).

Literature review

Wildfires have emerged as a critical challenge for infrastructure resilience and emergency management, with increasing frequency and intensity globally. This section reviews the existing literature on wildfire modeling, energy system resilience, and optimization approaches for emergency rescue operations, highlighting the gaps that this paper addresses.

Wildfire modeling has traditionally focused on predicting fire spread and intensity based on environmental factors such as vegetation, topography, and meteorological conditions. Among the most widely used models are those based on anisotropic heat equations, which simulate the directional spread of fires influenced by wind and terrain. Studies by¹² and¹³ emphasize the role of wind-driven fire dynamics, showing that wind speed and direction can significantly amplify fire intensity, particularly in regions with dense vegetation. Additionally, tools like FARSITE and FlamMap have been extensively utilized to predict fire behavior in various geographic contexts, providing foundational insights for risk assessment^14,15. However, existing models often operate in isolation, focusing on fire behavior without integrating the cascading effects on critical infrastructure. Research by¹⁶ highlights the limitations of static fire modeling approaches, which fail to account for dynamic interactions with energy systems and emergency operations. While advancements in real-time data integration from satellite imagery and meteorological sensors have improved prediction accuracy, there remains a gap in leveraging these data for coupled system analysis, such as the interaction between fire spread and energy supply reliability.

The resilience of energy systems in wildfire-prone regions has been a growing area of interest, particularly with the increasing adoption of microgrids and renewable energy technologies. Microgrids, characterized by their decentralized architecture, offer enhanced reliability and flexibility compared to traditional centralized grids. Studies by¹⁷ demonstrate that microgrids can maintain critical energy loads during wildfires by isolating themselves from the broader grid (islanding). However, the resilience of microgrids is significantly influenced by the location of energy resources, their capacity, and the fire’s impact on infrastructure. Previous works, such as those by¹⁸, have proposed optimization models for microgrid operations under disaster scenarios. These models focus on maximizing energy supply and minimizing costs but often lack robust mechanisms to handle the uncertainties introduced by dynamic wildfire conditions. More recent studies, like those by¹⁹, have integrated stochastic optimization techniques to address uncertainty. However, these methods often assume predefined probability distributions, limiting their applicability in highly uncertain scenarios like wildfires, where fire spread, wind patterns, and infrastructure damage are difficult to predict with precision.

Emergency rescue operations during wildfires are critical for minimizing casualties and infrastructure losses. A significant body of research has focused on optimizing vehicle dispatch and route planning to ensure timely responses. Classic approaches include shortest path algorithms, such as Dijkstra’s²⁰, which have been widely applied in rescue logistics. However, these deterministic methods are insufficient in the context of wildfires, where road closures, fire spread, and changing conditions necessitate dynamic and adaptive solutions. Recent advancements in dynamic route optimization incorporate real-time data on road conditions and fire spread. For example²¹, proposed a dynamic programming model that adjusts vehicle routes based on fire progression maps. While effective, such models often lack integration with energy systems, which are critical for powering rescue operations and maintaining communication networks. Research by²² highlights the need for integrated models that consider both energy supply and rescue logistics, emphasizing the importance of real-time resource allocation under uncertainty.

Problem formulation

To provide a clear overview of the proposed modeling framework, we begin by describing the logical connection between the wildfire spread model, microgrid energy system, and emergency resource allocation mechanisms. These three components are jointly formulated under an integrated optimization structure that dynamically responds to evolving fire conditions. The wildfire model serves as the primary driver of environmental uncertainty, simulating the spatial and temporal progression of fire intensity based on wind speed, vegetation density, terrain slope, and ignition probability. The outputs of the wildfire model-specifically fire intensity maps, predicted infrastructure exposure, and road closure risks-are passed to both the emergency logistics layer and the energy optimization layer.

In the emergency resource allocation model, rescue vehicle dispatch decisions are made in real time by incorporating updated accessibility maps and risk zones derived from fire dynamics. Road closure probabilities and fire proximity directly influence route feasibility and travel time penalties in the dispatch model. Simultaneously, the energy system model, which includes microgrid generation, storage, and load balancing, is informed by infrastructure exposure data and demand volatility caused by evacuation behavior or fire-induced outages.These three subsystems interact through shared inputs and feedback loops: the wildfire model informs risk propagation; the rescue operation model schedules vehicle actions under safety and access constraints; and the microgrid optimization ensures critical loads are met despite fluctuating supply and damage risks. This coupled formulation is solved using a Differentiable Distributionally Robust Optimization (DRO) framework, enabling coordinated decision-making under uncertainty.

To address the intertwined challenges of energy system operation and emergency resource coordination under wildfire threats, we formulate a set of mathematical models grounded in multi-layer dynamic optimization. The proposed formulation captures the propagation of wildfires, the operational constraints of microgrids, and the routing of emergency rescue vehicles, all within a unified framework. Each sub-component is coupled through real-time data and jointly optimized to ensure timely responses, minimal infrastructure loss, and resilient energy service under stochastic fire conditions. The core of this framework is a Differentiable DRO model that handles parameter uncertainty while maintaining optimization tractability. We now describe the key objective functions and constraints that structure the integrated decision-making process.

$$\begin{aligned} \begin{aligned} \min _{\varvec{\tau }, \varvec{\chi }}&\sum _{v \in \mathcal {V}} \sum _{r \in \mathcal {R}} \int _{0}^{T} \left( \phi _v^{(r)}(t) + \eta _v^{(r)}(t) \cdot \psi _v^{(r)}(t) \right) \, dt \\&+ \sum _{v \in \mathcal {V}} \sum _{r \in \mathcal {R}} \left[ \omega _v^{(r)} \cdot \int _{0}^{T} \gamma _v^{(r)}(t) \cdot \exp \left( \kappa _v^{(r)} \cdot \Delta _v^{(r)}(t)\right) dt \right] , \end{aligned} \end{aligned}$$

(1)

The first component of the optimization framework models the scheduling of fire rescue vehicles. This subproblem seeks to minimize overall travel time while accounting for delays caused by fire-affected road closures and the relative fire risk of each route. The objective function includes both baseline travel durations and dynamic penalties for proximity to high fire intensity areas. Equation (1) minimizes the total travel time for all rescue vehicles across all routes while incorporating penalties for delays caused by fire impact. The term $\phi _v^{(r)}(t)$ represents the baseline travel time for vehicle $v$ on route $r$ at time $t$, while $\eta _v^{(r)}(t) \cdot \psi _v^{(r)}(t)$ captures additional delays due to dynamic fire conditions, where $\eta _v^{(r)}(t)$ is a fire severity factor and $\psi _v^{(r)}(t)$ models its influence on route accessibility. The second term introduces weighted penalties $\omega _v^{(r)}$ for vehicles exposed to high fire risk, scaled by the exponential factor $\exp \left( \kappa _v^{(r)} \cdot \Delta _v^{(r)}(t)\right)$, where $\Delta _v^{(r)}(t)$ represents the proximity of fire to the vehicle. This comprehensive model ensures optimal rescue timing under dynamically evolving fire conditions.

$$\begin{aligned} \begin{aligned} \min _{\varvec{\mu }, \varvec{\zeta }}&\sum _{m \in \mathcal {M}} \int _{0}^{T} \left( \lambda _m(t) \cdot \pi _m(t) + \theta _m(t) \cdot \max \left( 0, d_m(t) - s_m(t) \right) \right) dt \\&+ \sum _{m \in \mathcal {M}} \beta _m \int _{0}^{T} \left( \rho _m(t) \cdot \left( \sigma _m^{+}(t) + \sigma _m^{-}(t) \right) ^2 \right) \, dt, \end{aligned} \end{aligned}$$

(2)

The second objective function addresses energy dispatch optimization within microgrids during wildfire events. This model ensures economic efficiency, supply-demand balancing, and system stability while accounting for uncertainties in demand and generation. Equation (2) minimizes energy costs for microgrid operations, where $\lambda _m(t)$ represents the marginal energy dispatch cost for microgrid $m$ at time $t$, and $\pi _m(t)$ captures energy prices. The term $\theta _m(t) \cdot \max \left( 0, d_m(t) - s_m(t) \right)$ penalizes unmet demand, where $d_m(t)$ is the demand and $s_m(t)$ the supply. An additional penalty term is included to minimize variability, where $\rho _m(t)$ is a sensitivity parameter and $\sigma _m^{+}(t), \sigma _m^{-}(t)$ represent deviations in supply over time. This approach ensures both economic and stable microgrid operations during fire-induced uncertainties.

$$\begin{aligned} \begin{aligned} \min _{\varvec{\delta }, \varvec{\pi }}&\int _{0}^{T} \sum _{b \in \mathcal {B}} \xi _b(t) \cdot \left( 1 - \exp \left( -\alpha _b \cdot \zeta _b(t) \cdot F_b(t)\right) \right) \, dt \\&+ \sum _{b \in \mathcal {B}} \int _{0}^{T} \gamma _b(t) \cdot \left( \vartheta _b(t) + \frac{\nu _b \cdot P_b(t)}{\left( 1 + \varepsilon _b \cdot \kappa _b(t)\right) } \right) \, dt, \end{aligned} \end{aligned}$$

(3)

The third objective focuses on protecting energy infrastructure from fire-related damage. It quantifies the expected losses based on fire intensity and the effectiveness of suppression efforts. Equation (3) minimizes fire-induced damage to infrastructure, where $\xi _b(t)$ represents the baseline cost of damage to building $b$ at time $t$, and $F_b(t)$ captures fire intensity. The term $\exp \left( -\alpha _b \cdot \zeta _b(t) \cdot F_b(t)\right)$ models the probability of damage mitigation based on suppression efforts $\zeta _b(t)$ and fire intensity. An additional term penalizes grid device failures, where $\vartheta _b(t)$ is the probability of failure, and $P_b(t)$ represents power flow. The fraction $\frac{\nu _b \cdot P_b(t)}{\left( 1 + \varepsilon _b \cdot \kappa _b(t)\right) }$ models the interaction between fire exposure $\kappa _b(t)$ and thermal stress on grid devices.

$$\begin{aligned} \begin{aligned} \max _{\varvec{\eta }, \varvec{\theta }}&\int _{0}^{T} \sum _{k \in \mathcal {K}} \chi _k(t) \cdot \left[ 1 - \Phi _k\left( \frac{\psi _k(t) - \mu _k}{\sigma _k} \right) \right] \cdot R_k(t) \, dt \\&- \sum _{k \in \mathcal {K}} \int _{0}^{T} \tau _k(t) \cdot \left( \beta _k^{+}(t) + \beta _k^{-}(t) \right) ^2 \cdot \Omega _k(t) \, dt, \end{aligned} \end{aligned}$$

(4)

Equation (4) maximizes the robustness of rescue and energy systems under uncertain conditions. The first term incorporates a DRO framework, where $\chi _k(t)$ represents a robustness metric for operation $k$ at time $t$, and $\Phi _k$ is the cumulative distribution function (CDF) for uncertainties in fire spread and energy demand. The second term penalizes variability in decision-making, where $\beta _k^{+}(t), \beta _k^{-}(t)$ represent deviations in robustness parameters, scaled by $\Omega _k(t)$. This ensures adaptive and robust responses to evolving uncertainties in fire scenarios.

$$\begin{aligned} \begin{aligned} \min _{\varvec{\pi }, \varvec{\lambda }}&\sum _{i \in \mathcal {I}} \int _{0}^{T} \xi _i(t) \cdot \Bigg ( 1 - \exp \Big (-\alpha _i \cdot \zeta _i(t) \cdot F_i(t) \cdot \mathcal {H}_i(t) \Big ) \Bigg ) \, dt \\&+ \int _{0}^{T} \sum _{j \in \mathcal {J}} \gamma _j(t) \cdot \left( \frac{\vartheta _j(t) + \rho _j(t) \cdot \kappa _j(t)}{1 + \epsilon _j \cdot P_j(t)} \right) \, dt, \end{aligned} \end{aligned}$$

(5)

Equation (5) captures the expected infrastructure damage cost as a function of fire progression. For infrastructure $i$, $\xi _i(t)$ represents the baseline damage cost, while the term $\exp \Big (-\alpha _i \cdot \zeta _i(t) \cdot F_i(t) \cdot \mathcal {H}_i(t) \Big )$ models the probability of damage mitigation, where $\zeta _i(t)$ is the suppression effort, $F_i(t)$ is the fire intensity, and $\mathcal {H}_i(t)$ is the heat transfer coefficient. For grid components $j$, the second term includes $\gamma _j(t)$, the expected failure cost, adjusted by $\vartheta _j(t)$ (failure probability), $\rho _j(t)$ (thermal stress), and $\kappa _j(t)$ (fire proximity), normalized by $P_j(t)$, the power transfer. This formulation evaluates the dynamic interaction between fire, suppression, and infrastructure impact over time.

$$\begin{aligned} \begin{aligned} \max _{\varvec{\psi }, \varvec{\phi }}&\int _{0}^{T} \sum _{k \in \mathcal {K}} \chi _k(t) \cdot \Bigg ( \min _{\mathbb {P} \in \mathcal {U}} \mathbb {E}_{\mathbb {P}} \Big [ \psi _k(t) \cdot \vartheta _k(t) - \frac{\rho _k(t)}{1 + \epsilon _k \cdot \delta _k(t)} \Big ] \Bigg ) \, dt, \end{aligned} \end{aligned}$$

(6)

Equation (6) employs a Differentiable Distributionally Robust Optimization (DRO) framework to enhance resilience against uncertainties in fire spread and energy operations. Here, $\chi _k(t)$ represents the robustness metric for operation $k$ at time $t$, and the inner minimization term considers the worst-case distribution $\mathbb {P}$ within the ambiguity set $\mathcal {U}$. The expectation $\mathbb {E}_{\mathbb {P}}$ accounts for the interaction of $\psi _k(t)$ (fire uncertainty) and $\vartheta _k(t)$ (system vulnerability), penalized by deviations in energy flow $\rho _k(t)$ and fire intensity $\delta _k(t)$. This ensures robust solutions even under worst-case disaster conditions.

$$\begin{aligned} \begin{aligned} \min _{\varvec{\theta }, \varvec{\omega }}&\int _{0}^{T} \sum _{l \in \mathcal {L}} \left( \beta _l(t) \cdot \left[ \left( \theta _l^{+}(t)\right) ^2 + \left( \theta _l^{-}(t)\right) ^2 \right] \cdot \Omega _l(t) \right) \, dt, \end{aligned} \end{aligned}$$

(7)

Equation (7) introduces a regularization term to enhance solution stability, penalizing fluctuations in the decision variables. Here, $\beta _l(t)$ is the penalty weight for operation $l$ at time $t$, and $\theta _l^{+}(t)$, $\theta _l^{-}(t)$ are deviations in the upper and lower bounds of decision variables, respectively. These are scaled by $\Omega _l(t)$, a time-varying sensitivity factor that captures the operational importance of specific variables. This term ensures smooth and stable solutions under dynamically changing disaster conditions.

$$\begin{aligned} \begin{aligned} \min _{\varvec{\xi }}&\int _{0}^{T} \Bigg ( \sum _{o \in \mathcal {O}} \phi _o \cdot \mathcal {L}_o(t) + \sum _{p \in \mathcal {P}} \psi _p \cdot \mathcal {E}_p(t) + \sum _{q \in \mathcal {Q}} \vartheta _q \cdot \mathcal {D}_q(t) \Bigg ) \, dt, \end{aligned} \end{aligned}$$

(8)

Equation (8) represents the weighted combination of all objectives to form a unified optimization function. The weights $\phi _o, \psi _p, \vartheta _q$ balance the relative importance of rescue time ($\mathcal {L}_o(t)$), energy cost ($\mathcal {E}_p(t)$), and infrastructure damage ($\mathcal {D}_q(t)$) across operations, energy systems, and infrastructure elements. By aggregating the objectives, the optimization achieves a Pareto-efficient solution, balancing competing priorities under disaster-driven uncertainties.

$$\begin{aligned} \begin{aligned} P_{\text {ignite}}(x, y, t) =&\, \int _{\mathcal {A}} \left( \rho _{\text {fuel}}(x', y', t) \cdot \gamma _{\text {temp}}(x', y', t) \cdot \lambda _{\text {humid}}(x', y', t) \right) \\&\cdot \exp \left( -\kappa _{\text {dist}} \cdot \sqrt{(x - x')^2 + (y - y')^2}\right) \, dx' \, dy', \end{aligned} \end{aligned}$$

(9)

Equation (9) models the probability of fire ignition $P_{\text {ignite}}(x, y, t)$ at location $(x, y)$ and time $t$. It integrates the effects of surrounding factors within an area $\mathcal {A}$, including $\rho _{\text {fuel}}(x', y', t)$ (fuel density), $\gamma _{\text {temp}}(x', y', t)$ (temperature effect), and $\lambda _{\text {humid}}(x', y', t)$ (humidity factor). The exponential term accounts for the influence of distance from neighboring points $(x', y')$, controlled by the decay parameter $\kappa _{\text {dist}}$. This formulation captures spatially distributed fire ignition potential under varying environmental conditions.

$$\begin{aligned} \begin{aligned} \mathcal {R}_{\text {spread}}(x, y, t) =&\, \int _{0}^{2\pi } \int _{0}^{\infty } \phi _{\text {wind}}(\theta , t) \cdot \psi _{\text {terrain}}(r, \theta ) \cdot \eta _{\text {fuel}}(r, \theta , t) \\&\cdot \exp \left( -\nu _{\text {atten}} \cdot r\right) \, r \, dr \, d\theta , \end{aligned} \end{aligned}$$

(10)

Equation (10) describes the wind-driven fire spread rate $\mathcal {R}_{\text {spread}}(x, y, t)$ at location $(x, y)$ and time $t$. The integral considers the anisotropic effects of wind direction and speed $\phi _{\text {wind}}(\theta , t)$, terrain slope $\psi _{\text {terrain}}(r, \theta )$, and fuel availability $\eta _{\text {fuel}}(r, \theta , t)$. The attenuation factor $\nu _{\text {atten}}$ governs the decay of fire spread intensity over distance $r$. This formulation captures the complex directional behavior of fire propagation influenced by environmental conditions.

$$\begin{aligned} \begin{aligned} S_{\text {rate}}(x, y, t) =&\, \mathcal {R}_{\text {spread}}(x, y, t) \cdot \Big ( 1 + \alpha _{\text {slope}} \cdot \tan (\theta _{\text {terrain}}) + \beta _{\text {veg}} \cdot \zeta _{\text {density}}(x, y) \Big ), \end{aligned} \end{aligned}$$

(11)

Equation (11) adjusts the fire spread rate $S_{\text {rate}}(x, y, t)$ based on terrain type and vegetation density. The base spread rate $\mathcal {R}_{\text {spread}}(x, y, t)$ is modified by $\alpha _{\text {slope}}$, a slope factor multiplied by the terrain gradient $\tan (\theta _{\text {terrain}})$, and $\beta _{\text {veg}}$, a vegetation factor scaled by density $\zeta _{\text {density}}(x, y)$. This formulation quantifies the acceleration or deceleration of fire spread due to local environmental features.

$$\begin{aligned} \begin{aligned} I_{\text {fire}}(x, y, t) =&\, \int _{0}^{t} \left( Q_{\text {heat}}(x, y, t') - \mathcal {L}_{\text {loss}}(x, y, t') \right) \, dt', \end{aligned} \end{aligned}$$

(12)

Equation (12) computes the fire intensity $I_{\text {fire}}(x, y, t)$ over time $t$ by integrating the net heat input $Q_{\text {heat}}(x, y, t')$ and losses $\mathcal {L}_{\text {loss}}(x, y, t')$. Heat input includes combustion energy, while losses account for radiation, convection, and conduction. This dynamic heat equation captures the time evolution of fire intensity at a given location.

$$\begin{aligned} \begin{aligned} \mathcal {C}_{\text {wind-fire}}(x, y, t) =&\, \phi _{\text {wind}}(t) \cdot \left[ I_{\text {fire}}(x, y, t) \cdot \cos (\theta _{\text {wind}} - \theta _{\text {terrain}}) \right] , \end{aligned} \end{aligned}$$

(13)

Equation (13) couples fire intensity with wind speed and direction, where $\mathcal {C}_{\text {wind-fire}}(x, y, t)$ represents the combined effect. $\phi _{\text {wind}}(t)$ is the wind speed, while the directional interaction depends on $\cos (\theta _{\text {wind}} - \theta _{\text {terrain}})$, capturing alignment between wind and terrain gradients.

$$\begin{aligned} \begin{aligned} Q_{\text {transfer}}(x, y, t) =&\, \kappa _{\text {conv}} \cdot I_{\text {fire}}(x, y, t) \cdot A_{\text {adjacent}}(x, y) \cdot \exp \left( -\mu _{\text {dist}} \cdot d\right) , \end{aligned} \end{aligned}$$

(14)

Equation (14) models heat transfer $Q_{\text {transfer}}(x, y, t)$ to adjacent buildings or grid devices. The convection coefficient $\kappa _{\text {conv}}$ scales the fire intensity $I_{\text {fire}}(x, y, t)$, while $A_{\text {adjacent}}(x, y)$ accounts for exposed surface area. The exponential term captures distance-based attenuation with decay parameter $\mu _{\text {dist}}$.

$$\begin{aligned} \begin{aligned} P_{\text {suppr}}(x, y, t) =&\, \frac{\eta _{\text {water}}(t) \cdot \psi _{\text {access}}(x, y)}{\left( 1 + \xi _{\text {fire}}(x, y, t) \cdot \delta _{\text {response}} \right) }, \end{aligned} \end{aligned}$$

(15)

Equation (15) evaluates fire suppression success probability $P_{\text {suppr}}(x, y, t)$. Suppression effectiveness depends on $\eta _{\text {water}}(t)$ (available water), $\psi _{\text {access}}(x, y)$ (accessibility), and the intensity factor $\xi _{\text {fire}}(x, y, t)$, scaled by response delays $\delta _{\text {response}}$. This equation quantifies dynamic suppression efficacy.

$$\begin{aligned} \begin{aligned} D_{\text {evolve}}(x, y, t) =&\, \int _{0}^{t} \Big ( \gamma _{\text {heat}}(x, y, t') \cdot Q_{\text {transfer}}(x, y, t') \cdot \psi _{\text {structure}}(x, y) \Big ) \, dt', \end{aligned} \end{aligned}$$

(16)

Equation (16) represents the damage evolution $D_{\text {evolve}}(x, y, t)$ in buildings or structures due to fire intensity over time. The damage rate is influenced by the heat transfer $Q_{\text {transfer}}(x, y, t')$, thermal conductivity of the structure $\gamma _{\text {heat}}(x, y, t')$, and structural vulnerability factor $\psi _{\text {structure}}(x, y)$. The integral ensures cumulative damage is captured dynamically as fire spreads.

$$\begin{aligned} \begin{aligned} P_{\text {fail,grid}}(x, y, t) =&\, \frac{\rho _{\text {thermal}}(x, y, t) \cdot I_{\text {fire}}(x, y, t)}{\sigma _{\text {grid}} \cdot \left( 1 + \mu _{\text {cool}} \cdot \psi _{\text {cooling}}(x, y)\right) }, \end{aligned} \end{aligned}$$

(17)

Equation (17) calculates the failure probability $P_{\text {fail,grid}}(x, y, t)$ for grid components. The thermal stress factor $\rho _{\text {thermal}}(x, y, t)$, coupled with fire intensity $I_{\text {fire}}(x, y, t)$, determines failure risk, mitigated by $\psi _{\text {cooling}}(x, y)$, which models cooling mechanisms such as insulation or airflow, scaled by the cooling factor $\mu _{\text {cool}}$.

$$\begin{aligned} \begin{aligned} P_{\text {fail,power}}(t) =&\, \prod _{i \in \mathcal {L}} \left[ 1 - \exp \left( -\nu _{\text {heat}} \cdot \phi _{\text {line}}(i, t) \cdot I_{\text {fire}}(i, t)\right) \right] , \end{aligned} \end{aligned}$$

(18)

Equation (18) models the failure probability $P_{\text {fail,power}}(t)$ of power lines. Here, $\phi _{\text {line}}(i, t)$ represents the susceptibility of line $i$ to thermal stress, while $\nu _{\text {heat}}$ scales the intensity of fire-induced damage. The exponential term captures the cumulative risk across all lines in the set $\mathcal {L}$.

$$\begin{aligned} \begin{aligned} \mathcal {I}_{\text {fire-grid}}(x, y, t) =&\, \kappa _{\text {spread}} \cdot \int _{\mathcal {N}} \psi _{\text {grid}}(x', y') \cdot \exp \left( -\alpha _{\text {dist}} \cdot d(x, y, x', y')\right) \, dx' \, dy', \end{aligned} \end{aligned}$$

(19)

Equation (19) represents the interaction $\mathcal {I}_{\text {fire-grid}}(x, y, t)$ between fire spread and energy infrastructure. It integrates the influence of grid components $\psi _{\text {grid}}(x', y')$ over neighboring regions $(x', y')$, with the interaction strength decaying exponentially over distance $d(x, y, x', y')$, controlled by $\alpha _{\text {dist}}$.

$$\begin{aligned} \begin{aligned} \mathcal {R}_{\text {closure}}(x, y, t) =&\, \mathcal {I}_{\text {fire-grid}}(x, y, t) \cdot \left( \frac{\phi _{\text {road}}(x, y)}{\left( 1 + \beta _{\text {risk}} \cdot P_{\text {ignite}}(x, y, t)\right) } \right) , \end{aligned} \end{aligned}$$

(20)

Equation (20) models the dynamic road closures $\mathcal {R}_{\text {closure}}(x, y, t)$ due to fire-induced risks. The interaction term $\mathcal {I}_{\text {fire-grid}}(x, y, t)$ reflects fire proximity to roads, scaled by $\phi _{\text {road}}(x, y)$, which represents road usability. The denominator incorporates ignition probability $P_{\text {ignite}}(x, y, t)$ and a risk adjustment factor $\beta _{\text {risk}}$.

$$\begin{aligned} \begin{aligned} \mathcal {P}_{\text {reroute}}(x, y, t) =&\, \sum _{r \in \mathcal {R}} \psi _{\text {alt}}(r, t) \cdot \exp \left( -\kappa _{\text {reroute}} \cdot \mathcal {R}_{\text {closure}}(r, t)\right) , \end{aligned} \end{aligned}$$

(21)

Equation (21) computes the probability of rerouting $\mathcal {P}_{\text {reroute}}(x, y, t)$ for rescue vehicles due to road closures. The alternative route feasibility $\psi _{\text {alt}}(r, t)$ is penalized exponentially by the closure impact $\mathcal {R}_{\text {closure}}(r, t)$, with $\kappa _{\text {reroute}}$ controlling sensitivity to closure intensity.

$$\begin{aligned} \begin{aligned} \mathcal {E}_{\text {damage}}(x, y, t) =&\, \int _{\mathcal {B}} \chi _{\text {structure}}(x', y') \cdot D_{\text {evolve}}(x', y', t) \cdot \exp \left( -\lambda _{\text {atten}} \cdot d(x, y, x', y')\right) \, dx' \, dy', \end{aligned} \end{aligned}$$

(22)

Equation (22) evaluates the total damage effect $\mathcal {E}_{\text {damage}}(x, y, t)$ on buildings caused by nearby fire evolution. Structural vulnerability $\chi _{\text {structure}}(x', y')$ and damage evolution $D_{\text {evolve}}(x', y', t)$ decay exponentially with distance $d(x, y, x', y')$, governed by $\lambda _{\text {atten}}$.

$$\begin{aligned} \begin{aligned} \mathcal {C}_{\text {fire-energy}}(x, y, t) =&\, \int _{\mathcal {N}} \phi _{\text {impact}}(n, t) \cdot \mathcal {I}_{\text {fire-grid}}(x', y', t) \, dx' \, dy', \end{aligned} \end{aligned}$$

(23)

Equation (23) calculates the cumulative interaction $\mathcal {C}_{\text {fire-energy}}(x, y, t)$ between fire spread and energy infrastructure. The fire-grid interaction term $\mathcal {I}_{\text {fire-grid}}(x', y', t)$ is weighted by the impact factor $\phi _{\text {impact}}(n, t)$ for each grid component $n$, capturing network-wide dependencies.

$$\begin{aligned} \begin{aligned} \mathcal {L}_{\text {closure}}(t) =&\, \sum _{i \in \mathcal {R}} \psi _{\text {traffic}}(i, t) \cdot \mathcal {R}_{\text {closure}}(i, t), \end{aligned} \end{aligned}$$

(24)

Equation (24) computes the total loss $\mathcal {L}_{\text {closure}}(t)$ due to road closures over all routes $i$. Traffic density $\psi _{\text {traffic}}(i, t)$ amplifies closure impacts, ensuring system-wide effects on mobility are captured.

$$\begin{aligned} \begin{aligned} \sum _{g \in \mathcal {G}} P_g(t) + \sum _{s \in \mathcal {S}} P_s(t) - \sum _{d \in \mathcal {D}} P_d(t) = 0, \quad \forall t \in \mathcal {T}, \end{aligned} \end{aligned}$$

(25)

Equation (25) ensures the microgrid energy balance at each time step $t$, where $\sum _{g \in \mathcal {G}} P_g(t)$ represents the power generated by distributed energy resources (DERs), $\sum _{s \in \mathcal {S}} P_s(t)$ is the power supplied from energy storage systems, and $\sum _{d \in \mathcal {D}} P_d(t)$ denotes the total demand across loads. This balance equation ensures the supply matches the demand within the microgrid.

$$\begin{aligned} \begin{aligned} P_g^{\text {min}} \le P_g(t) \le P_g^{\text {max}}, \quad \forall g \in \mathcal {G}, \; \forall t \in \mathcal {T}, \end{aligned} \end{aligned}$$

(26)

Equation (26) defines the dispatch limits for each DER $g$, bounded by $P_g^{\text {min}}$ and $P_g^{\text {max}}$. These limits account for the physical and operational constraints of renewable and conventional energy resources.

$$\begin{aligned} \begin{aligned} E_s(t+1) = E_s(t) - \eta _s^{\text {out}} \cdot P_s^{\text {out}}(t) + \eta _s^{\text {in}} \cdot P_s^{\text {in}}(t), \quad \forall s \in \mathcal {S}, \; \forall t \in \mathcal {T}, \end{aligned} \end{aligned}$$

(27)

Equation (27) models the state-of-charge dynamics of energy storage systems $s$, where $E_s(t+1)$ is the energy at the next time step, $P_s^{\text {out}}(t)$ and $P_s^{\text {in}}(t)$ are the discharge and charge power, respectively, and $\eta _s^{\text {out}}$ and $\eta _s^{\text {in}}$ are the respective efficiencies.

$$\begin{aligned} \begin{aligned} E_s^{\text {min}} \le E_s(t) \le E_s^{\text {max}}, \quad \forall s \in \mathcal {S}, \; \forall t \in \mathcal {T}, \end{aligned} \end{aligned}$$

(28)

Equation (28) enforces the storage capacity limits, ensuring the state-of-charge $E_s(t)$ remains within the minimum ($E_s^{\text {min}}$) and maximum ($E_s^{\text {max}}$) allowable bounds.

$$\begin{aligned} \begin{aligned} P_g(t) = \xi _g(t) \cdot P_g^{\text {rated}}, \quad \xi _g(t) \sim \mathcal {N}(\mu _g, \sigma _g^2), \quad \forall g \in \mathcal {G}, \; \forall t \in \mathcal {T}, \end{aligned} \end{aligned}$$

(29)

Equation (29) incorporates renewable energy generation variability, where $P_g(t)$ depends on the rated capacity $P_g^{\text {rated}}$ scaled by $\xi _g(t)$, a stochastic variable following a normal distribution with mean $\mu _g$ and variance $\sigma _g^2$. This accounts for uncertainties in renewable energy output under fire conditions.

$$\begin{aligned} \begin{aligned} \sum _{n \in \mathcal {N}} Y_{mn} \cdot V_m \cdot V_n \cdot \cos (\theta _m - \theta _n) = P_m(t), \quad \forall m \in \mathcal {N}, \; \forall t \in \mathcal {T}, \end{aligned} \end{aligned}$$

(30)

Equation (30) represents the power flow constraint for node $m$, where $Y_{mn}$ is the admittance between nodes $m$ and $n$, $V_m$ and $V_n$ are the voltage magnitudes, and $\theta _m, \theta _n$ are the voltage angles. This ensures energy distribution feasibility across the microgrid.

$$\begin{aligned} \begin{aligned} P_d(t) \le \alpha _d \cdot P_d^{\text {max}}, \quad \forall d \in \mathcal {D}, \; \forall t \in \mathcal {T}, \end{aligned} \end{aligned}$$

(31)

Equation (31) prioritizes load allocation under limited energy supply. $\alpha _d$ is the priority factor for load $d$, ensuring that higher-priority loads receive a greater share of available energy.

$$\begin{aligned} \begin{aligned} \min _{\mathbb {P} \in \mathcal {U}} \mathbb {E}_{\mathbb {P}} \Bigg [ \sum _{d \in \mathcal {D}} \Big ( \lambda _d(t) \cdot \big (P_d(t) - \hat{P}_d(t)\big )^2 \Big ) \Bigg ], \end{aligned} \end{aligned}$$

(32)

Equation (32) formulates a DRO-based allocation, where $\mathbb {P} \in \mathcal {U}$ is the worst-case distribution within the ambiguity set $\mathcal {U}$, $\lambda _d(t)$ is the penalty weight, and $\hat{P}_d(t)$ is the predicted demand. This ensures robustness in energy allocation under uncertain demands.

$$\begin{aligned} \begin{aligned} P_s^{\text {out}}(t) + P_s^{\text {in}}(t) \le \beta _s \cdot P_s^{\text {rated}}, \quad \forall s \in \mathcal {S}, \; \forall t \in \mathcal {T}, \end{aligned} \end{aligned}$$

(33)

Equation (33) limits the simultaneous charge and discharge rates of energy storage systems, where $\beta _s$ scales the rated capacity $P_s^{\text {rated}}$ for safety and operational efficiency.

$$\begin{aligned} \begin{aligned} \sum _{d \in \mathcal {D}_{\text {critical}}} P_d(t) \ge \gamma _{\text {reliability}} \cdot \sum _{d \in \mathcal {D}_{\text {critical}}} P_d^{\text {max}}, \quad \forall t \in \mathcal {T}, \end{aligned} \end{aligned}$$

(34)

Equation (34) enforces reliability constraints for critical loads, ensuring that a fraction $\gamma _{\text {reliability}}$ of their maximum demand $P_d^{\text {max}}$ is always met. This guarantees the continuous operation of vital services during disaster scenarios.

$$\begin{aligned} \begin{aligned} x_{v,r,t} \in \{0, 1\}, \quad&\forall v \in \mathcal {V}, \; \forall r \in \mathcal {R}, \; \forall t \in \mathcal {T}, \\&\text {subject to:} \; \sum _{r \in \mathcal {R}} x_{v,r,t} \le 1, \quad \forall v \in \mathcal {V}, \; \forall t \in \mathcal {T}, \end{aligned} \end{aligned}$$

(35)

Equation (35) introduces binary decision variables $x_{v,r,t}$, indicating whether rescue vehicle $v$ is dispatched to route $r$ at time $t$. The constraint ensures that each vehicle is assigned to at most one route at a given time. This binary assignment is crucial for modeling discrete vehicle dispatching decisions in rescue operations.

$$\begin{aligned} \begin{aligned} \sum _{v \in \mathcal {V}} \sum _{r \in \mathcal {R}} \Big ( c_v \cdot x_{v,r,t} \Big ) \le C_{\text {total}}, \quad&\forall t \in \mathcal {T}, \\ \sum _{v \in \mathcal {V}} \Big ( r_v \cdot x_{v,r,t} \Big ) \le R_{\text {total}}, \quad&\forall t \in \mathcal {T}, \end{aligned} \end{aligned}$$

(36)

Equation (36) enforces resource limits for rescue operations. The total vehicle capacity $C_{\text {total}}$ and resource availability $R_{\text {total}}$ are constraints on the number of vehicles $c_v$ and resources $r_v$ allocated across all routes and time periods. This ensures that rescue operations do not exceed logistical constraints.

$$\begin{aligned} \begin{aligned}&x_{v,r,t} \cdot \mathcal {B}_{r,t} \le \phi _{r,t}, \quad \forall v \in \mathcal {V}, \; \forall r \in \mathcal {R}, \; \forall t \in \mathcal {T}, \\&\phi _{r,t} = \exp \left( -\kappa _{\text {block}} \cdot \mathcal {R}_{\text {closure}}(r, t)\right) , \end{aligned} \end{aligned}$$

(37)

Equation (37) defines the feasibility of routes under fire-induced blockages, where $\mathcal {B}_{r,t}$ indicates the baseline route accessibility, and $\phi _{r,t}$ represents the fire-adjusted feasibility score. This score exponentially decays based on the route closure severity $\mathcal {R}_{\text {closure}}(r, t)$, scaled by $\kappa _{\text {block}}$. Vehicles are only dispatched to feasible routes.

$$\begin{aligned} \begin{aligned}&\tau _{v,r,t} = \frac{d_{v,r}}{v_{v,r,t}}, \quad&\forall v \in \mathcal {V}, \; \forall r \in \mathcal {R}, \; \forall t \in \mathcal {T}, \\&v_{v,r,t} = v_{\text {base}} \cdot \left( 1 - \lambda _{\text {fire}} \cdot \mathcal {I}_{\text {fire-route}}(r, t) \right) , \end{aligned} \end{aligned}$$

(38)

Equation (38) calculates travel time $\tau _{v,r,t}$ for vehicle $v$ along route $r$ at time $t$. The travel speed $v_{v,r,t}$ is adjusted from its base speed $v_{\text {base}}$ by a reduction factor proportional to the fire intensity impact $\mathcal {I}_{\text {fire-route}}(r, t)$, scaled by $\lambda _{\text {fire}}$. This dynamic adjustment reflects the delay due to fire spread.

$$\begin{aligned} \begin{aligned} \tau _{v,r,t} \le \tau _{\text {max}}, \quad&\forall v \in \mathcal {V}, \; \forall r \in \mathcal {R}, \; \forall t \in \mathcal {T}, \\ \tau _{\text {max}} = \frac{d_{v,r}}{\epsilon _{\text {min}} \cdot v_{\text {base}}}, \end{aligned} \end{aligned}$$

(39)

Equation (39) imposes an upper bound on travel time, $\tau _{\text {max}}$, determined by the minimum allowable efficiency $\epsilon _{\text {min}}$ of travel speed relative to the base speed $v_{\text {base}}$. This constraint ensures timely rescue operations even under challenging conditions.

$$\begin{aligned} \begin{aligned} \pi _{v,r,t} = \frac{\omega _r}{1 + \xi _{r,t}}, \quad&\forall v \in \mathcal {V}, \; \forall r \in \mathcal {R}, \; \forall t \in \mathcal {T}, \\ \text {maximize:} \;&\sum _{v \in \mathcal {V}} \sum _{r \in \mathcal {R}} \pi _{v,r,t} \cdot x_{v,r,t}, \end{aligned} \end{aligned}$$

(40)

Equation (40) defines priority scheduling for high-risk zones, where $\pi _{v,r,t}$ represents the priority of route $r$ at time $t$. The priority is inversely proportional to the suppression success factor $\xi _{r,t}$, ensuring high-risk routes with lower suppression success receive greater attention.

$$\begin{aligned} \begin{aligned} P_{v,r,t} = \frac{\tau _{v,r,t} \cdot \zeta _v}{\eta _v}, \quad&\forall v \in \mathcal {V}, \; \forall r \in \mathcal {R}, \; \forall t \in \mathcal {T}, \end{aligned} \end{aligned}$$

(41)

Equation (41) calculates energy consumption $P_{v,r,t}$ for vehicle $v$ on route $r$ at time $t$. The consumption depends on travel time $\tau _{v,r,t}$, vehicle load $\zeta _v$, and energy efficiency $\eta _v$. This ensures energy constraints are aligned with route and vehicle-specific factors.

$$\begin{aligned} \begin{aligned} \mathcal {R}_{\text {alloc}}(t) = \sum _{v \in \mathcal {V}} \sum _{r \in \mathcal {R}} \left( \phi _{v,r,t} \cdot \mathcal {I}_{\text {fire-route}}(r, t) \cdot x_{v,r,t} \right) , \quad&\forall t \in \mathcal {T}, \end{aligned} \end{aligned}$$

(42)

Equation (42) dynamically allocates resources based on fire conditions. $\mathcal {R}_{\text {alloc}}(t)$ aggregates the fire impact $\mathcal {I}_{\text {fire-route}}(r, t)$ for dispatched routes, weighted by vehicle feasibility $\phi _{v,r,t}$.

$$\begin{aligned} \begin{aligned} \mathcal {R}_{\text {update}}(t+1) = \mathcal {R}_{\text {alloc}}(t) + \lambda _{\text {adaptive}} \cdot \Delta _{\text {fire}}(t), \quad&\forall t \in \mathcal {T}, \end{aligned} \end{aligned}$$

(43)

Equation (43) updates resource allocation for the next time step, where $\Delta _{\text {fire}}(t)$ represents changes in fire conditions, scaled by $\lambda _{\text {adaptive}}$, the adaptability parameter. This ensures resource allocation is responsive to evolving disaster scenarios.

$$\begin{aligned} \begin{aligned} \sum _{t \in \mathcal {T}_{\text {window}}} x_{v,r,t} \le 1, \quad&\forall v \in \mathcal {V}, \; \forall r \in \mathcal {R}, \end{aligned} \end{aligned}$$

(44)

Equation (44) enforces time windows for rescue operations, ensuring that vehicles are dispatched only once within a predefined window $\mathcal {T}_{\text {window}}$. This guarantees efficient resource utilization across limited time periods.

The proposed framework is built upon several modeling assumptions to ensure computational feasibility and to reflect operational realities under wildfire scenarios. Wildfire propagation is modeled using anisotropic spread functions driven by wind direction, terrain, and fuel density, assuming homogeneous ignition probabilities within a local grid cell. Microgrids are assumed to operate in islanded mode once grid disruptions are detected, with dispatchable and renewable sources available at pre-specified capacities. Emergency vehicles are assumed to depart from known depots with fixed travel time limits and speed-reduction coefficients proportional to local fire intensity. All real-time data inputs, including wind vectors and fire front locations, are treated as time-discretized inputs updated hourly. Demand forecasts are perturbed under fire events, with higher demand predicted near evacuation shelters and hospitals. The DRO ambiguity sets are constructed using Wasserstein distance to capture distributional uncertainty in fire spread and energy demand.

Methodology

To enhance the contextual understanding of the simulated scenario, we first outline the timeline of the wildfire event and the associated emergency response phases. The case study considers a 48-hour high-risk wildfire event within Los Angeles County, beginning with a fire ignition at Hour 0 in a brush-heavy area under dry, windy conditions. Between Hour 0 and Hour 6, the fire spreads rapidly due to strong Santa Ana winds, prompting emergency alerts and early-stage containment planning. By Hour 12, the wildfire reaches critical infrastructure clusters, including distribution substations and key road segments, leading to partial power outages and blocked evacuation routes. At this stage, microgrids begin transitioning to islanded mode to supply hospitals and emergency shelters. Between Hour 18 and Hour 30, the fire evolves unpredictably, forcing adaptive rerouting of rescue vehicles and reallocation of energy to priority zones. Suppression efforts intensify, and by Hour 48, fire growth slows significantly, initiating system restoration planning. This timeline is used to structure the dynamic optimization and real-time response strategies evaluated in the following sections. This section outlines the methodology used to solve the integrated optimization problem for wildfire response and energy system management in Los Angeles. Leveraging predictive wildfire models, energy system dynamics, and advanced optimization techniques, the proposed approach employs Differentiable DRO layers to handle uncertainty and adapt to evolving conditions. Key components include the development of a dynamic scheduling algorithm for fire rescue vehicles, integration of renewable energy forecasts, and simulation-based validation using real-life data from Los Angeles wildfire events. The methodology ensures scalability and practical applicability to real-world scenarios.

$$\begin{aligned} \begin{aligned} \mathcal {U} = \Big \{ \mathbb {P} \in \mathcal {P}(\Theta ) :&\inf _{\mathbb {Q} \in \mathcal {P}(\Theta )} \int _{\Theta } \Vert \theta - \theta ' \Vert \, d\mathbb {Q}(\theta ') \le \delta , \\&\mathbb {E}_{\mathbb {P}}[\phi (\Theta )] = \mathbb {E}_{\mathbb {P}_0}[\phi (\Theta )] + \epsilon , \quad \forall \phi \in \mathcal {F} \Big \} \end{aligned} \end{aligned}$$

(45)

Equation (45) defines the ambiguity set $\mathcal {U}$ for the uncertain fire spread probabilities. The set $\mathcal {U}$ is constructed using a Wasserstein distance metric, where $\mathbb {P}_0$ represents the nominal distribution, and $\delta$ is the allowable deviation. The condition ensures that the expected values of functionals $\phi (\Theta )$ under $\mathbb {P}$ align with $\mathbb {P}_0$ within a tolerance $\epsilon$. This formulation encapsulates the worst-case uncertainty around fire propagation probabilities.

$$\begin{aligned} \begin{aligned} \mathbb {P}(\Theta , \mathcal {D}) =&\int _{\Theta } \int _{\mathcal {D}} f_{\Theta , \mathcal {D}}(\theta , d) \cdot g_{\Theta }(\theta ) \cdot h_{\mathcal {D}}(d) \, d\theta \, dd \end{aligned} \end{aligned}$$

(46)

Equation (46) models the joint uncertainty distribution $\mathbb {P}(\Theta , \mathcal {D})$ of fire propagation parameters $\Theta$ and energy demand $\mathcal {D}$. The joint density function $f_{\Theta , \mathcal {D}}(\theta , d)$ accounts for the dependency between $\Theta$ and $\mathcal {D}$, while $g_{\Theta }(\theta )$ and $h_{\mathcal {D}}(d)$ are their respective marginals. This representation captures the coupled uncertainty dynamics between fire spread and energy demands.

$$\begin{aligned} \begin{aligned} \min _{\pi \in \mathcal {X}} \max _{\mathbb {P} \in \mathcal {U}} \Bigg \{&\int _{\Theta } \int _{\mathcal {D}} \Big ( \alpha \cdot C_{\text {rescue}}(\pi , \theta ) + \beta \cdot C_{\text {energy}}(\pi , d) \\&+ \gamma \cdot R_{\text {fire}}(\theta , d) \Big ) \, d\mathbb {P}(\theta , d) \Bigg \} \end{aligned} \end{aligned}$$

(47)

Equation (47) establishes the DRO objective function to minimize worst-case expected costs. The objective comprises rescue costs $C_{\text {rescue}}(\pi , \theta )$, energy allocation costs $C_{\text {energy}}(\pi , d)$, and fire-induced risks $R_{\text {fire}}(\theta , d)$, weighted by $\alpha$, $\beta$, and $\gamma$, respectively. The inner maximization evaluates costs under the worst-case distribution $\mathbb {P}$ from the ambiguity set $\mathcal {U}$.

$$\begin{aligned} \begin{aligned} \min _{\pi \in \mathcal {X}} \max _{\mathbb {P} \in \mathcal {U}} \Bigg \{&\int _{\Theta } \int _{\mathcal {D}} \Big ( \alpha \cdot C_{\text {rescue}}(\pi , \theta ) + \beta \cdot C_{\text {energy}}(\pi , d) \Big ) \, d\mathbb {P}(\theta , d) \Bigg \} + \eta \cdot \Vert \pi - \pi _0 \Vert ^2 \end{aligned} \end{aligned}$$

(48)

This enhanced DRO formulation incorporates resilience metrics by adding a regularization term $\eta \cdot \Vert \pi - \pi _0 \Vert ^2$, which penalizes deviations from a baseline decision policy $\pi _0$. This promotes solution stability while minimizing costs across rescue and energy operations under uncertainty.

$$\begin{aligned} \begin{aligned} R_{\text {fire-risk}} = \int _{\Theta } \int _{\mathcal {Z}}&\Big ( \omega _{\text {infra}} \cdot D_{\text {infra}}(z, \theta ) + \omega _{\text {grid}} \cdot D_{\text {grid}}(z, \theta ) \Big ) \, g_{\Theta , \mathcal {Z}}(\theta , z) \, d\theta \, dz \end{aligned} \end{aligned}$$

(49)

The fire-risk factor $R_{\text {fire-risk}}$ quantifies the expected damage to infrastructure ($D_{\text {infra}}(z, \theta )$) and grid components ($D_{\text {grid}}(z, \theta )$), weighted by $\omega _{\text {infra}}$ and $\omega _{\text {grid}}$. The distribution $g_{\Theta , \mathcal {Z}}(\theta , z)$ models the joint uncertainty in fire parameters $\Theta$ and infrastructure exposure $\mathcal {Z}$. This term ensures fire-induced damages are prioritized in the optimization process.

$$\begin{aligned} \begin{aligned} \mathbb {P}_{\text {wind-fire}}(\Theta ) =&\int _{\Theta } \Bigg ( \phi _{\text {wind}}(\theta ) \cdot \exp \Big (-\kappa _{\text {spread}} \cdot R_{\text {fire}}(\theta )\Big ) \Bigg ) \, d\mathbb {P}_0(\theta ) \end{aligned} \end{aligned}$$

(50)

This equation models the influence of wind-driven fire propagation on the uncertainty distribution $\mathbb {P}_{\text {wind-fire}}(\Theta )$. The term $\phi _{\text {wind}}(\theta )$ scales the wind effect, while $\exp (-\kappa _{\text {spread}} \cdot R_{\text {fire}}(\theta ))$ captures the attenuation of fire risk with increasing distance from the origin.

To improve transparency and reproducibility, we provide further details on the predictive and optimization components of our framework. Wildfire propagation is modeled using a high-resolution cellular automata approach, which simulates spatiotemporal fire dynamics based on terrain gradient, wind direction, fuel density, and ignition probability. These simulations generate dynamic fire intensity maps that are updated every simulation cycle and used as real-time environmental input for both rescue and energy dispatch planning. For emergency vehicle scheduling, we implement a reinforcement learning-based policy using Proximal Policy Optimization (PPO), which enables agents to adaptively route rescue units while minimizing travel time and exposure to hazardous zones. The state space includes fire severity, road accessibility, and vehicle capacity, while the reward structure incentivizes timely arrival and full coverage of critical nodes.

Microgrid operation management is conducted using a mixed-integer linear programming (MILP) model that optimizes energy dispatch across distributed resources and storage units. The objective function balances operational cost, unmet load penalties, and load smoothing constraints, under the influence of dynamic fire-related uncertainties. The model is solved iteratively with real-time updates from the wildfire simulation engine and emergency logistics module.

$$\begin{aligned} \begin{aligned} \mathcal {R}_{\text {infra}}(\theta , t) = \int _{\mathcal {I}} \rho _{\text {damage}}(i, \theta ) \cdot \xi _{\text {resilience}}(i, t) \, di \end{aligned} \end{aligned}$$

(51)

Equation (51) quantifies the impact of fire intensity on infrastructure reliability. The resilience factor $\xi _{\text {resilience}}(i, t)$ adjusts for the ability of infrastructure $i$ to withstand fire-induced damage, scaled by the damage probability $\rho _{\text {damage}}(i, \theta )$ over all infrastructure components $\mathcal {I}$.

$$\begin{aligned} \begin{aligned} \mathcal {E}_{\text {demand}}(\Theta , t) = \int _{\mathcal {N}} \Big ( \lambda _{\text {fire}} \cdot \Delta _{\text {heat}}(n, \Theta ) + \mu _{\text {demand}}(n, t) \Big ) \, dn \end{aligned} \end{aligned}$$

(52)

Equation (52) captures fire-induced variability in energy demands. The term $\Delta _{\text {heat}}(n, \Theta )$ models fire-driven demand fluctuations for node $n$, scaled by $\lambda _{\text {fire}}$. The baseline demand $\mu _{\text {demand}}(n, t)$ integrates additional variability into the total demand calculation.

$$\begin{aligned} \begin{aligned} \mathcal {E}_{\text {alloc}}(\pi , \mathbb {P}) = \min _{\pi \in \mathcal {X}} \max _{\mathbb {P} \in \mathcal {U}} \Bigg \{&\int _{\mathcal {D}} \Big ( \lambda _{\text {reliability}} \cdot \mathbb {P}_{\text {load}}(d) \cdot P_{\text {alloc}}(\pi , d) \Big ) \, d\mathbb {P}(d) \Bigg \} \end{aligned} \end{aligned}$$

(53)

Equation (53) optimizes the allocation of energy resources $\mathcal {E}_{\text {alloc}}$ to maximize reliability under uncertain demand profiles. The term $\mathbb {P}_{\text {load}}(d)$ represents the probability distribution of demand $d$, and $P_{\text {alloc}}(\pi , d)$ is the allocated power based on decisions $\pi$. The parameter $\lambda _{\text {reliability}}$ emphasizes the importance of reliability.

$$\begin{aligned} \begin{aligned} \mathcal {C}_{\text {dispatch}} = \min _{\pi \in \mathcal {X}} \max _{\mathbb {P} \in \mathcal {U}} \Bigg \{&\int _{\mathcal {D}} \Big ( \alpha _{\text {dispatch}} \cdot C_{\text {dispatch}}(P, d) + \beta _{\text {unmet}} \cdot \max (0, d - s(P)) \Big ) \, d\mathbb {P}(d) \Bigg \} \end{aligned} \end{aligned}$$

(54)

Equation (54) balances energy dispatch costs $\alpha _{\text {dispatch}} \cdot C_{\text {dispatch}}(P, d)$ and penalties for unmet demand $\beta _{\text {unmet}} \cdot \max (0, d - s(P))$. Here, $s(P)$ represents the supply corresponding to power $P$, while the ambiguity set $\mathbb {P}$ handles uncertain demand distributions.

$$\begin{aligned} \begin{aligned} E_s(t+1) = E_s(t) + \eta _s^{\text {in}} \cdot P_s^{\text {in}}(t) - \eta _s^{\text {out}} \cdot P_s^{\text {out}}(t), \quad&E_s^{\text {min}} \le E_s(t) \le E_s^{\text {max}} \end{aligned} \end{aligned}$$

(55)

Equation (55) models the operational constraints of energy storage systems. The state-of-charge $E_s(t+1)$ depends on the previous state $E_s(t)$, energy charged $P_s^{\text {in}}(t)$, and energy discharged $P_s^{\text {out}}(t)$, scaled by charging/discharging efficiencies $\eta _s^{\text {in}}$ and $\eta _s^{\text {out}}$. The state-of-charge is constrained between $E_s^{\text {min}}$ and $E_s^{\text {max}}$.

$$\begin{aligned} \begin{aligned} \mathcal {R}_{\text {dispatch}}(\pi , \mathbb {P}) = \min _{\pi \in \mathcal {X}} \max _{\mathbb {P} \in \mathcal {U}} \Bigg \{&\int _{\mathcal {R}} \Big ( \xi _{\text {route}} \cdot \tau _{\text {travel}}(\pi , r) + \zeta _{\text {blockage}} \cdot \phi _{\text {access}}(\pi , r) \Big ) \, d\mathbb {P}(r) \Bigg \} \end{aligned} \end{aligned}$$

(56)

Equation (56) optimizes vehicle dispatch by minimizing travel times $\tau _{\text {travel}}(\pi , r)$ and penalties for route blockages $\phi _{\text {access}}(\pi , r)$, weighted by $\xi _{\text {route}}$ and $\zeta _{\text {blockage}}$. The distribution $\mathbb {P}$ handles uncertainties in route conditions.

$$\begin{aligned} \begin{aligned} \tau _{v,r,t} = \frac{d_{v,r}}{v_{\text {base}} \cdot \left( 1 - \lambda _{\text {fire}} \cdot \mathcal {I}_{\text {fire-route}}(r, t) \right) }, \quad&\tau _{v,r,t} \le \tau _{\text {max}} \end{aligned} \end{aligned}$$

(57)

Equation (57) adjusts travel times $\tau _{v,r,t}$ based on worst-case fire spread scenarios. The base speed $v_{\text {base}}$ is reduced by the fire impact $\mathcal {I}_{\text {fire-route}}(r, t)$, scaled by $\lambda _{\text {fire}}$. A constraint ensures travel times do not exceed the maximum allowable limit $\tau _{\text {max}}$.

$$\begin{aligned} \begin{aligned} \mathcal {P}_{\text {alloc}} = \sum _{r \in \mathcal {R}} \Big ( \pi _r \cdot \psi _{\text {risk}}(r) \cdot \phi _{\text {priority}}(r) \Big ), \quad \pi _r \in \{0, 1\} \end{aligned} \end{aligned}$$

(58)

Equation (58) allocates vehicles to high-risk areas based on risk factors $\psi _{\text {risk}}(r)$ and priority metrics $\phi _{\text {priority}}(r)$. The binary decision variable $\pi _r$ ensures that each route is either selected or not.

$$\begin{aligned} \begin{aligned} \mathcal {L}_{\text {reliability}} = \int _{\mathcal {D}_{\text {critical}}} \Big ( \lambda _{\text {critical}} \cdot P_{\text {supply}}(d) - \beta _{\text {failure}} \cdot \phi _{\text {fire}}(d) \Big ) \, dd, \quad \mathcal {L}_{\text {reliability}} \ge \gamma _{\text {threshold}} \end{aligned} \end{aligned}$$

(59)

Equation (59) models the minimum reliability threshold for critical energy loads. The reliability $\mathcal {L}_{\text {reliability}}$ depends on the supplied power $P_{\text {supply}}(d)$ and fire-induced failure probabilities $\phi _{\text {fire}}(d)$, scaled by $\lambda _{\text {critical}}$ and $\beta _{\text {failure}}$. It ensures the reliability remains above a predefined threshold $\gamma _{\text {threshold}}$.

$$\begin{aligned} \begin{aligned} \mathcal {E}_{\text {resilience}} = \int _{\mathcal {N}} \Big ( \rho _{\text {fire}}(n, t) \cdot \xi _{\text {response}}(n, t) \cdot P_{\text {allocated}}(n, t) \Big ) \, dn \end{aligned} \end{aligned}$$

(60)

Equation (60) updates energy reliability constraints by incorporating fire spread predictions. The resilience $\mathcal {E}_{\text {resilience}}$ is determined by fire severity $\rho _{\text {fire}}(n, t)$, system response $\xi _{\text {response}}(n, t)$, and allocated power $P_{\text {allocated}}(n, t)$.

$$\begin{aligned} \begin{aligned} \mathcal {R}_{\text {feasibility}}(t) = \int _{\mathcal {R}} \Big ( \phi _{\text {route}}(r, t) \cdot \psi _{\text {dispatch}}(r, t) \Big ) \, dr, \quad \mathcal {R}_{\text {feasibility}}(t) \ge \gamma _{\text {dispatch}} \end{aligned} \end{aligned}$$

(61)

Equation (61) ensures the feasibility of rescue operations under dynamically evolving fire conditions. The feasibility metric $\mathcal {R}_{\text {feasibility}}(t)$ integrates route accessibility $\phi _{\text {route}}(r, t)$ and dispatch success $\psi _{\text {dispatch}}(r, t)$, constrained to meet a minimum threshold $\gamma _{\text {dispatch}}$.

$$\begin{aligned} \begin{aligned} \mathcal {E}_{\text {realloc}}(t) = \sum _{n \in \mathcal {N}} \Big ( \psi _{\text {fire}}(n, t) \cdot P_{\text {available}}(n, t) - \lambda _{\text {demand}} \cdot P_{\text {required}}(n, t) \Big ) \end{aligned} \end{aligned}$$

(62)

Equation (62) reallocates energy resources dynamically among microgrid nodes based on fire conditions. The allocation $\mathcal {E}_{\text {realloc}}(t)$ considers fire severity $\psi _{\text {fire}}(n, t)$, available energy $P_{\text {available}}(n, t)$, and required demand $P_{\text {required}}(n, t)$, penalized by $\lambda _{\text {demand}}$. This ensures that nodes affected by severe fire conditions receive prioritized energy resources.

$$\begin{aligned} \begin{aligned} \mathcal {V}_{\text {dispatch}}(t) = \sum _{r \in \mathcal {R}} \Big ( \phi _{\text {priority}}(r, t) \cdot \psi _{\text {fire-intensity}}(r, t) \cdot x_r(t) \Big ) \quad x_r(t) \in \{0, 1\} \end{aligned} \end{aligned}$$

(63)

Equation (63) updates vehicle dispatch decisions based on real-time fire intensity maps. The decision variable $x_r(t)$ determines whether route $r$ is selected for dispatch, weighted by priority $\phi _{\text {priority}}(r, t)$ and fire intensity $\psi _{\text {fire-intensity}}(r, t)$.

$$\begin{aligned} \begin{aligned} \mathcal {L}_{\text {reg}} = \eta \cdot \Vert \pi - \pi _0\Vert ^2 + \zeta \cdot \Vert \mathbb {P} - \mathbb {P}_0\Vert ^2 \end{aligned} \end{aligned}$$

(64)

Equation (64) introduces a regularization term to stabilize DRO solutions. The first term $\eta \cdot \Vert \pi - \pi _0\Vert ^2$ penalizes deviations from the baseline decision policy $\pi _0$, while the second term $\zeta \cdot \Vert \mathbb {P} - \mathbb {P}_0\Vert ^2$ controls variability in the distribution $\mathbb {P}$ relative to the nominal distribution $\mathbb {P}_0$.

$$\begin{aligned} \begin{aligned} \mathcal {P}_{\text {penalty}} = \sum _{n \in \mathcal {N}} \Big ( \lambda _{\text {deviation}} \cdot \Vert P_{\text {allocated}}(n, t) - P_{\text {initial}}(n, t)\Vert \Big ) \end{aligned} \end{aligned}$$

(65)

Equation (65) introduces a penalty term $\mathcal {P}_{\text {penalty}}$ for deviations from initial resource allocations. The term penalizes discrepancies between allocated power $P_{\text {allocated}}(n, t)$ and initial allocations $P_{\text {initial}}(n, t)$, scaled by $\lambda _{\text {deviation}}$.

$$\begin{aligned} \begin{aligned} R_{\text {fire-risk}} = \int _{\mathcal {N}} \psi _{\text {damage}}(n) \cdot \phi _{\text {fire}}(n) \cdot \rho _{\text {impact}}(n) \, dn \end{aligned} \end{aligned}$$

(66)

Equation (66) evaluates the worst-case fire risk across all microgrid nodes. The risk $R_{\text {fire-risk}}$ integrates damage probability $\psi _{\text {damage}}(n)$, fire intensity $\phi _{\text {fire}}(n)$, and impact factor $\rho _{\text {impact}}(n)$ over all nodes.

$$\begin{aligned} \begin{aligned} \mathcal {P}_{\text {priority}} = \sum _{r \in \mathcal {R}} \Big ( \xi _{\text {urgency}} \cdot \phi _{\text {risk}}(r) \cdot \psi _{\text {impact}}(r) \Big ) \end{aligned} \end{aligned}$$

(67)

Equation (67) models risk-adjusted prioritization of rescue operations. The priority $\mathcal {P}_{\text {priority}}$ depends on urgency factor $\xi _{\text {urgency}}$, risk level $\phi _{\text {risk}}(r)$, and impact $\psi _{\text {impact}}(r)$ for each route $r$.

$$\begin{aligned} \begin{aligned} \mathcal {P}_{\text {predictive}}(t) = \sum _{g \in \mathcal {G}} \Big ( \phi _{\text {forecast}}(g, t) \cdot \xi _{\text {generation}}(g, t) \Big ) \end{aligned} \end{aligned}$$

(68)

Equation (68) integrates predictive models for renewable energy generation. The predictive output $\mathcal {P}_{\text {predictive}}(t)$ aggregates forecasts $\phi _{\text {forecast}}(g, t)$ and generation potential $\xi _{\text {generation}}(g, t)$ for each renewable source $g$.

$$\begin{aligned} \begin{aligned} \mathcal {D}_{\text {update}}(t) = \int _{\mathcal {N}} \Big ( \phi _{\text {fire-impact}}(n, t) \cdot \psi _{\text {demand-shift}}(n, t) \Big ) \, dn \end{aligned} \end{aligned}$$

(69)

Equation (69) updates demand forecasts dynamically based on fire spread. The updated demand $\mathcal {D}_{\text {update}}(t)$ considers fire impact $\phi _{\text {fire-impact}}(n, t)$ and demand shifts $\psi _{\text {demand-shift}}(n, t)$ across nodes.

$$\begin{aligned} \begin{aligned} \nabla _{\pi } \mathcal {L} = \mathbb {E}_{\mathbb {P}} \Big [ \nabla _{\pi } \Big ( \alpha \cdot C_{\text {rescue}} + \beta \cdot C_{\text {energy}} + \gamma \cdot R_{\text {fire}} \Big ) \Big ] \end{aligned} \end{aligned}$$

(70)

Equation (70) describes the gradient-based optimization for solving the DRO objective. The gradient $\nabla _{\pi } \mathcal {L}$ is computed as the expectation over $\mathbb {P}$ of the gradients of rescue cost $C_{\text {rescue}}$, energy cost $C_{\text {energy}}$, and fire risk $R_{\text {fire}}$, weighted by $\alpha$, $\beta$, and $\gamma$.

$$\begin{aligned} \begin{aligned} \Vert \nabla _{\pi } \mathcal {L} \Vert \le \epsilon _{\text {tol}}, \quad \Vert \mathbb {P} - \mathbb {P}_{\text {prev}} \Vert \le \delta _{\text {tol}} \end{aligned} \end{aligned}$$

(71)

Equation (71) defines convergence criteria for the iterative optimization process. The gradient norm $\Vert \nabla _{\pi } \mathcal {L} \Vert$ must fall below a tolerance $\epsilon _{\text {tol}}$, and the distributional shift $\Vert \mathbb {P} - \mathbb {P}_{\text {prev}} \Vert$ must not exceed $\delta _{\text {tol}}$.

$$\begin{aligned} \begin{aligned} \mathcal {C}_{\text {complexity}} = \mathcal {O} \Big ( |\mathcal {N}| \cdot |\mathcal {T}| \cdot |\mathcal {R}| \Big ) \end{aligned} \end{aligned}$$

(72)

Equation (72) quantifies the computational complexity of solving the DRO model. The complexity $\mathcal {C}_{\text {complexity}}$ depends on the number of nodes $|\mathcal {N}|$, time steps $|\mathcal {T}|$, and routes $|\mathcal {R}|$.

$$\begin{aligned} \begin{aligned} \mathcal {L}_{\text {decomp}} = \sum _{k=1}^{K} \mathcal {L}_k(\pi _k, \mathbb {P}_k) \quad \text {subject to } \sum _{k=1}^{K} \pi _k = \pi \end{aligned} \end{aligned}$$

(73)

Equation (73) introduces decomposition methods for simplifying high-dimensional optimization problems. The total objective $\mathcal {L}_{\text {decomp}}$ is split into smaller sub-problems $\mathcal {L}_k$, each defined over a subset of decisions $\pi _k$ and distributions $\mathbb {P}_k$. In this framework, emergency rescue operations are categorized into three primary types, each modeled with distinct operational objectives and associated resources. The first category involves evacuation support, which focuses on the safe transport of civilians from high-risk zones to designated emergency shelters. This includes the dispatch of buses, specialized transport vehicles, and staff coordination. The second category centers on fire suppression logistics, which incorporates the routing of fire engines, mobile water supply units, and aerial firefighting equipment to active wildfire fronts. The third category addresses medical and utility response, which includes sustaining the operation of critical healthcare facilities and mobile medical units, as well as restoring disrupted communication and utility nodes that are essential for ongoing emergency coordination. Each category relies on a tailored resource pool, constrained by availability and deployment feasibility, and is dynamically optimized based on wildfire progression, road conditions, and infrastructure status.

Case studies

The case study focuses on the Los Angeles region, which has faced unprecedented wildfire activity in late 2024 and early 2025, marking some of the most severe fire incidents in recent history. These wildfires, fueled by prolonged drought conditions, heat waves, and fierce Santa Ana winds, resulted in the destruction of over 250,000 acres and impacted thousands of residents across urban, suburban, and rural communities. The Los Angeles area, characterized by its dense population of 10 million people, urban sprawl, and proximity to fire-prone regions such as the San Gabriel Mountains and the Angeles National Forest, presents a complex and challenging testbed for the proposed Differentiable DRO framework. This region’s unique geography combines coastal plains, hills, and canyons, making it highly vulnerable to rapidly spreading fires driven by wind patterns and dry vegetation. The energy infrastructure in Los Angeles comprises a diverse network of 1,450 microgrids, each designed to improve energy resilience in this wildfire-prone area. Approximately 30% of these microgrids are powered by solar PV systems, leveraging Los Angeles’s 287 days of sunshine annually. Another 20% rely on wind turbines, strategically located in high-altitude regions where wind speeds often exceed 15 mph, while the remaining 50% utilize mixed sources such as natural gas and lithium-ion-based energy storage systems. Each microgrid supports critical infrastructure such as hospitals, emergency shelters, and evacuation centers, with backup capacity to sustain operations for 24–72 hours under emergency conditions. To enhance fire preparedness, real-time fire spread data is obtained from the California Department of Forestry and Fire Protection (CAL FIRE), which provides fire perimeters updated every 15 minutes. Additional datasets include high-resolution wind speed and direction information from the National Oceanic and Atmospheric Administration (NOAA) and vegetation heat maps derived from Landsat-9 satellite imagery, processed at a spatial resolution of 250 meters and a temporal resolution of hourly updates. For energy demand modeling, historical consumption patterns from 2022 to 2024 are combined with predictive models that simulate disruptions caused by evacuations, power outages, and increased cooling requirements, yielding node-specific load profiles for over 5,000 distribution nodes.

To capture the intricate interaction between wildfire dynamics and energy infrastructure, the study meticulously models 450 kilometers of power lines, of which 35% are located in high-risk zones identified by CAL FIRE’s Fire Hazard Severity Zones map. The remaining 65% traverse medium- and low-risk areas but are still susceptible to secondary fire effects, such as wind-driven embers and excessive heat exposure. Each microgrid is characterized by detailed parameters, including maximum capacity (ranging from 500 kWh to 1.5 MWh), renewable energy penetration (40–80%), and energy storage efficiency (85–95%). Fire propagation is simulated using a hybrid anisotropic heat equation, calibrated to incorporate terrain slope, vegetation density, and atmospheric conditions, capturing the fire’s complex and non-linear behavior. For example, wind speeds between 10–35 mph amplify the spread rate, creating highly dynamic fire perimeters that change every 5–10 minutes. The fire intensity’s impact on infrastructure is quantified by incorporating probabilities of failure for power lines (0.1–0.8) and critical energy loads (0.05–0.6) based on thermal exposure thresholds and proximity to fire perimeters. These probabilities are dynamically updated every 30 minutes using real-time fire data, allowing for adaptive optimization and resource allocation. The fire dataset further includes detailed suppression activity logs from CAL FIRE, such as deployment schedules for over 1,200 firefighting personnel, 75 aircraft, and 300 fire engines, integrated to evaluate the impact of suppression efforts on fire intensity and spread. Urban heat island effects in Los Angeles are also modeled, contributing to microgrid performance deviations due to elevated cooling loads. This holistic data setup ensures that the DRO framework reflects real-world complexities, allowing for robust modeling of energy resilience and emergency response strategies during wildfire disasters.

The computation environment consists of a high-performance computing (HPC) cluster configured with 64 Intel Xeon processors (3.0 GHz), 512 GB RAM, and 4 NVIDIA A100 GPUs for parallelized fire modeling and optimization tasks. The DRO framework is implemented in Python, using libraries such as PyTorch for differentiable optimization, Gurobi for mixed-integer programming, and Geopandas for geospatial data processing. The fire dynamics simulation leverages the FARSITE wildfire modeling tool, integrated with the energy optimization model. A total of 10,000 Monte Carlo simulations are run to evaluate the performance of the DRO framework under varying scenarios of fire spread, energy demand, and rescue operations. The computation runtime for each scenario averages 6–8 hours, with a total dataset size exceeding 5 TB, stored and processed using distributed computing frameworks such as Apache Spark.

Fig. 2

Cumulative Fire Propagation Heatmap with Wind Influence.

Figure 2 illustrates the cumulative propagation of fire intensity across a 10 km by 10 km region, aggregating data from five hourly intervals. The cumulative fire intensity, represented by the heatmap, highlights the spatial dynamics of fire spread over time. The central region of the fire experiences the highest intensity, with fire intensity values reaching a maximum of 1.8 arbitrary units, while the outer periphery demonstrates lower values ranging from 0.1 to 0.5. This gradient reflects the non-linear nature of fire growth, where the core of the fire burns more intensely due to sustained fuel availability and limited suppression. The grid resolution of 250 meters ensures sufficient granularity to capture spatial variations, providing detailed insights into the fire’s impact on localized areas. Wind vectors, overlaid in cyan, represent the overall wind influence during the fire propagation period. The predominant wind direction moves diagonally from the southwest (bottom-left) to the northeast (top-right), with wind speeds varying from 5 to 20 meters per second. This wind pattern amplifies the fire’s spread rate in the northeast direction, as indicated by the elongated contours of the high-intensity region in that area. The figure also demonstrates the role of wind-driven dynamics in creating asymmetric fire perimeters, which are essential for evaluating risks to critical infrastructure and microgrid nodes located in high-risk zones. Notably, areas directly downwind from the fire’s origin exhibit intensity values above 1.2, while regions perpendicular to the wind remain under 0.8, illustrating the directional impact of wind on fire propagation. To clarify the implementation of dynamic emergency resource allocation, our framework integrates a reinforcement learning-based dispatch strategy that continuously updates vehicle routing and deployment in response to real-time wildfire progression and road accessibility. Specifically, the decision space is represented as a time-varying graph, where nodes denote critical demand points (e.g., shelters, hospitals, fire suppression zones), and edges represent road segments with dynamically updated availability. The agent’s policy is optimized using proximal policy optimization (PPO), trained to minimize response time and maximize critical load coverage under uncertain fire dynamics.

Validation is conducted through a comparative analysis with two baseline strategies: (1) a static pre-scheduled dispatch plan, and (2) a rule-based heuristic that reallocates vehicles at fixed intervals without learning. As shown in Table X, our proposed approach achieves a 23.6]% reduction in average rescue response time and a 31.2% increase in priority zone coverage relative to the static baseline. These improvements highlight the significance of adaptive, fire-aware resource management in rapidly evolving disaster scenarios.

Fig. 3

Correlation of Fire Suppression Efforts and Fire Spread Over Time.

Figure 3 illustrates the dynamic relationship between fire suppression efforts, represented by the number of deployed personnel, and the cumulative fire-affected area over ten days during a wildfire event. The fire spread, shown in acres, rapidly accelerates in the first five days, growing from 100 acres on January 1 to 5,000 acres by January 5. During this period, the firefighting team scales up efforts significantly, increasing personnel from 50 to 700. This steep escalation highlights the critical phase when resources are heavily mobilized to combat rapid fire growth. The figure also shows a notable inflection point between January 5 and January 7. During this time, fire spread slows from an average daily increase of 1,500 acres in earlier days to just 2,000 acres over the two-day period. Concurrently, personnel deployment reaches 1,100. This slowdown coincides with the milestone of 50% containment on January 7, as annotated in the figure. The alignment between increased resources and reduced fire spread suggests that targeted suppression efforts were effective in curbing further escalation, particularly in high-priority containment zones. In the latter days, fire growth stabilizes, with only marginal increases from 9,000 acres on January 8 to 9,300 acres by January 10. Meanwhile, personnel deployment continues to rise, peaking at 1,700 on the final day. The containment milestones, marked at 20% on January 4, 50% on January 7, and 80% on January 9, illustrate key stages of progress. These annotations emphasize the importance of sustained and strategic resource allocation in achieving containment objectives. The interplay between fire suppression and fire spread provides actionable insights for optimizing firefighting strategies and resource planning in future wildfire scenarios.

Fig. 4

Enter Caption.

Probability of Damage to Energy Infrastructure Based on Fire Intensity and Proximity

Figure 4 provides a comprehensive visualization of the probability of damage to energy infrastructure as a function of fire intensity (measured in kilowatts per meter) and distance from the fire source (in meters). The damage probability is represented on the z-axis and ranges from 0 (no damage) to 1 (complete certainty of damage). The gradient color scheme transitions from light teal to dark teal, where darker shades indicate higher damage probabilities. The relationship reveals a clear interaction: as fire intensity increases and the distance to the infrastructure decreases, the likelihood of damage grows significantly. Examining the plot, for a fire intensity of 5 kW/m, infrastructure located within 20 meters shows a damage probability of approximately 0.7, while this probability drops to about 0.3 at a distance of 50 meters. For higher fire intensities, such as 9 kW/m, infrastructure within 10 meters faces near-certain damage with a probability exceeding 0.9. Conversely, at a fire intensity of 2 kW/m and a distance of 70 meters, the probability of damage remains below 0.1, emphasizing the importance of spatial separation and fire intensity control measures in reducing risk to critical infrastructure.

Fig. 5

Rescue Vehicle Dispatch Efficiency Over Time.

Figure 5 analyzes the efficiency of rescue vehicle dispatch operations during a 24-hour emergency response period. The bar chart displays the number of vehicles reaching their destinations on time, while the error bars illustrate delays caused by fire-induced road closures. The line graph overlays the average rescue time per vehicle, providing an additional dimension to evaluate the timeliness of operations. During the early hours, the number of vehicles dispatched remains steady at around 100, with delays affecting approximately 10 to 15 vehicles on average. However, as the emergency intensifies, the number of on-time vehicles decreases slightly, indicating the growing impact of road blockages. In the middle of the response window, between hours 8 and 16, the number of vehicles reaching on time shows a notable dip, dropping to approximately 70 vehicles in hour 12. This period also corresponds to an increase in average rescue time, peaking at over 85 minutes per vehicle. The delays are particularly pronounced during these hours, with nearly 30 vehicles per hour affected by road closures. This trend highlights the critical challenges of navigating infrastructure disruptions as the fire spreads, underscoring the need for real-time route optimization and additional resources to mitigate delays.

Fig. 6

Relationship Between Fire Intensity, Distance, and Damage Probability.

Figure 6 explores how fire intensity and proximity to the fire source affect the probability of damage to infrastructure. The X-axis represents fire intensity in kilowatts per square meter ($\hbox {kW}/\hbox {m}^{2}$), while the Y-axis indicates the distance from the fire source in meters. The color gradient, ranging from light green to dark blue, illustrates the damage probability, which spans from 0 (no damage) to 1 (certain damage). The contour lines, corresponding to critical thresholds of 0.5, 0.7, and 0.9, provide additional clarity on the impact levels. The plot reveals a steep gradient of damage probability near high fire intensities. For example, at an intensity of 8 $\hbox {kW/m}^{2}$, the damage probability exceeds 0.9 for distances within 10 meters, highlighting the vulnerability of close-range infrastructure under severe fire conditions. Conversely, at lower intensities of 2 $\hbox {kW/m}^{2}$, the probability drops below 0.5 even at distances as close as 20 meters, emphasizing the importance of managing fire intensity to reduce risks. The 0.5 contour line serves as a key demarcation, separating low-risk zones from areas requiring immediate attention.

Fig. 7

Fire Spread Intensity as a Function of Wind Speed and Direction.

Figure 7 demonstrates how fire spread intensity varies with wind speed and direction, offering insights into the dynamic interaction between meteorological factors and fire behavior. The X-axis represents wind speed in kilometers per hour, ranging from 0 to 50 km/h, while the Y-axis captures wind direction in degrees, spanning a full circular range of $0^{\circ }$ to $360^{\circ }$. The color gradient in the contour plot, ranging from light yellow to deep red, visualizes fire spread intensity in kilowatts per square meter, with darker shades corresponding to higher intensities. Cyan arrows overlaid on the plot represent wind vectors, showcasing the magnitude and direction of wind flow. The contour patterns reveal that fire spread intensity increases significantly with higher wind speeds, particularly when the wind direction aligns with the fire’s natural path (e.g., at $180^{\circ }$). For instance, at a wind speed of 40 km/h and a direction of $180^{\circ }$, the fire intensity exceeds 30 $\hbox {kW/m}^{2}$, highlighting the amplified risk under such conditions. In contrast, wind directions perpendicular to the fire’s path (e.g., $90^{\circ }$ or $270^{\circ }$) result in substantially lower intensities, even at higher wind speeds. This indicates that directional alignment is a critical factor in determining fire propagation behavior.

Fig. 8

Influence of Wind Speed and Suppression Resources on Fire Spread Rate.

Figure 8 illustrates the interplay between wind speed and suppression resource deployment in controlling fire spread rate, measured in meters per hour. The X-axis represents wind speed, ranging from 0 to 50 km/h, while the Y-axis denotes suppression resources deployed in terms of personnel or equipment per square kilometer, ranging from 0 to 100. The contour levels indicate fire spread rates, with values increasing from 0 to over 40 meters per hour as depicted by a gradient from lighter to darker shades. Cyan arrows overlay the plot to represent the combined directional effects of wind and suppression efforts on fire spread dynamics. The results highlight the critical influence of wind speed, where fire spread accelerates significantly as wind speed exceeds 30 km/h. At lower suppression resource levels, the fire spread rate can exceed 35 meters per hour for wind speeds above 40 km/h, underlining the challenges of managing high-intensity fires under strong wind conditions. Conversely, the deployment of sufficient suppression resources drastically reduces the spread rate. For instance, at a wind speed of 30 km/h, increasing suppression resources from 30 to 70 personnel per square kilometer lowers the spread rate from approximately 20 meters per hour to below 10 meters per hour, showcasing the effectiveness of well-planned resource allocation.

Fig. 9

Probability of Rescue Delay as a Function of Wind Speed and Fire Intensity.

Figure 9 captures how the probability of rescue delays is influenced by varying wind speeds and fire intensities. The X-axis represents wind speed, ranging from 0 to 50 km/h, while the Y-axis indicates fire intensity in kilowatts per square meter, spanning from 0 to 10 $\hbox {kW/m}^{2}$. The color gradient illustrates the probability of delays, with darker shades corresponding to higher probabilities, reaching up to 1. The critical scenarios are marked with white circles, highlighting combinations of wind speed exceeding 30 km/h and fire intensity above 8 $\hbox {kW/m}^{2}$. Annotated zones classify the plot into “High Risk” and “Low Risk” regions, providing clear visual segmentation of rescue challenges. The plot reveals that rescue delays are minimal under low wind speeds (e.g., below 10 km/h) and moderate fire intensities (e.g., 3 $\hbox {kW/m}^{2}$), with probabilities remaining under 0.3. However, as wind speeds increase beyond 30 km/h, the delay probabilities escalate sharply, exceeding 0.8 for fire intensities above 8 $\hbox {kW/m}^{2}$. For instance, at a wind speed of 40 km/h and fire intensity of 9 $\hbox {kW/m}^{2}$, the delay probability reaches approximately 0.9, marking a zone requiring immediate mitigation strategies. These findings emphasize the dual impact of wind and fire on the operational efficiency of rescue efforts.

Conclusion

This study addresses the urgent need for enhanced emergency response and energy system resilience in wildfire-prone urban areas, with a specific focus on Los Angeles. By integrating wildfire growth modeling, microgrid-based energy systems, and dynamic vehicle scheduling, the proposed framework offers a robust solution to mitigate the impacts of wildfires on critical infrastructure and human safety. The incorporation of real-life wildfire scenarios in Los Angeles highlights the practicality and adaptability of the approach, demonstrating its ability to prioritize resources for emergency shelters, hospitals, and rescue operations under extreme conditions. The results emphasize the critical role of predictive wildfire modeling in optimizing resource allocation and decision-making during disasters. This framework provides a valuable tool for urban planners and emergency responders to enhance preparedness and resilience against wildfires, offering a pathway for more effective disaster management in cities like Los Angeles and beyond. Future work will explore scaling the model to encompass regional wildfire impacts and refining the integration of predictive models with real-time data for greater precision.

While the proposed framework demonstrates promising results in simulation, several limitations must be acknowledged. First, the computational complexity of the reinforcement learning and MILP-based components may pose challenges for large-scale deployment in real-time scenarios. Model convergence time is sensitive to the number of agents, spatial resolution of the fire simulation, and update frequency of the road condition graph. Second, real-world deployment would depend heavily on the availability and fidelity of live wildfire data, including accurate forecasts of wind speed, humidity, and vegetation dryness. Current wildfire datasets are often sparse or delayed, which could limit the precision of real-time response. Third, assumptions such as fixed microgrid topology and uniform data availability across all regions may not fully hold in heterogeneous urban environments. Future work will focus on integrating drone-based sensing for live fire front detection, federated learning for distributed policy training, and adaptive zoning techniques to reduce computational load while maintaining local decision fidelity.

To explore the scalability of the proposed framework, it is important to consider its potential application to other wildfire-prone regions beyond Los Angeles. The modular structure of our approach, which decouples wildfire modeling, microgrid optimization, and emergency vehicle scheduling, enables adaptation to diverse geographic and infrastructural contexts. For example, in regions such as Northern California, Australia, or Southern Europe, fire behavior differs due to variations in vegetation type, climate patterns, and terrain complexity. These differences can be accommodated by retraining the fire propagation model on localized environmental data and adjusting infrastructure vulnerability parameters accordingly.

Moreover, the optimization layer can be reconfigured to reflect region-specific energy network topologies, resource availability, and emergency response protocols. The flexibility of the model allows it to incorporate localized constraints such as different road classifications, communication infrastructures, or evacuation strategies. This generalizability underscores the framework’s potential as a transferable decision-support tool for enhancing wildfire resilience in both urban and peri-urban settings.