Abstract
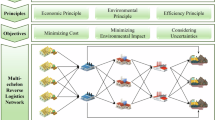
Considering the impact of environmental pollution and market competition on the business model of enterprises, a method of constructing sustainable supply chain network model under the price competition environment is proposed to achieve the balance of economic benefit, ecological benefit, environmental benefit and social benefit. Firstly, based on the concepts of sustainability and price competition, the model with maximum total network profit, minimum carbon emission and maximum social benefit is designed. Secondly, based on fuzzy programming theory, an expected value fuzzy chance constrained programming model with confidence measure is constructed to address the challenge of designing a sustainable closed-loop supply chain network in the face of uncertain conditions. Thirdly, the problems of premature convergence and slow convergence during the traditional particle swarm optimization algorithm and genetic algorithm are solved with the particle chaotic ant colony algorithm (PSCACO). Finally, taking a manufacturing enterprise as an example. By analyzing the different confidence level measures under single objective optimization and multi-objective optimization, sustainable closed-loop supply chain network planning method established is verified on feasibility and effectiveness.
Similar content being viewed by others
Introduction
In today’s world, the swift pace of economic growth and the rapid advancement of global integration have resulted in increasingly varied consumer demands for products, intensifying market competition. Additionally, as industrialization progresses quickly, climate change has become one of the most pressing challenges confronting humanity. Both society and businesses have focused on building an ecological civilization and protecting the environment, leading to widespread acceptance of sustainable development principles1,2,3,4. In 2015, the UN Development Summit adopted the 2030 Agenda for Sustainable Development, which sets out 17 global goals for sustainable development by 2030, covering many aspects such as economic development, social progress and environmental protection5. The goal of sustainability is to ensure that companies prioritize social benefits alongside their economic objectives. The ongoing pressures from market competition and environmental degradation have altered how businesses operate. A business model that solely focuses on financial performance is no longer sufficient to meet contemporary market needs. To enhance competitiveness effectively, a business strategy must simultaneously consider environmental impact, economic viability, and social responsibility. Meanwhile, if enterprises want to survive and develop, they must take competition into consideration in the design of supply chain network. Among them, price competition is common and easily affects demand. Competition leads to changes in demand, which determines the flow of goods and the location of facilities at different levels of the supply chain. As a complex dynamic network structure, the change of supply chain network directly affects income of whole chain, and has an important impact on society and environment. Therefore, by combining price competition to build a sustainable supply chain, companies can comprehensively enhance their core competitiveness and competitive advantage, improve their reputation, and position themselves in a more favorable manner.
In view of this, the following aspects are still worth exploring in the study of sustainable closed-loop supply chain network optimization:
(1) How to determine a reasonable index system for measuring sustainability of closed-loop supply chain network?
(2) How to establish a multi-objective fuzzy programming model based on the concept of sustainability in view of the ambiguity of network parameters?
(3) How to transform a multi-objective optimization problem into a single-objective numerical problem, that is, an optimization problem for solving satisfaction?
(4) What impact will price competition have on the closed-loop supply chain network?
(5) In terms of model solving, can we provide a new algorithm to solve the problem of low efficiency of traditional heuristic algorithm?
In the establishment of the closed-loop supply chain network model, this paper combined the concept of sustainability, constructed demand function considering the price competition factor, and established the multi-objective mixed integer programming model, which has the following three contributions:
(1) The index is designed to measure the sustainable development of economy, environment and society.
(2) Considering the fuzziness of network parameters, an expected value fuzzy opportunity constraint programming model based on credibility measurement is constructed based on fuzzy programming theory to achieve the goals of maximum network profit, minimum carbon emission and maximum network social benefit, in which the amount of jobs created is taken as measurement standard of social benefit.
(3) Using the characteristics of a multi-objective model, a membership function for multiple objectives is created, transforming the multi-objective optimization problem into a single-objective numerical problem.
(4) Exploring the influence of price competition on location selection results of supply chain network.
(5) In view of the inherent defects of particle swarm optimization and ant colony optimization, a fusion algorithm of particle swarm optimization and ant colony optimization is proposed.
Literature review
With the deepening of the concept of sustainable development, a sustainable supply chain network focuses on three of economy, environment and society. Eskandarpour et al.6 conducted a review of 87 studies related to supply chain network design, which included mathematical models that take into account economic, environmental, and social factors, and found that most studies focused on carbon emission and cost indicators, while other sustainability indicators were less present in the research on supply chain optimization. Some literature also considers social factors. At the social level, Lin et al.7 and Liang et al.8 have studied how to balance supply chain cost and carbon emissions. Qiu and colleagues9 introduced a fuzzy multi-objective model for sustainable supply chain networks that incorporates four key dimensions of collaborative modeling: economic costs, environmental impact, social effects, and corporate governance capacity. Yu et al.10 proposed a five-in-one sustainable closed-loop supply chain network model that carried out hierarchical analysis and weighted integration of five indicators: economic cost, compliance rectification and energy saving and emission reduction, green supply chain, promoting public green choice, and supply chain communication and transparency.
These scholars all consider economic, environmental, and social dimensions, but few consider the uncertainty in supply chain management. At present, the uncertainty processing of the network is mainly focused on robust optimization, random chance constraint and triangular fuzzy processing of uncertain parameters, and finally solved by algorithms or software. Zhang et al.11 established a multi-objective supply chain network planning model with minimum cost, minimum environmental damage and maximum social benefit. The uncertain parameters of Me measure were used for measurement, and the genetic whale algorithm was used to solve the model. Ren et al.12 built a multi-objective integer programming model based on epsilon constraints to solve the problem of water resources and carbon emissions in aluminum supply chain, and quantitatively evaluated the multi-objective optimization of supply chain economy and water resources under the influence of carbon emissions. Tirkolaee et al.13 introduced a fuzzy two-level decision support system (DSS) to optimize sustainable multilevel multi-product supply chain (SC) and intermodal network product distribution of perishable goods, and developed two MILP models to solve the sustainable development problem of this problem. Dehshiri et al.14 introduced blockchain technology to achieve supply chain sustainability, providing new applications for the use of blockchain in agricultural products.
At the same time, the competition faced by enterprises has changed from the competition among individual enterprises to the competition among the supply chain composed of downstream partners. Researchers have analyzed the supply chain from multiple perspectives, considering competitive elements. These investigations can be divided into three categories based on the competing entities: one category emphasizes competition among firms operating at the same level within the supply chain, where companies at a comparable tier compete for resources with those positioned at different levels of the supply chain15,16.; Competition among different levels in the supply chain: entities in one level make mutual choices with entities in another level, and the two levels are interdependent to achieve the maximum benefit of each other17,18,19. In this case, the supply chains competing against each other in terms of price, quality and other factors, and try to achieve a larger share of the market’s share20.
At present, the study of price competition in supply chain mainly focuses on supply chain coordination and decision-making, supply chain profit, supply chain model selection and traditional supply chain network design. Zhu et al.21 investigated the development of eco-friendly products within the supply chain amidst price and green competition, demonstrating through game theory that retailer-level price competition positively influences game equilibrium. Abhishek et al.22 discussed the problem of retail price competition between traditional distribution model and online channels, and believed that the intensified competition among retailers would make the platform tend to choose traditional distributors for sales. Tian et al.23 studied the choice of sales cooperation mode between the e-commerce platform and two suppliers under product price competition, and found that the choice of supplier mode depends on the tradeoff between the transfer of product pricing power and the cost of order fulfillment. Jena et al.24 analyzed the impact of price competition among manufacturers on profits in the omnichannel supply chain. Taleizadeh et al.25 developed a flexible supply chain model that addresses price competition and facility disruptions by employing the Stackelberg game approach. Matsui et al.26 designed a reverse supply chain network of recycling platform with dual recycling channels under consideration of acquisition price competition. Based on the characteristics of simultaneous price competition in the sales market and the recycling market, Wang et al.27 studied the decision-making problem under different models. Halat et al.28 examined the competition in pricing and subscriptions between two eco-friendly supply chains. They proposed a Stackelberg game involving a government agency and the two competing green supply chains.
To sum up, considering the economic benefits, environmental benefits and social benefits of enterprises, building a sustainable closed-loop supply chain is still a hot topic at present. However, less consideration is given to the impact of price competition. Therefore, in terms of price competition, this paper provides a supply chain network planning method that can bring more benefits to society and environment while ensuring the network economy.
Model building
Problem description and model assumption
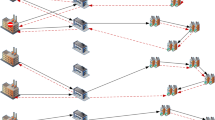
This paper establishes a sustainable closed-loop supply chain network as shown in Fig. 1, including multiple factories, multiple distribution points, multiple markets and multiple waste points. The network includes forward logistics network and reverse recovery network. The factory is responsible for the production of the product and at the same time for the secondary manufacturing of the product delivered at the recycling point; Distribution points transport new and remanufactured products from the factory to various markets; At the recycling point, EOL products in the consumer market will be recycled and tested, parts with reuse value will be refurbished, and the refurbished products will be sent to the factory for reproduction, and transport end-of-life products without reuse value to a designated waste collection point for proper disposal.
To aid in the construction of the model, the following assumptions are established based on the problem description:
Assumption 1: Capacity constraints are present at factories, distribution centers, recycling facilities, and waste disposal sites. Furthermore, the capacity allocation for both forward logistics and reverse logistics is equivalent.
Assumption 2: The production ratio of new products to raw materials is 1:1, regardless of the inventory of the production process29, waste items in the production process are recovered directly from the recycling point.
Assumption 3: The probable recovery rate of the product and the scrap rate of the parts are known.
Assumption 4: Take network carbon emission as environmental performance index, and the amount of labor created by network as social performance index.
Assumption 5: Unit transportation costs and carbon emissions remain the same when the routes are the same.
Assumption 6: Utilize the reconditioned components from the current period as the source for remanufactured products in the same period30.
Assumption 7: Each node is restricted to using a single type of transportation, and the transportation tool has a limited capacity.
Assumption 8: The factory location has been finalized, the positions of substitute distribution outlets and garbage disposal sites have been identified, along with a confirmed count of consumer markets29.
The cause of parameter fuzziness
It is assumed that market demand is completely determined by self-appropriate price and competitor price, so this paper does not take into account the ambiguity of requirements. However, the ambiguity of costs and recovery rates beyond demand is also quite common, so the fuzzy parameters mainly considered in this paper are the cost of facility establishment, the refurbishment cost of recycled products, and the recovery rate of EOL products. In addition, the ambiguity of carbon emission of facility establishment, the ambiguity of fixed labor amount created by facility establishment and the ambiguity of recycling product refurbishment rate are also considered. The causes of the ambiguity of the above parameters are shown in Table 1.
Symbol specification
See Table 2 for details.
Model construction
Demand function
The growing complexity of the market and heightened competition have led companies to strengthen relationships with both upstream suppliers and downstream distributors. This shift has turned competition into a contest between supply chains. The primary goal of business operations is to generate profits, which generally requires increasing market share. Engaging in price competition with similar or alternative products is the most effective way to boost market share. Thus, price competition among companies essentially becomes price competition among supply chains.
This paper mainly considers that there are sellers (competitors) of similar products in the market, whose direct competition is price competition, that is, price competition is a direct means for supply chain to win market share. With distributor profit maximization as the decision-making principle, the supply chain’s selling price in market c is pc32, the competitor’s selling price in market c is, and the basic demand of market c is \(\hat{p}_{c}\). In this paper, the sellers in the supply chain network compete with other sellers of similar products to gain more market share through price competition. Construct market demand function under price competition.
In formula (1), b represents product price sensitivity coefficient; drepresents the intensity of product competition between the supply chain and its competitors (competition coefficient). According to the demand function, the actual market demand declines as its own price sensitivity coefficient and price rise, while it increases with a higher fungibility coefficient and the sales prices of competitors33., which accords with the general market law. The supply chain network competition mode based on the above description is shown in Fig. 2.
By differentiating the supply chain price in Eq. (1), we can obtain:
Formula (2) shows that when other conditions remain unchanged, supply chain sales price pc in market c decreases by one unit, supply chain demand in market will increase by b + d. Among them, b is the new consumers attracted by the decline in the sales price of the product (customers who have no intention to consume before the price decline), and d is the consumers transferred from the competitor by the impact of the price decline (customers who have the intention to buy the product from the competitor before the price decline).
Construction of enterprise-environment-society three-goal collaborative model
Goal 1: The maximum total profit of the supply chain network. The network profit is equal to the operating income minus the cost. Including facility opening cost (FC), production technology introduction cost (IC), inter-node transport vehicle rental cost (ZC), product production cost (PC), product recovery cost (RC), product refurbishment cost (NC), product waste cost (DC), material transportation cost (TC) between nodes, and the use of refurbished parts Cost savings from remanufacturing (SC). Therefore, the maximization of closed-loop supply chain net-work profit is:
Goal 2: The least amount of carbon that the supply chain network emits overall. Including carbon emission from facility opening (FE), carbon emission from production technology introduction (IE), carbon emission from product production (PE), carbon emission from product refurbishment (NE), carbon emission from product waste treatment (DE) and carbon emission from transportation (TE). Therefore, the goal is to minimize the carbon emissions in closed-loop supply chain networks:
Goal 3: Network generates most labor possible, including the amount of labor created by opening fixed facilities (FL), the amount of labor created by introducing production technology (IL), the amount of labor increased by using technology t to produce products (QL), and the labor needed to upkeep transportation vehicles (GL). Therefore, the maximum amount of closed-loop supply chain network labor is:
The constraints are as follows:
Formula (26) indicates that the quantity of products transported from distribution points to markets must satisfy the actual market demand; Formula (27) indicates that the manufacturing and remanufacturing capacity of the factory cannot exceed its upper limit; Formula (28) shows that the amount of products accessible to the distributor is within its capacity constraints; Formula (29) indicates that the amount of EOL products recovered by recyclers from each market cannot exceed its recycling upper limit; Formula (30) indicates that the products that can be disposed of at the waste point cannot exceed the upper limit of disposal; Formula (31) indicates that the equilibrium between the production volume of goods from each factory utilizing technology t and the quantity of goods transported from each factory to distribution points; Formula (32) illustrates the balance between the amounts of products shipped from each factory to distribution centers and those distributed from these centers to individual markets; Formula (33) represents the balance between the amount of product shipped to market at the distribution center and amount of product recovered at the recycling point (the confidence of constraint realization is not less than σrc); Formula (34) represents the balance between the number of refurbished parts in the collection point and the number of refurbished parts shipped to each plant; Formula (35) represents the balance between the amount of EOL products that have no reuse value in the recycling point and the amount of products that are transported to the waste points for waste treatment (the confidence of the constraint realization is not less than σαj); Formula (36) represents that the constraint that each factory is limited to adopting a single technology; Formula (37) indicates that only the same means of transport can be selected between nodes. Formula (38) and (39) represent non-negative constraint and binary decision variables respectively.
Model transformation
Model equivalent transformation
The constructed mixed integer programming model with fuzzy parameters includes formula (3), Eq. (14), Eq. (21), constraint (28,29,30), constraint (33) and constraint (35). In order to effectively deal with fuzzy parameters in the model, the fuzzy variable is assumed to be trapezoidal fuzzy number. Based on fuzzy programming theory, a fuzzy variable is defined as η = (η1, η2, η3, η4)34, and η1 < η2 < η3 < η4. Based on the expected value of the trapezoidal fuzzy variable, the anticipated value of the fuzzy parameter η is given by E(η) = (η1 + η2 + η3 + η4)/4, the credibility measure based on trapezoidal fuzzy number is:
When \(\varphi \in (0.5,1]\), according to the formula (40–41):
The fuzzy parameters in the objective function in the sustainable supply chain network can be described as:
Based on the expected value theory and formula (44,45,46,47) of trapezoidal fuzzy numbers, the above mixed integer programming model is converted into the corresponding fuzzy expected value equivalent model, as shown below.
Based on the credibility fuzzy theory \(Cr\left( {\tilde{\xi } \le \eta } \right) \ge \varphi ,\forall j \in J\) can be seen that the conditions \(\eta \ge {2(1 - }\varphi )\eta {3} + ({2}\varphi { - 1)}\eta {4}\) must be satisfied in order to be established; \(Cr\left( {\tilde{\xi } \ge \eta } \right) \ge \varphi ,\forall j \in J\) can be seen that the conditions \(\eta \le ({2}\varphi { - 1)}\eta {1} + {2(1 - }\varphi )\eta {2}\) must be satisfied in order to be established; Therefore, constraints (28), (29), (30), (33), and (35) are further described as:
In Eq. (51,52,53,54,55), the confidence levels of chance constraints σi, σj, σw, σrc, σαj \(\in (0.5,1]\), while the other constraints remain unchanged.
Multi-objective transformation
Solution and the flexibility of decision makers, an interactive solution method is adopted to solve the above multi-objective trustworthy fuzzy programming model35. Based on the interactive solution method, decision makers can obtain satisfactory solutions meeting the conditions according to their preferences, and obtain the optimal solutions meeting the requirements by constantly adjusting parameters.
The optimization and resolution of the three objective functions in this research require the creation of membership functions for each function. This process turns the problem of multi-objective optimization into one of single-objective numerical optimization, specifically optimization of satisfaction36. Considering that the three performance metrics’ optimization goals differ-namely, maximizing social employment while minimizing supply chain total cost as well as carbon emissions—distinct membership functions are applied to each. The graphical representations of these membership functions for each objective are depicted in Fig. 3.
In this context, μ(Zi) indicates the objective function’s membership degree, which ranges from [0, 1] Zi denotes the objective function’s value, as well as Zi* signifies optimal value for single-objective optimization. Parameter θi reflects the maximum allowable deviation permitted by decision-makers. Membership functions corresponding to minimizing objective values are located on axis’s right side, while those associated with maximizing objective values are situated on the left side. The specific expressions for linear membership functions are as follows.
Sustainable supply chain network profit linear membership function:
Sustainable supply chain network carbon emission linear membership function:
Linear membership function of labor quantity in sustainable supply chain network:
Taking the average of membership functions for three objective functions to construct a satisfaction function, where the maximum satisfaction value corresponds to the optimal solution of the model with the corresponding maximum objective function value37:
In summary, an interactive fuzzy programming method based on credibility measure is obtained, its solution steps are as follows and the flow chart is shown in Fig. 4.
Step 1: Combining the chance constrained programming method and the expected value model, a credible fuzzy multi-objective chance constrained model is constructed;
Step 2: Perform a clear equivalence transformation on models with fuzzy parameters based on credibility fuzzy theory;
Step 3: Determine the optimal solution for each sub-objective function, meaning finding the best solution for every individual sub-objective Z1*, Z2* and Z3*;
Step 4: According to their own preferences and the company’s true state, decision-makers define the maximum permissible deviation from optimal values of each sub-objective function, namely θ1, θ2, θ3;
Step 5: Construct the membership functions for each sub-objective function based on multi-objective fuzzy optimization theory, namely μ(Z1), μ(Z2), μ(Z3);
Step 6: Solve the satisfactory function values based on Eq. (59), and obtain the sub-objective function values corresponding to the optimal satisfaction function values;
Step 7: When the decision maker is satisfied with the value of the objective function at this point, the value set is the optimal solution; When the decision maker is not satisfied, go to Step 4 and adjust θ1, θ2, and θ3 until you get a solution that satisfies the decision maker.
Particle chaotic ant colony algorithm design
Optimizing a sustainable closed-loop supply chain network is recognized as a classic NP-hard problem, typically addressed using both exact and heuristic algorithms. As the complexity of the problem grows, traditional exact algorithms often face challenges due to prolonged solving times. In contrast, heuristic algorithms are characterized by their robust parallel search capabilities, rapid computation speeds, and high solution quality, making them popular for tackling large-scale issues38. For instance, particle swarm optimization (PSO)39 and genetic algorithm (GA)40 have been effectively utilized to resolve various combinatorial optimization challenges with favorable outcomes. However, one limitation of heuristic methods is that they do not guarantee finding the global optimal solution during the resolution of combinatorial problems. To address this issue, this paper combines ACO with PSO, and makes use of the advantages of the two algorithms. Given that there tends to be little variation in pheromone concentration at the beginning stages of ant colony optimization—leading to increased randomness and reduced convergence speed—a novel particle chaotic ant colony optimization algorithm (PSCACO) has been introduced. This method incorporates chaotic variables to enhance pheromone allocation randomness and accelerate the search process within ant colonies.
Particle swarm optimization algorithm
The particle swarm optimization (PSO) algorithm, according to the inspection of bird flock behavior, utilizes information pooling among persons in population to achieve the group’s overall transition from disorder to order, thereby obtaining the optimal solution.
The particle swarm optimization algorithm based on social cognition perspective, wherein each individual in the group can learn from its neighboring individuals and draw lessons from their experiences, specifically by imitating the behavior of neighboring individuals, comparing their behaviors, and evaluating their motivation.
Suppose that a swarm of M particle individuals is performing a search in a D-dimensional space with a certain initial velocity. During the search, each particle dynamically adjusts its velocity based on its own flight experience and the movement experience of its neighboring particles. Variables involved include:
(1) Position of i-th particle at time t in D-dimensional space is:\(X_{{_{i} }}^{t} = \left( {x_{{_{i1} }}^{t} ,x_{{_{i2} }}^{t} ...x_{{_{iD} }}^{t} } \right)\), that is a potential solution.
(2) A single particle searches for the optimal value, which is personal optimal solution \(p_{i}^{t}\).
(3) The particle population searches for optimal value, \(p_{g}^{t}\) is global optimal solution.
(4) In D-dimensional space, the velocity \(V_{{_{i} }}^{t} = \left( {v_{{_{i1} }}^{t} ,v_{{_{i2} }}^{t} ,...v_{{_{iD} }}^{t} } \right)\) of a particle at time t and the location \(P_{i} = \left( {p_{i1} ,p_{i2} ,...p_{iN} } \right)\).
The particle swarm continuously modifies its position and speed to produce new particles. Here is the formula to update the particle swarm’s speed:
The formula for updating particle positions is:
In Eq. (60), ω means the inertia weight, while r1 as well as r2 are random values between 0 and 1, and c1 as well as c2 are the learning factors. It can be seen that the velocity of the next generation of particles hinges on the previous generation of particles’ velocities \(\omega V_{{_{id} }}^{t}\), individual memory \(c_{1} r_{1} \left( {p_{{_{id} }}^{t} - x_{{_{id} }}^{t} } \right)\) and the influence of group particles \(c_{2} r_{2} \left( {p_{g}^{t} - x_{{_{id} }}^{t} } \right)\), the inertia weight indicates what velocity of previous generation has on velocity of next generation. Figure 5 shows iterative process of particle swarm optimization. Flowchart of the PSO algorithm is shown in Fig. 6.
The biggest advantage of the PSO algorithm is its fast convergence rate, but this is also a limitation of the algorithm. When applying the PSO algorithm to resolve complex problems, it’s easy to encounter the problems of premature convergence.
(1) Premature development problem.
When solving the multi-peak function value again, the premature problem of the particle swarm optimization method is very obvious. Since the multi-peak problem has multiple local optimal solutions, particles are easily trapped in local optima during the re-search process. When particles cannot escape from the local optimal value, the early convergence phenomenon occurs.
(2) Convergence problems.
The problem arises due to the fact that during the later stages of the research, search direction of the individual optimal solution and the global optimal solution of the particles are opposite, causing the particles to oscillate within a certain range41.
If the PSO is solving a maximization problem, when the current position xd i of a particle is located between the individual optimal pd i and the population optimal pd g, but compared to that, xd i is closer to pd i, according to formula (61), the particle will be more influenced by the total swarm and move towards pd g. At this time, xd i is closer to pd i, and according to formula (61), the particle will be more influenced by the individual memory and move towards pd i, so that the phenomenon of moving back and forth will be repeated and the convergence of the algorithm will be reduced.
Ant colony optimization algorithm
The inspiration for the ant colony algorithm comes from real ant colony in nature, which seeks the optimal characteristics of the distance from the food source by exchanging pheromone information among individual ants.
Let K is the total number of ants in the colony, and n is the number of sites they must traverse. Distance between sites i and j is denoted as dij (i,j = 1,2,…,n), and the pheromone concentration on the path between sites i and j at time t is τijt. Initially, all paths have the same pheromone level: τij0 = τ0. Ant k (k = 1,2,…,k) decides its next location based on the pheromone concentration, with the transition probability Pijkt representing the likelihood of ant k moving from site i to site j at time t.
In this context, ηijt denotes the heuristic function, and Ak = (1,2,…,m) is set of locations for ant k to visit, initially containing n-1 elements. When Ak is empty, all locations have been visited. The parameter α indicates pheromone significance, with higher values enhancing the impact of information concentration on movement. β is the importance of the heuristic function, with greater values leading ants to prioritize closer sites. Pheromones on the connecting paths evaporate over time, with the evaporation rate represented by ρ (0 < ρ < 1), necessitating constant updates to the pheromone concentration along the paths42.
In Eq. (65),\(\Delta \tau_{ij}^{k}\) denotes the concentration of pheromones published by k ant in path of i as well as j; Q represents total amount of pheromones produced along the pathway where i is connected to j, and Lk is path length.
One of characteristics of the ACO is its initial delayed convergence due to the equal concentration of pheromone information in all paths, which leads to a strong contraction blindness and exploration at first. To solve this problem, a chaotic system is introduced, relying on the pervasiveness and randomness of the chaotic system to improve the pheromone information. A set of chaotic variables is introduced into formula (63). The expression of the chaotic variable is as follows:
In Eq. (66), Rt ij represents the chaotic variable; λ is the control variable that takes values in the range of [3.56, 4.0]. When the system reaches complete chaos, λ = 4.0. This paper adopts the Logistic map as a chaotic generator, and when the origin value is set to R0 ij = 0.42212, Fig. 7 displays the map’s bifurcation diagram.
The formula for updating pheromones based on chaotic perturbation can be further described as follows:
In Formula (67), ξ is an adjustable coefficient utilized to modulate impact of chaotic perturbations regarding pheromone levels. When chaotic variables are added, differential pheromone concentrations on the various paths in the origin stage can be reached, so that ant colony is able to evaluate and choose paths, which can improve convergence speed of algorithm.
Particle chaotic ant colony algorithm
The positions of particles obtained through the PSO act for ant colony. It is shown in Fig. 8.
The specific implementation steps of PSCACO are outlined as follows:
Step 1: Acquire pertinent parameters for supply chain network and define the algorithmic parameters, including T1 as the maximum iteration number for the PSO algorithm, T2 as the maximum iteration number for the ACO algorithm, K as the quantity of particles and ants, c1 and c2 as acceleration factors. Additionally, establish an initial inertia weight \(\omega\) while initializing particle velocity and position.
Step 2: Calculate fitness values for each initial particle to obtain individual and global optimal values.
Step 3: Update the velocity and position of particles, generate new positions for individuals, and compute the corresponding fitness values at their respective positions.
Step 4: Pre- and post-position update fitness values should be evaluated; the existing optimal solution should be maintained; the present iteration number t should be determined. If t < T, set t = t + 1 and return to step 4. If t > T1, then present the current optimal solution.
Step 5: The positions of particles obtained through the PSO act as initial solution set for ant colony.
Step 6: Establish the initial pheromone concentration for each path.
Step 7: Evaluate the fitness value and maintain present best solution.
Step 8: Update pheromones.
Step 9: Calculate the probability of transfer for the ant colony, update its position, determine the fitness value at this new location, compare fitness values from before as well as after the update, and keep current optimal solution.
Step 10: See if it satisfies the output condition. If t > T2, present current optimal solution; if not, set t = t + 1 and move on to step 9.
Algorithm performance evaluation
To assess the effectiveness of the suggested PSCACO algorithm, it’s applied to solve test functions of different dimensions, and its solution outcomes are contrasted to the optimization outcomes of MOPSO, CACO and GA algorithms. The parameter configurations for each algorithm are presented in Table 3.
The relevant information of test functions is shown in Table 4.
For each test function listed in Table 4, 10 optimization iterations were conducted, yielding the mean values and standard deviations for each algorithm, which are demonstrated in Table 5. Figure 9 shows the convergence curves for the single optimization results of each algorithm, where one randomly selected optimization result is illustrated in the same Fig. 14 test functions’ convergence speed and optimization ability under different algorithms are divided into three grades: excellent, good and general. The convergence between 0–20 iterations is excellent; It is good to achieve convergence between 20–40 iterations; It is common to achieve convergence between 40 and 60 iterations, and the Sankey diagram of each algorithm is shown in Fig. 10.
The best results in bold, the mean as well as standard deviation are presented from each algorithm in Table 5 over 12 tests. It is noteworthy, that the PSCACO algorithm achieves optimal solutions for functions f1, f2, f3, f7, f11, f13 and f14. In contrast, CACO algorithm performs well on f1, f2, f3 and f13, whilst MOPSO algorithm obtains optimal solutions for f1, f3 and f11. In f2, f9, and f14 the GA algorithm performs best. In addition, PSCACO obtains better average optimization results for f5, f6, f8, f10, and f12 than does CACO, MOPSO, and GA algorithm, and has a smaller distance between the approximate optimal solution and the true global optimal solution.
Based on the convergence curves depicted in Fig. 9, it is evident that PSCACO exhibits significantly enhanced convergence speed and optimization capability compared to the CACO algorithm, MOPSO algorithm, and GA algorithm. Furthermore, it demonstrates effective avoidance of local optima. From Fig. 10, it can be seen that the traffic distribution of the PSCACO algorithm is mainly concentrated on the excellent category and has the largest proportion. These findings lead to the conclusion that the PSCACO algorithm, which integrates PSO and ACO while introducing chaotic perturbation, has substantially improved its precision in optimization and convergence speed. It has also demonstrated its superiority in addressing various test functions.
Example analysis
Example description
The aim is supply chain network of a manufacturing enterprise, manufacturer of certain products, selling, and recycling. Based on the company’s actual circumstances, it is determined that the enterprise has 6 customers (c = 6), 3 processing plants (m = 3), and 7 alternative distribution points (i = 7), 4 alternative recycling points (j = 4), and 4 alternative waste points (w = 4). Based on this, the specific distances between nodes are shown in Table 6, Table 7, Table 8, Table 9, Table 10.
There are three kinds of transportation means for the network to choose (g = 3), and the numerical information of relevant parameters is shown in Table 11.
There are two types of manufacturing technologies (t = 2) that can be introduced into the network, with employment coefficients of 0.035 and 0.048 for products generated using different technologies, respectively, that is, QL1 = 0.035, QL2 = 0.048. Additionally, network parameters are randomly generated in a uniform distribution range of the real operational conditions of the enterprise. Among these, the fuzzy variable η = (η1, η2, η3, η4) is also sampled randomly from a uniform distribution interval and meets the condition η1 < η2 < η3 < η4, (The network fuzzy variables include: FCi, FCj, FCw, NCj, ECi, ECw, ECw, Li, Lj, Lw, CAi, CAj, CAw, rc, αj), Reference literatures43,44, the network parameters setting as shown in Table 12.
Market demand analysis under price competition
Based on the demand function formula (37), it can be seen that market demand is affected by the product’s own price and the selling price of competitors. When the basic market demand Ac is known, the actual market demand Dc of a product is jointly determined by the selling price pc of its own product, the selling price \(\hat{p}_{c}\) of competitors’ product, the price sensitivity coefficient b and the replaceable coefficient d. In order to directly represent the actual market demand under the combined action of the above parameters, the actual market demand under the interaction of pc, \(\hat{p}_{c}\) b, and d is described based on the scenario tree, as shown in Fig. 11.
Considering the actual situation of the product, the decision maker believes that the price sensitivity coefficient of the product itself ranges from [0.5, 0.8], the substitutability coefficient between the product and the competitive product ranges from [0.2, 0.8], and the market planned sales price ranges from [185,240]. Meanwhile, the existing distributors of similar products in the market have different selling prices. In order to simplify the operation, it is divided into three categories, and the specific value is given:
(1) Less than the supply chain network sales price, that is \(\hat{p}_{c} = 160 < p_{c} \in [185,240]\);
(2) In this paper, the supply chain network plan sales price range, that is \(\hat{p}_{c} = 195 \in p_{c} \in [185,240]\);
(3) Greater than the supply chain network sales price, that is \(\hat{p}_{c} = 250> p_{c} \in [185,240]\).
Based on the number of scenarios, 192 scenarios of actual market demand are described. By determining the minimum value of actual market demand Dc in the above scenaro is 2102 (b = 0.8, d = 0.8, pc = 240, \(\hat{p}_{c}\) = 160), and the maximum value is 2318 (b = 0.5, d = 0.8, pc = 185, \(\hat{p}_{c}\) = 250).
Single objective model solving
In this paper, the minimum cost profit function Z1, minimum carbon emission function Z2 and maximum labor quantity function Z3 are taken as the main objective functions of the decision. Based on the given parameters, PSCACO algorithm, CACO algorithm, MOPSO algorithm and GA algorithm were used to solve problem respectively, and optimal values of each objective function were obtained, as shown in Table 12, Table 13, Table 14, and the iteration diagram was shown in Fig. 13, Fig. 14, Fig. 15.
As can be seen from Table 13, Table 14, Table 15, the optimization effect of the three targets solved by the PSCACO algorithm is superior to that of the CACO algorithm, MOPSO algorithm and GA algorithm. When Z1 is the main objective function of the decision, the values of Z1, Z2 and Z3 are 1,259,252,272,058,4071 respectively. When Z2 is the main objective function of the decision, the values of Z1, Z2 and Z3 are 1,218,832, 258,547, 4243, respectively. When Z3 is the main objective function of the decision, the values of Z1, Z2 and Z3 are 1,227,543,263,911,4482, respectively. Optimal values of the sub-objective functions are conflicting and cannot be obtained simultaneously on their peaks.
As can be seen from Fig. 12, Fig. 13, Fig. 14 the convergence speed of PSCASO algorithm is superior to the other three algorithms. In the process of solving Z1*, PSCACO obtains the optimal solution around the 30 th generation, while CACO obtains the optimal solution around the 60 th generation. MOPSO obtained the optimal solution around the 40 th generation. The optimal solution of GA was obtained around the 70 th generation. In the process of solving Z2*, PSCASO algorithm is optimized with the fastest convergence speed. In the process of solving Z3*, PSCASO algorithm converges after 20 iterations, and obtains better labor quantity than PSCACO algorithm, CACO algorithm, MOPSO algorithm and GA algorithm. PSCACO algorithm shows better advantages in solving examples, and has the advantages of shorter running time and faster convergence speed.
Fig 15, Fig. 16, Fig. 17 shows the supply chain network planning scheme corresponding to each sub-objective function.
As can be seen from Fig. 15, Fig. 16, Fig. 17, in terms of reducing network costs, in order to achieve the optimal network profit, the number of facilities will be reduced as far as possible to reduce the fixed cost of network, and the calculation routes will be reduced to reduce the cost of means of transport. When the goal is to minimize network carbon emissions, they will choose a shorter route for transportation, and choose to open facilities with less carbon emissions as much as possible. Compared with the network planning scheme corresponding to the optimal supply chain profit and carbon emission, the number of facilities set up in the planning network aiming at the maximum number of supply chain network labor increases significantly, because the establishment of facilities will inevitably bring about an increase in the number of labor.
Multi-objective solution
In the case of a multi-objective optimization problem, it is not possible to achieve the optimal value for each individual subobjective; however, the decision maker can identify an optimal compromise solution using a multi-objective decision-making approach. Based on the single objective optimization results, the ideal values Z1*, Z2* and Z3* under PSCACO algorithm include: 1,259,252, 258,547, 4482, and under the assumption that the decision-maker sets the values of θ1, θ2, and θ3 to 45,000, 15,000, and 800 respectively, Fig. 18 illustrates the distribution of feasible solutions resulting in a total satisfaction level of μ > 0.6 under the PSCACO algorithm. Furthermore, Table 16 presents specific results regarding network profit, carbon emissions, and employment opportunities.
Based on Fig. 18 and Table 16, it is evident that there are eight feasible solutions with a satisfaction coefficient μ > 0.6 under the PSCACO algorithm. Among these, the optimal satisfaction coefficient value is μ = 0.71, resulting in a supply chain network profit of 125,057 yuan. This represents a reduction of 8745 yuan compared to the maximum supply chain network profit under single-objective conditions. Additionally, the carbon dioxide emissions amount to 261,318 g, which is an increase of 2771 g compared to the minimum emissions in the single-objective case. The network also provides employment opportunities for 4076 individuals, which is a decrease of 406 from the maximum employment opportunities available in the single-objective case. The fuzzy membership degree for both supply chain network profit and carbon emissions corresponding to this level of satisfaction exceeds 0.82; however, the fuzzy membership degree for network labor quantity stands at only 0.48.
Consequently, it can be inferred that this set of non-inferior solutions represents a sustainable supply chain network where lower labor satisfaction coefficients are traded off for higher levels of satisfaction regarding supply chain network profits and carbon emissions.
Furthermore, by utilizing fuzzy theory to construct membership degree functions, decision-makers can establish θ values based on their enterprise’s specific circumstances in order to obtain an overall maximized satisfaction coefficient for their network planning scheme as depicted in Fig. 19.
When compared to the optimal solution for a single objective, the optimal solution under multi-objective fuzzy membership achieves a more equitable distribution across the three sub-objectives, ensuring that the supply chain network profit, carbon emissions, and labor quantity all meet the decision-maker’s criteria.
The influence of price competition on supply chain network
In the supply chain network model considering price competition, pc is 150–300 yuan/piece, and the step size is 10. Take \(\hat{p}_{c}\) as 300 yuan/piece, b = 0.5, d = 0.8. The sensitivity analysis of pc was carried out to explore the impact of the change of sales price on the network model, and the average value of the Pareto optimal solution set was taken, as shown in Fig. 20.
As can be seen from Fig. 20, when the selling price of the supply chain products gradually decreases, the total profit of the sustainable supply chain network also gradually increases, and the total carbon emissions and jobs gradually increase, and then gradually decrease. This is because when its own selling price is reduced, the market demand for the supply chain products will increase, and the efficiency of the factory will be improved. But at the same time, with the increase of carbon emissions, if enterprises do not reduce carbon emissions, they need to bear more carbon tax costs under the same carbon emissions. Therefore, under the increasing cost of carbon tax, enterprises need to constantly adjust the layout of the supply chain network, constantly make the supply chain network low-carbon, and reduce the variable carbon emissions and fixed carbon emissions of the network. This also leads to a reduction in the number of fixed network infrastructure construction and a corresponding reduction in fixed jobs, thus reducing the total number of jobs.
Parameter fuzziness analysis
The network fuzzy variables include facility opening cost: FCi, FCj, FCw; Refurbishment cost of recycled products: NCj; Carbon emission: ECi, ECj, ECw; Amount of labor created by facility opening: Li, Lj, Lw; Facility capacity CAi, CAj, CAw, market recovery rate rc and recycled product refurbishment rate αj, supply chain network target model is expected value model, constraint is opportunity constraint, and credibility measure is used to represent the probability that fuzzy constraint is established. It is assumed that the pre-set confidence level of decision makers in the above solution process is 90%, that is, decision makers are more optimistic when making decisions. In order to analyze the influence of confidence level change (decision-maker’s optimistic—pessimistic level) on each objective function, the values of 0.75, 0.9, and 1 are respectively taken for \(\delta = \delta_{i} = \delta_{j} = \delta_{w} = \delta_{{r_{c} }} = \delta_{{\alpha_{j} }}\). The single-objective optimization results are shown in Table 17 and the multi-objective optimization results are shown in Table 18.
By analyzing the single objective and multi-objective optimization results of necessity measure, possibility measure and credibility measure under different confidence levels, it is found that the supply chain network profit and labor quantity under necessity measure constraint under 0.7, 0.8 and 0.9 measure is lower than that under possibility measure. The carbon emission of supply chain network constrained by necessity measure is higher than that constrained by possibility measure at the measurement levels of 0.7, 0.8 and 0.9, and the objective function value constrained by credibility measure is the average of necessity measure and possibility measure. In addition, the profit and labor quantity decrease with the increase of the measurement level, and the carbon emission increases with the increase of the measurement level. The above results are determined by the nature of each measure. The higher the measurement level, the higher the condition requiring the fuzzy constraint to be established, that is, the smaller the fuzzy deviation required. The decision goal under the constraint of necessity measure is more optimistic, and the decision goal under possibility measure is more pessimistic, and the reliability measure is a compromise of necessity measure and possibility measure, that is, the combination of pessimistic decision goal and optimistic decision goal.
Conclusions
With more and more enterprises acknowledging the significance of the benefits of economic, environmental and social aspects arising from development, there is an increasing interest in sustainable supply chain networks. In this paper, a sustainable closed-loop supply chain network model is constructed considering the price competition. The research results of this paper mainly include:
(1) Based on the principles of sustainability, a multi-objective fuzzy programming model was developed to address the complexities of multi-level and multi-transportation mode supply chain network structures. The primary objective was to achieve equilibrium among economic, environmental, and social factors within the system. While emphasizing the economic efficiency of the supply chain network, efforts were directed towards minimizing carbon emissions as an environmental performance indicator and maximizing job creation as a social benefit indicator in order to establish a sustainable supply chain network model. Additionally, demand theory-based price demand functions were employed alongside price competition in this sustainable supply chain network model. Furthermore, a multi-objective expected value model based on fuzzy expectation theory was constructed with an opportunity constraint derived from trustworthiness measurement. Uncertain variables were represented using trapezoidal fuzzy numbers, resulting in a clear equivalent conversion of the fuzzy model.
(2) According to the characteristics of PSO algorithm as well as ACO algorithm and introducing chaotic disturbance coefficient, a PSCACO is suggested by combining the two algorithms and introducing chaotic disturbance coefficient. The optimization results show that compared with CACO algorithm, MOPSO algorithm and GA algorithm, PSCACO algorithm has better optimization effect. The quality and speed of optimization are significantly improved, which is significantly better than the above comparison algorithm.
(3) By utilizing the PSCACO algorithm, we address the single-objective optimization issue by integrating instances and the actual range of demand distribution given self-price, competitor price, own price sensitivity coefficient, and substitute coefficient range in cases where demand is elastic. We derive network planning solutions to maximize supply chain network profit, minimize carbon emissions, and maximize network labor quantity for sustainable supply chain networks. Additionally, we employ the PSCACO algorithm to tackle multi-objective optimization problems, enabling decision-makers to identify viable solutions meeting specified allowable deviation ranges. Simulation results demonstrate that this approach effectively harmonizes multi-objective optimization problems of varying scales to achieve an overall optimal network solution.
(4) By comparing the change of the objective function value of opportunity constraint under necessity measure, possibility measure and credibility measure, the results show that the profit and network labor quantity decrease with the increase of measurement level, the carbon emission increases with the increase of measurement level, and the decision objective under necessity measure constraint is more optimistic. The decision goal under the possibility measure is more pessimistic, while the reliability measure is the compromise of necessity measure and possibility measure, that is, the combination of pessimistic decision goal and optimistic decision goal.
Therefore, for enterprises, while paying attention to their own interests, they should also look at the overall situation of the supply chain, pay attention to the overall profit of the supply chain network, strengthen cooperation with upstream and downstream enterprises of the supply chain, constantly improve the coordination level of supply chain management, and work with partners to build a green, stable and sustainable supply chain ecological environment.
This paper presents a sustainable closed-loop supply chain network model incorporating price competition, offering new insights for business development. Future research can build on this foundation in several directions. On the one hand, the model’s dimensions and indicator system can be expanded. For instance, in terms of environmental benefits, in addition to carbon emissions, indicators such as energy consumption and waste disposal could be included. Regarding social benefits, factors like community development and quality of life, alongside employment, could be considered. These additions would provide a more comprehensive reflection of sustainable development. On the other hand, future research could explore the integration of emerging technologies and management concepts. Investigating the application of big data, artificial intelligence, and blockchain in sustainable supply chain management, as well as their combination with green supply chains and intelligent manufacturing, would provide innovative and practical solutions for businesses aiming to achieve sustainable development.
Data availability
All data generated or analysed during this study are included in this published article.
References
Badri, H., Ghomi, S. M. T. F. & Hejazi, T. H. A two-stage stochastic programming approach for value-based closed-loop supply chain network design. Transp. Res. Part E 105, 1–17 (2017).
Jeihoonian, M., Zanjani, M. K. & Gendreau, M. Accelerating benders decomposition for closed-loop supply chain network design: Case of used durable products with different quality levels. Eur. J. Oper. Res. 251(3), 830–845 (2016).
Jin, Li. Multi-objective Robust Fuzzy optimization problem of closed-loop supply chain network design in low carbon environment. Control Decis. 2, 293–300 (2018).
Govindan, K., Soleimani, H. & Kannan, D. Reverse logistics and closed loop supply chain: A comprehensive review to explore the future. Eur. J. Oper. Res. 240(3), 603–626 (2015).
United Nations. Transforming our world: the 2030 Agenda for Sustainable Development[R]. New York, 2015.
Eskandarpour, M. et al. Sustainable supply chain network design: An optimization-oriented review. Omega 54, 11–32 (2015).
Lin, Q. et al. Collaborative emission reduction strategies of retailers considering carbon trading policies: financing emission reduction or technology emission reduction. Syst. Eng. Theo. Pract. 44(03), 986–1005 (2024).
Liang, J. et al. Pricing and distribution channel selection strategies of new products and reproducts under carbon emission reward and punishment mechanism. Syst. Eng. Theo. Pract. 43(04), 1116–1133 (2023).
Qiu, Y. et al. Integrated Multi-objective sustainable closed-loop supply chain network optimization based on Monte Carlo tree search. Comput. Integr. Manuf. Syst. 28(01), 269–293 (2022).
Qiu, Y. et al. Quadruple bottom line under fuzzy multi-objective sustainable supply chain network planning. J. Integr. Manuf. syst. 30(9), 3354–3387 (2024).
Zhang, X., Zhao, G. & Li, B. Multi-objective Fuzzy programming for sustainable closed-loop supply chain network design. Control Theo. Appl. 37(03), 513–527 (2019) ((in Chinese)).
Hong-Tao, R. et al. Multi-objective Optimization of green aluminum supply chain network design under resource constraints. Syst. Eng. Theo. Pract. 40(08), 2090–2103 (2020) ((in Chinese)).
Tirkolaee, E. B. & Aydin, N. S. Integrated design of sustainable supply chain and transportation network using a fuzzy bi-level decision support system for perishable products. Expert Syst. Appl. 195, 116628 (2022).
Dehshiri, S. J. H. & Amiri, M. Evaluation of blockchain implementation solutions in the sustainable supply chain: A novel hy-brid decision approach based on Z-numbers. Expert Syst. Appl. 235, 121123 (2024).
Wei, J. & Zhao, J. Pricing decisions with retail competition in a fuzzy closed-loop supply chain. Expert Syst. Appl. 38(9), 11209–11216. https://doi.org/10.1016/j.eswa.2011.02.168 (2011).
Sinha, S. & Sarmah, S. P. Coordination and price competition in a duopoly common retailer supply chain. Comput. Ind. Eng. 59(2), 280–295 (2010).
Xiao, T. & Qi, X. Strategic wholesale pricing in a supply chain with a potential entrant. Eur. J. Oper. Res. 202(2), 444–455. https://doi.org/10.1016/j.ejor.2009.05.023 (2010).
Zhang, J., Chiang, W. K. & Liang, L. Strategic pricing with reference effects in a competitive supply chain. Omega 44(2), 126–135. https://doi.org/10.1016/j.ejor.2009.05.023 (2014).
Xiao, T. & Qi, X. Price competition, cost and demand disruptions and coordination of a supply chain with one manufacturer and two competing retailers. Omega 36(5), 741–753. https://doi.org/10.1016/j.omega.2006.02.008 (2008).
Sheu, J. B. & Chen, Y. J. Impact of government financial intervention on competition among green supply chains. Int. J. Prod. Econ. 138(1), 201–213. https://doi.org/10.1016/j.ijpe.2012.03.024 (2012).
Zhu, W. G. & Ge, H. Y. Green product design in supply chains under competition. European J. Oper. Res. 18(6), 1342–1385 (2016).
Abhishek, V., Jerath, K. & Zhang, Z. J. Agency selling or reselling? Channel structures in electronic retailing. Manage. Sci. 62(8), 2259–2280 (2016).
Tian, L. et al. Marketplace, reseller, or hybrid: Strategic analysis of an emerging e-commerce model. Prod. Oper. Manag. 27(8), 1595–1610 (2018).
Jena, S. K. & Meena, P. Shopping in the omnichannel supply chain under price competition and product return. J. Retail. Consum. Serv. 65, 102848 (2022).
Taleizadeh, A. A., Ghavamifar, A. & Khosrojerdi, A. Resilient network design of two supply chains under price competition: game theoretic and decomposition algorithm approach. Oper. Res. https://doi.org/10.1007/s12351-020-00565-7 (2022).
Matsui, K. Dual-recycling channel reverse supply chain design of recycling platforms under acquisition price competition. Int. J. Prod. Econ. 259, 108769 (2023).
Wang, N., He, Q. & Jiang, B. Hybrid closed-loop supply chains with competition in recycling and product markets. Int. J. Prod. Econ. 217, 246–258 (2019).
Halat, K., Hafezalkotob, A. & Sayadi, M. K. The green supply chains’ ordering and pricing competition under carbon emissions regulations of the government. Int. J. Syst. Sci.: Oper. Log. 10(1), 1983884 (2023).
Mirzagoltabar, H. et al. Sustainable dual-channel closed-loop supply chain network with new products for the lighting industry. Comput. Ind. Eng. 162, 107781 (2021).
Liu, X. & Yang, Y. Multi-objective optimization of sustainable closed-loop supply chain Network. Comput. Eng. Appl. 58(19), 291–301 (2022) ((in Chinese)).
TOBISKOVAª1 N, HATTINGERª M, GULL E S. Sustainable Production through Advanced Manufacturing, Intelligent Automation and 419 Work Integrated Learning, J. Andersson et al.(Eds.) The Authors. This article is published online with Open Access by IOS Press and distributed under the terms of the Creative Commons Attribution Non-Commercial License 4.0 (CC BY-NC 4.0)[J].(2024).
Chen, Y., Sun, H. & Xu, H. Decomposition and discrete approximation methods for solving two-stage distributionally robust optimization problems. Comput. Optim. Appl. 78(1), 205–238 (2021).
Luo, H. & Sun, W. Supply chain with free-riding consideration under bops: Pricing/subsidy decision research[C]//2023 IEEE 11th joint international information technology and artificial intelligence conference (ITAIC). IEEE 11, 1318–1324 (2023).
Rostamzadeh, R. et al. A fuzzy decision-making approach for evaluation and selection of third party reverse logistics provider using fuzzy ARAS. Transport 35(6), 635–657 (2020).
Özceylan, E. & Paksoy, T. Interactive fuzzy programming approaches to the strategic and tactical planning of a closed-loop sup-ply chain under uncertainty. Int. J. Prod. Res. 52(8), 2363–2387 (2014).
Dai, Z. & Dai, H. Bi-objective closed-loop supply chain network design with risks in a fuzzy environment. J. Ind. Prod. Eng. 33(3), 169–180 (2016).
Lan, C. et al. Hyperbolic metamaterial based on anisotropic Mie-type resonance. Opt. Express 21(24), 29592–29600 (2013).
Jianting, Z., Shenglian, G. & Kebing, C. Gain distribution method for joint optimal operation of cascade reservoirs based on in-formation entropy. J. Hydel. Eng. 39(2), 94–102 (2020).
Fangfang, G., Hongwu, L. & Weilin, R. Dimensionality reduction algorithm for network security data based on supervised dis-criminant projection. J. Commun. 42(6), 84–93 (2021).
Croux, C., Filzmoser, P. & Fritz, H. Robust sparse principal component analysis. Technometrics 55(2), 202–214 (2013).
Chen, L. et al. [Retracted] A supply chain model based on data-driven demand uncertainty under the influence of carbon tax policy. Mob. Inf. Syst. 2022(1), 5960949 (2022).
Wang, F., Wang, J. & Chen, X. Evacuation entropy path planning model based on hybrid ant colony-artificial fish swarm algorithms[C]//IOP conference series: Materials science and engineering. IOP Publ. 563(5), 052025 (2019).
Tavana, M. et al. A comprehensive framework for sustainable closed-loop supply chain network design. J. Clean. Prod. 332, 129777 (2022).
Ala, A. et al. A fuzzy multi-objective optimization model for sustainable healthcare supply chain network design. Appl. Soft Comput. 150, 111012 (2024).
Funding
This research was funded by Basic scientific research project of higher education Department of Liaoning Province, grant number LJ212411035026; Liaoning Province Education Science"14 th Five-Year Plan", subject approval number JG22DB480.
Author information
Authors and Affiliations
Contributions
Conceptualization, T.Z. and Q.H.; methodology, T.Z. and Q.H and W.Z and M.W.; software, Q.H and W.Z.; validation, Q.H.; formal analysis, T.Z. and Q.H.; investigation, Q.H.; data curation, Q.H and W.Z and M.W.; writing—original draft preparation, T.Z. and Q.H and W.Z and M.W.; writing—review and editing, Q.H.; visualization, Q.H.; funding acquisition, T.Z. All authors have read and agreed to the published version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Zhang, T., He, Q., Zhao, W. et al. Sustainable closed-loop supply chain network planning considering price competition using particle chaotic ant colony algorithm. Sci Rep 15, 17964 (2025). https://doi.org/10.1038/s41598-025-02656-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-02656-x