Study of in situ stress inversion of deeply incised valleys considering the river evolution process

Abstract

The study of the in situ stress field is significant for the stability of large underground caverns near deep V-shaped valleys. Tectonic movements, gravity and river erosion have a great influence on the formation of the modern stress field. With the existing inversion method of the stress field in river valleys, it is assumed that the current stress field was formed in an ancient time. The inversion results are derived by first calculating the influence of tectonic movements and gravity on the ancient stress field, followed by simulating modern river erosion through multistep excavation. Thus, the influence of tectonic movements on the process of river erosion is ignored. To solve this problem, an optimized inversion method considering tectonic movements during different periods of river erosion (ORE) is proposed based on multistep excavation and a genetic algorithm (GA). In this method, unit extrusion, shear movements and gravity are carried out at different periods of valley evolution to simulate the effects of tectonic movements at different geological times on the current geostress field. The method is applied to the ground stress inversion of the Shuangjiangkou hydropower station, and the relative errors between the inversion results and the field-measured data are less than 30%. By comparing the results with those of the multiple regression method and multistep excavation method, it is found that the unloading phenomenon of slopes and the stress concentration phenomenon below the riverbed can be simulated with accuracy. This indicates that the proposed method can provide a reference for the design and construction of engineering work in similar locations. Finally, by analyzing the ground stress field of the underground main powerhouse in Shuangjiangkou, it is found that high-stress-induced disasters such as rock bursts and large deformations may occur in the area.

Introduction

In recent years, hydroelectric power has received increasing attention as a clean energy source. Alpine valleys are the main landform of Southwest China, which makes it naturally suitable for the construction of large hydropower projects. Due to the topographical constraints of mountainous areas, many main hydropower powerhouses are built on the sides of valleys. During the excavation of these underground caverns, high-geostress-induced phenomena such as rock burst and large deformation have been observed. Thus, it is of great significance to engineering to accurately obtain the initial stress field distribution characteristics. The most effective way to obtain the stress field is in situ stress measurement. The main methods of measurement are stress relief analysis, hydraulic fracturing tests, acoustic emission(AE) analysis and AE-based ground stress methods^1,2. However, due to constraints such as funding, time and topography, only a few caverns can be measured during exploration, and the available geostress data are too limited to estimate a reliable ground stress field from such measurements alone.

Numerical simulation inversion methods based on measured values are widely applied to clarify the in situ stress fields at research sites. The most classical in situ stress inversion method is the multiple regression method, which can simulate the effects of tectonic movements and gravity on the formation of the geostress field. The method is widely used in engineering, such as at the Xiluodu³, Laxiwa⁴, Xiaowan⁵, and Dagangshan hydropower stations⁶. Based on the idea of the multiple regression method, a large number of improved methods have been proposed and applied^7,8,9,10. The lateral pressure coefficient method is another widely used inversion method that obtains the ground stress field by calculating the relationship between different stress components and burial depth^11,12,13. The inversion process of this method is simple, but it has poor performance when the depth is not linearly related to the stress. With the development of computer and machine learning technology, some scholars have introduced artificial intelligence methods such as neural networks^14,15,16,17, genetic algorithms (GAs)^5,18,19, and generative adversarial networks (GANs)¹³, which provide a broader view for the development of ground stress inversion. Based on field results from hydraulic fracturing tests on tunnel ground stress, Zhang et al. (2024) used a GS-XGBoost regression algorithm to determine the optimal boundary conditions and perform 3D ground stress inversion in tunnel models²⁰. Yao et al. (2021) utilized neural networks to establish the relationship between burial depth, measurement point positions, tectonic stresses, and geo-stress distribution¹⁸. Qian et al. (2021) focused on lateral stress coefficients as key internal variables to relate burial depth to lateral stress coefficients, enabling the inversion of the overall stress field distribution¹³. Pu et al. (2021) utilized a decision tree regression model to establish a nonlinear relationship between the six initial geo-stress components and the three displacement components, subsequently achieving geo-stress inversion for the mine area²¹. Zhang et al. (2016) developed a nonlinear model using support vector machines (SVM) to describe the relationship between estimated boundary conditions and actual measured stresses²².

Although machine learning has been increasingly applied in geo-stress inversion, existing studies focus on tectonic movements’ effects on the geo-stress field, overlooking the impact of fluvial erosion. Research on in situ stress has shown that river erosion significantly affects stress distribution, especially in areas with river valley topography²³. In deep V-shaped valleys influenced by tectonic movements, river erosion can cause stress release in shallow rock masses. The slopes in these areas usually undergo significant stress release phenomena, with stress concentration zones below the riverbed^24,25. To simulate this, zones of planation and terraces were created in a numerical calculation model to simulate river erosion with step-by-step excavation^8,26. This approach assumed that the ground stress field was formed in ancient times and ignored the influence of tectonic movements on the stress field during the evolution of river valley topography. To move past this assumption, a new inversion method that considers the different periods of river erosion was proposed. The effects of tectonic movements and gravity on ground stress during different periods of river valley evolution are simulated in this method, and the current stress field is calculated by GAs to grasp the characteristics of ground stress distribution in the research area. This method was applied to the ground stress inversion of Shuangjiangkou hydropower station, and its reliability was verified by comparing it with the field-measured data, multiple regression method and existing inversion method that considers river erosion. The inversion result can provide a reference for the design and construction of hydropower projects in the region.

Engineering background

Project layout

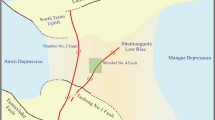
The Shuangjiangkou hydropower station is located in the upper reaches of the Dadu River in Aba Prefecture, Sichuan Province, China. The valley in the research area is narrow and has an asymmetric “V” shape, with slope angles of 40 ~ 60°, as shown in Fig. 1. There are VI river terraces in the valley near the dam site area, indicating that the river has evolved through several different stages. The geological profile of the river valley area is provided in Table 1. The river section in the dam area features a deep-cut, curved river valley geomorphology. The lower part of the valley exhibits a distinct ‘V’-shaped profile, with sections that are locally canyon-like. In contrast, the middle and upper parts of the valley are characterized by a wider valley. Along both riverbanks, there are residual terraces (I-VI), which were formed in the discontinuous belts between the Q4 and Q2 geological periods. The height differences of the terraces range from 3 m to 5 m, 12 m to 24 m, 50 m to 60 m, 85 m to 130 m, 252 m to 268 m, and 376 m to 390 m. The Level I terraces are primarily composed of accumulation terraces, while the Level II and III terraces are mostly base terraces or are embedded within accumulation terraces. The Level IV and V terraces are predominantly eroded terraces, with some sections being base terraces. And the formation age, uplift height and rate of the terraces are shown in Table 2.

Table 1 Comparison table of stratigraphic division in the reservoir area.

Fig. 1

Engineering location and river valley topography.

The underground cavern group of this hydropower project located in the mountain on the left bank of the Dajinchuan River valley mainly consists of three major caverns, which are the main powerhouse chamber, the main transformer chamber and the tailwater surge chamber. The directions of the long axes of the three main caverns are all N10°W.

Table 2 Information of the terraces.

Regional tectonic geological setting

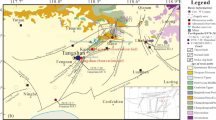
The research area is located in the tectonically active Sichuan‒Tibet region in Southwest China, as shown in Fig. 2. As a result of the northward collision of the Indian Ocean plate with the Eurasian plate, neotectonic movements characterized by fault zone activity have occurred in the region. Many large faults near the research area are active, the most influential of which is the Xianshuihe fault zone, as shown in Fig. 3. The horizontal rate of crustal movement of the Xianshuihe fault is approximately 10 ± 2 mm/a. Although the engineering area is in a relatively intact plate and a certain distance from the Xianshuihe fault, it is still influenced by tectonic movements.

Fig. 2

Tectonic stress map of China (According to Reference²⁷, created using PowerPoint, https://www.microsoft.com/powerpoint).

Fig. 3

Horizontal velocity of crustal deformation around the research area (According to Reference²⁸, created using PowerPoint, https://www.microsoft.com/powerpoint).

Results and analysis of in situ stress measurements

To grasp the characteristics of the in situ stress distribution in the research area, seven in situ stress measurement points were set on the left bank of the river valley. The locations of the measurement points are shown in Fig. 4, and the results are shown in Table 3. The ranges of maximum principal stress σ₁, intermediate principal stress σ₂ and minimum principal stress σ₃ are 15.98 ~ 32.91 MPa, 8.53 ~ 24.24 MPa and 3.14 ~ 16.41 MPa, respectively. The direction of σ₁ is consistently NNW ~ SSE, and the direction of the regional tectonic movement is generally consistent with that. The range of the strength/stress ratio σ_c/σ_max is 2.69 ~ 5.54, where σ_c (σ_c = 88.53 MPa) is the uniaxial compressive strength and σ_max is σ₁ in Table 3. According to GB/T 50,218 − 2014²⁹, the typical damage phenomena of high in situ stress zones, such as rock burst, spalling and large deformation of the rock, could have occurred in the research site during the construction period. For inversion with the numerical simulation software, the in situ stress measurements are converted to the in situ stress values of the calculated coordinate, as shown in Table 4. The range of σ_zz/σ_g is 1.12 ~ 2.71, which indicates that the research site has experienced overburden unloading due to river erosion. The relationships between principal stress and depth are shown in Fig. 5. The magnitude of the principal stress tends to increase with increasing depth; however, the correlation of σ₁ and σ₃ with burial depth is poor, with R² values of 0.65 and 0.75, respectively. Furthermore, the ranges of the lateral stress coefficients in the X-, Y- and Z-directions are 1.39 ~ 3.88, 1.22 ~ 3.80 and 1.12 ~ 2.71, respectively, which are all greater than 1.0. From the above phenomenon, it can be seen that the in situ stress distribution is strongly influenced by the tectonic movements at the research site.

Fig. 4

Engineering geological section in the horizontal direction and the calculation range of the model.

Table 3 3D principal in situ stress measurement.

Table 4 Stress components for measured in situ stress in calculation coordinate.

Fig. 5

The relationship between principal stress and depth.

In situ stress inversion method for the deep V-shaped Valley

Multiple linear regression method

Multiple linear regression has been widely applied to in situ stress field inversion^30,31. The main steps of multiple regression are as follows: Create a numerical calculation model with the factors that may lead to the initial stress field as undetermined coefficients. Then, a multiple regression equation between the predicted and measured stress fields is determined using the least squares method. The distribution of the initial geostress field is mainly influenced by many factors, such as the topography, lithology, geology, earthquake activity, tectonic movement, river erosion, and ground temperature and groundwater conditions. The effects of ground temperature and groundwater on the in situ stress field in most areas are relatively small and difficult to quantify, so they are generally neglected³². In some cases, the long-term rheology of the rock also has the potential to affect the distribution of the in situ stress field³³. Especially in soft rocks, this phenomenon may cause the geostress in the sedimentary strata to vary in the vertical direction^34,35. Natural gas-methane gas production and gas excavation processes in the V-shaped valley-lacustrine settings in orogenic uplifting areas that also strongly affect in situ stress field due to Methane explosion-related soft-sediment deformation processes (e.g., gas migraton, seepages, pockmarks, bathymetric lows, microfractures-faults)³⁶.

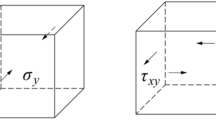
In general, gravity and tectonic motion are the main considerations of the multiple linear regression method^37,38. Six conditions that can influence the formation of ground stress were identified, as shown in Fig. 6. In Fig. 6, (a) represents the uniform extrusion tectonic motion U_x along the X-direction; (b) represents the uniform extrusion tectonic motion U_y along the Y-direction; (c) represents gravity G; (d) represents the shear tectonic motion U_yz in the XZ-plane, perpendicular to the Y-direction and along the Z-direction; (e) represents the shear tectonic motion U_xz in the YZ-plane, perpendicular to the X-direction and along the Z-direction; and (f) represents the shear tectonic motion U_xy in the XZ- and YZ-planes, along the X- and Y-direction, respectively. The stress fields caused by the above gravity and tectonic motion at the measurement point are considered undetermined coefficients, and the regression equation is established with the measured stress values. The stress field obtained by the inversion can be expressed as:

$${\sigma _{MR}}={b_1}{\sigma _{xx}}+{b_2}{\sigma _{yy}}+{b_3}{\sigma _{zz}}+{b_4}{\tau _{yz}}+{b_5}{\tau _{xz}}+{b_6}{\tau _{xy}}+{b_7}$$

(1)

where σ_MR is the stress field inverted by the multiple linear regression method, σ_xx is the stress field caused by the tectonic motion perpendicular to the X-direction and along the X-direction, σ_yy is the stress field caused by the tectonic motion perpendicular to the Y-direction and along the Y-direction, σ_zz is the stress field caused by gravity perpendicular to the Z-direction and along the Z-direction, τ_yz is the stress field caused by the shear tectonic motion perpendicular to the Y-direction and along the Z-direction, τ_xz is the stress field caused by the shear tectonic motion perpendicular to the X-direction and along the Z-direction, τ_xy is the stress field caused by the shear tectonic motion along the X- and Y-directions, and b_1~7 are coefficients.

The residual sum of squares Q is minimized by the least squares method to obtain the expression of the present ground stress field. The residual sum of squares Q is expressed as:

$$Q=\sum\limits_{k} {{{\left( {{\sigma _k} - \sigma _{k}^{\prime }} \right)}^2}}$$

(2)

where σ_k is the stress value calculated by Eq. (1) at the measurement points and σ_k’ is the stress value measured on site.

Fig. 6

Simulation of gravity and tectonic motion with the multiple regression method.

Multiple linear regression method considering river erosion

In areas with river valley topography, river erosion has a strong influence on the distribution of the in situ stress field^24,39,40. The difference between the inversion method considering the river valley evolution process and the above multiple regression method is that (1) the numerical model is created based on engineering geological data to establish the planation above the river; (2) the river erosion process is simulated by multistep excavation; and (3) the present stress field is assumed to have been formed in an ancient time, i.e., before the planation in the numerical model was excavated. The factors considered in this method are gravity, tectonic movements and river erosion. The inversion steps of this method are as follows: (1) in the numerical model containing planation, the effects of gravity and tectonic motion on the ground stress field are calculated separately, as shown in Fig. 7; (2) the expression for in situ stress is calculated by Eqs. (1) and (2); and (3) the planation and terraces are excavated in the numerical model until the current river valley topography is approximated.

Fig. 7

Simulation of gravity and tectonic motion considering the river erosion.

The optimized in situ stress inversion method considering river erosion

An important assumption of the inversion method in Sect. 3.2, which considers river erosion, is that the present ground stress field was formed in ancient times. Therefore, the tectonic motion and gravity are simulated in the model with planation. Even if the movements of the plates are consistent, and it still has a large effect on the ground stress field during the evolution of the river. The influence of tectonic movements on the in situ stress field should be considered during the different periods of river valley evolution. Based on the above theory, an optimized inversion method of the ground stress field considering river erosion (ORE) is proposed. The influences of gravity and tectonic movements on the ground stress field during the different stages of valley evolution are considered. As shown in Fig. 8, taking the uniform extrusion tectonic motion in the Y-direction as an example, the tectonic motion in the Y-direction is simulated during an ancient period, the river evolution period and the present river valley topography period. Then, the expression for the present stress field can be expressed as:

$$\sigma _{ORE}^{} = \left[ {b_{ij}^0{\text{ }}b_{ij}^1{\text{ }}...{\text{ }}b_{ij}^N} \right]\left[ \begin{gathered} \sigma _{ij}^0 \hfill \\ \sigma _{ij}^1 \hfill \\ ... \hfill \\ \sigma _{ij}^N \hfill \\ \end{gathered} \right]$$

(3)

where σ_ORE is the stress field inverted by the optimized inversion method of the ground stress field considering river erosion, σN ij is the stress field caused by the ij tectonic motion during the N period; the subscript “ij” represents the stress fields caused by different tectonic motions and gravity (σ_ij can be σ_xx, σ_yy, σ_zz, σ_yz, σ_xz and σ_xy); the superscripts 0 to N represent a total of (N + 1) excavations in the numerical simulation from the ancient period to the present topographic period, for example, σN xx is the stress field caused by the X-directional tectonic motion of the current valley topography; and bN ij represents the undetermined coefficients of the ij tectonic stress in the current topography.

Fig. 8

The tectonic movements at different periods of river valley evolution.

It is important to note the following simplifying assumptions made in the simulations of tectonic motion and erosion presented in Fig. 8: (1) Tectonic motion occurs simultaneously with surface erosion; (2) Tectonic motion is modeled through unit displacements in the numerical simulations, achieved by applying a constant normal-phase velocity at the boundary. In practice, tectonic movements and surface erosion do not necessarily occur simultaneously. However, accurately determining the relationship between erosional processes and tectonic movements is challenging. Therefore, we have made the simplifying assumption that tectonic movements and surface erosion occur concurrently. Additionally, the velocity of tectonic movement varies significantly across different historical periods. The assumption of constant velocity is employed here to facilitate the simulation of the ground stress field and to enable its application across various engineering contexts.

In Eq. (3), there are multiple factors influencing the stress field caused by the tectonic motion in each direction, so there are more undetermined coefficients. To improve the accuracy of the solution, a GA was used. GAs are inspired by Darwinian theory and are often used to estimate the global optimum^41,42,43. This introduces the concepts of gene coding, chromosome crossover, gene variation and natural selection into the process of solving optimization problems, and through continuous “population evolution”, the optimal solution of the problem is finally obtained. The process of GA is as follows:

Step 1: Initialization of Population: A random initial population is generated, where each individual (chromosome) represents a potential solution.

Step 2: Fitness Evaluation: Each individual is evaluated for its fitness, which measures how good the individual is at solving the problem. To accommodate the geo-stress inversion problem and Eq. (3), the fitness function can be defined as:

$$fitness=\hbox{min} {(\frac{1}{M}\sum\limits_{{k=1}}^{M} {({\gamma _k}{F_{uk}} - {F_{mk}}} )^2})$$

(4)

where M is the number of measurement points; k can be 1 to M; γ_k is an undetermined coefficient; F_uk is a matrix of the unit tectonic motion-induced and gravity-induced ground stresses at the measurement points for different periods; and F_mk is the stress measured at the measurement points.

Step 3: Selection Operation: Individuals are selected for reproduction based on their fitness. Common selection methods include roulette wheel selection and tournament selection. The goal is to retain individuals with higher fitness to pass their genes to the next generation.

Step 4: Crossover Operation: Selected individuals undergo crossover to produce new individuals.

Step 5: Mutation Operation: New individuals undergo mutation to increase population diversity. Mutation involves randomly altering some genes of the individual.

Step 6: Replacement Operation: The new individuals replace the old ones, forming a new population.

Step 7: Termination Condition: Check if the termination condition is met. Termination conditions include reaching a maximum number of generations, achieving a preset fitness threshold.

Step 8: Output Results: Output the optimal solution or the best individual.

The flow of the Genetic Algorithm (GA) is illustrated in Fig. 9 (A). The workflow of the ORE method is shown in Fig. 9(B), and the steps are as follows:

Step 1

Create the numerical simulation model with the planation and terrace zones.

Step 2

Simulate he effects of tectonic movements and gravity on the in situ stress field in the ancient surface period.

Step 3

Excavate the first terrace to simulate river erosion.

Step 4

Apply the tectonic movements and gravity in the model without terrace I excavated in Step 3.

Step 5

Repeat Step 3 and Step 4 until the model reflects the present river valley topography.

Step 6

Solve the undetermined coefficient in Eq. (3) by GA.

Step 7

Calculate the stress field and introduce it to the model. After the stress equilibrium calculation, a relatively accurate in situ stress field that can reflect the evolution of the river valley should be obtained.

Fig. 9

(A) The process of the GA (B) The process of the ORE method.

Engineering application

Numerical model

FLAC^3D is finite element calculation software that is based on the fast Lagrange method, which has been widely used for in situ stress inversion in geotechnical engineering^6,43. To study the influence of river evolution and tectonic movements on the geostress, a 3D numerical model was created with FLAC^3D (FLAC^3D version 9.0, https://www.itascacg.com/software/FLAC3D), as shown in Fig. 10(A). According to the geological investigation data in Table 1, the model was divided into 4 steps of excavation and excavated in the numerical software step by step in sequence until the present river valley topography was formed. To compare the effects of river erosion on the distribution of geostress, a numerical calculation model without ancient strata was created, as shown in Fig. 10(B). The horizontal dimensions of both models were 3200 m×1600 m (X×Y), and the coordinate in the Z-direction was the same as the actual elevation. The Mohr‒Coulomb constitutive model was applied in the calculation model. The computational model in FLAC^3D has a length of 1600 m and a width of 3200 m, as illustrated in Fig. 11. The element sizes vary across different weathering zones: the unweathered region has a element size ranging from 100 m to 10 m, the weakly weathered area has an element size between 20 m and 10 m, and the strongly weathered area features an element size of 5 m to 10 m. FLAC^3D exhibits significant mesh size sensitivity, with smaller mesh dimensions leading to exponentially increased computational time, and different grid resolutions for identical models potentially resulting in several-fold variations in solution duration^13,18,44. ​​Grid independence verification was conducted for three mesh densities: coarse (300,000 elements), medium (400,000 elements), and fine (500,000 elements). The results demonstrate that stress values at seven monitoring points stabilized after mesh refinement, with the maximum relative error difference between the coarse and fine meshes being < 5%, as presented in Table 5.​ This confirms that the selected mesh density achieves sufficient accuracy and satisfies grid independence criteria. The total number of elements in the computational model is 508,452.

Table 5 Verification of grid independence.

Table 6 Mechanical parameters of rock masses under different weathering conditions.

Fig. 10

(A) FLAC3D (version 9.0, https://www.itascacg.com/software/FLAC3D) Numerical calculation model with ancient strata. (B) FLAC3D (version 9.0, https://www.itascacg.com/software/FLAC3D) Numerical calculation model without ancient strata.

Fig. 11

FLAC3D (version 9.0, https://www.itascacg.com/software/FLAC3D) model for geo-stress inversion..

The mechanical parameters of the numerical model are shown in Table 6. The unweathered rock specimens are obtained from the exploration flat caves within the project area of the underground cavern, primarily consisting of fresh granite. Details of the mechanical testing conducted on this granite can be found in previous work⁴⁵. The weakly weathered rock consists primarily of weakly altered granite, interspersed with fine-grained granite crystals, pegmatite veins, and fissure-developed micro-new granite. The strongly weathered rock is mainly composed of strongly altered granite, interlayered with granite and pegmatite veins. Their mechanical parameters are obtained through field deformation tests⁴⁵. The fault primarily consists of crushed and fractured rock that is strongly weathered and rusted. The particle size distribution is as follows: gravel content greater than 60 mm ranges from 5.51 to 9.25%, gravel content between 60 mm and 2 mm is 63.49–80.55%, sand content between 2 mm and 0.075 mm is 8.79–27.37%, fines content smaller than 0.075 mm is 1.39–3.64%, and particles smaller than 5 mm make up 19.91–42.49%. The final mechanical parameters of the fault were determined through high-pressure infiltration and deformation tests on in-situ samples, as well as direct shear tests on the fault rocks conducted in the laboratory.

In situ stress inversion of the research site

The ORE method is applied to the numerical model in Fig. 10(A) for in situ stress field inversion in research area. The specific inversion process is as follows:

Step 1

A uniform tectonic motion and gravity are applied to obtain the corresponding ground stress field.

Step 2

The first step is excavated, and the stress equilibrium calculation is carried out. A stress field influenced by erosion of terrace “Q2-1” is formed. On the basis of this model, the effects of tectonic movement and gravity on the geostress field are simulated.

Step 3

Terrace “Q2-2 ~ Q4” is excavated, and the effects of tectonic movement and gravity on the geostress field are simulated. Thus, a total of 30 geostress fields under the influence of tectonic movements and gravity were obtained for the 5 periods ranging from terrace “Q2-1” to the present river valley topography.

Step 4

The obtained stress field is introduced into Eq. (3), and the GA algorithm is used to obtain the optimal solution for the undetermined coefficients.

Step 5

The calculated stress field is introduced into the numerical model, and the new inversion of the stress field is obtained by performing stress equilibration.

The undetermined coefficients calculated by GA are shown in Table 7. The inversion of the stress field can be calculated by Eq. (3). For section AA’ (Fig. 4), the distribution of σ₁ of the research site is shown in Fig. 12. The relative errors and root mean square error (RMSE) of the inversion results calculated by the ORE method and the measured values at the measurement point are shown in Tables 7 and 8. The relative error and RMSE are calculated as follows:

$$\left\{ \begin{gathered} \Delta =\frac{{{{\left\| {{\text{Calculated value}} - {\text{Measured value}}} \right\|}_2}}}{{{{\left\| {{\text{Measured value}}} \right\|}_2}}} \hfill \\ RMSE=\sqrt {\frac{1}{n}\sum\limits_{{i=1}}^{n} {{{\left( {{\text{Calculated value}} - {\text{Measured value}}} \right)}^2}} } \hfill \\ \end{gathered} \right.$$

(5)

where || ||₂ is the 2-norm, n represents the number of the measured points.

The inversion results are generally considered acceptable in engineering when the relative error is less than 30%⁴⁶. From Table 8, the range of relative error is 17.10%~27.84%, less than 30%. The relative error at point 6 is the largest, reaching 27.84%. The primary reason for this significant error is the uneven distribution of measurement points. Specifically, point 6 is located at the northernmost edge of the river’s left bank, while the nearest valley area in its vicinity lacks any measurement points. When using the principal stresses for error assessment, the relative errors remained consistently below 30%. Specifically, the minimum error is reduced to 7.63%, while the maximum error is 24.38%. Additionally, the RMSE values averaged around 3 MPa. The minimum RMSE, recorded at measurement point No. 6, is 0.81 MPa, while the maximum RMSE, observed at measurement point No. 3, is 4.77 MPa. Overall, these values suggest that the errors fall within a relatively reasonable range. This indicates that the result obtained by the ORE can reflect the actual distribution of the stress field. The following conclusions can be drawn from Fig. 12:

• (1) A large stress concentration zone exists below the river valley, with stresses ranging from 28.0 ~ 35.0 MPa. This is consistent with the view of many studies on the existence of a stress concentration zone below the riverbed in areas of river valley topography^4,26,47.

• (2) In the shallow part of the mountain, stress relaxation zones are distributed, mainly due to the release of the original high geostress in the rock due to river erosion. Thus, these areas can lead to the deterioration of the rock strength, and eventually, a low-stress zone is formed.

• (3) High-stress zones with stresses = greater than 30 MPa exist in the deeply buried areas of both the left and right banks of the valley, which is consistent with the conclusion in Sect. 3.2 that ground stress is positively correlated with burial depth.

• (4) At a fault, there is a stress relief phenomenon because of its poor mechanical properties. However, in a near-fault zone, a certain degree of stress concentration occurs due to extrusion.

• (5) The formation of stress concentration zones beneath river valleys arises from the ​​synergistic interplay between tectonic forces and surface erosion​​, where three sequential mechanisms dominate: Initially, tectonic loading from crustal uplift or plate convergence generates regional compressive stress fields (e.g., thrust fault systems). Subsequently, fluvial incision and gravitational erosion remove overlying rock mass, creating localized stress release zones and weakening subsurface support. When tectonic loading outpaces erosional unloading, elastic strain energy accumulates within the rock mass; if sustained for 10–100 thousand years, this time-lagged stress imbalance ultimately breaches shear zone activation thresholds, producing localized stress concentrations (2–3× background stress) at valley bottoms through tectonic-erosional energy redistribution.

Table 7 The coefficients calculated by GA in the ORE method.

Fig. 12

FLAC3D (version 9.0, https://www.itascacg.com/software/FLAC3D) model for geo-stress inversion..

Table 8 Geo-stress inversion values and inversion errors (Stress components).

Table 9 Geo-stress inversion values and inversion errors (Principle stress).

To further investigate how changes in the distribution of ground stress evolved during the process of surface erosion, Fig. 13 illustrates the spatiotemporal evolution of the ground stress field in the river valley from the Early-Middle Pleistocene transition (c. 780 ka) to the present. The figure demonstrates that during the Early-Middle Pleistocene boundary (Q2-1 to Q2-2, c. 780–128 ka), the valley bottom exhibited no distinct stress concentration zone; stress release was predominantly concentrated near the surface, likely due to limited incision and tectonic inheritance. Following valley morphogenesis in the Middle-Late Pleistocene (Q2-2 to Q3, c. 128–11.7 ka), the V-shaped valley became structurally defined. During this phase, the valley-bottom stress concentration began to detach from the left high-geostress region, while the right-side stress release zone became modulated by mountain morphology. From the Late Pleistocene to Holocene (Q3 to Q4, c. 11.7 ka–present), progressive riverbed incision amplified stress concentration at the channel axis, which gradually decoupled from the right mountain high-stress zone. By the Holocene (post-Q4, c. 11.7 ka–present), the deep V-shaped valley stabilized, with the area exceeding 35 MPa undergoing substantial expansion across the riverbed, which was spatially isolated from adjacent mountain blocks. This spatiotemporal coupling between erosion-driven topographic evolution and geostress reorganization underscores the necessity of integrating paleogeomorphic timelines into geomechanical simulations.

Fig. 13

(A): Distribution of the ground stress field following the evolution of the valley from Q2-1 to Q2-2. (B): Distribution of the ground stress field following the evolution of the valley from Q2-2 to Q3. (C): Distribution of the ground stress field following the evolution of the valley from Q3 to Q4.

To verify the reliability and superiority of the ORE method, its results are compared with those of the multiple regression (MR) method in Sect. 3.1 and the inversion method considering river evolution (RE) in Sect. 3.2. The numerical model in Fig. 10(B) is used for the MR method, and the model in Fig. 10(A) is used for the RE method.

$${\sigma _{MR}}=4.12{\sigma _{xx}}+2.24{\sigma _{yy}}+1.45{\sigma _{zz}}+0.83{\tau _{yz}}+3.15{\tau _{xz}}+0.36{\tau _{xy}}$$

(6)

$${\sigma _{RE}}=1.62{\sigma _{xx}}+1.30{\sigma _{yy}}+1.58{\sigma _{zz}} - 2.36{\tau _{yz}} - 0.57{\tau _{xz}}+0.12{\tau _{xy}}$$

(7)

where σ_MR is the stress field obtained by the MR method and σ_RE is the stress field obtained by the RE method.

The distributions of σ₁ calculated by the MR and RE methods in section AA’ are shown in Figs. 14 and 15, respectively. By comparing Figs. 12, and 15, the following observations were made: (1) Obvious stress relaxation and concentration zones appear in Fig. 14, but the predicted magnitude of in situ stress is relatively small and the accuracy is poor compared to the measured stresses. (2) A relatively obvious stress concentration zone does not form below the riverbed in Fig. 15, and the overall stress in the right bank of the mountain is relatively large.

Fig. 14

The distribution of σ1 obtained by the RE method in section AA’.

Fig. 15

The distribution of σ1 obtained by the RE method in section AA’.

Fig. 16

Comparison of the relative errors of the ORE method and the RE method.

A comparison of the relative errors of the ORE and RE methods is shown in Fig. 16, where the result of MR is not plotted because the overall stress distribution is obviously different from the measured values. The relative errors of the RE method are all greater than those of the ORE method, and most errors are greater than 30%. This indicates that the ORE method, which considers the effects of river erosion, tectonic movements and gravity on ground stress, provides an accurate inversion. The result of the ORE method can be used to advise the construction and design of engineering projects in similar settings.

The ORE method considers the impacts of tectonic movement, gravity, and river erosion on geostress fields during different periods, demonstrating higher inversion accuracy compared to existing methods like the RE method (e.g., GAN inversion) that account for valley excavation. Unlike other approaches that neglect excavation effects (e.g., BP Neural Network), the ORE method incorporates tectonic movement influences between consecutive excavation phases, more realistically reflecting the river valley evolution process. By integrating genetic algorithms, the simulation results are further enhanced in reliability.

Influence of the in situ stress field on the main powerhouse

The maximum principal stress σ₁ and minimum principal stress σ₃ distribution characteristics along the long axis of the main powerhouse are shown in Fig. 17(A) and Fig. 17(B). From the figures, the following can be concluded: (1) In the main powerhouse area, the range of maximum principal stress σ₁ magnitudes is 17.5 ~ 28.0 MPa, and the range of minimum principal stress σ₃ magnitudes is 10.0 ~ 16.0 MPa. The strength/stress ratio is 3 ~ 5; thus, there is a high probability of high-stress-induced phenomena such as rock burst and spalling during construction, especially in the area along the positive direction of the Y-axis. (2) Fault “f1” passes under the main powerhouse and has a relatively small effect on σ₁ in the area. Near the fault, a certain degree of stress concentration is observed in the minimum principal stress field. The stability of the underground cavern is mainly controlled by σ₁, so the influence of fault “f1” on the stability of the surrounding rock of the main powerhouse is relatively small.

Fig. 17

(A) The distribution of σ1 in section BB’. (B) The distribution of σ3 in section BB’.

Sensitivity analysis of parameters

To investigate which input parameters most significantly impact the accuracy of the stress inversion, we modified the mechanical parameters of the unweathered rock mass. The adjusted parameters included Poisson’s ratio, cohesion, and the internal friction angle. Poisson’s ratio was varied from 0.2 to 0.4 in increments of 0.1; cohesion was adjusted from 1 MPa to 5 MPa in increments of 2 MPa; and the internal friction angle was set between 40 and 60 degrees in increments of 10 degrees. This resulted in a total of 12 sensitivity analysis scenarios, as shown in Table 10. And the geo-stress inversion errors for various mechanical parameter values are shown in Table 11.

After adjusting the bulk modulus, the average relative error ranged from 40 to 50%, with the maximum error reaching 50.29% when the bulk modulus is set to 30 GPa. For both Poisson’s ratio and cohesion, the average error remained around 40%. In contrast, the largest average error for the internal friction angle occurred at 30 degrees, with a value of 72.32%. When the internal friction angle drops sharply from a higher value (e.g., 40°) to 30°, the shear strength of the rock mass decreases significantly. The strength deterioration induces stress redistribution, resulting in substantial discrepancies between numerically predicted stress values and field measurements. Additionally, the average relative error at an internal friction angle of 70° is significantly higher than those observed when adjusting the bulk modulus, Poisson’s ratio, and cohesion. This suggests that the accuracy of the internal friction angle’s parameter determination is highly sensitive to the results of the geo-stress inversion. Therefore, special attention should be given to accurately calibrating this parameter during the inversion process.

To further assess the impact of the internal friction angle on geo-stress inversion, Fig. 18 illustrates the distribution of σ₁ in the valley area when the internal friction angle is set to 30°, which corresponds to the working condition with the largest relative error in the inversion. In contrast to Fig. 13, the most significant difference is the disappearance of the stress concentration zone beneath the river valley, or alternatively, a marked downward shift in its location. Additionally, σ₁ in this stress concentration area decreases substantially from 35 MPa to 25 MPa. This altered stress distribution does not align with the actual geological conditions, highlighting the need for greater attention to the internal friction angle during parameter calibration.

Table 10 The sensitivity analysis scenarios.

Table 11 Geo-stress inversion errors for various mechanical parameter values.

Fig. 18

Distribution of σ1 in the valley region with an internal friction angle of 30°.

Limitations of the model and corresponding engineering recommendations

The inversion method proposed in this paper is applicable to geo-stress inversion tasks in the deep V-valley region, particularly in areas where significant surface erosion has occurred. However, the effectiveness of this method requires further investigation in regions with less pronounced topographic relief, where surface erosion is minimal, or in other types of river valley topographies, such as U-shaped valleys.

For the selection of geo-stress measurement points, it is recommended to prioritize ​in-situ testing at the valley floor​ (e.g., 1 km downstream of the Shuangjiangkou Dam site, spaced at 50 m intervals) to capture stress concentration gradients. When arranging additional measurement points, ​dynamic drilling campaigns​ should be implemented with variable depths (e.g., 3–5 m intervals) and lateral offsets (1–3 times valley width) to account for lateral stress variations. Regarding engineering design, ​split-set grouting combined with rock bolts​ (6–9 m length, 1.5 × 1.5 m grid) is advised for high-stress zones (> 30 MPa), as validated in the Shuangjiangkou Dam foundation stabilization project. This approach will provide a more comprehensive understanding of geo-stress distribution in the study area, laying a solid foundation for more accurate geo-stress inversion work and enhancing our overall understanding of geo-stress patterns.

Conclusion

In this paper, a new in situ stress inversion method that can simulate the tectonic movement, gravity and evolution process of river valleys was proposed. The in-situ stress inversion analysis of the Shuangjiangkou hydropower area based on this method was carried out, and the main conclusions are as follows:

• (1) Tectonic movements, gravity and river erosion have a great influence on the formation of the modern stress field in this area with valley topography. The topographic changes from ancient times to modern times are caused by river erosion, which contributes to the stress relaxation in the slope and the formation of a stress concentration zone below the riverbed.

• (2) The new method proposed in this paper takes into account the effects of tectonic movements, gravity and river erosion on ground stress at different periods, which gives it a higher inversion accuracy than that of the existing valley excavation method. The average error of the ORE method is 15% lower than that of the RE method. Compared with the method that does not account for excavation, the multistep excavation method is more reflective of the known the river evolution.

• (3) The maximum principal stress σ₁ is 17.5 ~ 28.0 MPa at the main powerhouse of the Shuangjiangkou hydropower station, and the strength/stress ratio is 3 ~ 5, which indicates that high-stress-induced phenomena such as rock burst, spalling, and large deformation may occur. For future cavern excavation projects, enhanced displacement monitoring should be prioritized, with particular emphasis on implementing support systems that require appropriate reinforcement–specifically, split-set grouting combined with rock bolts (length: 6–9 m; grid spacing: 1.5 × 1.5 m) is recommended for high-stress zones exceeding 30 MPa.