Probabilistic failure assessment of bolt-stabilized pro-dip slopes considering shear effect

Abstract

This study presents a probabilistic failure assessment model for bolt-stabilized pro-dip slopes, explicitly addressing the critical yet overlooked shear effect in conventional stability analyses. Conventional analytical approaches oversimplify the mechanical interactions between sliding slope masses and stabilizing bolts through the assumption of uniaxial tensile loading, thereby neglecting the combined tensile-shear stress states observed in real-world scenarios. To bridge this gap, the proposed model integrates force and moment equilibrium analyses, adopts the von Mises strength criterion for bolt rupture assessment, and systematically incorporates bedrock stratigraphy through differentiated parameter assignments. A comprehensive Monte Carlo simulation framework quantifies failure probabilities across three dominant modes: tensile-shear failure of bolts, rock-grout bond failure, and grout-bolt bond failure. Validation through the Freeway No.3 landslide case study demonstrates that shear-inclusive calculations yield significantly higher failure probabilities (exceeding 80% underestimation in shear-neglected models under high groundwater conditions). Parametric analyses reveal distinct behavioral regimes governed by bolt inclination, fixed length, and hydrological factors. The results emphasize that shear effect fundamentally alters failure mode dominance, with bolt failure becoming predominant under realistic stress conditions. This work provides a critical advancement in reliability-based design for pro-dip slopes, offering engineers a tool to mitigate catastrophic risks through physics-informed probabilistic assessments.

Introduction

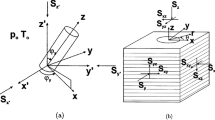
Pro-dip slopes, characterized by rock strata dipping in the same direction as the slope face, are inherently prone to large-scale shear sliding along weak interlayers or bedding planes^1,2,3,4,5. This type of geological structures predominate in mining and civil engineering projects, where catastrophic failures can lead to severe economic losses and safety hazards^6,7,8,9. To mitigate such risks, bolt stabilization techniques, including fully grouted rock bolts and anchor cables, have been widely adopted as cost-effective reinforcement measures^10,11. The installation procedure of the rock bolt involves inserting a steel bar into pre-drilled boreholes, grouting to bond the bolt with surrounding rock, and finally anchoring the bolt head at slope surface. A schematic diagram of typical pro-dip slope stabilized by steel bolts is shown in Fig. 1.

Fig. 1

Sketch of a pro-dip slope stabilized by bolts.

Understanding the failure mechanisms of bolted pro-dip slopes are crucial for maintaining the engineering operations. Both field investigations and physical model tests consistently demonstrate a critical mechanical behavior during bedding plane-controlled slope sliding: rock bolts are subjected not merely to tensile forces, but rather to a combined tension-shear stress state^{12,13,14,15,16}. This composite loading effect exhibits particular intensity at shear interfaces within rock masses, challenging the conventional pure-tension assumption in bolt design. Laboratory shear tests on bolted joints further reveal that the strength of anchored steel bars under combined tension-shear loading shows significant reduction compared to pure tensile conditions^{17,18,19,20,21}. These findings underscore the imperative to account for shear effects in stability analyses of bolted pro-dip slopes.

Recent advances in slope reliability research emphasize probabilistic approaches to quantify uncertainties including strength parameter variability, bolt corrosion rates, and interfacial shear characteristics^22,23,24,25. However, prevailing geomechanical models oversimplify bolt-slope interaction mechanisms by predominantly considering tensile resistance while neglecting the critical role of shear effects in load transfer systems. Such simplifications may lead to substantial underestimation of failure probabilities, particularly in steeply dipping strata. Furthermore, existing methodologies inadequately address the stratified nature of mechanical parameters in bedrock formations, resorting to homogenized treatments instead. Clearly, for bolted pro-dip slopes, it is necessary to establish a failure probability assessment model that more closely aligns with the real situation.

This study addresses these critical gaps through three contributions: (1) Incorporation of both force equilibrium and moment equilibrium analysis in geomechanical modeling to characterize the actual tension-shear states of rock bolts; (2) Adoption of the von Mises strength criterion replacing conventional tensile strength criteria for bolt rupture assessment; (3) Systematic consideration of bedrock stratigraphy through differentiated parameter assignments in failure probability evaluations. Building upon these advancements, a probabilistic failure evaluation model for bolt-stabilized pro-dip slope is established and validated through a practical case study. Furthermore, parametric sensitivity analysis was conducted to investigate the influences of key parameters on model outcomes.

Materials and methods

Mechanical analysis

The mechanical model of a bolt-stabilized pro-dip slope is schematically illustrated in Fig. 2. The slope exhibits potential sliding along a weak interlayer, accompanied by a deep rear fissure formation. The structural fissures create preferential pathways for water infiltration and storage. The governing forces acting on the potential sliding mass include:

Fig. 2

Forces on potentially sliding slope stabilized by bolts.

(a) Gravitational force (G): Represented as a concentrated force at the centroid, calculated by:

$$G=\gamma bV$$

(1)

where γ denotes the average unit weight of slope rock, b is the horizontal bolt spacing, and V represents the cross-sectional area of the potential sliding masses.

(b) Hydrostatic pressure in rear fissure (E): Exhibiting triangular distribution from the phreatic surface to the weak interlayer, with resultant force located at one-third the water column height. The magnitude is given by:

$$E=\frac{1}{2}{\gamma _{\text{w}}}bh_{{\text{w}}}^{2}$$

(2)

where ${\gamma _{\text{w}}}$ is the unit weight of water, ${h_{\text{w}}}$denotes water column height in the fissure.

(c) Pore water pressure along weak interlayer (P): Characterized by linear increase from zero to ${\gamma _{\text{w}}}{h_{\text{w}}}$ along the interface. The resultant force acts at one-third length from the fissure:

$$P=\frac{1}{2}{\gamma _{\text{w}}}b{h_{\text{w}}}{l_{\text{S}}}$$

(3)

where ${l_{\text{S}}}$ is the weak interlayer length.

• a. (d) Normal force (N): Perpendicular to the weak interlayer, assumed acting at the intersection point between the interface and the vertical line through the centroid. This parameter is determined through mechanical equilibrium analysis.

• b. (e) Resisting force (S): Parallel to the weak interlayer, calculated using the Mohr-Coulomb criterion:

$$S=N\tan \varphi +cb{l_{\text{S}}}$$

(4)

where φ and c represent the friction angle and the cohesion of the weak interlayer, respectively.

(f) Bolt reinforcement forces: As depicted in Fig. 3, each bolt sustains composite tension-shear loading. Previous studies^23,24,25 assumed pure axial tension ($\varepsilon \approx 0$), which is inadequate for pro-dip slopes where multidirectional loading occurs. Our model explicitly considers both axial tensile force (${R_i}$) and transverse shear force (${Q_i}$), normalized per unit width as ${R_i}/{w_i}$ and ${Q_i}/{w_i}$ respectively, where ${w_i}$ represents horizontal bolt spacing.

Fig. 3

Sketch of the forces on a bolt: (a) shear effect considered; (b) shear effect ignored (ε denotes the angle between the bolt and the resultant force acting on it).

Force equilibrium equations are established as:

$$\sum {{F_x}=0\;\;\;\;\;\;\;} \sum {{Q_i}\sin \alpha } /{w_i}+\sum {{R_i}\cos \alpha /{w_i}} +S - G\sin \beta - E\cos \beta =0$$

(5)

$$\sum {{F_y}=0\;\;\;\;\;\;\;} \sum {{Q_i}\cos \alpha /{w_i}} - \sum {{R_i}\sin \alpha /{w_i}} +N - G\cos \beta +E\sin \beta +P=0$$

(6)

$$\sum {M=0\;\;\;\;} \sum {{R_i}{l_i}\sin \alpha /{w_i}} - \sum {{Q_i}{l_i}\cos \alpha /{w_i}} - N{l_{\text{N}}}+G{l_{\text{G}}} - E\left( {{l_{\text{S}}}\sin \beta +\frac{{{h_{\text{w}}}}}{3}} \right) - \frac{2}{3}P{l_{\text{S}}}=0$$

(7)

where $\alpha$ is the angle between the bolt and weak interlayer, yielding $\alpha =\beta +\delta$. Substituting Eqs. (1)-(4) into Eqs. (5)-(7), yield the matrix formulation:

$$\left[ \begin{gathered} {a_{11}}\;\;{a_{12}}\;\;{a_{13}} \hfill \\ {a_{21}}\;\;{a_{22}}\;\;{a_{23}} \hfill \\ {a_{31}}\;\;{a_{32}}\;\;{a_{33}} \hfill \\ \end{gathered} \right]\;\left[ \begin{gathered} {Q_i} \hfill \\ {R_i} \hfill \\ N \hfill \\ \end{gathered} \right]=\left[ \begin{gathered} {b_{11}} \hfill \\ {b_{21}} \hfill \\ {b_{31}} \hfill \\ \end{gathered} \right]$$

(8)

where coefficient matrix elements are defined as:

${a_{11}}=n\sin (\beta +\delta )/{w_i}$,${a_{12}}=n\cos (\beta +\delta )/{w_i}$,${a_{13}}=\tan \varphi$,${a_{21}}=n\cos (\beta +\delta )/{w_i}$,${a_{22}}= - n\sin (\beta +\delta )/{w_i}$,${a_{23}}=1$${a_{31}}= - \sum {{l_i}\cos (\beta +\delta )} /{w_i}$,${a_{32}}=\sum {{l_i}\sin (\beta +\delta )} /{w_i}$,${a_{33}}= - {l_{\text{N}}}$,${b_{11}}=\gamma bV\sin \beta +\frac{1}{2}{\gamma _{\text{w}}}bh_{{\text{w}}}^{2}\cos \beta - cb{l_{\text{S}}}$,${b_{21}}=\gamma bV\cos \beta - \frac{1}{2}{\gamma _{\text{w}}}bh_{{\text{w}}}^{2}\sin \beta - \frac{1}{2}{\gamma _{\text{w}}}b{h_{\text{w}}}{l_{\text{S}}}$,

${b_{31}}=\frac{1}{2}{\gamma _{\text{w}}}bh_{{\text{w}}}^{2}\left( {{l_{\text{S}}}\sin \beta +\frac{{{h_{\text{w}}}}}{3}} \right)+\frac{1}{3}{\gamma _{\text{w}}}b{h_{\text{w}}}l_{{\text{S}}}^{2} - \gamma bV{l_{\text{G}}}$, n is the number of bolts in the selected profile.

The values of ${Q_i}$, ${R_i}$ and ${N}$ can be derived by the matrix transformation of Eq. (8).

Failure modes and failure functions

Due to the complexity of the failure mechanism of a slope-bolt system, Sabatini et al.²⁶ summarized four failure modes, i.e., failure of the steel bolt, failure of the rock mass, failure of the rock-grout bond, and failure of the grout-bolt bond. The failure of the rock mass, even in the case of fractured rock, seldom occurs owing to the fact that the bond strength between the rock and grout or the grout and bolt is much lower than the rock strength²⁶. Considering this reason, we focus on the other three failure modes in the present study, as sketched in Fig. 4. The three failure modes have also been confirmed through laboratory direct shear tests on bolted joints^{17,18,19,20,21}.

Fig. 4

Failure modes of the slope-bolt system.

Mode 1: Tensile-shear failure of the bolt at weak interlayer.

Although the majority of the rock bolt is subjected to tensile loading, it will experience a combined tension-shear effect at the weak interlayer of the pro-dip slope due to sliding. Combined tension-shear stress may induce bolt yielding, subsequently leading to slope instability. The shear effect on the rock bolt was largely overlooked in previous stability evaluation models of slope-bolt systems. In the present study, the actual stress situation of the bolt is fully considered.

For failure Mode 1, slope failure initiates when the resultant tension-shear stress of rock bolt intensifies to exceed the material yield threshold. The corresponding limit state function can be formulated using the von Mises criterion as:

$${Z_1}={\sigma _{\text{f}}} - \sqrt {{{\left( {\frac{{{R_i}}}{{{A_{\text{S}}}}}} \right)}^2}+4{{\left( {\frac{{{Q_i}}}{{{A_{\text{S}}}}}} \right)}^2}}$$

(9)

where ${\sigma _{\text{f}}}$ and ${A_{\text{s}}}$ denote the yield strength and the cross-sectional area of the steel bolt, respectively. The positive and negative values of ${Z_1}$ represent the stable and unstable state of the slope, respectively.

Mode 2: Failure of the rock-grout bond.

The load-transfer integrity of slope-bolt systems relies on grout-mediated interfacial bonding between bolts and bedded rock masses. Progressive interfacial degradation occurs when interfacial shear stresses surpass the stratum-specific bond strength, ultimately destabilizing the slope through interfacial decoupling. While existing models acknowledged grout bonding quality, their reliance on homogenized geological conditions critically oversimplified bedrock heterogeneity^18,24,27. To resolve this limitation, we establish a multi-stratum analytical model accounting for lithological stratification, with the corresponding limit state function expressed as:

$${Z_2}=\sum {\pi {D_j}{L_j}{u_j}} - {R_i}$$

(10)

where ${D_j}$ and ${L_j}$ are the outer diameter and the length of the grout fixed in the jth stratum of bedrock, ${u_j}$ denotes the bond strength between the bolt and the jth stratum. The failure of the rock-grout bond would occur under the condition of ${Z_2}<0$, and vice versa.

Mode 3: Failure of the grout-bolt bond.

In contrast to Mode 2, tensile forces transfer through shear-dominant load mechanisms at the grout-bolt interface. Catastrophic pull-out failure ensues when shear stress intensities exceed the grout-bolt bond capacity, manifesting as progressive bolt-grout decoupling. The governing limit state criterion is formulated as:

$${Z_3}=\pi d{L_0}v - {R_i}$$

(11)

where d and ${L_0}$ represent the diameter and fixed length of rock bolt, respectively, and v is the bond strength between the grout and bolt. If ${Z_3}<0$, the grout-bolt bond breaks, and if ${Z_3} \geqslant 0$, the bond remains effective.

By sequentially evaluating tensile-shear forces from Eq. (8) through failure functions (9)-(11), the stability state of the slope-bolt system can be diagnostically determined. Notably, these failure modes exhibit mutual exclusivity - the onset of any single failure mechanism suffices to trigger global system instability.

Probabilistic failure assessment

Conventional deterministic analyses operate under the assumption of fixed input parameters, neglecting two fundamental uncertainty sources: (1) inherent geospatial heterogeneity of rock mass properties, and (2) observational uncertainties systematically introduced through geological investigation and construction processes.

Notwithstanding these pervasive uncertainties, their statistical regularity enables probabilistic reliability quantification through multivariate integration:

$${P_{\text{f}}}=\int {I\left[ {Z(\chi )} \right]f(\chi )d\chi }$$

(12)

where ${P_{\text{f}}}$ denotes failure probability, $f(\chi )$ and $Z(\chi )$respectively represent probability density function and failure function of random vector $f(\chi )$, while $I[Z(\chi )]$ serves as a binary indicator enforcing limit state conditions:

$$I\left[ {Z(\chi )} \right]=\left\{ \begin{gathered} 0\;\;\;\;{\text{when}}\;Z(\chi ) \leqslant 0 \hfill \\ 1\;\;\;\;{\text{when}}\;Z(\chi )>0 \hfill \\ \end{gathered} \right.$$

(13)

The Monte Carlo simulation (MCS), which is widely used in reliability computations, is performed to operationalize Eq. (12). It constructs a probability model of certain actual problem and simulates the behavior of the system through random sampling to obtain an approximate solution to the problem. The basic procedures include: constructing or describing the probability process, implementing sampling from given probabilistic distributions, and establishing various estimators. Based on the MCS, a large sets of physical parameters are generated randomly which are substituted into the failure functions to evaluate the stability of the slope. This yields mode-specific failure probabilities:

$$P_{{\text{f}}}^{r} \approx \frac{1}{m}\sum\limits_{{k=1}}^{m} {I\left[ {{Z_r}({\chi _k})} \right]}$$

(14)

where$P_{{\text{f}}}^{r}$and ${Z_r}$ respectively denote the failure probability and failure function for Mode r (r = 1, 2, 3), m is the quantity of samples, and${\chi _k}$denotes the kth sample of$\chi$.

Considering system-level failure as a series system, the global failure probability ($P_{{\text{f}}}^{{\text{s}}}$) elevates beyond individual mode probabilities:

$$P_{{\text{f}}}^{{\text{s}}} \approx \frac{1}{m}\sum\limits_{{k=1}}^{m} {I\left[ {{Z_1}({\chi _k})\left| {{Z_2}({\chi _k})} \right.\left| {{Z_3}({\chi _k})} \right.} \right]}$$

(15)

This probabilistic framework not only assesses system reliability, but also pinpoints critical failure modes, delivering practical guidance for slope reinforcement design.

Workflow for engineering practice

The computational framework proposed in this study demonstrates significant applicability for engineering implementation through the following systematic workflow:

Step 1

Establish geomechanical model.

Develop the slope-bolt system model by consulting existing design specifications and construction records. Particular attention should be paid to validating the model’s geological fidelity through comprehensive field investigations, including borehole logging and geophysical surveys.

Step 2

Parameter acquisition and characterization.

Acquire material parameters through field measurements (geotechnical mapping, in-situ testing) and laboratory experimentation (triaxial tests, shear strength assessments). Categorize parameters as deterministic (fixed values) or stochastic (statistical distributions), with particular emphasis on establishing appropriate probability density functions for uncertain parameters.

Step 3

Stochastic parameter sampling.

Implement Monte Carlo simulation to generate m stochastic realizations of uncertain parameters, ensuring statistical convergence through Kolmogorov-Smirnov testing.

Step 4

System reliability analysis.

Execute batch computations by incorporating each parameter set into the mechanical framework established in Sect. "Mechanical analysis". For each realization: (1) compute critical stability indicators, (2) evaluate failure modes per Sect. "Failure modes and failure functions" criteria, and (3) quantify failure function values.

Step 5

Failure probability assessment.

Process all computational outcomes to determine: system-level failure probability (Eq. (15)) Mode-specific failure likelihood (Eq. (14)).

While this methodology features an intuitive workflow, particular attention must be given to parameter uncertainty quantification which collectively govern result reliability and engineering decision confidence. For slope-bolt systems, the stochastic variabilities propagate through three primary domains:

• i) Slope geomechanical parameters: Unit weight dispersion, strength parameter stochasticity at weak interlayers, stratigraphic thickness variability, and groundwater table fluctuation;

• ii) Bolt mechanical properties: Yield strength scattering, bedrock anchorage length tolerance, cross-sectional area manufacturing deviations;

• iii) Interface bonding characteristics: Rock-grout and grout-bolt bond strength randomness.

Case study

In this section, the proposed model is applied to a failure case of the bolted pro-dip slope - the Freeway No.3 landslide that occurred in Taiwan on April 25, 2010. Through comparative calculations, we demonstrate the critical importance of considering shear effects in such scenarios. Numerous studies have investigated this landslide, with detailed descriptions available in the existing literature^28,29,30,31.

The catastrophic event involved approximately half of the mountain slope collapsing, with over 200,000 m³ of soil and rock inundating the highway and destroying an interchange bridge. Figure 5(a) presents a panoramic view of the landslide scene. During highway construction, excavation was implemented at the mountain foot, followed by the stabilization of 572 bolts at the slope front. The rock bolts were arranged with a horizontal spacing of approximately 2.6 m and a vertical spacing of 1.8 m. Post-failure field investigations revealed that only 58 bolts remained at their original positions. Among the remaining bolts, 48% exhibited fracture failure of steel strands. Figure 6 illustrates the geological profile and bolt arrangement in the slope area. The excavated slope reveals six distinct strata from top to bottom: Overburden soil (OB), Sandstone with vertical joints (SS), Alternations of thin sandstone and shale (SS/SH), Dark gray shale (SH), Sandstone with trace fossils (SS-f), and Alternations of thin sandstone and shale (SS/SH). The slip surface is believed to develop at the interface between the third and fourth layers, specifically along the top of the dark gray shale layer. Core drilling investigations identified clay seams at the slip surface depth in several boreholes. These weak clay seams have been recognized as a potential contributor to slope failure.

Fig. 5

(a) Panoramic photograph of Freeway No. 3 landslide in Taiwan; (b) Site photograph showing the vertical tension joints developed in the second stratum (SS)²⁹.

Fig. 6

(modified from Wang et al.²⁹ and Chen et al.³⁰

Cross-sections of the slope on Freeway No. 3 before failure: (a) full profile; (b) profile showing the strata and bolting structures at the front edge.

Notably, the second and third strata (SS and SS/SH) exhibit significantly higher permeability compared to the underlying fourth stratum (SH). Post-event investigations revealed extensive vertical joints within the sandstone as shown in Fig. 5(b). This evidence strongly suggests that groundwater accumulation occurred in the strata above the shale, generating horizontal pressures at joints and uplift pressure along the slip surface. In this case study, we assume the presence of a tension joint at the trailing edge of the profile shown in Fig. 6(b), subsequently assessing the failure probability of the bolted slope under varying groundwater levels. The computational parameters, primarily reported by Wang et al.²⁹, are summarized in Table 1.

Table 1 Parameter values for the analysis of the failure probability of freeway no. 3 slope²⁹.

Figure 7 presents a comparative analysis of slope-bolt system failure probabilities with respect to groundwater level variations in trailing edge joint, contrasting computational models incorporating shear effects with those neglecting such mechanical considerations. The probabilistic curves demonstrate a biphasic characteristic: an initial gradual escalation below 6.0 m groundwater level transitions to an exponential growth phase beyond this critical threshold. Notably, while the divergence between shear-inclusive and shear-neglected models remains marginal (< 0.03 relative difference) under low hydraulic head conditions (${h_{\text{w}}}$< 5 m), pronounced discrepancies emerge at elevated groundwater levels. Specifically, shear-considered calculation yield failure probability surpassing their shear-neglected counterparts by 0.4 at ${h_{\text{w}}}=10\;{\text{m}}$. This critical observation underscores that conventional computational approaches omitting shear mechanisms may systematically underestimate failure risks in bolted pro-dip slopes by over 80% under extreme hydrological conditions - a potentially catastrophic oversight in geotechnical design for Freeway No.3 landslide. These findings also demonstrate the validity of the proposed model.

Fig. 7

Failure probability comparison of Freeway No.3 landslide with/without shear effect considered during groundwater variation.

Discussion

In the present study, a pro-dip slope stabilized by bolts is employed for the discussion. The differences in the computational results with and without considering shearing effect will be compared, and the influences of varying parameters on the failure probability will be explored. In this case, the slope developed in sedimentary strata with an inclination of 27°. The slope is prone to sudden failure due to its downward creep along a weak interlayer. A vertical fissure with 9.6 m in depth is generated at the rear top of the slope, which provides the pathway for groundwater infiltration. The potentially sliding slope mass is composed of siltstone, and the underlying strata are mudstone, silty mudstone, sandstone, breccia, and limestone in vertical sequence. For the sake of stabilization, the slope is excavated into a stepped shape and then anchored by the bolts. Two rows of bolts are installed on every step surface for a total of four steps. Both the longitudinal and transverse spacing of the bolts are 3 m. The front view and A1-A2 profile of the bolted slope are illustrated in Fig. 8. Tables 2 and 3 present the parameter values of the slope-bolt system.

Fig. 8

(a) Front view and (b) A1-A2 profile of the study slope.

Table 2 Parameter values of the slope and bolt.

Table 3 Parameter values of the bedrock.

Shear effect

A mechanical model was developed for the bolted pro-dip slope through explicit consideration of shear interactions between the potentially sliding mass and stabilization elements. Monte Carlo simulations were subsequently performed to quantify the statistical characteristics of bolt forces and failure functions, with particular emphasis on comparative analysis between scenarios incorporating and neglecting shear effects.

Figure 9(a) illustrates the evolution of tensile, shear, and resultant forces in the rock bolts with respect to the friction angle of the weak interlayer. All three force components exhibit approximately linear reductions as the friction angle increases. Notably, while the resultant forces under both consideration scenarios demonstrate comparable magnitudes (< 10% variation), their mechanical compositions differ fundamentally. The shear-inclusive condition produces composite tension-shear loading, contrasting with pure tensile loading observed when neglecting shear effects. Of particular note is the observation of the greater shear force than the tensile force in the shear-inclusive condition. This finding highlights the critical importance of incorporating shear interactions in stability assessments.

Fig. 9

(a) Comparison of forces on the bolt with/without shear effect considered; (b) Comparison of the mean values of the failure function for three modes with/without shear effect considered.

Figure 9(b) compares failure function means (z_r) for three distinct failure modes. Lower z_r values indicate higher failure susceptibility. For Mode 1 (bolt failure), z_r values under shear consideration are systematically lower than those in shear-neglected scenarios. Conversely, Modes 2 (rock-grout bond failure) and 3 (bolt-grout bond failure) exhibit inverse trends. This suggests that shear interactions significantly alter failure mode dominance: bolt failure becomes predominant when considering shear effects, whereas bond failures govern system behavior when shear effects are neglected.

Influence of the fixed length

The parametric study focuses on the influences of the fixed length and inclination of the bolt, and the groundwater level on the failure probabilities.

The parametric analysis reveals a characteristic trilinear (Z-shaped) relationship between fixed length (L₀) and failure probabilities (Fig. 10). Three distinct behavioral regimes emerge:

Fig. 10

Variation of failure probabilities for slope-bolt system and three failure modes with fixed bolt length.

(1) Unstable regime (L₀ < 1.5 m): System failure probability ($P_{{\text{f}}}^{{\text{s}}}$) remains saturated at 1.0;

(2) Transitional regime (1.5 m < L₀ < 3.75 m): $P_{{\text{f}}}^{{\text{s}}}$decreases progressively, exhibiting strong correlation with Mode 2 probabilities ($P_{{\text{f}}}^{2}$<$P_{{\text{f}}}^{3}$);

(3) Stabilized regime (L₀ > 3.75 m): $P_{{\text{f}}}^{{\text{s}}}$ converges to Mode 1 probability (≈ 0.19), indicating bolt failure becomes the governing mechanism.

Influence of the bolt inclination

Figure 11 demonstrates the coupled effects of bolt inclination and fixed length on system reliability. Two characteristic behaviors emerge: For L₀ < 3.5 m: system reliability shows high sensitivity to δ; For L₀ > 3.5 m: reliability becomes less δ-dependent.

Fig. 11

Variation of failure probability for slope-bolt system with bolt inclination and fixed bolt length.

Notably, for any given δ, $P_{{\text{f}}}^{{\text{s}}}$ follows a biphasic relationship with L₀: initial reduction phase (L₀ < 3.5 m) governed by bond failure mechanism, followed by asymptotic stabilization (L₀ > 3.5 m) controlled by bolt strength limitations.

Influence of the groundwater

Figure 12 shows the variations of failure probabilities of the three modes with groundwater level. With the rise of the groundwater level, the failure probability of Mode 1 is much larger than those of the other two modes, implying that the failure probability of the system is the same as that of Mode 1. The groundwater influence analysis identifies four characteristic phases i.e., stable phase (${h_{\text{w}}} \leqslant 3\;{\text{m}}$): $P_{{\text{f}}}^{{\text{s}}}$ remains at 0, initiation phase ($3\;{\text{m}}<{h_{\text{w}}} \leqslant 5.5\;{\text{m}}$): $P_{{\text{f}}}^{{\text{s}}}$ slowly increases, critical phase ($5.5\;{\text{m}}<{h_{\text{w}}} \leqslant 8\;{\text{m}}$): $P_{{\text{f}}}^{{\text{s}}}$ accelerates, and failure phase (${h_{\text{w}}}>8\;{\text{m}}$): $P_{{\text{f}}}^{{\text{s}}}$ approaches saturation. In practice, we must pay attention to the steep rise of the failure probability, which indicates the system fails suddenly.

Fig. 12

Variation of failure probabilities for slope-bolt system and three failure modes with groundwater level.

Conclusion

This study establishes a probabilistic framework for evaluating the stability of bolted pro-dip slopes, addressing critical limitations in conventional approaches through three key advancements: (1) To accurately reflect the tensile-shear stress state of rock bolts, the geomechanic analysis incorporates both force equilibrium and moment equilibrium of the slope mass, thereby enabling precise calculation of tensile and shear forces acting on the bolts. (2) The von Mises strength criterion is adopted to analyze bolt conditions, replacing conventional tensile strength criteria. (3) The probabilistic failure assessment comprehensively considers the stratigraphic properties of bedrock formations and implements differentiated parameter assignments. A comprehensive Monte Carlo simulation framework quantifies failure probabilities across three dominant modes: tensile-shear failure of bolts, rock-grout bond failure, and grout-bolt bond failure.

The effectiveness of the proposed model was validated through a case study of the Freeway No.3 landslide in Taiwan. The investigation revealed that while computational results considering versus neglecting shear effects exhibited minor discrepancies under lower groundwater levels, the former demonstrated substantially greater values compared to the latter under elevated groundwater conditions.

The parametric study was conducted to investigate the influences of bolt inclination, bolt length, and groundwater level on the failure probability of stabilized slopes, which further revealed how parameter variations induced transitions among three distinct failure modes.

Practical implications of this study include: mandatory inclusion of shear effects in bolt design criteria for pro-dip slopes, optimization of bolt inclination and fixed length to minimize failure risks implementation of real-time groundwater monitoring at critical thresholds. Future work should address dynamic loading effects and corrosion-induced strength degradation.