Bolt loosening evaluation method based on normalized screw root equivalent stress and loosening life curve

Bolts are subject to complex loads and prone to loosening failure in transverse random service environments. To establish a loosening life evaluation method applicable to different types of bolts, numerous bolt clamping-force recession curves were obtained by bolt-loosening tests, and the relationship between the transverse displacement external load and loosening life (D–N curve) was established. Subsequently, an equivalent model of the bolt external load and screw load was established based on Castigliano’s theorem, and an equivalent model of the screw load and screw-tooth root stress was established based on the deformation coordination equation of elastic mechanics. Based on the above bolt-load equivalent models, the screw-tooth root stresses were equivalently characterized by the transverse displacement of the bolted connection, and then the screw-tooth root equivalent stress–loosening life curve (S_u–N curve) was established to normalize the D–N curves with different bolt diameters. Finally, a bolt-loosening bench test of an antenna bracket under transverse random vibration was performed, and the loosening life of the bolts was evaluated using the S_u–N curve. The maximum relative error between the test and theoretically predicted lives was only 6.26%, which verified the accuracy of the bolt-loosening life evaluation method based on the bolt-load equivalence and provided a certain reference for the bolt-loosening life evaluation and anti-loosening design in a random vibration environment.

Introduction

Bolted connections are one of the most commonly used connection methods in mechanical systems and are widely used in civil engineering, aerospace, rail transportation, automobiles, and ships because of their easy disassembly, high reliability, and good fastening ability^1,2,3,4,5. The main role of a bolted connection is to ensure that a structure remains sufficiently stable. Bolted connections must maintain a sufficient clamping force at all times while transmitting force or moment⁶. However, in practical engineering, bolts are often subjected to harsh service environments with random vibrations, and their loading characteristics are complex. Screws are subjected to a bending moment under the action of a reciprocating transverse load, which causes bending deformation. Simultaneously, the screw tooth also generates alternating stress and elastic–plastic deformation, and the contact surface of the screw tooth exhibits fretting wear⁷. With the accumulation of elastic–plastic deformation and fretting wear of the screw, the contact surface of a bolted connection exhibits a relative sliding phenomenon that reduces the clamping force. If the clamping force decreases significantly during service, bolt loosening or fatigue fractures occur⁸.

Bolt loosening generally occurs before fatigue fracture; therefore, bolt loosening is the primary failure mode^9,10. Many factors affect bolt loosening, including the initial preload^11,12,13, bolt specification^14,–17, load form^18,19,20, contact surface condition^21,22,23, and service environment temperature^24,25,26, making it difficult to monitor and evaluate bolt loosening. In important mechanical structures, bolt loosening may cause major accidents; therefore, it is very important to study the evaluation method of bolt-loosening life.

In the theoretical analysis of bolt loosening, Sopwith²⁷ investigated the load distribution of each screw tooth in a threaded pair through theoretical analysis in the early stage. The strain behavior was expressed by the elongation and compression of the bolt and nut in the axial direction, and a corresponding analytical model was established. Yamamoto et al.²⁸ conducted an in-depth study on the deformation behavior of a screw tooth during bolt loosening and regarded bolt loosening as a process of energy accumulation and release after reaching a critical value. They proposed that the root cause of bolt loosening was owing to the elastic properties of the screw; the screw bends and deforms under transverse excitation and stores a certain amount of torsional deformation energy. With the continuous excitation, the stored deformation energy gradually increases and is released when it reaches a certain critical value. The released energy causes the screw contact surface to rotate, resulting in bolt loosening. They established a formula for calculating the transverse critical load that causes bolt loosening and a calculation method for the bearing capacity of each screw tooth based on its mechanical characteristics and verified the correctness of the method through bolt-loosening tests²⁹. Subsequently, Sakai³⁰ indicated that during the bolt-loosening process under a transverse load, the sliding direction of the threaded surface was consistent with the load direction, and the contact surface between the bolt head and the clamped part slid along the circumferential direction. At the same time, the calculation formulas of the critical loosening moment and angle were established according to the mechanical equilibrium theory, and it was found that the theoretical results were consistent with the test results. Zhang et al.³¹, Jiang et al.³², and Yang et al.³³ established models for calculating the critical loosening load of bolts by considering the thread properties and load forms. Krenevicius et al.³⁴ defined the relationship between the load-bearing capacity of a screw tooth and the rotation angle as a polynomial function and derived the screw loads under the simultaneous action of bending load, axial force, and transverse force. In summary, it can be seen that energy accumulation and release are the main failure mechanisms of bolt loosening, and the loosening critical load obtained based on the theoretical mechanical model has a certain guiding significance for preventing bolt loosening. However, limitations still exist in quantitatively characterizing the cumulative characteristics of the bolt-loosening process.

Goodier and Sweeney³⁵ developed a bolt axial tension test device for testing bolt loosening at the earliest stage. Through multiple bolt axial loading tests, it was found that the nut rotated in the initial stage. The maximum and minimum loosening rotation angles of the nut were measured using two pointers fixed on the outer ring of the nut at 2° and 0.7°, respectively. Subsequently, Sauer et al.³⁶, Clark and Cook³⁷, and Gambrell³⁸ improved Goodier and Sweeney’s test method and found that axial excitation did not easily lead to the complete loosening of bolts through axial-loosening tests. To investigate the effect of transverse excitation on bolt loosening, Junker³⁹ used a bolt transverse vibration test to completely loosen a bolt under transverse excitation, and its degree of loosening was much greater than that under axial excitation. Through the relationship between the displacement amplitude and the number of vibrations, it was found that the bolt loosening was due to the relative slip between the contact surface of the bolt and the clamped part, which was generated by the driving force of the external excitation being greater than the friction force between the threaded pairs. Jiang et al.⁴⁰ found that plastic deformation occurred first because of the stress concentration at the root of the screw tooth through a transverse vibration test and finite element simulation and that the plastic region was mainly concentrated at the root of the first ring of the working screw tooth. Plastic deformation gradually accumulates under the ratchet effect, resulting in a gradual reduction in the clamping force. Jiang et al.⁴¹ found that the complete loosening process of a bolt consisted of two stages: material loosening and structural loosening. The clamping-force recession in the material-loosening stage was caused by the plastic deformation of the material, but relative rotation between the threaded pairs did not occur. The clamping-force recession in the structural-loosening stage was caused by the relative rotation between the threaded pairs, and the bolt was completely loosened during this stage. To further clarify the mechanism of bolt loosening, Zhang et al.^42,43 found that fretting wear occurred on the thread surface under transverse excitation. The degree of wear deepened with the continuous loading of excitation and eventually caused the recession of the clamping force. In summary, the transverse load is the main cause of bolt loosening, and the bolt-loosening process can be divided into material-loosening and structural-loosening stages. Experimental research can accurately characterize the degree of bolt loosening; however, the relative displacement of a bolted connection and the screw-tooth stress are difficult to obtain in practical engineering applications. Therefore, the key to accurately predicting bolt-loosening life is to obtain the bolt load and stress under service conditions.

In terms of bolt-loosening life prediction, Li et al.¹¹ realized a synchronous measurement of the bolt clamping force and transverse displacement by modifying the Junker test machine. Through a transverse loosening test of M16 bolts under different preloads, it was found that in the initial stage, the clamping force of the bolts exhibited a double exponential recession trend with an increase in vibration time. Later, Zhang et al.⁴⁴ used a bolt simulation model to simulate the fretting wear of a threaded surface during the recession of the bolt clamping force and then established a bolt-loosening life prediction method that predicted the degree of wear of the threaded surface. The simulation prediction results were consistent with the experimental results, thereby verifying the accuracy of the method. However, this method has high modeling accuracy requirements, and different bolts with different specifications must be modeled differently, which is time-consuming. On this basis, Jiang et al.⁴⁵ constructed D–N curves with different loosening states through transverse variable-amplitude bolt-loosening tests and found that the curves were similar to the material stress–fatigue life curves, both of which showed obvious high- and low-cycle boundaries and bilinear characteristics. Through transverse vibration tests, Yang et al.⁴⁶ found that bolts did not loosen when the transverse displacement amplitude was less than a certain critical value, which is similar to the fatigue limit of the material; simultaneously, the displacement–life curves of the M6 and M8 bolts were established. Yang et al.⁴⁷ established a linear cumulative model of bolt loosening through high-low-amplitude and low-high-amplitude transverse loading tests of bolts and proved that the model can accurately predict the bolt-loosening life through bolt-loosening tests. The test proved that the model could accurately predict the loosening life of bolts. In summary, current bolt-loosening prediction methods are still mainly based on D–N curves, but it is difficult to obtain the relative displacement of a bolted connection in an actual structure; therefore, practical applications in engineering still face many challenges. Because the D–N curve of bolt loosening is similar to the S–N curve of material fatigue, engineering applications would be simplified if a normalized bolt-loosening life prediction curve can be established using a theoretical model.

As a closed fastening system, a bolted connection is subject to complex loads influenced by numerous factors. The bolt-loosening process is closely related to the contact characteristics and deformation state of the screw pair, whereas the stress state of the screw teeth is complex and difficult to obtain. The traditional bolt-loosening life evaluation method primarily uses the displacement load of a bolt to establish a life evaluation model. Although it has a certain theoretical significance, the displacement load of a bolted connection in an actual structure cannot be accurately obtained, and it is difficult to apply it in an actual engineering environment. Therefore, it is necessary to consider the loading behavior of screw teeth as the base point to establish a simple and effective numerical method to characterize the relationship between screw-tooth stress and bolt-loosening life, which is of great scientific significance for evaluating the bolt-loosening life in a transverse random vibration environment.

In this study, the D–N curve was obtained by performing bolt-loosening tests. Subsequently, an equivalent model of the bolt external load and screw load was established based on Castigliano’s theorem, and an equivalent model of the screw load and screw-tooth root stress was established based on the deformation coordination equation of elastic mechanics. Subsequently, based on the bolt-load equivalent models, a method for obtaining the screw-tooth root stress was proposed, and the S_u–N curve was established to normalize the D–N curves with different bolt diameters. Finally, the accuracy of the bolt-loosening life evaluation method based on the bolt-load equivalent model was verified by performing a bolt-loosening bench test of an antenna bracket.

Bolt-loosening test

Test details

To obtain the relationship between the transverse vibration load and loosening life of bolts, a loosening-life test was performed using 8.8 grade M16 × 120 high-strength bolts as test specimens. As shown in Fig. 1, the test was performed on an MTS 809 tensile-torsional fatigue testing machine, and the bolt was tightened on a single-lap L-type fixture with high stiffness. To avoid the influence of the frictional force of the fixture contact surface on the applied load during the testing process, rolling needles were arranged on the overlapping surface of the fixture, and lubricating oil was applied. The two ends of the fixture were assembled on the fixed and actuating ends of the testing machine, and an alignment groove was set on the side of the fixture to ensure consistent fit clearance. The bolts were connected in series to a small gasket, fixture, pressure sensor, and large gasket. In general, the gaskets are never used for the important bolted connections. However, in this study, the large and small gaskets were installed on one side of the pressure sensor. The main purpose was to ensure that the bolt pressure was more evenly transmitted to the pressure sensor and to guarantee the accuracy of the pressure data. Additionally, the small gasket under the bolt head was mainly used to protect the surface of the connecting components from being scratched by the bolt head, ensuring consistent test conditions for each test.

The transverse load of the bolt was input in the form of sinusoidal transverse displacement excitation, and six excitation levels of 0.25 mm, 0.3 mm, 0.4 mm, 0.5 mm, 0.6 mm, and 0.8 mm were set. According to the mechanical design standard, considering factors such as the yield strength of the bolt material and effective cross-sectional area, the pre-tightening force of the bolt was set at 60 kN, and the pre-tightening force of each test was precisely controlled by a torque wrench and EVT-14 TP-12 T pressure sensor. The dynamic change in the clamping force of the bolt during the test was recorded in real time using a DH5902 N portable data collector with a 200-Hz sampling frequency, and the test was stopped when the bolt fractured.

Fig. 1

Bolt-loosening test tooling.

Test results

A typical clamping-force recession process of a bolt under the action of a transverse load is shown in Fig. 2. According to the competitive failure analysis theory of bolts in⁴⁸, the intersection point (N_D point) of the clamping-force recession curve and the 45° tangent line was used as the boundary point between the structural-loosening and fatigue-fracture stages. Before the N_D point, the bolt mainly exhibited fretting wear, contact surface slip, and thread pair slip, whereas after the N_D point, the bolt mainly exhibited crack propagation and fracture behavior. The clamping force of the bolt continued to decrease under the repeated action of the transverse displacement load, and the recession rate showed a fast-slow-fast non-linear characteristic. The bolt fracture was located at the transition fillet under the bolt head or the root of the first ring of the working screw tooth, which indicated that when the bolt was subjected to a transverse load, the force was the greatest at these two locations.

Fig. 2

Bolt clamping-force recession process.

Transverse load mainly leads to bolt loosening, whereas axial load mainly leads to bolt fatigue fracture. Therefore, the damage caused by transverse loads is different from that caused by axial loads, and the transverse damage mainly leads to changes in the roughness and friction coefficient of the thread contact interface. Consequently, in the structural-loosening stage, the bolt underwent fretting wear and transverse damage accumulated, resulting in the slip of the contact interface. Simultaneously, owing to the complex meshing state of the thread pairs, the evident deformation characteristics in this area directly affected the decline in the clamping force and was the root cause of bolt loosening. Therefore, in this study, the loosening life of bolts was studied based on the load characteristics of the screw teeth.

The bolt-clamping force recession curves for different transverse displacement amplitudes are shown in Fig. 3. Under the same pre-tightening force, the bolt-loosening life was negatively correlated with the transverse displacement amplitude. The higher the transverse displacement amplitude, the greater the transverse load and additional bending moment of the bolt, which increases the deformation of the screw teeth and makes the bolt more prone to loosening. From the first 5000 vibration cycles of the intercepted bolt clamping-force recession curve, the transverse displacement amplitudes of 0.25 mm, 0.3 mm, 0.4 mm, 0.5 mm, 0.6 mm, and 0.8 mm correspond to clamping force variation amplitudes of 1.4 kN, 1.9 kN, 2.1 kN, 2.6 kN, 2.8 kN, and 6.3 kN, respectively. As the transverse displacement amplitude increased, the amplitude of the clamping-force variation also increased because an increase in the transverse displacement amplitude leads to an increase in the contact force of each contact surface of the bolted connection, and the bolt clamping force will also increase under the influence of the contact force.

Fig. 3

Bolt clamping-force recession curves under different transverse displacement amplitudes.

To further investigate the correlation characteristics between bolt-loosening life and the transverse displacement, the D–N curve of an M16 bolt was constructed by extracting the vibration cycles of the loosening state when the clamping force declined to 95% of the initial pre-tightening force and was compared with the D–N curve of the M10 bolt in reference⁴⁵. One of the reasons for choosing the D–N curve of the loose state when the clamping force was reduced to 95% of the initial pre-tightening force was to compare it with the D–N curve of M10 bolts to find out the loosening characteristics of both types of bolts. Another reason was to convert the D–N curve of the loose state when the clamping force was reduced to 95% of the initial pre-tightening force into the S_u–N curve in order to evaluate the loosening life of the subway bogie antenna bracket bolts in Sect. 4.2. The parameters of the two types of bolts are listed in Table 1, and their D–N curves are shown in Fig. 4. The loosening life of the two types of bolts increased as the transverse displacement amplitude decreased and also showed the same characteristics of high- and low-cycle boundaries and bilinearity. In Fig. 4, the obvious inflection point of the D–N curve was used as the demarcation point between the low-cycle region and high-cycle region. Due to the dispersion of the D–N curve, the demarcation point is a fuzzy qualitative point in the D–N curve rather than a precise quantitative point. After converting the D–N curve of different types of bolts into a normalized S_u–N curve, this demarcation point becomes a precise quantitative point.

Table 1 Comparison of bolt parameters.

Fig. 4

D–N curves of M10 and M16 bolts.

For service bolts in actual engineering structures, the loosening life can be evaluated using the D–N curve if the relative displacement of the clamped parts is known. However, different D–N curves are required to calculate the bolt-loosening life according to different bolt types, pre-tightening forces, and clamping thicknesses, and obtaining each D–N curve requires complicated and tedious bolt-loosening tests. This method is not only time-consuming and laborious but also not universal. Therefore, based on the bolt-loosening theory and the characteristics of screw-tooth root stress, it is important to establish a bolt-loosening life-prediction curve that can be applied to different types of bolts and loading conditions. However, because a bolted connection is a closed system with complex screw pairs, it is impossible to directly measure the dynamic changes in the screw-tooth root stresses during the loading process. Therefore, it is necessary to obtain the equivalent relationship between the bolt external load and screw-tooth root stresses based on the bolt-load equivalent model to obtain a normalized S_u–N curve.

Screw-tooth root equivalent stress–loosening life curve

Bolt-load equivalent model

A completely bolted connection system primarily consists of bolts, nuts, and clamped parts. After the bolts are pre-tightened, the components contact each other and generate interaction forces, thereby achieving a force balance and maintaining sufficient tightness and stability. Hashimura and Socie⁴⁹ found that damage such as crack nucleation at the root of the first thread is not be observed in the low cycle under transverse load, and loosening is caused by bolt rotation. In the high cycle, a crack is observed at the root of the first thread. Loosening occurs due to loss of bolt stiffness caused by crack nucleation and propagation, which then leads to bolt rotation. This conclusion is highly consistent with the conclusion of this study that the loosening life of bolts shows the characteristics of high- and low-cycle boundaries and bilinearity. The stress state of each contact surface of a bolted connection changes under the action of a transverse external load. Bolt-loosening failure occurs when the transverse external load exceeds the critical load required for bolt loosening. When the transverse external load is less than that of the critical load, although it does not immediately lead to bolt loosening, it causes an irreversible fastening deterioration of the bolts. The repeated accumulation of fastening deterioration eventually leads to bolt-loosening failure, and this loosening situation accounts for most engineering cases. Therefore, the stress state of bolts with transverse loads less than that of the critical load of loosening was analyzed in this study.

Because the bolted connection of mechanical equipment is always in a fastening state during service, the space of the screw pair is closed, and the load state of the screw tooth cannot be obtained directly by a measuring instrument. Therefore, based on strict mechanical theory, bolt-load equivalent models were constructed in this study, and the local stress state of the screw tooth was equivalent to the bolt external load or screw load, which can be directly measured. As shown in Fig. 5, the bolt-load equivalent model is a numerical model that uses the screw load as a bridge to achieve an equivalent conversion between the bolt external load and the screw-tooth root stress. The load transfer process of a bolted connection is divided into two stages: transfer of the bolt external load to the screw load and transfer of the screw load to the screw-tooth root stress.

Fig. 5

Bolt-load equivalent model¹⁹.

In transfer stage I, the screw undergoes bending deformation under the action of transverse displacement and leads to the corresponding bending moment at each position of the screw along the axial direction. The bending moments at both ends of the screw are the largest, and the bending moment at the central section of the screw is the smallest. Based on Castigliano’s theorem, an equivalent model of the bolt external load and screw load is established as

$$\:M={(x}_{3}-\frac{3{I}_{Z1}{l}_{2}^{2}}{\left(6{{l}_{2}I}_{Z1}+{l}_{1}{I}_{Z2}\right)})\frac{12D{E}_{b}{I}_{Z2}(6{l}_{2}{I}_{Z1}^{2}+{l}_{1}{I}_{Z2}{)}^{2}}{(6{l}_{2}{I}_{Z1}^{2}+{l}_{1}{I}_{Z2}{)}^{2}{l}_{2}^{3}+3{{l}_{1}^{2}I}_{Z2}^{2}{l}_{2}^{3}}$$

(1)

where M is the bending moment of the screw, l₁ is the fit clearance of the bolt hole, l₂ is the clamping length, x₃ is the distance from any position on the screw to the bolt head, I_Z1 is the axial section inertial moment of the bolt head, I_Z2 is the transverse section inertial moment of the screw, E_b is the elastic modulus of the screw, and D is the transverse displacement.

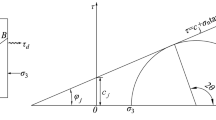
In transfer stage II, when the screw load is transferred to the screw tooth, the screw-tooth surface is subjected to a force generated by the pre-tightening force, bending moment, and transverse force expressed as S₁, S₂, and S_T, respectively. In the direction of the force, S₁ and S₂ are perpendicular to the inclined plane of the screw tooth, and the resultant force can be represented by S_A. The direction of S_T is consistent with that of the transverse external load. Based on the deformation coordination equation of elastic mechanics, the calculation expressions for the three forces were obtained, and the equivalent model of the screw load and screw-tooth root stress was established as¹⁹

$$\:\left\{\begin{array}{l}{S}_{1}\left(z\right)={\lambda\:}_{1}{F}_{P}\frac{tan\beta\:}{{cos}\alpha\:}\left[\frac{{cos}h({\lambda\:}_{1}L)}{{sin}h({\lambda\:}_{1}L)}{cos}h({\lambda\:}_{1}z)-{sin}h{(\lambda\:}_{1}z)\right]\\\:{S}_{2}\left(z\right)=-\sqrt{{\lambda\:}_{2}}\left[(M-\frac{M}{1-{e}^{-2\sqrt{{\lambda\:}_{2}}L}}){e}^{\sqrt{{\lambda\:}_{2}}z}-\frac{M}{1-{e}^{-2\sqrt{{\lambda\:}_{2}}L}}{e}^{-\sqrt{{\lambda\:}_{2}}z}\right]\frac{2{sin}\beta\:}{{d}_{2}{cos}\alpha\:}\\\:{S}_{T}\left(z\right)=-\sqrt{{\lambda\:}_{3}}\left[({F}_{T}-\frac{{F}_{T}}{1-{e}^{-2\sqrt{{\lambda\:}_{3}}L}}){e}^{\sqrt{{\lambda\:}_{3}}z}-\frac{{F}_{T}}{1-{e}^{-2\sqrt{{\lambda\:}_{3}}L}}{e}^{-\sqrt{{\lambda\:}_{3}}z}\right]{sin}\beta\:\end{array}\right.$$

(2)

Among them,

$$\:\left\{\begin{array}{l}{\lambda\:}_{1}=\sqrt{(\frac{1}{{A}_{b}{E}_{b}}+\frac{1}{{A}_{n}{E}_{n}})\frac{1}{(\frac{{k}_{b}}{{E}_{b}}+\frac{{k}_{n}}{{E}_{n}})tan\beta\:}}\\\:{\lambda\:}_{2}=(\frac{1}{{I}_{by}}+\frac{1}{{I}_{ny}})\frac{{d}_{2}^{2}}{4{(k}_{b}+{k}_{n}){sin}\beta\:}\\\:{\lambda\:}_{3}=\frac{2(1+\nu\:)}{({k}_{b}^{r}+{k}_{n}^{r}){sin}\beta\:}(\frac{{f}_{b}}{{A}_{b}}+\frac{{f}_{n}}{{A}_{n}})\end{array}\right.$$

(3)

where α is the half-thread angle, β is the thread rise angle, d₂ is the middle diameter of the bolt, and z is the distance from the screw tooth to the top surface of the nut in the load direction. A_b and A_n, E_b and E_n, I_by and I_ny, f_b and f_n, and G_b and G_n are the cross-sectional areas, elastic moduli, moments of inertia relative to the y-axis, shear-shaped coefficients, and shear moduli of the bolt and nut, respectively. v_b, v_n, k_b, and k_n are Poisson’s ratios and elastic deformation coefficients of the bolt and nut, respectively.

In order to solve the deformation parameters v_b, v_n, k_b, and k_n caused by the inclination of the bolt head and engaging thread under transverse load. Yamamoto and Kasei²⁹ proposed that the deformation of a unit width screw is caused by five conditions: bending, shear, thread inclination, thread shear, and radial force, as shown in Eqs. (4)–(6).

External thread:

$$\:\left\{\begin{array}{l}{\delta\:}_{1b}=0.034w\:{cos}\:\alpha\:\frac{1-{\nu\:}_{b}^{2}}{{E}_{b}}\\\:{\delta\:}_{2b}=1.08w\:{cos}\:\alpha\:\frac{1+{\nu\:}_{b}}{{E}_{b}}\\\:{\delta\:}_{3b}=0.229w\:{cos}\:\alpha\:\frac{1-{\nu\:}_{b}^{2}}{{E}_{b}}\\\:{\delta\:}_{4b}=1.18w\:{cos}\:\alpha\:\frac{1-{\nu\:}_{b}^{2}}{{E}_{b}}\\\:{\delta\:}_{5b}=1.003w\:{cos}\:\alpha\:\frac{1-{\nu\:}_{b}}{{E}_{b}}\end{array}\right.$$

(4)

Internal thread:

$$\:\left\{\begin{array}{l}{\delta\:}_{1n}=0.073w\:{cos}\:\alpha\:\frac{1-{\nu\:}_{n}^{2}}{{E}_{n}}\\\:{\delta\:}_{2n}=1.15w\:{cos}\:\alpha\:\frac{1+{\nu\:}_{n}}{{E}_{n}}\\\:{\delta\:}_{3n}=0.294w\:{cos}\:\alpha\:\frac{1-{\nu\:}_{n}^{2}}{{E}_{n}}\\\:{\delta\:}_{4n}=1.14w\:{cos}\:\alpha\:\frac{1-{\nu\:}_{n}^{2}}{{E}_{n}}\\\:{\delta\:}_{5n}=1.003w\:{cos}\:\alpha\:\frac{1.69+{\nu\:}_{n}}{{E}_{n}}\end{array}\right.$$

(5)

$$\:\left\{\begin{array}{c}{\delta\:}_{b}={\delta\:}_{1b}+{\delta\:}_{2b}+{\delta\:}_{3b}+{\delta\:}_{4b}+{\delta\:}_{5b}=w\:{cos}\:\alpha\:\frac{{k}_{b}}{{E}_{b}}\\\:{\delta\:}_{n}={\delta\:}_{1n}+{\delta\:}_{2n}+{\delta\:}_{3n}+{\delta\:}_{4n}+{\delta\:}_{5n}=w\:{cos}\:\alpha\:\frac{{k}_{n}}{{E}_{n}}\end{array}\right.$$

(6)

where w is the unit force. k_b and k_n can be obtained by introducing Eqs. (4) and (5) into Eq. (6).

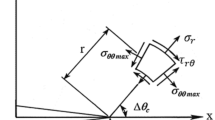
To obtain the screw-tooth root stresses, the forces S_A and S_T were converted into the principal stress S_n perpendicular to the surface of the screw tooth, the shear stress S_τ along the radial direction, and the shear stress S_b along the tangential direction as¹⁹

$$\:\left\{\begin{array}{l}{S}_{n}=-{S}_{T}\:{sin}\:\alpha\:-S\:{cos}\:\beta\:\\\:{S}_{\tau\:}=S\:{sin}\:\beta\:(1-\frac{\mu\:{S}_{n}}{\sqrt{(S{sin}\beta\:{)}^{2}+(-{S}_{T}{cos}\alpha\:{)}^{2}}})\\\:{S}_{b}=-{S}_{T}\:{cos}\:\alpha\:(1-\frac{\mu\:{S}_{n}}{\sqrt{(S{sin}\beta\:{)}^{2}+(-{S}_{T}{cos}\alpha\:{)}^{2}}})\end{array}\right.$$

(7)

where µ is the static friction coefficient.

Based on the tensor characteristic equation, the three principal stresses σ₁, σ₂, and σ₃ were solved for the above forces, and the screw-tooth root nominal equivalent stress was obtained as

$$\:{\sigma\:}_{n}=\sqrt{\frac{1}{2}\left[({\sigma\:}_{1}-{\sigma\:}_{2}{)}^{2}+({\sigma\:}_{2}-{\sigma\:}_{3}{)}^{2}+({\sigma\:}_{3}-{\sigma\:}_{1}{)}^{2}\right]}$$

(8)

By introducing the stress concentration factor K_t into Eq. (8), and the true stress of the screw-tooth root was obtained as follows:

$$\:{\sigma\:}_{t}={K}_{t}\sqrt{\frac{1}{2}\left[({\sigma\:}_{1}-{\sigma\:}_{2}{)}^{2}+({\sigma\:}_{2}-{\sigma\:}_{3}{)}^{2}+({\sigma\:}_{3}-{\sigma\:}_{1}{)}^{2}\right]}$$

(9)

Based on the above bolt-load equivalent models, an equivalent transformation relationship between the bolt external load and the screw-tooth root stress can be established for bolted connections with different bolt types, pre-tightening forces, and clamping thicknesses. In addition, the prediction of bolt-loosening life in this study draw on the prediction method of bolt fatigue life, and the difference from the prediction method of fatigue life is as follows: First, the D–N curves of bolts should be transformed into M–N curves (the relationship curves between the screw bending-moment amplitudes and vibration times), and then the M–N curves should be transformed into normalized S_u–N curve. In this process, the true stress of the screw-tooth root is obtained based on the nominal equivalent stress and stress concentration coefficient. Then, the rain flow counting is performed on the true stress-time histories of the screw-tooth root under transverse random vibration. Finally, the accumulated loosening damage is calculated according to the rain flow counting results, and then the bolt-loosening life is obtained. Therefore, the action of cyclic stress and the process of damage accumulation of bolts are reflected in the process of rain flow counting of the true stress-time histories of the screw-tooth root. Therefore, in this study, the stress concentration factor K_t is used to calculate the true stress of the screw-tooth root.

Normalized screw-tooth root equivalent stress–loosening life curve

The D–N curves of the M16 bolts were obtained by the bolt-loosening life tests described in the previous section and compared with the D–N curve of the M10 bolts. To obtain the normalized bolt-loosening life evaluation curve, the D–N curves of the two types of bolts were converted into S_u–N curves based on the bolt-load equivalent models described in this section, and their normalized analysis was performed.

The conversion process is as follows. First, based on the equivalent model of the bolt external load and screw load, the transverse displacement amplitudes of the D–N curve (Fig. 4) were converted to screw bending-moment amplitudes. Based on this, the M–N curves were established by combining them with the results of the bolt-loosening life test as shown in Fig. 6a. Then, based on the equivalent model of the screw load and screw-tooth root stress, the loads superimposed by the bending moment and clamping force were equivalently converted into the screw-tooth root stresses, and the relationship curves (S_u–N curves) between the screw-tooth root stresses and vibration times were obtained as shown in Fig. 6b. The conversion processes for the bolt external load, screw load, and screw-tooth root stress are listed in Table 2.

Fig. 6

Screw load/screw-tooth root stress–life curves. (a) Screw load–loosening life curves. (b) S_u–N curves.

Table 2 Results during bolt-load conversion process.

As shown in Fig. 6b, the S_u–N curves of the M10 and M16 bolts showed obvious high- and low-cycle boundaries and bilinear characteristics, and the consistency of the two curves was high; that is, the stress level at the root of the screw tooth and the corresponding loosening life of the two types of bolts under a transverse load were basically the same. Based on this, a normalized S_u–N curve was established as shown in Fig. 7.

Fig. 7

Normalized S_u–N curve for different types of bolts.

Validation of bolt-loosening life evaluation method

Bolt-loosening bench test under transverse random vibration

The normalized S_u–N curve was obtained through a bolt-loosening life test and the bolt-load equivalent models described in the previous section. To verify the accuracy of the application of the curve, a transverse random vibration bolt-loosening bench test was performed with the antenna bracket of a subway bogie as the test object.

The test was performed on a 3ES-40–370-VT0505 multi-axis synchronous vibration-testing machine, and two transverse fastening bolts connecting the antenna bracket to the subway bogie were used as the test evaluation bolts as shown in Fig. 8. Consistent with the bolt-loosening test bolts, the bench test bolts were 8.8 grade M16 × 120 high-strength bolts. To facilitate the analysis, the two bolts were defined as Bolts I and II. The clamping forces of the bolts were monitored and recorded in real-time using pressure sensors. Force-measuring bolts were used in the test bolts to accurately obtain the screw load. A force-measuring bolt was used to attach four strain gauges spaced 90° apart in the circumferential direction of the polished rod; then the bending strain of the screw was measured, and the bolt bending moment was calculated using Eq. (10). During the test, the vibration table applied a transverse random vibration excitation to the antenna bracket, and the force-measuring bolt bore a transverse shear load. As the vibration time increased, loosening damage gradually accumulated, and the bolt clamping force gradually declined.

Fig. 8

Transverse random vibration bolt-loosening bench-test tooling.

$$\:{M}_{c}=EW\sqrt{(\frac{{\epsilon\:}_{1}-{\epsilon\:}_{3}}{2}{)}^{2}\:+\:(\frac{{\epsilon\:}_{2}-{\epsilon\:}_{4}}{2}{)}^{2}}$$

(10)

where M_c is the measured bending moment of the screw, ε₁, ε₂, ε₃, and ε₄ are the strain values in four directions around the circumference of the bolt, E is the elastic modulus of the bolt, and W is the bending section coefficient.

Because the pre-tightening force of the M16 bolts in the loosening life tests was 60 kN, to verify the accuracy of the normalized S_u–N curve for evaluating the bolt-loosening life of the same bolt under different pre-tightening forces, the pre-tightening force of the bolt was set to 20 kN in the bench test. In addition, the excitation of the bench test used the random vibration acceleration test spectrum in the EN61373:2010 standard, with an RMS of 15 m/s² and a 12-h vibration time.

The process for predicting the bolt-loosening life in this study is as follows:

• (1) The D–N curves were obtained through the bolt-loosening tests.

• (2) Based on the equivalent model of the bolt external load and screw load, the D–N curves were converted to the M–N curves.

• (3) Based on the equivalent model of the screw load and screw-tooth root stress, the M–N curves were converted to the normalized S_u–N curve.

• (4) The transverse random vibration bolt-loosening bench test was carried out, and the axial force-time histories and bending moment-time histories of the screws were obtained by the force-measuring bolts.

• (5) The axial force-time histories and bending moment-time histories of the screws were converted into the stress-time histories of the screw-tooth root through the equivalent model of the screw load and screw-tooth root stress.

• (6) The rain flow counting was performed on the stress-time histories of the screw-tooth root.

• (7) Taking the S_u–N curve as input, the cumulative loosening damage of the bolt was calculated based on the rain flow counting results, and the bolt-loosening life was obtained by taking the reciprocal of the cumulative loosening damage.4.2. Bench test results.

The clamping-force recession curves of the bolts obtained from the transverse random vibration bolt-loosening bench test are shown in Fig. 9. As the vibration time increased, the clamping force exhibited decaying characteristics; it first decreased rapidly and then decreased slowly. Evident material- and structural-loosening stages existed that were consistent with that of the typical bolt clamping-force recession curve under transverse vibration. After 12 h of vibration, the clamping force of Bolts I and II finally decreased to 94% and 91.5% respectively. Therefore, the bolt-loosening life was evaluated using an S_u–N curve with a 95% loosening state.

Fig. 9

Bolt-loosening life calculation process.

The analysis of the bending strain–time histories of the screw collected from the force-measuring bolts shown in Fig. 9 show that the strain ranges of the two bolts at 0° and 180° were larger than those at 90° and 270°. This is because when the bolt was initially tightened, the directions of the 0° and 180° strain gauges of the screw were parallel to the direction of the vibration excitation, and the directions of the 90° and 270° strain gauges were perpendicular to the excitation direction. Therefore, the bending deformations of the screw in the 0°and 180° directions were larger, and the bending moment was also larger, which verified the rationality of the bench test.

First, the bending moment–time histories of the screws were obtained by introducing the bending strain–time histories into Eq. (1). Subsequently, the axial force–time histories and bending moment–time histories of the bolts were transformed into the screw-tooth root stress–time histories using an equivalent model of the screw load and screw-tooth root stress. Similar to material fatigue theory, the higher the stress level, the greater the degree of bolt loosening.

Finally, the vibration times under different stress levels were obtained by rain flow counting of the screw-tooth root stress–time histories based on the S_u–N curve. The calculated bolt-loosening lives are listed in Table 3. The hourly damage values of Bolts I and II were 0.366 and 0.746, respectively, which correspond to the predicted loosening lives of 2.73 h and 1.34 h, respectively. Meanwhile, the clamping-force recession curve shows that the vibration times of Bolts I and II when the clamping force declined to the loosening state of 95% of the pre-tightening force were 2.82 h and 1.43 h, respectively. The consistency between the predicted and test bolt-loosening lives was high, with a maximum relative error of only 6.26%, which verifies the accuracy of the bolt-loosening life evaluation method based on the normalized S_u–N curve.

Table 3 Comparison of predicted and tested bolt-loosening lives.

In summary, the S_u–N curve obtained by load equivalence and normalization of D–N curves of different types of bolts can effectively evaluate the loosening life of bolts under a transverse random vibration environment. To further improve the evaluation accuracy, more D–N curves for different types of bolts should be obtained through bolt-loosening tests and then normalized to obtain more accurate S_u–N curves. This bolt-loosening life evaluation method can serve as a reference for engineering applications.

Conclusions

In this study, the loosening behavior of bolts under transverse vibration was investigated, an S_u–N curve normalized to D–N curves with different bolt diameters was constructed, and a bolt-loosening life evaluation method based on load equivalence was proposed. The major conclusions of this study are as follows:

• (1) Through bolt-loosening tests, it was found that the root of the first ring of the working screw tooth was the main location of bolt fracture, indicating that this area, which was subject to severe loads and permanent plastic deformation, was the root cause of bolt loosening.

• (2) By comparing the D–N curves of two types of bolts, the trends of the two D–N curves tended to be consistent, showing clear high- and low-cycle boundaries and bilinear characteristics. However, the calculation of the bolt-loosening life of a specific structure requires a specific D–N curve, which is time-consuming and laborious and cannot meet engineering requirements.

• (3) An equivalent model of the bolt external load and screw load was established based on Castigliano’s theorem, and an equivalent model of the screw load and screw-tooth root stress was established based on the deformation coordination equation of elastic mechanics. Bolt-load equivalent models can equivalently convert the bolt external load into screw-tooth root stress.

• (4) Based on the bolt-load equivalent models, the D–N curves of two types of bolts were equivalently converted into S_u–N curves, and it was found that the stress level at the root of the screw tooth and the corresponding loosening life of the different types of bolts under a transverse load were basically the same; thus, a normalized S_u–N curve was established.

• (5) The loosening life of the fastening bolts of an antenna bracket was evaluated based on a normalized S_u–N curve and compared with the results of a bolt-loosening bench test under transverse random vibration. It was found that the maximum error between the theoretically predicted and tested loosening lives was only 6.26%, which verified the accuracy of the bolt-loosening life evaluation method based on the bolt-load equivalence.

This study demonstrates the existence of a normalized S_u–N curve for bolted connections that can be used to evaluate the loosening life of different types of bolts. This greatly reduces the time and test cost of obtaining a specific bolt-load loosening life curve through bolt-loosening tests and has some reference significance for engineering applications. Owing to the limitations of the test conditions, loosening life tests of more types of bolts were not performed in this study, and additional tests are required to further improve and obtain more accurate normalized S_u–N curves. Also, a loosening life evaluation method for bolts under composite excitation can be further studied in the future.