Introduction

The Davey–Stewartson equations are higher-dimensional generalizations of the nonlinear Schrödinger equation that are crucial models for a variety of non-linear phenomena in plasma physics, including nonlinear optics and hydrodynamics1. The impact of multiplicative noise on exact stochastic soliton solutions, especially using the modified extended direct algebraic method, has not been thoroughly investigated, although the deterministic Davey–Stewartson equations have been the topic of much research, and stochastic versions have been studied using a variety of numerical and analytical techniques. Researchers have not fully investigated how multiplicative Brownian motion affects stabilizing processes in dark, bright, rational, and periodic wave solutions of these equations. This paper fills the existing research gap through the application of a modified extended direct algebraic method to obtain exact stochastic soliton solutions for the Davey–Stewartson equations with multiplicative noise. The paper examines how multiplicative Brownian motion stabilizes dark, singular, rational, and periodic wave solutions. The research adds new analytical solutions along with insights into the complex noise-wave dynamics in higher-dimensional systems where multiplicative noise proves essential for stabilizing wave structures. The investigation under It\(\hat{o}\) calculus explores the stochastic DS equation which includes multiplicative noise2,3,4,5,6,7,8,9,10. In 1974, Davey and Stewartson developed the Davey–Stewartson equation (DSE). The DSE equation illustrates the time-varying evolution of a three-dimensional wave packet in shallow water. Hydrodynamics, non-linear optics, plasma physics, and other disciplines have used the deterministic Davey–Stewartson equations (1) and (2), or \(\sigma = 0\). For example, the interaction between microwaves and a properly matched spatio-temporal optical pattern may be explained by the DDSE solutions11,12. We consider the following Davey–Stewartson equations that are affected by multiplicative noise in the stochastic sense:13

$$\begin{aligned} & i\Psi _t + \frac{1}{2} \alpha ^2 (\Psi _{xx} + \alpha ^2 \Psi _{yy}) + {{\lambda }} |\Psi |^2 \Psi - \Phi \Psi + i\sigma \Psi \Xi _t = 0, \end{aligned}$$
(1.1)
$$\begin{aligned} & \Phi _{xx} - \alpha ^2 \Phi _{yy} - 2{{\lambda }} (|\Psi |^2)_{xx} = 0, \end{aligned}$$
(1.2)

In Eqs. (1.1) and (1.2), \(\Psi (x, y, t)\) represents the complex wave amplitude, while \(\Phi (x, y, t)\) is a real-valued potential. The parameter \(\alpha\) determines the type of Davey–Stewartson equation: \(\alpha = 1\) corresponds to the DS-I equation, whereas \(\alpha = i\) yields the DS-II equation14,15,16,17. The cubic non-linearity is governed by the constant \(\lambda\), where \(\lambda = +1\) and \(\lambda = -1\) represent the focusing and defocusing cases, respectively. The noise intensity is denoted by \(\sigma\), which scales the influence of the multiplicative noise term \(\Xi _t\) in the It\(\hat{o}\) sense, and it is the time derivative of Brownian motion \(\Xi (t)\), that is, \(\Xi _{t} = \dfrac{d \,\Xi }{dt}\) and \(\Xi (t)\) is also called the standard Wiener process. It depends only on t18. Physically, the terms involving \(\Psi _{xx}\) and \(\Psi _{yy}\) represent dispersion in the x and y directions, respectively. The term involving \(\Phi\) accounts for a self-induced potential, and the noise term \(i\sigma \Psi \Xi _t\) represents the influence of random fluctuations on wave dynamics.

The stochastic DS-equations maintain integrability based on the characteristics of introduced stochastic noise and system nonlinearity. The deterministic DS-I and DS-II equations possess integrable solutions when specific conditions apply, whereas inverse scattering methods together with soliton and rational solutions become available. When Brownian motion serves as the multiplicative noise input the equations lose their integrability properties which hinders the application of inverse scattering transform methods. Most noise perturbations eliminate strict integrability but some specific noise structures or weak stochastic disturbances enable partial integrability and exact solutions. The noise characteristics determine whether integrable properties can be preserved because additive noise preserves integrability better than multiplicative noise. The MEDA method and other analytical approaches enable researchers to obtain exact or semi-analytical solutions even after full integrability is lost. Numerical methods including Monte Carlo simulations deliver important statistical data about solution behavior when studying stochastic systems. The analytical and numerical tractability of stochastic DS equations with multiplicative noise remains intact despite their lack of integrability properties.

The introduction of the Wiener process within our model is unique as it breaks away from deterministic definitions. It is possible to model structures changing over time using mathematical tools such as random processes, and the Wiener process in particular. This continuous-time stochastic process, which is utilised in stochastic calculus and has many applications in the social sciences, physical sciences, and quantitative finance, can be thought of as a continuous deformation of the fundamental random walk. This continuous-time stochastic process, which can be viewed as a continuous variation of the basic random walk, plays a crucial role in stochastic calculus and has found applications in diverse fields, from quantitative finance to physical sciences and social sciences. It makes possible to obtain the stochastic solutions in the sense of It\(\hat{o}\) calculus which is useful to study various processes like the formation of the ocean waves, the processes related to optical communication, the phenomena connected with the wave collapses in the astrophysics. We investigate the interplay between stochastic and random noise components and their link to physical properties to gain a better understanding of how these two types of factors affect wave behaviour.

Consider a Wiener process \(\Xi (t)\) that is non-differentiable and has the following characteristics:19,20

$$\begin{aligned} & \lim _{\Delta t \rightarrow 0} \Delta \Xi (t) = 0; \end{aligned}$$
(1.3)
$$\begin{aligned} & \lim _{\Delta t \rightarrow 0} \frac{(\Delta \Xi (_t))^N}{\Delta t} = {\left\{ \begin{array}{ll} 1, & N = 2 \\ 0, & N = 3, 4, \dots \end{array}\right. } \end{aligned}$$
(1.4)

A stochastic process \((\Xi _t)_{t \le 0}\) is said to be Brownian motion if the following criteria are met:

  • \(\Xi _t\) is a continuous function for \(t \le 0\).

  • \(\Xi _0 = 0\).

  • For \(t_1 < t_2\), \(\Xi _{t_2} - \Xi _{t_1}\) is independent.

  • \(\Xi _{t_2} - \Xi _{t_1}\) has a normal distribution \(\kappa (0, t_2 - t_1)\).

The fundamental nature of expectation lies at the core of probability theory as well as stochastic analysis when solving stochastic differential equations. Expectation enables analysis of average results obtained from multiple iterations of the random process. Stochastic wave equations require expectation to understand the statistical attributes of wave solutions which occur when noise act on them.25,26,27,28 There have been several effective techniques suggested, including the new extended direct algebraic method29, \(\phi ^6\)-expansion method30, Hirota bilinear method31,32,33, fractional modified Sardar subequation method and fractional enhanced modified extended tanh-expansion method34, generalized exponential rational function method35, generalized tanh-coth method36, generalized Kudryashov method37, improved \(\tan (\frac{\phi }{2}\)-expansion method38, new modified exponential Jacobi technique39 and so on. Here, we apply a powerful technique known as the modified extended direct algebraic method40,41,42,43 to build a variety of exact soliton solutions for the nonlinear partial differential equation.

The modified extended direct algebraic method represents an effective method to solve nonlinear partial differential equations including stochastic Davey–Stewartson equations. This method delivers three main benefits which include exact solution-finding capabilities and efficient nonlinearity management and stochastic system compatibility that makes it ideal for practical usage. The method shows flexibility for use in plasma physics nonlinear optics and hydrodynamics because of its ability to analyze wave phenomena and soliton dynamics. The modified extended direct algebraic method delivers an improved understanding of random wave stabilization effects through its use of multiplicative noise, thus becoming an essential tool for studying stochastic wave systems

Algorithm for modified extended direct algebraic method

We provide the modified extended direct algebraic method44,45,46,47 in this section. It is also referred to as the modified extended \(\tanh\)-function method48,49,50,51,52,53,54. The following steps outline the main steps in this technique, which we summarize here:

Suppose the following nonlinear partial differential equation

$$\begin{aligned} E(u,u_{t},u_{x},u_{tt},u_{xx},u_{x t},\cdots ) =0, \end{aligned}$$
(2.1)

E is a polynomial in \(u=u(x,t)\) and its numerous partial derivatives, which involve nonlinear terms and the highest order derivatives, whereas \(u = u(x,t)\) is a wave function.

Step 1. For wave solutions, apply the following wave transformation.

$$\begin{aligned} u=U({\zeta }), \,\,\,\,\,\,\,\, {\zeta } = x-v\,t. \end{aligned}$$
(2.2)

where v is the wave speed.

Step 2. A nonlinear ordinary differential equation is obtained by plugging Eq. (2.2) into Eq. (2.1).

$$\begin{aligned} O(U, U', U'',U''',\cdots )=0. \end{aligned}$$
(2.3)

Step 3. Let \(U({\zeta })\) be the next variable that can be expressed as a polynomial in \(\eta ({\zeta })\)

$$\begin{aligned} U({\zeta }) ={{B}}_{{0}}+\sum _{i=1}^{M}{{B}}_{{i}} \eta ^{i} +{{C}}_{{i}} \eta ^{-i}, \end{aligned}$$
(2.4)

where \(\eta ^{\prime }\) satisfies the nonlinear ODE, whereas there \({{B}}_{0}, {{B}}_{i}, {{C}}_{i},\) are unknown constants to be found later.

$$\begin{aligned} \eta '={{\rho }}+\eta ^{2}, \end{aligned}$$
(2.5)

where \({{\rho }}\) is an arbitrary constant, and \(\eta '= \frac{d\eta }{d{\zeta }}\).

Step 4. Considering the homogeneous balance between the non-linear terms and the highest-order derivatives present in Eq. (2.3), one can deduce the value of the natural number M. To obtain a system of algebraic equations with respect to \({B}_{i},{C}_{i}\), and \({{\rho }}\) where \(i = 1,2,3,\cdots M\), plug Eq. (2.4) into Eq. (2.2) and Eq. (2.5). At this stage, we shall determine \({{B}}_{0}\), \({{B}}_{{i}}\), \({{C}}_{{i}}\), \({{\rho }}\), and v since all the coefficients of \(\eta ^{i}\) must vanish. The general solutions to Eq. (2.5) are as follows:

Family 1. If \({{\rho }}<0\), we have

$$\begin{aligned} \eta \left( {\zeta } \right) = {-\sqrt{-{{\rho }}}\tanh \left( \sqrt{-{{\rho }}}{\zeta } \right) } \,\,\,\,\,\,\, \texttt {or} \,\,\,\,\,\,\,\, \eta ({\zeta }) = -\sqrt{-{{\rho }}}\coth \left( \sqrt{-{{\rho }}}{\zeta } \right) . \end{aligned}$$
(2.6)

Family 2. If \({{\rho }} >0\), we have

$$\begin{aligned} \eta ({\zeta }) = {\sqrt{{{\rho }}}\tan \left( \sqrt{{{\rho }}}{\zeta } \right) } \,\,\,\,\,\,\, \texttt {or} \,\,\,\,\,\,\,\, \eta ({\zeta }) = -\sqrt{{{\rho }}}\cot \left( \sqrt{{{\rho }}}{\zeta } \right) , \end{aligned}$$
(2.7)

Family 3. If \({{\rho }} =0\), we have

$$\begin{aligned} \eta \left( {\zeta } \right) = -\dfrac{1}{{\zeta }}. \end{aligned}$$
(2.8)

Application of the Davey–Stewartson equations affected by multiplicative noise in the It\(\hat{o}\) calculus sense

Making stochastic wave transformation for Eqs. (1.1) and (1.2)

$$\begin{aligned} \Psi (x,y,t) = U(\zeta ) e^{(i\Omega - \sigma \Xi (t) - \sigma ^2 t)}, \quad \Phi (x,y,t) = V(\zeta ) e^{-2\sigma \Xi (t) - 2\sigma ^2 t}, \end{aligned}$$
(3.1)

with

$$\begin{aligned} \zeta = \zeta _1 x + \zeta _2 y - \zeta _{3} t, \quad \text {and} \quad \Omega = {k}x +{w} y + {\theta } t, \end{aligned}$$

where \(\zeta\), \(\Omega\) are deterministic functions and \(\{ \zeta _1, \zeta _2, \zeta _3 \}\), \(\{ k, w, \theta \}\) are nonzero constants. Putting Eq. (3.1) into Eq. (1.1) and Eq. (1.2) respectively, then we obtain for the real part

$$\begin{aligned}&\left( \frac{1}{2} \zeta _1^2 \alpha ^2 + \frac{1}{2} \zeta _2^2 \alpha ^4 \right) {U}'' - \left( \theta + \frac{1}{2} \alpha ^2 {{k}}^2 + \frac{1}{2} \alpha ^4 {{w}}^2 \right) {U} + \left( {{k}} {U}^3 - {UV} \right) e^{(-2 \sigma \Xi (t) - 2 \sigma ^2 t)} = 0, \end{aligned}$$
(3.2)
$$\begin{aligned}&\left( \zeta _1^2 - \alpha ^2 \zeta _2^2 \right) {V}'' - 2 \zeta _1 {{k}} ({U}^2)'' = 0, \end{aligned}$$
(3.3)

and, imaginary part,

$$\begin{aligned} \left( -\zeta _3 + 2 \zeta _1 {{k}} + 2 \zeta _2 {{w}} \right) {U}'&= 0. \end{aligned}$$
(3.4)

From Eq. (3.4), we obtain

$$\begin{aligned} \zeta _3&= 2 \zeta _1 {{k}} + 2 \zeta _2 {{w}}. \end{aligned}$$
(3.5)

Now, integrating Eq. (3.3) once, we attain

$$\begin{aligned} V = \frac{2 \zeta _1^2 {{k}}}{(\zeta _1^2 - \alpha ^2 \zeta _2^2)} {U}^2. \end{aligned}$$
(3.6)

Substituting Eq. (3.6) into Eq. (3.2) , we obtain

$$\begin{aligned} {U}'' - \mu _2 {U} + \mu _1 {U}^3 e^{-2\sigma \Xi (t) - 2\sigma ^2 t} = 0, \end{aligned}$$
(3.7)

where

$$\begin{aligned} \mu _1 = \frac{2{{\lambda }}}{\alpha ^2(\zeta _1^2 - \alpha ^2 \zeta _2^2)},\, \mu _2 = \frac{2\theta + \alpha ^2 {{k}}^2 + \alpha ^4 {{w}}^2}{\zeta _1^2 \alpha ^2 + \zeta _2^2 \alpha ^4},\, \mu _{3}=\frac{2 \zeta _1^2 {{k}}}{(\zeta _1^2 - \alpha ^2 \zeta _2^2)}. \end{aligned}$$
(3.8)

We take the expectation on both sides

$$\begin{aligned} {U}'' - \mu _2 {U} - \mu _1 {U}^3 e^{-2\sigma ^2 t} E\left( e^{-2\sigma \Xi (t)}\right) = 0. \end{aligned}$$
(3.9)

Since \(\Xi (t)\) is normally distributed, so \(E\left( e^{-2\sigma \Xi (t)}\right) = e^{2\sigma ^2 t}\). Hence, Eq. (3.9) becomes

$$\begin{aligned} {U}'' - \mu _1 {U}^3 - \mu _2 {U} = 0. \end{aligned}$$
(3.10)

Balancing the highest degree derivative \(U^{\prime \prime }\) along with the nonlinear term \(U^3\) in Eq. (3.10), we obtain \(M = 1\). Hence the formal solution of Eq. (3.10) is

$$\begin{aligned} U(\zeta ) = \beta _{0} + \beta _{1} \eta (\zeta ) + \frac{\beta _{2}}{\eta (\zeta )} \end{aligned}$$
(3.11)

Plugging Eq. (3.11) along with Eq. (2.5) into Eq. (3.10) will provide these constants, as well as collecting all terms with the same power of \(\eta ^{i}, i = 0, 1,\cdots , M\) and setting every coefficient equal to zero, hence the following collection of algebraic equations is obtained

$$\begin{aligned} {\left\{ \begin{array}{ll} - \mu _1 \beta _1^3 + 2\beta _1 & = 0, \\ - 3\mu _1 \beta _1^2 +\beta _2 - \mu _2 \beta _1 + 2\beta _1 \rho - 3\mu _1 \beta _0^2 \beta _1 & = 0, \\ - \mu _2 \beta _0 - \mu _1 \beta _0^3 - 6\mu _1 \beta _0 \beta _1 \beta _2 & = 0, \\ - 3\mu _1 \beta _0^2 \beta _2 + 2\beta _2 \rho - \mu _2 \beta _2 - 3\mu _1 \beta _1 \beta _2^2 & = 0, \\ 2\beta _2 \rho ^2 - \mu _1 \beta _2^3 & = 0. \end{array}\right. } \end{aligned}$$
(3.12)

The following set of solutions are possible for solving the (3.12) using Maple.

Case I. If \(\beta _{2}=0\) then (3.12) gives: \(\beta _0 = \frac{\sqrt{-\mu _1 \mu _2}}{\mu _1},\)   \(\beta _1 = \pm \frac{\sqrt{2}}{\sqrt{\mu _1}}.\)

Case II. If \(\beta _{0}=0\) then (3.12) gives: \(\beta _1 =\pm \frac{\sqrt{2}}{\sqrt{\mu _1}},\)    \(\beta _{{2}}=\frac{2\,\rho -\alpha _{2}}{3\sqrt{\mu _{1}}}\).

Case III. If \(\beta _{1}=0\) then (3.12) gives: \(\beta _2 =\pm \frac{\sqrt{2} \, \rho }{\sqrt{\mu _1}}\),     \(\beta _0 = \pm \frac{1}{\sqrt{3}}\frac{\sqrt{\mu _1(2\rho -\mu _2)}}{\mu _1}\).

Using cases I, II, and III, we can obtain the following stochastic soliton solutions.

Case (I)

Family (I) provides the following dark (\(\Psi _{{1}}\),\(\Phi _{{1}}\)) and singular (\(\Psi _{{2}}\),\(\Phi _{{2}}\)) stochastic soliton solitons for \(\rho <0\),

$$\begin{aligned} \Psi _{{1}}= \bigg [\pm \frac{\sqrt{-\mu _1 \mu _2}}{\mu _1} \pm \frac{\sqrt{2}}{\sqrt{\mu _1}}\left( -\sqrt{-\rho } \tanh \left( \sqrt{-\rho } \zeta \right) \right) \bigg ] e^{(i({k}x +{w} y + {\theta } t) - \sigma \Xi (t) - \sigma ^2 {t})}, \end{aligned}$$

or

$$\begin{aligned} \Psi _{{2}}= \bigg [\pm \frac{\sqrt{-\mu _1 \mu _2}}{\mu _1} \pm \frac{\sqrt{2}}{\sqrt{\mu _1}}\left( -\sqrt{-\rho } \coth \left( \sqrt{-\rho } \zeta \right) \right) \bigg ] e^{(i({k}x +{w} y + {\theta } t) - \sigma \Xi (t) - \sigma ^2 {t})}, \end{aligned}$$

and

$$\begin{aligned} \Phi _{{1}}= \mu _{3}\left( \bigg [\pm \frac{\sqrt{-\mu _1 \mu _2}}{\mu _1} \pm \frac{\sqrt{2}}{\sqrt{\mu _1}}\left( -\sqrt{-\rho } \tanh \left( \sqrt{-\rho } \zeta \right) \right) \bigg ]\right) ^2 e^{-2\sigma \Xi (t) - 2\sigma ^2 { t}}, \end{aligned}$$

or

$$\begin{aligned} \Phi _{{2}}= \mu _{3}\left( \bigg [\pm \frac{\sqrt{-\mu _1 \mu _2}}{\mu _1} \pm \frac{\sqrt{2}}{\sqrt{\mu _1}}\left( -\sqrt{-\rho } \coth \left( \sqrt{-\rho } \zeta \right) \right) \bigg ]\right) ^2 e^{-2\sigma \Xi (t) - 2\sigma ^2 { t}}. \end{aligned}$$

Family (II) provides the following (\(\Psi _{{3}}\),\(\Phi _{{3}}\), \(\Psi _{{4}}\),\(\Phi _{{4}}\)) periodic stochastic soliton solitons for \(\rho >0\),

$$\begin{aligned} \Psi _{{3}}= \bigg [\pm \frac{\sqrt{-\mu _1 \mu _2}}{\mu _1} \pm \frac{\sqrt{2}}{\sqrt{\mu _1}}\left( \sqrt{\rho } \tan \left( \sqrt{\rho }\zeta \right) \right) \bigg ] e^{(i({k}x +{w} y + {\theta } t) - \sigma \Xi (t) - \sigma ^2 {t}) }, \end{aligned}$$

or

$$\begin{aligned} \Psi _{{4}}= \bigg [\pm \frac{\sqrt{-\mu _1 \mu _2}}{\mu _1} \pm \frac{\sqrt{2}}{\sqrt{\mu _1}}\left( -\sqrt{\rho } \cot \left( \sqrt{\rho }\zeta \right) \right) \bigg ] e^{(i({k}x +{w} y + {\theta } t) - \sigma \Xi (t) - \sigma ^2 {t})}, \end{aligned}$$

and

$$\begin{aligned} \Phi _{{3}}= \mu _{3}\left( \bigg [\pm \frac{\sqrt{-\mu _1 \mu _2}}{\mu _1} \pm \frac{\sqrt{2}}{\sqrt{\mu _1}}\left( \sqrt{\rho } \tan \left( \sqrt{\rho }\zeta \right) \right) \bigg ] \right) ^2 e^{-2\sigma \Xi (t) - 2\sigma ^2 { t}}, \end{aligned}$$

or

$$\begin{aligned} \Phi _{{4}}= \mu _{3}\left( \bigg [\pm \frac{\sqrt{-\mu _1 \mu _2}}{\mu _1} \pm \frac{\sqrt{2}}{\sqrt{\mu _1}}\left( -\sqrt{\rho } \cot \left( \sqrt{\rho }\zeta \right) \right) \bigg ] \right) ^2 e^{-2\sigma \Xi (t) - 2\sigma ^2 { t}}. \end{aligned}$$

Family (III) provides the following (\(\Psi _{{5}}\),\(\Phi _{{5}}\)) rational stochastic soliton solitons for \(\rho =0\),

$$\begin{aligned} & \Psi _{{5}}= \bigg [\pm \frac{\sqrt{-\mu _1 \mu _2}}{\mu _1} \pm \frac{\sqrt{2}}{\sqrt{\mu _1}} \left( -\frac{1}{\zeta }\right) \bigg ] e^{(i({k}x +{w} y + {\theta } t) - \sigma \Xi (t) - \sigma ^2 {t})}, \\ & \Phi _{{5}}= \mu _{3}\left( \bigg [\pm \frac{\sqrt{-\mu _1 \mu _2}}{\mu _1} \pm \frac{\sqrt{2}}{\sqrt{\mu _1}} \left( -\frac{1}{\zeta }\right) \bigg ] \right) ^2 e^{-2\sigma \Xi (t) - 2\sigma ^2 { t}}, \end{aligned}$$

Case (II)

Family (I) provides the following dark (\(\Psi _{{6}}\),\(\Phi _{{6}}\)) and singular (\(\Psi _{{7}}\),\(\Phi _{{7}}\)) stochastic soliton solitons for \(\rho <0\),

$$\begin{aligned} \Psi _{{6}}= \bigg [\pm \frac{\sqrt{2}}{\sqrt{\mu _1}} \left( -\sqrt{-\rho } \tanh \left( \sqrt{-\rho }z \right) \right) \pm \frac{2\,c-\mu _{2}}{3\sqrt{\mu _{1}}}\left( \sqrt{-\rho } \tanh \left( \sqrt{-\rho } \zeta \right) \right) ^{-1}\bigg ] e^{(i({k}x +{w} y + {\theta } t) - \sigma \Xi (t) - \sigma ^2 {t})}, \end{aligned}$$

or

$$\begin{aligned} \Psi _{{7}}= \bigg [ \pm \frac{\sqrt{2}}{\sqrt{\mu _1}} \left( -\sqrt{-\rho } \coth \left( \sqrt{-\rho }z \right) \right) \pm \frac{2\,c-\mu _{2}}{3\sqrt{\mu _{1}}}\left( -\sqrt{-\rho } \coth \left( \sqrt{-\rho } \zeta \right) \right) ^{-1}\bigg ] e^{(i({k}x +{w} y + {\theta } t) - \sigma \Xi (t) - \sigma ^2 {t})}, \end{aligned}$$

and

$$\begin{aligned} \Phi _{{6}}=\mu _{3}\left( \bigg [\pm \frac{\sqrt{2}}{\sqrt{\mu _1}} \left( -\sqrt{-\rho } \tanh \left( \sqrt{-\rho }z \right) \right) \pm \frac{2\,c-\mu _{2}}{3\sqrt{\mu _{1}}}\left( \sqrt{-\rho } \tanh \left( \sqrt{-\rho } \zeta \right) \right) ^{-1}\bigg ] \right) ^2 e^{-2\sigma \Xi (t) - 2\sigma ^2 { t}}, \end{aligned}$$

or

$$\begin{aligned} \Phi _{{7}}=\mu _{3}\left( \bigg [ \pm \frac{\sqrt{2}}{\sqrt{\mu _1}} \left( -\sqrt{-\rho } \coth \left( \sqrt{-\rho }z \right) \right) \pm \frac{2\,c-\mu _{2}}{3\sqrt{\mu _{1}}}\left( -\sqrt{-\rho } \coth \left( \sqrt{-\rho } \zeta \right) \right) ^{-1}\bigg ] \right) ^2 e^{-2\sigma \Xi (t) - 2\sigma ^2 { t}}. \end{aligned}$$

Family (II) provides the following (\(\Psi _{{8}}\),\(\Phi _{{8}}\), \(\Psi _{{9}}\),\(\Phi _{{9}}\)) periodic stochastic soliton solitons for \(\rho >0\),

$$\begin{aligned} \Psi _{{8}}= \bigg [ \pm \frac{\sqrt{2}}{\sqrt{\mu _1}} \left( \sqrt{\rho } \tan \left( \sqrt{\rho }\zeta \right) \right) \pm \frac{2\,c-\mu _{2}}{3\sqrt{\mu _{1}}}\left( \sqrt{\rho } \tan \left( \sqrt{\rho }\zeta \right) \right) ^{-1}\bigg ] e^{(i({k}x +{w} y + {\theta } t) - \sigma \Xi (t) - \sigma ^2 {t})}, \end{aligned}$$

or

$$\begin{aligned} \Psi _{{9}}= \bigg [ \pm \frac{\sqrt{2}}{\sqrt{\mu _1}} \left( -\sqrt{\rho } \cot \left( \sqrt{\rho }\zeta \right) \right) \pm \frac{2\,c-\mu _{2}}{3\sqrt{\mu _{1}}}\left( -\sqrt{\rho } \cot \left( \sqrt{\rho }\zeta \right) \right) ^{-1}\bigg ] e^{(i({k}x +{w} y + {\theta } t) - \sigma \Xi (t) - \sigma ^2 {t})}, \end{aligned}$$

and

$$\begin{aligned} \Phi _{{8}}=\mu _{3}\left( \bigg [ \pm \frac{\sqrt{2}}{\sqrt{\mu _1}} \left( \sqrt{\rho } \tan \left( \sqrt{\rho }\zeta \right) \right) \pm \frac{2\,c-\mu _{2}}{3\sqrt{\mu _{1}}}\left( \sqrt{\rho } \tan \left( \sqrt{\rho }\zeta \right) \right) ^{-1}\bigg ] \right) ^2, \end{aligned}$$

or

$$\begin{aligned} \Phi _{{9}}=\mu _{3}\left( \bigg [ \pm \frac{\sqrt{2}}{\sqrt{\mu _1}} \left( -\sqrt{\rho } \cot \left( \sqrt{\rho }\zeta \right) \right) \pm \frac{2\,c-\mu _{2}}{3\sqrt{\mu _{1}}}\left( -\sqrt{\rho } \cot \left( \sqrt{\rho }\zeta \right) \right) ^{-1}\bigg ] e^{-2\sigma \Xi (t) - 2\sigma ^2 { t}}\right) ^2, \end{aligned}$$

Family (III) provides the following (\(\Psi _{{10}}\),\(\Phi _{{10}}\)) rational stochastic soliton solitons for \(\rho =0\),

$$\begin{aligned} & \Psi _{{10}}= \bigg [\pm \frac{\sqrt{2}}{\sqrt{\mu _1}} \left( -\frac{1}{\zeta }\right) \pm \frac{2\,c-\mu _{2}}{3\sqrt{\mu _{1}}} \left( -\frac{1}{\zeta }\right) ^{-1}\bigg ] e^{(i({k}x +{w} y + {\theta } t) - \sigma \Xi (t) - \sigma ^2 {t})}, \\ & \Phi _{{10}}=\mu _{3}\left( \bigg [\pm \frac{\sqrt{2}}{\sqrt{\mu _1}} \left( -\frac{1}{\zeta }\right) \pm \frac{2\,c-\mu _{2}}{3\sqrt{\mu _{1}}} \left( -\frac{1}{\zeta }\right) ^{-1}\bigg ] \right) ^2 e^{-2\sigma \Xi (t) - 2\sigma ^2 { t}}. \end{aligned}$$

Case (III)

Family (I) provides the following dark (\(\Psi _{{11}}\),\(\Phi _{{11}}\)) and singular (\(\Psi _{{12}}\),\(\Phi _{{12}}\)) stochastic soliton solitons for \(\rho <0\),

$$\begin{aligned} \Psi _{{11}}= \bigg [ \frac{1}{\sqrt{3}}\frac{\sqrt{\mu _1(2\rho -\mu _2)}}{\mu _1} \pm \frac{-\sqrt{2} \, c}{\sqrt{\mu _1}} \left( -\sqrt{-\rho } \tanh \left( \sqrt{-\rho } \zeta \right) \right) ^{-1}\bigg ] e^{(i({k}x +{w} y + {\theta } t) - \sigma \Xi (t) - \sigma ^2 {t})}, \end{aligned}$$

or

$$\begin{aligned} & \Psi _{{12}}= \bigg [ \frac{1}{\sqrt{3}}\frac{\sqrt{\mu _1(2\rho -\mu _2)}}{\mu _1} \pm \frac{-\sqrt{2} \, c}{\sqrt{\mu _1}}\left( -\sqrt{-\rho } \coth \left( \sqrt{-\rho } \zeta \right) \right) ^{-1}\bigg ] e^{(i({k}x +{w} y + {\theta } t) - \sigma \Xi (t) - \sigma ^2 {t})}, \\ & \Phi _{{11}}=\mu _{3}\left( \bigg [ \frac{1}{\sqrt{3}}\frac{\sqrt{\mu _1(2\rho -\mu _2)}}{\mu _1} \pm \frac{-\sqrt{2} \, c}{\sqrt{\mu _1}} \left( -\sqrt{-\rho } \tanh \left( \sqrt{-\rho } \zeta \right) \right) ^{-1}\bigg ] \right) ^2 e^{-2\sigma \Xi (t) - 2\sigma ^2 { t}}, \end{aligned}$$

or

$$\begin{aligned} \Phi _{{12}}=\mu _{3}\left( \bigg [ \frac{1}{\sqrt{3}}\frac{\sqrt{\mu _1(2\rho -\mu _2)}}{\mu _1} \pm \frac{-\sqrt{2} \, c}{\sqrt{\mu _1}}\left( -\sqrt{-\rho } \coth \left( \sqrt{-\rho } \zeta \right) \right) ^{-1}\bigg ] \right) ^2 e^{-2\sigma \Xi (t) - 2\sigma ^2 { t}}. \end{aligned}$$

Family (II) provides the following (\(\Psi _{{13}}\),\(\Phi _{{13}}\), \(\Psi _{{14}}\),\(\Phi _{{14}}\)) periodic stochastic soliton solitons for \(\rho >0\),

$$\begin{aligned} \Psi _{{13}}= \bigg [\frac{1}{\sqrt{3}}\frac{\sqrt{\mu _1(2\rho -\mu _2)}}{\mu _1} \pm \frac{-\sqrt{2} \, c}{\sqrt{\mu _1}}\left( \sqrt{\rho } \tan \left( \sqrt{\rho }\zeta \right) \right) ^{-1}\bigg ] e^{(i({k}x +{w} y + {\theta } t) - \sigma \Xi (t) - \sigma ^2 {t})}, \end{aligned}$$

or

$$\begin{aligned} & \Psi _{{14}}= \bigg [ \frac{1}{\sqrt{3}}\frac{\sqrt{\mu _1(2\rho -\mu _2)}}{\mu _1} \pm \frac{-\sqrt{2} \, c}{\sqrt{\mu _1}}\left( -\sqrt{\rho } \cot \left( \sqrt{\rho }\zeta \right) \right) ^{-1}\bigg ] e^{(i({k}x +{w} y + {\theta } t) - \sigma \Xi (t) - \sigma ^2 {t})}, \\ & \Phi _{{13}}=\mu _{3}\left( \bigg [\frac{1}{\sqrt{3}}\frac{\sqrt{\mu _1(2\rho -\mu _2)}}{\mu _1} \pm \frac{-\sqrt{2} \, c}{\sqrt{\mu _1}}\left( \sqrt{\rho } \tan \left( \sqrt{\rho }\zeta \right) \right) ^{-1}\bigg ] \right) ^2 e^{-2\sigma \Xi (t) - 2\sigma ^2 { t}}, \end{aligned}$$

or

$$\begin{aligned} \Phi _{{14}}=\mu _{3}\left( \bigg [ \frac{1}{\sqrt{3}}\frac{\sqrt{\mu _1(2\rho -\mu _2)}}{\mu _1} \pm \frac{-\sqrt{2} \, c}{\sqrt{\mu _1}}\left( -\sqrt{\rho } \cot \left( \sqrt{\rho }\zeta \right) \right) ^{-1}\bigg ] \right) ^2 e^{-2\sigma \Xi (t) - 2\sigma ^2 { t}}. \end{aligned}$$

Family (III) provides the following (\(\Psi _{{15}}\),\(\Phi _{{15}}\)) rational stochastic soliton solitons for \(\rho =0\),

$$\begin{aligned} & \Psi _{{15}}= \bigg [\pm \frac{1}{\sqrt{3}}\frac{\sqrt{\mu _1(2\rho -\mu _2)}}{\mu _1} \pm \frac{-\sqrt{2} \, c}{\sqrt{\mu _1}} \left( -\frac{1}{\zeta }\right) ^{-1}\bigg ] e^{(i({k}x +{w} y + {\theta } t) - \sigma \Xi (t) - \sigma ^2 {t})}, \\ & \Phi _{{15}}=\mu _{3}\left( \bigg [\pm \frac{1}{\sqrt{3}}\frac{\sqrt{\mu _1(2\rho -\mu _2)}}{\mu _1} \pm \frac{-\sqrt{2} \, c}{\sqrt{\mu _1}} \left( -\frac{1}{\zeta }\right) ^{-1}\bigg ] \right) ^2 e^{-2\sigma \Xi (t) - 2\sigma ^2 { t}}. \end{aligned}$$

The graphical representation

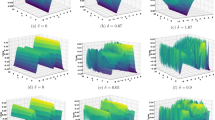
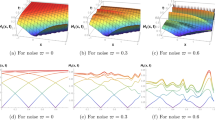
To visualize and analyze the impact of noise, MATLAB tool has been employed to plot the three-dimensional, two-dimensional as well as contour plots of the obtained solutions. These plots give a better picture of how solitons respond to under the various noise intensities. The waveforms are plotted in 3 dimensions in order to reveal the temporal and spatial changes and how they converge to be stable around the zero. Two-dimensional cross-sections bring out the amplitude variations clearly; contour maps provide a better view of structure of the wave and variation of intensity.

Results and discussion

This section of our work consists of the results and a literary comparison. The classical Davey–Stewartson (DS) equation which Davey and Stewartson developed in 1974 underwent extensive research in recent years. Through their work Yan et al.55 discovered high-order lump solutions of the DS model while Behera and Virdi56 deployed the \(\frac{G'}{G}\) -model expansion method to obtain soliton solutions. Ding et al.57 studied dark and anti-dark solitons whereas Coppini et al.58 developed N-breather anomalous wave solutions. The analysis of Lie point symmetries together with similarity reductions and conservation laws for the DS equation appears in Guo et al.59. Liu and Li60 analyzed the DS equation as it interacted with time-noise effects at the multiplicative level. The research examines the stochastic Davey–Stewartson (SDS) equation through the application of the MEDA method to discover diverse exact stochastic soliton solutions. Using this approach we obtained diverse solution types such as dark ones as well as trigonometric ones, rational solutions, and periodic wave solutions. We investigate multiple physical consequences of noise on these solutions. We use MATLAB software to draw graphical representations of soliton solutions which show how they act with varying noise strength. Our findings yield traditional stochastic soliton solutions of the DS equation as the noise parameter reaches zero value. These findings serve to advance dynamical systems research in noisy conditions by offering important observations regarding future investigation.

Physical interpretation

A dark stochastic soliton is a soliton that moves in a nonlinear dispersive medium that contains fluctuations or random noise. Even if random influences vary the position, depth, phase, etc. of these solitons, they do not significantly change their general form of localized dip on a continuous wave background. On a continuous wave background, they occur in localized dips, although random variables might cause variations in their characteristics (position, depth, or phase). With a focus on how these solitons behave to stochastic perturbations, they are studied in systems where a random character is inherent, such as optical fibers, Bose-Einstein Condensates etc. Multiplicative noise introduces random disturbances to amplitudes, depths, phases, and positions, which can disrupt the soliton’s localised dip and deform dark stochastic solitons. Soliton broadening, energy exchange with the background, or a transition to chaotic dynamics under high noise intensities. These effects are important for investigations of soliton stability in stochastically nonlinear media. A periodic stochastic soliton undergoes random perturbations that periodically alter its amplitude, phase, or velocity, among other properties. They are studied in fields like optical communications, quantum fluids, and plasma physics; often, stochastic effects necessitate the use of analytical solutions. They are typically represented by stochastic nonlinear partial differential equations as the nonlinear Schrödinger equation with noise. A stochastic soliton solution of rational type is one in which the soliton is represented by rational functions, with a profile consisting of a ratio of functions. It differs from conventional exponential or trigonometric soliton solutions in that it uses stochastic variables for building algebraic patterns. Figures 1, 6, 10, 15, 20, and 25 display dark stochastic soliton solutions while Figs. 2, 7, 11, 16, 21 and 26 display singular stochastic soliton solutions. Similarly Figs. 3, 4, 8, 12, 13, 17, 18, 22, 23, 27, and 28 display periodic stochastic soliton solutions. Furthermore the Figs. 5, 9, 14, 19, 24, and 29 display rational stochastic soliton solutions.

Fig. 1
figure 1

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Psi _{1}\left( x,y,t\right) |\) for \(\sigma = 0.08, \zeta _{1}=0.5, \zeta _{2}=0.7, {{w}}=8.7, k=3, \lambda = 0.25, \theta =0.2, \rho =-0.5, y=1, z = 0,\) and \(\Xi (t) =\)randn.

Full size image
Fig. 2
figure 2

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Psi _{2}\left( x,y,t\right) |\) for \(\sigma = 0.08, \zeta _{1}=0.5, \zeta _{2}=0.7, {{w}}=8.7, k=3, \lambda = 0.25, \theta =0.2, \rho =-0.5, y=1, z = 0,\) and \(\Xi (t)\)randn.

Full size image
Fig. 3
figure 3

(Matlab R2017a (9.2.0.538062))The 3 dim, contour and line plots of \(|\Psi _{3}\left( x,y,t\right) |\) for \(\sigma = 0.08, \zeta _{1}=0.15, \zeta _{2}=1.7, {{w}}=5.7, k=1.63, \lambda = 10.25, \theta =0.2, \rho =125.5, y=1, z = 0,\) and \(\Xi (t)\)randn.

Full size image
Fig. 4
figure 4

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Psi _{4}\left( x,y,t\right) |\) for \(\sigma =0.09, \zeta _{1}=0.15, \zeta _{2}=1.7, {{w}}5.7, k=2.63, \lambda =20.25, \theta =0.02, \rho =2.06, y=1, z=0,\) and \(\Xi (t)\)randn.

Full size image
Fig. 5
figure 5

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Psi _{5}\left( x,y,t\right) |\) for \(\sigma =0.08, \zeta _{1}=0.15, \zeta _{2}=1.7, {{w}}4.7, k=2.63, \lambda =10.25, \theta =1.02, \rho =0, y=1, z=0,\) and \(\Xi (t)=\)randn.

Full size image
Fig. 6
figure 6

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Psi _{6}\left( x,y,t\right) |\) \(\sigma =0.09, \zeta _{1}=10.5, \zeta _{2}=10.7, {{w}}=4.7, k=2, \lambda =0.25, \theta =0.02, \rho =-98825.5, y=1, z=0,\) and \(\Xi (t)=\)randn.

Full size image
Fig. 7
figure 7

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Psi _{7}\left( x,y,t\right) |\) \(\sigma =0.05, \zeta _{1}=10.4, \zeta _{2}=10.8, {{w}}=10.7, k=5, \lambda =2.25, \theta =0.02, \rho =-10.5, y=1, z=0,\) and \(\Xi (t)=\)randn.

Full size image
Fig. 8
figure 8

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Psi _{8}\left( x,y,t\right) |\) \(\sigma =0.09, \zeta _{1}=10.15, \zeta _{2}=3.7, {{w}}=15.7, k=5.63, \lambda =0.025, \theta =0.02, \rho =98800, y=1, z=0,\) and \(\Xi (t)=\)randn.

Full size image
Fig. 9
figure 9

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Psi _{10}\left( x,y,t\right) |\) \(\sigma =0.16, \zeta _{1}=2.4, \zeta _{2}=2.8, {{w}}=5.7, k=2.8, \lambda =5.25, \theta =20.02, \rho =0 y=1, z=0,\) and \(\Xi (t)=\)randn.

Full size image
Fig. 10
figure 10

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Psi _{11}\left( x,y,t\right) |\) \(\sigma =0.09, \zeta _{1}=10.5, \zeta _{2}=10.7, {{w}}=5.7, k=2, \lambda =5.25, \theta =0.02, \rho =-0.5, y=1, z=0,\) and \(\Xi (t)=\)randn.

Full size image
Fig. 11
figure 11

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Psi _{12}\left( x,y,t\right) |\) \(\sigma =0.09, \zeta _{1}=10.5, \zeta _{2}=10.7, {{w}}=6.7, k=3.5, \lambda =5.25, \theta =0.02, \rho =-0.5, y=1, z=0,\) and \(\Xi (t)=\)randn.

Full size image
Fig. 12
figure 12

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Psi _{13}\left( x,y,t\right) |\) \(\sigma =0.09, \zeta _{1}=10.5, \zeta _{2}=10.7, {{w}}=6.7, k=3.5, \lambda =5.25, \theta =0.02, \rho =2.5, y=1, z=0,\) and \(\Xi (t)=\)randn.

Full size image
Fig. 13
figure 13

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Psi _{14}\left( x,y,t\right) |\) \(\sigma =0.09, \zeta _{1}=10.5, \zeta _{2}=10.7, {{w}}=8.7, k=4.5, \lambda =5.85, \theta =0.02, \rho =2.5, y=1, z=0,\) and \(\Xi (t)=\)randn.

Full size image
Fig. 14
figure 14

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Psi _{15}\left( x,y,t\right) |\) \(\sigma =0.09, \zeta _{1}=10.5, \zeta _{2}=10.7, {{w}}=8.7, k=0.5, \lambda =0.85, \theta =0.02, \rho =0, y=1, z=0,\) and \(\Xi (t)=\) randn.

Full size image
Fig. 15
figure 15

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Phi _{1}\left( x,y,t\right) |\) for \(\sigma =0.09, \zeta _{1}=10.5, \zeta _{2}=10.7, {{w}}=8.7, k=0.5, \lambda =0.85, \theta =0.02, \rho =-190.6, y=1, z=0,\) and \(\Xi (t)=\)randn.

Full size image
Fig. 16
figure 16

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Phi _{2}\left( x,y,t\right) |\) for \(\sigma =0.06, \zeta _{1}=0.150, \zeta _{2}=1.7, {{w}}=10.7, k=5, \lambda =0.125, \theta =3.02, \rho =-190.6, y=1, z=0,\) and \(\Xi (t)=\)randn.

Full size image
Fig. 17
figure 17

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Phi _{3}\left( x,y,t\right) |\) for \(\sigma =0.08, \zeta _{1}=0.150, \zeta _{2}=1.70, {{w}}=6.7, k=2.63, \lambda =2.25, \theta =3.02, \rho =125.6, y=1, z=0,\) and \(\Xi (t)=\)randn.

Full size image
Fig. 18
figure 18

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Phi _{4}\left( x,y,t\right) |\) for \(\sigma =0.09, \zeta _{1}=0.150, \zeta _{2}=1.7, {{w}}=5.7, k=2.63, \lambda =10.25, \theta =0.02, \rho =2.06, y=1, z=0,\) and \(\Xi (t)=\)randn.

Full size image
Fig. 19
figure 19

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Phi _{5}\left( x,y,t\right) |\) for \(\sigma =0.08, \zeta _{1}=0.150, \zeta _{2}=1.7, {{w}}=4.7, k=2.63, \lambda =10.25, \theta =1.02, \rho =0, y=1, z=0,\) and \(\Xi (t)=\)randn.

Full size image
Fig. 20
figure 20

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Phi _{6}\left( x,y,t\right) |\) for \(\sigma =0.09, \zeta _{1}=10.50, \zeta _{2}=10.70, {{w}}=4.7, k=2, \lambda =2.25, \theta =0.02, \rho =-98825.5, y=1, z=0,\) and \(\Xi (t)=\)randn.

Full size image
Fig. 21
figure 21

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Phi _{7}\left( x,y,t\right) |\) for \(\sigma =0.05, \zeta _{1}=-10.150, \zeta _{2}=10.70, {{w}}=10.7, k=5, \lambda =2.25, \theta =0.02, \rho =-10.5, y=1, z=0,\) and \(\Xi (t)=\)randn.

Full size image
Fig. 22
figure 22

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Phi _{8}\left( x,y,t\right) |\) for \(\sigma =0.09, \zeta _{1}=10.150, \zeta _{2}=3.7, {{w}}=15.7, k=5.63, \lambda =0.025, \theta =0.02, \rho =98800, y=1, z=0,\) and \(\Xi (t)=\)randn.

Full size image
Fig. 23
figure 23

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Phi _{9}\left( x,y,t\right) |\) for \(\sigma =0.16, \zeta _{1}=1.40, \zeta _{2}=1.80, {{w}}=6.7, k=2.35, \lambda =1.025, \theta =30.02, \rho =0.0005, y=1, z=0,\) and \(\Xi (t)=\)randn.

Full size image
Fig. 24
figure 24

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Phi _{10}\left( x,y,t\right) |\) for \(\sigma =0.16, \zeta _{1}=2.40, \zeta _{2}=2.80, {{w}}=10.7, k=5.7, \lambda =0.85, \theta =20.02, \rho =0, y=1, z=0,\) and \(\Xi (t)=\)randn.

Full size image
Fig. 25
figure 25

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Phi _{11}\left( x,y,t\right) |\) for \(\sigma =0.09, \zeta _{1}=10.150, \zeta _{2}=10.70, {{w}}=5.7, k=2.0, \lambda =2.25, \theta =0.02, \rho =0.02, y=1, z=0,\) and \(\Xi (t)=\)randn.

Full size image
Fig. 26
figure 26

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Phi _{12}\left( x,y,t\right) |\) for \(\sigma =0.09, \zeta _{1}=10.150, \zeta _{2}=10.70, {{w}}=6.7, k=3.5, \lambda =5.25, \theta =0.02, \rho -0.5, y=1, z=0,\) and \(\Xi (t)=\)randn.

Full size image
Fig. 27
figure 27

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Phi _{13}\left( x,y,t\right) |\) for \(\sigma =0.06, \zeta _{1}=10.150, \zeta _{2}=10.70, {{w}}=10.70, k=3.5, \lambda =5.25, \theta =0.02, \rho =2.5, y=1, z=0,\) and \(\Xi (t)=\)randn.

Full size image
Fig. 28
figure 28

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Phi _{14}\left( x,y,t\right) |\) for \(\sigma =0.09, \zeta _{1}=10.150, \zeta _{2}=10.70, {{w}}=6.7, k= 6.7, \lambda =5.25, \theta =0.02, \rho =2.5, y=1, z=0,\) and \(\Xi (t)=\)randn.

Full size image
Fig. 29
figure 29

(Matlab R2017a (9.2.0.538062)) The 3 dim, contour and line plots of \(|\Phi _{15}\left( x,y,t\right) |\) for \(\sigma =0.09, \zeta _{1}=10.150, \zeta _{2}=10.70, {{w}}=8.7, k=0.5, \lambda =0.85, \theta =0.02, \rho =0, y=1, z=0,\) and \(\Xi (t)=\)randn.

Full size image

In conclusion, all figures pertaining to dark, singular, periodic, and rational solitons in different kinds of plots are essential tools to investigate nonlinear systems. They are employed to illustrate underlying patterns in situations where it is difficult to recognise new connections; practically, they support research goals in domains ranging from plasma physics to quantum mechanics and optics by providing reasoning, prediction, and validation for new ideas. The observations show that multiplicative noise creates various impacts on dark, periodic and rational solitons across multiple ways. The soliton starts to disperse due to the introduced dispersive effects which lead to its reduced localization. The bright peak along with the dark dip becomes increasingly wider due to this effect. The combination of noise with other factors reduces the amplitude levels of bright as well as dark components thus weakening the soliton structure fundamentally. The transmission of noise causes structural definition loss which makes bright-dark area boundaries fade into each other in the optical field. The delicate nonlinear balance needed for sustaining the soliton’s shape becomes disturbed by random fluctuations that arise from noise-induced perturbations. Noise drives unnecessary distribution of energy that pulls away from the localized soliton structure which then results in its deterioration. The effects demonstrate why noise plays such an important part in controlling the stability and movement patterns of soliton solutions.

Conclusion

We studied the stochastic Davey–Stewartson equations which serve as a fundamental tool for studying complex wave phenomena in environments affected by noise. The MEDA method provided exact stochastic soliton solutions which included bright, dark, singular, rational and periodic waveforms. The mathematical simulations showed that Brownian motion which models multiplicative noise causes major modifications to the solutions that lead toward zero-stabilization as their primary outcome. MATLAB-generated graphical analysis demonstrates the detailed relationship of noise with nonlinear wave patterns effectively. Such findings generate ramifications that enhance our knowledge about noisily driven wave phenomena across the fields of plasma physics and nonlinear optics alongside fluid dynamics of complex systems. The field benefits from this research which offers an essential fundamental view of randomness effects on soliton motion by surpassing the current perturbative and numerical methods. Multiplicative noise produces observed wave stabilization effects indicating a potential process for noise-driven order which might lead to practical wave structure control within stochastic systems. The construction of exact stochastic solutions in this work provides an essential basis which supports future investigations of wave propagation under random disturbances. Related works studied stochastic NLS and DS equations yet they withheld the approach for developing exact stochastic soliton solutions of Davey–Stewartson equations with multiplicative noise through MEDA methodology. Future investigations should analyze more progressive noise models beyond white noise using fractional Brownian motion together with colored noise since they better reproduce diverse stochastic processes. The investigation of control methods which strengthen soliton stability under random external disturbances shows potential for practical realization. Exact stochastic solutions derived in this work function as reference points for verifying numerical methods while helping in developing stable control strategies for noisy nonlinear systems. Future investigations should apply the discovered stochastic soliton solutions to actual situations involving optical fiber communication and wave propagation through turbulent plasmas.