Risk evaluation of metro tunnel shield construction based on game variable weight extension cloud theory

Abstract

To address the issues of fuzziness and randomness in risk evaluation for subway shield construction, this study proposes a risk assessment model integrating variable weight theory and an extension cloud model to enable a more scientific and effective evaluation. Firstly, the WBS-RBS (Work Breakdown Structure-Risk Breakdown Structure) method was employed to establish a risk evaluation index system for metro tunnel construction, with risk levels classified into Grades I-V. Secondly, the ordinal relationship method (G1) and entropy weight method were applied to calculate the fixed weights of the evaluation indexes. The comprehensive fixed weights are determined based on the game theory, considering the dynamic changes of the evaluation indexes, and the optimal dynamic, comprehensive weights are calculated based on this combined with the variable weight theory. Finally, comprehensive affiliation degrees were obtained through the extension cloud model, and the comprehensive evaluation grade was determined according to the principle of maximum affiliation. The model was applied to the submarine tunnel section of Qingdao Metro Line 8. The results indicate that the risk level of the project is Grade III, which aligns with the actual construction conditions. This consistency validates the rationality and feasibility of the proposed method, offering a novel approach to guide safety management and risk decision-making in metro tunnel construction projects.

Introduction

With the rapid development of cities, the metro has become an important part of public transport. Since the construction of Beijing Metro Line 1 was started in 1965, by the end of 2023, 338 urban rail transit lines with a total length of 11224.54 km have been opened in 59 cities in Chinese Mainland¹. Metro not only drives economic development but eases traffic congestion. At the same time, construction risk also exists. By searching for accident statistics released by the Ministry of Emergency Management of the People’s Republic of China, accident investigation reports released by the government, and publicly available literature^2,3,4, a total of 192 subway tunnel construction accidents in China from 2010 to 2023 were retrieved, which is an incomplete statistic. The results are shown in Fig. 1a. Classify the number of accidents according to construction methods, and see Fig. 1b for the proportion of accidents caused by different construction methods. As shown in the pie chart, the open cut method and shield method are the two construction methods with more construction accidents, accounting for over 50% of the total accidents.

Fig. 1

(a) Statistics on the number of subway tunnel construction accidents and fatalities in China from 2010 to 2023; (b) Proportion of construction accidents caused by different construction methods.

The shield method is one of the mostly used methods for metro shield tunnel construction. Due to shield tunnel construction process having the characteristics of uncertainty, irreversibility, technical difficulty, danger, etc. Once an accident occurs, it directly threatens the personal safety of the construction workers and the surrounding people, which has a significant impact on society⁵. For example, in 2007, the collapse of Metro Line 4 in Sao Paulo killed seven people; in 2018, the water penetration collapse of Metro Line 2 in Foshan, China, killed 11 people and injured eight; and in 2023, a landslide in an under-construction metro in India trapped 41 people. There are many hidden dangers during the construction of metro tunnels, and the possibility of various types of accidents is high. It is necessary to carry out a risk valuation of the construction of metro tunnels to determine the potential dangers.

For the risk assessment of metro shield construction, domestic and foreign scholars carry out relevant research from the three aspects: constructing the evaluation index system, calculating the weights of the indicators and selecting the evaluation model. The construction of the evaluation index system is the main foundation for risk assessment, and most scholars construct it through literature review, the Delphi method, on-site analysis, or with the help of risk identification methods. Forcael et al.⁶ identified and classified 36 metro risk factors based on survey data from tunnel companies. Guo et al.⁷ constructed a risk assessment framework for shield tunneling through buildings from five dimensions. Liu et al.⁸ established a safety assessment system for metro tunnel construction from four aspects, based on considering the complexity of the metro tunnel construction environment under extreme rainfall weather conditions. Luo et al.⁹ utilized fishbone diagram analysis and fault tree analysis to analyze the causes of explosions in natural gas spherical tanks. Nezarat et al.¹⁰ identified and assessed the risk factors of tunneling through MCDM techniques and analyzed them about the Golab Tunnel in Iran and achieved certain results. Yao et al.¹¹ analyzed the factors influencing metro stations based on the FTA-BN method. Yang¹² used the Hazard and Operability Analysis Method (HAZOP) to identify the metro shield tunnel construction risk. Li et al.¹³ constructed a spatial network model within subway stations based on complex network theory, and evaluated the importance indicators of each subspace in the network. Although all of these methods play a crucial role in risk identification and system construction, they are limited to building frameworks from a single perspective and have little analysis of changes in risk factors. The WBS-RBS method can decompose the construction process and potential risks from top to bottom and deeply analyze the coupling relationship between the two, which can be applied to a complex evaluation system like the metro.

The calculation of the weights of the indicators will directly affect the accuracy of the risk evaluation in metro tunnel construction. The calculation of weights is mainly divided into three methods: subjective weights, objective weights, and combined weights. Jbaihi et al.¹⁴ evaluated the technical potential of large-scale CSP power plants using the AHP method. Hu et al.¹⁵ improved the AHP by incorporating positive and negative weights of the indicators. Cong¹⁶ calculated the indicator weights of metro shield construction based on the structural entropy weight method. Chen et al.¹⁷ utilized a combination of AHP and the entropy weight method to determine the weights according to the safety evaluation standards for metro projects. Guan et al.¹⁸ proposed an evaluation method combining RF and Triangular Fuzzy Number Hierarchical Analysis (TFNAHP), and used it for metro shield flood risk evaluation. Wang et al.¹⁹ employed the OWA operator and simple correlation function method to carry out a scientific and effective evaluation of metro shield construction risk. Xiong et al.²⁰ used the Combined Ordered Weighted Average (C-OWA) operator to weaken the influence of subjective factors and establish an interaction matrix. Kong et al.²¹ proposed the AHP-EWM-GFCE model to evaluate the performance of four novel medical waste gasification low-carbon multigenerational systems. The combination assignment method, while addressing the limitations of a single method, does not consider the balance between the combined weights²². None of the above weight calculation methods are sufficiently precise, whereas game theory can optimize deviations between combined and individual weights by adjusting coefficients to minimize dispersion.

The selection of evaluation models is the core of the risk assessment process, and commonly used risk evaluation models include hierarchical analysis model²³, TOPSIS model²⁴, Fuzzy Analytic Hierarchy Process(FAHP)²⁵, fuzzy analysis network (FANP)^26,27,28, system dynamics model (SD)²⁹, grey cluster analysis^30,31,32, coupling theory^33,34, Bayesian network^35,36 and topology theory³⁷, etc. The above theories and models have greatly improved the risk assessment of metro tunnel construction, but they do not fully consider the uncertainty of construction risk. The cloud model can describe the ambiguity and randomness of uncertain decision-making systems³⁸, which can make up for the limitations of the above assessment models. Liu et al.³⁹ used a cloud model for the coupled analysis of microenvironmental health vulnerability (MMHV) in the metro, which provides effective guidance for taking precise measures for metro operations. Cao et al.⁴⁰ adopted an extension cloud model to evaluate government ecological performance, which is important for achieving carbon neutrality. Chen et al.⁴¹ applied a cloud model to assess the risks of shield tunnel boring beneath existing tunnels and verified the model’s effectiveness. Gao⁴² applied the cloud model to analyze risks in oil tanker cargo handling operations, using the model to translate expert qualitative judgments on factor significance into quantitative assessments. It is evident that the application of cloud models across various fields demonstrates their strong applicability and effectiveness.

Metro shield tunnel boring is a dynamic process, and the weights of evaluation indicators also vary dynamically⁴³. Based on the above research, this paper proposes a metro shield construction risk evaluation model incorporating variable weight theory and an improved cloud model. This model accounts for the dynamic nature of tunnel shield construction and enables dynamic analysis of risk evaluation indicator weights. By integrating quantitative and qualitative analyses, it effectively addresses the uncertainty and ambiguity in the evaluation system. Furthermore, it mitigates the limitations of single-method evaluation approaches and enhances the reliability of evaluation results.

Method

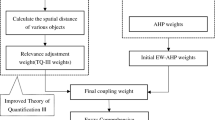
This paper adopts the Work Breakdown Structure and Risk Breakdown Structure (hereinafter referred to as WBS-RBS) method to distinguish the hazard factors, based on which it constructs the risk evaluation index system of shield construction in metro tunnels and divides the risk level of the indexes according to the relevant standards and experts’ opinions. The game combination assignment of the G1-entropy weight method is used to balance the weights of both, and variable weight theory is introduced to dynamically adjust the weights of indicators. In addition, the extension cloud evaluation method is used to measure the fuzziness and randomness of the indicators, transforming the qualitative concepts into quantitative representations and constructing an underground tunnel construction risk evaluation model based on variable weight theory and extension cloud model to optimize the risk assessment. Finally, the model is applied to the submarine tunnel project of Qingdao Metro Line 8 to verify the practicality and effectiveness of the risk evaluation model. The specific research framework is shown in Fig. 2.

Fig. 2

Research framework.

Construction specification

At present, shield method construction is one of the most commonly used methods in urban rail transit construction. Scientific, systematic, and comprehensive risk assessment for shield construction projects can reduce the adverse effects of accidents. In order to achieve this goal, this article referred to the “Work Safety Law of the People’s Republic of China” when constructing the risk assessment index system. And it divides five risk levels according to GB 50715 − 2011 ‘Standard for Construction Safety Assessment of Metro Engineering’⁴⁴. According to GB 50157 − 2013 ‘Code for Design of Metro’⁴⁵ the risk indicator evaluation standard for metro shield construction in metro tunnels is established.

Data processing

The research data in this paper mainly consists of two parts. The first part is the original scoring data, using the Delphi method to score the risk level of risk indicators. In order to make indicators with different scales comparable, the data need to be standardized and mapped to the [0, 1] interval. This paper invited ten experts in the field of tunnels. The standardized measures are:${r_{ij}}=({d_{ij}} - \hbox{min} {d_i})/(\hbox{max} {d_i} - \hbox{min} {d_i})$ for positive indicators, ${r_{ij}}=(\hbox{max} {d_i} - {d_{ij}})/(\hbox{max} {d_i} - \hbox{min} {d_i})$ for negative indicators.

The second part is to distinguish the importance of the neighboring indicators. Firstly, experts are invited to rank the importance of each indicator. Then they assigned values to the ordinal relationship of the indicators, whose assignment criteria are referred to in the literature⁴⁶. The above data were used in the G1 method to calculate weights.

Risk evaluation model for metro shield construction in metro tunnels

Identification of risk factors

Due to the complicated and numerous processes of the metro shield construction, the risk will also be different as the project is in different stages of construction⁴⁷. This article selects the combination of WBS method and RBS method to identify risk factors. WBS is to divide the project level by level into several more manageable subsystems, and divide the work of the project into different levels from the whole to the details⁴⁸. RBS classifies risks according to different perspectives to comprehensively identify and analyze risks⁴⁹. Although WBS can decompose the project into manageable work packages, it may ignore potential risks. By mapping RBS to each level of WBS, the specific risks that may be faced by each sub project can be systematically identified, which greatly reduces the possibility of risk omission in the identification process. When facing complex subway engineering projects, it can clearly and intuitively present various risks that the project may face at any stage. Moreover, it can balance the overall situation and reflect details, providing a new analytical method for identifying such risks⁵⁰. The decomposition diagram is shown in Fig. 3.

Fig. 3

(a) Schematic diagram of WBS decomposition structure tree; (b) Schematic diagram of RBS decomposition structure tree; (c) WBS-RBS decomposition tree.

The specific steps for identifying risk factors include:

(1) Preliminary identification. Based on the statistics of subway construction accidents, collect and analyze the main causes of 58 shield tunneling accidents, obtain preliminary identified risk factors, and form a preliminary list of risk factors, as shown in Table 1.

Table 1 Preliminary list of risk factors.

(2) Secondary identification. The initially identified risk factors are used as secondary indicators for RBS, and the WBS-RBS method is applied to construct a risk coupling matrix to complete the secondary identification of risk indicators.

In view of the construction characteristics of subway shield tunnel projects, such as long construction lines and complex construction technology, this paper adopts the WBS method of “process decomposition & division and subdivision” to carry out risk decomposition. The work breakdown structure of the project is divided into three main stages based on the process flow of subway tunnels and GB 50,446 “Code for Construction and Acceptance of Shield Tunnels”⁵¹. It is divided into three main stages: pre construction stage, beginning and diving stage and shield arrival stage. Each stage contains $\:n$ sub items. Based on preliminary identification of risk factors and expert opinions, the risks of shield tunneling construction are decomposed into five categories: Personnel Operational Risks, Environmental Risks, Construction Technology Risks, Management Risks, and Emergency Risks, denoted as $\:{R}_{k}$,$k=1,2,3,4,5$. Each type of risk factor is further subdivided into $\:{R}_{km}$ sub risk factors, $m=1,2,3, \cdots$. Perform WBS decomposition and RBS decomposition separately for subway tunnel shield construction, as shown in Fig. 4.

Fig. 4

(a) Tunnel construction work breakdown tree; (b) Tunnel construction risk breakdown tree.

Take the last elements of WBS and RBS in Fig. 4 as columns and rows of the matrix respectively, then cross them pairwise and analyze whether there is any risk at the intersection⁵². The element values of the coupling matrix are determined through an expert survey method. Ten deputy-senior-level experts, all with extensive experience in subway engineering construction, were surveyed. The questionnaire survey form can be found in Appendix 1. The specific steps of the expert survey method are as follows:

• (1) If the expert believes that there are relevant risks at the intersection, the element value of the coupling matrix is marked as “√”, if there is no or negligible associated risk, do not fill in.

• (2) Ten questionnaires were collected. For matrix element values at the same location, if one expert considers them relevant, it is recorded as “1”. If all 10 experts consider them unrelated, it is recorded as “0”^53,54.

Taking W₁₁R₂₁ as an example, if the geological survey before construction is inaccurate and the geological conditions are not ideal, water seepage and collapse accidents may occur during the construction process. Two experts in the collected questionnaire believed that the coupling of the two would lead to accidents, so the matrix element value at the W₁₁R₂₁ coupling point is “1”. The final WBS-RBS risk identification matrix for shield method tunneling is shown in Fig. 5.

Fig. 5

WBS-RBS construction risk identification matrix.

Establishment of a risk evaluation index system

The coupling results of WBS-RBS construction risk identification matrix are summarized. Based on the “4M1E” theory and literature review^55,56, following the principles of scientificity, objectivity, and feasibility in establishing indicators, a subway tunnel construction risk assessment index system consisting of 5 primary indicators and 19 secondary indicators is constructed. Among it, the primary indicators mainly include personnel factors, mechanical equipment factors, environmental factors, management factors, and contingency factors, as shown in Fig. 6.

Fig. 6

Metro tunnel construction risk evaluation index system.

Classification of risk levels

According to relevant norms and previous research on risk identification and grading in tunnel shield construction⁵⁷, the risk levels are classified into I-V, representing low risk, lower risk, medium risk, higher risk, and high risk, respectively. The evaluation thresholds for each level are (4.5, 5], (3.5, 4.5], (2.5, 3.5], (1.5, 2.5], and (0, 1.5]. For qualitative risk scoring, a semi-quantitative method is adopted, categorizing risks into the five levels mentioned above based on qualitative descriptions. The assignment intervals are determined through consultations with on-site personnel and industry experts^58,59. The specific definitions and treatments for each level are presented in Table 2.

Table 2 Risk level intervals and their definitions.

In the constructed evaluation index system, risk indicators are classified into subjective and objective indicators. Subjective indicators are scored based on the practical experience of metro safety managers and experts, while objective indicators are graded according to their actual values. Following the ‘Code for Design of Metro’, the risk indicator evaluation standard, risk level interval, and related description of metro shield construction are established, as shown in Table 3.

Table 3 Evaluation guidelines for safety evaluation indexes of metro shield construction in metro tunnels.

Calculation of indicator weights

Calculation of fixed weight

Sequential relationship method

The G1 method can flexibly analyze the importance of different indicator weights in different environments, and has the advantages of fast counting rate and without consistency test⁶⁰. It is suitable for the decision analysis process in which the evaluation indicators are random and fuzzy, and the number of indicators is large. The specific steps are as follows:

(1) Ranking the importance of evaluation indicators.

(2) Importance discrimination of neighboring indicators. If the rate of the importance of the evaluation indicator$\:\:{X}_{i-1}^{*}\:$to $\:{X}_{i}^{*}$ in the ordinal relationship is given as $\:\frac{{w}_{i-1}}{{w}_{i}}$, then the judgment ratio is:

$${r_i}=\frac{{{w_{i - 1}}}}{{{w_i}}}\begin{array}{*{20}{c}} {}&{} \end{array}$$

(1)

where$\:{\:w}_{i}$ is the weight of the $\:i$-th evaluation indicator in the ordinal relationship, and $\:{r}_{i}\:\:$is the assignment of the importance of the ordinal relationship evaluation indicator $\:{X}_{i-1}^{*}$ to $\:{X}_{i}^{*}$.

(3) Compute the subjective weight of each indicator. According to the given $\:{r}_{i}\:$assignment, the weights of evaluation indicators are calculated as follows:

$${w_i}={\left( {1+\sum\limits_{{i=2}}^{k} {\prod\limits_{{s=1}}^{k} {{r_s}} } } \right)^{ - 1}}$$

(2)

$${w_{i - 1}}={w_i}{r_i}\begin{array}{*{20}{c}} {}&{\left( {i=k,k - 1, \cdots ,2} \right)} \end{array}$$

(3)

Entropy weight method

The entropy weight method is a method of determining the weights of indicators based on their information entropy⁶¹. The weight reflects the effective amount of information provided by the index, while other methods (such as the coefficient of variation method) only focus on the degree of dispersion. In addition, it can objectively reflect the relative importance of the index in comprehensive evaluation^62,63. If the information entropy of the indicator is smaller, it shows that the degree of variability of this index is higher, the more information the indicator provides, and the more useful it is in the evaluation process⁶⁴. The specific calculations are as follows:

(1) Construct the judgment matrix $B = (b_{{ij}} )_{{m \times n}}$ of the evaluation index from the raw scoring data.

(2) Normalize matrix $R = (r_{{ij}} )_{{m \times n}}$.

(3) Calculate the information entropy of the index.

$${e_i}= - \frac{{\sum\nolimits_{{j=1}}^{m} {{p_{ij}}\ln {p_{ij}}} }}{{\ln m}}$$

(4)

$${p_{ij}}=\frac{{{r_{ij}}}}{{\sum\nolimits_{{j=1}}^{m} {{r_{ij}}} }}$$

(5)

Where$\:\:{p}_{ij}$ is the indicator ratio of the $\:j$-th evaluation indicator of the $\:i$-th evaluation item, $\:{r}_{ij}$ is the scoring value of the $\:j$-th indicator by the $\:i$-th expert, $\:m$ is the number of evaluation indicators.

(4) Compute the objective weights of indicators.

$${w_i}=\frac{{1 - {e_i}}}{{m - \sum\nolimits_{{i=1}}^{m} {{e_i}} }}$$

(6)

Comprehensive constant power based on game theory

The combination weighting of game theory is a method for solving practical problems by solving linear equations; it introduces the idea of game theory⁶⁵. The G1 method relies on expert experience, and the weighting results may vary due to different understandings of expert experience. The entropy weight method is more objective, and the weight coefficients are based on a strict algorithmic process. Combining subjective and objective assignment methods, game theory is introduced to determine the comprehensive weights $\:{w}_{i}^{*}$ of indicators in order to minimize linear errors. This method can combine the advantages of subjective and objective weighting methods, and adjust the combined weights in real time to achieve dynamic weighting⁶⁶.

Assume that $\:L$ methods are used to assign weights to the indicators and obtain the weight vectors ${w_i}$of $\:i$ indicators. In this paper, L is taken as 2, i is taken as 19, and then the comprehensive weight is:

$$w_{i}^{ * } = \sum\limits_{{i = 1}}^{L} {\alpha _{i} } w_{i}^{T} ,\alpha _{i} > 0$$

(7)

Where $\:{w}_{i}^{*}$ is the integrated weight vector, ${\alpha _i}$ is the linear combination coefficient.

According to the game theory, to find the most satisfactory weight vector, so that the deviation of $\:{w}_{i}^{*}$ from $\:{w}_{i}$ is extremely minimal, that is:

$$\hbox{min} {\left\| {\sum\limits_{{i=1}}^{L} {{\alpha _i}w_{i}^{T} - {w_i}} } \right\|_2},i=1,2, \cdots ,L$$

(8)

${\alpha _i}$ is obtained by calculation, further normalization is performed to obtain $\alpha _{i}^{ * }$, and the combined indicator weight $\:{w}^{*}$ is found with the following formula:

$$\alpha _{i}^{ * }=\frac{{{\alpha _i}}}{{{\alpha _1}+{\alpha _2}}},i=1,2$$

(9)

$${w^ * }=\alpha _{1}^{ * }w_{1}^{T}+\alpha _{2}^{ * }w_{2}^{T}$$

(10)

Calculation of variable weight

The theory of variable weights can calculate the equilibrium factor based on the actual values of various risk assessment indicators, thereby overcoming the bias caused by normal weight evaluation⁶⁷. Therefore, variable weight theory is applied in the risk evaluation of metro shield construction, which can reduce the assessment bias caused by the fixed weight and dynamically analyze the risk factors of the construction process.

Denote $W\left( X \right)=\left[ {{w_1}\left( X \right),{w_2}\left( X \right), \cdots ,{w_n}\left( X \right)} \right]$ as a set of variable weight vectors, and for any fixed weight vector ${W^0}=\left( {{w_1},{w_2}, \cdots ,{w_n}} \right)$, the variable weight vector ${W_i}\left( X \right)$ of the $\:i$-th evaluation indicator can be obtained.

$${W_i}\left( X \right)=\frac{{W_{i}^{0} \cdot {R_i}\left( X \right)}}{{\sum\limits_{{j=1}}^{n} {\left[ {W_{j}^{0} \cdot {R_j}\left( X \right)} \right]} }}$$

(11)

Where $W_{i}^{0} \cdot {R_i}\left( X \right)=\left[ {{w_1} \cdot {R_1}\left( X \right),{w_2} \cdot {R_2}\left( X \right), \ldots ,{w_n} \cdot {R_n}\left( X \right)} \right]$.

The following are the steps in the variable weighting calculation:

(1) Determine the weighting factor. The fixed-weight coefficient $W_{i}^{0}$ in this paper is the combination weight ${w^ * }$, obtained based on game theory, and the calculation process is shown in Eq. (7) to Eq. (10).

(2) Establish the variable weight vector. The types of variable weight vectors are mainly linear, exponential, logarithmic, and so on. Considering the engineering situation and the literature⁶⁸, the exponential type function is chosen to calculate the variable weight vector ${R_i}\left( X \right)$.

$${R_i}\left( X \right)=\left\{ \begin{gathered} {e^{\alpha \left( {\beta - {x_{ij}}} \right)}} \hfill \\ 1 \hfill \\ \end{gathered} \right.\begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} {{x_{ij}} \leqslant \beta } \\ {{x_{ij}}>\beta } \end{array}} \end{array}$$

(12)

Where $j=1,2, \ldots ,n$, $\alpha \geqslant 0$, $0<\beta \leqslant 1$. $\:\beta\:$ is the lower limit value of alert; $\:\alpha\:$ is the punishment factor. The larger $\:\alpha\:$ becomes, the more significant the punishment effect is as well.

(3) Calculate the variable weight vector. Combine the combination weight $W_{i}^{0}$ with ${R_i}\left( X \right)$ to calculate the variable weight vector ${W_i}\left( X \right)$, shown in Eq. (11).

Improved object element extension cloud model

The extension theory describes things based on matter-element and solves the contradiction problem from two different dimensions: qualitative and quantitative. Its essence is coupling extension and cloud model, and it uses matter-element extension theory to analyze the cloud model⁶⁹. After calculating the comprehensive affiliation degree of the object and determining the rating class to which it belongs, the eigenvalues of the class variables can then be calculated. And by using the eigenvalues of the class variables, the degree of bias of the object towards the two nearest classes can thus be determined. The extension cloud model can be expressed as a matrix:

$$R=\left( {A,B,V} \right)=\left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} A&{{B_1}}&{\left( {{E_{{x_1}}},{E_{{n_1}}},{H_{{e_1}}}} \right)} \end{array}} \\ {\begin{array}{*{20}{c}} {}&{{B_2}}&{\left( {{E_{{x_2}}},{E_{{n_2}}},{H_{{e_2}}}} \right)} \end{array}} \\ \vdots \\ {\begin{array}{*{20}{c}} {}&{{B_n}}&{\left( {{E_{{x_n}}},{E_{{n_n}}},{H_{{e_n}}}} \right)} \end{array}} \end{array}} \right)$$

(13)

Where R is the evaluation level set matrix, $\:{C}_{i}(i=\text{1,2},\cdots\:,n)$is the evaluation indicator, $\:{E}_{{x}_{j}},{E}_{{n}_{j}}{,H}_{{e}_{j}}$is the numerical characteristics value of cloud model for the evaluation index $\:{C}_{i}$.

Numerical characteristics of the cloud model

According to the known value range of the corresponding grade of each risk evaluation index in Sect. 3.3, the numerical characteristics of the cloud model are calculated by Eq. (14). Then, MATLAB is applied to generate the standard cloud diagram of each evaluation index to make the evaluation results visualized. The calculated cloud digital features are shown in Table 4.

$$\left\{ {\begin{array}{*{20}{c}} {{E_{\text{x}}}=\frac{{{D_{\hbox{min} }}+{D_{\hbox{max} }}}}{2}} \\ {{E_n}=\frac{{{D_{\hbox{max} }} - {D_{\hbox{min} }}}}{6}} \\ \begin{gathered} \hfill \\ {H_{\text{e}}}=p{E_n} \hfill \\ \end{gathered} \end{array}} \right.$$

(14)

Where $\:{D}_{max}$、$\:{D}_{min}$ is the upper and lower limits of each grade interval, p is the fuzziness and randomness of the indicator, and 0.5 is taken in this paper.

Table 4 Numerical characteristics of cloud models for indicators at all levels in the evaluation of metro shield construction in metro tunnels.

Based on the cloud eigenvalues $\:{E}_{x}$, $\:{E}_{n}$ and $\:{H}_{e}$ in Table 4, a cloud diagram is generated using MATLAB as shown in Fig. 7. The horizontal coordinate of the cloud diagram indicates the score of the risk evaluation indicator, and the vertical coordinate indicates the affiliation degree of this risk indicator in different score ranges.

Fig. 7

Ranking cloud for risk evaluation indicators.

Calculation of composite affiliation degree and assessment of risk level

Replace the correlation degree between the object elements with the hierarchical affiliation degree of the indicator. MATLAB was used to generate normally distributed random numbers $\:{E}_{n}^{{\prime\:}}$ with $\:{E}_{n}$ as the expected value and $\:{H}_{e}$ as the standard deviation, and the deterministic value in the risk level to be tested is $\:{x}_{i}$. The rank affiliation degree corresponding to the cloud droplet $\:{x}_{i}$ was calculated from Eq. (15).

$${k_i}=\exp \left[ { - \frac{{{{({x_i} - {E_x})}^2}}}{{2{{(E_{{{n_i}}}^{\prime })}^2}}}} \right]$$

(15)

Where ($\:{x}_{i},{k}_{i}$) is the cloud droplets, this paper takes 2000 cloud droplets, in which $\:{x}_{i}$ is the value of the evaluation index, ${E_{{x_i}}}$is the variance, and $E_{n}^{\prime }$is the random number that obeys the normal distribution.

The cloud affiliation degree of the second-level indexes is normalized. The dynamic comprehensive weights are combined with that result of normalization to calculate the comprehensive judgment vector B, determining the comprehensive affiliation degree of the evaluation object.

$$B=\sum\limits_{{i=1}}^{m} {{V_i}} S$$

(16)

Where $\:{V}_{i}\:$is the set of dynamic, comprehensive weight vectors for each indicator, and$\:\:S$ is the extension cloud matrix composed of cloud correlations.

Calculate level variable eigenvalues

From the eigenvalues $\:{i}^{*}$ of the level variables, it is possible to determine the degree of bias of the actual risk level of the evaluation object towards the two neighboring risk levels.

$$\bar{k}_{{iv}} = \frac{{k_{{iv}} - \min \left( {k_{{iv}} } \right)}}{{\max (k_{{iv}} ) - \min \left( {k_{{iv}} } \right)}}$$

(17)

$${i^ * }=\frac{{\sum\nolimits_{{v=1}}^{5} {i \times \overline {{{k_{iv}}}} } }}{{\sum\nolimits_{{v=1}}^{5} {\overline {{{k_{iv}}}} } }}$$

(18)

Where $v=1,2,3,4,5$, $\:i$ is the level evaluation threshold, and $\:{i}^{*}$ is the eigenvalue of the level variable of the object to be evaluated.

Application

Engineering background

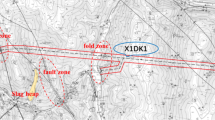
In this paper, the Qingdao Metro Line 8 submarine tunnel construction section between Dayang Station and Qingdao North Station is selected for risk assessment. The geology of Line 8 cross-sea section is complex and variable, with most of them being soft rocks, accompanied by medium-coarse sand layer, powdery clay layer and other weak strata⁷⁰. The construction section passes through nine fault fracture zones. The formation fissures of the faults located in the sea area are large, which are prone to mud escape and sea water reverse storage, and the construction is very difficult.

Calculation of indicator weights

Calculation of weighting

The G1 method is chosen to determine the subjective weights of the secondary indicators. This paper invites ten experts to rank the indicators and assign values. To neutralize the subjectivity of the experts’ ranking, the subjective weights of each group of data are computed by Eq. (3) and then averaged as the final subjective weights$\:{\:w}_{1}$ of the secondary indicators. According to the initial expert scoring data, the objective weight vector $\:{w}_{2}$ is calculated by Eq. (6).

Taking the reliability of B₆ Equipment Reliability as an example, the optimal linear combination coefficient $\:{\alpha\:}_{1}^{*}$=$\:{\alpha\:}_{2}^{*}$=0.5 is calculated using game theory Eq. (8). By substituting the weights of the subjective and objective factors and the optimal linear combination coefficient into Eq. (9), the comprehensive weight value of B₆ is determined to be 0.1329. From a data perspective, the game-theoretic results exhibit a bias toward objective weights, as the entropy weight method reveals risks that were underestimated by subjective judgments, thereby shifting the comprehensive weights toward the objective direction. Game theory prioritizes ensuring the true risks reflected in data while respecting expert experience through balanced allocation. The comprehensive weighting value $\:{w}^{*}$of the remaining secondary indicators is shown in Table 5.

Table 5 Constant and variable weights of evaluation indicators.

Variable weighting

The risk evaluation indicators were normalized according to the methodology presented in Sect. 3.5.2 and then subjected to variable weighting calculations. Among them, B₂ and B₈ belong to inverse type indicators, B₁、B_3 − 7 and B_9 − 19 belong to positive type indicators. And considering the balanced value of variable weights, at this time, $\:\alpha\:$ is taken to be 0.5, and $\:\beta\:$ is taken to be the edge of the medium risk interval. The variable weight vector is solved by Eq. (11), and the calculation results are shown in Table 5. In this study, a total of four different assignment methods, namely, the sequential relationship method (G1), the entropy weight method (EWM), the game theory combination weighting method (CWGT), and the variable weighting calculation are analyzed, and a comparison diagram is plotted as shown in Fig. 8.

Fig. 8

Comparison of weight values under different methods.

Calculation of single-indicator rank affiliation degree

The risk level of each indicator depends on their level of membership. Firstly, the average of the original scoring values of the secondary indicators is calculated, and the correlation between the secondary indicators and the evaluation level is calculated according to Eq. (15). The membership results are shown in Table 6.

Table 6 Rank affiliation degree for each level of the indicator.

Calculation of combined certainty

According to the dynamic optimal weight $\:{W}_{i}\left(X\right)$ of each indicator calculated in Sect. 4.2.2 and the single-indicator rank affiliation degree in Table 6, the comprehensive certainty degree of the evaluation object under different grades can be obtained from Eq. (16).Taking the human factors as an example, according to Eq. (16), the affiliation degree vector of A₁ is calculated as [0.0080,0.1838,0.2465,0.0008,1.9989e-14]^T. This factor belongs to the risk of class III, and similarly the rank degree of the rest of the first-level indicators can be obtained. MATLAB is used to calculate the integrated affiliation vector B=[0.0398,0.0439,0.24031,0.0608,2.3500e-09]^T of the evaluation project and the evaluation level. After then, by the principle of maximum affiliation degree, the risk level of evaluation project will be known.

Calculation of variable characteristic value

From the comprehensive affiliation degree vector B, the rank variable eigenvalue $\:{i}^{*}$ of the construction project is then calculated according to Eq. (17) and Eq. (18), which is used to judge the degree of bias of the object to be evaluated towards the two neighboring grades. After calculation, $\:{i}^{*}$=2.8369 is obtained. Based on the level variable characteristic values and the evaluation thresholds of each level, a comparison map of the evaluation cloud map and the level concept cloud map is generated by the forward cloud generator, which is shown in Fig. 9.

Fig. 9

Comparison of evaluation cloud map and hierarchical conceptual cloud map.

Discussion

WBS and RBS were employed to decompose the tunnel construction process and construction risks, respectively. The bottom-level decomposition factors were coupled to generate the WBS-RBS matrix in Fig. 5. The risk factors corresponding to each ‘1’ element in the matrix are as follows: W₁₄R₁₁, (W₂₁R₁₂, W₂₂R₁₂, W₂₄R₁₂, W₂₅R₁₂, W₃₃R₁₂), and (W₁₄R₁₃, W₂₉R₁₃), meaning that workers are unqualified to operate, there are violation operation in their tunnelling process and they are lack of safety awareness; (W₁₁R₂₁, W₂₄R₂₁, W₂₆R₂₁, W₂₈R₂₁), W₂₆R₂₂, and (W₂₆R₂₃, W₂₈R₂₃), representing complex geological conditions; (W₂₆R₃₁, W₂₈R₃₁, W₃₂R₃₁), W₁₃R₃₂, and (W₁₂R₃₃, W₂₂R₃₃, W₂₈R₃₃), suggesting machinery failure or improper equipment usage; (W₁₄R₄₁, W₁₅R₄₁), W₁₄R₄₂, and W₂₆R₄₃, reflecting poor site management; (W₂₆R₅₁, W₂₈R₅₁), W₁₅R₅₂, and (W₂₃R₅₃, W₂₆R₅₃, W₂₈R₅₃, W₃₁R₅₃), demonstrating inadequate emergency plans.

This study integrates variable weight theory with extension cloud theory to comprehensively account for uncertainties in the construction process, thereby achieving dynamic risk assessment. Fig. 8 demonstrates the differences in indicator weights calculated using various assignment methods. The results reveal significant discrepancies between subjective and objective normal weights for certain indicators. Through game theory-based deviation minimization, an optimal balanced comprehensive normal weight is obtained. Following variable weight processing, the dynamic weights exhibit the following characteristics: (1) Most indicators demonstrate reduced weights compared to their fixed counterparts; (2) Indicators B₈, B₉, and B₁₅ maintain equivalent values between variable and fixed weights; (3) Indicator B₁₃ displays an increased variable weight relative to its fixed weight. The variable weight theory effectively mitigates weight imbalance phenomena, yielding more rational weight distributions. The dynamically optimized comprehensive weights follow this descending order: B₆ (0.1528) > B₉> B₁₈> B₇> B₄> B₁₃> B₃> B₁₁> B₁> B₁₇> B₁₄> B₅> B₁₂> B₁₆> B₁₀> B₂> B₁₉> B₈> B₁₅. Notably, B₆ (Equipment Reliability) possesses the highest weight, followed by B₉ (Hydrogeological Factors).

Fig. 10

(a) Distribution of affiliation degree and risk level maps for each secondary indicator; (b) Distribution of affiliation degree and risk level maps for each level of indicator.

The affiliation degree distribution of the secondary indicators is shown in Fig. 10(a), where the horizontal coordinates are the secondary evaluation indicators of the risk of metro shield construction in metro tunnels, and the vertical coordinates are the distribution of the basic certainty degree of different indicators. The risk level of each index can be seen according to the longitudinal distribution and color of the membership scatter of each index. Combined with Table 6, it is concluded that the risk level of the three indicators B₆, B₉ and B₁₃ is IV, which belong to the higher risk. So they need to be focused on. B_3 − 5, B₈, B_{10 − 12}, B_{14 − 19} belong to the III level of risk, which are unlikely to occur but still need to be paid attention to them. Figure 10 (b) shows the distribution of the affiliation degree of the first-level indicators, from which it can be seen that the first-level indicators in the III-level risk account for the majority. After calculation, the affiliation degree vector of A₁ is [0.0080 0.1838 0.2465 0.0008 1.9989e-14] ^T, the affiliation degree vector of A₂ is [0.1527 0 0.0028 0.0858 0] ^T, the affiliation degree vector of A₃ is [0 0.0012 0.1331 0.0254 0] ^T, the affiliation degree vector of A₄ is [0 0 0.2048 0.2927 0] ^T, and the affiliation degree vector of A₅ is [0 0 0.4263 0 0] ^T. Among them, A₂ is a level I risk indicator, A₁, A₃, and A₅ belong to the level III risk indicator, and the management factor of A₄ is a level IV risk indicator, i.e. higher risk. The construction unit must focus on establishing and implementing the safety education management system to reduce the risk of loss.

Based on the membership degree of each index, the membership degree is transformed into the overall certainty degree of construction project risk. According to the principle, the comprehensive risk assessment grade of Qingdao Metro Line 8 undersea tunnel shield construction is III. In Sect. 4.5, $\:{i}^{*}$=2.8369 is calculated. Combined with Fig. 9, it can be seen that the risk of the evaluation object belongs to grade III, and it is towards grade III, which is in a stable state. As Qingdao Metro Line 8 summarizes the construction experience of Line 2, Line 3, and Line 13, and adds many safety measures to greatly reduce the construction risk, the evaluation results are in line with the actual safety level of the project.

Conclusion

• (1) Based on a review of metro construction literature and practical considerations, the construction process using the shield method was decomposed into three first-level stages: the preparation stage, the tunneling stage, and the shield arrival stage, along with 17 second-level work breakdown structures. According to the literature and experts’ experience, five major risk categories of people, materials, environment, management, and contingency are gotten, and refined them into 15 risk factors, based on which the risk evaluation index system of Metro Shield construction is established.

• (2) Based on the variable weight theory, the game combination of the G1 method and the entropy weight method of constant power is dynamically adjusted to avoid weight imbalance. Preliminarily, the indicators that affect the safety of metro shield construction are safety knowledge of personnel, equipment reliability, hydrogeological factors, safety education, and contingency factors. In that, the combined fixed weight of equipment reliability is 0.1533, which is changed to 0.1528 after dynamic correction. However, it is still the maximum weight value, so the equipment reliability still needs to be focused on.

• (3) The improved extension cloud model is used to assess the construction risk of Qingdao Metro Line 8 cross-sea interval. Finally, the mechanical equipment is a level I risk indicator, and the management factors are the IV level risk indicator, which indicates that the mechanical equipment has negligible impact on the construction of metro shield and the management factors have the largest impact on it. By the principle of maximum affiliation degree, the risk level of the evaluation project is III, which belongs to medium risk. The eigenvalue of the variable for the assessed project is 2.8369, indicating that the risk level of the assessed project is at the level of III and is biased towards level III, with no tendency to change to other levels.

This paper constructs a risk evaluation model for metro shield construction based on game-variable weight extension cloud theory. This model is of great significance for clarifying construction risk and taking effective measures to prevent accidents. Based on the research, the early warning function can be integrated according to the risk evaluation level to ensure construction safety better.