Introduction

With a material composition gradation spanning six orders of magnitude, debris flow is primarily a high-concentration, wide-graded, multi-phase, inhomogeneous fluid that is created by heavy rainfall or snowmelt. Its formation and movement process are extremely complex, frequently involving rapid mobility, strong impact, and sudden erosion of mountainous environments, which has a strong destructive effect and is challenging to manage1. Thus, it is crucial for early warning systems and debris flow disaster prevention to predict the spatial probability of debris flow occurrence through debris flow susceptibility evaluation studies. This is also a challenging and popular research topic. With the intensification of extreme weather in recent years2, the situation of debris flow disaster in China, which is already severe, has become more and more serious. It is also more challenging to precisely assess and evaluate debris flow susceptibility using conventional techniques, so knowing how to appropriately characterize debris flow susceptibility is crucial in this situation.

The expert scoring method, hierarchical analysis method, fuzzy comprehensive judgment method, weighted information entropy method, and multiple regression method are some of the traditional techniques frequently used in the evaluation of debris flow susceptibility3,4,5,6,7,8,9,10,11. Factor weights can be determined in two ways: first, using the expertise of the factors to allocate weights; second, using the expertise in conjunction with mathematical and statistical analysis techniques to derive factor weights. The fundamental idea behind both approaches is to evaluate the susceptibility of debris flows by calculating the factor weights. Nevertheless, due to the limitations of expertise, these approaches have limited applicability and are challenging to implement broadly in various geographic contexts12. For a considerable amount of time, this approach has been crucial, particularly in situations where data are scarce and technological resources are inadequate. However, because extreme weather events occur frequently and debris flows suddenly and quickly, traditional methods are frequently slow to react to disasters in real time and do not offer enough timely and accurate predictions. In recent times, machine learning algorithms have also become more popular for use in determining debris flow susceptibility. Convolutional neural networks, decision trees, random forests, artificial neural networks, and support vector machines have all been effectively used in the analysis of geologic hazards13,14,15,16,17,18. Both traditional assessment methods and disaster prediction accuracy can be greatly enhanced by machine learning models19. A single machine learning algorithm might not be able to sufficiently capture the best-fit function of the sample set in the hypothesis space or the real distribution due to the limited and extremely complex training data for the debris flow prediction problem, which would affect the prediction accuracy20. Consequently, by combining the benefits of several models, ensemble learning enhances prediction performance even more21. The primary techniques used in ensemble learning are Bagging (e.g., Random Forest), which trains several models of the same kind and averages or votes their outputs to lower the variance and overfitting risk of a model, and Boosting (e.g., Extreme Gradient Boosting), which builds upon the accuracy and stability of a model through iterative training to target the inaccurate predictions of the preceding model cycle; Stacking, in contrast, integrates various base model types and leverages a meta-model to learn from these base models’ outputs in order to achieve a more robust integrated prediction capability22. Ensemble learning improves the robustness and interpretability of geohazard prediction while also reducing bias and variance and handling intricate interactions between various features.

The training set for ensemble learning techniques typically includes a sizable percentage of both non-mudslide events (negative samples) and mudslide events (positive samples)23. When it comes to debris flow susceptibility assessment, researchers typically pay little attention to the negative samples that won’t occur in a disaster and instead concentrate only on the positive samples that have occurred or will occur in various investigations24. The negative samples needed for modeling were frequently selected at random from unlabeled samples in earlier research25,26. The irrational negative sample acquisition strategy is one of the primary sources of noise in the dataset due to this approach’s treatment of high-quality positive samples equally with negative samples from potentially noisy data27,28. This frequently results in issues like model overfitting. As a result, one of the main areas of focus for machine learning research is how to optimize the sample pool to enhance model performance. 2019 Zhu et al. presented a buffer zone control-based sampling technique that allows negative samples to be taken from outside the buffer zone. This technique is based on the fundamental idea that the area surrounding a disaster site is similar to the geoenvironmental conditions that caused the disaster29. In 2021, Liang et al. suggested a different sampling strategy based on buffer zone control, in which negative samples can be drawn from outside the buffer zone by first creating an initial susceptibility map, and in order to enhance the performance of the model, negative samples can then be chosen from the samples with the lowest susceptibility rank30. The interference of noisy data on the model can be greatly decreased by enhancing the negative sample selection strategy, which will further enhance the use of machine learning in the assessment of debris flow susceptibility. This enhances the model’s usefulness in practice and offers a wider outlook for debris flow hazard prediction.

Active seismic zones frequently affect the complex natural geologic structure of the upper Minjiang River region, and the area frequently experiences mudslide disasters due to the mountainous area’s delicate ecological balance. In order to assess the debris flow susceptibility in the study area, this paper takes into account the complex natural geographic conditions of the area and combines with the actual situation. It then determines 14 evaluation factors, including area, gully density, roundness, Melton ratio, lithology, distance from road, distance from fault, aspect, NDVI, SPI, TWI, rainfall, land use type, and curvature. Finally, it uses the Spy Technique to construct dependable non - debris flow samples and adopts the ensemble learning model to assess the susceptibility of debris flow in the upper Minjiang River basin based on the watershed unit as the evaluation unit. The evaluation results can serve as a basis for future debris flow disaster prevention and control in the area. In addition, the integration of the SPY technology and the integrated learning method in this paper has opened up a new path for similar studies in complex geological regions. In the future, continuous exploration will be carried out focusing on the optimization of the model structure and the improvement of prediction accuracy, which will contribute to the development of the technology for evaluating debris flow disasters.

Study area

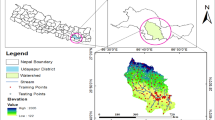
The coordinates of the Upper Minjiang River basin are 30°45’37 “N − 33°69’35 “N and 103°33’46 ‘E − 104°10’36 “E. In the Aba Tibetan and Qiang Autonomous Prefecture of Sichuan Province, the basin includes the counties of Wenchuan, Mao, and Songpan. The Minjiang River’s upper reaches are situated in an alpine canyon zone that is typical of the Sichuan Basin and the eastern edge of the Tibetan Plateau. The elevation changes sharply from 750 m to 5200 m over a 40–50 km horizontal range, with notable variations in surface relief. This area is mainly exposed in Paleozoic and Mesozoic clastic and carbonate rocks, mainly composed of sandstone slate, schist, shale, dry sandstone, marble and metamorphic rocks, which are extremely broken. The region is also in the western Sichuan trench area, which has seen numerous tectonic movements that have left behind fractured geological formations and shaky foundations. Additionally, summers are frequently marked by heavy rainfall due to the influence of the monsoon climate. This uneven distribution of precipitation increases the risk of natural disasters like debris flow. The Minjiang River, a significant tributary of the Yangtze River’s upper reaches, serves as the study area’s principal river. With a watershed area of 7326 km2, the upper reaches of the Minjiang River in the study area span approximately 295 km. The main stream can be separated into the northern, middle, and southern sections from the upper reaches to the lower reaches based on the longitudinal profile characteristics of the main stream channel (Fig. 1).

Fig. 1
figure 1

Geographic location of the upper Minjiang River region and the distribution of debris flow basins. Created by ArcGIS Pro 3.0.1 https://www.esri.com/en-us/arcgis/products/arcgis-pro/overview.

Full size image

Data and research methodology

Data

Debris flow dataset

The debris flow susceptibility evaluation model is built using the debris flow dataset, which aids in locating the occurrence of debris flow and determining the correlation between debris flow occurrence and indicator factors. Remote sensing images clearly show the geomorphological characteristics of debris flow, which can be specifically identified as the debris flow formation area, circulation area, and accumulation area31. This paper therefore makes use of the upstream 2021 Gaofen-2 satellite imagery of the Minjiang River, field research, and other methods. The base map of the map is combined with the DEM data obtained from the Chinese Academy of Sciences’ Resource and Environmental Science and Data Center (https://www.resdc.cn/) with a resolution of 12.5 m x 12.5 m. A total of 113 debris flow events were interpreted within the study area.

Evaluation factor

In accordance with the circumstances surrounding the formation of debris flow in the sub-watershed, fourteen evaluation factors were chosen from five categories of topography and geomorphology, rainfall, geology, vegetation cover, and human activities. (1) Topographic and geomorphologic data, based on the DEM data with a spatial resolution of 12.5 m in the study area, were extracted by Arcgis10.8 to obtain the watershed area, gully density, roundness, Melton ratio, slope direction, curvature, and hydrological processing to obtain the streamflow power index (SPI) and topographic wetness Index (TWI) of the watersheds; (2) Rainfall data, which were obtained through Arcgis10.8 cropping of the average annual rainfall in Sichuan Province (National Meteorological Science Data Center) to get the average annual rainfall vector data in the study area; (3) geomorphology: from the Chinese Academy of Sciences Resources and Environment Science and Data Center (http://www.resdc.cn/) to obtain the study area faults and stratigraphic rock body data, through the coordinate transformation to get the distance from the faults, the stratigraphic rock body data; (4) Vegetation cover data, the Landsat8 near-infrared and far-infrared bands with a resolution of 30 m in August 2024 were selected to obtain the normalized difference vegetation index (NDVI); the vector data of land use types in the study area were obtained by cropping the global 30-meter surface cover data (http://www.globeland30.org/home/background.aspx); (5) human activity, the 2021 Gaofen-2 satellite image was used to extract information about the study area’s roads and as well as the distance from each road.

Fig. 2
figure 2

Debris flow watershed factor classification map.

Full size image

Methodology

Evaluation units

A suitable choice of evaluation units, which typically includes raster units, slope units, special condition units, and watershed units, is essential for geohazard susceptibility modeling32,33,34,35. The watershed unit is capable of encapsulating the geometric properties of debris flows and elucidating their correlation with associated indicators, among other things36. Thus, the chosen watershed unit serves as the primary research foundation for this work, and the 12.5 m DEM data of the research unit is delineated using the hydrological processing method of ArcGIS10.8. In hydrological analysis, the selection of thresholds is essential for the delineation of watershed units. Thresholds are typically used in hydrological processing methods to identify accumulation areas within a watershed. By setting an appropriate threshold, the accumulation areas can be accurately delineated, ensuring the avoidance of excessive subdivision or oversimplification of watershed units. The study’s findings indicate that the ideal threshold is 5000 through threshold selection. The final study area was defined in 226 sub-watershed units using the Gaofen-2 satellite images. As shown in Fig. 1.

A total of fourteen index factors were discretized based on the watershed unit using the regional statistics function of the ArcGIS 10.8 software. The values of the corresponding factors in the watershed unit were averaged for area, gully density, roundness, Melton ratio, distance to road, distance to fault, NDVI, SPI, TWI, rainfall, and curvature. The most frequent values within the watershed unit were used to determine the values of stratigraphic rocks and land use types. As illustrated in Fig. 2, the spatial resolution was unified to 12.5 m×12.5 m after all raster layers were reclassified using the natural discontinuity method.

Ensemble learning

Multiple base learners are employed in ensemble learning, and a unifying approach is used to aggregate their findings for regression or classification tasks. Generally, ensemble learning exhibits better overall performance in terms of generalization than individual learners. Ensemble learning can be divided into three main categories: serial-sequence methods, where the base learners exhibit significant interdependencies, such as Boosting, exemplified by XGBoost; parallel methods, where there are no substantial dependencies between the base learners, like Bagging, symbolized by Random Forest; and Stacking, which combines the outputs of diverse types of base learners37.

The Random Forest (RF) algorithm builds multiple classifiers and combines their predictions to increase overall prediction accuracy. A subset of the available features is randomly selected during the construction of each decision tree, thereby assisting in the reduction of overfitting. Several subsets are randomly selected from the original dataset to serve as training sets, and for each training set, a decision tree is built using a random subset of features38. The training set is used to train each decision tree until the stopping condition is met. Voting or averaging is used to determine the classification or regression results of the final predicted values when predictions are made for new data. The training results of each decision tree are combined based on the Bagging integration concept39.

Based on Gradient Boosting Decision Tree (GBDT), Extreme Gradient Boosting Tree (XGBoost) is an enhanced optimization algorithm40. XGBoost and GBDT are similar in that they are both serial serialization algorithms based on the concept of Boosting integration. Based on the residuals between the previous decision tree and the actual value of the prediction results for the decision tree’s training, they fit the residuals through a number of iterations to continuously approximate the actual value until they reach the set value or the number of iterations after the training ends. The final prediction of this sample in the entire integrated model is determined after the weighted and summed individual decision tree results are forecast. The distinction is that, in solving the loss function, XGBoost employs Taylor’s second-order expansion to streamline the calculation and adds regular terms, like L1 and L2, to the objective value to manage the model’s complexity and avoid overfitting41. The XGBoost algorithm has greater computational efficiency and the ability to prevent overfitting when compared to the conventional GBDT algorithm42.

By combining multiple learning models and using their predictions as inputs, the stacking principle aims to train a meta-learner to make final predictions. The fundamental idea of stacking, in contrast to bagging and boosting, is to use a new model to learn how to efficiently integrate predictions from other models. The basic steps are as follows: first, train multiple base models (e.g., Random Forest, Extreme Gradient Boosting Tree, and Linear Regression) on the original dataset; second, create a new dataset using the predictions of these base models as new features; and third, train a meta-model on the new dataset to produce the final prediction. By using this method, stacking can improve overall prediction performance and generalization ability by fully utilizing the benefits of each base model43,44. Figure 3 illustrates the stacking modeling procedure used in this work.

Fig. 3
figure 3

stacking modeling flowchart.

Full size image

Spy technology

A negative sample acquisition strategy based on the SPY technique is as follows: First, a predetermined percentage (15% in this paper based on prior research) of debris flow samples are chosen and fed into the unlabeled samples. These samples will be treated as spy samples along with the unlabeled samples in order to train a classifier to predict all the samples. The lowest probability of the spy samples is used as the value, and the probability value is lower than the samples with the threshold value are considered as reliable negative samples45. The main premise of this approach is that reliable negative samples can be filtered out by looking at the probability threshold of the spy samples, and that spy samples and potential debris flow samples in unlabeled samples will behave similarly in the classifier’s prediction.

Model accuracy evaluation

(1) Accuracy, precision, recall and F1 score.

The process of assessing debris flow susceptibility involves validating and evaluating the model’s performance. A confusion matrix is typically used to evaluate a binary classification model’s performance46. Four parameters comprise the confusion matrix: True Positive (TP) represents the number of debris flow that the model predicts to be mudslides and that are actually mudslides; False Negative (FN) represents the number of non-mudslides that the model predicts to be mudslides but that are actually mudslides; False Positive (FP) represents the number of mudslides that the model predicts to be mudslides but are actually non-mudslides; True Negative (TN) is the number of mudflows that the model predicts to be non- mudslides but are in fact mudslides. Based on this, four statistical metrics (accuracy, precision, recall, and F1 score) were used to assess each model’s performance. Each metric’s description is displayed in Table 1.

Table 1 Model accuracy evaluation indicators.
Full size table

The True Positive Rate (TPR) and False Positive Rate (FPR), which show how well the model performs at various classification thresholds, are represented on the vertical and horizontal axes, respectively, of the ROC curve. The percentage of samples that are wrongly predicted to be positive is known as the False Positive Rate, while the percentage of samples that are correctly predicted to be positive is known as the True Positive Rate. The model performs better the closer the ROC curve is to the upper left corner47. The Area Under the Curve (AUC) value, which offers a thorough evaluation of the model’s performance, is the area under the ROC curve. When the AUC value is 0, the model’s predictions represent perfect misclassification, meaning the predictions are completely opposite to the actual outcomes. In such a case, reversing the predictions would result in a perfect model. In contrast, an AUC value of 0.5 indicates random guesswork, where the model cannot distinguish between positive and negative samples. On the other hand, an AUC value of 1 reflects perfect discrimination between positive and negative samples. The closer the AUC value is to 1, the better the model performs in terms of prediction.

Research process

Figure 4 shows a schematic representation of the technical route flow for this study.

Fig. 4
figure 4

Schematic diagram of the technology route flow.

Full size image

Debris flow susceptibility analyses

Correlation analysis of indicators for evaluating susceptibility to debris flow

In order to select the evaluation factors with the most predictive ability and to improve the accuracy of model prediction, correlation analysis was performed on the 14 factors initially selected. The matrix of correlation coefficients between the 14 influencing factors can be obtained and visualized to create Fig. 5 using the Correlation Plot plug-in of Origin plotting software. In the graph, negative correlations are displayed in blue, and positive correlations are displayed in red. The image’s size and the correlation coefficient’s magnitude are directly correlated. The figure illustrates that all evaluation factors have correlation coefficients that are less than 0.54. The weaker correlation coefficients suggest that factor interactions are smaller and the evaluation factors that were chosen are more rational.

Fig. 5
figure 5

Correlation analysis of debris flow evaluation factors.

Full size image

Multi-Collinearity test

In a regression model, multicollinearity is defined as a strong linear relationship between independent variables. In addition to making it challenging to distinguish between the various effects on the dependent variable, this circumstance may raise standard errors and cast doubt on the regression coefficients. Typically, the variance inflation factor (VIF) and tolerance (TOL) are used to evaluate the covariance between variables. A high correlation or lack of precision between the variables is indicated when the VIF is less than 5 and the TOL is greater than 0.2, respectively; the opposite suggests that an issue exists. The chosen evaluation factors for multiple covariance are analyzed using SPSS 27 software in this paper (Table 2). The minimum value of TOL in the indicator system is 0.304, and the maximum value of VIF is 3.290, and the results demonstrate that there is no covariance issue in the indicator factor system, further confirming the rationality of the evaluation factors that were chosen.

Table 2 Analysis of factor covariance in debris flow watersheds.
Full size table

Model construction

The debris flow susceptibility assessment problem became a dichotomous problem when watersheds experiencing debris flow events were labeled as ' 1 ' and watersheds not experiencing debris flow events were labeled as ' 0 ‘, in accordance with the classification requirements of the ensemble learning model48. A sample dataset with an equal number of positive and negative samples was created by taking the 113 watersheds that had experienced debris flow out of the 226 sub-watershed units in the study area and another 113 watersheds that had not. In the process of constructing the sample dataset into a training set and a test set, a reasonable allocation of the division ratio is crucial, because an unreasonable division ratio may significantly affect the precision and accuracy of the model. As a result, the base dataset is split with reference to the studies in related literature, with 70% going toward the training set and 30% going toward the test set. This division strategy not only maintains sample balance but also gives the ensemble learning model for debris flow susceptibility assessment a solid foundation for training and testing, enhancing the model’s capacity for generalization and prediction accuracy49.

In accordance with the research methodology for ensemble learning suggested in 2.2.2, in this paper, we select RF model based on Bagging integration idea, XGBoost model based on Boosting integration idea, and construct Stacking-RF and Stacking-XGBoost models based on Stacking integration idea with RF and XGBoost as the base model and RF and XGBoost as the meta-model respectively.

Following the suggested SPY debris flow negative sample collection strategy outlined earlier, the process of obtaining trustworthy negative samples for our base dataset can be broken down into two stages: (1) Designate 15% of the debris flow samples as spy samples and non-mudflow samples to create a negative sample pool. This collection contains 129 samples in our analysis, with the remaining 85% of the samples serving as debris flow positive samples (consisting of 97 samples). By integrating RF, XGBoost, Stacking-RF, and Stacking-XGBoost models, we assign a probability value to each sample within the study area. (2) Identify the lowest probability associated with the spy samples, and all samples with probabilities lower than this threshold are deemed reliable negative samples. The probability thresholds derived from the RF, XGBoost, Stacking-RF, and Stacking-XGBoost models for spy sample prediction are 0.294, 0.228, 0.23, and 0.05, respectively. Consequently, all samples in the study area below these probability thresholds are recognized as reliable negative samples. To maintain balance, an equal number of positive samples are randomly selected from the pool of mudflow positive samples, resulting in the creation of the base dataset for SPY-RF, SPY-XGBoost, SPY-Stacking-RF, and SPY-Stacking-XGBoost models in equal proportions, as shown in Table 3. Ultimately, this base dataset is split into a 70% training set and a 30% test set, which are utilized for the training and testing of the constructed debris flow susceptibility assessment ensemble learning models.

Table 3 Model-Specific dataset size and sample composition based on spy technique.
Full size table

Debris flow susceptibility mapping

Following the development of the ensemble learning principle-based debris flow susceptibility model, the model was used to determine the debris flow susceptibility index for each watershed unit in the study area. As illustrated in Fig. 6, the debris flow susceptibility index was divided into five grades based on the natural breakpoint method in ArcGIS 10.8 software. These grades are very low, low, moderate, high, and very high in that order. The debris flow susceptibility grading map in the study area demonstrates that the range of very high susceptibility zones that actually occur and the mudslide susceptibility zones derived based on the SPY-RF model are roughly consistent. This outcome offers a crucial foundation for managing the risk of debris flow and further validates the model’s validity.

Fig. 6
figure 6

Debris flow susceptibility grading map.

Full size image

The evaluation results of debris flow susceptibility can also be analyzed using statistical methods. Table 4 analyzes the number of watershed units in each model’s debris flow susceptibility level, the area occupied by each level, and the corresponding debris flow events. It calculates the ratio between the proportion of debris flow events in each susceptibility level and the corresponding area proportion. Debris flow density is defined as the ratio of the number of debris flow events in each susceptibility level to the corresponding area. Figure 7 presents the statistical results of debris flow susceptibility for each model. From Table 4; Fig. 7, the distribution characteristics and density differences of debris flows within each susceptibility level can be observed.

For the RF model, the area of high susceptibility regions is 2135.76 km², with a debris flow density of 2.20; for very high susceptibility regions, the area is 1829.57 km², with a density of 2.40. The SPY-RF model shows a high susceptibility area of 1374.51 km² and a density of 1.38; the very high susceptibility area is 2893.50 km², with a density of 2.49. For the Stacking-RF model, the high susceptibility area is 1029.02 km², with a density of 1.26; the very high susceptibility area is 4251.15 km², with a density of 2.02. The SPY-Stacking-RF model has a high susceptibility area of 574.69 km², with a density of 1.22; the very high susceptibility area is 3519.44 km², with a density of 2.02. The XGBoost model shows a high susceptibility area of 3641.39 km², with a density of 2.11; the very high susceptibility area is 781.48 km², with a density of 2.30. The SPY-XGBoost model has a high susceptibility area of 765.18 km², with a density of 1.96; the very high susceptibility area is 4832.82 km², with a density of 1.61. For the Stacking-XGBoost model, the high susceptibility area is 444.00 km², with a density of 1.35; the very high susceptibility area is 4804.30 km², with a density of 1.96. Finally, the SPY-Stacking-XGBoost model has a high susceptibility area of 66.51 km², with a density of 3.01; the very high susceptibility area is 3568.33 km², with a density of 2.21.

Overall, the SPY-RF model performs better across different risk levels and exhibits the highest debris flow density in extremely high susceptibility areas. This model can more comprehensively reflect the debris flow risk across various susceptibility levels, making it suitable for a wider range of application scenarios. It is not only adept at precise predictions focused on high-risk areas but also demonstrates higher sensitivity and predictive capability in low-risk regions.

Table 4 Different modelled debris flow susceptibility classes and characteristics of debris flow distribution.
Full size table
Fig. 7
figure 7

Debris Flow Vulnerability Statistical Chart.

Full size image

Model accuracy verification

In accordance with the prior research methodology, this study builds 70% of the training dataset and 30% of the testing dataset using a 7:3 sample dataset. As demonstrated in Table 5 and Figure.8, the model performance metrics accuracy, precision, recall, and F1 score were computed based on the counts of TP, FN, FP, and TN, respectively.

Table 5 Accuracy of each integrated learning model.
Full size table
Fig. 8
figure 8

Model performance metrics.

Full size image
Fig. 9
figure 9

ROC curves for each integrated learning.

Full size image

In the model accuracy validation, the overall performance of SPY-RF surpasses that of other models. While RF excels in recall, the high accuracy, precision, and F1 score of SPY-RF make it more advantageous for practical applications. Although RF can identify all susceptibility areas, the comprehensive advantages of SPY-RF indicate that it can provide more balanced and reliable evaluation results in real-world applications.

The ROC curve of the debris flow susceptibility evaluation model based on ensemble learning is shown in Fig. 9. The AUC value of the SPY-RF model is 0.93, slightly higher than that of the SPY-XGBoost model, which is 0.92. Considering the performance of the aforementioned ensemble learning models in debris flow susceptibility evaluation, the SPY-RF model is the best. Therefore, the subsequent analysis will utilize the evaluation results of the SPY-RF model to examine debris flow susceptibility and the contribution rates of the evaluation factors.

Analysis of the contribution rates of debris flow evaluation indicators

Based on the Random Forest model, the contribution rates of different factors influencing debris flow susceptibility were generated using the feature_importances function in Python software. The calculation is expressed in Eq. (1):

$$\:\begin{array}{c}I{P}_{i}=\frac{I{P}_{i}}{\sum\:_{i=1}^{N}\:I{P}_{i}}\#\left(1\right)\end{array}$$

In the equation: \(\:I{P}_{i}\)—— Contribution rate of the \(\:i\)th factor;

The analysis results of the contribution rates of debris flow evaluation indicators in the study area indicate that, as shown in Fig. 10, the four factors with the highest contribution rates to debris flow susceptibility are SPI, rainfall, curvature, and watershed area, with contribution rates of 0.21, 0.18, 0.09, and 0.09, respectively. In contrast, factors with lower contribution rates include land use type, slope aspect, distance from faults, and rock mass.

Fig. 10
figure 10

Debris Flow Basin Factor Contributions.

Full size image

Discussion

This study selects the RF model based on Bagging ensemble ideas, the XGBoost model based on Boosting ensemble ideas, and constructs Stacking models using RF and XGBoost as base models, namely Stacking-RF and Stacking-XGBoost, for mapping debris flow susceptibility in the upper Minjiang River Basin. The results indicate that high susceptibility areas are consistent with previous studies16;50;51. A comparison of model accuracy shows that the SPY-RF model performs better across different risk levels and exhibits the highest debris flow density in very high susceptibility areas. This model can more comprehensively reflect the debris flow risk across various susceptibility levels, making it suitable for a wider range of application scenarios. Previous methods for studying debris flow susceptibility largely relied on traditional statistical analyses or single machine learning algorithms. However, given the suddenness and rapidity of debris flow events, these methods often appear lagging in responding to emergencies, lacking sufficient accuracy and timeliness52,53,54. Additionally, due to data scarcity and complexity in debris flow predictions, single machine learning models often fail to capture the underlying patterns in the data, affecting prediction outcomes. In contrast, ensemble learning effectively integrates multiple algorithms, addressing complex interactions between features, reducing model bias and variance, thereby enhancing robustness and interpretability. By combining the predictions of multiple base models, ensemble learning provides a more reliable basis for decision-making. Thus, ensemble learning plays a crucial role in debris flow prediction, offering significant support for the early warning and prevention of geological disasters.

In the research on debris flow susceptibility evaluation, researchers typically focus on positive samples that have occurred or are likely to occur, while paying less attention to negative samples where disasters are not expected55,56,57. This study employs SPY technology to select reliable negative samples and constructs a foundational dataset for debris flow susceptibility evaluation. As shown in Table 4; Fig. 7, the SPY-XGBoost model can more accurately identify debris flow events in very high susceptibility areas compared to the XGBoost model, significantly reducing the likelihood of non-susceptible areas being misclassified as susceptible, thereby enhancing the reliability of risk assessment. Moreover, the model based on SPY technology outperforms the original model in terms of accuracy, precision, recall, and AUC value. This performance improvement is attributed to the advantages of SPY technology in negative sample selection and feature extraction, allowing the model to more precisely distinguish between susceptible and non-susceptible areas. Additionally, SPY technology enhances the representativeness of the dataset, improving the model’s learning capability, which further increases overall predictive reliability. These results further validate the effectiveness of using SPY technology for debris flow susceptibility assessment, providing important theoretical support for future research.

Stacking is an ensemble learning method that improves overall model performance by combining the predictions of multiple base learners. The fundamental idea is to train different types of models on the same dataset, and then use the outputs of these models as new features input into a higher-level model for final predictions58. In this study, Stacking models were constructed based on RF and XGBoost as base models, with RF and XGBoost serving as meta-models for Stacking-RF and Stacking-XGBoost, respectively. The results indicate that both Stacking-RF and Stacking-XGBoost models do not perform well. Several reasons may contribute to this finding: the output features of the base learners may exhibit high correlation, preventing the meta-model from extracting new information. The meta-model requires a sufficiently diverse set of features to learn effectively. If the output features of the base learners are similar, the learning effectiveness of the meta-model may be limited. Additionally, the insufficient number of debris flow data samples results in a small training dataset, making it challenging for the meta-model to learn effective combination patterns, which leads to a decline in performance. Therefore, in future research, it is important to select multiple base models based on feature and data types, considering the strengths and weaknesses of different algorithms, such as logistic regression, support vector machines, and KNN. Alternatively, more complex meta-models, such as neural networks, could be employed to ensure diversity among the models, aiming for improved predictive performance.

In the analysis of the contribution rates of debris flow evaluation indicators in this study, the SPI has the highest contribution rate, indicating that water flow intensity plays a crucial role in the occurrence of debris flows, as strong water flow can exacerbate soil erosion and the formation of debris flows. The contribution rate of rainfall follows closely, demonstrating the direct impact of rainfall on debris flow occurrence. Curvature and watershed area also significantly influence debris flow susceptibility, particularly as curvature reflects the effect of terrain undulation on debris flows, while watershed area affects the scale of water flow convergence. However, factors with lower contribution rates include land use type, slope aspect, distance from faults, and rock mass. The low contributions of land use type and slope aspect may relate to the relative uniformity of these factors in the study area or the prominence of other factors influencing debris flow occurrence. The contribution rates of distance from faults and rock mass are the lowest, suggesting that in this specific study area, the spatial distribution of faults and rock mass may not have formed significant patterns of debris flow susceptibility. If the occurrence of debris flows in the study area is primarily influenced by factors such as rainfall and topography, and the distribution of faults and rock mass does not exhibit clear impact characteristics, their contribution rates are naturally low. This analytical result provides important evidence for the selection and application of influencing factors in future research.

Conclusion

This study uses watershed units as evaluation units and proposes SPY technology to construct reliable non-debris flow samples. It employs the Random Forest (RF) model based on Bagging ensemble ideas, the XGBoost model based on Boosting ensemble ideas, and constructs Stacking models using RF and XGBoost as base models, with RF and XGBoost serving as meta-models for Stacking-RF and Stacking-XGBoost, respectively. The evaluation of debris flow susceptibility in the upper Minjiang River Basin, combined with watershed evaluation factors, yielded the following results:

  1. (1)

    This study establishes a debris flow susceptibility evaluation model for the Upper Minjiang River Basin, incorporating hyperparameter tuning and negative sample optimization. The AUC values for the RF, SPY-RF, XGBoost, SPY-XGBoost, Stacking-RF, SPY-Stacking-RF, Stacking-XGBoost, and SPY-Stacking-XGBoost models were 0.82, 0.93, 0.72, 0.87, 0.80, 0.92, 0.71, and 0.90, respectively. The SPY-RF model outperforms others across various risk levels, providing a more comprehensive representation of debris flow risk. Models utilizing SPY technology consistently perform better than their original counterparts, indicating that SPY significantly enhances the quality of negative samples, improving prediction accuracy and reliability.

  2. (2)

    Although the Stacking-RF and Stacking-XGBoost models were designed to improve predictive performance, the high correlation between the base learner outputs hindered the meta-model from extracting new information, leading to poor performance. Furthermore, the limited number of debris flow data samples restricted the model’s learning capacity, affecting the effective learning of combination patterns. Future research should focus on model diversity by selecting base models from various algorithms (such as logistic regression, support vector machines, and KNN) or by adopting more complex meta-models (such as neural networks) to ensure model diversity and enhance predictive performance and robustness.

  3. (3)

    The contribution analysis of debris flow evaluation indicators revealed that the top four contributing factors are SPI, rainfall, curvature, and area, while the bottom four are land use type, slope aspect, distance to faults, and rock mass. For debris flow risk management in the Upper Minjiang River Basin, attention should be focused on rainfall and topography, as these primary factors significantly influence debris flow occurrence, while other factors play a lesser role. Therefore, targeted optimization of rainfall management and terrain modification measures will be crucial for improving debris flow prevention and control in the watershed.