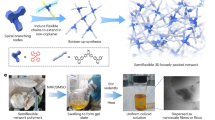
Abstract
Conventional polymeric membrane manufacturing faces significant limitations, including reliance on harsh chemicals, limited geometrical shapes (primarily flat sheets and hollow fibers), low resolution, and slow production speeds. This study introduces an innovative approach for 3D printing complex-shaped membranes with tailored properties, utilizing polymerization-induced phase separation (PIPS) and masked stereolithography (MSLA). The influence of processing parameters, including resin volume, irradiation duration, and temperature, on membrane characteristics—such as pore size, porosity, thickness, surface morphology, water permeability, and rejection rate— is systematically investigated. The findings indicate that this method can fabricate membranes with a wide range of pore sizes and porosities. The membrane architecture comprises interconnected nodules, the dimensions of which are contingent upon the processing conditions. Furthermore, the study demonstrates that PIPS facilitates the phase inversion of thermosets and the incorporation of environmentally friendly biobased solvents, thereby broadening the scope of membrane fabrication with novel polymers.
Similar content being viewed by others
Introduction
Membrane science and technology has made tremendous progress to fulfil separation and purification requirements in different fields including desalination, wastewater treatment, dairy industry etc. Sustainable progress of membrane science and technology, however, is strongly associated with the availability of better membrane fabrication techniques, which are green and capable of producing complex shapes. It is well-acknowledged that the fabrication of complex-shaped membranes can enhance the membrane efficiency by improving the mass or heat transport across the membrane1,2, fouling mitigation3,4,5, cell adhesion6,7,8 and lower or higher membrane wettability of the membranes9,10. However, state-of-the-art membrane fabrication techniques lack the versatility of fabricating membranes with shapes more complex than flat sheets or hollow fibers11,12. Conventionally, polymeric membranes are mainly prepared by using phase inversion methods such as non-solvent induced phase separation (NIPS), thermally induced phase separation (TIPS), evaporation induced phase separation (EIPS) or vapor induced phase separation (VIPS). These techniques employ the de-solvation of polymers by either thermal or non-solvent means to induce precipitation of the polymer13,14, which generates a porous membrane15. These methods lack the capability of making complex shapes and they also require harsh chemicals to dissolve the polymer, thus, the processes are not aligned with a green and sustainable transition16.
Additive manufacturing or its more conventional name 3D printing is a highly precise fabrication method for producing complex structures17. Therefore, 3D printing is considered as a potential new method for creating new membranes with complex topology and shape. Currently, the most accurate commercial 3D-printing method is vat polymerization through stereolithography (SLA) or masked stereolithography (MSLA) for production of structures with microscopic pores. However, this method is limited by its current resolution (i.e., the smallest possible 3D printable detail), which on most commercially available printers typically does not allow to produce a pore size typically below 50 microns18. This resolution does not fulfill the requirements for most membrane applications such as ultrafiltration (0.01 μm to 0.1 μm) or microfiltration (0.1 μm to 10 μm)19. Resin printing by two-photon polymerization (TPP) has successfully created geometries down to 9 nm, which is sufficient for both microfiltration and ultrafiltration20,21,22. TPP is constrained by processing speed due to the laser’s small spot size, making large-scale membrane fabrication challenging. Ignoring the typical buildplate size of 1 mm² to 10 mm² commonly cited in literature, fabricating a 1 m² membrane with a thickness of 250 μm would take approximately 1.5 months2,23,22. However, new and advanced equipment, such as beam splitters, are emerging in the market that may enhance fabrication efficiency and reduce processing time24.
One rarely explored phase inversion method in membrane fabrication is PIPS. The PIPS process follows the theory of polymers changing solubility due to a change in their molecular weight as explained by Flury-Huggins25,26. Due to the decreased solubility with increasing molecular weight, the polymer precipitates out of solution as a nucleate. These nucleates either grow, agglomerate, or coalesce while simultaneously solidifying due to continuous increase in molecular weight until completely solidifying into a solid-porous structure27. Therefore, by rapidly increasing the polymer molecular weight, the polymer can be forced out of solution and a porous membrane is produced. The resulting pore sizes can reach the nanometer range28. Like the conventional phase inversion techniques, the properties of the membrane can be modified by the processing variables including synthesis temperature, solvent concentration and polymer concentration29,30. Therefore, this method is potentially suitable to customize membrane parameters such as porosity and pore size. PIPS can be initiated with UV radiation through radical polymerization. This makes PIPS usable for lithography-based 3D printing unlike other phase inversion methods. Therefore, combining PIPS with the commercially available and commonly used MSLA technique, it is potentially possible to generate nano sized pores while also retaining the ability to create membrane shapes more complex than hollow fiber or flat sheet. This combination also potentially increases the processing speed significantly compared to TPP. Since in PIPS the polymer starts more soluble, less harsh chemicals can potentially be used for this type of membrane manufacturing, since the polymers used for PIPS are easier to dissolve31,32,33,2,34.
The tunability and printability of these membranes open new avenues for the fabrication of innovative membrane types with diverse applications. Therefore, we have shown the fabrication and testing of membranes through PIPS by using sustainable bio-based solvents and a thermosetting polymer. Furthermore, we have demonstrated the proof-of-concept of combining PIPS with MSLA for making 3D printed membranes with macrostructures. The effect of solution compositions and processing variables (operating temperature and UV radiation time) on properties of the produced membranes has also been investigated.
Materials and methods
Simulation of the Flory-Huggins and Cahn-Hillard model effect on PIPS
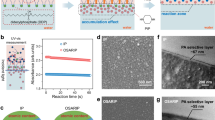
To explore the factors of resin concentration, temperature and irradiation time and their effects on membrane properties a simulation of the Flory-Huggins and Cahn-Hillard model of simple phase inversion was performed. The simulation was based on the driving force described by a simplified Flory-Huggins for a binary system.
Where, f(c) is a simplified expression for the double-well free energy density correlation, in this equation W is an expression for the thermodynamic barrier height and c is the concentration of compound 1 (resin) in compound 2 (porogen), going from 0 to 1. F(c) is an expression for total free energy here and κ is an expression for interfacial energy.
The total kinetics of the phase separation and coarsening of the polymer mix is described by the following Cahn-Hillard Eq.
Here M is a mobility coefficient describing the molecular mobility.
The simulations are performed using a Python script from Soares et al.35 with varying polymer concentration, time before solidification and molecular mobility. The parameters M, c, W and dt was set to be 1, 0.5, 2 and 1000 as a standard if nothing else is stated and all parameters are in arbitrary unit. These simulations will be compared to the experimental data of the membrane fabrication as described below.
Membrane material
Anycubic clear resin thermosetting monomer blend was chosen as thermosetting resin for MSLA purposes due to its cheap and easy commercial availability. The Anycubic clear resin blend is composed of 50% Resin epoxy (CAS: 61788-97-4) as the main monomer, 45% Tri(propylene glycol) diacrylate (CAS: 42978-66-5) as crosslinker and 5%. 1-Hydroxycyclohexyl phenyl ketone (CAS: 947-19-3) as the photo initiator. Decan-1-ol was chosen as a bio-based solvent and acetone was used as a washing agent. These were chosen in order to promote a sustainable membrane preparation method by greatly reducing the amount of petroleum-based materials36.
Flatsheet membrane synthesis—PIPS
Following the principle of PIPS, the resin was dissolved in the solvent using a magnetic stirrer for 30 min at 400 RPM. The solution was then placed on a UV-screen of a Creality LD-002 H resin printer and polymerization was initiated via irradiation from the UV-LCD screen with an intensity of 8000uW/cm2. The membrane was then readily formed, and the resin turned opaque white in color, indicating microporosity37. After polymerization, the decan-1-ol and residue resin blend were removed by placing the membrane in acetone for 48 h. This induces residue removal inside the pores through solvent extraction into the acetone solution. Thereafter, the acetone was further removed by placing the membrane in a container filled with demineralized water for 24 h. Different flat sheet membranes were fabricated by changing the resin to solvent ratio, irradiation time and temperature. The effect of resin amount was tested by making different resin concentrations based on volume fractions of resin to decan-1-ol (30%, 33.3%, 37.5%, 40%, 42.9%, 46.2% and 50%). The irradiation time and temperature were kept at 90s and 22 °C, respectively for these experiments. The membrane fabrication at different UV irradiation times was investigated at 10s, 20s, 45s, 90s and 180s to study the effect of irradiation time at the set resin volumetric amount and temperature of 42.9% and 22 °C, respectively. Finally, the effect of temperature was tested at five different temperatures, i.e., 22 °C (room temperature), 30 °C, 40 °C, 50 °C and 60 °C since the temperature influences both the solubility of the polymer and the phase inversion. The resin concentration and irradiation time were kept at 42.9% and 90s respectively.
3D printed membrane PIPS-MSLA
Three disk-shaped membranes with a 5 cm diameter and 1 mm, 2 mm and 3 mm thickness were fabricated (cf. Figure 1). The CAD files were sliced in Shitubox with a 100 μm layer height and a UV exposure time of 8s per layer. The MSLA apparatus was Creality ld-002 H. The resin volume was kept at 42.9% and the synthesis was performed at room temperature. The disks were subsequently tested for permeability as explained in Sect. 2.4. Furthermore, a CAD-file of a 2.3 mm thick 65 mm x 50 mm square membrane with macro topology consisting of rows of triangular prisms with a 200 μm half-width and a 200 μm height was generated. This membrane was prepared with the same settings as the disks.
Membrane characterization
The membrane morphologies were observed through a Zeiss evo 60 scanning electron microscope (SEM). The membrane samples were coated with a thin gold layer by plasma sputtering. The membrane thickness was measured with a Mitutoyo 543-391B micrometer. Porosity was measured by completely wetting the membranes with demineralized water and subsequent evaporation by drying the wetted membrane at 100 °C for 48 h. The mass difference before and after evaporation corresponded to the total mass of water in the pores, which can be converted to total void volume. Porosity was then calculated by the following equation:
where Φ is the porosity, Vvoid is pore volume, Vtotal is the membrane volume, dmevap is the mass loss from evaporation, mtot is the total sample mass, ρwater is water density set to 1.00 g/ml and ρpoly is the polymer density found to be 1.23 g/ml.
Pore size was analyzed by capillary porometry with complete wetting of the membranes in propan-1-ol. Pressure of nitrogen gas was slowly increased by increments of 0.1 bar/min. Bubbles appeared at the largest pore size (\(\:{D}_{L}\)). The mean pore size (\(\:{D}_{mean})\) was found as the mean of increased gasflow. Pore size was then calculated from the pressure using the Youngs-Laplace equation (Eq. 5).
Where \(\:{D}_{pore},\:\gamma\:,\theta\:\:and\:P\:\)is the pore diameter at the given pressure, the surface tension of the wetting agent (propan-1-ol: 0.022 N/m), the contact angle (propan-1-ol: 10.1°) and the gas pressure, respectively.
The water permeability was tested by a dead-end setup under three different pressures of 1, 1.5 and 2 bar. The exposed membrane area was 28.3 mm2.
The rejection of the membranes was tested using three different compounds with different sizes. These compounds were Nano-clay (Sigma), magnetite (Sigma), and bovine-hemoglobin (Sigma) with 600, 100 − 50 and 5 nm size, respectively. All particles were dispersed in water at concentrations of 0.5 g/L. To generate a stable suspension for magnetite, 10 ppm tween-80 (Sigma) was added. The hydrodynamic size of the particle’s agglomerates was determined with SLS apparatus Malvern ZS Nanosizer. The permeate concentration was measured by UV-VIS spectroscopy with a Varian Cary 50 BIO UV-Visible Spectrophotometer.
Results and discussion
Simulation of the Flory-Huggins and Cahn-Hillard model effect on PIPS
The kinetics of the liquid-liquid state can be explained by a combination of expression for mixing energy from Flory-Huggins and system dynamics expression from Cahn-Hillard25. A Flory-Huggins and Cahn-Hillard model of simple phase inversion with varying polymer concentration, time before solidification and molecular mobility in length directions x and y in arbitrary units is illustrated in Fig. 2.
The phase inversion in PIPS is induced by polymerization, which decreases the miscibility of the system and gradually solidifies. In the early stages of phase inversion, the two phases (polymer-rich and polymer-poor) will both be liquid before the polymer-rich domains (sometimes also the polymer-poor) solidify completely and “freeze” the structure38,39. Due to the gradual coalescence of the individual phases, it is usually in the mobile liquid-liquid state where the membrane structure is determined. However, as polymerization usually happens over time, growth can likely also happen in the liquid-solid phase post phase inversion, which contributes to morphological change. The effects of changing the resin concentration, radiation time and temperature are described in the following sections through experimental analysis.
Resin concentration
Different membranes were fabricated at various resin volumetric amounts and the permeability, thickness, porosity, the mean pore size (Dmean) and the largest pore size (DL) of the prepared membranes are shown in Fig. 3. The water permeability decreases from 1235 ± 45 to 65 ± 4 LMH/bar with increasing resin to solvent ratio of 30–50%, respectively (Fig. 3). This decrease in permeability corresponds with the trends of decreasing pore size, decreasing porosity and increasing membrane thickness as shown in Fig. 3(b-d), respectively. Dmean decreases from 667 nm to 108 nm with increasing resin concentration from 30 to 50% as illustrated in Fig. 3(a). Similarly, the DL decreases from 2889 nm to 408 nm (Fig. 3(b)). Therefore, DL and Dmean reduces with higher concentrations of resin. As can be seen in Fig. 3(c), the porosity likewise decreases from 0.81 to 0.60 with increasing amount of resin. The decrease in pore size and porosity suggests densification of the membrane with increased amount of resin. This densification corresponds to other phase inversion methods where a low concentration of polymer leads to more polymer poor zones which will subsequently lead to a bigger pore size and higher porosity40,41,42.
The membrane thickness increases from 0.223 ± 7 to 0.310 ± 6 mm by increasing the resin concentration from 30 to 50% (Fig. 3(d)). This change in thickness is likely due to the increased polymerization induced by the increased concentration of resin. This results in more quantity of polymer being generated due to high growth occurring at the interphase of the membrane i.e., a thicker membrane.
The effects of the resin concentration on the top and bottom surface morphologies of the membrane can be seen in Fig. 3a. Though very similar in structure, it is observed the topside of the membranes become more porous with bigger gaps between the polymer with decreasing resin concentration, thus illustrating the densification effect reflected by the increased porosity and increased permeability with lower resin concentrations. This is reflected in Fig. 2, where decreasing the polymer concentration will lead to less polymer rich zones and therefore bigger gaps between the polymer. Furthermore, decreasing the resin concentration might lead to longer time before solidification, which will further lead to more time for coalescence and therefore even bigger gaps between the polymer zones.
It can further be noticed that the densification effect is less pronounced at the screen side of the membrane leading to some asymmetry between the top and screen side of the membrane. This asymmetry between the screen side and the top side seems to increase with higher resin concentrations. This asymmetry could therefore be caused by post-solidification growth by migration of monomers and post polymerization growth at the membrane surface, which would be more pronounced with more available monomers as it is the case with higher resin concentrations.
Radiation time
Different membranes were prepared by varying the UV-irradiation time and the permeability, thickness, porosity, and DL and Dmean of the prepared membranes are shown in Fig. 4. The permeability of the membranes decreases from 471 ± 32 to 225 ± 6 LMH/bar when irradiation time is increased from 10 s to 180 s. This decrease in permeability corresponds with the increase in membrane thickness and decreased porosity and pore size, thus, the membrane becomes denser with increasing irradiation time. The densification of the membranes caused by the increased amount of irradiation time is likely due to the increased amount of polymerization, similarly, to increasing the amount of resin. This suggests two effects; (i) growth of pre-existing nodules, which would result in densification and pore narrowing; (ii) generation of additional layers of polymer, narrowing the pores of the membrane and increasing the membrane thickness.
It can be seen in Fig. 4, that the effect of further irradiation has less effect on thickness, porosity and pore size with increasing irradiation. This is likely a result of the membrane becoming thicker and thereby shielding the resin-membrane interphase from the UV irradiation.
The effect of UV-radiation time on the membrane morphology can be seen in Fig. 4a. The nodules do not change much in structure or in size on the screen-side. A slight difference is observed on the membrane topside, where larger nodules are observed with increasing irradiation time. This increase in nodule size on the top side of the membrane is likely because of growth caused by coalescence and densification of the polymer. This suggests that the main reason for a decrease in permeability, pore size and porosity is the densification at the topside of the membrane caused by the dissipating UV intensity leading to a slower polymerization at the topside of the membrane and as can be observed in Fig. 2, this will lead to a more coalesced structure.
Temperature
The permeability, thickness, porosity, DL and Dmean of the membranes prepared at different temperatures are shown in Fig. 5. Compared to other parameters, the synthesis temperature influences the membrane permeability, porosity and pore size parabolically. The permeability of the membranes increases from 270 ± 2 to 357 ± 10 LMH/bar with increase in the synthesis temperature from 22 °C to 30 °C and subsequently a decrease to 27 ± 4 LMH/bar at 60 °C. The same trend is observed for DL and Dmean (Fig. 5(a-b)) with an initial increase of Dmean from 228 nm to 248 nm (from 22 °C to 30 °C). From 30 to 60 °C, Dmean decreases drastically to 120 nm. The porosity increases from 0.66 to 0.68 from 22 °C to 30 °C and then subsequently decreases to 0.62 by increasing the temperature to 60 °C (Fig. 5(c)). As illustrated in Fig. 5(d), the thickness only increases with increasing temperature, which is due to the polymerization process being catalyzed by heat, thus creating a thicker membrane.
The topology of the membrane (Fig. 5a) becomes more open and porous, and the nodules becomes slightly enlarged by increasing the temperature from 22 °C to 30 °C. The observed effect suggests that heating from 22 to 30 °C promotes growth of the nucleate through Ostwald ripening and coalescence. This could be explained by the increased molecular mobility caused by temperature increase, which would in turn lead to a more porous structure as seen in Fig. 2. This explains the larger pore size, porosity and permeability even though the membrane gets thicker. A further increase of synthesis temperature from 30 °C to 60 °C causes a denser membrane. It is also observed that the nodules almost disappear, leaving a denser morphology. Similar effects are observed in literature43. The densification caused by increased temperature could be explained by the increased polymerization rate, which would lead to less time before solidification which is illustrated in Fig. 2.
Rejection properties
The membranes were tested for their rejection using nanoclay, magnetite and hemoglobin (Table 1). It is found that the hydrodynamic diameter for nanoclay is 494 ± 102 nm and the rejection of these particles is > 99.9%, which is expected due to the average pore size of the membrane being lower (228 nm). Two hydrodynamic diameters are found in the solution of magnetite particles suspended in 10 ppm tween-80, these are 145 ± 23 nm and 8.7 ± 1.8 nm, respectively. DLS analysis of a 10ppm tween solution without magnetite showed that the 8.7 ± 1.8 nm corresponds to a solution with pure surfactant suggesting tween-80 micelles. Therefore, only the 145 ± 23 nm corresponds to magnetite agglomerates. The rejection of magnetite is > 99.9%, even though the magnetite suspended agglomerates had a smaller diameter than the 228 nm pore size. This is likely due to agglomeration at the membrane surface, as magnetite particles agglomerate and sediment easily (hence the necessity of tween-80 as surfactant). The hemoglobin suspension was found to contain particles with a hydrodynamic diameter of 531 ± 78 nm, which is much larger than the diameter of a single hemoglobin protein of 5 nm. However, contrary to its large agglomeration size, permeation through the membrane is observed. It is found that the membrane rejects 35.1 ± 1.1% of the initial concentration. This indicates that the agglomerates of hemoglobin break and pass through the membrane. This was confirmed as two hydrodynamic particle sizes were found in the permeate (92 ± 10 nm and 5 ± 1 nm, respectively) with majority of particles with sizes of 5.4 nm corresponding to hemoglobin’s actual size emphasizing de-agglomeration effect. The rejection tests prove the complexity of size exclusion but together with the pore sizes analysis suggests the membranes to be in the ultrafiltration and microfiltration range.
3D printed membranes
The 3D printed disks with different sizes, along with their pure water permeability, can be seen in Fig. 6. The printing time of the discs where 120s, 240s and 360s for the 1 mm, 2 mm and 3 mm discs respectively of which 80s, 160s and 240s is the respective UV curing times. The permeability was 155 ± 6, 92 ± 1 and 42 ± 1 LMH/bar for thicknesses of 1 mm, 2 mm and 3 mm, respectively. These results prove the possibility of using PIPS integrated with MSLA. There is a dramatic decrease in permeability of 471 ± 32 LMH/bar to 155 ± 6LMH/bar from the flat sheet membrane with 10s irradiation time to the 1 mm thick 3D printed disk. Despite that the disks were exposed to a lower irradiation time, which from the previous data results in higher permeability, the thickness of the membranes causes a higher influence on the permeability.
The main motivation of applying 3D printing for membrane fabrication is to fabricate complex structures and surface patterns. Therefore, to confirm the useability of the method for fabrication of porous 3D-printing of complex shapes, a CAD-file of a 2.3 mm thick, 65 mm x 50 mm square membrane was prepared. The purpose was to fabricate a macro topology consisting of rows of triangular prisms with a 200 μm half-width and 200 μm height through MSLA with 42.9% resin concentration.
The fabricated membranes with surface topology are shown in Fig. 7 with a triangular pattern. The membrane itself took a total of 276s to make, compared to the membrane disc of similar thickness of 2 mm, the membrane area of the prism membrane is 1.65 times the area of the disc. This highlights that MSLA is only limited in processing speed by the thickness of the membrane and a 1 mm thick membrane will take 120s regardless of the total membrane area.
The SEM analysis of the membrane made through PIPS-MSLA printing with complex topology reveals that the porous structure of this membrane resembles with those prepared by using solely PIPS. The membranes were too fragile to use a capillary flow porometer for determining the exact pore size. This demonstrates that the PIPS- MSLA method can make complex topological membranes, which can greatly benefit the membrane processes for instance in reducing concentration polarization, acting as a spacer, inducing nucleation in membrane assisted crystallization processes, etc.
Conclusion
Porous hydrophilic flat sheet membranes were demonstrated to be synthesized through the PIPS method using commercially available resin and subsequently integrated with MSLA 3D printing. It was demonstrated that it is possible to use sustainable solvents and washing agents as decan-1-ol and acetone for the manufacturing and thereby exclude petroleum-based chemicals. Membrane parameters were modified by changing resin concentration and compared to a Flory Huggins and Cahn Hillard simulation of a phase inversion system. It was found that UV-irradiation time and temperature resulting in membranes ranging from MF down to UF process in a process that was in agreement with the phase inversion simulation. The membranes had pore size, porosity and permeability ranging from < 108 nm to 666 nm, 0.60 to 0.81 and 27 ± 4 to 1235 ± 45 LMH/bar, respectively, demonstrating the versatility of the process. The membrane structure was found to be composed of an interconnected network of nodules without any macro voids, which will change into a more spinodal structure with an increase in temperature or resin concentration. The membranes also demonstrated very good rejection towards different compounds with different particle sizes; thus, a rejection of > 99.9, > 99.9 and 35.1 ± 1.1 of the nano clay, magnetite and hemoglobin particles, respectively was observed.
Furthermore, it was shown that PIPS was a feasible method for fabricating membranes through 3D printing by MSLA. However, the number of layers decreases the permeability of the final 3D printed membrane due to increased thickness and composition change in the resin during the manufacturing. This must be optimized and controlled during fabrication. In perspective, the use of MSLA-3D can benefit membrane processes in terms of increased permeability, minimizing fouling, etc. Furthermore, PIPS enables the use of various new polymers, including thermoplastics, for membrane synthesis. These polymers are typically incompatible with conventional phase inversion techniques.
Data availability
Data sets generated during the current study are available from the corresponding author on reasonable request.
References
Low, Z. X. N. et al. Perspective on 3D printing of separation membranes and comparison to related unconventional fabrication techniques. J Memb. Sci 523, (2016).
Tijing, L. D. et al. 3D printing for membrane separation, desalination and water treatment. Appl. Mater. Today. 18, 100486 (2020).
Maruf, S. H., Wang, L., Greenberg, A. R., Pellegrino, J. & Ding, Y. Use of nanoimprinted surface patterns to mitigate colloidal deposition on ultrafiltration membranes. J. Memb. Sci. 428, 598–607 (2013).
Maruf, S. H., Greenberg, A. R., Pellegrino, J. & Ding, Y. Critical flux of surface-patterned ultrafiltration membranes during cross-flow filtration of colloidal particles. J. Memb. Sci. 471, 65–71 (2014).
Jung, S. Y. et al. Particle deposition on the patterned membrane surface: simulation and experiments. Desalination 370, 17–24 (2015).
Lu, N. et al. Fabrication of PDMS surfaces with micro patterns and the effect of pattern sizes on bacteria adhesion. Food Control. 68, 344–351 (2016).
Hou, S., Gu, H., Smith, C. & Ren, D. Microtopographic patterns affect Escherichia coli biofilm formation on Poly(dimethylsiloxane) surfaces. 27, 2686–2691 (2011).
Ding, Y. et al. Thermodynamic underpinnings of cell alignment on controlled topographies. Adv. Mater. 23, 421–425 (2011).
Ochs, M. et al. Wetting-Controlled localized placement of surface functionalities within nanopores. Small 16, 1906463 (2020).
Kim, K. Y., Srivastava, R. P. & Khang, D. Y. Oleophilic to oleophobic wettability switching of isoporous through-hole membranes by surface structure control for low-voltage electrowetting-based oil-water separation. J Memb. Sci 646, (2022).
Koo, J. W. et al. A review on spacers and membranes: conventional or hybrid additive manufacturing? Water Res. 188, 116497 (2021).
Khalil, A., Ahmed, F. E. & Hilal, N. The emerging role of 3D printing in water desalination. Sci. Total Environ. 790, 148238 (2021).
Dong, X., Lu, D., Harris, T. A. L. & Escobar, I. C. Polymers and solvents used in membrane fabrication: A review focusing on sustainable membrane development. Membr. 2021. 11, Page 309 (11), 309 (2021).
Kim, J. F. Recent progress on improving the sustainability of membrane fabrication Article info. J. Membrane Sci. Res. 6, 241–250 (2020).
Hołda, A. K. & Vankelecom, I. F. J. Understanding and guiding the phase inversion process for synthesis of solvent resistant nanofiltration membranes. J. Appl. Polym. Sci. 132, 1–17 (2015).
Lee, W. J., Goh, P. S., Lau, W. J. & Ismail, A. F. Hilal, N. Green approaches for sustainable development of liquid separation membrane. Membr. 2021. 11, Page 235 (11), 235 (2021).
Ngo, T. D., Kashani, A., Imbalzano, G., Nguyen, K. T. Q. & Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Compos. B Eng. 143, 172–196 (2018).
Luongo, A. et al. Microstructure control in 3D printing with digital light processing. Comput. Graphics Forum. 39, 347–359 (2020).
Wang, L. H. & Y.-T. S. N. K. Advanced Physicochemical Treatment Processes. (Handbook of environmental engineering, (2006).
Bougdid, Y. & Sekkat, Z. Voxels optimization in 3D laser Nanoprinting. Sci. Rep. 10, 1–8 (2020).
Fritzler, K. B. & Prinz, V. Ya. 3D printing methods for micro- and nanostructures. Uspekhi Fizicheskih Nauk. 189, 55–71 (2019).
Fiedor, P. & Ortyl, J. A new approach to micromachining: High-precision and innovative additive manufacturing solutions based on photopolymerization technology. Materials 13, 1–25 (2020).
Low, Z. X. et al. Perspective on 3D printing of separation membranes and comparison to related unconventional fabrication techniques. J. Memb. Sci. 523, 596–613 (2017).
UpNano GmbH. NanoPro VT. https://www.upnano.com/nanopro-vt/ (2025). Last accessed: 01-05-2025.
Wang, F., Ratke, L., Zhang, H., Altschuh, P. & Nestler, B. A phase-field study on polymerization-induced phase separation occasioned by diffusion and capillary flow—a mechanism for the formation of porous microstructures in membranes. J. Solgel Sci. Technol. 94, 356–374 (2020).
Leguizamon, S. C. et al. Polymerization-Induced phase separation in Rubber-Toughened Amine-Cured epoxy resins: tuning morphology from the Nano- to Macro-scale. Macromolecules 54, 7796–7807 (2021).
Young, T. H. & Chen, L. W. Pore formation mechanism of membranes from phase inversion process. Desalination 103, 233–247 (1995).
Dong, Z. et al. 3D printing of inherently nanoporous polymers via polymerization-induced phase separation. Nature Communications 2021 12:1 12, 1–12 (2021).
Nakanishi, K. Pore structure control of silica gels based on phase separation. J. Porous Mater. 4, 67–112 (1997).
Boots, H. M. J., Kloosterboer, J. G., Serbutoviez, C. & Touwslager, F. J. Polymerization-Induced phase separation. Convers. – Phase Diagrams Undefined 29. 1, 7683–7689 (1996).
Post, W., Susa, A., Blaauw, R., Molenveld, K. & Knoop, R. J. I. A Review on the Potential and Limitations of Recyclable Thermosets for Structural Applications. (2019). https://doi.org/10.1080/15583724.2019.1673406 60, 359–388.
Abdelghafour, M. M. et al. The effect of molecular weight on the solubility properties of biocompatible Poly(ethylene succinate) Polyester. Polym. 2021. 13, 2725 (2021).
Chai, X. S., Hou, Q. X. & Schork, F. J. Determination of the solubility of a monomer in water by multiple headspace extraction gas chromatography. J. Appl. Polym. Sci. 99, 1296–1301 (2006).
Kozuch, D. J., Zhang, W. & Milner, S. T. Predicting the Flory-Huggins Χ parameter for polymers with stiffness mismatch from molecular dynamics simulations. Polym. 2016. 8, 241 (2016).
Soares, E. A., Barreto, A. G. & Tavares, F. W. Exponential Integrators for Phase-Field Equations using Pseudo-spectral Methods: A Python Implementation. ArXiv ID: 2305.08998, (2023). https://github.com/elvissoares/PyCahnHilliard. 1–12.
Dong, X., Lu, D., Harris, T. A. L. & Escobar, I. C. Polymers and solvents used in membrane fabrication: A review focusing on sustainable membrane development. Membranes vol. 11 Preprint at (2021). https://doi.org/10.3390/membranes11050309
James, A. M., Dawson, R., James, A. M. & Dawson, R. Efficient and tunable White-Light emission using a dispersible porous polymer. Macromol. Rapid Commun. 41, 2000176 (2020).
Wang, F. et al. Progress report on phase separation in polymer solutions. Adv. Mater. 31, 1806733 (2019).
Strathmann, H. & Kock, K. The formation mechanism of phase inversion membranes. Desalination 21, 241–255 (1977).
Hołda, A. K., Aernouts, B., Saeys, W. & Vankelecom, I. F. J. Study of polymer concentration and evaporation time as phase inversion parameters for polysulfone-based SRNF membranes. J. Memb. Sci. 442, 196–205 (2013).
Vandezande, P., Li, X., Gevers, L. E. M. & Vankelecom, I. F. J. High throughput study of phase inversion parameters for polyimide-based SRNF membranes. J. Memb. Sci. 330, 307–318 (2009).
Doménech-Carbó, M. T., Aura-Castro, E. & Domenech-Carbo, M. T. Evaluation of the phase inversion process as an application method for synthetic polymers in conservation work. Stud. Conserv. 44, 19 (1999).
Yan, Y., Zhang, R., Liang, Q., Liu, J. & Han, Y. Control the interplay of crystallization and phase separation of conjugated polymer blends by the relative rate of nucleation and growth. Polymer (Guildf) 182, (2019).
Acknowledgements
The authors are greatly thankful to the Poul Due Jensen Foundation for funding this work through the project “Membrane Distillation and Membrane Crystallization for recovery of water and minerals from waste streams”.
Author information
Authors and Affiliations
Contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript. BSK: methodology, experimental work, analysis, writing. AA: methodology, analysis, writing, supervision, CAQJ: methodology, analysis, writing, supervision.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Kirkebæk, B.S., Ali, A. & Quist-Jensen, C.A. Masked stereolithography and polymerization induced phase separation for 3D printing of membranes. Sci Rep 15, 18776 (2025). https://doi.org/10.1038/s41598-025-03527-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-025-03527-1