Introduction

In the next millennium, electricity production is dominated by renewable energy sources. There are about 3.2 EJ/year of energy that reaches the earth’s surface. The surface of the Earth is abundant with energy, and extraction of a small portion of the same can resolve the energy crisis. The photovoltaic system processes solar energy into electrical energy1,2,3. The photovoltaic system consists of the fundamental components of a photovoltaic cell. The grouping of cells leads to the photovoltaic array4,5. To optimum voltage and current, photovoltaic modules are connected in series and parallel. Table represents symbols and abbreviations used in the paper.

In grid-connected systems6,7,8, converters can be used to ensure that the electricity produced is compatible with the grid9,10,11. Comparison of photovoltaic cells is analyzed using spectral distribution. Data sheets provide for parameters under standard test conditions. The following are the nominal (standard) test conditions:

$$\begin{aligned} Irradiance (Gn) = 600-1000 W \end{aligned}$$
(1)
$$\begin{aligned} Temperature (T) = {25}^{\circ } C \end{aligned}$$
(2)

One of the indirect forms of energy is the wind energy caused due to the uneven heating of the earths surface by the sun. Considering a wind energy system12,13,14 in a grid-connected hybrid energy system helps to provide a continuous source of power supply to the load. Designing a wind model within a microgrid setup involves the analysis of wind speed, turbine characteristics, and the yaw control mechanism.

Fig. 1
figure 1

Aerodynamic characteristic of the wind turbine.

Full size image

The permanent magnet synchronous generator fed wind turbine yields a turbine output power versus turbine speed characteristics as shown in Fig. 1 Compared to a photovoltaic system, the15 wind energy conversion system can act as a micro-power service provider for the hybrid system due to erratic variations in the wind speed.

The chosen reference DC bus voltage is an LVDC equal to 48 V. Obtaining power from solar and wind power with their intermittency conditions and maintaining the DC bus voltage at 48 V is a demanding task.16,17,18 Hence, a storage system helps to provide the energy required by the load system. By providing gating signals to the switches, power electronic converters help to manage the bidirectional power flow between the source and the load, as shown in Fig. 2.

Fig. 2
figure 2

Circuit of bidirectional power flow using DC–DC Converter.

Full size image

As shown in Fig. 2 based on the switching of the S1 and S2, the D1 and D2 batteries are charged or discharged19. Power flow management occurs according to the reference criteria chosen for the battery. SoC, \(I_{b}\) and \(V_{b}\) are the reference measurements for the battery20,21. In charging mode, S1 is turned on and the battery current is negative22. In discharging mode, S2 is turned off and the battery current is positive.

In this paper, two modes of control mechanism are provided, one with the PI controller and the other with the model reference adaptive controller23,24,25. A 48V DC bus voltage is maintained on the bus by using the operation of Bidirectional DC–DC Converter with the help of the PI or the adaptive PI controller. In the first proposed simulation, a micro grid system comprising DER’s connected to grid tied system with Bidirectional DC–DC Converter and ESS is implemented. The solar and wind system is controlled using an MPPT controller to attain maximum power output at all given input conditions26,27,28,29. In the second proposed simulation, the model reference adaptive controller (MRAC) is implemented to enhance the resiliency and stability of the grid connection system. A conceptual comparison of PI and MRAC is shown in Table 1.

The rest of the paper is organized as follows: the second section gives the analysis of the working of the PV cell, the third section gives the modeling of the wind energy conversion system as these two will form the distributed energy resources. fourth section interprets the operation of battery system. fifth section follows with the modeling of the system by giving a comparison between PI and MRAC controller. The sixth part gives the concept of model reference adaptive controller and its importance. The seventh part presents a detailed analysis of power flow management by producing simulated results and outputs using MATLAB Simulink, and the final section provides the conclusion of the research work carried out.

Table 1 Comparison of PI controller and model reference adaptive controller.
Full size table

PV cell modeling

In essence, a photovoltaic cell is a semiconductor diode with light exposure at the p–n junction. Various types of semiconductor30 are used in the production of photovoltaic cells, employing different manufacturing techniques. Currently, the only silicon cells available on a commercial basis are monocrystalline and31,32 a thin film or a layer of bulk silicon joined to electric terminals makes up silicon photovoltaic cells.

PV cell model equations

  1. 1.

    Photocurrent (\(I_{ph}\)):

    $$\begin{aligned} I_{ph} = I_{sc} + k_i(T - T_{ref}) \end{aligned}$$
    (3)

    where short-circuit current is \(I_{sc}\), temperature coefficient of the short-circuit current is \(k_i\), cell temperature is \(T\) , and reference temperature is \(T_{ref}\)

  2. 2.

    Diode current (\(I_d\)):

    $$\begin{aligned} I_d = I_0 \left( e^{\frac{qV_d}{nkT}} - 1 \right) \end{aligned}$$
    (4)

    where Reverse saturation current is \(I_0\), electron charge is \(q\), diode voltage is \(V_d\), ideality factor is \(n\), Boltzmann constant is \(k\), and cell temperature is \(T\)

  3. 3.

    Shunt current (\(I_{sh}\)):

    $$\begin{aligned} I_{sh} = \frac{V + IR_s}{R_{sh}} \end{aligned}$$
    (5)
  4. 4.

    PV cell output current (\(I\)):

    $$\begin{aligned} I = I_{ph} - I_d - I_{sh} \end{aligned}$$
    (6)

    By substituting \(I_d\) and \(I_{sh}\) the equation yields:

    $$\begin{aligned} I = I_{ph} - I_0 \left( e^{\frac{q(V + IR_s)}{nkT}} - 1 \right) - \frac{V + IR_s}{R_{sh}} \end{aligned}$$
    (7)

The photovoltaic effect is the fundamental idea behind the operation of a photovoltaic cell. The necessary power is produced by this current and the voltage that is produced by its inherent electric fields33,34,35.

Characteristics of PV cell

Three key elements make up a PV characteristic36,37: MPP, Voc, and Isc. Typically, manufacturers include these specifications for a specific PV cell or module in their data sheets. A basic model can be created using these parameters with greater accuracy utilizing additional data.

Fig. 3
figure 3

IV–PV characteristics of PV cell.

Full size image

I–V characteristic based fundamental equation is as shown in Fig. 3 of the ideal solar cell mathematically comes from the theoretical operation38,39of semiconductors and is as follows:

$$\begin{aligned} I = Ipv - Io[exp(qV/nkT)-1] \end{aligned}$$
(8)

Modeling of the wind energy system

Due to the widespread concern about environmental issues such as pollution and depletion of natural resources caused by conventional resources to generate electricity, as well as the growing cost of these fuels, the area has been shifted to find new thoroughly, environmentally and environmentally accurate sources of power40. Wind energy is the economical source of energy41. There are two classifications of wind turbines: fixed-speed and variable-speed wind turbines42.

Wind energy conversion system

The converted wind power is43:

$$\begin{aligned} P_w = \frac{1}{2} \rho S v^3 c_p \end{aligned}$$
(9)

where wind speed = v, air density = \(\rho\), covered surface of the turbine = S, and conversion coefficient of power = \(c_p\)

Wind turbine

Conversion from wind energy to mechanical energy. The mechanical power of the turbine obtained from wind power can be used to calculate the mechanical torque of the turbine44. The power coefficient of the turbine—the ratio of mechanical power to wind power, or \(c_p\). Pitch angle (\(\beta\)), is denoted as the angle of the turbine blade, and tip speed (\(\lambda\)) denotes the power coefficient, while tip speed is product of rotational speed and wind speed, as expressed by

$$\begin{aligned} c_p(\lambda , \beta ) = c_1 \left( c_2 \frac{1}{\lambda _i} - c_3 \beta - c_4 \beta ^x - c_5 \right) e^{-c_6 \frac{1}{\lambda _i}} \end{aligned}$$
(10)

The coefficients \(c_1\) to \(c_6\) and \(x\) values change for various turbines depending on the wind turbine rotor and blade design. The parameter \(\frac{1}{\lambda _i}\) is defined as

$$\begin{aligned} \frac{1}{\lambda _i} = \frac{1}{(\lambda + 0.08\beta )} - \frac{0.035}{(1 + \beta ^3)} \end{aligned}$$
(11)

The power coefficient is given by

$$\begin{aligned} c_p = \frac{P_m}{P_w}, \quad c_p < 1 \end{aligned}$$
(12)
$$\begin{aligned} P_m = c_p(\lambda , \beta ) \frac{\rho S}{2} v^3 \end{aligned}$$
(13)

where

$$\begin{aligned} P_m = \text {the mechanical output power of the turbine}, \quad T_m = \frac{P_m}{\omega } \end{aligned}$$

PMSG in wind turbine

The voltage equations of PMSG are45,46,47:

$$\begin{aligned} \frac{d}{dt} i_d = \frac{1}{L_d} v_d - \frac{R}{L_d} i_d + \frac{L_q}{L_d} p \omega _r i_q \end{aligned}$$
(14)
$$\begin{aligned} \frac{d}{dt} i_q = \frac{1}{L_q} v_q - \frac{R}{L_q} i_q + \frac{L_d}{L_q} p \omega _r i_d - \frac{\lambda p \omega _r}{L_q} \end{aligned}$$
(15)
$$\begin{aligned} T_e = 1.5 p [\lambda i_q + (L_d - L_q) i_d i_q] \end{aligned}$$
(16)
$$\begin{aligned} \frac{d}{dt} \omega _r = \frac{1}{J} (T_e - F \omega _r - T_m) \end{aligned}$$
(17)

The dynamic equations are given by:

$$\begin{aligned} \frac{d}{dt} \theta = \omega _r \end{aligned}$$
(18)

where \(J =\) inertia of the rotor, \(F =\) friction of the rotor, and \(\theta =\) angular position of the rotor.

Battery system

A rechargeable battery is an electrochemical device that, when charged, transforms electrical energy into chemical energy and, when discharged, returns chemical energy to electrical energy48,49. By storing energy in battery packs, renewable energy sources reduce dependency on fossil fuels. In technological terms, rechargeable batteries have advanced from lead acid to nickel-based batteries and then to lithium–ion batteries (li–ion)50,51. Precise battery data, including state-of-charge (SOC), voltage, and current, are essential for circuit designers to control the energy usage of battery-powered devices. In addition, careful battery management is required to avoid overcharging or over discharging. An accurate battery model is essential for circuit design52. Numerous research works on battery modeling methods have been published in various scholarly journals53. The suggested comparable circuit model for a battery is precise and easy to understand54. The basic equivalent circuit model equations are as shown:

Open-circuit voltage determines the equation in terms of state of charge:

$$\begin{aligned} V_{oc}&= f(SOC) \end{aligned}$$
(19)

The terminal voltage across the equivalent circuit is given by:

$$\begin{aligned} V_t&= V_{oc} - I \cdot R_{int} \end{aligned}$$
(20)

State of charge of a battery is:

$$\begin{aligned} SOC(t)&= SOC(0) - \frac{1}{C} \int _0^t I(\tau ) \, d\tau \end{aligned}$$
(21)

Current derived from ohm’s law for internal resistance:

$$\begin{aligned} I&= \frac{V_t - V_{oc}}{R_{int}} \end{aligned}$$
(22)

SoC estimate

State of charge is calculated using the said equations. The system has two inputs: current (I) and initial SOC (SOC0). The effect of the rate capacity of a battery55 is characterized by a lookup table. The real-time SOC is the output of the subsystem.

$$\begin{aligned} {SoC}(t) = \frac{Q_{\text {remaining}}(t)}{Q_{\text {max}}(t)} \times 100\% \end{aligned}$$
(23)

System model

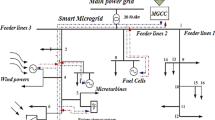
An important advantage for developing a DC microgrid in India is to provide electricity to rural areas. A DC microgrid as shown in Fig. 4 consists of generating sources, an energy storage system, loads, energy management, and an independent power system56,57. A system like that might or might not be linked to the grid. Grid-connected systems are found mainly in urban areas, with isolated areas or partially served villages. In areas where grid-connected electricity is available, the region’s social and economic development is hampered by a low-quality and time-limited supply.

Fig. 4
figure 4

System model for delivering the power at all variable conditions.

Full size image

Microgrid systems are reliable and affordable and contribute to environmental sustainability, rather than environmental damage. They are also not restricted to a particular area. DC microgrid powered by renewable energy sources utilizes boundless energy sources that are abundant and cost-free. Using DC–DC power converters with an efficiency greater than 95% DC microgrid can eliminate the need for AC/DC converters. In the generalized block schematic of a DC micro grid shown, the permanent magnet synchronous generator (PMSG) has several benefits over other WTG topologies, it can be employed as a generating source in a micro grid. With PMSG, the variable speed topology is fully controllable and full power converters (Voltage Source Converter) are utilized.

$$\begin{aligned} P_{in} = P_{out} + P_{loss} \end{aligned}$$
(24)
$$\begin{aligned} P_{in} = \sum _{i=1}^{n} P_{i,gen} - \sum _{j=1}^{m} P_{j,load} \end{aligned}$$
(25)
$$\begin{aligned} P_{out} = \sum _{k=1}^{p} P_{k,storage} \end{aligned}$$
(26)
$$\begin{aligned} P_{loss} = \sum _{l=1}^{q} P_{l,line} \end{aligned}$$
(27)
$$\begin{aligned} P_{balance} = P_{in} - (P_{out} + P_{loss}) \end{aligned}$$
(28)

When there is a significant energy demand, fuel cells can supply enormous amounts of power, while batteries are typically used as a backup. The proposed attributes of a DC microgrid are as follows. A DC microgrid must be reliable. A reasonable degree of quality of the power supply should be maintained.

  • The DC microgrid must be robust. Since solar and wind energy are sporadic, it should withstand dynamic load circumstances and variations in power generation.

  • The system needs to require the least amount of maintenance and installation money.

  • The DC microgrid must retain its adaptability even after initial installation and sizing. Changes in generation or storage capacity, as well as adjustments to the load

The summary of the primary contributions of the planned work:

  • To satisfy the increasing load demand, a hybrid DC microgrid system based on photovoltaic, wind, and ESS is being developed.

  • To improve the PV output voltage and produce high-gain outputs, an MPPT controller is suggested. This helps in stabilizing the DC link voltage of the microgrid.

  • Furthermore, DFIG-based WECS utilizes an additional MPPT approach to properly regulate DC link voltage in all operating situations.

  • For ESS, a BMS-based control method is suggested to sufficiently increase the DC link voltage when PV and WECS are not producing enough power.

  • In addition, all these systems are connected to a Microgrid system through a DC link, where it is converted to a three-phase supply to the three-phase load.

Fig. 5
figure 5

Conditions for power flow management.

Full size image

Case 1 represents the power balance equation for a DC microgrid system, where: Vdc = DC bus voltage, Idc = DC bus current, Ppv = power generated by the solar photovoltaic system, Pw = power generated by the wind energy system, Pbat = power supplied (+) or absorbed (−) by the battery storage system, Pgrid = Power exchanged with the grid (positive when exporting power, negative when importing power). Cases 2 and 3 represent the equations when generation is greater than Demand, Generation is less than demand, respectively.

The data taken for both systems are real data taken from actual panel ratings and readings achieved over a week. In the simulation, one-day readings for both wind energy and photovoltaic energy are considered, respectively. Figure 5 represents the three different cases of power flow management in a DC microgrid.

Proposed methodology

Model reference adaptive controller

Changes in the process dynamics are adjusted by an adaptive controller. Variations can be intriguing from a number of places. Ex: unaccounted dynamics in the systems. A controller is required to handle these variations. The said parameter can be executed efficiently by using a robust controller. As the range of uncertainty grows, designing a single controller becomes more and more complex. In MRAC, consider a reference model with the closed-loop system. In Fig. 6, subtract the two outputs to produce an error signal E such that the error is zero. The uncertainty in the system is represented as f(x).

Fig. 6
figure 6

Representation of model reference adaptive controller.

Full size image

The reference model in a MRAC describes as follows:

$$\begin{aligned} {\dot{x}}_m(t)&= A_m x_m(t) + B_m r(t) \end{aligned}$$
(29)
$$\begin{aligned} y_m(t)&= C_m x_m(t) \end{aligned}$$
(30)

The system is typically controlled by:

$$\begin{aligned} {\dot{x}}(t)&= A x(t) + B u(t) \end{aligned}$$
(31)
$$\begin{aligned} y(t)&= C x(t) \end{aligned}$$
(32)

There exists a control law in MRAC to reduce the error between the output of the plant and the reference model chosen. The control law is given by:

$$\begin{aligned} u(t)&= \phi (t) \theta ^T(t) \end{aligned}$$
(33)

In order to reduce the error, adaptation law is given by:

$$\begin{aligned} {\dot{\theta }}(t)&= -e(t) \gamma \phi (t) \end{aligned}$$
(34)

Mathematical model of adaptive PI controller

The standard PI controller equation is given by:

$$\begin{aligned} u(t) = K_p e(t) + K_i \int e(t) dt \end{aligned}$$
(35)

where \(u(t)\) is the control output, \(e(t)\) is the error signal, \(e(t) = r(t) - y(t)\), \(K_p\) is the proportional gain, \(K_i\) is the integral gain.

For an **Adaptive PI Controller**, the gains \(K_p\) and \(K_i\) dynamically change according to system conditions. The MRAC-PI adapts its parameters dynamically based on the reference model to minimize error. The adaptive control law is:

$$\begin{aligned} u(t) = K_p(t) e(t) + K_i(t) \int e(t) \, dt \end{aligned}$$
(36)

where Kp(t)K_p(t) and Ki(t)K_i(t) are time-varying gains that adjust based on the adaptation law:

$$\begin{aligned} {\dot{K}}_p(t) = -\gamma _p e(t) \varphi (t) \\ {\dot{K}}_i(t) = -\gamma _i e(t) \int e(t) \, dt \end{aligned}$$

where, \(\gamma _p\) and \(\gamma _i\) are adaptive learning rates, \(\varphi (t)\) is the basis function (typically chosen as e(t) for direct adaptation). Adaptive error minimization condition: The adaptation law ensures that the tracking error \(e_m = y - y_m\) approaches zero asymptotically.

$$\begin{aligned} V(e) = \frac{1}{2} e^2 \\ {\dot{V}}(e) = -\gamma _p e^2 - \gamma _i e \int e \, dt \le 0 \end{aligned}$$

This guarantees the stability of the system and improved performance over the conventional PI controller.

Error dynamics and adaptive law:

Error dynamics:

The error dynamics is derived on the basis of the difference between the actual system response and the reference model response. Let the state of the system be represented as:

$$\begin{aligned} {\dot{x}} = Ax + Bu \end{aligned}$$

and the reference model as:

$$\begin{aligned} {\dot{x}}_m = A_m x_m + B_m r \end{aligned}$$

where \(x\) is the state of the system, \(x_m\) is the state of the reference model, \(A\) and \(B\) are the system matrices, \(A_m\) and \(B_m\) are the desired model matrices, \(r\) is the reference input. The tracking error is defined as:

$$\begin{aligned} e = x - x_m \end{aligned}$$

Taking the derivative,

$$\begin{aligned} {\dot{e}} = {\dot{x}} - {\dot{x}}_m \end{aligned}$$

Substituting the system and reference model equations,

$$\begin{aligned} {\dot{e}} = Ax + Bu - (A_m x_m + B_m r) \end{aligned}$$

Since \(u\) is controlled by an adaptive PI controller,

$$\begin{aligned} u = K_p e + K_i \int e \, dt \end{aligned}$$

where \(K_p\) and \(K_i\) are the proportional and integral adaptive gains. Thus, the error dynamics becomes:

$$\begin{aligned} {\dot{e}} = (A + BK_p) e + BK_i \int e \, dt - A_m x_m - B_m r \end{aligned}$$

Adaptive law: The adaptive law updates the controller gains \(K_p\) and \(K_i\) using Lyapunov stability criteria. Consider the Lyapunov function:

$$\begin{aligned} V = \frac{1}{2} e^T P e + \frac{1}{2} {\tilde{K}}_p^T \Gamma ^{-1} {\tilde{K}}_p + \frac{1}{2} {\tilde{K}}_i^T \Gamma ^{-1} {\tilde{K}}_i \end{aligned}$$

where \(P\) is a positive definite matrix, \(\Gamma\) is the adaptation gain, \({\tilde{K}}_p = K_p - K_p^*\) and \({\tilde{K}}_i = K_i - K_i^*\) are the parameter estimation errors. Differentiating \(V\),

$$\begin{aligned} {\dot{V}} = e^T P {\dot{e}} + {\tilde{K}}_p^T \Gamma ^{-1} {\dot{K}}_p + {\tilde{K}}_i^T \Gamma ^{-1} {\dot{K}}_i \end{aligned}$$

To ensure stability, the adaptation laws are chosen as:

$$\begin{aligned} {\dot{K}}_p = -\Gamma e^T P B \\ {\dot{K}}_i = -\Gamma e^T P B \int e \, dt \end{aligned}$$

These laws adjust the controller parameters dynamically to minimize the tracking error.

Fig. 7
figure 7

Boost converter system with control structure.

Full size image

Results

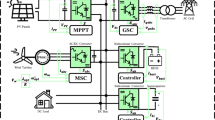
DC microgrid structure consists of the PV array output, the WECS output, the battery output and the DC bus, and the grid connection depending on the power flow from either of the sources. Figure 7 represents the Boost converter system with control structure. Flowchart determines the power management in the hybrid system. Therefore, there is a continuous supply to the grid under all circumstances.

Fig. 8
figure 8

Flowchart of power management in the system.

Full size image

As seen in the flow chart in Fig. 8, the suggested system operates in three different ways. All three systems-the photovoltaic or solar cell for the first power, the wind system for the second power, and the battery for the third power-are connected to a common DC connection, which supplies the voltage for the grid system.

Fig. 9
figure 9

Hardware setup of PV and Wind system.

Full size image

The system is run by two controllers. An PI controller being former and an adaptive controller being later. This paper compares the results of a simulation that was conducted using these two controllers to construct two systems. Figures 9 and 10 denotes the hardware setup and weather monitoring system displayed in the computer software, respectively. Figures 11 and 12 represent the actual wind and photovoltaic data observed using weather link software, respectively.

Fig. 10
figure 10

Weather monitoring system displayed onto the computer software.

Full size image

The original system is considered by feeding the real-time values through the signal builder. An average of a single day data of around 1000 to 2000 points is converted to a single value for a day length.

Fig. 11
figure 11

Actual data of Wind energy conversion system observed in weather link software.

Full size image

The real value of the photovoltaic system shown in Fig. 12 is taken for 3 days that has more than 1000 points, which is converted to the average and fed to the system. The representation of the photovoltaic system for each day, for example, is Monday, Tuesday, Wednesday, as shown in Fig. 12.

Similarly, the image shown in Fig. 11 is for the real value of the wind systems that are being fed to the proposed system.

Fig. 12
figure 12

Actual data of photovoltaic system observed in weather link software.

Full size image
Fig. 13
figure 13

Adaptive PI controller-based DC microgrid system in MATLAB Simulink.

Full size image

The real-time values of the photovoltaic and wind subsystem remain the same for both proposed systems, and the simulation is run on the basis of these values to verify optimized power flow management within the system. The waveforms represent the operation and analysis of the Adaptive PI controller and PI controller for variable values of irradiance and wind speed.

Fig. 14
figure 14

Solar irradiance profile represented through signal builder in W/m2.

Full size image

The DC microgrid system based on the adaptive PI controller in MATLAB is shown in Fig. 13. The maximum value of radiation is 958 W/m2 as shown in Figure 14 and the values are represented by the signal builder. Its been observed that due to the MPPT tracking system the maximum output voltage gathered is equal to 31.06V. Similarly, with increasing irradiance, the current through the system also increases, and the maximum current obtained is 35.59A. The variation of the reference and actual current in the adaptive system accounts for between 3 and 4%. The actual current is taken from the proposed system, and the reference current is generated from the PI/Adaptive PI controller of the controller system. These two are compared and generated from the PI/Adaptive PI controller to give them to the gate of the transistors used in the system to control the battery output. The Soc in the PI system has a difference of about 0.8 when measured from peak to last value, while the Adaptive PI system resulted in about 0.6 of the difference.

Fig. 15
figure 15

PV array output in watts supplied to the grid in case of adaptive PI controller.

Full size image

The PV system outputs power with the recorded irradiance of both the PI controller system and the Adaptive PI controller system. The PV power for the adaptive PI controller system is 1.022 kW for the selected irradiance as shown in Fig. 15.

Fig. 16
figure 16

MATLAB output of DC Bus voltage compared with reference voltage in PI controller.

Full size image

Figure 16 shows an error difference of 7.65% between the reference voltage and the acquired dc bus voltage using a PI controller. To sustain a constant dc bus voltage of 48 V at the load, tuning of PI is not sufficient to produce the required output. Hence, the adaptive PI controller helps in creating a reference model based on which tuning happens to bring the output dc bus voltage approximately to 48 V as shown in Fig. 17.

Fig. 17
figure 17

MATLAB output of DC bus voltage compared with reference voltage in adaptive PI controller.

Full size image
Fig. 18
figure 18

Battery discharging and charging based on the load demand.

Full size image

Figure 18 represents the discharging and charging of the battery according to the load requirement. During 0 to 18 s, the minimum irradiance and wind speed are not sufficient to feed the load; therefore, the battery is discharged by feeding the load. From time 18 to 40 s, with the given wind profile, PV has a maximum insolation level sufficient to meet the load requirement and charge the battery. The latter part satisfies Case-2.

Fig. 19
figure 19

Battery showing negative current during charging condition.

Full size image

Figure 19 represents the maximum battery current to be − 7.183 A. The battery charging condition is denoted by a negative sign. In Fig. 19 from 14 to 25 s battery is shifting from discharging state to charging state, 25 s onward battery is moving towards discharging condition. Variations occur due to the load requirement and the operation of the network.

Fig. 20
figure 20

Power outputs under Case-1.

Full size image
Fig. 21
figure 21

Power outputs under Case-2.

Full size image
Fig. 22
figure 22

Power outputs under Case-3.

Full size image
Fig. 23
figure 23

Grid output voltage.

Full size image
Fig. 24
figure 24

Grid output current.

Full size image

The wind system also plays the same important role as the PV system, as this system is a hybrid model combining renewable systems and grid systems. A Voltage Source Inverter (VSI) that takes in the gate pulses from the pulse generator through a sinusoidal pulse width modulation (SPWM) methodology. The DC link power is passed through it and hence the distortion is removed by passing through a filter system present at the three-phase inverter output. Figures 20, 21, and 22 represent the three cases of power flow management. In Fig. 20 the photovoltaic power is 1.1 kW, the wind power is 110 W, the grid power is 902 W; therefore, it satisfies the condition Pdc = Ppv + Pw - Pgrid. In Fig. 21 It satisfies the configuration Ppv + Pw> Pgrid. In Fig. 22 It satisfies the condition Ppv + Pw< Pgrid. Hence, power management is successfully implemented in the given DC microgrid system using an adaptive PI controller. The final voltage of the grid and the current measured through the VI measurement block are shown in Figs. 23 and 24 for an adaptive PI controller system.

Figure 25 represents the THD value of the PI controller system, which resulted in a value of approximately 0.87.

Fig. 25
figure 25

THD of Grid voltage for PI controller system.

Full size image

Figure 26 represents the THD value of the adaptive PI controller system, which resulted in a value of only 0.26.

Fig. 26
figure 26

THD of Grid voltage for Adaptive PI controller system.

Full size image

Both the PI system and the adaptive PI controller have been shown in the form of waveforms comparing the PV system, the wind system, the battery system, and the grid system. The tabulated values of all these systems for both controllers are shown in Table 2.

Table 2 Performance comparison of PI and model reference adaptive controller.
Full size table

Table 2 mathematically proves that MRAC-PI dynamically adjusts its gains, improves tracking performance, and reduces steady-state error compared to the fixed-gain PI controller.

Conclusion

This paper introduces a model reference-based adaptive controller to contribute to efficient, resilient, and reliable power flow management in a microgrid system. Initially, a comparison of PI and MRAC is analyzed to check which controller offers better results by taking a variable input from laboratory data. Since real-time values are involved as the uncertainty grows, so is the stability of the system. To make the microgrid system more stable, an effective controller is chosen. The implementation of the microgrid system uses photovoltaic and wind as port-1 and port-2, respectively, while the battery system acts as a port-3 unit. All three ports are connected to an LVDC bus of 48 V, from the LVDC bus a tapping is taken and given to a grid-connected system. The platform used to implement the data is MATLAB Simulink. Photovoltaic and wind equipment is equipped with MPPT controller and the battery for bidirectional power flow to switch the battery from charging to discharging and vice versa based on the requirement. The initial proposed controller is a PI controller which plays a crucial role in regulating bus voltage by taking reference of bus voltage and bus current, Soc. The PI controller gives an error in the output voltage of around 30–40%. The model reference adaptive controller is implemented to overcome the error superiority of dealing with uncertainty in a dynamic way. The proposed simulation gives the operation of a DC microgrid system for various real-time values of irradiance and wind speed data collected from the laboratory. From the simulation results, MRAC provides reliable data when it comes to maintaining the DC bus voltage at 48V. The robustness of the model is analyzed using the predictive analysis of an MRAC which produces a stable output for variable conditions of the input.