Strong ground motion prediction model for EPA in Loess Plateau of Northwestern China

Abstract

Utilizing the database of seismic landslides and strong motion records from the Loess Plateau, 81 earthquakes with magnitudes ranging from 3.0 to 7.1 were undertaken. Furthermore, 2802 strong ground motion records were chosen as the focal points of our investigation. Through analysis of the variation pattern of effective peak acceleration (EPA) values, an EPA prediction model for the Loess Plateau was developed using both surface wave magnitude (M_s) and Das magnitude (M_wg). Furthermore, the study examines the discrepancies between this model and two other attenuation models. The results show that (1) the $\overline{\beta }$_max (maximum average amplification factor) values employed for the Loess Plateau differ from those specified in other established standards and span from 2.15 to 2.40 in the horizontal and vertical directions. (2) A negative correlation between EPA values and epicentral distance. The magnitudes and directions influence the rates of change of the fitting curves. (3) A positive correlation between the EPA values and earthquake magnitudes. The change rates of the fitting curves tend to increase first and then decrease, with the horizontal directions always being higher than the vertical directions. (4) The prediction equation based on M_wg exhibits residual standard deviations in the range of 0.493–0.536, which optimizes the fitting results and simplifies the fitting procedure to some extent. (5) The prediction model for the Loess Plateau differs from the reference models, with its fitting EPA values and attenuation rates being relatively lower.

Introduction

As a particular type of soil, loess is widely distributed in the Loess Plateau region of China, covering areas such as Shaanxi, Shanxi, Gansu, and Ningxia. Its total area is approximately 630,000 square kilometers, with significant thickness, vast coverage, and a network of ravines and gullies. Owing to its location in the seismic zones of both northern and southern China, as well as the northeastern margin of the Tibetan Plateau, the Loess Plateau is an area of active tectonic movement, frequent earthquakes, and significant secondary geological hazards^1,2,3,4. In conjunction with the region’s complex terrain and geological conditions, the loose and porous structural characteristics of loess sites induce a distinct dynamic response under seismic excitation. This interaction leads to modifications in the propagation path and amplification effects of ground motion^3,5,6,7. As crucial indices for assessing seismic intensity, spectral characteristics, propagation effects, and ground motion parameters accurately reflect the impact of ground motion on soil and structures. Therefore, conducting in-depth analysis and study of ground motion characteristics at Loess Plateau is paramount for the scientific and rational implementation of earthquake disaster prediction and mitigation measures in loess regions.

Research on ground motion prediction models primarily focuses on peak ground acceleration (PGA), peak ground velocity(PGV), response spectral, and seismic intensity^8,9,10,11,12. However, studies on effective peak acceleration (EPA) are relatively lacking. Among various ground motion parameters, EPA is a key index for reflecting ground motion intensity¹³. Unlike PGA, determined by the high-frequency peak of ground motion, EPA is essentially calculated by processing specific ground motion records to derive acceleration values that strongly correlate with structural response and the potential for ground motion-induced damage¹⁴. Therefore, the concept of EPA plays a crucial role in accurately reflecting the acceleration response of ground motion on building structures, predicting seismic intensity, and assessing the potential risk of damage and failure in structures¹⁵. On the basis of ground motion acceleration records from various periods and regions, numerous standards and scholars, both domestically and internationally, have studied the EPA from different perspectives. The calculation of EPA values was first defined in the Tentative Provisions for the Development of Seismic Regulations for Buildings, issued by the U.S. Applied Technology Council¹⁶ and the U.S. Geological Survey’s National Seismic-Hazard Maps: documentation¹⁷. It has been continuously applied in subsequent studies and remains an important reference for the current EPA calculation formula. For the definition of the maximum value of the seismic acceleration time history, the Seismic Ground Motion Parameters Zonation Map of China (GB 18306-2015) specifies that "the peak acceleration of ground motion is determined as 1/2.5 times the maximum value of the normalized ground motion acceleration response spectrum with a damping ratio of 5%"¹⁸. In the Chinese Code for Seismic Design of Buildings (GB 50011-2010) (2016 Edition)¹⁹, the effective peak acceleration (EPA) is determined by the maximum value of the seismic acceleration time history. Specifically, the maximum value of the seismic influence coefficient is divided by the amplification factor 2.25¹⁹. With respect to the influencing factors and variation patterns of the EPA, Chen et al.²⁰ argued that seismic waves with high frequencies attenuate rapidly, and the influence of vibrations with frequencies far from the structure’s natural frequency is minimal. Therefore, the EPA is a design parameter that reflects the impact of earthquakes. Matheu et al.²¹ demonstrated how to generate standard response spectra and the EPA under various earthquake scenarios, emphasizing the importance of the EPA in assessing earthquake hazards and improving seismic design standards. Based on seismic hazard analysis, Zhong et al.²² obtained PGA and EPA values for 12 engineering sites in the Jinsha River Basin. They investigated the influencing factors and the relationship between the two parameters, providing a theoretical foundation for understanding the variation in the EPA under different seismic conditions. Long et al.²³ analyzed the correlation between the EPA and seismic intensity via strong ground motion data from two seismic events in Sichuan Province as examples. Based on 666 strong ground motion records, Cao et al.²⁴ compared the EPA definitions and parameters in China and the United States, revealing the differences in EPA calculations under different definitions and their impacts on engineering design. Peng²⁵ studied the amplitude modulation of the EPA in selecting strong motion records and proposed a new amplitude modulation method to improve the accuracy and reliability of ground motion simulations. Using the finite element method, Zhang et al.²⁶ selected 100 actual ground motion records as seismic inputs to simulate and examine the response of the EPA to soil slopes under different definitions of seismic action. Additionally, Wan et al.²⁷ analyzed and evaluated the attenuation of the EPA across different directions by selecting 645 strong earthquake records from the Pazarcik earthquake in Turkey and developed a prediction model for EPA.

Currently, most existing studies focus on the definition of the EPA and compare calculation methods. Some studies rely on conversion fitting methods, using historical seismic data from various countries to establish prediction models, typically for bedrock sites. Research on EPA prediction models for soil sites, particularly loess sites, remains insufficient. Therefore, based on strong motion records from Loess Plateau, this paper investigates and establishes the relationships among the EPA, earthquake magnitudes, and epicentral distance. These findings provide a crucial basis for exploring the ground motion characteristics of Loess Plateau and enhancing the assessment and prevention capabilities for seismic geological disasters.

Strong motion records of the Loess Plateau

The data for this study are derived from the database of seismic landslides and strong motion records in the Loess Plateau, constructed by the author’s research group. The database includes information on 142 earthquakes on the Loess Plateau between 2001 and 2019, with magnitudes ranging from 2.4 to 7.1 and source depths between 4 and 33 km. The strong motion record database contains 3,144 three-direction strong motion records. Each record includes basic information such as the earthquake occurrence time, epicenter location, surface wave magnitude (M_s), epicentral distance (R_epi), source depth, number of trigger stations, station name and code, site conditions (the classification sites are based on V_S20 from the Chinese Code for Seismic Design of Buildings (GB 50011-2010) (2016 Edition)¹⁹, recording model, sampling interval of the strong motion accelerometer, and recording time²⁸.

Based on the existing database, this study utilizes SeismoSignal software (v2022) and follows the PEER NGA-West2 standard²⁹ to conduct baseline correction using linear polynomials (y = a₀ + a₁x). Meanwhile, to mitigate the impact of baseline drift on integral displacement, preserve the sensitive frequency band relevant to engineering structures, and minimize the interference of instrumental noise, a fourth-order Butterworth band-pass filter is applied to the selected strong motion records. The filter bandwidth is set to 0.1–25 Hz^30,31.

This approach corrects zero drift and deflection errors generated during data recording and removes low-quality records, such as those with incomplete waveforms or damaged channels. Owing to the limited distribution of strong earthquake stations and data collection constraints, relatively few stations exist at Class I and III sites, and the distributions of earthquake magnitudes and epicentral distances are not uniform. To explore the EPA prediction model for Loess Plateau reasonably and minimize the influence of anomalous earthquakes on the fitting process, a total of 81 earthquakes with magnitudes ranging from 3.0 to 7.1, recorded between 2008 and 2019, and with site conditions of Class II at the strong motion stations, were selected as the research data. There are 2802 strong ground motion records from the EW, NS, and UD directions, and epicentral distances ranging from 1 to 551 km. Table 1 describes the selected earthquakes’ names, occurrence dates, epicentral locations, source depths, and other information.

Table 1 List of earthquakes information.

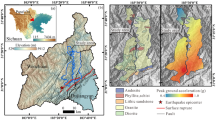
Using the database of seismic landslides and strong motion records in the Loess Plateau²⁸, spatial visualization was performed with ArcGIS 10.2 under the WGS84 geographic coordinate system. The epicenter locations of 81 earthquakes and the distribution of the triggered strong motion stations on the Loess Plateau were mapped, as shown in Fig. 1. A total of 358 Class II site strong motion stations were involved, distributed across Gansu (149), Sichuan (35), Shanxi (33), Shaanxi (31), Qinghai (45), Neimenggu (16), and Ningxia (49). For better visual observation, the epicentral locations were classified according to the magnitude categories of 3.0 ≤ M_s < 4.0, 4.0 ≤ M_s < 5.0, 5.0 ≤ M_s < 6.0, and M_s ≥ 6.0, represented by red dots of varying sizes.

Fig. 1

The epicentral locations and the distribution of strong motion stations for 81 earthquakes (This map was created using ArcGIS 10.2 (https://desktop.arcgis.com)).

Methods

The EPA is an energy index used to evaluate the acceleration response of ground motion on structures. It employs the response spectrum to derive the peak acceleration of ground motion, which reflects the average significance of the ground motion’s effect with the unit in gal¹³. Compared with the traditional PGA, the EPA considers a broader range of factors, including the amplitude and frequency characteristics of acceleration, making it an essential parameter for enhancing the safety and reliability of seismic engineering. The EPA values in different domestic and international specifications are calculated via the acceleration response spectrum with a damping ratio of 5%. The primary expression is provided in Eq. (1).

$${\text{EPA}} = \frac{{\overline{S}_{a} (T^{\prime })}}{{\overline{\beta }_{\max } (T^{\prime })}}$$

(1)

where $\overline{\beta }_{\max }$ represents the maximum value of the average amplification coefficient of the standard acceleration response spectrum. T' is the corresponding period to $\overline{\beta }_{\max }$. $\overline{S}_{a} (T^{\prime })$ is the value of the average acceleration response spectrum of the ground motion with a damping ratio of 0.05 at period T'.

However, the values of $\overline{\beta }_{\max }$ and T' have not been uniformly defined in the current mainstream domestic and international specifications. To explore the variations in EPA values for Loess Plateau in China reasonably and address the issue of the differing definitions and values of $\overline{\beta }_{\max }$ and T' in various specifications, this paper draws on relevant specifications from China and the United States. Additionally, it references current research on the design ground motion parameters for Loess Plateau³⁰, considering the differences in EPA definitions and the extent of variation in parameter values. Specifically, the period corresponding to T′ is defined as [0.1 s, T_g], and $\overline{\beta }_{\max }$ is the maximum average amplification factor of the standard acceleration response spectrum within the T′ frequency band.

For the $\overline{\beta }_{\max }$ value, this study employs the Nelder-Mead simplex algorithm. It converges faster on Loess Plateau as a local optimization method, with a slight standard deviation between the results and the actual response spectrum³². The calculation formula is shown in Eq. (2). The design response spectrum curve consists of three parts, a straight-line rising section, a platform section, and an exponential falling section, as shown in Fig. 2. After the design response spectrum and corresponding β_max values are obtained, a statistical analysis is performed to derive the results³³.

$$\begin{array}{*{20}l} {\beta {(}T{)} = \left\{ \begin{gathered} {1} + \frac{{\beta_{{{\text{max}}}} - {1}}}{{T_{{0}} }} \\ \beta_{{{\text{max}}}} \\ \beta_{{{\text{max}}}} \mathop {\left( {\frac{{T_{{\text{g}}} }}{T}} \right)}\nolimits^{\gamma } \\ \end{gathered} \right.} \hfill & \begin{gathered} 0 \, \le \, T \, \le \, T_{0} \\ T_{{0}} \, \le \, T \, \le \, T_{{\text{g}}} \, \\ \, \\ T_{{\text{g}}} \, \le \, T \, \le \, T_{{\text{m}}} \\ \end{gathered} \hfill \\ \end{array}$$

(2)

Fig. 2

Design response spectrum curve.

In Eq. (2), β(T) is the amplification factor of the response spectrum to the peak ground acceleration. β_max is the maximum amplification factor of the design response spectrum, also known as the plateau value. T₀ is the period corresponding to the intersection of the straight-line rising section and the platform section. T_g is the characteristic period. γ is the attenuation index of the design response spectrum.

After the corresponding EPA values are obtained, selecting the appropriate fitting methods and evaluation metrics is crucial for exploring the attenuation model. In this study, the least squares method is employed for data fitting, and the model parameters are iteratively adjusted to minimize the sum of the squared residuals between the observed and predicted values³⁴. The adjusted R² is used to evaluate the goodness of fit between the model and the data, aiming to explore the attenuation relationship between the amplitude or epicentral distance and the EPA values. The calculation process is shown in Eqs. (3) and (4).

$$R^{2} { = 1} - \frac{{\sum\limits_{i = 1}^{n} {(y_{i} - \mathop y\limits^{ \wedge }_{i} )^{2} } }}{{\sum\limits_{i = 1}^{n} {(y_{i} - \mathop y\limits^{ - }_{i} )^{2} } }}$$

(3)

In Eq. (3), y_i represents the i-th observed value, $\mathop y\limits^{ \wedge }_{i}$ represents the i-th predicted value, and $\mathop y\limits^{{ - }}_{i}$ represents the mean value of the observed values.

$${\text{Adjusted}}\;{ }R^{2} = 1 - \left( {\frac{{(1 - R^{2} )(n - 1)}}{n - p - 1}} \right)$$

(4)

In Eq. (4), n represents the number of observed data points, and p represents the number of independent variables. The adjusted R² value ranges from 0 to 1. A value closer to 1 indicates that the predicted values can effectively describe the changes in the observed values, whereas a value closer to 0 suggests that the model is not optimal.

Results

The values are first classified according to different directions to characterize the EPA values’ distribution range and variation characteristics accurately. The classification of magnitudes follows the criteria shown in Fig. 1, categorized into 3.0 ≤ M_s < 4.0, 4.0 ≤ M_s < 5.0, 5.0 ≤ M_s < 6.0, and M_s ≥ 6.0. The epicentral distances are divided into 0 ≤ R_epi < 30 km, 30 ≤ R_epi < 50 km, 50 ≤ R_epi < 100 km, and R_epi ≥ 100 km. The $\overline{\beta }_{\max }$ values for each direction are obtained via the Nelder-Mead simplex algorithm, as shown in Table 2.

Table 2 The calculation results of different direction $\overline{\beta }_{\max }$ values in loess site.

Compared with the $\overline{\beta }_{\max }$ values calculated from the ground motion data in this study, the results for the horizontal directions are close to the reference value of 2.5 provided by the United States National Seismic Hazard Maps¹⁷, Engineering Seismology¹³, and the Seismic Ground Motion Parameters Zonation Map of China (GB 18306-2015)¹⁸. The vertical direction value is 2.15, which is closer to the value of 2.25 specified in the Chinese Code for Seismic Design of Buildings (GB 50011-2010) (2016 Edition)¹⁹.

Based on the $\overline{\beta }_{\max }$ values, the EPA values for 745 sets of strong ground motion records are calculated, each containing two horizontal directions and one vertical direction. According to the classification method used in this study, Table 3 presents the mean EPA values for Class II sites under different ranges of magnitude and epicentral distance.

Table 3 The mean EPA values for different magnitudes and epicentral distances.

The mean EPA values in the EW direction range from 2.42 to 57.24 gal, in the NS direction range from 2.50 to 53.40 gal, and in the UD direction span from 0.98 to 68.19 gal. The mean EPA values in the horizontal direction are approximately 1.26 times greater than that in the vertical direction. It is worth noting that the differences in seismic wave propagation paths between different directions result in distinct characteristics for the average EPA values in the EW and NS directions. Therefore, discussing them separately to observe their differences is still meaningful. Overall, the mean EPA values in the horizontal direction are smaller than those in the vertical direction only when M_s ≥ 6.0 and 0 ≤ R_epi < 30 km. In all other cases, the mean EPA values in the horizontal direction exceed that in the vertical direction. When the magnitude is constant, the mean EPA values in each direction decrease with increasing epicentral distance, and the attenuation rate increases progressively as the magnitude range expands. Conversely, when the epicentral distance is constant, the mean EPA values in each direction increase with magnitude, but the attenuation rate gradually decreases as the epicentral distance range increases.

Relationships between EPA and epicentral distance

Building upon the existing mainstream EPA prediction results and considering the effect of near-field high-frequency ground motion saturation^35,36,37, the EPA prediction model proposed in this study is presented in Eq. (5) while maintaining consistent site conditions. To accurately construct the EPA prediction model, this study integrates the application of seismic prediction models in earthquake engineering³⁸ and employs the stepwise regression method proposed by Xiao and Yu³⁹. This approach accounts for the impact of parameter regression error on the overall error, effectively controlling potential multicollinearity in the fitting process. In the regression procedure, specific parameters are incrementally introduced step by step since the impact of the error of each parameter on the variance of the outcomes varies. In order to avoid parameter coupling and the uncertainties inherent in direct fitting, parameters that have the least influence in terms of error are first identified. Subsequently, the regression analysis is carried out in an orderly manner. It commences with the epicentral distance term and is followed by the magnitude term.

For the selection of distance parameters, to accurately describe the attenuation characteristics of near-field high-frequency ground motion, it is generally recommended to use either the fault rupture distance (R_RUP) or the Joyner-Boore distance (R_JB), which represents the shortest horizontal distance from the station to the surface projection of the fault⁴⁰. In this study, due to the paucity of seismic fault data and the fact that most of the earthquakes considered are shallow and in the far-field, the difference between the fault distance or fault projection distance and the epicentral distance (R_epi) is negligible. Therefore, the R_epi is chosen as the distance parameter. Taking practical applications into account, this study employs the widely-used surface wave magnitude (M_s) as a parameter to represent the source radiation energy. Meanwhile, it still adheres to the magnitude and epicentral distance classification criteria established above.

$$\ln {\text{EPA = }}c_{{1}} { + }c_{2} M_{{\text{s}}} + c_{3} M_{{\text{s}}}^{2} + c_{4} \ln [R_{{{\text{epi}}}} + c_{5} \exp (c_{6} M_{{\text{s}}} )] + \delta$$

(5)

M_s represents the surface wave magnitude, R_epi represents the epicentral distance, and c₁, c₂, c₃, c₄, c₅, and c₆ represent the regression constants, δ represents fitting error.

The specific operational procedure is as follows: First, only the geometric diffusion and non-elasticity attenuation of energy are considered, simplifying the prediction model to Eq. (6)¹³. Then, the least squares method is employed to compute the R² value between the fitting curve and the actual EPA values, thereby assessing the influence of the epicentral distance. In the equation, f(R_epi) is a function of the epicentral distance, and a, b, and i are regression constants.

$$f{(}R_{{{\text{epi}}}} {\text{) = lnEPA = }}i{ + }a{\text{ln(}}R_{{{\text{epi}}}} { + }b{)}$$

(6)

The EPA values in the EW, NS, and UD directions for different magnitude ranges are shown in Figs. 3, 4, 5, 6. The vertical axis represents the EPA values, while the horizontal axis represents epicentral distance. The red line represents the fitting curve.

Fig. 3

The EPA values for each direction and the corresponding fitting curves with epicentral distance when the M_s is between 3.0 and 4.0.

Fig. 4

The EPA values for each direction and the corresponding fitting curves with epicentral distance when the M_s is between 4.0 and 5.0.

Fig. 5

The EPA values for each direction and the corresponding fitting curves with epicentral distance when the M_s is between 5.0 and 6.0.

Fig. 6

The EPA values for each direction and the corresponding fitting curves with epicentral distance when the M_s is greater than or equal to 6.0.

When the M_s range is 3.0 to 4.0, the EPA values for the EW, NS, and UD directions vary from 0.63 to 30.92 gal, 0.46 to 41.69 gal, and 0.18 to 19.73 gal, respectively, with the horizontal direction EPA values generally higher than the vertical direction values. Consistent with the trend in the mean EPA values, the EPA values for different directions decrease as the epicentral distance increases. Based on the fitting results, the equations for each direction’s fitting curve are as follows, lnEPA = 7.78 − 1.70ln(R_epi + 12.32), lnEPA = 6.75 − 1.47ln(R_epi + 9.29), and lnEPA = 6.06 − 1.55ln(R_epi + 7.12), corresponding to R² values of 0.90, 0.88, and 0.89, respectively. When the epicentral distance is less than 10 km, the EPA values for all directions decrease at the slowest rate, after which the decay rate gradually increases, indicating a distinct nonlinear relationship. However, when the directions are compared, the EPA value decays more slowly in the vertical direction than in the horizontal direction.

When the M_s range is 4.0 to 5.0, the EPA values for the EW, NS, and UD directions vary from 0.26 to 142.22 gal, 0.24 to 146.81 gal, and 0.16 to 70.52 gal, respectively, with the horizontal direction EPA values again being higher than the vertical direction values. The EPA values for all directions tend to decrease with increasing epicentral distance. Based on the fitting results, the equations for each direction’s fitting curve are as follows, lnEPA = 6.84 − 1.25ln(R_epi + 11.53), lnEPA = 7.13 − 1.30ln(R_epi + 12.30), and lnEPA = 5.04 − 1.01ln(R_epi + 2.06), corresponding to R² values of 0.92, 0.90, and 0.93 respectively. The attenuation rate of the UD component EPA values shows slight variation with increasing epicentral distance. In contrast, the attenuation rate in the horizontal direction is generally faster than that in the vertical direction. Taking 100 km as a boundary, the EPA value decay rates before and after this distance show an increasing nonlinear relationship.

When 5.0 ≤ M_s < 6.0, the EPA values for the three directions (EW, NS, UD) range from 0.30 to 175.28 gal, 0.31 to 130.04 gal, and 0.12 to 111.26 gal, respectively, although the horizontal directions still present higher EPA values than the vertical direction does, the overall difference is relatively minor. The EPA values for all directions consistently decrease with increasing epicentral distance. The equations are as follows, lnEPA = 7.29 − 1.30ln(R_epi + 0.55), lnEPA = 8.20 − 1.44ln(R_epi + 9.86), and lnEPA = 6.76 − 1.35ln(R_epi + 2.55), corresponding to R² values of 0.88, 0.92, and 0.91, respectively. Concerning the attenuation rates, the horizontal directions continue to decay faster than the vertical direction. However, unlike earlier findings, the attenuation rates of the EPA values in all directions do not change significantly as the epicentral distance increases.

When M_s ≥ 6.0, the EPA values for the three directions (EW, NS, UD) vary from 0.25 to 47.15 gal, 018 to 49.17 gal, and 0.10 to 28.38 gal, respectively, and the EPA values for the different directions exhibit an inverse relationship with the epicentral distance. However, owing to the limited data collected in the near-field range for this magnitude range, the overall EPA values are lower than those for the previous magnitude range, and differences between the directions remain. The horizontal directions have higher EPA values than the vertical direction. The equations are as follows, lnEPA = 9.07 − 1.50ln(R_epi + 14.56), lnEPA = 9.10 − 1.65ln(R_epi + 14.09), and lnEPA = 8.92 − 1.58ln(R_epi + 13.86), corresponding to R² values of 0.90, 0.92, and 0.90, respectively. The attenuation rate of the vertical direction’s EPA values is lower than that of the horizontal directions, which remains consistent with previous trends. The EPA attenuation rate is approximately linearly related, similar to the trend observed for 5 ≤ M_s < 6.

Overall, the fitted curves, considering the earthquake magnitude, can effectively reflect the variation of the actual EPA values. Although there may be some differences within different magnitude ranges, the overall trend shows that, with increasing epicentral distance, the EPA values generally decrease. Regarding attenuation rates, the horizontal directions consistently exhibit higher attenuation rates than the vertical direction.

Although variations may occur across different magnitude ranges, the overall trend indicates that the EPA values decrease with increasing epicentral distance. Additionally, the horizontal components consistently exhibit a lower attenuation rate than the vertical component. This finding is consistent with the stipulation in the Chinese Code for Seismic Design of Buildings (GB 50011-2010) (2016 Edition)¹⁹, which mandates that the ratio of horizontal to vertical design acceleration is 2/3. Moreover, it indirectly validates the resemblance between the EPA and the PGA.

Relationships between EPA and M _s

Similarly, fitting is performed based on the classification of epicentral distance and considering the effects of magnitude and characteristics of near-field ground motion, and the R² values of the fitting curves are also calculated for analysis¹³. The predictive equation is expressed in the form of Eq. (7)¹³, f(M_s) is the function related to magnitude, and d, e, h are the regression constants. The EPA values for the EW, NS, and UD directions at different epicentral distances are presented in Figs. 7, 8, 9, 10. The ordinate represents the EPA value in these figures, and the abscissa denotes the magnitude. The red line represents the fitting curve.

$$f{(}M_{{\text{s}}} {\text{) = lnEPA = }}d{ + }eM_{{\text{s}}} { + }hM_{s}^{2}$$

(7)

Fig. 7

The EPA values for each direction and the fitting curves with M_s when the R_epi is between 0 and 30 km.

Fig. 8

The EPA values for each direction and the fitting curves with M_s when the R_epi is between 30 and 50 km.

Fig. 9

The EPA values for each direction and the fitting curves with M_s when the R_epi is between 50 and 100 km.

Fig. 10

The EPA values for each direction and the fitting curves with M_s when the R_epi greater than or equal to 100 km.

When the R_epi ranges from 0 to 30 km, the EPA values for the EW, NS, and UD directions vary from 0.53 to 183.65 gal, 0.36 to 232.75 gal, and 0.35 to 111.27 gal, respectively. The EPA values for the horizontal directions are consistently higher than those for the vertical direction. The fitting equations for each direction are lnEPA = − 10.60 + 5.33M_s − 0.47(M_s)², lnEPA = − 9.93 + 5.08M_s − 0.45 (M_s)², and lnEPA = − 10.78 + 5.13M_s − 0.45(M_s)², corresponding to R² values of 0.89, 0.90, and 0.93, respectively. The fitting curves represent the trends of the EPA values well. As the magnitude increases, the EPA values for all directions show an increasing trend. The results of the fitting curves are generally consistent with the trend shown in Table 3. When 3.0 ≤ M_s < 5.0, the EPA values increase significantly, with the fastest growth rate observed, whereas for M_s ≥ 5.0, the increase in the EPA values slows, with the increase gradually decreasing.

When the R_epi ranges from 30 to 50 km, the EPA values for the EW, NS, and UD directions vary from 0.71 to 84.89 gal, 0.84 to 89.68 gal, and 0.30 to 28.38 gal, respectively. Compared with those in the 0–30 km range, the horizontal direction EPA values in this range are significantly greater than the vertical direction values, although the overall EPA values decrease. The fitting equations for each direction are lnEPA = − 7.62 + 3.73M_s − 0.32(M_s)², lnEPA = − 8.60 + 4.10M_s – 0.35(M_s)², and lnEPA = − 8.98 + 3.84M_s – 0.32(M_s)², corresponding to R² values of 0.91, 0.90, and 0.89, respectively. The fitting results for the EPA values as a function of magnitude are similar to those shown in Table 3. For 3.0 ≤ M_s < 4.0, the EPA values increase significantly, with the fastest growth rate, whereas for M_s ≥ 4.0, the rate of increase begins to slow.

When the R_epi ranges from 50 to 100 km, the EPA values for the EW, NS, and UD directions vary from 0.52 to 66.66 gal, 0.63 to 31.97 gal, and 0.27 to 16.84 gal, respectively. Compared with the values in the previous two epicentral distance ranges, the horizontal direction EPA values in this range are still higher than the vertical direction values. However, owing to the increased epicentral distance, the EPA values show a further decreasing trend. The fitting equations for each direction are lnEPA = − 11.50 + 4.62M_s − 0.38(M_s)², lnEPA = − 5.26 + 2.40M_s − 0.19(M_s)², and lnEPA = − 5.07 + 2.05M_s − 0.16 (M_s)², corresponding to R² values of 0.89, 0.93, and 0.93, respectively. The nonlinear variation in the EPA values with magnitude weakens in this range, with only the EPA values in the EW direction showing a significant increase when 3.0 ≤ M_s < 4.0. The growth rates of the EPA values and the magnitudes in the other directions are relatively moderate.

When the R_epi greater than or equal to 100 km, the EPA values for the EW, NS, and UD directions vary from 0.26 to 32.12 gal, 0.24 to 46.52 gal, and 0.10 to 15.92 gal, respectively. The EPA values for the horizontal directions are still higher than those for the vertical directions. Compared with those in the previous three epicentral distance ranges, the EPA values in all directions decreased to their lowest values. The fitting equations for each direction are lnEPA = − 12.39 + 4.55M_s − 0.37(M_s)², lnEPA = − 11.86 + 4.41M_s − 0.36(M_s)², and lnEPA = − 7.71 + 2.60M_s − 0.19(M_s)², corresponding to R² values of 0.88, 0.90, and 0.91, respectively. The curve shows a significant increase when M_s < 4.0, after which the growth rate decreases. The EPA values exhibit an approximately linear growth trend as the magnitude increases.

Based on the results presented in Figs. 7, 8, 9 and 10, intuitively, the fitting curves considering the magnitude well reflect the actual changes in EPA values. Firstly, the EPA values in the horizontal directions are consistently higher than in the vertical direction. Moreover, the EPA values in every direction escalate as the earthquake magnitude increases, which is in excellent accordance with the general tendency of the average EPA values. These results show a positive correlation between the EPA value and the earthquake’s magnitude. The larger the magnitude, the higher the EPA value.

This phenomenon is in line with the existing research results as well. The magnitude of an earthquake is intimately associated with the energy released during the seismic event, and this released energy has a direct bearing on the peak ground motion parameters. Many studies have demonstrated a positive correlation between the PGA or the EPA and the earthquake magnitude. Nevertheless, it should be noted that this correlation is not a straightforward linear relationship⁴¹. Theoretically speaking, as the earthquake magnitude increases, the energy released at the seismic source also escalates, and both the PGA and the EPA are inclined to exhibit an approximately linear increasing trend. Nevertheless, as the magnitude continues to rise, the energy released at the rupture surface of the source might be distorted as a result of inaccurate energy estimation. This distortion can cause the values of PGA or EPA to show a bias towards lower magnitudes. This particular phenomenon is referred to as the energy saturation effect⁴². Within a given range of epicentral distances, the rate of change in EPA values gradually decreases as earthquake magnitude increases. However, in this study, the M_s range is only from 3.0 to 7.1, and higher magnitudes are not considered. As a result, to comprehensively understand how the energy saturation effects specifically influence the variation pattern of the EPA values for earthquakes of higher magnitudes, additional in-depth research is essential.

The EPA prediction model based on M _s

After integrating the surface wave magnitude to represent the source effect and considering the epicentral distance to reflect the impact of the propagation medium, and with the site conditions remaining constant, the calculated regression coefficients for various directions in the final EPA prediction equations are shown in Table 4. The residuals between the actual EPA values and the predicted values are computed to evaluate the goodness of the regression outcomes for the attenuation relationship. As illustrated in Fig. 11, the correlations among the EPA residual, M_s, and R_epi are depicted. Moreover, the standard deviation of the residual(σ) is incorporated as an assessment criterion to verify the regression performance of the prediction model put forward in this research. The range of the residuals is from − 1.50 to 1.24 in the EW direction, from − 1.45 to 1.36 in the NS direction, and from − 1.43 to 1.35 in the UD direction. Upon calculation, the σ errors is 0.555 in the EW direction, 0.567 in the NS direction, and 0.504 in the UD direction. The points in the residual figures are mostly centered within a horizontal band, and the mean residuals for each direction are close to zero, indicating that the deviation in predicting the EPA values for different magnitudes and epicentral distances on Loess Plateau is relatively small.

Table 4 Calculation results of the EPA prediction model parameters for each direction under M_s.

Fig. 11

Distribution of the residuals for EPA values of each direction under M_s with earthquake magnitude and epicentral distance.

To reflect the attenuation of EPA values in different directions with epicentral distance under the M_s magnitudes, representative magnitudes of 3.5, 4.5, 5.5, and 6.5 are selected for calculation, corresponding to the magnitude ranges of 3.0 ≤ M_s < 4.0, 4.0 ≤ M_s < 5.0, 5.0 ≤ M_s < 6.0, and M_s ≥ 6.0, respectively, based on the magnitude classification criteria and Table 4 in this paper. The results are presented in Fig. 12. When the epicentral distance is 1 km, the EPA values range from 19.86 to 407.72 gal in the EW direction, from 21.25 to 333.37 gal in the NS direction, and from 12.95 to 189.42 gal in the UD direction. As both magnitude and epicentral distance increase, the EPA values gradually decrease.

Fig. 12

Based on the regression results, the attenuations of EPA values in different directions with epicenter distances are fitting when 3.0 ≤ M_s < 4.0, 4.0 ≤ M_s < 5.0, 5.0 ≤ M_s < 6.0 and M_s ≥ 6.0.

The EPA prediction model based on M _wg

However, it is widely recognized that the magnitude selection plays a pivotal role in formulating an EPA prediction equation. Existing studies have shown that the approximate maximum saturation limit of the M_s is around 8.3⁴³. This situation makes it challenging to predict the relevant parameters for earthquakes with higher magnitudes accurately. Kanamori⁴⁴ introduced the moment magnitude (M_w) to address this issue to mitigate the magnitude saturation phenomenon at large magnitudes. The M_w is solely determined by the seismic moment (M₀), which depends on the shear modulus, rupture area, and slip amount near the fault, and is not sensitive to the temporal characteristics of fault rupture and source depth⁴⁴. As M₀ reflects the seismic energy released by fault slip, it primarily derives from the low-frequency components of seismic wave amplitudes. Although M_w mitigates the effects of magnitude saturation, it tends to introduce inherent amplification when used to invert seismic moments for earthquakes with M_w < 7.5⁴⁵. This phenomenon can increase magnitude estimation errors for small to moderate earthquakes and limit its ability to accurately characterize the variability of near-field and high-frequency ground motions^43,46. In addition, the scaling coefficient of M_w is typically derived based on the assumption of an average stress drop at the global or regional scale, which may result in significant deviations when applied to other regions. Furthermore, many historical earthquakes in China with strong-motion records lack calibrated moment magnitudes, further limiting M_w's applicability as a regression parameter in regional ground motion studies.

To address this issue, this study introduces the Das magnitude (M_wg), which is not derived from seismic source parameters but obtained through a weighted inversion of observed ground motion records⁴⁶. M_wg aims to characterize the features of strong ground motion records more accurately⁴⁷. It can be interpreted as an optimal magnitude solution tailored to each earthquake, effectively capturing the response characteristics of medium and high-frequency ground motions, eliminating the constraints imposed by the upper limit of surface wave integration, and avoiding the magnitude saturation effect⁴⁸. This feature makes M_wg particularly suitable for regions with frequent small to moderate magnitude earthquakes and infrequent large events. Recent studies have shown that the M_wg integrates the understanding of global tectonic processes, accounts for the influence of source depth, and distinguishes the spectral attenuation characteristics of shallow and intermediate-to-deep earthquakes through a frequency band weighting factor, thereby offering advantages in evaluating earthquakes across different tectonic environments^49,50,51. Moreover, since it is derived from directly observed seismic data, it exhibits a stronger correlation with other magnitude scales, thereby overcoming the limitations of both M_s and M_w^46,47.

To ensure the prediction results reasonably capture the attenuation trend of EPA at large magnitudes, a prediction model with strong regional adaptability, low residuals, and high predictive capability is developed. This study introduces M_wg as a parameter to represent the radiation energy of the seismic source. Based on the research findings of Das et al.⁴³, the existing M_s values are converted to M_wg.

When M_s ≤ 6.1, the specific conversion formulas are presented in Eq. (8).

$$M_{{{\text{wg}}}} = 0.688M_{{\text{s}}} + 1.672$$

(8)

When M_s ≥ 6.2, the specific conversion formulas are presented in Eq. (9).

$$M_{{{\text{wg}}}} = 1.073M_{{\text{s}}} - 0.646$$

(9)

While maintaining the original classification intervals for epicentral distance, the relationship between EPA values and M_wg is further examined using Eq. (7)¹³. The fitting curves’ R² values are also calculated for analysis¹³. As shown in Figs. 13, 14, 15, 16, the variation trends of EPA values concerning M_wg are illustrated for the EW, NS, and UD directions across different ranges of epicentral distance. The vertical axis represents the EPA values, the horizontal axis represents M_wg, and the red line indicates the fitting curve.

Fig. 13

The EPA values for each direction and the fitting curves with M_wg when the R_epi is between 0 and 30 km.

Fig. 14

The EPA values for each direction and the fitting curves with M_wg when the R_epi is between 30 and 50 km.

Fig. 15

The EPA values for each direction and the fitting curves with M_wg when the R_epi is between 50 and 100 km.

Fig. 16

The EPA values for each direction and the fitting curves with M_wg when the R_epi greater than or equal to 100 km.

When 0 ≤ R_epi < 30 km, the EPA values in the EW, NS, and UD directions range from 0.53 to 183.65 gal, 0.36 to 232.75 gal, and 0.35 to 111.27 gal, respectively. The corresponding fitting equations for each direction are lnEPA = − 25.77 + 10.73M_wg − 0.95(M_wg)², lnEPA = − 16.81 + 7.28M_wg − 0.63(M_wg)², and lnEPA = − 36.61 + 14.30M_wg − 1.25(M_wg)², with R² values of 0.90, 0.91, and 0.92, respectively. The EPA values in different directions positively correlate with Mwg, and the growth rate is significantly higher in the 3.0 ≤ M_wg < 5.0 range than for M_wg ≥ 5.0.

When 30 ≤ R_epi < 50 km, the EPA values in the EW, NS, and UD directions range from 0.71 to 84.89 gal, 0.84 to 89.68 gal, and 0.30 to 28.38 gal, respectively. The corresponding fitting equations for each direction are lnEPA = − 18.27 + 7.40M_wg − 0.62(M_wg)², lnEPA = − 18.96 + 7.64M_wg − 0.64(M_wg)², and lnEPA = − 12.85 + 4.79M_wg − 0.36(M_wg)², with R² values of 0.93, 0.93, and 0.92, respectively. The EPA values in all directions increase with M_wg, and the rate of increase is greater in the range of 3.0 ≤ M_wg < 5.0 than for M_wg ≥ 5.0.

When 50 ≤ R_epi < 100 km, the EPA values in the EW, NS, and UD directions range from 0.52 to 66.66 gal, 0.63 to 31.97 gal, and 0.27 to 16.84 gal, respectively. The corresponding fitting equations for each direction are lnEPA = − 25.77 + 10.73M_wg − 0.95(M_wg)², lnEPA = − 16.81 + 7.28M_wg − 0.63(M_wg)², and lnEPA = − 36.61 + 14.30M_wg − 1.25(M_wg)², with R² values of 0.90, 0.91, and 0.92, respectively. The EPA values in all directions increase with increasing M_wg, but the growth rate gradually decreases as M_wg becomes larger.

When R_epi ≥ 100 km, the EPA values in the EW, NS, and UD directions range from 0.52 to 66.66 gal, 0.63 to 31.97 gal, and 0.27 to 16.84 gal, respectively. The corresponding fitting equations for each direction are lnEPA = − 4.62 + 0.94M_wg − 0.07(M_wg)², lnEPA = − 6.11 + 2.22M_wg − 0.15(M_wg)², and lnEPA = − 6.23 + 1.95M_wg − 0.13(M_wg)², with R² values of 0.90, 0.91, and 0.92, respectively. The EPA values in different directions positively correlate with M_wg, while the growth rate decreases as M_wg increases, indicating a negative correlation between growth rate and M_wg.

According to the results presented in Figs. 13, 14, 15, 16, the fitting curves based on M_wg effectively capture the variation in EPA values and exhibit trends similar to those based on M_s. Additionally, influenced by seismic wave energy, EPA values in the horizontal directions are generally higher than those in the vertical direction, and EPA values increase with increasing earthquake magnitude. Moreover, under varying epicentral distances, the growth rate of EPA values gradually decreases with increasing M_wg.

On this foundation, to formulate more suitable attenuation equations for predicting the EPA values under the condition of the M_wg. It is necessary to utilize the standard deviation σ to investigate the sensitivity of the geometric mean moment magnitude M_wg to the magnitude saturation term c₃M² in Eq. (5) based on the current fitting method. Upon calculation, if the original equation is still used for fitting, the sigma in each direction increases significantly by approximately 0.3, indicating a rise in the uncertainty of the prediction results. Consequently, removing the c₃M² term in the subsequent fitting process is essential. The final fitting equation is presented in Eq. (10).

$$\ln {\text{EPA = }}c_{{1}} { + }c_{2} M_{{{\text{wg}}}} + c_{4} \ln [R_{{{\text{epi}}}} + c_{5} \exp (c_{6} M_{{{\text{wg}}}} )] + \delta$$

(10)

M_wg represents the Das magnitude scale, R_epi represents the epicentral distance, and c₁, c₂, c₄, c₅, and c₆ represent the regression constants, δ represents fitting error.

The calculation results of the regression coefficients in different directions are shown in Table 5. The residuals in different directions, along with the magnitude and epicentral distance, are also expanded along the x-axis symmetry, as shown in Fig. 17. The residual range in the EW direction is − 1.11 to 1.35, in the NS direction is − 1.35 to 1.37, and in the UD direction is − 1.33 to 1.35. The EW, NS, and UD directions σ are 0.536, 0.547, and 0.493, respectively. Compared to the prediction results based on M_s, the residual range and residual standard deviation of the prediction results using M_wg in the three directions show little difference. However, the prediction results with M_wg are greater, especially for small epicentral distances and large magnitudes, where the errors are smaller than those obtained with M_s.

Table 5 Calculation results of the EPA prediction model parameters for each direction under M_wg.

Fig. 17

Distribution of the residuals for EPA values of each direction under M_wg with earthquake magnitude and epicentral distance.

The variation characteristics of EPA values under different M_wg magnitudes are based on the calculation results presented in Table 5. For the magnitude intervals of 3.0 ≤ M_wg < 4.0, 4.0 ≤ M_wg < 5.0, 5.0 ≤ M_wg < 6.0, and M_wg ≥ 6.0, representative M_wg values of 3.5, 4.5, 5.5, and 6.5, respectively, are selected for analysis. The results are shown in Fig. 18. When the epicentral distance is 1 km, the EPA values in the EW direction range from 17.13 to 435.09 gal, in the NS direction from 12.91 to 354.84 gal, and in the UD direction from 15.02 to 189.78 gal. The EPA values show a negative correlation with both magnitude and epicentral distance. However, regarding numerical value, the EPA values based on M_wg are slightly lower than those based on M_s.

Fig. 18

Based on the regression results, the attenuations of EPA values in different directions with epicenter distance are fitting when 3.0 ≤ M_wg < 4.0, 4.0 ≤ M_wg < 5.0, 5.0 ≤ M_wg < 6.0 and M_wg ≥ 6.0.

Discussion

In this study, ground motion prediction equations for EPA were developed using both M_s and M_wg. While M_s has been widely employed in ground motion parameter modeling, it exhibits notable limitations. Due to magnitude saturation, M_s tends to underestimate the energy release of large earthquakes and becomes unreliable for small events (M_s < 4.0) where surface wave signals are weak or absent^43,48. In contrast, M_wg, derived from body wave characteristics, is less affected by saturation and remains consistent across a wider magnitude range and varying focal depths, including deep-focus events⁴⁶.

Through the analysis and comparison of the residual standard deviation and the fitting degree of the two magnitude models, we found that, compared to the M_s, the residual standard deviations of the M_wg are reduced by 0.011–0.040, while the R² values of the fitting curves at different epicentral distance ranges increase by 0.01–0.02. These results indicate that the M_wg exhibits slightly better fitting and predictive performance, confirming its reliability and applicability at loess sites. Therefore, M_wg is considered a more suitable magnitude parameter for ground motion modeling in such regions.

Meanwhile, this study selects two prediction models for reference to validate the accuracy and variability of the calculation results. One of the prediction models is that of Yu et al.³⁷, which uses the seismic zone as the basic unit and fully considers the regional differences in strong ground motion attenuation. Based on this approach, China is divided into four regions. According to the collected bedrock ground motion records, the EPA attenuation relationship for different regions of China is provided and applied in the Seismic Ground Motion Parameters Zonation Map of China (GB 18306-2015)¹⁸. The other model is from Wang¹, who based his work on the bedrock ground motion records from the Loess Plateau. This model primarily focuses on the attenuation characteristics of PGA in the Loess Plateau, mainly attention to the prediction results of PGA. Moreover, by combining the proportional relationship between EPA and PGA, the EPA attenuation relationship for the region is derived.

To ensure the validity of the model comparison, the selected EPA values were excluded from the model fitting process. The EPA attenuation results of the prediction equation under M_wg are then compared with the results of the two models at magnitudes 5.3 and 6.7, respectively. The results are shown in Figs. 19 and 20, where the orange points represent the actual EPA values, and the blue curve represents the EPA attenuation results calculated via the prediction model proposed in this study. The red dotted line represents the EPA attenuation curves obtained via the prediction model of Yu et al.³⁷ The green dotted line represents the EPA attenuation curves obtained by Wang¹. To better compare the degree of correspondence between the three prediction models and the actual EPA values, the corresponding R² values are also provided in the legend.

Fig. 19

The attenuation curves based on M_wg (M_s = 5.3) are compared with those of Yu et al.³⁵ and Wang¹ models, as well as the fitting conditions with the actual EPA values in different directions.

Fig. 20

The attenuation curves based on M_wg (M_s = 6.7) are compared with those of Yu et al.³⁵ and Wang¹ models, as well as the fitting conditions with the actual EPA values in different directions.

When the M_s is 5.3, the R² range of the fitting curve in this paper is 0.88–0.90, which is higher than the two reference models in all directions. The model’s horizontal and vertical attenuation curves in this study are lower than those of Yu et al.³⁷ and Wang¹ models when the R_epi is less than approximately 22 km and 11 km, respectively. When the R_epi is in the range of 23 to 150 km and 11 to 147 km, the horizontal and vertical attenuation curves of the model in this study start to be higher than those of the Wang¹ model but remain lower than those of the Yu et al.³⁷ model. When the R_epi exceeds 120 km and 106 km, the attenuation curves of the model in this study are higher than both reference models in all directions.

When the M_s is 6.7, the R² range of the fitting curve in this paper is 0.83–0.88, which is also higher than the two reference models in all directions. The model’s horizontal and vertical attenuation curves in this study are lower than those of Yu et al.³⁷ and Wang¹ models when the R_epi is less than approximately 201 km, 236 km, and 197 km, respectively. When the R_epi is between 354 and 300 km, the horizontal attenuation curves of the model in this study start to be higher than that of the Wang¹ model. When the R_epi exceeds 425 km, it becomes higher than both reference models. The vertical attenuation curve, however, only becomes higher than the Wang¹ model when the R_epi exceeds 198 km but overall remains lower than the Yu et al.³⁷ model.

The EPA values from the reference models and the model in this study exhibit a consistent overall trend under different magnitudes, gradually decreasing as the epicentral distance increases. However, there are differences in the initial values and attenuation rates. When the epicentral distance is small, the EPA values of the bedrock are higher than that of the loess site. As the seismic intensity decreases, the damping effect in the nonlinear behavior of the soil layer diminishes, and the amplifying effect becomes more pronounced, leading to relatively larger EPA values for the loess site. Moreover, as the magnitude increases, the epicentral distance corresponding to this phenomenon tends to move backward. In terms of attenuation rate, compared to the two reference models, the attenuation curves in this study model exhibit slower decay with increasing distance for different magnitudes and directions. Overall, the model whole shows the characteristics of long-distance and slow attenuation. This result is generally consistent with the attenuation results for the PGA at Loess Plateau obtained by Li et al.³⁰ Compared with the reference models, the attenuation trend predicted by the model in this study better matches the observed changes in EPA values, providing a more accurate reflection of the EPA value variations in the Loess Plateau region.

Furthermore, several aspects remain worthy of consideration in this research. Firstly, within the current magnitude range, the prediction equation obtained by fitting with the M_wg does not exhibit substantial differences compared to the equation based on the M_s. Nevertheless, as a component of scientific advancement, it not only alleviates the magnitude saturation effect seen in the original equation but also reduces the complexity of the model’s prediction process. This further highlights the global applicability of M_wg. Notwithstanding these merits, owing to the scarcity of ground motion data from near-field large earthquakes in the Loess Plateau, the model requires further refinement to improve its prediction accuracy.

Secondly, although this study employs a new model algorithm to reduce uncertainty, the incompleteness of the database still results in systematic differences between the predicted EPA values and observed data, which need further refinement. Additionally, the calculated $\overline{\beta }_{\max }$ values in all directions are lower than the reference values specified in current regulations. According to existing research, loess sites’ unique dynamic characteristics and high-frequency attenuation phenomena contribute to this discrepancy. Compared with hard soil or bedrock sites, the thickness of the overburdened soil layer is a key factor influencing the $\overline{\beta }_{\max }$ values and the deviation of the predicted results⁵².

Given this, future research should focus on collecting more representative strong ground motion records under various site conditions in the Loess Plateau to gain a comprehensive and in-depth understanding of ground motion characteristics. Additionally, improving the fundamental data of relevant seismic monitoring stations is essential. These efforts will be crucial for optimizing the prediction equations, enhancing the accuracy and reliability of predictions, and ultimately enabling a more precise evaluation of the seismic response of loess sites.

Conclusions

This study is based on 81 earthquakes in the Loess Plateau region of Northwestern China. Using the existing EPA calculation theory and the least squares fitting method, this study explores the variation in EPA values with magnitude and epicentral distance. It provides an EPA prediction model applicable to the Class II sites of Northwestern China. The main conclusions are as follows.

• (1) The EPA values for different directions of Loess Plateau, which are calculated via the Nelder-Mead simplex algorithm, differ from those specified in current relevant standards. The range of the $\overline{\beta }_{\max }$ values for the different directions is between 2.15 and 2.40, which is slightly lower than the required values of 2.5 and 2.25 specified in the United States National Seismic Hazard Maps, Engineering Seismology, Seismic Ground Motion Parameters Zonation Map of China, and Chinese Code for Seismic Design of Buildings.

• (2) The EPA values across the four magnitude ranges decrease with increasing epicentral distance, and the effect of the epicentral distance on the EPA values is modulated by magnitude. Overall, the decay rate of the fitting curve in the horizontal direction is higher than that in the vertical direction. As the epicentral distance increases, the attenuation rate of EPA values also becomes more pronounced. The fitting parameter i ranges from 5.04 to 9.11, parameter a ranges from − 1.70 to − 1.01, parameter b ranges from 0.55 to 12.32, and the R² ranges from 0.88 to 0.93.

• (3) The EPA values, calculated based on strong motion records from the Loess Plateau, increase nonlinearly with increasing magnitude. The growth rate of EPA values demonstrates a progressively decreasing trend. The EPA values for the horizontal directions are consistently higher than those for the vertical direction across different epicentral distance ranges. When the magnitude is M_s, the fitting parameter d ranges from − 12.39 to − 5.07, parameter e ranges from 2.05 to 5.33, parameter h ranges from − 0.47 to − 0.16, and the R² ranges from 0.88 to 0.93. As for the M_wg magnitude, the fitting parameter d ranges from − 36.61 to − 4.62, parameter e ranges from 0.94 to 14.30, parameter h ranges from − 1.25 to − 0.07, and the R² ranges from 0.90 to 0.94.

• (4) The EPA prediction models proposed in this study, based on M_s and M_wg, can accurately capture the variations in actual EPA values across different directions. Compared with the prediction model in the current standard, the EPA values derived from M_wg fitting and their attenuation rates with distance are generally lower. This discrepancy may be attributed to the dynamic characteristics of the Loess Plateau and the influence of overlying soil thickness.

• (5) Introducing M_wg improves prediction accuracy to a certain extent based on the comparison results. The residual range in each direction is reduced from − 1.50–1.36 to − 1.35–1.37, and the range of residual standard deviations is decreased from 0.504–0.576 to 0.493–0.536. Moreover, the calculated results align well with the actual observations, further validating the applicability of M_wg​ in loess sites. This finding offers a new perspective and approach for refining current ground motion parameter equations and updating related specifications.