Introduction

The onset of the COVID-19 pandemic in 2020 induced a vast surveillance effort to track both individual and populational impact of the SARS-CoV-2 virus circulation and to guide public policy toward individual and collective interventions1. In France, a near real time passive surveillance system for infections was created, collating data on every infection diagnostic test in a single information system (SI-DEP)2. This extensive data collection included for each tested subject their age, sex and day of testing, and for the first time in France standardized postal addresses allowing for the systematic geocoding of cases. The spatial unit at which data was made available is the Îlot de Regroupement pour l’Information Statistique (IRIS). It is a statistical unit aiming to subset administrative towns into small (~ 1500 residents in average) homogenous units from an urban planning standpoint (commonality of housing, economic activities…). The IRIS is also the unit at which census-based and derived indicators are mostly available. Hence, for the purpose of epidemic management, there was a keen interest by public health professional in using neighbourhoods’ socio-economic composition as a predictor of the risk of infection at a small geographical scale. Although the published literature is rich with ecological analyses of case incidence explained by socio-economic indicators3,4,5,6,7,8,9, analyses conducted at such a fine geographical scale are scarcely reported, and when they are reported an adequate measurement of the predictive quality of the models are rarely given. Therefore, we aimed to assess the ability of local socio-demographic and economic indicators measured at a population level to explain the observed SARS-CoV-2 infection incidence.

Materials and methods

We conducted a retrospective, ecological analysis of the count of incident cases of infection by SARS-CoV-2 within the Auvergne-Rhône-Alpes French region, to assess the association between infection rate and socio-economic indicators from census data. The study region accounted for 12% of the total metropolitan French population, with 8.1 million inhabitants in 2022. Our study was conducted for a time period between May 13th, 2020 and February 14th, 2021, covering most of the second wave in France. The study time frame was divided in four epidemics periods matching the dynamic of the second wave: a low incidence period up to July 26th 2020, the second wave growth phase up to October 25th, the peak and decrease period marked by local curfews followed by a national confinement up to December 13th and the stabilization phase up to February 14th 2021. No confinement or curfews were in effect aside from the third period, which starts at the epidemic peak of the second wave.

The infection case data (defined as a positive PCR or antigenic based test conducted by a health care professional) was extracted from the SI-DEP information system and aggregated over each epidemic period and spatial unit. No reliable test data were available due to technical limitations and a changing definition of the count of individuals tested over the study period, leading to only the positive test being analysed. Case counts between 1 and 5 were censored by the provider to prevent reidentification of subjects. 2% of all cases were censored and were imputed following a procedure detailed in the Supplementary Material. No age-sex stratified data has been considered, because it would have led to important loss of information due to statistical censorship.

The socio-economic indicators evaluated as predictors of the distribution of infection cases were the proportion of migrants, the proportion of unemployed individuals, the proportion of single person homes, the proportion of households without a child, the proportion of car ownership, the proportion of individuals without a high school diploma, and the proportion of overpopulated homes. Two other indicators were included for population mobility in volume and nature, i.e. the proportion of individuals working outside of their residency town, and the proportion of individuals travelling to work by car. All above mentioned indicators were obtained from the 2017 population census data from the French National Institute of Statistics and Economic Studies (INSEE, Data Availability statement).

To quantify the association between the socio-economic indicators and case incidence, four parametric models were defined for each period. The null model (M1) was a generalized linear model with the counts of cases following a Poisson distribution, estimating the expected incidence rate for one person-week per IRIS. The offset is the log of the product of the IRIS population and the duration of the period (in weeks). The linear predictor for all four models is the following, with \(\mu\) the intercept, \({\varvec{X}}{\varvec{\beta}}\) the fixed effects of covariates and \({\varvec{\phi}}\) a conditional autoregressive (CAR) random effect:

$${\mathcal{M}}_{1}:offset+\mu$$
$${\mathcal{M}}_{2}:offset+\mu +{\varvec{X}}{\varvec{\beta}}$$
$${\mathcal{M}}_{3}:offset+\mu +{\varvec{\phi}}$$
$${\mathcal{M}}_{4}:offset+\mu +{\varvec{X}}{\varvec{\beta}}+{\varvec{\phi}}$$

CAR random effects allow for the decomposition of the between IRIS residual variance in two components: one spatially autocorrelated, with the correlation structure defined by a neighbourhood matrix and one uncorrelated. The CAR random effect proposed by Leroux and MacNab10,11 was used, providing two parameters to estimate with a direct interpretation: \({\tau }^{2}\) the total between-unit variance and \(\rho\) the spatial autocorrelation coefficient controlling how \({\tau }^{2}\) is distributed between correlated and uncorrelated effects (0 giving fully uncorrelated effects, and 1 fully correlated effects). The neighbourhood matrix between spatial units was defined on a travel-time-based metric. All IRIS within 60 min of each other were considered neighbours, with a weight defined as the inverse of the computed travel time separating each other. The matrix was standardized to ensure a mean sum of rows equal to one, rendering the \({\tau }^{2}\) parameter directly interpretable on the scale of the predicted incidence rates of infection cases.

To assess the functional forms of the covariates, we used a penalized spline regression on the model M2 (covariates only) in each period, with a response following a negative binomial distribution. The estimation procedure in penalized spline regression12 provides the effective degrees of freedom (edf) for each covariate. This estimation and the graphical analysis of the corresponding functional forms were used to guide the choice of the degree of freedom used in the final models, implemented using orthogonal polynomials. The definitive degrees of freedom were selected empirically to maintain the most notable functional forms while not compromising the convergence of the Bayesian sampling procedure.

\(\beta\) parameters quantifying the association between the incidence rates of cases and the evaluated covariates were set to follow a centred normal prior distribution of variance 1000, and \({\tau }^{2}\) followed an Inverse-Gamma prior, with shape 0.1 and scale 1. The prior for \(\rho\) is set internally in the package as a uniform distribution in [0,1]. For each model fitting, 3 parallel Monte-Carlo Markov Chains were generated to produce 6,000 samples from the posterior distribution for each parameter. Convergence was assessed using Gelman plots and the potential scale reduction factor13. For the random effects’ parameters (\({\tau }^{2}, \rho\)) the median of the posterior distribution of the parameters was used as punctual estimate, and the credibility interval was built using the 2.5th and 97.5th centiles of the posterior distribution. The random variance \({\tau }^{2}\) is presented as a standard deviation \(\tau\), additive on the log-incidence scale and as \(\text{exp}\left(2\tau \right)\), multiplicative on the incidence scale. For the fixed effects of covariates, the estimated incidence rate ratios (IRR) for a covariate \(p\) were defined as the ratio between the predicted incidence rate at a given value of the covariate over the incidence rate at the mean value of the covariate, and plotted. The predicted IRR for each IRIS and period, using the overall mean predicted incidence rate as a denominator, was presented using cartography.

One major hypothesis in Poisson process modelling is that the probability of the next event is independent from the number of events which occurred previously. When modelling counts of cases aggregated over time as is the case in our study, this implies that the number of expected cases in one given IRIS is strictly proportional to the number of subjects at risk in this IRIS. For an infectious disease, this is not the case as the probability of contamination within one IRIS is a function of the number of contacts between residents and the number of infectious residents, which themselves may vary as a function of total population within this IRIS. To relax this hypothesis, models M2 and M4 include as a predictor the number of person-week centred on the mean person-week count per IRIS in the study region. The resulting IRR estimates the effect of the size of the population in a given IRIS upon the infection risk of an individual living in this IRIS.

Each model was evaluated by computing the Moran index of the residuals to assess whether the model was successful in accounting for the spatial autocorrelation, 1 indicating a complete positive autocorrelation and 0 no autocorrelation. We used the deviance explained to measure and compare, for each period, the goodness-of-fit of the models. The deviance explained by models M2, M3, and M4 compared to the null (M1) was used to assess the improvement in goodness-of-fit, with 1 indicating a perfect fit and 0 a fit no better than the null model. Predictive quality was evaluated using the quantile of the observed count of cases in the posterior predictive distribution of the counts for each unit. The observed value was classified in three categories: under the 5th or above the 95th quantile giving a poor prediction, under the 25th or above the 75th quantile giving a mediocre prediction, and within the interquartile range giving a satisfying prediction.

Detailed models’ specification, weight matrix computation, results from the edf determination (Figure S1) and evaluation of the MCMC sampling and of the priors’ influence (Figure S2) are reported in Supplementary Material. All analysis was conducted using R software (4.4.0). Travel times were computed using the Conveyal R5 routing engine14. Geographic data was extracted from the OpenStreetMap dataset. The model parameters were estimated using the package CARBayes15, and the functional form exploration was conducted using package mgcv.

The dataset of infection cases used in this study is composed of aggregated counts with censorship of statistical units for which there was between 1 and 5 observations. Therefore, we deemed the data anonymized16, with no further Institutional Review Board approval necessary under French law. The infection data collection in France was mandatory for the study period and a default authorization for the reuse of data for research purposes was included in the relevant law and subsequent decree2.

Results

The study region is composed of 5,410 IRIS, with 5,069 for which all variables were available, and 7,917,997 individuals at risk, for an average of 1,562 individuals per available IRIS. The 341 IRIS with missing data for the covariates were in highly rural and mountainous areas with very low population count. The total number of cases observed during the study period was 562,376, of which 438,992 cases could be attributed to an IRIS and used in this study (78%). The median proportion of single person homes was 31% (IQR 25–39), and the median proportion of families without child was 50% (IQR 45–57) (Table 1). Regarding transportation, the median proportion for working outside of the residency town was 59% (IQR 37–72), 83% (IQR 73–89) for travelling to work by car, and 93% (IQR 87–96) for car ownership. The median proportion for home overcrowding was 1.6% (IQR 0–3.5).

Table 1 Description of the demographic and socio-economic characteristics of the IRIS (infra-municipal spatial units) of the French region Auvergne-Rhône-Alpes.
Full size table

The effect of the socio-economic indicators was found to be varying across periods, with several noticeable trends by the full model (M4, Fig. 1). The proportion of immigrants and households without child were found to have similar effects across periods, in shape and magnitude. The incidence rate was positively associated with the proportion of immigrants in a near linear fashion, negatively associated with the proportion of households only for values above 50%, and negatively associated with the proportion of households owning a car only during the Growth period. The effect of the IRIS population on the incidence rate is found to be of consistent shape across periods, with a sharp reduction of incidence rate in IRIS with a low population count compared to the regional mean, and an increase in incidence rate with a population between 1 and 4 times the mean value. Finally, regarding the Low Incidence period, although no significant association is found (no credibility intervals are displayed to improve readability), the incidence rate seems to increase with the proportion of overcrowded homes.

Fig. 1
figure 1

Estimated incidence rate ratios for each covariate in the full model (M4), and their credibility intervals at 95%. The credibility interval for the Low incidence period is not shown to maintain clarity. Interpretation: during the Low incidence period, in an IRIS with around 17% of immigrants, the Incidence Rate is about 1.25 times that in an IRIS at the mean proportion of immigrants (about 7%). During the Peak and decrease period, in an IRIS with a population a quarter that of the regional mean (1,562), the Incidence Rate is about 0.75 times that in an IRIS with the population at the regional mean.

Full size image

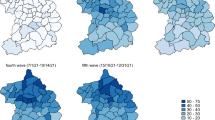
Table 2 presents the estimations by the full model (M4) for the parameters of the CAR random effects and the mean predicted incidence rate over the study. The spatial correlation coefficient is found to be moderate during the Low Incidence and Stabilization periods (0.46 and 0.59 respectively), indicating a similar share of spatially correlated and uncorrelated variance across IRIS. During the Growth and Peak and decrease periods, a strong spatial autocorrelation was found (0.78 and 0.88), indicating a strong spatial structure of the incidence rate across the study region. The between-IRIS variance in incidence rates, presented as standard deviation, is found to be 1.16 for the Growth period and between 0.51 and 0.58 for the last three periods, implying a dispersion of the IRIS’ predicted incidence rates by a factor of 10.2 and by a factor of about 3 respectively. Figure 2 provides a map by period of the predicted IRR by the full model. The high degree of spatial autocorrelation for periods 2 and 3 is strongly visible on panels B and C, with a grouping of IRIS with elevated IRR along urban areas as illustrated by the railway network on the map. Insets for the named metropolitan areas are presented in Supplementary Material (Figures S3 to S6).

Table 2 Mean predicted incidence rate per period for the entire study area (for 1,000 person-week), and CAR random effects parameters estimated by the full model (M4) with their 95% credibility interval.
Full size table
Fig. 2
figure 2

Predicted incidence rate ratio of SARS-CoV-2 infection for the IRIS (infra-municipal spatial unit) of the French region Auvergne-Rhône-Alpes during the second epidemic wave: model with covariates and spatial effect (M4). From A to D: Low incidence, Growth, Peak and decrease, and Stabilization periods. Insets for each of the metropolitan areas labelled on the map (Clermont-Ferrand, Lyon, Grenoble, Saint-Etienne) are presented in the Supplementary material (Fig. S3 to S6). Produced in R, with packages ggplot2 (3.5.1), sf (1.0.16), ggrepel (0.9.5), ggspatial (1.1.9), and patchwork (1.2.0) (https://cran.r-project.org/).

Full size image

Models’ residuals for the Low incidence and Stabilization periods exhibited a minimal spatial autocorrelation, even for the null model M1 (0.028 and 0.072 respectively, Table 3). For the Growth and Peak and Decrease periods, both the inclusion of a spatial effect and the inclusion of covariates were able to mitigate the residual autocorrelation indicating a spatial structure of the covariate distribution. The fit for the Growth period was also noticeably improved by the introduction of covariates (M2), with the deviance explained reaching 0.15. For the Peak and decrease and Stabilization periods, the fit improved only with the addition of a spatial effect to the model, with no relevant difference between M3 and M4. During the Low incidence period, the deviance explained showed marginal improvement between M3 and M4, with a small benefit from the covariates’ addition, but the proportion of IRIS with a poor prediction remained above 80% in all cases. Regarding the three others periods, only the models with a CAR random effect provide a high proportion of satisfying predictions (above 81% satisfying, under 8% poor), whereas the models M1 and M2 are producing poor predictions for 43–58% of the IRIS, with a maximum of 21% of satisfying predictions. For all periods, the null model and the model with covariates only were very close regarding predictive quality. The best improvement of M2 over M1 was an increase from 14 to 19% of satisfying predictions during the Growth period.

Table 3 Moran indices, deviance explained and distribution of prediction quality for each model fitted on the observed data, by epidemic period.
Full size table

Discussion

Our main result is an inability of our ecological covariates alone to raise the proportion of satisfying prediction above 21%, indicating a predictive performance on the observed data barely superior to that of the simple estimated mean incidence over the study region. Putting aside the Low Incidence period for which cases are extremely sparse across the study region, the addition of spatial random effect produced major increases in predictive quality. In conjunction with the notable improvement in explained deviance with the spatial effects, this suggests our choice of a travel time metric for the neighbourhood matrix is appropriate. However, a proper assessment of this adequacy remains to be done.

The present literature remains scarce regarding small-area modelling of infectious disease, limiting our ability to compare the present results appropriately. We identified a handful of authors reporting on small-area analysis about COVID-19 incidence7,8,17,18 but without providing a quantitative estimation of the predictive ability of the fixed effects in each model. Our report therefore brings to the literature a quantification of the potential for ecological variables to contribute to infection risk prediction, although our initial aim of providing proper estimates of risk on which the local authorities could act was not reached. We can however strongly stress the necessity to present an exhaustive panel of model performance metrics when conducting this type of ecological analysis at a small spatial scale.

The results found regarding the socio-economic and mobility indicators are less clear, with only two indicators maintaining a relatively constant and significant effect across study periods: the proportion of immigrants and the proportion of families without a child. The protective effect of families without a child may be related to the family size (i.e. number of family sources) and lack of exposure to school-based contamination thus limiting household transmissions19. Our results are concordant with other findings that identified higher risk of Covid-19 infection among immigrants20. Time-varying effects of the ecological covariates could be related to changes in behaviour within specific populations, as was described in Germany during the first wave in 20203, or ultimately to unmeasured confounding.

Our study has several limitations. First, for reasons of personal data protection, we were unable to conduct an analysis standardized for age and sex. More than 30% of cases observed during the entire study period would have been censored. Estimates of age-related risk of infection suggests a upward trend in risk with increasing age21, indicating a potential excess of cases in units where the elderly are overrepresented, and the opposite in areas inhabited by a younger population. With regards to the sex-related risk, other studies found variable results, with a tendency toward a higher risk of positivity among males compared to females6,22.

Our second caveat is the absence of availability of the counts of individuals tested for SARS-CoV-2 infection. Indeed, assuming a homogeneous testing rate across all spatial unit is a strong hypothesis5. Moreover, similar work on French data has established a variation of the testing rate according to socio-economic level, with a decrease in testing with the increase in deprivation7. It is therefore reasonable to suspect the counts of infection cases to be underestimated in more deprived areas, which could lead to bias the estimates of the association between incidence rates and socio-economic indicators.

In conclusion, the present findings suggest the insufficiency of using ecological indicators at a small-area scale (1000–10,000 inhabitants) to predict incidence rates during an infectious disease, at least when applied to a respiratory infectious disease such as Covid-19. As modelling strategies in disease mapping frequently involve the use of random effects to account for excess variability and autocorrelation, it appears advisable when analysing aggregated data at a fine geographic resolution to thoroughly assess whether the fixed effects estimated are relevant to the global model performance.