PMSM sensorless control based on super-twisting algorithm sliding mode observer with the IAORLS parameter estimations

Abstract

This paper addresses the high-frequency oscillations issue commonly associated with the sliding mode observer (SMO) algorithm in sensorless control of surface-mounted permanent magnet synchronous motor (SPMSM) and the problem of parameter variation caused by magnetic saturation and temperature rise during motor operation. A novel information acquisition optimized recursive least squares (IAORLS) algorithm, which incorporates an IAO optimized forgetting factor, is proposed to identify motor parameters. The identified parameters are utilized in conjunction with the Super Twisting Algorithm Sliding Mode Observer (STA-SMO) for motor control. By discretizing the stator voltage equations of the SPMSM via the forward Euler method, IAORLS enables efficient parameter identification. These parameters are then integrated into the STA-SMO, allowing the observer to receive real-time updates, thereby preventing performance degradation due to parameter mismatches. Additionally, the method reduces high-frequency oscillations when the motor’s extended back electromotive force (back-EMF) is observed, improving the accuracy of rotor position and speed estimation. Simulations and experimental results confirm the effectiveness and reliability of the proposed approach.

Introduction

Owing to their high power density, simple structure, high torque, high efficiency, and rapid dynamic response, surface-mounted permanent magnet synchronous motor (SPMSM) have been widely adopted in industries such as robotics manufacturing, servo motors, and electric vehicles, receiving significant positive feedback¹. A model-based sensorless PMSM requires precise motor parameters for high-performance operation. However, some of the parameters of SPMSM can vary during motor operation. For example, magnetic saturation can cause changes in inductance, and temperature increases can lead to variations in stator resistance and magnetic flux², ultimately reducing motor efficiency. Therefore, real-time parameter identification ensures the motor’s high-performance operation.

Sensorless control strategies for SPMSM are generally categorized into two broad approaches: high-frequency signal injection methods and fundamental model-based methods³. The fundamental model-based method is often applied in the medium and high-speed ranges, where the approach involves detecting the current and voltage signals in the motor stator windings and then using either open-loop or closed-loop methods to directly compute extended back electromotive force (back-EMF) or flux information, thereby enabling rotor position and speed observations through a position or speed observer⁴. However, a significant challenge arises when these methods are applied to low- or zero-speed operations, where the signal-to-noise ratio is often too low for extracting useful signals, leading to degraded performance in rotor position and speed estimation.

The motivation for advancing these methods stems from the critical need for accurate and reliable rotor position and speed detection. Commonly used position estimation algorithms include the sliding mode observer⁵, extended kalman filter (EKF) algorithm⁶, model reference adaptive system (MRAS) algorithm⁷, and luenberger observer algorithm⁸. Most of these algorithms require estimation of the back-EMF, which is then utilized to detect the rotor position and speed. These methods depend on updated electrical parameters, specifically the stator resistance and d-axis inductance used for speed and position estimation. However, after the motor has been in operation for some time, magnetic saturation and temperature variations can occur, resulting in changes to the motor parameters and ultimately leading to a decline in dynamic control performance⁹. In other words, variations in the stator resistance and inductance values can cause inaccuracies in back-EMF estimation, reducing the reliability of the observed rotor position¹⁰.

This parameter dependency highlights the core motivation behind ongoing research: the need to develop more robust methods that can adapt to changes in motor parameters over time. Variations in stator resistance and inductance values can lead to a decline in the dynamic control performance, making accurate parameter identification crucial for maintaining stable control and efficient operation.

To address this challenge, parameter identification techniques have been developed alongside advances in modern control theory¹¹. Depending on the process and approach, parameter identification can be classified into offline and online methods. Offline parameter identification provides only static or specific operating point estimates, making it unsuitable for real-time changes in motor operating conditions, potentially resulting in inaccurate parameter estimation during actual operation. On the other hand, online parameter identification collects real-time sensor data such as current and voltage and uses algorithms to update motor parameter estimates continuously. Compared with offline methods, online parameter identification monitors the motor’s operating state in real time and facilitates the real-time update of controller parameters, thereby enabling adaptive control.

In permanent magnet synchronous motor online parameter identification, model reference adaptive system¹², recursive least squares (RLS)¹³, extended kalman filter¹⁴, and particle swarm optimization (PSO)¹⁵ each have their unique advantages.

MRAS constructs a reference model and an adjustable model, using the error between them to drive parameter updates, achieving real-time estimation with high online identification capability. EKF, on the other hand, leverages state-space models and stochastic signal processing to update parameters through recursive prediction and correction, offering strong noise resistance and high identification accuracy, making it suitable for dynamically changing systems. PSO, as a swarm intelligence optimization algorithm, simulates the iterative updates of particles in the search space to find the global optimal solution. It effectively identifies motor parameters even when the initial conditions are uncertain, making it particularly suitable for scenarios requiring global optimization.

By feeding the identified motor parameters back into the system, the disturbances caused by parameter variations can be mitigated, ensuring stable system operation. Reference¹⁶ proposed a model reference adaptive system-based parameter identification method that considers inverter nonlinearity for SPMSM, identifying stator resistance and inductance. However, this method faces the challenges of rank deficiency and slow convergence speed. Further, reference¹⁷ introduces an affine projection algorithm for identifying stator resistance and d-axis inductance online, which improves system robustness. However, the algorithm’s lack of general applicability limits its use in diverse operational conditions. This underscores the ongoing motivation for further developing and optimizing online parameter identification techniques that are both fast-converging and robust, to enhance the reliability and accuracy of sensorless control systems, especially under varying and unpredictable operating conditions.

This paper presents a super-twisting algorithm sliding mode observer with the IAORLS parameter estimations for sensorless control of SPMSM. The IAORLS algorithm is employed for parameter identification, offering faster convergence and more minor steady-state errors than other methods. It also dynamically updates parameter estimates in real-time data streams while maintaining a lower computational cost, improved numerical stability, and greater adaptability. The super-twisting sliding mode algorithm mitigates typical high-frequency oscillations in conventional sliding mode control. By continuously feeding the parameters identified by the RLS algorithm back to the observer in real time, the proposed approach addresses the effects of parameter variations caused by magnetic saturation and temperature rise, enhancing motor efficiency.

Electrical model

Since the SPMSM does not exhibit saliency, the d-axis and q-axis inductance are equal, i.e., ${L_d} = {L_q} = L$. To simplify the subsequent analysis and simulation experiments, the SPMSM has a symmetrical structure, and core losses due to eddy currents and hysteresis are neglected. The stator voltage equations of the SPMSM in the two-phase stationary reference frame are as follows:

$$\begin{aligned} \left\{ \begin{array}{l} u_{\alpha }=Ri_{\alpha }+L\frac{di_{\alpha }}{dt}+e_{\alpha }\\ u_{\beta }=Ri_{\beta }+L\frac{di_{\beta }}{dt}+e_{\beta } \end{array} \right. \end{aligned}$$

(1)

where ${u_{\alpha ,\beta }}$ represent the $\alpha \beta$-axis stator voltages, respectively, L denotes the stator inductance, R represents stator resistance, ${i_{\alpha ,\beta }}$ represents the $\alpha \beta$-axis currents and ${e_{\alpha ,\beta }}$ are the back-EMF for the $\alpha \beta$-axis. and their expressions are as follows:

$$\begin{aligned} \left\{ \begin{array}{l} e_\alpha =-\omega _e\psi _f\sin \theta _e\\ e_\beta =\omega _e\psi _f\cos \theta _e \end{array} \right. \end{aligned}$$

(2)

where ${\omega _e}$, ${\psi _f}$ , ${\theta _e}$ are the electrical rotor velocity, permanent magnet flux linkage and electrical rotor position, respectively. To facilitate the use of STA-SMO for observing the back-EMF. Equation (1) is reformulated into the current equation form as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \frac{{d{i_\alpha }}}{{dt}} = - \frac{R}{L}{i_\alpha } + \frac{1}{L}{u_\alpha } - \frac{1}{L}{e_\alpha }\\ \frac{{d{i_\beta }}}{{dt}} = - \frac{R}{L}{i_\beta } + \frac{1}{L}{u_\beta } - \frac{1}{L}{e_\beta } \end{array} \right. \end{aligned}$$

(3)

STA-SMO

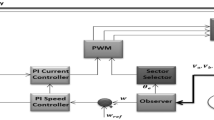
Figure 1 illustrates the conventional sliding mode observer (SMO) of the SPMSM system. The conventional SMO is an estimator based on sliding mode theory. In sensorless control of the SPMSM, using a conventional SMO to estimate the rotor speed and position often presents a challenge: sliding mode control is frequently associated with high-frequency oscillations, which can result in errors in the estimated rotor position, thereby degrading system performance.

Figure 1

Block diagram of the conventional sliding mode observer of the SPMSM.

Super-twisting algorithm observer

The super-twisting sliding mode observer is based on the super-twisting algorithm (STA), which Professor A. Levant introduced in 1993¹⁸. This algorithm effectively suppresses the high-frequency oscillations problem commonly seen in conventional sliding mode observers. Additionally, the stability of this algorithm has been proven via the Lyapunov method, as shown in¹⁹. The expression for the STA is as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \frac{{d{x_1}}}{{dt}} = - {k_1}|{{\bar{x}}_1}{|^{\frac{1}{2}}}{\textrm{sgn}}({{\bar{x}}_1}) + {x_2} + {\rho _1}({x_1},t)\\ \frac{{d{x_2}}}{{dt}} = - {k_2}{\textrm{sgn}}({{\bar{x}}_2}) + {\rho _2}({x_2},t) \end{array} \right. \end{aligned}$$

(4)

where ${x_{1,2}}$ is the control input of the system, ${k_{1,2}}$ is the sliding mode gains, ${\mathop \textrm{sgn}} ( \cdot )$ is the sign function and ${\rho _{1,2}}$ represent system disturbances. ${\bar{x}_1}$ denotes the difference between the estimated and actual values (${\bar{x}_1} = {\hat{x}_1} - {x_1}$), which also serves as the sliding surface. Equation (4), we can see that the high-gain switching function is transformed into the derivative of ${x_2}$ and then integrated back into ${x_1}$, which is somewhat equivalent to a low-pass filter (LPF) for the high-gain switching function. This fundamentally suppresses high-frequency oscillations²⁰. Assume that the disturbance term in (4) is globally bounded, i.e.,

$$\begin{aligned} {\rho _1} \le {\delta _1}|{x_1}{|^{\frac{1}{2}}},{\rho _2} = 0 \end{aligned}$$

(5)

where ${\delta _1}$ is an arbitrary positive real number. The sliding mode gain ${k_{1,2}}$ should satisfy

$$\begin{aligned} k_1>2\delta _1,k_2>k_1\frac{5\delta _1k_1+4\delta _1^2}{2(k_1-2\delta _1)} \end{aligned}$$

(6)

The system subsequently converge to the sliding mode surface in finite time. This implies that the error reaches zero and that the estimated value converges to the actual value. By combining (3) and (4), the stator current observer expression for the sensorless control of the SPMSM based on the STA-SMO can be derived as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \frac{{d{{\hat{i}}_\alpha }}}{{dt}} = - \frac{R}{L}{{\hat{i}}_\alpha } + \frac{1}{L}{u_\alpha } + \frac{1}{L}{k_1}|{{\bar{i}}_\alpha }{|^{\frac{1}{2}}}{\textrm{sgn}}({{\bar{i}}_\alpha }) + \frac{1}{L}\int {{k_2}} {\textrm{sgn}}({{\bar{i}}_\alpha })dt\\ \frac{{d{{\hat{i}}_\beta }}}{{dt}} = - \frac{R}{L}{{\hat{i}}_\beta } + \frac{1}{L}{u_\beta } + \frac{1}{L}{k_1}|{{\bar{i}}_\beta }{|^{\frac{1}{2}}}{\textrm{sgn}}({{\bar{i}}_\beta }) +\frac{1}{L}\int {{k_2}} {\textrm{sgn}}({{\bar{i}}_\beta })dt \end{array} \right. \end{aligned}$$

(7)

The input to the system is the estimated $\alpha \beta$-axis current ${\hat{i}_{\alpha ,\beta }}$. By comparing (4) and (7), we can observe that the disturbance term of the system at this point is

$$\begin{aligned} \left\{ \begin{array}{l} \rho ({{\hat{i}}_\alpha },t) = - \frac{R}{L}{{\hat{i}}_\alpha } + \frac{1}{L}{u_\alpha }\\ \rho ({{\hat{i}}_\beta },t) = - \frac{R}{L}{{\hat{i}}_\beta } + \frac{1}{L}{u_\beta } \end{array} \right. \end{aligned}$$

(8)

By subtracting (3) from (7), the error equation can be obtained as

$$\begin{aligned} \left\{ \begin{array}{l} \frac{{d{{\bar{i}}_\alpha }}}{{dt}} = - \frac{R}{L}{{\bar{i}}_\alpha } + \frac{1}{L}({k_1}|{{\bar{i}}_\alpha }{|^{\frac{1}{2}}}{\textrm{sgn}}({{\bar{i}}_\alpha }) + \int {{k_2}} {\textrm{sgn}}({{\bar{i}}_\alpha })dt + {e_\alpha })\\ \frac{{d{i_\beta }}}{{dt}} = - \frac{R}{L}{{\bar{i}}_\beta } + \frac{1}{L}({k_1}|{{\bar{i}}_\beta }{|^{\frac{1}{2}}}{\textrm{sgn}}({{\bar{i}}_\beta }) + \int {{k_2}} {\textrm{sgn}}({{\bar{i}}_\beta })dt + {e_\beta }) \end{array} \right. \end{aligned}$$

(9)

When the system reaches the equilibrium point, and the current error reaches the sliding mode surface, i.e., ${\bar{i}_{\alpha ,\beta }}$, according to the equivalent control principle of sliding mode control, the back-EMF can be regarded as

$$\begin{aligned} \left\{ \begin{array}{l} {{\hat{e}}_\alpha } = - {k_1}|{{\bar{i}}_\alpha }{|^{\frac{1}{2}}}{\textrm{sgn}}({{\bar{i}}_\alpha }) - \int {{k_2}} {\textrm{sgn}}({{\bar{i}}_\alpha })dt\\ {{\hat{e}}_\beta } = - {k_1}|{{\bar{i}}_\beta }{|^{\frac{1}{2}}}{\textrm{sgn}}({{\bar{i}}_\beta }) - \int {{k_2}} {\textrm{sgn}}({{\bar{i}}_\beta })dt \end{array} \right. \end{aligned}$$

(10)

Typically, ${k_2}$ is greater than ${k_1}$, because ${k_2}$ acts as a high-gain switching term, which is added to the calculation through integration. In (10), the integration and the larger ${k_2}$ help reduce high-frequency oscillations caused by the sign function, whereas ${k_1}$ ensures the fast dynamic response of the observer. Therefore, the estimation of the extended back electromotive force is influenced by both ${k_1}$ and ${k_2}$.

Rotor position and velocity calculate

From Eq. (10), we can see that the equivalent extended back electromotive force is a discontinuous high-frequency signal exhibiting a certain degree of distortion. This signal distortion can cause the observed extended back electromotive force to discontinuous. Therefore, adding a low-pass filter here can make the waveform continuous, i.e.,

$$\begin{aligned} \left\{ \begin{array}{l} {Z_\alpha } = \frac{{{\omega _e}}}{{s + {\omega _e}}}{{\hat{e}}_\alpha }\\ {Z_\beta } = \frac{{{\omega _e}}}{{s + {\omega _e}}}{{\hat{e}}_\beta } \end{array} \right. \end{aligned}$$

(11)

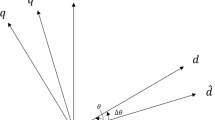
Then, the rotor position information can be estimated using the arctangent function

$$\begin{aligned} \hat{\theta }= \arctan \left( - \frac{{{Z_\alpha }}}{{{Z_\beta }}}\right) \end{aligned}$$

However, the range of the arctangent function is $( - \frac{\pi }{2},\frac{\pi }{2})$, while the actual motor operates in the range $(0,2\pi )$. Therefore, after calculating the angle using the arctangent function, a compensation value needs to be added or subtracted based on the sign of ${Z_\beta }$, i.e.,

$${\hat{\theta }_e} = \arctan \left( - \frac{{{Z_\alpha }}}{{{Z_\beta }}}\right) + \frac{{ - {Z_\beta } + \mid {Z_\beta }\mid }}{{2\mid {Z_\beta }\mid }}$$

By differentiating the rotor position, the rotor speed can be obtained

$$\begin{aligned} {\hat{\omega }_e} = \frac{{d{{\hat{\theta }}_e}}}{{dt}} \end{aligned}$$

Parameter identification

The precise control and operation of a PMSM rely heavily on accurately identifying key parameters, including the stator resistance, inductance, and rotor flux. While conventional identification methods have proven effective, they face significant challenges in accommodating real-time motor dynamics influenced by temperature variations, magnetic saturation, and load fluctuations. To address these limitations, this paper presents an innovative approach that integrates the strengths of the recursive least squares (RLS) algorithm with the adaptive capabilities of the information acquisition optimizer (IAO) for the identification of the motor’s permanent magnet flux, inductance, and stator resistance.

Recursive least squares

The least squares (LS) method was first proposed by Gauss in 1795 in his renowned study on predicting celestial body motion. Since then, the LS method has gradually become a cornerstone of estimation theory. Its concise principles, rapid convergence speed, and ease of implementation have led to its widespread application in system parameter estimation²¹. In real-time control systems, estimating and adjusting the system parameters to adapt to dynamic changes and external environmental influences is often necessary. The recursive least squares method can dynamically update parameter estimates on basis of collected data in real-time, enabling more precise control of the control system. The basic idea of the recursive least squares algorithm can be summarized as follows:

$$\begin{aligned} \hat{\mu }(k)=\hat{\mu }(k-1)+\mu _{com}(k) \end{aligned}$$

(12)

where ${\mu _{com}}(k)$ is the correction term.

The form of the recursive least squares method is as follows:

$$\begin{aligned} \left\{ \begin{array}{l} Y(k) = {\mu ^T}(k)\varphi (k)\\ \hat{\mu }(k) = \hat{\mu }(k - 1) + K(k)[y(k) - {\varphi ^T}(k)\hat{\mu }(k - 1)]\\ K(k) = \frac{{P(k - 1)\varphi (k)}}{{\lambda + {\varphi ^T}(k)P(k - 1)\varphi (k)}}\\ P(k) = \frac{1}{\lambda }[I - K(k){\varphi ^T}(k)]P(k - 1) \end{array} \right. \end{aligned}$$

(13)

where $Y$ is the output signal, $\hat{\mu }$ is the parameter to be estimated in the model, $\lambda$ is the forgetting factor, $I$ is the identity matrix, $\varphi$ is the input vector, $P$ is the covariance matrix, and $K$ is the gain matrix. Before using the mentioned recursive least squares method, it is necessary to determine the initial values $P(0)$, $\hat{\mu }(0)$ and $\lambda$, which are generally set to

$$\begin{aligned} \left\{ \begin{array}{l} P(0) = \alpha I\\ \hat{\mu }(0) = \varepsilon \\ \lambda = 1 \end{array} \right. \end{aligned}$$

(14)

where $\alpha$ is a sufficiently large positive real number (ranging from 10$^4$ to 10$^10$), and $\varepsilon$ is a zero vector or a sufficiently small positive vector.

In most cases, the forgetting factor $\lambda$ is typically set to 1, meaning that the RLS algorithm does not disregard past data and that all the data points contribute equally to the parameter estimation. However, as the number of historical observations increases, the influence of recent data on the algorithm’s convergence weakens. Since only the most current parameters identified by RLS can accurately reflect the present state of convergence, fixing the forgetting factor at one is only suitable for systems with stable characteristics and low data noise. The PMSM is a complex, nonlinear, and highly coupled system, using a fixed forgetting factor of 1 is unsuitable. To improve the convergence speed of RLS when identifying PMSM parameters and to reduce steady-state error, the algorithm must be optimized, with the critical factor being the determination of the forgetting factor. The forgetting factor directly affects both the update speed and adaptability of the RLS. Choosing an appropriate forgetting factor balances tracking rapidly changing system parameters and avoiding excessive fluctuations.

Information acquisition optimizer

The IAO, a metaheuristic optimization algorithm introduced by Xiao Wu in 2024²², is designed to explore search spaces efficiently via an adaptive search mechanism. It iteratively updates by acquiring and filtering new information from the system, enabling it to escape local optima and converge rapidly toward the global optimum. The methodology can be summarized in three stages.

The first stage of IAO involves information collection, where agents gather data from various sources via different methods. This process is effectively a variant of differential evolution, governed by the following formula:

$$\begin{aligned} x_i^{{\textrm{iter}} + 1} = x_i^{{\textrm{iter}}} + \sigma \times \left( x_i^{r1} - x_i^{r2}\right) \end{aligned}$$

(15)

where iter denotes the current iteration number, $x_i^{{\textrm{iter}}}$ represents the state of the information body at the iter iteration, $x_i^{iter+1}$ refers to the state of the information entity after the initialization of information collection. $x_i^{r1}$ and $x_i^{r2}$ are two randomly generated information bodies during the iteration, and $\sigma$ is a random number between [0, 1] that characterizes the influencing factors in the information collection process.

The second stage involves information filtering and evaluation. This process is a crucial mechanism that enables individuals to rapidly identify relevant and valuable information. It eliminates inaccurate and misleading data and significantly enhances the overall quality of the information. The process is mathematically represented as follows:

$$\left\{ {\begin{array}{{l}} {x_i^{{\textrm{iter}} + 1} = x_i^{{\textrm{iter}}} - \Delta \times {\textrm{rand}} \times \left( x_i^{{\textrm{rand}}} - x_i^{{\textrm{iter}}}\right) ,{\textrm{if rand}} < 0.5}\\ {x_i^{{\textrm{iter}} + 1} = x_i^{{\textrm{iter}}} + \Delta \times {\textrm{rand}} \times \left( x_i^{{\textrm{rand}}} - x_i^{{\textrm{iter}}}\right) ,{\textrm{otherwise}}} \end{array}} \right.$$

where rand is the random number generated in [0,1], and $\Delta$ represents the error caused by subjective factors in filtering and evaluating information, which is defined by:

$$\begin{aligned} \Delta =\frac{\cos \left( \frac{\pi }{2}\times \sqrt{\mid \Gamma \mid }\right) }{\Xi } \end{aligned}$$

(16)

where $\Xi$ represents the subjective influence factor, a critical quantitative measure of personal subjectivity. It captures how individual preferences, experiences, emotions and preconceived notions can lead to overly optimistic or pessimistic judgments about information, thus affecting its final acquisition and application. Moreover, owing to cognitive limitations and contextual influences, $\Xi$ potential errors in information processing may arise sporadically or be the result of systemic biases, such as confirmation bias or groupthink. The randomness associated with $\Xi$ highlights the inherent uncertainty in filtering and evaluating information, indicating that even when exposed to the same data, different individuals or the same individual at different times may determine it differently owing to variations in the subjective state. This factor can be expressed as:

$$\begin{aligned} \Xi =2\times \textrm{mod}\left( \left( 3.468\times v\times (1-\beta )\times \left(a\cos (\tau \times 10^4)\right)\right) ,1\right) \end{aligned}$$

(17)

where $v$, $\beta$ and $\tau$ are random numbers generated between [0, 1].

$\Gamma$ is defined as the reliability factor, with its mathematical model inspired by the human capacity for dynamic adjustment during information filtering and evaluation. As the process progresses, the complexity of the information decreases, and the model is simplified accordingly. thus represents the algorithm’s ability to self-adjust on basis of the quality of information at various stages of iteration, optimizing its performance. This enhances the algorithm’s adaptability and flexibility, significantly improving the reliability and accuracy of the results. The calculation is provided in Eq. (22):

$$\Gamma = \sin \left( {\left( \frac{\pi }{4}\right) ^{\frac{{{\textrm{iter}}}}{{{\mathrm{Max\_iter}}}}}}\right) + \Phi + \frac{{{{\log }_{10}}\frac{{{\textrm{iter}}}}{{{\mathrm{Max\_iter}}}}}}{8}$$

where Max_iter represents the maximum number of iterations. The mathematical model of $\Gamma$ is composed of three primary components: a sinusoidal function, a logarithmic function, and the information quality factor. The information quality factor $\Phi$ is calculated as follows:

$$\Phi = \cos (2 \times \delta + 1) \times \left( 1 - \frac{{{\textrm{iter}}}}{{{\mathrm{Max\_iter}}}}\right)$$

where $\delta$ is a random number generated between [0, 1]. The quality factor $\Phi$ is dependent on the number of iterations (iter), influencing the phase and amplitude of the cosine function to regulate the precision of information acquisition. Furthermore, $\Phi$ directly impacts the eigenvalue $x_i^{{\textrm{iter}} + 1}$ by adjusting the reliability factor $\Gamma$ throughout the iteration. The IAO algorithm simulates the adaptive adjustment behavior of individuals when confronted with varying information, thus enabling optimal information acquisition. The third stage involves information analysis and organization. Its purpose is to extract useful information from the filtered data and to transform the transferable information identified in the previous stage into actionable insights. The process is mathematically represented as follows:

$$\left\{ {\begin{array}{*{20}{l}} {x_i^{{\textrm{iter}} + 1} = x_i^{{\textrm{best}}} \times \cos \left( \frac{\pi }{2} \times \sqrt{{\Lambda ^{\frac{1}{3}}}} \right) - \varepsilon \times \left( \frac{1}{D}\sum \nolimits _{i = 1}^d {x_i^{{\textrm{best}}} - x_i^{{\textrm{best}}}} \right) ,{\textrm{if}}\;\Phi \ge 0.5}\\ {x_i^{{\textrm{iter}} + 1} = x_i^{{\textrm{best}}} \times \cos \left( \frac{\pi }{2} \times \sqrt{{\Lambda ^{\frac{1}{3}}}} \right) - 0.8 \times \left( \zeta \times \kappa \times \frac{1}{D}\sum \limits _{i = 1}^d {x_i^{{\textrm{best}}}} - (2 \times \omega - 1) \times x_i^{{\textrm{best}}}\right) ,{\textrm{otherwise}}} \end{array}} \right.$$

where $x_i^{\textrm{best}}$ represents the best information body generated in the previous iteration process, $\frac{1}{D}\sum \nolimits _{i = 1}^d {x_i^{\textrm{best}}}$ represents the average value of the best information bodies generated in the last iteration, and $\varepsilon$, $\zeta$, $\omega$ and $\kappa$ are random numbers generated between [0, 1]. $\Lambda$ represents the control factor for analyzing and organizing information, and is defined as follows:

$$\begin{aligned} \Lambda =2^{\left( \sqrt{|\Gamma |}-2\right) } \end{aligned}$$

(18)

During information organization and analysis, the depth and breadth of these processes can be dynamically optimized on basis of the quality and reliability of the information, significantly enhancing the accuracy and effectiveness of the final output. This adaptive adjustment mechanism is embodied in $\Lambda$; by dynamically adjusting the value of $\Gamma$ (the reliability factor), $\Lambda$ modifies the rigor and granularity of information processing. A higher $\Gamma$ value, indicating more excellent information reliability, leads to a corresponding increase in $\Lambda$, enabling the algorithm to perform deeper information mining and more extensive integration.

IAORLS design

Optimizing the forgetting factor $\lambda$ of the RLS algorithm via the IAO enables adaptive adjustment of the forgetting factor, thereby enhancing the accuracy and performance of parameter identification. First, the mean square error is used as the loss function to assess estimation accuracy, as shown in (4.2)

$$\begin{aligned} J(\lambda )=\frac{1}{N}\sum _{k=1}^N\left( y(k)-\hat{y}(k,\lambda )\right) ^2 \end{aligned}$$

(19)

where $y(k)$ represents the output of the system, $\hat{y}(k,\lambda )$ is the output based on the current forgetting factor $\lambda$ and $N$ is the maximum number of iterations.

Next, initialize the forgetting factor $\lambda _0$ (typically a value close to 1, with $\lambda _0 = 0.98$ in this paper), the learning rate $\alpha$ and the maximum number of iterations $N$. At each time step $k$, the RLS update process depends on the current forgetting factor $\lambda$. The output error is then calculated, and the loss function is estimated based on this forgetting factor. Finally, the IAO continuously adjusts the forgetting factor according to the loss function value, minimizing the RLS parameter estimation error. The procedure for identifying the SPMSM parameters via the IAORLS algorithm is illustrated in Fig. 2.

Figure 2

Structure of the SPMSM parameter identification flowchart of the IAORLS algorithm.

Figure 3 presents a performance comparison between the RLS and IAORLS algorithms on basis of mean square error (MSE) evaluation. In the first 100 iterations, the IAORLS algorithm shows a significantly faster convergence rate than the conventional RLS algorithm does, with a more rapid reduction in MSE, indicating superior performance in managing initial noise or errors. In the later stages, although both algorithms stabilize, IAORLS achieves a lower steady-state error than RLS does, demonstrating a clear advantage in accuracy. Overall, the IAORLS algorithm outperforms the RLS algorithm in terms of both the speed of initial error convergence and the steady-state error.

Figure 3

Average convergence curves of IAORLS and conventional RLS.

Motor parameter identification

The stator voltage equation of the SPMSM in the synchronous rotating coordinate system is given by

$$\begin{aligned} \left\{ \begin{array}{l} \frac{{d{i_d}}}{{dt}} = \frac{{{u_d}}}{L} + {{\hat{\omega }}_e}{i_q} - \frac{R}{L}{i_d}\\ \frac{{d{i_q}}}{{dt}} = \frac{{{u_q}}}{L} + {{\hat{\omega }}_e}{i_d} + \frac{{{{\hat{\omega }}_e}}}{L}{\varphi _f} - \frac{R}{L}{i_q} \end{array} \right. \end{aligned}$$

(20)

where ${i_{d,q}}$ and ${u_{d,q}}$ represent the $dq$-axis stator current and stator voltage, respectively.

By applying the forward Euler method for discretization, the discrete form of the stator current equation for the SPMSM is obtained as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \begin{array}{l} i_d(k + 1) = \left( 1 - \frac{{R{T_s}}}{L}\right) {i_d}(k) + {T_s}{{\hat{\omega }}_e}{i_q}(k) - \frac{{{T_s}}}{L}{u_d}(k)\\ {i_q}(k + 1) = \left( 1 - \frac{{R{T_s}}}{L}\right) {i_q}(k) - {T_s}{{\hat{\omega }}_e}{i_d}(k) + {{{T_s}}}{L}\left( {u_q}(k) - {{\hat{\omega }}_e}{\psi _f}\right) \end{array} \end{array} \right. \end{aligned}$$

(21)

Using the $i_d=0$ control method and considering that the q-axis current remains approximately constant in the steady state, the equation for $i_q$ in (21) can be further simplified to

$$\begin{aligned} {u_q}(k) = {\hat{\omega }_e}(k){\psi _f} + {i_q}(k)R \end{aligned}$$

(22)

Thus, on basis of the above equation, the $q$-axis current $i_q$ and rotor speed $\hat{\omega }_e$ can be collected as input variables. In contrast, the $q$-axis voltage $u_q$ is collected as the output variable, enabling the identification of the magnetic flux linkage $\psi _f$ and resistance parameters $R$.

Using the S-function to implement the IAORLS, sample ${\hat{\omega }_e}$, ${i_q}(k)$ and ${u_q}(k)$, output the identified parameters ${\psi _f}$ and R.

Since the $q$-axis stator voltage equation contains the positional parameter of the permanent magnet flux linkage $\psi _f$, the inductance can only be identified via this equation.

When $i_d=0$, (21) with respect to $i_d$ can be simplified to

$$\begin{aligned} {u_d}(k) = - {i_q}(k){\hat{\omega }_e}L \end{aligned}$$

(23)

The IAORLS algorithm is still implemented using an S-function, with $-i_q(k)$ and $u_d(k)$ as inputs, and the identified parameters $L$ as outputs.

Simulation and experimental

Simulation results

To demonstrate the effectiveness of the proposed method, this paper conducts a comparative experiment between conventional SMO, STA-SMO without identification and STA-SMO with IAORLS, utilize field-oriented control (FOC) as the primary control strategy and employ space vector pulse width modulation (SVPWM) to improve voltage utilization. The method was simulated in Simulink. Figure 4 shows the block diagram of the sensorless control method for the SPMSM using the STA-SMO with IAORLS parameter identification.

Figure 4

Structure of STA-SMO with IAORLS parameter identification sensorless control of SPMSM.

Table 1 Parameter of the SPMSM.

Table 1 shows the parameters of the SPMSM used in the simulation and experimental. The simulation time is set to 0.1 s, with an initial speed of 500 r/min, increasing to 1000 r/min at 0.05 s.

Figure 5 shows the simulation results of the conventional SMO. It is obvious that high-frequency oscillations is experienced in the rotor position estimated by the SMO during the motor startup phase, primarily due to the low back-EMF and the discontinuity introduced by the sign function.

Figure 5

Simulation results of the conventional SMO for SPMSM sensorless control: (a) Rotor position; (b) Rotor position error.

Figures 6 and 7 show the simulation results of STA-SMO with conventional RLS parameter identification. The use of the STA-SMO algorithm combined with conventional RLS parameter identification results in a relatively long stabilization time and significant overshoot, both during the motor’s initial speed attainment and sudden acceleration. The high-frequency oscillations caused by SMO is eliminated. The stabilization time is approximately 0.007 s, with a maximum overshoot of approximately 15.2%. The motor speed error is relatively large at startup, reaching 12.6 r/min at its peak.

Figure 6

Simulation result of STA-SMO with conventional RLS for SPMSM sensorless control: (a) Rotor speed; (b) Rotor speed error.

Figure 7

Simulation result of STA-SMO with conventional RLS for SPMSM sensorless control: (a) Rotor position; (b) Rotor position error.

However, after running for a while, the STA-SMO with conventional RLS demonstrates good rotor speed tracking, with the speed error controlled within the range of 0–5 r/min. Rotor position tracking also shows good performance, with the error maintained between 0.040 rad and 0.047 rad.

On the basis of simulation results shown in Figs. 8 and 9, applying the STA-SMO with IAORLS parameter identification in sensorless control of the SPMSM outperforms the STA-SMO method. This method demonstrates greater accuracy in motor speed and rotor position estimation.

Figure 8

Simulation results of STA-SMO with IAORLS parameter identification for SPMSM sensorless control: (a) rotor speed; (b) rotor speed error.

Figure 9

Simulation results of STA-SMO with IAORLS parameter identification for SPMSM sensorless control: (a) rotor position; (b) rotor position error.

The system’s stabilization time is approximately 0.0075 s, with the maximum overshoot reduced to approximately 5%. With respect to speed estimation, the peak rotor speed error is just 4.2 r/min, and compared with those of STA-SMO method, the speed ripples are significantly diminished. The rotor speed error is nearly zero once the motor reaches a steady state.

Additionally, the STA-SMO with IAORLS parameter identification excels in terms of rotor position tracking performance. Its maximum position error is only approximately 0.0125 rad, and after the system stabilizes, the error remains approximately 0.001 rad. This is a significant improvement over the STA-SMO with conventional RLS, confirming this approach’s precise control and error reduction advantages. In summary, STA-SMO with IAORLS parameter identification enhances the performance of sensorless control for the SPMSM in various aspects, including the accuracy and stability of speed and position estimation.

Figure 10

Extended back electromotive force of the SPMSM: (a) with RLS parameter identification; (b) with IAORLS parameter identification.

Figure 10 shows the estimated values of the back-EMF under STA-SMO with conventional RLS and IAORLS parameter identification. With IAORLS parameter identification, the extended back-EMF waveform is smoother, and spikes are suppressed.

Figure 11 shows the motor parameters identified by the different methods, including IAORLS, RLS, MRAS, EKF, and PSO. The observers adopted by the system when using these parameter identification methods are all STA-SMO.Among them, both MRAS and EKF have inherent limitations that prevent them from identifying the permanent magnet flux linkage.

The magnetic field generated by the permanent magnets is relatively constant. When the motor operates, the magnetic field of these permanent magnets remains unchanged, so the rotor flux linkage also remains steady. The IAORLS estimated flux linkage is approximately 0.172 Wb, which differs from the actual flux linkage by 0.003 Wb, resulting in an error of approximately 1.7%.

As shown in Table 2, the IAORLS method outperforms RLS in terms of the identification accuracy of both stator resistance and stator inductance. Although the accuracy of the permanent magnet flux linkage identified by IAORLS is lower than that of RLS, the identification time is significantly shorter. Overall, IAORLS demonstrates superior performance compared to RLS. The IAORLS method not only provides the most accurate parameter estimations for resistance, inductance, and flux linkage but also offers the fastest identification time, making it the most efficient method for motor parameter identification when compared to the other methods considered in this study.

As the motor operating, the increase in motor temperature and magnetic saturation causes the stator resistance and inductance variations. The figures show that the IAORLS estimated stator resistance increased from 0.75 to 0.77 $\Omega$, while the inductance decreased from 0.0109 to 0.0098 H. These findings demonstrates that the IAORLS algorithm has good tracking ability for parameter variations.

Table 2 Motor parameters identified by different methods.

Figure 11

SPMSM parameters identified via IAORLS, MRAS, EKF, PSO, RLS: (a) resistance; (b) flux linkage; (c) inductance.

Experimental results

Figure 12 presents the experimental system’s configuration. The SPMSM is controlled by an STMicroelectronics STM32G474CET6 and fed by an STMicroelectronics STGIB10CH60TS-L intelligent power module. The control system’s switching and sampling frequencies are set to 10 kHz.

Figure 12

SPMSM experimental platform.

Figures13 and 14 present the estimated rotor speed, target rotor speed, and error of the conventional RLS parameter identification and IAORLS parameter identification under no load conditions. The IAORLS algorithm outperforms the conventional RLS algorithm in terms of speed estimation accuracy and error stability. IAORLS achieves faster convergence to the target speed with reduced fluctuations, resulting in more reliable performance in motor control applications. In contrast, while the RLS algorithm is effective, it results in more significant error variability, indicating lower precision in speed estimation than IAORLS.

Figure 13

Rotor speed experimental results of STA-SMO with conventional RLS (a) rotor speed (b) rotor speed error.

Figure 14

Rotor speed experimental results of STA-SMO with IAORLS (a) rotor speed (b) rotor speed error.

Conclusion

This paper proposes a STA-SMO with the IAORLS parameter identification for sensorless control of the SPMSM. Compared to MRAS, EKF, RLS, and PSO methods, the IAORLS algorithm provides a more efficient identification of the motor parameters of the SPMSM used in the experiments, including stator resistance, inductance, and permanent magnet flux linkage. Furthermore, after a period of operation, the method can still accurately identify the changed parameter values due to magnetic saturation and temperature increases. The real-time identified motor parameters are fed back into the super-twisting sliding mode observer, enhancing its performance.

The simulation and experimental results demonstrate that the STA-SMO with IAORLS parameter identification sensorless control for SPMSM effectively suppresses the high-frequency oscillations issues commonly associated with conventional sliding mode control, while also improving the dynamic performance and efficiency of the motor.