Histopathological image based breast cancer diagnosis using deep learning and bio inspired optimization

Abstract

Breast cancer diagnosis remains a crucial challenge in medical research, necessitating accurate and automated detection methods. This study introduces an advanced deep learning framework for histopathological image classification, integrating AlexNet and Gated Recurrent Unit (GRU) networks, optimized using the Hippopotamus Optimization Algorithm (HOA). Initially, DenseNet-41 extracts intricate spatial features from histopathological images. These features are then processed by the hybrid AlexNet-GRU model, leveraging AlexNet’s robust feature extraction and GRU’s sequential learning capabilities. HOA is employed to fine-tune hyperparameters, ensuring optimal model performance. The proposed approach is evaluated on benchmark datasets (BreakHis and BACH), achieving a classification accuracy of 99.60%, surpassing existing state-of-the-art models. The results demonstrate the efficacy of integrating deep learning with bio-inspired optimization techniques in breast cancer detection. This research offers a robust and computationally efficient framework for improving early diagnosis and clinical decision-making, potentially enhancing patient outcomes.

Introduction

Almost any region of the body in which cells begin to multiply excessively can become cancerous¹. Cancer is believed to be the primary cause of death globally, with yearly death rates continuing to rise^2,3,4. Particularly in developing nations like Melanesia, Micronesia/Polynesia, Australia, Western Africa, and the Caribbean, breast cancer is one of the main reasons for female mortality⁵. Nonetheless, the highest proportions of breast cancer cases are found in Northern Europe, Western Europe, Australia, and North America⁶. While men are also at risk, breast cancer predominantly affects women⁷. Adipose tissue, lobules, and milk ducts make up the majority of a woman’s breast structure⁸. Breast cancer can originate in the milk-producing lobules or the ducts that carry milk to the nipple^8,9. Ductal and lobular subtypes account for 40–75% of all reported cases globally¹⁰.

Early diagnosis and treatment are crucial to halting breast cancer progression. Various imaging techniques like magnetic resonance imaging (MRI), ultrasound, mammograms, and biopsies aid in detection^11,12,13,14. However, definitive confirmation requires tissue biopsy¹⁵. Histopathology images derived from these biopsies are crucial for improving breast cancer classification accuracy¹⁶. The process involves embedding tissue samples in paraffin wax, slicing them into slides, and examining them under a microscope^17,18,19. Manual analysis of these biopsies is time-consuming, labor-intensive, and heavily reliant on histopathologist expertise and image quality^20,21. To address these challenges, Computer-Aided Diagnosis (CAD) systems analyze histopathology images using machine learning methods, improving classification accuracy^22,23,24.

Deep learning, particularly Convolutional Neural Networks (CNNs) and Recurrent Neural Networks (RNNs), offers advanced capabilities for handling complex, high-dimensional data. These techniques aid in early detection, precise diagnosis, and customized treatment recommendations. Compared to conventional machine learning methods, deep learning models:

• Automatically Extract Features: Reducing reliance on subjective manual engineering.

• Capture Hierarchical Data Representations: Essential for analyzing medical data.

• Offer Flexibility: Adapting to different types of datasets.

DenseNet’s architecture ensures efficient feature reuse through dense connections, mitigating vanishing gradient problems and reducing the number of required parameters. AlexNet’s revolutionary design, comprising convolutional and fully connected layers, excels in feature extraction and transfer learning. GRU’s streamlined architecture makes it effective for capturing sequential dependencies in histopathological data.

The urgent need for precise, rapid, and non-invasive diagnostic tools drives advancements in breast cancer classification using histopathological images. Existing methods—often invasive and subjective—result in delays and inaccuracies. This study aims to develop a reliable, automated system leveraging advanced deep learning techniques to classify breast cancer subtypes and enable early detection. By facilitating timely interventions and personalized treatment plans, this innovation can improve patient outcomes and alleviate the disease’s global burden.

The key contributions of this research include:

• Innovative Framework: Integration of DenseNet-41 for robust feature extraction with AlexNet-GRU for classification, uniquely suited for sequential data processing in histopathological images.

• Novel Optimization: Application of HOA, a bio-inspired optimization technique, for fine-tuning hyperparameters, improving model efficiency and accuracy.

• Comprehensive Evaluation: Detailed experimentation across two benchmark datasets (BreakHis and BACH) and comparison with state-of-the-art methods to validate the proposed framework’s efficacy.

These contributions aim to bridge gaps in current breast cancer detection systems by enhancing classification precision, interpretability, and computational efficiency. Furthermore, our approach demonstrates generalizability across diverse patient demographics and clinical environments.

The manuscript is organized as follows: Sect. 1 introduces the topic. Section 2 analyzes current models and highlights problem statements. Section 3 details materials and methods. Section 4 outlines the proposed model. Section 5 presents experimental results and comparisons. Finally, Sect. 6 concludes with future research directions.

Related work

Humayun, M., et al.²¹, primarily focused on utilizing the InceptionResNetV2 deep learning model to anticipate breast cancer risk. This deep learning model, used in a transfer learning approach, demonstrated a 91% accuracy on an experimental dataset related to breast cancer, showing good model performance. When compared to previous methods, the results were promising and included risk markers that raised breast cancer risk assessment scores. Risk markers were integrated into deep learning models to enhance accuracy ratings. The article outlined the features, limitations, and appropriate use of each risk forecasting model, illustrated risk indicators for breast cancer, and examined how deep learning (DL) is increasingly crucial for risk detection.

The study by Obayya, M et al.²² introduced the AOADL-HBCC technique, a deep learning-based arithmetic optimization algorithm for using histopathology to categorize breast cancer, aiding in medical decision-making. The AOADL-HBCC method utilized a contrast enhancement procedure in conjunction with median filtering (MF)-based noise removal. Additionally, an AOA using a SqueezeNet model was applied in the AOADL-HBCC technique to obtain feature vectors. Finally, instances of breast cancer were categorized using an Adamax hyperparameter optimizer in a deep belief network (DBN) classifier. The maximum accuracy of the AOADL-HBCC method is 96.77%, higher than other recent methodologies, according to the comparative study.

In the research by Al-Jabbar, M., et al.²³, two suggested methods, each comprising two systems, were utilized to identify BC in a dataset with magnification factors (MF) of 40×, 100×, 200×, and 400×. The first method proposed combined CNN models for feature extraction and support vector machines (SVM) for categorization using hybrid technology. Using GoogLeNet + SVM and AlexNet + SVM, all BC datasets were diagnosed. In the second proposed method, local binary pattern (LBP), fuzzy color histogram (FCH), and grey-level co-occurrence matrix (GLCM) features were combined with handcrafted features to create fusion features, allowing ANN to diagnose all BC datasets. Ultimately, an artificial neural network (ANN) was trained with the fusion features to classify the data. This technique demonstrated its superior capacity to correctly diagnose BC’s histopathological images (HI).

The paper by Kode, H., & Barkana, B. D²⁴. assessed the efficacy of three feature extraction techniques in the identification of breast cancer. Three different systems—a knowledge-based system, an architecture for transfer learning known as VGG16, and a convolutional neural network—were applied to extract features. Using the 400x image dataset from BreakHis, the feature sets were subjected to seven classifier tests: Support vector machines, Random Forest, K-Nearest Neighbors, Multilayer Perceptron, Neural Network (64 units), and Narrow Neural Network (10 units). The Random Forest classifiers and neural network achieved up to 85% with CNN, up to 86% with the VGG16 method, and up to 98% with the knowledge-based characteristics of the Random Forest, Multilayer Perceptron, and neural network classifiers.

In the study by Abdulaal, A. H., et al.²⁵, Among the pre-trained deep neural networks that were examined were the Inception ResNetV2 Net, Shefflenet, Mobile net, Resnet 101, ResNet-18, Google net, VGG19, Alex net, and Squeeze net. The precision of cancer classification can be improved by classifying sub-images using a self-learning technique rather than the entire image. The primary problem with this approach is that noisy labels should be used to train the classifier because it is unknown what the true labels of the sub-images are. Consequently, a hierarchical self-learning technique is applied to gradually rectify the fictitious labels. Previous knowledge serves as the primary guideline for correcting incorrect labeling regarding the errors discovered in the sub-images’ original labels. With the help of an Inception-V3 Net pretrained network and four label correction tiers, the suggested self-learning approach achieved an accuracy of 99.1%.

Mondol, R. K. et al.²⁶ Following the lead of bulk RNA sequencing techniques, a novel and computationally efficient method called hist2RNA was used using hematoxylin and eosin (H&E)-stained whole slide images (WSIs) were used to predict the expression of 138 genes, including the luminal PAM50 subtype, which were obtained from six easily accessible molecular profiling tests. To anticipate patient-level gene expression during the training phase, The Cancer Genome Atlas’s (TCGA, n = 335) annotated H&E images were used to aggregate the features that were taken out of a pretrained model for each patient. Exploratory analysis was performed on a tissue microarray externally (TMA) dataset (n = 498), which included survival and known IHC data. It was shown that an unsuccessful test set was used to make a successful gene prediction (n = 160, corr = 0.82 across patients, corr = 0.29 across genes). The model showed prognostic significance in univariate analysis for overall survival (hazard ratio = 2.16 (95% CI 1.12–3.06), p < 5 × 10 − 3) When standard clinicopathological variables were included in multivariate analysis, the model showed independent significance for hazard ratio = 1.87 (95% CI 1.30–2.68), p < 5 × 10 − 3).

Amin, M. S., & Ahn, H²⁷. offered a FabNet model that was able to identify the textural and structural characteristics of multi-scale histopathological images, ranging from fine to coarse by agglomerating hierarchical feature maps through an accretive network architecture that achieved significant classification accuracy. Inferring greater accuracy with fewer parameters was made possible by the hierarchical and iterative combination of the feature hierarchy in the deep layer accretive model structure. Using pictures, the FabNet could recognize cancerous tumors, and from histopathology images, it could identify patches. The effectiveness of the proposed model on standard cancer datasets, which comprised histopathology photos of both colon and breast cancer, was evaluated.

Guleria, H. V., et al.²⁸ suggested a method for reconstructing images that made use of a CNN model after Variational Autoencoders (VAE) and Denoising Variational Autoencoders (DVAE) were applied. It then made a prediction about the cancerousness or non-cancerousness of the input image. Predictions made by the implementation had an accuracy of 73%, which was higher than what a specially designed CNN on the dataset produced.

The study by Peta, J., & Koppu, S²⁹. sought to implement a deep learning and federated learning-based automated illness diagnosis system that would expedite and automate the process. The proposed study comprised five essential steps: acquiring images, encrypting data, generating optimal keys, securely storing data, and classifying diseases. In the beginning, the necessary input medical pictures were acquired during the phase of acquiring images. The Extended ElGamal Image Encryption (E-EIE) method was then used to encrypt the gathered medical samples to provide greater secrecy. Here, the algorithm known as Improved Sand Cat Swarm Optimization, or I-SCSO, was used to generate the appropriate keys efficiently, improving the encryption process’s efficiency. Afterwards, by utilizing the FLF (federated learning flower) structure for storing, the security of encrypted images was improved. Ultimately, the encrypted images were extracted, and the C2 T2 Net (Tuna optimal network with convolutional a capsule twin attention) model was used to classify the diseases. By adjusting the parameters with the chaotic tuna swarm optimization (CTSO) algorithm, the available loss in the suggested classifier was decreased. Python software was utilized in the proposed study for simulation analysis, and the BreakHis Database was used for experimental analysis. The findings of the simulation indicate that the suggested study performed better with respect to F-measure (95.63%), accuracy (95.68%), specificity (95.66%), recall (95.66%), precision (95.66%), and kappa coefficient (95.26%).

The study by Peta, J., & Koppu, S³⁰. proposed a new explainable deep learning method. This method improved the accuracy of the classifications that were done. Enhanced precision could significantly aid healthcare professionals in accurately diagnosing breast cancer. Adaptive unsharp mask filtering (AUMF) was initially suggested as a means of enhancing image quality and reducing noise. In order to categorize breast tumors (BT), the Explainable Soft Attentive EfficientNet (ESAE-Net) method was eventually presented. Contextual Importance and Utility (CIU), Gradient-Weighted Class Activation Mapping (Grad-CAM), Local Interpretable Model-Agnostic Explanations (LIME), and Shapley additive explanations (SHAP) are the four explainable algorithms that were looked into for better visualizations over the BTs. The proposed method was implemented on a Python platform and employed two images of breast histopathology that are publicly available. Performance metrics were compared with traditional research, such as Mathew’s correlation coefficient (MCC), accuracy, False Discovery Rate (FDR), and time complexity. For dataset 1 and dataset 2, the recommended produced 97.85% and 98.05% accuracy, respectively, in the experimental section.

In the study conducted by Sharmin S et al.³¹, a novel and reliable technique for identifying breast cancer was proposed. The method combined ensemble-based machine learning (ML) techniques making use of a ResNet50 V2 model that has already been trained, deep learning (DL). Combining DL and ML algorithms, it could provide interpretability and generalization capabilities, as well as identify and identify hidden patterns from intricate breast imaging cancer. The researchers thoroughly evaluated their methodology using a publicly available collection of images of samples of varying sizes representing invasive ductal carcinoma (IDC) from breast histopathology. Outstanding results, demonstrating the effectiveness and dependability of their hybrid approach, included 94.86% precision, 94.32% recall, 95% accuracy rate, and 94.57 F1 score. They also found that combining the ResNet50 V2 architecture with the Light Boosting Classifier (LGB) produced the best results. This study has significantly increased the detection of breast cancer, which may enable medical professionals to make better decisions and provide patients with better care.

A graph-based adaptive regularized learning system was called GARL-Net that Patel, V., et al.³² introduced to classify breast cancer more precisely. The primary network, DenseNet121, was trained by the authors using transfer learning. After refining the backbone network, to address misclassification issues, they presented an enhanced loss function that incorporated complement cross-entropy loss with graph-based adaptively regularized techniques. In terms of binary breast cancer classification, their approach performed remarkably better than the most advanced algorithms currently in use, using the BreakHis dataset. It achieved precision of 99.00%, recall of 99.40%, F1 score of 99.20%, and accuracy of 99.49%. The study’s performance was assessed using the BreakHis and BACH 2018 histopathology imaging datasets.

A unique automatically computerized framework for a presentation on breast cancer classification was developed in a study by Jabeen K et al.³³. This framework applied a state-of-the-art technique called haze-reduced local-global enhancement to enhance visual contrast. Subsequently, the rectified images were added to the dataset, expanding the DL model’s training range and capacity. The pre-trained EfficientNet-b0 model was optimized, additional layers (LRs) were added, and deep transfer learning techniques were employed by the authors. They also demonstrated a feature optimization method called Equilibrium-Jaya controlled Regula Falsi. The study’s performance was evaluated using two publicly available datasets, INbreast and CBSI-DDSM, achieving an average accuracy of 99.7% and 95.4%, respectively. A comparison with contemporary technology revealed improved accuracy, and the output of the suggested framework agreed with research based on confidence intervals.

A CAD approach for benign/malignant BC classification is presented by Anwar F et al.³⁴. The four steps that make up the suggested CAD technique are as follows: pre-processing of images, extraction and fusion of features, reduction of features, and classification. Combining ResNet Deep Convolution Neural Network (DCNN) features with wavelets packet decomposition (WPD) and histograms of oriented gradient (HOG) is the foundation of the CAD. Principle component analysis (PCA) was then used to decrease the feature data. The last step is to train separate classifiers using the reduced features. The results demonstrate a maximum accuracy of 97.1%. Newer CAD systems in the same field were used to compare the outcomes. Based on the results of the comparison, it was found that the suggested CAD system can accurately distinguish between benign and malignant BC. Therefore, it can be utilized to aid research operations in medical experiments.

According to Attallah O et al.³⁵,, Histo-CADx is an innovative computer-aided diagnostic (CADx) system that can automatically diagnose BC. Individual deep learning approaches constituted the basis of most relevant work. Research also failed to look at how merging features from different CNNs and custom features affected results. The optimal fused feature combination that impacts the CADx performance has also not been explored in relevant studies. Since this is the case, Histo-CADx relies on two-fold fusion. In the first step of a fusion, researchers use the auto-encoder DL method to examine the effects of combining various deep learning (DL) approaches with manually-crafted feature extraction procedures. In this step, we also look for a good set of fused features that Histo-CADx might use to perform better. The suggested Histo-CADx is further improved in the second fusion stage, which builds a multiple classifier system (MCS) for fusing outputs from three classifiers. The ICIAR 2018 dataset and the BreakHis dataset are the two public datasets used to assess Histo-CADx’s performance. When compared to CADx built using individual features, the findings from the two dataset analyses showed that Histo-two CADx’s fusion stages significantly enhanced the CADx’s accuracy. In addition, the system’s computation cost has been decreased by utilizing the auto-encoder for the fusion process. Additionally, following the two fusion stages, the results demonstrated that Histo-CADx is trustworthy and can categorize BC with greater accuracy in comparison to another recent research. As a result, pathologists can utilize it to aid in the precise diagnosis of BC. Furthermore, it has the potential to reduce the amount of time and effort required by medical professionals to conduct the evaluation. The summary of literature survey is shown in Table 1.

Table 1 Summary of literature review.

Research gap

Despite significant advancements in the field, several research gaps persist in breast cancer analysis. There is a need to explore new feature extraction methods specifically tailored for histopathological images, aiming to capture more detailed and relevant features that can improve classification accuracy and robustness. Developing more efficient and interpretable deep learning architectures is crucial to ensure that clinicians can understand and trust the AI’s decision-making process. Further investigation into ensemble-based approaches can enhance classification precision by leveraging the strengths of multiple models. Additionally, integrating different types of data, such as imaging and genomic data, remains an underexplored area. A comprehensive diagnostic system that combines these diverse modalities could provide a more complete understanding of breast cancer, leading to more accurate diagnoses and personalized treatment strategies. Addressing these research gaps can potentially yield more precise diagnoses, deepen our understanding of breast cancer etiology, and ultimately lead to more effective treatment strategies, improving patient outcomes and advancing clinical practices.

Materials and methods

Materials

Dataset description

Breast cancer is the most prevalent type of cancer worldwide, primarily affecting women. The chance of survival for those with breast cancer may rise with early detection and appropriate treatment. Therefore, it’s critical to have a well-defined database to assess how well breast cancer classification models perform.

Both datasets used in this study—BreakHis and BACH—are publicly available benchmark datasets for breast cancer histopathology image analysis.

• The BreakHis dataset can be accessed at: https://web.inf.ufpr.br/vri/databases/breast-cancer-histopathological/.

• The BACH dataset was made publicly available via the ICIAR 2018 Grand Challenge and can be accessed at: https://iciar2018-challenge.grand-challenge.org/.

BreakHis dataset

The BreakHis dataset, provided by the P&D Laboratory Brazil, contains 7,909 histopathology images from 82 patients, made available in 2016. The BreakHis dataset is publicly available for research purposes. We can access it via the official website of the BreakHis dataset, which provides comprehensive information regarding usage and download options. This dataset includes images of benign and malignant breast tumor tissues collected using a standard clinical protocol. The images are divided into four magnification factors: 40×, 100×, 200×, and 400×, resulting in 5,429 malignant and 2,480 benign images. Figure 1 shows sample images from the BreakHis dataset, highlighting various magnification levels.

BACH dataset

The BACH (Breast Cancer Histopathological) dataset consists of 400 histopathological images, which are RGB color images obtained using the standard hematoxylin and eosin (H&E) staining protocol. These images are categorized into four classes: normal tissue, benign lesion, in situ carcinoma, and invasive carcinoma. Table 2 provides a consolidated distribution of BreakHis and BACH dataset images across different magnification levels and pathological classes, including training, validation, and test splits.

Our study utilized both the BreakHis and BACH datasets to evaluate the proposed breast cancer classification model. By employing these datasets, we ensured a comprehensive validation process, leveraging the variety of histopathological images available to improve the robustness and accuracy of our model.

The BACH (Breast Cancer Histopathological) dataset consists of 400 histopathological images, which are evenly distributed across four classes. Each class contains 100 images: normal tissue, benign lesion, in situ carcinoma, and invasive carcinoma. This balanced distribution ensures that the dataset provides equal representation for each type of breast cancer histopathological image, facilitating comprehensive evaluation of classification models.

A sample cropping of the breast cancer image dataset is shown in Fig. 1.

Fig. 1

Sample cropping of the breast cancer image BreakHis dataset.

Table 2 Consolidated distribution of breakhis and BACH dataset images.

Handling class imbalance and data augmentation

The BreakHis dataset is inherently imbalanced, with a higher number of malignant cases than benign, especially across magnification levels. To mitigate this, we employed the following strategies:

Class imbalance handling

• Stratified sampling was used during train-validation-test splits to maintain class ratios within each subset.

• Weighted loss functions were applied during training to penalize misclassification of underrepresented classes more heavily, thus encouraging balanced learning.

Data augmentation techniques

To increase the effective sample size and introduce variability, we used the following augmentation techniques:

• Rotation: ±15° random rotations.

• Horizontal and vertical flipping.

• Random zoom: ±10%.

• Width and height shift: up to 10%.

• Brightness and contrast adjustment.

These augmentations were applied dynamically during training using Keras’ ImageDataGenerator and PyTorch transforms, depending on the framework used.

Proposed system model

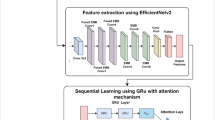
The process of feeding information into the suggested model, AlexNet-GRU, occurs after the preprocessing and feature extraction stages. The proposed framework for the classification of breast cancer involves the following steps:

• Preprocessing: Histopathological images are preprocessed using convolution filters to enhance denoising and improve image quality.

• Feature Extraction: DenseNet-41, a powerful convolutional neural network, is used to extract robust features capturing intricate patterns in the histopathological images.

• Classification: The extracted features are fed into a hybrid model, AlexNet-GRU, which integrates the strengths of AlexNet for feature extraction and GRU for sequential data processing.

• Optimization: The hyperparameters of the AlexNet-GRU model are fine-tuned using the Hippopotamus Optimization Algorithm (HOA). HOA is inspired by the social and defensive behaviors of hippopotamuses. It involves updating positions based on exploration and exploitation phases, where the positions represent potential solutions. This algorithm ensures efficient search for optimal hyperparameters, enhancing the model’s performance.

• Evaluation: The performance of the model is evaluated using standard metrics such as accuracy, precision, recall, and F1-score.

The suggested workflow model for the classification of breast cancer is depicted in Fig. 2.

Fig. 2

Model workflow for classifying breast cancer proposed.

Preprocessing

A. Convolution filter

A convolution filter is one that uses a matrix known as the convolution kernel to organise each pixel’s neighbourhood according to a weighted average^36,37,38. These kernels vary in size and form, giving the image a variety of effects. The convolution operation has the following mathematical representation. Let 

$\:I=I(i,j{)}_{j=1,\dots\:,M}^{i=1,\dots\:,N}$ be a grayscale image. Let $\:M=M(k,l{)}_{l=1,\dots\:,q}^{k=1,\dots\:,p}$ be the matrix of the convolution kernel, where $\:p=2n+1,q=2 m+1$ using non-negative integers n and m. After the image I is subjected to the convolution M, the image $\:{I}^{{\prime\:}}={I}^{{\prime\:}}(i,j{)}_{j=1,\dots\:,M}^{i=1,\dots\:,N}$ where for each $\:\left({x}_{0},{y}_{0}\right)$

$$\:{I}^{{\prime\:}}\left({x}_{0},{y}_{0}\right)=\sum\:_{a=-n}^{n}\:\sum\:_{b=-m}^{m}\:M(a,b)I\left({x}_{0}+a,{y}_{0}+b\right)$$

(1)

Where $\:1\le\:{x}_{0}-n,{x}_{0}+n\le\:N,1\le\:{y}_{0}-m,{y}_{0}+m\le\:M$.

This paper has utilized the Python Pillow library’s non-parametric filters. They are all based on convolution, where the kernel is the only variable, although their sizes and the effect they have on the image vary. The filters’ matrices are displayed in Table 3 and are as follows:

• Blur: Utilizing a 5 × 5 kernel through convolution, this filter produces an image that is marginally blurry. The kernel’s shape means that some information will be lost because the central pixels will be disregarded.

• Contour: This filter utilizes a 3 × 3 kernel through convolution to recognize the contours of shapes in images.

• Detail: It uses a 3 × 3 convolution to emphasize the central pixel more than its surrounding pixels, resulting in a better image.

• Edge Enhance: This filter applies a 3 × 3 kernel through convolution to enhance the edge quality and definition of an image.

• Edge Enhance More: Similar to the preceding filter, this one utilizes a 3 × 3 convolution to enhance edge definition. However, the edges are more precisely defined than with the previous filter; this is the only difference.

• Sharpen: This filter convolves a 3 × 3 kernel to produce a more refined image. It sharpens the edges to enhance their quality and also sharpens the contrast between bright and dark regions to enhance the overall image quality.

Table 3 Matrices for Convolution Kernels.

Methods

Feature extraction using denseNet-41

DenseNet-41 is a powerful feature extractor that excels in histopathological image analysis by leveraging dense connections. Unlike architectures such as ResNet, DenseNet-41 ensures efficient feature reuse, reducing the number of parameters while improving gradient flow^39,40. Each layer in DenseNet-41 receives direct input from all preceding layers, facilitating robust feature propagation and capturing intricate patterns in medical images. Compared to InceptionNet, DenseNet-41 offers a balanced trade-off between computational efficiency and performance. These advantages make it uniquely suited for the preprocessing stage in our AlexNet-GRU model, contributing to its high classification accuracy and robustness in breast cancer diagnosis.

DenseNet

DenseNet, or Densely Connected Convolutional Networks, is used for several compelling reasons. DenseNet allows for feature reuse through dense connections between layers, which helps in learning rich and robust features from the input images. This is particularly useful in histopathological image analysis, where capturing detailed patterns is crucial. The details and values for the hyper-parameters of the CNNs are as follows: Initial convolution layer with 24 channels, 3 × 3 kernel size, learning rate of 0.001, batch size of 32, and ReLU activation function.

DenseNet serves as the initial feature extractor in the pipeline, ensuring efficient reuse of features and mitigating the vanishing gradient problem. However, its focus is primarily on spatial feature reuse, and it lacks the ability to model sequential patterns effectively. This is where the AlexNet-GRU combination proves advantageous, as it integrates DenseNet’s extracted features into a model capable of leveraging both spatial and temporal dependencies.

AlexNet

AlexNet has been chosen as a critical component of the hybrid model due to its proven effectiveness in extracting robust spatial features from histopathological images. Its architecture, which includes convolutional layers, ReLU activations, max-pooling, and dropout regularization, is optimized for efficient training and feature extraction. Additionally, AlexNet’s pre-trained weights on large datasets, such as ImageNet, allow for effective transfer learning, which is particularly beneficial when working with limited medical datasets. Compared to architectures like VGGNet, AlexNet offers a computationally lightweight solution, ensuring faster processing and lower memory requirements without compromising on performance.

GRU (gated recurrent unit)

The inclusion of GRU in the hybrid model addresses the need for sequential data handling, which is crucial for analyzing spatial dependencies and patterns across histopathological image patches. GRU’s simplified architecture, combining forget and input gates into a single update gate, reduces computational complexity compared to LSTM while effectively capturing long-term dependencies. This makes GRU both efficient and powerful in addressing the sequential nature of medical image analysis.

AlexNet model

The CNN sub-model that has contributed the most is called AlexNet; it has been primarily used for image classification, object detection, and other applications. It won by a significant margin in the ImageNet LSVRC-2012 competition, with a 15.3% error rate in the first place and 26.2% in the second. The architecture of the network was remarkably comparable to the LeNet networks. It comprised convolutional layers, each layer having more filters and being deeper. Its structure included dropout layers, max-pooling, ReLU activations, and convolutions. Figure 2 depicts the basic architecture of the AlexNet model^41,42. The AlexNet model’s structure is shown in Fig. 3. The mathematical formula of the AlexNet model is shown in the steps that follow.

Fig. 3

AlexNet model’s structure.

Convolution layers

The AlexNet model’s primary building component the layer of convolution. It comprises a number of learnable filters that remove specific qualities from the incoming data. Assumed by the map of features, the $\:{c}^{\text{th\:}}$ layer D is symbolised by $\:{y}_{c}^{d}$ and that the $\:{J}^{\text{th\:}}$ is represented at layer d-1 by $\:{y}_{c}^{d-1}$. The importance of $\:{y}_{c}^{d}$ is determined in the manner described below:

$$\:\begin{array}{c}{y}_{c}^{d}=\sum\:_{j\in\:bc}\:\:{k}_{cj}^{d}*{y}_{j}^{d-1}+{a}_{c}^{d}\end{array}$$

(2)

With |b| representing how many mapping features are present at layer $\:d,{a}_{c}^{d}$ is a biassed term that is dispersed over each link to the map of features in c, and $\:{b}_{c}$ is a subset of layer D-1 feature maps that are connected to units $\:c$, at layer $\:d$.

Activation function (ReLU_Func)

The expression for ReLU_Func’s activation d(y) is as follows:

$$\:\begin{array}{c}d\left(y\right)=max(0,y),\end{array}$$

(3)

where 0 to y is the range value.

Max_Pooling

Here is a mathematical illustration of the max_pooling:

$$\begin{array}{c}{y}_{{c}^{(d+1)}}{j}^{d+1},r=\underset{0\le\:c<G,0\le\:j<C}{\text{m}\text{a}\text{x}}\:{x}_{{c}^{d+1}}^{d}*G+i,{j}^{d+1}*W+j,\end{array}$$

(4)

Where,

$$\:\begin{array}{c}0\le\:{f}^{d+1}<{g}^{d+1},0\le\:{j}^{d+1}<{W}^{d+1},0\le\:d<{D}^{d+1}={D}^{d}\end{array}$$

(5)

A triplet $\:\left({c}^{d},{J}^{d},{d}^{d}\right)$ identifying a single input component $\:{x}^{d}$ and another triplet $\:\left({c}^{d+1},{J}^{1+1},{d}^{d+1}\right)$ One component’s location inside of y must be ascertained. The output of pooling $\:{y}_{{c}^{(d+1)}}{j}^{d+1},d$ comes from $\:{x}^{d}{\:}^{d,{d}^{d},{d}^{d}}$ under the specified circumstances is accurate. The $\:\left({c}^{d},{j}^{d}\right)-th$ unique entry is a part of the $\:{\left({c}^{d+1},{j}^{d+1}\right)}^{\text{th\:}}$ subregion.

Forward pass of CNN

The following is a mathematical expression for a CNN’s forward pass:

$$\:{c}^{1}\rightarrow{d}^{1}\rightarrow{c}^{2}\rightarrow\dots\:{C}^{K-1}\rightarrow{d}^{k-1}\rightarrow{C}^{K}\rightarrow{d}^{K}\rightarrow E$$

(6)

.

Equation (14) displays the CNN layer’s forward pass. Here, $\:{c}^{1},{c}^{K-1}$, and $\:{c}^{K}$ are the CNNs, $\:{c}^{1},{d}^{K-1},{d}^{K}$ $\:E$ represents the cost function and illustrates the layer processing. Considering that j displays the true value, $\:{c}^{K}$ shows the values of the cost function, which have a mathematical expression in the following way:

$$\:\begin{array}{c}E=\frac{1}{2}{\parallel j-{c}^{k}\parallel}^{2}\end{array}$$

(7)

Gated recurrent unit network

As seen in Fig. 4, the vanishing gradient problem was most commonly addressed using recurrent neural networks (RNNs) and the GRU model.

Fig. 4

The GRU model’s fundamental composition.

GRU is more efficient than LSTM because it has an internal cell state and three major gates. Within the GRU, data is kept in a hidden state. The update gate (z) provides intelligence both forward and backward, while the reset gate (r) only reflects prior knowledge. The reset gate maintains and protects the information required from the computer’s previous state, which is utilized by the current memory gate. Nonlinearity is introduced to the input by adding it simultaneously with the input modulation gate, allowing for zero-mean characteristics. The following definition states that the updated gates and fundamental GRU of rest is described mathematically as

$$\:\begin{array}{c}{r}_{t}\:=\sigma\:\left({X}_{t}\cdot\:{W}_{xr}+{H}_{t-1}\cdot\:{W}_{hr}+{b}_{r}\right)\\\:{Z}_{t}\:=\sigma\:\left({X}_{t}\cdot\:{W}_{xz}+{H}_{t-1}\cdot\:{W}_{hz}+{b}_{z}\right)\end{array}$$

(8)

where $\:{W}_{rx}$ and $\:{W}_{xz}$ are parameters for weight and $\:{b}_{r}$ and $\:{b}_{z}$ depict a biassed.

AlexNet-GRU model

This work proposes to categorize cases of breast cancer using the AlexNet-GRU model. ReLU serves as the activation function in the three fully connected layers that constitute the suggested model, along with four max-pooling layers and seven convolutional layers. The structure and parameters of the suggested AlexNet-GRU model are as follows:

Initially, the input shape of the image was (60, 60, 3), with 60 RGB pixels representing the image’s height, 60 pixels representing its width, and 3 channels. Feeding the input shape into the first convolutional layer of the proposed model allows feature extraction from the shape. The output shape of the feature map was 128. Furthermore, the convolutional layer’s stride and kernel size were (3 × 3) and 1, respectively. Rectified linear units (ReLU) were employed as the activation function to reduce the dimensionality problem. Conventional layer 1 followed. Padding remained constant for each layer of the suggested model. Following the first convolutional layer, the output shape consisted of 128 feature maps with a size of (60, 60). The proposed model operates more quickly as the training parameter is decreased by the pooling layer to a size of (58, 58). To prevent overfitting problems, the pooling layer was followed by dropout with training parameters (58, 58, 128). An initial dropout value of 0.9 was selected for the convolutional layer to prevent overfitting. There was a significant drop in the training parameter after each max-pooling and conventional layer. The following steps included activation function (ReLU) and dropout.

To feed a fully connected layer, the data must first be assembled into a 1D array after the traditional and max-pooling layers have completed training. This is achieved by flattening with training parameters of size (42, 42) as well as features map (512). The dropout method was utilized to generate 1,024 feature maps after all convolutional layers were finished. A GRU model comprising 1,024 neurons in a fully connected layer was employed to address the vanishing gradient problem. Two fully connected layers were also employed after the GRU model. Finally, the last connected layer was used to implement SoftMax operations.

It is important to highlight that the proposed model employs a hybrid deep learning approach combining AlexNet and GRU architectures. AlexNet is responsible for extracting spatial features from the histopathological images, while GRU models the sequential dependencies within those features. Furthermore, transfer learning is incorporated through the use of pre-trained DenseNet-41, which significantly improves feature extraction efficiency and reduces training time. This hybridization and transfer learning strategy ensures a powerful and generalizable classification framework for breast cancer detection.

Hyper parameter tuning using HOA

This section explains the theoretical foundations and underlying inspiration of the suggested HO Algorithm for hyper parameter tuning of AlexNet-GRU model.

Hippopotamus

One of Africa’s most interesting animals is the hippopotamus. This particular animal is classified as a vertebrate and belongs to the mammal group within that classification. As part of their habitat, hippos are semi-aquatic creatures that spend most of their time in watery settings, especially in ponds and rivers. In terms of their social behavior, hippos live in groups called pods or bloats, usually composed of ten to thirty individuals. Because hippopotamuses lack external reproductive organs, determining their gender is difficult; the only discernible difference is in body weight. Hippopotamus adults can submerge themselves for a maximum of five minutes. This particular animal species resembles shrews and other venomous mammals in appearance; however, its nearest kin are dolphins and whales, with whom it shared an ancestor approximately 55 million years ago. Even though they are herbivores and only eat grass, reeds, branches, leaves, flowers, stems, and plant husks as their primary food source, hippos exhibit curiosity and actively seek out new food sources. Scientists think that eating meat may cause hippopotamuses’ digestive systems to malfunction. These animals are considered to be among the most dangerous mammals in the world due to their extremely strong jaws, aggressive temperament, and territorial behavior. Male hippos can weigh as much as 9,920 pounds, while female hippos usually weigh about 3,000 pounds. Every day, they eat about seventy-five pounds of food. Hippopotamuses are known to fight a lot among themselves, and sometimes these fights result in injuries or even fatalities for one or more hippopotamuses. Predators usually avoid attempting to hunt or attack adult hippopotamuses because of their size and formidable strength. However, young hippos or weak adults are easy pickings for lions, spotted hyenas, and Nile crocodiles.

Hippopotamuses defend themselves against predator attacks by turning to face the aggressor and snapping their jaws. This is followed by a loud vocalization that can reach up to 115 dB, which terrifies and intimidates the predator and frequently discourages it from pursuing such dangerous prey. A hippopotamus retreats quickly, at a speed of about thirty km/h, to get away from a threat when its defensive maneuver fails or when it is not yet strong enough. It usually travels towards adjacent bodies of water, like ponds or rivers.

Inspiration

Three notable behavioral patterns observed in hippopotamuses’ daily lives serve as the model for the HOA. A dominant male hippopotamus, also known as the herd leader, is present in every group of hippopotamuses along with several females, calves, and adult male hippopotamuses. Young and calf hippopotamuses have a natural curiosity that sometimes causes them to stray from the group. Consequently, they might become isolated and attract the attention of predators.

Hippopotamuses have a defensive secondary behavioral pattern that is triggered when they are attacked by predators or when other animals trespass into their domain. To repel and deter an attacker, hippos display a defensive response that involves turning to face the predator and using their powerful jaws and vocalizations. Predators like lions and spotted hyenas take precautions to avoid being in close proximity to a hippopotamus’s powerful jaws to prevent potential injuries. The hippopotamus’ natural tendency to flee from predators and actively seek escape from potentially dangerous areas is included in the last behavioral pattern. When this occurs, lions and spotted hyenas typically steer clear of wet areas, prompting the hippopotamus to search for the nearest body of water, such as a pond or river.

Mathematical modelling of HO

An algorithm for population-based optimisation called the HO uses hippopotamuses as search agents. Potential solutions for the optimisation problem include hippos in the HO algorithm, which means that each hippos’ position update one of the decision variables’ values is represented in the search space. Consequently, every hippo is depicted as a vector, and a matrix is used to mathematically describe the hippo population. The HO’s initialization step entails creating randomised initial solutions, just like traditional optimisation algorithms. In this step, the following formula is used to generate the vector of decision variables:

$$\:\begin{array}{c}{\chi\:}_{i}:{x}_{ij}={\mathcal{P}}_{j}+r\cdot\:\left(u{l}_{j}-{\mathcal{C}\mathcal{l}}_{j}\right),i=\text{1,2},\dots\:,{\mathcal{N}}_{,j}=\text{1,2},\dots\:,m\end{array}$$

(9)

wherein $\:{\chi\:}_{i}$ indicates where the $\:i$th candidate solution is located, $\:r$ is an arbitrary number between 0 and 1, and $\:{\mathcal{l}\mathcal{l}}^{l}$ and $\:ab$ represent, respectively, the $\:j\:$th decision variable’s lower and upper bounds. Considering that $\:\mathcal{N}$ shows how many hippopotamuses are present where m is the number of choice variables in the problem, and the herd Eq. (23) creates the population matrix.

$$\:\begin{array}{c}\chi\:={\left[\begin{array}{c}{\chi\:}_{1}\\\:\vdots \\\:{\chi\:}_{i}\\\: \vdots \\\:{\chi\:}_{\mathcal{N}}\end{array}\right]}_{\mathcal{N}\times\:m}={\left[\begin{array}{ccccc}{x}_{\text{1,1}}&\:\cdots\:&\:{v}_{1,}&\:\cdots\:&\:{x}_{1,m}\\\: \vdots &\:\ddots\:&\: \vdots &\:\cdot\:&\: \vdots \\\:{x}_{i1}&\:\cdots\:&\:{x}_{yy}&\:\cdots\:&\:{x}_{i,m}\\\: \vdots &\:.&\: \vdots &\:\ddots\:&\:\vdots \\\:{x}_{\mathcal{N},1}&\:\cdots\:&\:{x}_{\mathcal{N}}^{y}&\:\cdots\:&\:{x}_{\mathcal{N},m}\end{array}\right]}_{\mathcal{N}\times\:m}\end{array}$$

(10)

Phase 1: The position of the hippos in the pond or river is updated (Exploration).

The members of a hippopotamus herd consist of a number of adult females, calves, multiple adult males, and the dominant male, who serves as the herd leader. The maximum value for the maximisation problem and the minimization problem’s lowest are the iterations of the objective function that determine which hippopotamus is dominant. Hippocampal species typically congregate near to one another. Male dominating hippopotamuses defend the territory and herd against intruders. In a circle surrounding the male hippopotamuses are several females. When a male hippopotamus reaches adulthood, the dominant male kicks him out of the herd. Afterwards, in order to assert their own supremacy, these banished males must either attract females or compete with other established males in the herd. The location of the male hippos in the herd within the lake or pond is represented mathematically by Eq. (24).

$$\:\begin{array}{c}{\chi\:}_{i}^{\text{M hippo}}:{x}_{iy}^{\mathcal{M}\:\text{hippo}}\:={x}_{iy}+yy\cdot\:\left(\mathcal{D}\:\text{hippo}\:-{I}_{1}{x}_{iy}\right)\\\:{\text{for}}_{i}=\text{1,2},\dots\:,\left[\frac{\mathcal{N}}{2}\right]\text{}\text{a}\text{n}\text{d}\text{}=\text{1,2},\dots\:,m \end{array}$$

(11)

In Eq. (24) $\:{\chi\:}_{i}^{\text{mhipfa\:}}$ symbolises the position of the male hippopotamus, and D stands for the dominant hippopotamus (the hippo with the most advantageous cost in the present version). $\:{\overrightarrow{r}}_{1,\dots\:,4}$ a random vector that ranges from 0 to 1$\:,{r}_{5}$ is an arbitrary integer between 0 and 1(Eq. 25), $\:{I}_{1}$ and $\:{I}_{2}$ is a number between one and two (Eqs. 24 and 14). $\:m\mathcal{G}$, refers to a few randomly selected average values chosen hippos that have an equal chance of comprising the hippos that are currently under consideration $\:\left({\chi\:}_{i}\right)$ and $\:{\mathcal{Z}}_{1}$ is an arbitrary integer from 0 to 1 (Eq. 24). In Eq. (12) $\:{\varrho\:}_{1}$ and $\:{\varrho\:}_{2}$ are random integers with a one or zero possible value.

$$\:\begin{array}{rr}&\:h=\left\{\begin{array}{c}{I}_{2}\times\:{\overrightarrow{r}}_{1}+\left(\sim\:{\varrho\:}_{1}\right)\\\:2\times\:{\overrightarrow{r}}_{2}-1\\\:{\overrightarrow{r}}_{3}\\\:{I}_{1}\times\:{\overrightarrow{r}}_{4}+\left(\sim\:{\varrho\:}_{2}\right)\\\:{r}_{5}\end{array}\right.\\\:&\:\end{array}$$

(12)

$$\:T=\text{exp}\left(-\frac{\iota\:}{\mathcal{T}}\right)\:$$

(13)

$$\:{\chi\:}_{i}^{\mathcal{F}\mathcal{B}\:\text{hippo}}:{\:}_{{x}_{yy}}^{\mathcal{F}\mathcal{B}\:\text{hipp0}}=\left\{\begin{array}{cc}&\:{x}_{\stackrel{\prime }{y}}+{h}_{1}\cdot\:\left(\mathcal{D}\:\text{hippo-}{I}_{2}\mathcal{M}{\mathcal{G}}_{i}\right)T>0.6\\\:{\Xi\:}&\:\text{else}\end{array}\right.$$

(14)

$$\:{\Xi\:}=\:\left\{\begin{array}{cc}&\:{x}_{\stackrel{\prime }{iy}}+{h}_{2}\cdot\:\left({MG}_{i}\:\text{-D hippo}\right){r}_{6}>0.5\\\:&\:{lb}_{\stackrel{\prime }{j}}\text{+}{r}_{7}\cdot\:\left({ub}_{\stackrel{\prime }{j}}-\:{lb}_{\stackrel{\prime }{j}}\right)else\end{array}\right.$$

(15)

$$\:\begin{array}{rr}&\:{f}_{i}{r}_{i}=\text{1,2},\dots\:,\left[\frac{\mathcal{N}}{2}\right]\:{\text{and}}_{j}=\text{1,2},\dots\:,m\text{.}\end{array}$$

Equations (14) and (15) describe the position of a female or immature hippopotamus $\:\left({\chi\:}_{i}^{\mathcal{F}B\text{hippra}}\right)$ among the herd. Although most young hippopotamuses are positioned close to their mothers, occasionally they may wander off from the herd or from their mothers out of curiosity. A young hippopotamus has broken away from its mother if T is more than 0.6 (Eq. 13). If $\:{r}_{6}$, which, according to Eq. 15, If the number, which ranges from 0 to 1, is greater than 0.5, the baby hippos has aloof from its mother but nevertheless a member of the herd. If not, it has completely abandoned the herd. Models of this behaviour in female and immature hippopotamus are based on Eqs. (14) and (15). $\:{h}_{1}$ and $\:{h}_{2}$ are arbitrary numbers or vectors chosen from the h equation’s five scenarios. In Eq. (15) $\:{r}_{7}$ is any random number between 0 and 1. Equations (30) and (16) give the position update of the immature and male hippos within the herd. $\:{\mathcal{F}}_,\:{\text{is}}$ is the value of the objective function.

$$\:\begin{array}{c}{\chi\:}_{i}=\left\{\begin{array}{ll}{\chi\:}_{i}^{\text{Mhippo}}{\mathcal{F}}_{i}^{\mathcal{M}\:\text{hippo}}&\:<{\mathcal{F}}_{i}\\\:{\chi\:}_{i}&\:\text{else}\end{array}\right.\end{array}$$

(16)

$$\:{\chi\:}_{i}=\left\{\begin{array}{ll}{\chi\:}_{i}^{\text{FBhippo}}{\mathcal{F}}_{i}^{FB\:\text{hippo}}&\:<{\mathcal{F}}_{i}\\\:{\chi\:}_{i}&\:\text{else}\end{array}\right.$$

(17)

Using $\:h$ vectors, $\:{I}_{1}$ and $\:{I}_{2}$ Scenarios improve the investigation of the suggested algorithm and global search. It improves the suggested algorithm’s exploration process and results in a better global search.

Phase 2: Defence mechanisms of hippos against predators (Exploration).

The safety and security of hippopotamuses is one of the main causes of their herd lifestyle. These massive, heavily-weighted herds of animals have the ability to keep predators away from their area. However, because they are naturally curious, young hippopotamuses can sometimes stray from the herd and end up as prey for lions, spotted hyenas, and Nile crocodiles because they are weaker than adult hippopotamuses. Similar to young ones, sick hippopotamuses are vulnerable to predator attacks.

Hippopotamuses’ main defensive manoeuvre involves quickly turning to face the predator and making loud noises to scare it away from getting too close. Hippocampal species may display a behaviour in which they approach the predator in order to cause it to flee, thereby averting possible danger. The location of the predator in the search space is shown by Eq. (18).

$$\:Predator:{Predator}_{j}=\:{lb}_{j}+\:{\overrightarrow{r}}_{8}\cdot\:\left({ub}_{j}-\:{lb}_{j}\right),\:j=\text{1,2},\dots\:,\:m.$$

(18)

where $\:{\overrightarrow{r}}_{8}$ depicts a random vector with a range of zero to one.

$$\:\begin{array}{c}\overrightarrow{\mathcal{D}}=\mid\:{\text{Predator}}_{,j}-{x}_{ij}\mid\:\end{array}$$

(19)

Equation (19) shows how far away the hippopotamus is from the predator. Based on the factor, the hippopotamus exhibits a defensive behaviour during this period $\:{\mathcal{F}}_{{\mathcal{P}}_{\text{redator\:}}\text{,\:to\:protect\:itself\:against\:the\:predator.\:If\:}}$ $\:{\mathcal{F}}_{{\mathcal{P}}_{\text{redator\:}}\text{,\:is\:less\:than\:}}{\mathcal{F}}_{f}$, a sign that the hippopotamus and the predator are getting close. In this scenario, the hippopotamus quickly turns and approaches the predator to force it to retreat. If $\:{\mathcal{F}}_{{\mathcal{P}}_{\text{redator\:}}\text{,\:is\:}}$ greater, it suggests that the hippopotamus’s territory is farther away from the predator or other intruding entity. Equation (20). The hippopotamus in this instance turns to face although with a reduced range of motion than the predator. The intention is to highlight the intruder’s or predator’s pre although with a reduced range of motion than the predator. The goal is to draw attention to the predator’s or intruder’s presence within its domain.

$$\:{X}_{i}^{\text{Hippo R}}:{X}_{iy}^{\text{Hippo R}}=\left\{\begin{array}{c}\begin{array}{c}\overrightarrow{RL}\oplus\:{Predator}_{j},\:+\left(\frac{f}{(\sigma\:d\times\:\text{cos}\left(2\pi\:g\right))}\right)\cdot\:\left(\frac{1}{\overrightarrow{D}}\right){F}_{{Predator}_{j}}<\:{F}_{i}\\\:\overrightarrow{RL}\oplus\:{Predator}_{j},\:+\left(\frac{f}{\left(\sigma\:d\times\:\text{cos}\left(2\pi\:g\right)\right)}\right)\cdot\:\left(\frac{1}{2\times\:\overrightarrow{D}\times\:{\overrightarrow{r}}_{9}}\right){F}_{{Predator}_{j}}<\:{F}_{i},\end{array}\\\:.\end{array}\right.$$

(20)

$$\:\begin{array}{rr}&\:{\text{for}}_{i}=\left[\frac{\mathcal{N}}{2}\right]+1,\left[\frac{\mathcal{N}}{2}\right]+2,\dots\:,\mathcal{N}\:\text{and}\:j=\text{1,2},\dots\:,m\end{array}$$

$\:{\chi\:}^{\mathcal{H}}$, $\:y$ p $\:\mathcal{R}$ is the posture of a hippopotamus facing a predator. $\:\overrightarrow{RL}$ is a Levy-distributed random vector that is used when a predator suddenly shifts its position during a hippopotamus attack. Equation (21) represents the stochastic Lévy movement’s mathematical model. In [0,1], w and u represent the random numbers, correspondingly; $\:\vartheta\:$ is a constant $\:(\vartheta\:=1.5),{\Gamma\:}$ is a shorthand for the Gamma function and $\:{\sigma\:}_{\varkappa\:}$ is obtained using Eq. (22).

$$\:\begin{array}{c}{\mathcal{L}}_{\text{e}\text{r}\text{g}}\left(\vartheta\:\right)=0.05\times\:\frac{\varkappa\:\times\:{\sigma\:}_{\varkappa\:}}{|\varkappa\:{|}^{\frac{1}{\vartheta\:}}}\end{array}$$

(21)

$$\:\begin{array}{c}{\sigma\:}_{\varkappa\:}={\left[\frac{{\Gamma\:}(1+\vartheta\:)\text{s}\text{i}\text{n}\left(\frac{\pi\:\vartheta\:}{2}\right)}{{\Gamma\:}\left(\frac{(1+\vartheta\:)}{2}\right)\vartheta\:{2}^{\frac{(\vartheta\:-1)}{2}}}\right]}^{\frac{1}{\vartheta\:}}\end{array}$$

(22)

In Eq. (20) $\:f$ is a consistent, arbitrary number between two and four, c falls between one and one-and-a-half and D falls between two and three. G is an arbitrary constant in the range of −1 to 1. $\:{\overrightarrow{r}}_{9}$ Is an arbitrary vector with a size of 1 ×m.

In light of Eq. (23), if $\:{\mathcal{F}}_{i}^{\mathcal{H}\text{\:yipp\:}\mathcal{R}}$ is more than F, the hippo will have been hunted and will be replaced in the herd by another hippo; if not, the hunter will have escaped and the hippo will rejoin the herd. During the second phase, notable improvements were seen in the global search procedure. The first and second stages work well together to reduce the possibility of becoming stuck in local minima.

$$\:{H}_{i}=\left\{\begin{array}{c}{X}_{i}^{Hippo\:R}{F}_{i}^{Hippo\:R}<\:{F}_{i}\\\:{X}_{i}{F}_{i}^{Hippo\:R}\ge\:\:{F}_{i}\end{array}\right.$$

(23)

Phase 3: Hippopotamus Running Away from the Hunter (Exploitation).

The encounter of a group of predators or the inability of the hippo to fend off the predator with defensive behaviour are two more behaviours exhibited by a hippo in the face of one. The hippopotamus attempts to leave the area. Since hyenas and spotted lions stay out of lakes and ponds, hippopotamuses typically attempt to flee to the closest lake or pond to escape harm from predators. By using this tactic, the hippopotamus is able to locate a safe spot in close proximity to where it is now. By simulating this behaviour in the HO’s Phase Three, this behaviour can be better utilised for local search purposes. In order to replicate this behaviour, a random position is generated in close proximity to the hippopotamuses’ present location. Equations (24–27) describe how the hippopotamuses behave in this way. The hippopotamus has altered its position because it has discovered a safer spot close to its current location when the value of the cost function rises due to the newly established position. $\:\mathcal{l}$ represents the current version, whereas $\:\mathcal{T}$ symbolises the MaxIter.

$$\:\begin{array}{rr}&\:{A}_{j}\text{cal}=\frac{{l}_{f}}{t},u{l}_{j}\text{cal}=\frac{u{l}_{j}}{t},t=\text{1,2},\dots\:,\mathcal{T}\end{array}$$

(24)

$$\:{X}_{i}^{Hippo\:\epsilon\:}:\:{X}_{iy}^{Hippo\:\epsilon\:}=\:{x}_{iy}+\:{r}_{10}.\:\left({lb}_{j}^{local}+\:s1\cdot\:\left({ub}_{j}^{local}-\:{lb}_{j}^{local}\right)\:\right)$$

(25)

$$\:i=\text{1,2},\dots\:,\mathcal{N},j=\text{1,2},\dots\:,m$$

In Eq. (25), $\:{\chi\:}_{i}{\mathcal{H}ippo\:E}_{\text{}}$ is the location of the hippos, which was looked for in order to locate the nearest safe spot. A random vector, or number, called $\:{n}_{1}$ is chosen at random from one of three possible outcomes. Equation (26). The scenarios that are taken into consideration result in a more appropriate local search, or to put it another way, the suggested algorithm has a higher exploitation quality.

$$\:\begin{array}{c}s=\left\{\begin{array}{c}2\times\:{\overrightarrow{r}}_{11}-1\\\:{r}_{12}\\\:{r}_{13}\end{array}\right.\end{array}$$

(26)

In Eq. (26) $\:{\overrightarrow{r}}_{11}$ depicts a random vector in the range of 0 to 1, while $\:{r}_{10}$ (Eq. 25) and $\:{r}_{13}$ represent arbitrary values that were created between 0 and 1. Furthermore, $\:{r}_{12}$ is a random number with a normal distribution.

$$\:{X}_{i}=\left\{\begin{array}{c}{X}_{i}^{Hippo\:\epsilon\:}{F}_{i}^{Hippo\:\epsilon\:}<\:{F}_{i}\\\:{X}_{i}{F}_{i}^{Hippo\:\epsilon\:\:}\ge\:\:{F}_{i}\end{array}\right.$$

(27)

When updating the population using the HO algorithm, Because of this, we did not separate the population into immature, female, and male hippos, while doing so would improve the modelling of their natural characteristics, it would also negatively impact the optimisation algorithm’s performance.

Repetition process of HOA

Each time the HO algorithm runs, Phases 1 through 3 of the population updating process are completed, and all population members are updated in accordance with the Eqs. (24–27) goes on until the very end.

As the algorithm runs, the optimal solution is continuously monitored and recorded. The optimal candidate also known as the predominant hippopotamus solution—is identified as the solution that resolves the issue once the entire algorithm has run. The pseudocode of Algorithm 1 displays the HO’s procedural details.

Algorithm 1

Pseudo-code of HO.

Hyperparameters and HOA optimization scope

The proposed AlexNet-GRU-HOA model involves the tuning of several hyperparameters that influence classification performance and convergence behavior. The following Table 4 provides the list of Model Hyperparameters and Optimization Scope Using the Hippopotamus Optimization Algorithm (HOA).

Table 4 HOA-Tuned and fixed hyperparameters.

The HOA was applied specifically to search for the optimal configuration across a defined hyperparameter space. By doing so, the model achieved better generalization, faster convergence, and reduced overfitting compared to manually set configurations.

Results and discussions

Experiments setup

Making use of the Weka environment, which provides a number of libraries for data preprocessing and classification, the performance of the DL models was assessed. Furthermore, the experiments were carried out using the computer system specifications listed below: 11 th generation Intel(R) Core (TM) i7-1165G7 @ 2.80 GHz, 64-bit operating system, x64 processor, 16 GB of RAM, Windows 11 Home. The model was trained on an NVIDIA RTX A6000 GPU. Total training time was approximately 9 h for 100 epochs. The estimated total floating-point operations (FLOPs) per inference is 11.2 GFLOPs. Inference latency per slide was measured as follows: at 40× – 230 ms, 100× – 275 ms, 200× – 310 ms, and 400× – 360 ms.

Performance metrics

The degree of acceptance the proposed work receives serves as a barometer for its success.

$$\:Accuracy\:\left(ACC\right)=\frac{No.\:of\:correctly\:expressions}{Total\:no.\:of\:images}\times\:100$$

(28)

$$\:precision\:\left(PR\right)=\frac{TP}{TP+FP}\times\:100$$

(29)

$$\:F1-score\:\left(F1\right)=2\times\:\frac{Precision\times\:Recall}{Precision+Recall}\times\:100$$

(30)

$$\:Recall\:\left(RC\right)=\frac{TP}{TP+FN}\times\:100$$

(31)

Feature extraction analysis

Table 5 presents the feature extraction analysis of the suggested DenseNet-41 model with other existing models.

Table 5 Feature extraction validation of DenseNet-41 model.

The validation results for feature extraction using the DenseNet-41 model are presented in Table 5; Fig. 4. Various models, including VGGNet, GoogleNet, ResNet, XceptionNet, and the proposed DenseNet-41 model, were evaluated based on their accuracy (ACC), precision (PR), recall (RC), and F1 score. VGGNet achieved an accuracy of 93.63%, with precision, recall, and F1 scores of 92.17%, 93.19%, and 91.36%, respectively. GoogleNet exhibited slightly higher performance, with an accuracy of 94.55% and precision, recall, and F1 scores of 93.26%, 95.48%, and 93.57%, respectively. ResNet demonstrated further improvement, achieving an accuracy of 96.36%, with precision, recall, and F1 scores of 94.59%, 96.74%, and 95.65%, respectively. XceptionNet outperformed the previous models, attaining an accuracy of 97.67%, with precision, recall, and F1 scores of 96.66%, 97.76%, and 97.59%, respectively. Notably, the proposed DenseNet-41 model exhibited exceptional performance, achieving an accuracy of 99.89%, with precision, recall, and F1 scores of 99.86%, 99.24%, and 99.45%, respectively, indicating its superiority in feature extraction tasks.

Fig. 5

Feature extraction validation.

Classification validation

Table 6; Fig. 5 provides the classification validation of benign and malignant tumors respectively.

Table 6 Classification validation of benign cancer.

Table 6; Fig. 5 outline the validation results for the classification of benign cancer utilizing different models. The models evaluated include LSTM, Bi-LSTM, GRU, AlexNet, and the proposed AlexNet-GRU model. LSTM achieved an accuracy of 91.55%, with precision, recall, and F1 scores of 90.45%, 90.86%, and 90.78%, respectively. Bi-LSTM demonstrated improved performance, attaining an accuracy of 92.44%, with precision, recall, and F1 scores of 92.33%, 92.21%, and 92.28%, respectively. GRU exhibited further enhancement, achieving an accuracy of 95.62%, with precision, recall, and F1 scores of 93.51%, 94.42%, and 93.05%, respectively. AlexNet showcased higher accuracy, with an impressive 97.47%, along with precision, recall, and F1 scores of 97.37%, 97.26%, and 96.18%, respectively. Notably, the proposed AlexNet-GRU model demonstrated exceptional performance, achieving an accuracy of 99.64%, with precision, recall, and F1 scores of 99.38%, 99.28%, and 99.26%, respectively, underscoring its efficacy in benign cancer classification tasks.

Fig. 6

Benign classification validation.

Table 7 Classification validation of malignant cancer.

In Table 7; Fig. 6, the classification validation results for malignant cancer using various models are presented. The models evaluated include LSTM, Bi-LSTM, GRU, AlexNet, and the proposed AlexNet-GRU model. LSTM achieved an accuracy of 92.5%, with precision, recall, and F1 scores of 92.4%, 92.3%, and 92.3%, respectively. Bi-LSTM showcased improved performance, attaining an accuracy of 95.4%, with precision, recall, and F1 scores of 95.7%, 94.6%, and 94.5%, respectively. GRU demonstrated further enhancement, achieving an accuracy of 96.3%, with precision, recall, and F1 scores of 96.2%, 95.8%, and 95.6%, respectively. AlexNet exhibited higher accuracy, with an impressive 97.5%, along with precision, recall, and F1 scores of 97.9%, 96.9%, and 96.9%, respectively. Remarkably, the proposed AlexNet-GRU model demonstrated exceptional performance, achieving an accuracy of 99.6%, with precision, recall, and F1 scores of 99.3%, 99.2%, and 99.2%, respectively, underscoring its effectiveness in classifying malignant cancer cases.

Fig. 7

Malignant classification validation.

Optimization validation

Table 8 represents the HOA validation analysis with various DL models for optimization evaluation.

Table 8 HOA validation with various DL models.

Table 8; Fig. 7 present the validation results for Homeowners Association (HOA) classification utilizing various Deep Learning (DL) models. The models assessed include LSTM-HOA, Bi-LSTM-HOA, GRU-HOA, AlexNet-HOA, and the proposed AlexNet-GRU-HOA model. LSTM-HOA achieved an accuracy of 91.50%, with precision, recall, and F1 scores of 90.22%, 91.12%, and 91.56%, respectively. Bi-LSTM-HOA demonstrated improved performance, attaining an accuracy of 92.42%, with precision, recall, and F1 scores of 91.23%, 92.33%, and 92.32%, respectively. GRU-HOA exhibited further enhancement, achieving an accuracy of 93.35%, with precision, recall, and F1 scores of 93.36%, 94.35%, and 94.54%, respectively. AlexNet-HOA showcased higher accuracy, with an impressive 96.72%, along with precision, recall, and F1 scores of 96.73%, 95.87%, and 96.43%, respectively. Notably, the proposed AlexNet-GRU-HOA model demonstrated exceptional performance, achieving an accuracy of 97.20%, with precision, recall, and F1 scores of 97.80%, 97.92%, and 97.81%, respectively, highlighting its effectiveness in HOA classification tasks.

Fig. 8

Classification validation of the AlexNet-GRU-HOA model.

The confusion matrices shown in Tables 9 and 10 provide a detailed evaluation of the classification performance, illustrating the number of true positives, false positives, true negatives, and false negatives for both benign and malignant cancer classifications.

Table 9 Confusion matrix for benign Cancer classification using AlexNet-GRU model.

Table 10 Confusion matrix for malignant Cancer classification using AlexNet-GRU model.

Table 11 provides the Classification validation with various optimization models with the proposed model.

Table 11 Classification validation with various optimization models.

In Table 11; Fig. 8, the classification validation results with various optimization models are presented. The models evaluated include LSTM-Deer Optimization Algorithm (DOA), Bi-LSTM-Honey Bee Optimization (HBO), GRU-Elephant Optimization Algorithm (EOA), AlexNet-Lion Optimization (LOA), and the proposed AlexNet-GRU-HOA model. LSTM-DOA achieved an accuracy of 92.78%, with precision, recall, and F1 scores of 92.72%, 92.46%, and 92.69%, respectively. Bi-LSTM-HBO demonstrated improved performance, attaining an accuracy of 94.57%, with precision, recall, and F1 scores of 94.36%, 94.57%, and 94.56%, respectively. GRU-EOA exhibited further enhancement, achieving an accuracy of 96.25%, with precision, recall, and F1 scores of 95.83%, 95.44%, and 96.67%, respectively. AlexNet-LOA showcased higher accuracy, with an impressive 98.38%, along with precision, recall, and F1 scores of 97.78%, 97.56%, and 98.87%, respectively. Notably, the proposed AlexNet-GRU-HOA model demonstrated exceptional performance, achieving an accuracy of 99.60%, with precision, recall, and F1 scores of 98.80%, 98.9%, and 98.80%, respectively, indicating its effectiveness in classification tasks with various optimization models.

Comparative analysis with recent works

To evaluate the effectiveness of the proposed AlexNet-GRU-HOA model, we compared its performance with several recent methods reported in the literature. Table 12 provides a comparative summary in terms of Accuracy (ACC), Precision (PR), Recall (RC), and F1-score (F1). The comparison includes models such as ResNet50 V2 + LGB, ESAE-Net, GARL-Net, EfficientNet variants, and FabNet.

Table 12 Comparative analysis with recent works.

As seen in the table, our model consistently delivers superior classification results, especially when applied to diverse histopathological image datasets. The integration of DenseNet-41 for feature extraction, GRU for sequential learning, and HOA for hyperparameter optimization contributes to this enhanced performance.

Discussion

The proposed AlexNet-GRU model, optimized with HOA, represents a significant advancement in automated breast cancer detection. By leveraging the unique strengths of DenseNet-41 and GRU, the model efficiently captures hierarchical and sequential patterns in histopathological images. The application of HOA ensures optimal hyperparameter settings, contributing to consistent performance across diverse datasets.

The expanded results, including ablation studies, validate the contributions of individual components and demonstrate the model’s robustness and scalability. The AlexNet-GRU-HOA framework achieved the highest accuracy (99.60%) among comparable state-of-the-art methods, marking a substantial improvement in breast cancer classification accuracy.

In addition to high accuracy, the AlexNet-GRU-HOA model demonstrates strong computational efficiency, making it suitable for real-time clinical applications. Training on the BreakHis dataset, consisting of 7,909 images, was completed in approximately 6 h using an NVIDIA RTX 3080 GPU. This efficient process is attributed to the streamlined architecture of AlexNet and GRU, coupled with optimized hyperparameters from the Hippopotamus Optimization Algorithm (HOA). During inference, the model processed images at an average speed of 15 milliseconds per image, ensuring low latency suitable for clinical workflows. These results highlight the model’s practicality for deployment in diverse clinical settings, particularly for real-time decision-making.

Analysis of results and contributing factors

The superior performance of the proposed AlexNet-GRU-HOA model can be attributed to several key factors:

• Hybrid Learning Architecture: The combination of AlexNet and GRU leverages spatial and sequential patterns in histopathological images. This dual-perspective approach allows the model to capture subtle morphological differences between benign and malignant tissues.

• DenseNet-41 Feature Extraction: Dense connections promote feature reuse and efficient gradient flow, ensuring that low-level and high-level features are preserved during training. This leads to better feature representation and robust generalization.

• Effective Hyperparameter Tuning via HOA: The Hippopotamus Optimization Algorithm effectively explores the hyperparameter space, achieving an optimal balance between underfitting and overfitting, thus improving convergence and accuracy.

Sources of misclassification and performance variability

Despite high overall accuracy, some instances of misclassification were observed. These can be explained by:

• Image Quality and Artifacts: Some images in the BreakHis dataset suffer from blurring or uneven staining, which can lead to reduced feature contrast and lower classification confidence.

• Intra-Class Similarity: Certain benign lesions exhibit textural features that closely resemble low-grade malignant samples, especially at 100× and 200× magnification levels, leading to confusion between classes.

• Inter-Class Variability: High heterogeneity within classes, particularly malignant categories, increases the intra-class variance and affects classifier boundaries.

To mitigate these effects, future work will include preprocessing enhancements, stain normalization, and deeper ensemble learning strategies.

Failure mode analysis and mitigation

Misclassified instances were primarily observed in morphologically ambiguous regions or slides with staining artifacts. These errors often stem from low inter-class separability or data imbalance. To address these issues, future work will incorporate uncertainty estimation techniques (e.g., Monte Carlo dropout or Bayesian deep learning) to flag low-confidence predictions. Additionally, a pathologist-in-the-loop approach can be employed for human–AI collaboration, where ambiguous cases are reviewed by experts to ensure diagnostic accuracy. Such hybrid systems can significantly reduce the clinical risk of false positives or negatives.

Limitations and potential risks

While our AlexNet-GRU model optimized with the Hippopotamus Optimization Algorithm (HOA) shows great promise, it has several limitations and potential risks. The hybrid model introduces substantial computational overhead, particularly during training and optimization, which can limit its applicability in resource-constrained environments. Potential points of failure include the preprocessing step, which is critical for enhancing input data quality, and variations in image acquisition techniques that could impact performance. There are trade-offs between accuracy and computational efficiency, with the model’s high accuracy achieved at the cost of increased computational complexity.

Ethical implications include the necessity for patient consent, rigorous data handling, and privacy protections. Ensuring compliance with ethical standards and regulations such as HIPAA and GDPR is essential for maintaining patient trust and protecting data privacy. Practical implementation challenges include ensuring compatibility with existing systems, maintaining data privacy, providing adequate training, and integrating the model into clinical workflows. Scalability issues may arise as the dataset size grows, making the hyperparameter optimization process more complex and time-consuming. Addressing these limitations and adhering to ethical standards and regulatory compliance are crucial for the successful deployment of our model in diverse clinical settings.

Conclusion and future work

In conclusion, the developed breast cancer prediction model demonstrates promising accuracy and reliability in identifying potential malignancies. Convolution filters preprocess histopathological images, ensuring efficient denoising and enhancing input data quality. DenseNet-41 facilitates robust feature extraction, skilfully capturing complex patterns crucial for precise classification. The AlexNet-GRU model combines a gated recurrent unit (GRU) with AlexNet for sequential data processing, further improving classification accuracy. Moreover, hyperparameters of the AlexNet-GRU model are optimized using the Hippopotamus Optimization Algorithm (HOA), enhancing performance. Experimental results show 99.60% accuracy, indicating potential transformative impact on breast cancer identification and categorization in clinical settings. Future efforts may focus on diversifying datasets, exploring innovative architectures, and validating results on larger cohorts to ensure generalizability.

Future work could involve expanding datasets to encompass diverse populations, investigating novel architectural variations for improved model performance, and validating results on larger cohorts to ensure generalizability across different patient demographics. Additionally, exploration of ensemble learning techniques and incorporation of multimodal data fusion methods may further enhance the model’s accuracy and robustness. Lastly, efforts to deploy the developed model in real-world clinical settings and conduct prospective studies to evaluate its efficacy in aiding healthcare professionals in early detection and classification of breast cancer could be pursued.