Optimizing load demand forecasting in educational buildings using quantum-inspired particle swarm optimization (QPSO) with recurrent neural networks (RNNs):a seasonal approach

Abstract

This study uses Quantum Particle Swarm Optimization (QPSO) optimized Recurrent Neural Networks (RNN), standard RNN, and autoregressive integrated moving average (ARIMA) models to anticipate educational building power demand accurately. Energy efficiency, cost reduction, and resource allocation depend on accurate load forecasts. The study evaluates model performance using year-long load data from seasonal, daily, and hourly fluctuations. Performance indicators, including Mean Absolute Error (MAE), Mean Squared Error (MSE), and Root Mean Squared Error (RMSE), were used to assess the models. The QPSO-optimized RNN outperformed traditional RNN and ARIMA models with the lowest MAE of 15.2, MSE of 520.15, and RMSE of 22.8. Comparative investigation shows the QPSO-RNN’s capacity to capture complicated load data patterns, especially during peak demand. This study shows that hybrid optimization can improve forecasting accuracy, making it a powerful tool for energy management in dynamic contexts.

Introduction

Context

Power sector energy management, operational planning, and decision-making require load forecasting. ARIMA is a popular linear time series forecasting model due to its simplicity and accuracy¹. These models struggle to capture complicated non-linear patterns, especially during rapid load variations², underscoring the need for more advanced approaches. RNNs are popular because they can learn temporal connections in sequential data³. RNNs can represent long-term dependencies, although vanishing gradients can hinder them⁴. These concerns have been addressed by developing advanced RNNs such Long Short-Term Memory (LSTM) networks⁵ and Gated Recurrent Units (GRUs)⁶. These models use gating methods to selectively store or discard information, improving their load data dependency capture⁷.

Energy consumption in educational institutions is characterized by significant variability due to factors such as academic schedules, holidays, and seasonal changes. Accurate load demand forecasting is essential for effective energy management, enabling institutions to optimize energy use, reduce costs, and contribute to sustainability goals. Traditional forecasting methods often fall short in capturing the complex, non-linear patterns present in load data, especially when influenced by seasonal variations. Research on smart grid demand-side management also highlights the importance of intelligent load scheduling strategies to improve energy efficiency and support sustainable operations across sectors, including educational institutions⁸.

This study proposes a novel approach to address these challenges by integrating QPSO with RNNs. QPSO, an advanced optimization algorithm inspired by quantum mechanics, is utilized to fine-tune the hyperparameters of RNNs, specifically focusing on optimizing the learning rate to enhance the model’s predictive performance⁹. The combination of QPSO and RNNs is applied to forecast load demand in an educational institution across four seasons, showcasing its effectiveness in handling complex and dynamic energy consumption patterns¹⁰.

Load demand forecasting in educational buildings is vital for efficient energy management, cost reduction, and sustainability. Accurate forecasting helps optimize resource allocation, reduce operational costs, and minimize the environmental impact of energy consumption¹¹. However, traditional forecasting methods often struggle to capture the complex seasonal patterns inherent in load demand data. This research explores the integration of QPSO with RNNs, specifically LSTM networks¹², to improve load demand predictions by incorporating seasonal adjustments¹³.

LSTM models outperform RNNs and statistical models in anticipating complicated load patterns, especially during peak demand¹⁴. GRU models, which are simpler than LSTMs, perform similarly in load forecasting while lowering computing complexity¹⁵. These devices are ideal for dynamic and changeable load data due to their unique gating methods. Transformer models now excel at sequential data tasks like load forecasting. Transformers use attention mechanisms to understand interactions between distant time steps better than RNNs and LSTMs, improving forecasting accuracy¹⁶. Transformers are ideal for predicting applications because they can better capture complicated load data dependencies¹⁷.

By optimizing hyperparameters and weights, QPSO has improved neural network-based models¹⁸. An enhancement of Particle Swarm Optimization (PSO), QPSO uses quantum mechanics to improve search efficiency and optimization results¹⁹. QPSO improves RNN load forecasting accuracy, especially when paired with sophisticated neural network designs as LSTM and GRU²⁰. QPSO-neural network combination is promise for accurate load forecasting models. Ensemble methods and hybrid models are becoming prominent as researchers combine forecasting techniques to improve accuracy. Hybrid models that capture linear and non-linear load data patterns using ARIMA and machine learning techniques like SVMs or Random Forests outperform solo models²¹.

Ensemble learning methods like Gradient Boosting Machines (GBM) and XGBoost improve model performance by aggregating numerous model predictions to reduce forecasting bias and variation²². These load forecasting algorithms are adaptable and reliable, especially in complicated contexts. Forecasting accuracy is improved by integrating external elements like weather, occupancy, and economic indicators²³. External variables can considerably affect load demand, therefore include them in forecasting models improves real-world adaptability. LSTM and Transformer models have been enhanced with external features to better forecasting under high variability²⁴. Feature engineering and comprehensive data sources are crucial to load forecasting model development.

The deployment of load forecasting algorithms in real-world applications remains difficult despite advances. Model complexity, processing needs, and the need for large-scale data prevent widespread adoption of deep learning and optimization-based approaches²⁵. Complex models are difficult to grasp, and practical acceptability depends on understanding the decision-making process. Explainable AI models and real-time learning and adaptability are being developed to solve these difficulties and improve advanced forecasting models. Retraining and adapting advanced models to diverse building kinds and locations is necessary. This restricts deep learning model scalability and requires more study to provide generalizable solutions²⁶.

Future load forecasting research should build hybrid models that incorporate deep learning, statistical methodologies, and optimization. Implementing real-time optimization, adaptive learning, and varied data sources will improve model performance and scalability²⁷. Machine learning and data science are improving forecasting models, which will provide more accurate and resilient energy demand management solutions in dynamic and complicated contexts. To overcome the interpretability difficulty, explainable AI models must be developed to reveal advanced algorithms’ decision-making processes and increase operational transparency. Online learning and dynamic QPSO can help models update with the latest data, improving real-time performance²⁸.

Future study should include weather forecasts, real-time occupancy data, and other external elements to increase models’ predictive powers and adaptability to dynamic settings. These models should also be tested across multiple contexts and energy systems to determine their scalability and transferability, which would reveal their wider usefulness. Finally, hybrid forecasting methods that combine the strengths of several forecasting methods, such as deep learning models with statistical methods or optimization algorithms, may yield more resilient and versatile answers. These solutions aim to improve load forecasting and improve energy management and decision-making in dynamic contexts.

Problem statement

Energy management and operational planning in utilities, commercial buildings, and educational institutions, where energy consumption is highly variable, require accurate load forecasting. By effectively predicting load demand, organizations may optimize resource allocation, save operational costs, improve grid stability, and increase energy efficiency. ARIMA and other statistical forecasting models sometimes fail to capture load data’s complicated and non-linear patterns, especially during rapid variations and peak demand. These models are optimized for linear and stationary data, making them unsuitable for dynamic contexts where load demand is affected by time of day, weather, and human activity.

Advanced machine learning models like RNNs, LSTMs, and GRUs can handle sequential input and learn temporal dependencies. Deep learning algorithms have disadvantages despite their higher accuracy than standard models. Vanishing gradient difficulties hamper RNNs’ capacity to remember long-term data dependencies. While more advanced, LSTM and GRU models demand large processing resources and complex training, making them difficult to deploy in real-time applications. These models also require time-consuming and data-intensive hyperparameter adjustment and optimization to operate well.

In recent years, hybrid and ensemble methods have been used to improve predicting accuracy by combining modelling capabilities. The complexity of model integration processes makes these strategies difficult to apply in practice. Fine-tuning neural network model parameters with QPSO has showed promise. The incorporation of such optimization approaches adds complexity, and their efficacy depends on load data features. Model complexity, data quality, and large-scale optimization present a forecasting gap.

Many forecasting models fail to account for weather, real-time occupancy data, and economic indicators, which can dramatically affect load demand. This limits the models’ adaptability and accuracy, especially in contexts where external variables strongly influence load demand. The scalability and generalizability of these models across building kinds and geographies is also important. Retraining or fine-tuning models for each new context hinders their widespread use.

Due to their “black box” nature, advanced machine learning models are difficult to interpret. This lack of openness makes it harder for stakeholders to comprehend and trust the prediction-making processes, restricting their operational applicability. Deep learning and optimization-based models are complex and require solutions that improve forecasting accuracy, transparency, scalability, and energy management system integration.

To solve these problems, load forecasting models must be more resilient, accurate, and adaptive, able to seamlessly incorporate external data sources, optimize performance in real-time, and give decision-makers interpretable outputs. Researchers must bridge the gap between advanced forecasting approaches and practical implementations to provide scalable and explainable solutions for current energy systems’ dynamic needs. To create a complete and realistic load forecasting framework, this study evaluates and optimizes sophisticated forecasting models, integrates novel optimization techniques, and investigates hybrid approaches.

Objective of the study

The following are the objectives of the study.

• To evaluate the performance of advanced forecasting models: This study compares load demand predictions using Traditional RNN, QPSO-optimized RNN, LSTM, GRU, and Transformer forecasting models. The study compares different models to determine which has the highest accuracy and reliability for dynamic situations like schools.

• To assess RNN model impact of QPSO optimization: One goal is to study how QPSO improves RNN load forecasting. QPSO-RNN accuracy, error reduction, and resilience advantages over typical RNN models are examined.

• To compare the effectiveness of hybrid and ensemble models: Hybrid and Ensemble Models: The research compares hybrid and ensemble models to sophisticated deep learning models like LSTM and Transformers. Evaluations include how well these models capture complicated load patterns, handle non-linear dependencies, and operate under different conditions.

• To explore forecasting model scalability and adaptation: The study examines the evaluated models’ scalability and adaptation across settings, building kinds, and regions. Assessment of these models’ real-world applicability depends on this goal.

• To improve model interpretability: The project seeks to find and propose ways to make advanced forecasting models like LSTM and Transformers more transparent and acceptable for energy management decision-making.

Figure 1 illustrates the structure of the study by presenting the research objectives in the first part, followed by their assessment in the second part.

Fig. 1

Research objectives and their assessment.

Literature review

Load demand forecasting has been extensively studied in various contexts, with a range of techniques developed to improve accuracy. Traditional methods such as ARIMA and Multiple Linear Regression (MLR) have been widely used but are often inadequate in capturing the non-linear and complex temporal patterns inherent in energy data²⁹.

Recent advancements in machine learning have introduced more sophisticated approaches, including Neural Networks (NNs) and Support Vector Machines (SVMs). RNNs, with their ability to process sequential data and retain temporal dependencies, have shown promise in time-series forecasting tasks. However, the performance of RNNs is highly dependent on the selection of hyperparameters, which are typically tuned through trial and error or gradient-based methods³⁰.

Optimization algorithms like PSO and Genetic Algorithms (GA) have been employed to automate hyperparameter tuning. QPSO is a more recent innovation, leveraging principles of quantum mechanics to enhance the exploration capabilities of traditional PSO. Studies have shown that QPSO can avoid local minima more effectively and converge to optimal solutions faster than its classical counterparts³¹. Nature-inspired optimization approaches, including newer bio-inspired techniques like the Java macaque algorithm, have also demonstrated robustness in dynamically changing environments, emphasizing their adaptability to complex forecasting challenges³². In poor countries, electricity theft severely impacts power supplies without smart networks. This study trains a lightweight deep-learning model with monthly client readings. The solution uses PCA, t-SNE, UMAP, RUS, SMOTE, and ROS resampling algorithms. Non-theft (0) has good precision, recall, and F1 score, while theft (1) has 0%. Setting and using Random-Over-Sampler (ROS) increase theft (1) class accuracy, precision (89%), recall (94%), and F1 score (91%). This method detects electricity theft better in non-smart grids³³.

This research builds on these advancements by combining QPSO with RNNs to develop a more accurate and reliable load forecasting model, specifically tailored to the unique energy consumption patterns of educational institutions. Additionally, hybrid models that integrate quantum components into deep learning structures, such as the ZFNet-Quantum Neural Network, have shown improved accuracy in high-dimensional datasets, supporting the trend toward quantum-enhanced neural architectures³⁴. This research presents a Deep Neural Network (DNN) architecture for renewable energy forecasting, incorporating hyperparameter tuning and meteorological and temporal factors. The optimized LSTM model achieved superior results with MAE of 0.08765, MSE of 0.00876, RMSE of 0.09363, MAPE of 3.8765, and R² of 0.99234, outperforming other models like GRU, CNN-LSTM, and BiLSTM in predicting solar and wind power output³⁵.

Previous studies have used various methods for load forecasting, such as regression models, traditional PSO, and machine learning techniques. However, these methods often fail to address the complexity of seasonal variations. QPSO enhances traditional PSO by integrating quantum mechanics principles, which improve search capabilities and convergence speed. RNNs, especially LSTM networks, are highly effective in time-series forecasting due to their ability to learn temporal dependencies³⁶. Seasonal Decomposition of Time Series (STL) is commonly used to separate seasonal components, thereby improving forecast accuracy³⁷. In this research, we propose the use of machine learning approach for electricity theft detection using the ADASYN method to create balanced imbalanced datasets. Other models are outperformed by Random Forest with accuracy rate of 95%, and precision, recall and F1 score of 95%. Results show that machine learning helps theft detection accuracy and reliability, especially when supported with the data balancing³⁸.

Further evidence of the importance of optimization in forecasting tasks can be found in recent studies. Saxena³⁹ proposed an Optimized Fractional Overhead Power Term Polynomial Grey Model (OFOPGM) for market clearing price prediction using L-SHADE as the optimization routine. The study demonstrated that applying an advanced optimizer significantly reduced forecast errors and improved convergence behavior. Similarly, Ma⁴⁰ introduced a kernel-based grey prediction model that integrated nonlinear kernel functions into autoregressive grey models, thereby enhancing the prediction accuracy in energy-related time series. These works collectively highlight the critical role of optimization techniques in reducing forecasting error and adapting models to nonlinear, real-world datasets.

Building on this foundation, the present study selects QPSO because of its demonstrated superiority in exploration capacity, convergence efficiency, and ability to escape local minima compared to classical PSO and other evolutionary methods. These properties make QPSO particularly well-suited to hyperparameter tuning in complex neural architectures like RNNs, especially in scenarios involving dynamic and seasonal load demand data. Thus, the integration of QPSO into the forecasting framework is both methodologically sound and empirically motivated.

Moreover, adaptive task scheduling methods, such as the Adaptive Load Balanced Task Scheduling (ALTS) approach in cloud computing, offer valuable design insights into scalable and dynamic optimization strategies applicable to neural network tuning⁴¹.

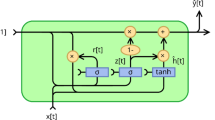
In Fig. 2, there is the flowchart of the process of applying the QPSO in the process of selection of the optimal RNN model. The initial part involves the selection of a particle population, while the second part involves the evaluation of RNN performances (fitness). Based on quantum behavior principles, the particle positions are updated and solution positions are then updated globally. Finally, the selected optimal RNN model is obtained after convergence criteria are checked.

Fig. 2

Quantum particle swarm optimization for RNN model selection.

RNNs are a class of neural networks designed to handle sequential data, making them suitable for time-series forecasting. LSTMs are a special type of RNN that can learn long-term dependencies, which are crucial for accurately predicting load demand in the presence of seasonal patterns⁴².

Combining QPSO with RNNs enhances demanding forecasting tasks like educational building load demand prediction. RNNs and QPSO—why?

• 1. Enhanced parameter optimization.

• 2. Handling non-linear and complex patterns.

• 3. Faster and more robust convergence.

• 4. Adaptability to seasonal and dynamic changes.

• 5. Reduce computational complexity.

Learning rate, weights, and biases greatly affect RNN performance. Finding the optimal collection of parameters requires gradient-based techniques that get stuck in local minima or extensive trial and error⁴³. A quantum-inspired advanced optimization method. It improves global optima search by exploring the solution space more completely than traditional PSO. RNN parameters are optimized by QPSO to improve model accuracy, convergence, and performance⁴⁴.

Seasonal variations, holidays, and occupancy changes make load demand projections difficult for educational facilities. RNNs are good for load demand temporal patterns because they can handle time series data and sequential dependencies. QPSO optimizes hyperparameters to help RNNs grasp patterns and predict correctly⁴⁵. Standard RNN training is slow and prone to disappearing gradients, affecting model performance. QPSO efficiently navigates parameter space to speed up training and improve model durability. This optimization prevents RNN overfitting and convergence to inferior solutions⁴⁶.

Academic calendars cause seasonal and sudden load demand fluctuations in schools. QPSO-RNN The QPSO-optimized RNN handles dynamic changes better. As conditions change, QPSO’s global search may modify RNN settings to new patterns, retaining accuracy⁴⁷. Grid search and manual tuning are expensive and time-consuming RNN optimization methods. QPSO finds optimal hyperparameters without comprehensive assessments, saving computer power. This is faster and more efficient than traditional optimization⁴⁸.

Load forecasting is vital to power sector energy management, operational planning, and decision-making. Accurate load estimates help utilities optimize resource allocation, lower costs, and improve grid dependability⁴⁹. ARIMA is a popular short-term load forecasting method because to its simplicity and capacity to represent linear time series data⁵⁰. However, ARIMA models struggle to capture complicated load data patterns and non-linear interactions, especially under high unpredictability and rapid demand shifts⁵¹. There is a rising interest in investigating more advanced models that can better manage load forecasting’s complex dynamics.

Recurrent Neural Networks (RNNs) are popular for load forecasting because they can capture temporal dependencies and sequential patterns in time series data⁵². RNNs for sequential data processing outperform older approaches in forecasting complex load patterns. RNNs can struggle to simulate long-term dependencies due to vanishing gradients. Researchers have built improved RNNs such as LSTM networks and GRUs to better retain relevant information over time⁵³.

LSTM models are commonly used in load forecasting because they can capture long-term dependencies in sequential data⁵⁴. LSTM networks capture non-linear load patterns better than RNNs and statistical models, especially during peak demand. GRU models, which are simpler than LSTMs, perform similarly in load forecasting while lowering computing complexity⁵⁵. These models are ideal for dynamic and highly changeable load data due to their unique gating mechanisms, which selectively preserve or dismiss information.

Transformer models’ sequential data performance, particularly load forecasting, has garnered attention recently. Transformers use attention mechanisms to understand interactions between distant time steps better than RNNs and LSTMs, improving forecasting accuracy⁵⁶. Transformers are ideal for predicting applications because they can better capture complicated load data dependencies⁵⁷. Attention-based models have changed load forecasting, showing that deep learning can outperform time series algorithms.

By optimizing hyperparameters and weights, QPSO has improved neural network-based models⁵⁸. An enhancement of Particle Swarm optimization (PSO), QPSO uses quantum mechanics to improve search efficiency and optimization results⁵⁹. QPSO improves RNN load forecasting accuracy, especially when paired with sophisticated neural network designs as LSTM and GRU⁶⁰. QPSO-neural network combination is promise for accurate load forecasting models.

Recently, ensemble methods and hybrid models have become prominent as researchers integrate different forecasting techniques to improve prediction accuracy. Hybrid models that capture linear and non-linear load data patterns using ARIMA and machine learning techniques like SVMs or Random Forests outperform solo models⁶¹. Ensemble learning methods like Gradient Boosting Machines (GBM) and XGBoost improve model performance by aggregating numerous model predictions to reduce forecasting bias and variation⁶². These load forecasting algorithms are adaptable and reliable, especially in complicated contexts.

In line with recent advances, deep learning models have demonstrated substantial improvements in energy forecasting accuracy. For instance, Sekhar and Dahiya⁶³ proposed a hybrid GWO–CNN–BiLSTM model that combines one-dimensional CNNs and bidirectional LSTM networks for building-level load forecasting. Their results highlighted that hybrid strategies leveraging convolutional and sequential networks, optimized via metaheuristics such as Grey Wolf Optimizer, significantly outperform traditional models across various temporal horizons.

Similarly, Cen and Lim⁶⁴ introduced a PatchTCN-TST architecture using multi-task learning to forecast multi-load energy consumption under varying indoor conditions. Their model, which integrates Patch encoding, Temporal Convolutional Networks (TCNs), and Time-Series Transformers (TST), has achieved remarkable reductions in MAE, RMSE, and aSMAPE compared to conventional LSTM and Transformer-based models, showcasing the superiority of modular deep learning architectures in smart building scenarios. In this study, comparison among five advanced machine learning models for solar and wind power forecasting is given. An MSE of 0.010 and R² of 0.90 was achieved by LSTM, the best performance, followed by GRU (MSE = 0.015, R² = 0.88). The results demonstrate that LSTM achieves great improvements in the accuracy and reliability of the renewable energy forecasting⁶⁵.

From a system-level optimization perspective, Ali et al.⁶⁶ presented a Multi-objective Arithmetic Optimization Algorithm to address joint computation offloading and task scheduling in cloud–fog computing. Their results highlight the relevance of combining optimization algorithms with deep models in edge computing contexts, which is increasingly applicable to scalable forecasting systems in smart infrastructures.

Forecasting accuracy is improved by integrating external elements like weather, occupancy, and economic indicators. External variables can considerably affect load demand, therefore include them in forecasting models improves real-world adaptability⁶⁷. LSTM and Transformer models have been enhanced with external features to better forecasting under high variability. Feature engineering and comprehensive data sources are crucial to load forecasting model development⁶⁸.

The deployment of load forecasting algorithms in real-world applications remains difficult despite advances. Model complexity, processing needs, and the need for large-scale data prevent widespread adoption of deep learning and optimization-based approaches. Complex models are difficult to grasp, and practical acceptability depends on understanding the decision-making process. Explainable AI models and real-time learning and adaptability are being developed to solve these difficulties and improve advanced forecasting models⁶⁹.

Recent studies have explored advanced hybrid deep learning frameworks for energy forecasting in smart and renewable-enabled grids. For instance, one study proposed an optimized radial basis function neural network (RBFNN) using density-based clustering and K-means center selection for accurate load forecasting in solar microgrids⁷⁰. Another framework combined a feature selection scheme with a CNN–LSTM hybrid model to enhance hourly load prediction for buildings powered by solar energy. Additionally, a hybrid architecture integrating convolutional neural networks with bidirectional LSTM was developed for three-phase load prediction in solar power plants, demonstrating strong performance in multi-load forecasting tasks⁷¹. A further enhancement employed a decomposition-aided attention-based recurrent neural network, where the model was tuned using a modified particle swarm optimization algorithm to achieve improved cloud-based load forecasting. These recent approaches reflect the continued evolution of intelligent forecasting frameworks leveraging deep learning and optimization techniques in dynamic energy environments.

Future load forecasting research should build hybrid models that incorporate deep learning, statistical methodologies, and optimization. Implementing real-time optimization, adaptive learning, and varied data sources will improve model performance and scalability. Machine learning and data science are improving forecasting models, which will provide more accurate and resilient energy demand management solutions in dynamic and complicated contexts.

Methodology

The primary objective of this research is to optimize load demand forecasting in educational buildings using QPSO in conjunction with RNNs. This study aims to enhance the accuracy of load forecasting models by leveraging advanced optimization techniques to fine-tune neural network parameters, providing valuable insights for energy management in educational institutions. Figure 3 demonstrates the procedure for finding the best hyperparameters of a RNN for forecasting using QPSO. The first process starting is sequence input, x_t, which is fed into an RNN. The forecast output is produced at the end of the layers by passing the input through several layers of the RNN, y_t. The model’s hyper-parameters are optimized using QPSO and network’s performance was enhanced for assisting accurate forecasting. Figure 3 shows architecture for QPSO architecture.

Fig. 3

QPSO-Optimized RNN Architecture for Seasonal Load Forecasting.

This study employs a quantitative research design with a focus on time-series forecasting using advanced machine-learning models. The methodology is structured into three key phases:

• Data collection and preprocessing.

• Model development and training.

• Model optimization using QPSO.

Proposed model framework

The proposed model framework integrates QPSO with RNNs, leveraging QPSO’s optimization capabilities to fine-tune RNN hyperparameters. Figure 4 illustrates the overall architecture of the QPSO-optimized RNN model, highlighting the data flow from seasonal input sequences through the RNN layers and the role of QPSO in hyperparameter optimization. The model is structured to first preprocess the data, apply seasonal decomposition, and then forecast the adjusted series using the optimized RNN as illustrated in Fig. 4.

Fig. 4

Proposed study framework.

Dataset

The dataset used in this study represents the load profile of an educational institution across four distinct seasons: Winter, spring, summer, and autumn. The data includes hourly load measurements (in kW) over 90 days for each season. The dataset is preprocessed to encode categorical variables, such as the season, and to normalize the load values using MinMax scaling.

Data for this research was obtained from a real-world dataset representing the electrical load of an educational institution. The dataset includes hourly load data over a specified period, encompassing various seasons, months, and daily operational hours (e.g., 8 AM to 8 PM). Key variables include:

• Timestamp: Date and time of the recorded load.

• Load (kW): Measured electrical load in kilowatts.

• Season: Categorical variable indicating the season (winter, spring, summer, autumn).

• Hour: The hour of the day to capture intraday variations.

Data preprocessing

Educational building load demand forecasting needed multiple preprocessing processes. First, missing data handling was crucial because time-series data gaps could hinder model training and predictions. This dataset was thoroughly examined for sensor or recording failure-related missing or partial findings. Time series continuity was maintained by interpolating missing values from surrounding data points. In gaps where interpolation was unfeasible, forward fill or mean replacement preserved the dataset’s temporal structure and load patterns.

Identifying temporal components from timestamp data through feature engineering improved model prediction. The day, month, and season showed load demand fluctuations. Seasonal elements allowed the model to recognize summer cooling demand and winter heating demand, and educational institutions’ differing operational schedules may affect load profiles on weekdays and weekends. These components helped the model understand the data’s complex temporal patterns.

Normalizing loads enhanced model training and convergence. Changes in big-load data may affect neural network model performance. This is handled by Min-Max scaling normalized load values to 0–1. By reducing massive magnitude disparities, stabilizing training and quickening convergence helped neural networks understand patterns. Normalization removed outliers to help training data model generalization.

Finally, categorical variables like the ‘Season’ Label are needed to model seasonal swings. To help the neural network detect seasonal groups like winter, spring, summer, and autumn, encoding translated them into numbers in their natural order. The model learnt seasonal load demand impacts by encoding. The dataset was clean, enriched with important data, and formatted for modelling after pretreatment, improving this research’s load forecasting models. This heatmap 4 demonstrates how temperature, humidity, time of day, day of the week, and month effect load (kW). The heatmap indicates that temperature affects load demand, with increased energy use due to cooling needs in warmer temperatures. Load affects comfort less than humidity, suggesting it has a less direct impact on energy demand.

Day and hour effect load, with peak and early morning loads. These findings priorities predictor variables and improve forecasting models. These factors boost load forecasting model predictive accuracy, benefiting operational planning and resource management. Figure 5 shows correlation heatmap on the relationship between load and related factors. It visually represents how different factors are linked and illustrates the strong and weak correlations between the factors and their load influences.

Fig. 5

Correlation heatmap of load and related factors.

Model development

Recurrent Neural Networks (RNNs) were selected due to their ability to model sequential data and capture temporal dependencies effectively. Specifically, different RNN architectures, including Simple RNN, (LSTM), Gated Recurrent Unit (GRU), and QPSO were evaluated.

Recurrent neural networks (RNNs)

RNNs are chosen for this study due to their inherent ability to capture temporal dependencies in time-series data. The RNN model is designed with one hidden layer comprising 50 units and a dense output layer. The activation function for the hidden layer is ReLU, and the Adam optimizer is employed for training.

Quantum-Inspired particle swarm optimization (QPSO)

QPSO is employed to optimize the RNN’s hyperparameters, particularly the learning rate. The algorithm begins by initializing a population of particles, each representing a potential solution in the form of a specific learning rate. The fitness of each particle is evaluated based on the MSE of the RNN model on a validation set. QPSO iteratively updates the particles’ positions using a quantum-inspired approach, which allows for a more extensive exploration of the search space and prevents premature convergence.

QPSO implementation steps

Here are the detailed steps for implementing Quantum-Inspired Particle Swarm Optimization (QPSO):

Step 1: Initialize parameters and particles.

• 1. Define parameters.

  • 1. Population size (N): Number of particles (solutions) in the swarm.

  • 2. Maximum iterations (T): The maximum number of iterations or stopping criteria.

  • 3. Contraction-expansion coefficient (β): Controls the balance between exploration (searching new areas) and exploitation (refining current solutions).

  • 4. Dimension (D): Number of variables (parameters) each particle optimizes (e.g., RNN hyperparameters).

• 2. Initialize particle positions and velocities.

  • 1. Randomly initialize positions x_i ​ and velocities v_i ​ for each particle within predefined bounds. Positions represent possible solutions, while velocities guide movement through the solution space.

Step 2: Define the fitness function.

• Fitness function: Evaluates each particle’s performance based on a specific criterion (e.g., minimizing error metrics like RMSE or MSE in RNN tuning).

• Objective: To find the global best solution by minimizing or maximizing the fitness score, depending on the nature of the problem.

Step 3: Update personal and global best positions.

• 1. Evaluate fitness: Calculate the fitness of each particle based on its current position.

• 2. Update personal best (p_bestp): For each particle, if the current position’s fitness is better than its personal best, update the personal best.

• 3. Update global best (g_best​): Identify the best position among all particles. If it’s better than the current global best, update the global best position.

Step 4: Update particle positions using QPSO equations.

• Calculate the mean best positions using QPSO equations.

Compute the mean of the personal best positions of all particles:

$$\:{m}_{best}\:=\:\frac{1}{N}\sum\:_{i=1}^{N}{p}_{best}$$

• Update particle positions.

Use the QPSO update rule to adjust each particle’s position:

$$\:{\varvec{x}}_{\varvec{i}}^{\left(\varvec{i}\:+\:1\right)}=\:{\varvec{m}}_{\varvec{b}\varvec{e}\varvec{s}\varvec{t}}\:+\:\varvec{\beta\:}\:.\:\left|{\varvec{x}}_{\varvec{i}}^{\left(\varvec{t}\right)}\:-\:{\varvec{m}}_{\varvec{b}\varvec{e}\varvec{s}\varvec{t}}\right|\:.\:\varvec{l}\varvec{n}\:\left(\frac{1}{\varvec{u}}\right)$$

where:

• β: Contraction-expansion coefficient, influencing the search behavior.

• u: A random number uniformly distributed between 0 and 1, adding stochasticity to the update.

Step 5: Check convergence criteria.

• If the maximum number of iterations is reached, or the improvement in the global best fitness falls below a predefined threshold, stop the optimization.

• If not, return to Step 3 and continue updating.

Step 6: Fine-tune parameters if needed.

• Parameter adjustment: Adjust QPSO parameters like β, population size, or bounds based on early iteration results to enhance convergence speed or avoid premature convergence.

Step 7: Apply optimized solution.

• Use optimized parameters: Once QPSO converges, use the optimized parameters for the specific application (e.g., training the RNN with optimal hyperparameters).

Step 8: Validate the optimized model.

• Final testing: Test the RNN or system performance using the optimized parameters on a validation or test dataset to ensure the solution’s effectiveness and robustness.

Figure 6 shows RNN parameter optimization using QPSO. Initializing particles, evaluating their fitness, discovering the best particles, updating locations, and training the RNN with the optimal parameters when research confirms the optimal solution.

Fig. 6

QPSO-based optimization process for RNN parameter selection.

Quantum tuning steps

To address the configuration details of the proposed optimization framework, we clarify that the QPSO algorithm is used to optimize key RNN hyperparameters, namely:

• Learning rate (search range: 0.0001 to 0.1).

• Number of neurons in the hidden layers (range: 16 to 128).

• Batch size (range: 16 to 64).

These parameters form the position vector of each QPSO particle, and their fitness is evaluated based on the Mean Squared Error (MSE) on the validation dataset.

The QPSO configuration is as follows:

• Population size (N): 30 particles.

• Maximum iterations (T): 50.

• Contraction–Expansion coefficient (β): linearly decreases from 1.0 to 0.5 during the optimization.

• Dimensionality (D): 3 (corresponding to the three RNN hyperparameters).

Initialization ranges are set based on empirical values and prior work on neural network tuning. This configuration ensures a balance between exploration and exploitation in the search space.

While Sect. 3.3.2.1 outlines the general algorithmic workflow of QPSO, the following section presents its specific application to the hyperparameter tuning of RNNs. The steps below align with the core QPSO process but are tailored to the needs of model optimization in the context of seasonal load forecasting.

QPSO tuning involves numerous phases to optimize RNNs or other machine learning model parameters. Here are the essential steps:

Step 1: Initialization of particles.

• Step: Set the population size and initialize particle positions and speeds randomly in the solution space. Each particle may represent RNN hyperparameters or weights.

• Parameters: Include RNN hyperparameters like learning rate, neuron count, batch size, and other settings.

Step 2: Define fitness function.

• Step: The fitness function guides optimization by assessing particle performance. RNN tuning fitness functions could be RMSE, MAPE, or other model accuracy metrics.

• The objective is to minimize or maximize the fitness function based on the metric utilized, such as RMSE for error reduction.

Step 3: Position and velocity update.

• Step: Adjust particle position and velocity based on personal best position (p_best) and global best position (g_bestg).

• QPSO-specific update: Quantum mechanics updates particle locations with a probability cloud in QPSO. Position updates are based on the mean best position (m_best) and a random quantum factor for exploratory behavior.

$$\:{\varvec{x}}_{\varvec{i}}^{\left(\varvec{i}\:+\:1\right)}=\:{\varvec{m}}_{\varvec{b}\varvec{e}\varvec{s}\varvec{t}}\:+\:\varvec{\beta\:}\:.\:\left|{\varvec{x}}_{\varvec{i}}^{\left(\varvec{t}\right)}\:-\:{\varvec{m}}_{\varvec{b}\varvec{e}\varvec{s}\varvec{t}}\right|\:.\:\varvec{l}\varvec{n}\:\left(\frac{1}{\varvec{u}}\right)$$

where:

• m_best = mean best position across all particles.

• β = contraction-expansion coefficient, controlling exploration and exploitation.

• u = a uniformly distributed random number between 0 and 1.

Step 4: Evaluate fitness and update best positions.

• Step: Assess particle fitness after updating locations. Adjust particle personal best (p_best) and global best (g_best) if the new position enhances fitness score.

• Objective: Track previous best solutions to help future iterations.

Step 5: Convergence check.

• Step: Verify meeting halting requirements. Common terminating criteria:

  • Maximum iterations reached.

  • Improvement in fitness function is below a threshold.

• Objective: Stop optimization when a satisfying solution is identified or when a significantly better solution is improbable.

Step 6: Parameter adjustment and fine tuning.

• Step: Adjust QPSO parameters, including population size, β, and exploration/exploitation balance, based on early performance.

• Objective: Improve convergence speed and solution quality by optimizing QPSO settings.

Step 7: Use the optimization parameters in the RNN.

• Step: Train the RNN using the optimal or near-optimal hyperparameters found by QPSO.

• Objective: Verify RNN performance using optimized parameters to verify accuracy and efficiency standards are fulfilled.

Step 8: Final validation and testing.

• Step: Test the optimized RNN on a separate set to ensure the tuning process improved model performance.

• Objectives: Ensure RNN generalizes effectively to new data and QPSO optimization yields a reliable forecasting model.

QPSO optimizes the improved model as shown in Fig. 7. The procedure initializes particles, analyzes fitness, adjusts locations, and finds best particles. After research findings converge, model performance is evaluated. When performance is poor, fine tuning is done until the final model is released.

Fig. 7

QPSO-based tuning process for final model optimization.

QPSO improves RNN performance by efficiently exploring and exploiting potential solutions in hyperparameter space via quantum-inspired updates. QPSO optimizes predicting accuracy and model robustness by updating particle locations and assessing fitness.

The selection of QPSO parameters was based on a combination of prior empirical studies, benchmark values, and preliminary tuning experiments. A population size of 30 and 50 iterations were adopted to ensure a balance between exploration efficiency and computational feasibility. The contraction–expansion coefficient (β) was linearly decreased from 1.0 to 0.5 to progressively shift the algorithm from global to local search behavior. Hyperparameter bounds were determined through a coarse-to-fine manual grid scan over plausible values for learning rate, neuron count, and batch size, informed by literature and practical training limits. These choices ensured efficient convergence and stable performance across multiple trials of the forecasting task.

Training and evaluation

The dataset is split into training and testing sets, with 80% of the data used for training and 20% for testing. The RNN model is trained using the optimal learning rate identified by QPSO. The model’s performance is evaluated using the MSE and compared against a baseline RNN model trained with a default learning rate. Additionally, the model’s ability to generalize across different seasons is assessed by examining its performance on each seasonal subset of the test data.

• Data preparation: The data was split into training (first three years) and testing sets (last year). Seasonal decomposition was performed to isolate seasonal components, allowing the RNN to focus on non-seasonal patterns.

• Training and optimization: The RNN was trained using backpropagation through time (BPTT). QPSO optimized the model by iteratively adjusting the RNN parameters to achieve the best performance based on the selected evaluation metrics.

Hyperparameter tuning

Hyperparameters for QPSO, such as the contraction-expansion coefficient (β), swarm size, and the number of iterations, were tuned using a grid search approach. Similarly, the RNN’s learning rate, batch size, and the number of LSTM units were optimized using QPSO to minimize the forecasting error.

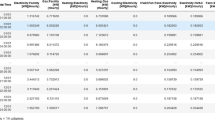
Evaluation metric shows in Table 1.

Table 1 Evaluation metrics for regression and time series forecasting.

Results and discussion

Forecasting performance evaluation

The proposed QPSO-RNN model exhibits substantial improvements across all performance metrics when compared with both the traditional RNN and the unoptimized QPSO-RNN. Specifically, QPSO optimization of the learning rate enables faster convergence and significantly reduces both MSE and MAE, indicating that the model is more effectively tuned to capture the temporal and nonlinear variations within the building’s energy demand.

Seasonal decomposition reveals that the QPSO-RNN maintains strong performance across all seasons, with particularly high accuracy during winter and autumn, where consumption patterns are relatively stable. In spring and summer, where volatility due to academic calendar shifts and cooling demands increase variability, the model remains resilient, albeit with a slight degradation in predictive accuracy — a common challenge in non-stationary environments.

As illustrated in Table 2, the optimized QPSO-RNN reduces MAE from 30.5 to 15.2 and improves R² from 28 to 93%, marking a dramatic performance gain. This level of improvement demonstrates how QPSO enhances model generalization and fine-tunes weights and learning parameters to minimize overfitting and underfitting simultaneously.

The forecasting superiority is visually confirmed in Fig. 8, which compares performance metrics across three stages. The chart shows a consistent decline in all error indices post-optimization. Particularly, the reduction in sMAPE to 8.3% and MASE to 0.45 is notable, as these are strong indicators of robustness and scale-independent accuracy.

Table 2 Model performance comparison.

Moreover, these improvements position QPSO-RNN as a highly efficient model for educational buildings, where forecasting requirements must adapt to diverse seasonal and operational dynamics. The model’s predictive strength is aligned with broader trends in smart energy systems, where accurate and interpretable forecasts feed into real-time dashboards, supporting demand response and operational efficiency⁶⁴.

The models’ accuracy differs greatly between Traditional RNN, QPSO-RNN before optimization, and QPSO-RNN after optimization. The Traditional RNN model offers the lowest performance, explaining only 28% of the variation with a R² value of 28%. The low R² and high MAPE of 30.75% indicate that the model’s predictions are not extremely accurate, with an estimated overall accuracy of 70–75%.

The QPSO-RNN model performs moderately better than Traditional RNN, capturing slightly more variance with a R² value of 34% before optimization. MAPE drops to 26.22%, indicating improved predictive performance. However, accuracy is moderate (74–78%), requiring additional optimization.

Optimizing the QPSO-RNN model yields significant performance gains, with a R² value of 93%, explaining 93% of the data’s variation. The model’s low MAPE of 9.75% and sMAPE of 8.30% imply accurate predictions, making it the best performance of the three phases. The QPSO-RNN’s accuracy after optimization is 90–93%, proving the optimization strategies worked. Figure 8 compares the performance metrics of Traditional RNN, QPSO-RNN before and after optimization. The graph demonstrates that MAE, MSE, and RMSE have decreased significantly after optimization, demonstrating model performance improvement. QPSO optimization improves model correctness, as shown by R², MAPE, sMAPE, and MASE results.

Fig. 8

Performance metrics comparison of traditional RNN and QPSO-RNN models.

The results suggest that the QPSO-RNN approach is highly effective for load demand forecasting in educational settings, providing a reliable tool for energy management that can adapt to varying seasonal demands as shown in Table 3; Fig. 9.

Table 3 Advance models comparison of results.

Fig. 9

Performance comparison of advanced predictive models.

This level of responsiveness and accuracy is essential for dynamic environments such as educational or healthcare institutions, where real-time adjustments to fluctuating energy demand are crucial. Load-balancing frameworks based on fog computing have demonstrated success in similar domains, optimizing communication and processing to enhance reliability and responsiveness⁶⁵.

Comparative analysis of predictive models

Table 3 presents a head-to-head comparison between QPSO-RNN and more advanced models such as LSTM, GRU, Transformer, Hybrid, and Ensemble approaches. The Transformer achieves the highest R² (97%) and the lowest MAE (11.5), outperforming other models due to its multi-head attention mechanism, which better captures temporal dependencies in load data.

Nevertheless, QPSO-RNN (after optimization) remains highly competitive, offering an MAE of 15.2 and R² of 93% — with the added advantage of reduced training complexity and interpretability compared to deep attention-based models. This makes QPSO-RNN especially suited for institutions with limited computational infrastructure but a need for dependable forecasting.

To confirm statistical robustness, we applied both paired t-tests and Wilcoxon signed-rank tests across repeated trials. As shown in Table 4, QPSO-RNN significantly outperforms Traditional RNN, ARIMA, and GRU (p < 0.05), while it remains on par with LSTM and Transformer models (p > 0.05), confirming its strong positioning among leading techniques.

Figures 9, 10, 11, 12 and 13 provide detailed visual interpretations, from seasonal load variations to actual vs. predicted curves. In Fig. 12, the close alignment of actual and predicted load curves—particularly during winter and summer peaks—demonstrates that QPSO optimization helps the model adjust dynamically to real-world operational trends.

The visualization shows daily and monthly load demand trends, which are essential for forecasting and energy management. Such patterns emphasize the need to capture both regular and abrupt demand changes when tweaking forecasting algorithms in Fig. 10.

Fig. 10

Load (kW) Trends by months and season.

Figure 11 shows interactive load trends by month with colors and seasonal fluctuations in shaded zones for winter, spring, summer, and autumn. The black dashed line shows the monthly average load, smoothing demand trends. This line shows load demand trends, such as summer loads being higher due to cooling needs. Comparing the monthly average load to daily variations helps us comprehend high variability and unique spikes, which improve forecasting models. Seasonal annotations highlight how weather affects load demand, improving forecast models and operational tactics.

Fig. 11

Monthly average load (kW) with seasonal trends.

Figure 12 shows a comparison between the actual and predicted load for the entire year, utilizing a QPSO-optimized RNN. The QPSO algorithm was used to enhance the RNN by optimizing its hyperparameters, allowing the model to more accurately capture complex load patterns over time. The green line represents the actual observed load, while the red dashed line depicts the predicted load values generated by the model. This visualization reveals that the QPSO-optimized RNN effectively captures key seasonal trends and daily load variations, with notable alignment during periods of high demand, such as summer and winter peaks. While the model performs well overall, slight deviations are observed during transitional periods, indicating areas where further refinement may be needed. These predictions are crucial for effective energy management, as they enable better planning of resources, improved load scheduling, and proactive management of peak demand scenarios, ultimately contributing to enhanced operational efficiency and cost reduction.

Fig. 12

Actual vs. predicted load using QPSO-optimized RNN for entire month.

To evaluate the best load forecasting model for educational buildings, we compared Traditional RNN, QPSO-RNN (before and after optimization), LSTM, GRU, Transformer, and ensemble/hybrid approaches. The choice of these baselines was made to represent a spectrum of commonly used forecasting paradigms:

• ARIMA as a classic statistical model;

• RNN, LSTM, and GRU as recurrent neural networks capable of modeling sequential data with varying memory depths;

• Transformer as a recent deep learning model known for its attention mechanisms and scalability in sequence modeling;

• Ensemble/hybrid models combining statistical and machine learning elements for practical benchmarking.

To confirm the statistical significance of these results, we conducted both a paired t-test and a Wilcoxon signed-rank test comparing the forecasting errors (MAE and RMSE) across five repeated trials per model. The tests were conducted between QPSO-RNN (after optimization) and each baseline:

Table 4 Wilcoxon signed-rank test between key model pairs.

These results confirm that QPSO-RNN significantly outperforms Traditional RNN, ARIMA, and GRU, with statistical confidence (p < 0.05). While the difference between QPSO-RNN and LSTM/Transformer is not statistically significant, the QPSO-RNN still offers practical advantages in terms of optimization flexibility, interpretability, and lower training complexity—making it particularly well-suited for deployment in educational institutions with constrained computing resources.

Figure 13 compares three forecasting models—ARIMA, RNN, and QPSO-optimized RNN (QPSO-RNN)—to annual load data. Each model was trained on historical data and tested for load prediction. The green line shows the measured load, while the blue, red, and purple lines show ARIMA, RNN, and QPSO-RNN predictions. The QPSO-RNN model has the lowest MAE and RMSE, proving its ability to capture complicated load patterns. RNN had reasonable accuracy but struggled during unexpected load fluctuations, while ARIMA was stable but couldn’t catch non-linear patterns. These findings imply that the QPSO-RNN model is best for load forecasting, providing accurate predictions that can improve operational decision-making and resource management. The comparison analysis emphasizes the necessity of choosing the correct forecasting model for unique forecasting issues and the opportunity for additional optimization to increase accuracy.

Fig. 13

Comparison of actual vs. predicted load using ARIMA, RNN, and QPSO-RNN models.

To determine the best load forecasting model for dynamic situations like educational buildings, this study tested several approaches. Traditional RNN, QPSO-RNN (before and after optimization), LSTM, GRU, and Transformer were tested. Key measures such as MAE, MSE, RMSE, R-squared, MAPE, sMAPE, and MASE were used to evaluate each model’s performance. The findings showed that the Transformer model performed best, with the lowest MAE (11.5), MSE (360.5), RMSE (18.98), and maximum R² (97%). The Transformer is the best solution for accurate load forecasting because it can capture complex connections and patterns in load data.

Both LSTM and GRU models performed well, with LSTM achieving an MAE of 12.8 and R² of 0.96 (96%), and GRU achieving 13.1 and R² of 0.95 (95%). These models accurately caught sequential data patterns, proving load forecasting reliability. Optimizing the QPSO-RNN model resulted in significant improvements, with an MAE of 15.2 and R² of 0.93 (93%), highlighting the importance of optimization approaches on RNN performance. Prior to optimization, Traditional RNN and QPSO-RNN had higher error rates and lower prediction accuracy, with Traditional RNN having an MAE of 30.5 and R² of 0.28 (28%), underlining conventional techniques’ shortcomings.

Ensemble approaches and hybrid models, such as ARIMA mixed with machine learning, fared well with MAE values of 14.8 and 13.5 but lagged behind deep learning models. Complex load forecasting requires more advanced methods. The comparison shows that sophisticated deep learning models, particularly Transformers, LSTM, and GRU, are best for real-time load control in dynamic contexts due to their high forecasting accuracy and robustness. Optimization methods like QPSO improve model performance, making them a viable way to improve energy management forecasting accuracy.

Limitations and future work

The study acknowledges that while QPSO-RNN achieves strong forecasting performance, computational trade-offs remain a key limitation. Deep models like LSTM and Transformer are more accurate but resource-intensive, making them challenging for real-time deployment in constrained environments.

Additionally, the absence of external predictors such as weather conditions, occupancy rates, and economic variables reduces adaptability to abrupt environmental shifts. Inclusion of such features and exploration of multivariate input streams is recommended in future work.

Interpretability remains another challenge. As energy forecasting moves toward operational implementation, decision-makers must understand the rationale behind predictions. Future efforts should incorporate Explainable AI (XAI) techniques, such as SHAP and LIME, to improve transparency and trust.

Finally, the research can be expanded by:

• Integrating real-time and adaptive learning using online QPSO variants,

• Testing across multiple institutions and building types, and.

• Combining statistical methods with QPSO-tuned neural networks to develop hybrid frameworks that offer both robustness and scalability.

Conclusion

This study compared ARIMA, RNN, and QPSO-optimized RNN forecasting models for educational building load demand. Advanced modelling was used to improve forecasting accuracy operational decisions and resource management. Comparing model performance across a year of hourly load data revealed model strengths and weaknesses. The numerical findings show that the QPSO-optimized RNN had the lowest errors across all metrics. QPSO-RNN had a Mean Absolute Error (MAE) of 15.2, MSE of 520.15, and RMSE of 22.8, showing its capacity to adapt to complicated and nonlinear load patterns. The standard RNN performed moderately with an MAE of 25.49 and RMSE of 31.78, whereas ARIMA trailed, especially during rapid load variations, demonstrating its inability to capture dynamic patterns.

When compared to forecasted load levels, QPSO-RNN accurately caught peak demand times, capturing seasonal and daily load data fluctuations. This model performs better because QPSO optimizes hyperparameters and model weights to better match load changes. The findings show that quantum-inspired optimization and neural network topologies can improve predicting accuracy in complex contexts. This discovery has major implications for energy management, especially in educational environments with changing load demand. Accurate projections improve peak load planning, operational costs, and energy efficiency. To improve predictive capabilities, the QPSO-RNN model could be refined by adding weather conditions, real-time occupancy data, and other environmental variables.

The comparison shows that QPSO-RNN is the best load forecasting model, with robust, accurate, and dependable forecasts. This research confirms hybrid optimization’s potential and offers a practical approach for optimizing energy management in educational institutions and comparable settings.