Optical solitons, bifurcation, and chaos in the nonlinear conformable Schrödinger equation with group velocity dispersion coefficients and second-order spatiotemporal terms

Abstract

In this study, we utilize the new direct mapping method to derive optical soliton solutions for the nonlinear conformable Schrödinger equation, which accounts for group velocity dispersion coefficients and second-order spatiotemporal terms. Leveraging bifurcation and chaos theories, we conduct an in-depth analysis of the planar dynamical system associated with the equation, providing detailed graphical representations of chaotic solutions for the perturbed system. The time series of the planar system, along with a sensitivity analysis of the perturbed system, is visualized through various graphical illustrations to underscore the model’s significance and its dynamic behavior in practical applications. We derive a new family of soliton solutions including bell-shaped, dark-bright, and mixed dark-bright solitons which have not been previously reported in the literature. Further, the influence of the conformable derivative parameter and temporal dynamics on these soliton solutions is systematically investigated, highlighting the system’s importance in real-world contexts. The results highlight the potential of the proposed model in advancing optical fiber communication technologies, especially for the efficient transmission and control of ultra-fast pulses. This work contributes both theoretical novelty and practical insights into nonlinear wave propagation in advanced photonic systems.

Introduction

Nonlinear partial differential equations (NPDEs) are commonly employed to depict many dynamic phenomena in engineering and applied sciences. The construction of nonlinear equations for evolution is essential for gaining a deeper understanding of intricate natural events in disciplines such as physics, applied mathematics, and engineering. Soliton theory is crucial for deriving analytical approaches for nonlinear partial differential equations, as it reveals fundamental details about phenomena like optical fibers^1,2, plasma physics⁵, biomedical science^3,4, and others. Many scholars have devised numerous analytical strategies to obtain the analytic solutions of NPDEs^{6,7,8,9,10,11,12}. Appropriate conversions are necessary to translate the NPDEs into ordinary differential equations (ODEs) in order to analyze the exact soliton solutions. The efficacy of the exact solutions in tackling these issues greatly depends on the parameters and coefficients used in the transformations. The parameters and coefficients are essential factors in the practical implementation of the models. Investigating and applying soliton solutions in nonlinear evolution systems (NLESs) has opened up new research and development opportunities across various scientific and technological fields. Understanding and controlling soliton solutions not only enhances fundamental scientific knowledge but also offers practical possibilities for advancing technologies like long-distance communication systems and optical signal processing. As researchers continue to explore the characteristics and dynamics of solitons in NLESs, new methods and approaches are constantly being refined and developed. This ongoing research into soliton solutions in NLESs drives innovation and paves the way for significant advancements in multiple areas of science and engineering. Many analytical methods have been employed to construct soliton solutions of nonlinear evolution equations, such as the modified Jacobi elliptic function expansion method¹³, the trial equation method¹⁴, the new extended direct algebraic approaches¹⁵, the extended sinh-Gordon equation expansion method¹⁶, the sub equation method¹⁷, the generalized Kudryashov method¹⁸, and the enhanced algebraic method¹⁹.

Bifurcation refers to a qualitative change in the structure of solutions to a differential equation as a parameter is varied. In the case of the nonlinear Schrödinger equation, bifurcations typically occur when certain critical values of parameters group velocity dispersion and nonlinearity are reached, leading to a sudden change in the behavior of the soliton solutions. Chaos in the nonlinear Schrödinger equation describes a highly sensitive dependence on initial conditions, where small perturbations can lead to drastically different outcomes. This chaotic behavior is indicative of the complex and unpredictable nature of soliton dynamics under certain conditions.

The main aim of this study is to analyze the bifurcation, chaos, and optical soliton solutions of the time-fractional nonlinear Schrödinger equation in optical fibers using the newly improved direct mapping method by Wang in 2022²⁰, is used to construct various soliton solutions for this type of nonlinear Schrödinger equation. Compared to traditional methods such as the inverse scattering transform, Hirota’s bilinear method, or the variational approach, the direct mapping method is more straightforward, less computationally intensive, and highly adaptable to equations involving conformable derivatives and higher-dimensional structures. Further, it provides exact solutions without requiring restrictive ansatz assumptions or extensive symbolic computation, making it a practical and efficient tool for analyzing complex nonlinear wave phenomena. Consider the following nonlinear Schrödinger equation with group velocity dispersion coefficients and second-order spatiotemporal terms²¹:

$$\begin{aligned} i\left( \frac{\partial \rho (x,t)}{\partial x}+{{\eta }_{1}}\frac{{{\partial }^{\alpha }}\rho (x,t)}{\partial {{t}^{\alpha }}}\right) +{{\eta }_{2}}\frac{{{\partial }^{2\alpha }}\rho (x,t)}{\partial {{t}^{2\alpha }}}+{{\eta }_{3}}\frac{{{\partial }^{2}}\rho (x,t)}{\partial {{x}^{2}}}+{{\left| \rho (x,t) \right| }^{2}}\rho (x,t)=0, 0< \alpha \le 1, \end{aligned}$$

(1)

where the function $\rho (x,t)$ is a complex-valued function. The order of the conformable fractional derivative is denoted by $\alpha$. The spatial dispersion is represented by ${{\eta }_{3}}$, while ${{\eta }_{2}}$ represents the group velocity dispersion. The ratio of group speed is proportional to ${{\eta }_{1}}$. The present type of the nonlinear Schrödinger equation models the propagation of nonlinear optical pulses in dispersive media such as fiber-optic channels. The inclusion of conformable fractional derivatives allows for the incorporation of memory and hereditary effects, making this model particularly relevant for ultra-fast and nonlocal optical pulse dynamics in modern photonic systems. The current model is analyzed utilizing the extended direct algebraic method to generate different types of soliton solutions, including dark, mixed bright, and complex solitons²². The soliton solutions for the time-fractional nonlinear Schrödinger equation with includes group velocity dispersion coefficients and second-order spatiotemporal terms are studied in Ref.²³. In Ref.²⁴, the present problem is analyzed using the auxiliary equation technique to derive many solutions in the form of traveling waves. The current model, discussed in reference²⁵, is seen as capable of explaining pulse occurrences that extend beyond the conventional slowly-varying envelope approximation. Furthermore, the research examines the spatial and temporal attributes of the issue, as well as its aspects of transition. The amplitude ansatz approach is used to detect many types of optical soliton solutions, such as bright,dark-bright, and dark solitons in Ref.²⁶. The impact of the fractional order on the bright soliton and W-soliton solution of this model is investigated in Ref.²⁷. In addition, the authors of²⁸ examined the modulation instability of the existing model and employ the F-expansion method to produce various exact solutions. The authors in Ref.²⁹ investigate many new solitons for the present equation employing the Sine-Gordon expansion approach. The modified extended direct algebraic technique was used to produce several optical soliton solutions for a range of nonlinear Schrödinger equations, as demonstrated in Ref.³⁰. In a recent study, researchers discovered numerous new exact solutions for the present form of Schrödinger model. These solutions include dark, singular, bright,wave, and dark-bright solutions³¹.

Definition 1.1

Let $\psi :(0,\infty )\rightarrow R$. The definition of the conformable fractional derivative of order $\alpha$ is defined as follows:

$$\begin{aligned} {{L}_{\alpha }}\left( \psi \right) (x)=\underset{I\rightarrow 0}{\mathop {\lim }}\,\frac{\psi (x+I{{x}^{1-\alpha }})-\psi (x)}{I}, \end{aligned}$$

(2)

for all $x>0$ and $\alpha \in (0,1]$³².

Assume that ${{\psi }_{1}}$ and ${{\psi }_{2}}$ are conformable differentiable of order $\alpha$, and ${{\rho }_{1}},{{\rho }_{2}}\in R$. We have

• 1. ${{L}_{\alpha }}({{\rho }_{1}}{{\psi }_{1}}+{{\rho }_{2}}{{\psi }_{2}})={{\rho }_{1}}{{L}_{\alpha }}({{\psi }_{1}})+{{\rho }_{2}}{{L}_{\alpha }}({{\psi }_{2}}).$

• 2. ${{L}_{\alpha }}({{x}^{\lambda }})=\lambda {{x}^{\lambda -\alpha }}$ for all $\lambda \in R.$

• 3. ${{L}_{\alpha }}({{\psi }_{1}}{{\psi }_{2}})={{\psi }_{2}}{{L}_{\alpha }}({{\psi }_{1}})+{{\psi }_{1}}{{L}_{\alpha }}({{\psi }_{2}}).$

• 4. ${{L}_{\alpha }}\left( \frac{{{\psi }_{1}}}{{{\psi }_{2}}} \right) =\frac{{{\psi }_{2}}{{L}_{\alpha }}({{\psi }_{1}})-{{\psi }_{1}}{{L}_{\alpha }}({{\psi }_{2}})}{\psi _{2}^{2}}.$

The application of conformable derivatives extends to other fields, including physics, engineering, economics, and biology, highlighting its potential importance as a powerful tool for understanding complex systems^33,34. This paper provides an introduction to the fundamental concepts of conformable derivatives. Furthermore, it helps us understand the complexities of physical phenomena. The wide range of conformable derivative applications demonstrates the need for more precise mathematical methods for handling real-world objects and processes.

The direct mapping method

In this section, we derive a range of innovative optical soliton solutions for the studied model, obtained using the direct mapping method. We posit that the solution to (1) can be represented as the following series:

$$\begin{aligned} W(\sigma )=\sum \nolimits _{j=0}^{N}{{{d}_{j}}}{{\left( \Lambda (\sigma ) \right) }^{j}},\,{{d}_{N}}\ne 0, \end{aligned}$$

(3)

where ${{d}_{0}},{{d}_{1}},...,{{d}_{N}}$ are real constants, N denotes a balancing parameter, and $\Lambda (\sigma )$ satisfies the following relation:

$$\begin{aligned} {{\left( \frac{d\Lambda (\sigma )}{d\sigma } \right) }^{2}}={r_{1}{u }^{2}}{{\Lambda }^{2}}(\sigma )+\frac{r_{2}(u)^{2}}{p^{2}} {{\Lambda }^{4}}(\sigma ). \end{aligned}$$

(4)

Here, the solutions of the above equation are defined as follows:

$$\begin{aligned} \Lambda _{1}(\sigma )=p\operatorname {sech}(u \sigma ), \end{aligned}$$

(5)

where $r_{1}=1$ and $r_{2}=-1.$

$$\begin{aligned} \Lambda _{2}(\sigma )=p\operatorname {csch}(u \sigma ), \end{aligned}$$

(6)

where $r_{1}=1$ and $r_{2}=1.$

$$\begin{aligned} \Lambda _{3}(\sigma )=p\operatorname {sec}(u \sigma ), \end{aligned}$$

(7)

where $r_{1}=-1$ and $, r_{2}=1$.

$$\begin{aligned} \Lambda _{4}(\sigma )=p\operatorname {csc}(u \sigma ), \end{aligned}$$

(8)

where $r_{1}=-1$ and $r_{2}=1.$

Application to the perturbed time-fractional nonlinear Schrödinger equation for optical fibers

Here, we utilize the new direct mapping method to generate several accurate answers in closed-form for the current time-fractional nonlinear Schrödinger problem. The inquiry begins by employing the following wave transformations:

$$\begin{aligned} \begin{aligned}&\rho (x,t)=W(\sigma ){{e}^{i\varphi (x,t)}}, \\&\sigma =x-s\frac{{{t}^{\alpha }}}{\alpha }, \quad \varphi (x,t)=-\kappa x+w\frac{{{t}^{\alpha }}}{\alpha }. \end{aligned} \end{aligned}$$

(9)

The symbol $W(\sigma )$ represents the phase component, w represents the wave number, $\kappa$ represents the frequency of solitons, and s represents the speed of the moving wave. By substituting the above transformations into the nonlinear Schrödinger equation (1), resulting in the following real part and imaginary part, respectively:

$$\begin{aligned} ({{\eta }_{2}}{{s}^{2}}+{{\eta }_{3}}){W}''(\sigma )+(\kappa -{{\eta }_{1}}w-{{\eta }_{2}}{{w}^{2}}-{{\eta }_{3}}{{\kappa }^{2}})W(\sigma )+{{W}^{3}}(\sigma )=0, \end{aligned}$$

(10)

and

$$\begin{aligned} (1-s{{\eta }_{1}}-2(sw{{\eta }_{2}}+{{\eta }_{3}}\kappa )){W}'(\sigma )=0. \end{aligned}$$

(11)

From the above equation, we obtain the following condition:

$$\begin{aligned} s=\frac{1-2{{\eta }_{3}}\kappa }{{{\eta }_{1}}+2w{{\eta }_{2}}}. \end{aligned}$$

(12)

By substituting the value of s into (10), we obtain the following equation:

$$\begin{aligned} ({{\eta }_{2}}{{A}_{2}}+{{\eta }_{3}}{{A}_{1}}){W}''(\sigma )+{{A}_{1}}{{A}_{3}}W(\sigma )+{{A}_{1}}{{W}^{3}}(\sigma )=0, \end{aligned}$$

(13)

where ${{A}_{1}}={{({{\eta }_{1}}+2\kappa {{\eta }_{2}})}^{2}}$, ${{A}_{2}}={{(1-2{{\eta }_{3}}\kappa )}^{2}}$ , and ${{A}_{3}}=(\kappa -{{\eta }_{1}}w-{{\eta }_{2}}{{w}^{2}}-{{\eta }_{3}}{{\kappa }^{2}})$.

In order to calculate the homogeneous balancing constant in (13), we focused on the term with the highest order $W''(\sigma )$, as well as the highest nonlinear term $W^{3}(\sigma )$. Thus, we establish the equation $N + 2 = 3N$. Therefore, applying the balance principle, the solution for N is determined to be 1. Therefore, the series in (3) is reduced to the following form:

$$\begin{aligned} W(\sigma )={{d}_{0}}+{{d}_{1}}\Lambda (\sigma ). \end{aligned}$$

(14)

Substituting (4) and (14) into (13) and then organizing the coefficients of ${{W}^{i}}(\sigma )$, where $i=0,1,2,...$, we obtain the following set of non-linear equations:

$$\begin{aligned}&(\Lambda (\sigma ))^{0}= \left( 2\,\eta _{2}\,w+\eta _{1} \right) ^{2} \left( {{ d_{0}}}^{3}+ \left( -\eta _{2}\,{w}^{2}-\eta _{3}\,{\kappa }^{2}-\eta _{1}\,w+\kappa \right) { d_{0}}\right) =0\\&(\Lambda (\sigma ))^{1}= { d_{1}} \left( 2\,\eta _{2}\,w+\eta _{1} \right) ^{2}\left( -\eta _{2}\,{w}^{2}-\eta _{3}\,{\kappa }^{2}+3\,{{ d_{0}}}^{2}-\eta _{1}\,w+\kappa \right) +{ d_{1}}\,{ r_{1}}\,{u}^{2} ( 4\,{\eta _{2}}^{2}\eta _{3}\, {w}^{2}+4\,\eta _{2}\,{\eta _{3}}^{2}{\kappa }^{2}+4\,\eta _{1}\,\eta _{2}\,\eta _{3}\,w\\&+{\eta _{1}}^{2}\eta _{3}-4\,\eta _{2}\,\eta _{3}\,\kappa +\eta _{2} ) =0,\\&(\Lambda (\sigma ))^{2}=3{ d0}\,{{ d1}}^{2}\, \left( 2\,\eta 2\,w+\eta 1 \right) ^{2}=0,\\&{{( \Lambda (\sigma ) )}^{3}}={{ d_{1}}}^{3} \left( 2\,\eta _{2}\,w+\eta _{1} \right) ^{2}+{\frac{2\,{ d_{1}}\,{u}^{2} { r_{2}}\,}{{p}^{2}}} \left( 4\,{\eta _{2}}^{2}\eta _{3}\,{w}^{2}+4\,\eta _{2}\,{\eta _{3}}^{2}{\kappa }^{2}+4\,\eta _{1}\,\eta _{2}\,\eta _{3}\,w+{\eta _{1}}^{2}\eta _{3}-4\,\eta _{2}\,\eta _{3}\,\kappa +\eta _{2} \right) =0. \end{aligned}$$

The subsequent outcomes are derived from solving this system:

Fig. 1

The bell-shape plots of ${{\left| {{\rho }_{1}}(x,t) \right| }^{2}}$, where $\alpha = 1,w= -1,\eta _{2}=1,{\eta }_{1}=0.5,\kappa = 0.3,$ and $u= -0.36$.

Fig. 2

The mixed dark-bright plots of $\operatorname {Re}({{\rho }_{1}}(x,t))$, where $\alpha = 1,w= -1,\eta _{2}=1,{\eta }_{1}=0.5,\kappa = 0.3,$ and $u= -0.36$.

Fig. 3

The dark-bright plots of $\operatorname {Im}({{\rho }_{5}}(x,t))$, where $\alpha = 1,w= 1.1,\eta _{3}=1,{\eta }_{1}=0.9,\kappa =0.1,$ and $u= -0.1$.

Fig. 4

The comparison of bright plots of $|{{\rho }_{9}}(x,t)|^2$ , where $w=2,\eta _{3}=1,{\eta }_{2}=1,\kappa =-0.9,w=2$ and $u= -0.1255$.

Result 1.

$$\begin{aligned} \begin{aligned}&\eta _{3}=-{\frac{4\,{w}^{2} \left( { r_{1}}\,{u}^{2}-{\kappa }^{2} \right) {\eta _{2}}^{2}+ \left( 4\,\eta _{1}\,{ r_{1}}\,{u}^{2}w-4\,\eta _{1}\,{\kappa }^{2}w-4\,\kappa \,{ r_{1}}\,{u}^{2} \right) \eta _{2}+ \left( { r_{1}}\,{u}^{2}-{\kappa }^{ 2} \right) {\eta _{1}}^{2} +\sqrt{{ K_{1}}}}{8{u}^{2} { r_{1}}\,\eta _{2}\, {\kappa }^{2}}},d_{0}=0,\\&d_{1}={\frac{\sqrt{\eta _{2}\,{ r_{2}}\, \left( -4\,{w}^{2} \left( { r_{1}}\,{u}^{2}+{\kappa }^{2} \right) {\eta _{2}}^{2}+ \left( -4\,\eta _{1}\,{ r_{1}}\,{u}^{2}w-4\,\eta _{1}\,{\kappa }^{2}w+4\, \kappa \,{ r_{1}}\,{u}^{2} \right) \eta _{2}+ \left( { r_{1}}\,{u}^{2}-{ \kappa }^{2} \right) {\eta _{1}}^{2} +\sqrt{{ K_{1}}} \right) }}{2\eta _{2}\,u{ r_{1}}\,p}}, \end{aligned} \end{aligned}$$

(15)

where

$K_{1}=\left( 16\, \left( { r_{1}}\,{u}^{2}+{\kappa }^{2} \right) ^{2} \left( {w}^{2}{\eta _{2}}^{2}+\frac{{\eta _{1}}^{2}}{4}\right) +16\, \left( { r_{1}}\,{u}^{2}+{\kappa }^{2} \right) \left( \eta _{1}\,{ r_{1}}\,{u}^{2}w+ \eta _{1}\,{\kappa }^{2}w-2\,\kappa \,{ r_{1}}\,{u}^{2} \right) \eta _{2} \right) \left( \eta _{2}\,w+\frac{\eta _{1}}{2} \right) ^{2} .$

From (5), (9), (12), (14), and 15, we can have the following optical soliton solution:

$$\begin{aligned} \begin{aligned}&\rho _{1}(x,t)=\frac{\sqrt{-\eta _{2}{(-4\,{w}^{2} \left( {\kappa }^{2}+{u}^{2} \right) {\eta _{2}}^{2}+ \left( -4 \,\eta _{1}\,{\kappa }^{2}w-4\,\eta _{1}\,{u}^{2}w+4\,\kappa \,{u}^{2} \right) \eta _{2}+{\eta _{1}}^{2}{u}^{2}-{\eta _{1}}^{2}{\kappa }^{2} )}+\sqrt{{ K_{2}}}}}{\eta _{2}u}\\&\,\operatorname {sech}(({-\frac{ \left( {\kappa }^{2}-{u}^{2} \right) \left( 4\,{w}^{2}{ \eta _{2}}^{2}+4\,w\eta _{1}\,\eta _{2}+{\eta _{1}}^{2} \right) +8\,\eta _{2}\,\kappa \,{u} ^{2}+\sqrt{{ K_{2}}}}{4\eta _{2}\,\kappa \,{u} \left( 2\,\eta _{2}\,w+\eta _{1} \right) }})\frac{t^{\alpha }}{\alpha })+x) \textrm{e}^{i ( -\kappa \,x+w\frac{t^{\alpha }}{\alpha } )}. \end{aligned} \end{aligned}$$

(16)

From (6), (9), (12), (14), and 15, we can have the following optical soliton solution:

$$\begin{aligned} \begin{aligned}&\rho _{2}(x,t)=\frac{\sqrt{\eta _{2}{(-4\,{w}^{2} \left( {\kappa }^{2}+{u}^{2} \right) {\eta _{2}}^{2}+ \left( -4 \,\eta _{1}\,{\kappa }^{2}w-4\,\eta _{1}\,{u}^{2}w+4\,\kappa \,{u}^{2} \right) \eta _{2}+{\eta _{1}}^{2}{u}^{2}-{\eta _{1}}^{2}{\kappa }^{2} )}+\sqrt{{ K_{2}}}}}{\eta _{2}u}\\&\,\operatorname {csch}(({-\frac{ \left( {\kappa }^{2}-{u}^{2} \right) \left( 4\,{w}^{2}{ \eta _{2}}^{2}+4\,w\eta _{1}\,\eta _{2}+{\eta _{1}}^{2} \right) +8\,\eta _{2}\,\kappa \,{u} ^{2}+\sqrt{{ K_{2}}}}{4\eta _{2}\,\kappa \,{u} \left( 2\,\eta _{2}\,w+\eta _{1} \right) }})\frac{t^{\alpha }}{\alpha })+x) \textrm{e}^{i ( -\kappa \,x+w\frac{t^{\alpha }}{\alpha } )}, \end{aligned} \end{aligned}$$

(17)

where

$K_{2}=\left( 16\,\eta _{2}\, \left( {\kappa }^{2}+{u}^{2} \right) \left( \left( \eta _{2}\,w+\eta _{1} \right) \left( w{\kappa }^{2}+{u}^{2}w \right) -2\,\kappa \,{u}^{2} \right) +4\,{\eta _{1}}^{2} \left( u-\kappa \right) ^{ 2} \left( u+\kappa \right) ^{2} \right) \left( \eta _{2}\,w+\frac{\eta _{1}}{2} \right) ^{2}.$             

From (7), (9), (12), (14), and (15), we can have the following optical soliton solution:

$$\begin{aligned} \begin{aligned}&\rho _{3}(x,t)=-\frac{\sqrt{\eta _{2}{(-4\,{w}^{2} \left( {\kappa }^{2}+{u}^{2} \right) {\eta _{2}}^{2}+ \left( -4 \,\eta _{1}\,{\kappa }^{2}w-4\,\eta _{1}\,{u}^{2}w+4\,\kappa \,{u}^{2} \right) \eta _{2}-{\eta _{1}}^{2}{u}^{2}-{\eta _{1}}^{2}{\kappa }^{2} )}+\sqrt{{ K_{3}}}}}{\eta _{2}u}\\&\,\operatorname {sec}(({\frac{ \left( {\kappa }^{2}+{u}^{2} \right) \left( -4\,{w}^{2} {\eta _{2}}^{2}-4\,w\eta _{1}\,\eta _{2}-{\eta _{1}}^{2} \right) +4\,\eta _{2}\,\kappa \,{u }^{2}+\sqrt{{ K_{3}}}}{4\eta _{2}\,\kappa \,{u} \left( 2\,\eta _{2}\,w+\eta _{1} \right) }} )\frac{t^{\alpha }}{\alpha })+x) \textrm{e}^{i ( -\kappa \,x+w\frac{t^{\alpha }}{\alpha } )}. \end{aligned} \end{aligned}$$

(18)

From (8), (9), (12), (14), and (15), we can have the following optical soliton solution:

$$\begin{aligned} \begin{aligned}&\rho _{4}(x,t)=-\frac{\sqrt{\eta _{2}{(-4\,{w}^{2} \left( {\kappa }^{2}+{u}^{2} \right) {\eta _{2}}^{2}+ \left( -4 \,\eta _{1}\,{\kappa }^{2}w-4\,\eta _{1}\,{u}^{2}w+4\,\kappa \,{u}^{2} \right) \eta _{2}-{\eta _{1}}^{2}{u}^{2}-{\eta _{1}}^{2}{\kappa }^{2} )}+\sqrt{{ K_{3}}}}}{\eta _{2}u}\\&\,\operatorname {csc}(({\frac{ \left( {\kappa }^{2}+{u}^{2} \right) \left( -4\,{w}^{2} {\eta _{2}}^{2}-4\,w\eta _{1}\,\eta _{2}-{\eta _{1}}^{2} \right) +4\,\eta _{2}\,\kappa \,{u }^{2}+\sqrt{{ K_{3}}}}{4\eta _{2}\,\kappa \,{u} \left( 2\,\eta _{2}\,w+\eta _{1} \right) }} )\frac{t^{\alpha }}{\alpha })+x) \textrm{e}^{i ( -\kappa \,x+w\frac{t^{\alpha }}{\alpha } )}, \end{aligned} \end{aligned}$$

(19)

where

$K_{3}=16\, \left( \eta _{2}\,w+\frac{\eta _{1}}{2} \right) ^{2} \left( \eta _{2}\, \left( u- \kappa \right) \left( \left( {w}^{2}\eta _{2}+\eta _{1}\,w-2\,\kappa \right) {u}^{2}-w \left( \eta _{2}\,w+\eta _{1} \right) {\kappa }^{2} \right) \left( u+\kappa \right) +\frac{{\eta 1}^{2} }{4}\left( {\kappa }^{2}+{u}^{2} \right) ^{2} \right) .$

Result 2.

$$\begin{aligned} d_{0}=0,\eta _{2}=0,\kappa =\kappa ,w={\frac{\eta _{3}\,{ r_{1}}\,{u}^{2}-\eta _{3}\,{\kappa }^{2}+\kappa }{\eta _{1}}}, d_{1}={\frac{u\sqrt{-2\,\eta _{3}\,{ r_{2}}}}{p}}. \end{aligned}$$

(20)

Fig. 5

The mixed dark-bright plots of $\operatorname {Im}({{\rho }_{9}}(x,t))$, where $w=2,\eta _{3}=1,{\eta }_{2}=1,\kappa =-0.9,w=2,u= - 0.1255$ and $t=2$.

Fig. 6

The 2D plots of ${{\left| {{\rho }_{9}}(x,t) \right| }^{2}}$ and $\operatorname {Im}({{\rho }_{9}}(x,t))$, where $w=2,\eta _{3}=1,{\eta }_{2}=1,\kappa =-0.9,w=2,u= -0.1255$ and $t=2$.

From (5), (9), (12), (14), and (20) , we can have the following optical soliton solution:

$$\begin{aligned} \begin{aligned}&\rho _{5}(x,t)=\sqrt{2\eta _{3}} u \textrm{sech} \left( u \left( x +{\frac{ \left( 2\, \eta _{3}\,\kappa -1 \right) {t}^{\alpha }}{\alpha \,\eta _{1}}} \right) \right) {\textrm{e}^{i \left( -\kappa \,x+{\frac{ \left( -\eta _{3}\,{\kappa }^ {2}+\eta _{3}\,{u}^{2}+\kappa \right) {t}^{\alpha }}{\alpha \,\eta _{1}}} \right) }}. \end{aligned} \end{aligned}$$

(21)

From (6), (9), (12), (14), and (20) , we can have the following optical soliton solution:

$$\begin{aligned} \begin{aligned}&\rho _{6}(x,t)=\sqrt{-2\eta 3} u \textrm{csch} \left( u \left( x +{\frac{ \left( 2\, \eta _{3}\,\kappa -1 \right) {t}^{\alpha }}{\alpha \,\eta _{1}}} \right) \right) {\textrm{e}^{i \left( -\kappa \,x+{\frac{ \left( -\eta _{3}\,{\kappa }^ {2}+\eta _{3}\,{u}^{2}+\kappa \right) {t}^{\alpha }}{\alpha \,\eta _{1}}} \right) }}. \end{aligned} \end{aligned}$$

(22)

From (7), (9), (12), (14), and (20) , we can have the following optical soliton solution:

$$\begin{aligned} \begin{aligned}&\rho _{7}(x,t)=\sqrt{-2\eta _{3}} u \textrm{sec} \left( u \left( x +{\frac{ \left( 2\, \eta _{3}\,\kappa -1 \right) {t}^{\alpha }}{\alpha \,\eta _{1}}} \right) \right) {\textrm{e}^{i \left( -\kappa \,x+{\frac{ \left( -\eta _{3}\,{\kappa }^ {2}-\eta _{3}\,{u}^{2}+\kappa \right) {t}^{\alpha }}{\alpha \,\eta _{1}}} \right) }}. \end{aligned} \end{aligned}$$

(23)

From (8), (9), (12), (14), and (20) , we can have the following optical soliton solution:

$$\begin{aligned} \begin{aligned}&\rho _{8}(x,t)=\sqrt{-2\eta 3} u \textrm{csc} \left( u \left( x +{\frac{ \left( 2\, \eta _{3}\,\kappa -1 \right) {t}^{\alpha }}{\alpha \,\eta _{1}}} \right) \right) {\textrm{e}^{i \left( -\kappa \,x+{\frac{ \left( -\eta _{3}\,{\kappa }^ {2}-\eta _{3}\,{u}^{2}+\kappa \right) {t}^{\alpha }}{\alpha \,\eta _{1}}} \right) }}. \end{aligned} \end{aligned}$$

(24)

Result 3

$$\begin{aligned} d_{0}=0,\eta _{2}=0, d_{1}={\frac{\sqrt{-2\,\eta _{3}\,{ r_{2}}}u}{p}}, \eta _{1}={\frac{ \left( { r_{1}}\,{u}^{2}-{\kappa }^{2} \right) \eta _{3}+\kappa }{w }}. \end{aligned}$$

(25)

From (5), (9), (12), (14), and (25) , we can have the following optical soliton solution:

$$\begin{aligned} \begin{aligned}&\rho _{9}(x,t)=\sqrt{2\eta _{3}}u\textrm{sech} \left( u \left( x+{\frac{ \left( 2\, \eta _{3}\,\kappa -1 \right) w{t}^{\alpha }}{\alpha \, \left( \left( -{ \kappa }^{2}+{u}^{2} \right) \eta _{3}+\kappa \right) }} \right) \right) \textrm{e}^{i ( -\kappa \,x+{\frac{w{t}^{\alpha }}{\alpha }} ) }. \end{aligned} \end{aligned}$$

(26)

From (6), (9), (12), (14), and (25), we can have the following optical soliton solution:

$$\begin{aligned} \begin{aligned}&\rho _{10}(x,t)=\sqrt{-2\eta _{3}}u\textrm{csch} \left( u \left( x+{\frac{ \left( 2\, \eta _{3}\,\kappa -1 \right) w{t}^{\alpha }}{\alpha \, \left( \left( -{ \kappa }^{2}+{u}^{2} \right) \eta _{3}+\kappa \right) }} \right) \right) \textrm{e}^{i ( -\kappa \,x+{\frac{w{t}^{\alpha }}{\alpha }} ) }.\\ \end{aligned} \end{aligned}$$

(27)

From (7), (9), (12), (14), and (25), we can have the following optical soliton solution:

$$\begin{aligned} \begin{aligned}&\rho _{11}(x,t)=\sqrt{-2\eta _{3}}u\textrm{sec} \left( u \left( x+{\frac{ \left( 2\, \eta _{3}\,\kappa -1 \right) w{t}^{\alpha }}{\alpha \, \left( \left( -{ \kappa }^{2}-{u}^{2} \right) \eta _{3}+\kappa \right) }} \right) \right) \textrm{e}^{i ( -\kappa \,x+{\frac{w{t}^{\alpha }}{\alpha }} ) }.\\ \end{aligned} \end{aligned}$$

(28)

From (8), (9), (12), (14), and (25), we can have the following optical soliton solution:

$$\begin{aligned} \begin{aligned}&\rho _{12}(x,t)=\sqrt{-2\eta _{3}}u\textrm{csc} \left( u \left( x+{\frac{ \left( 2\, \eta _{3}\,\kappa -1 \right) w{t}^{\alpha }}{\alpha \, \left( \left( -{ \kappa }^{2}-{u}^{2} \right) \eta _{3}+\kappa \right) }} \right) \right) \textrm{e}^{i ( -\kappa \,x+{\frac{w{t}^{\alpha }}{\alpha }} ) }.\\ \end{aligned} \end{aligned}$$

(29)

Fig. 7

Phase portraits of the system’s bifurcations are depicted under different conditions for $\mu _{1}$ and $\mu _{2}$, using various parameter values for Case 5.1 and Case 5.2.

Fig. 8

Phase portraits of the system’s bifurcations are depicted under different conditions for $\mu _{1}$ and $\mu _{2}$, using various parameter values for Case 5.3 and Case 5.4.

Results and discussion

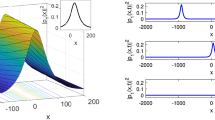
In this section, we chose specific values for the physical parameters to emphasize the importance of the conformable Schrödinger equation system. Various graphs have been employed to analyze the properties of the novel optical solutions and demonstrate their physical significance. We examine how the conformable order derivative, denoted as $\alpha$, and the time variable t affect the present soliton solutions. This analysis is depicted through a collection of two-dimensional, contour, and three-dimensional plots, which are presented in the present figures. The bell-shaped optical solution of ${{\left| {{\rho }_{1}}(x,t) \right| }^{2}}$ with the effect of temporal parameter t is given in Figure 1 graph (a) and graph (b), respectively. Figures 2a,b, 5a,b illustrate the mixed dark-bright solutions of $\operatorname {Re}({{\rho }_{1}}(x,t))$ and $\operatorname {Im}({{\rho }_{9}}(x,t))$ with the effect of temporal parameter t, respectively. Further, in Fig. 3a the mixed dark-bright soliton solutions to $\operatorname {Im}({{\rho }_{5}}(x,t))$ with the contour plot is depicted. The stability of the current optical soliton solutions is evident as they remain stable over long distances. The figures demonstrate how the topological features of these soliton solutions behave as the temporal parameter varies. In practical scenarios, mixed dark-bright optical solutions are composed of a combination of dark and bright solutions. The dark solutions exhibit lower intensity, while the bright solutions display higher intensity, both coexisting within the same wave function. This combination creates areas with both decreased and increased amplitude or intensity, leading to intricate interactions between the dark and bright components. The comparison of solution ${{\left| {{\rho }_{9}}(x,t) \right| }^{2}}$ for two distinct values of $\alpha$ is given in Fig. 4a,b. The presence of bell-shaped solitons suggests that the system supports different types of coherent structures that can move while preserving both their form and speed. By modifying the parameters that influence dark soliton propagation, engineers can tailor optical fiber systems to suit particular communication needs (Fig. 5).

Figure 6a,b illustrate the variation in the topological characteristics of various soliton solutions as the conformable derivative parameter $\alpha$ is changed. The results illustrated are novel and do not align with any previously published studies. The figures offer a dynamic representation of different soliton solutions, including periodic, bright, singular, combo bright-dark, and dark optical solitons. These solutions are of physical importance; for instance, the hyperbolic secant is relevant in the profile of a laminar jet mirror. It can be claimed that the results presented in this study are novel and have not been previously reported in the existing literature, particularly when compared with the findings in Refs.^{25,26,27,28,29}.

Fig. 9

In this figure, we identify the chaotic behavior of the system (32) using various methods of chaos detection. (a) Three-dimensional phase picture, (b) two-dimensional phase portrait, (c) time series of t compared to W(t), and (d) time series of t compared to U(t) with physical parameters ${{\mu }_{1}}=1$, ${{\mu }_{2}}=-1$, $\gamma =0.001$ ,and $\varepsilon =\pi$.

Bifurcation

This section provides a bifurcation analysis of the dynamical system described by (13). Firstly, by applying the Galilean transformation to (13), we derive the dynamical system in the following manner:

$$\begin{aligned} \begin{aligned}&{W}'=U, \\&{U}'=-{{\mu }_{1}}W-{{\mu }_{2}}{{W}^{3}}, \\ \end{aligned} \end{aligned}$$

(30)

where ${{\mu }_{1}}=\frac{{{A}_{1}}{{A}_{3}}}{{{\eta }_{2}}{{A}_{2}}+{{\eta }_{3}}{{A}_{1}}}=\frac{{{({{\eta }_{1}}+2w{{\eta }_{2}})}^{2}}(\kappa -{{\eta }_{1}}w-{{\eta }_{2}}{{w}^{2}}-{{\eta }_{3}}{{\kappa }^{2}})}{({{\eta }_{2}}{{(1-2{{\eta }_{3}}\kappa )}^{2}}+{{\eta }_{3}}{{({{\eta }_{1}}+2w{{\eta }_{2}})}^{2}})}$ and ${{\mu }_{2}}=\frac{{{A}_{1}}}{{{\eta }_{2}}{{A}_{2}}+{{\eta }_{3}}{{A}_{1}}}=\frac{{{({{\eta }_{1}}+2w{{\eta }_{2}})}^{2}}}{({{\eta }_{2}}{{(1-2{{\eta }_{3}}w)}^{2}}+{{\eta }_{3}}{{({{\eta }_{1}}+2w{{\eta }_{2}})}^{2}})}$.

The Hamiltonian function for (30) is expressed as follows:

$$\begin{aligned} G(W,U)=\frac{{{U}^{2}}}{2}-{{\mu }_{1}}\frac{{{W}^{2}}}{2}-{{\mu }_{2}}\frac{{{W}^{4}}}{4}=g, \end{aligned}$$

(31)

where g is the Hamiltonian constant. We will analyze the phase graphs of system (30) within the parameter space determined by ${{\mu }_{1}}$ and ${{\mu }_{2}}$. The collected results are ascertained through qualitative analysis. We resolve the system.

$$\begin{aligned} \begin{aligned}&U=0,\\&-\mu _{1}W-\mu _{2}W^{3}=0.\\ \end{aligned} \end{aligned}$$

(32)

To determine the equilibrium points of Eq. (30). The calculated equations are: (0, 0) and $(\pm \sqrt{\frac{-{{\mu }_{1}}}{{{\mu }_{2}}}},0)$.

Fig. 10

In this figure, we identify the chaotic behavior of the system (32) using various methods of chaos detection. Figure 10a three-dimensional phase picture, Fig. 10b two-dimensional phase portrait, Fig. 10c time series of t compared to W(t), and Fig. 10d time series of t compared to U(t) with physical parameters ${{\mu }_{1}}=1$, ${{\mu }_{2}}=-1$, $\gamma =0.1$, and $\varepsilon =\pi$.

The determinant of the Jacobian matrix for system 30 is

$$\begin{aligned} D(W,U)=\left| \begin{matrix} 0 & 1 \\ -{{\mu }_{1}}-3{{\mu }_{2}}{{W}^{2}} & 0 \\ \end{matrix} \right| ={{\mu }_{1}}+3{{\mu }_{2}}{{W}^{2}}. \end{aligned}$$

(33)

Fig. 11

In this paper, we identify the chaotic behavior of the system (32) using various methods of chaos detection. (a) Three-dimensional phase picture, (b) two-dimensional phase portrait, (c) time series of t compared to W(t), and (d) time series of t compared to U(t) with physical parameters ${{\mu }_{1}}=1$, ${{\mu }_{2}}=-1$, $\gamma =0.4$ and $\varepsilon =\pi .$.

Fig. 12

In this figure, we identify the chaotic behavior of the system (32) using various methods of chaos detection. (a) Three-dimensional phase picture, (b) two-dimensional phase portrait, (c) series of time of t compared to W(t), and (d) time series of t compared to U(t) with physical parameters ${{\mu }_{1}}=1$, ${{\mu }_{2}}=-1$, $\gamma =0.4$ and $\varepsilon =2\pi$.

It is established that:

• 1. (W, U) is a saddle point if $D(W,U)<0$.

• 2. (W, U) is a center point if $D(W,U)>0$.

• 3. (W, U) is a cuspidal point if $D(W,U)=0$.

The potential results that can be achieved by modifying the relevant parameter are outlined below.

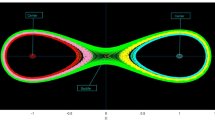
• 1. Case 5.1: ${{\mu }_{1}}<0$ and ${{\mu }_{2}}>0$. By specifying the values of the parameters $\kappa =-1$, ${{\eta }_{1}}=-1$, ${{\eta }_{2}}=0$, ${{\eta }_{3}}=-1$, $w=-1$, and $s=1$, we determine that there are three equilibrium points, namely $(1,0),(-1,0)$, and (0, 0), as illustrated in Fig. 6a. Clearly, the point (0, 0)is the center point, and the points (1, 0) and $(-1,0)$are saddle points.

• 2. Case 5.2: ${{\mu }_{1}}>0$ and ${{\mu }_{2}}<0$. Upon choosing the parameters $\kappa =-1$, ${{\eta }_{1}}=0.04$, ${{\eta }_{2}}=-1$, ${{\eta }_{3}}=0$, $w=-\frac{1}{2}$, and $s=1$, we can notice the existence of three equilibrium points, namely specifically (0, 0), $(-1,0)$ , and (1, 0). Among these, the position (0, 0)functions as a saddle point, as depicted in Fig. 6b. In addition, the coordinates (1, 0) and $(-1,0)$ serve as center points.

• 3. Case 5.3: ${{\mu }_{1}}<0$ and ${{\mu }_{2}}<0$. By specifying the values of the parameters $\kappa =1$, ${{\eta }_{1}}=0.04$, ${{\eta }_{2}}=-0.5$, ${{\eta }_{3}}=0.5$, $w=-\frac{1}{2}$, and $s=1$, we determine that the sole noncomplex real equilibrium poin is located at coordinates (0, 0), as shown in Fig. 7a. Clearly, the point (0, 0) corresponds to the saddle point.

• 4. Case 5.4: ${{\mu }_{1}}>0$ and ${{\mu }_{2}}>0$. By choosing specific values for the parameters $\kappa =-1$, ${{\eta }_{1}}=-1$, ${{\eta }_{2}}=0$, ${{\eta }_{3}}=1$, $w=-1$, and $s=1$, we find that the only actual equilibrium point is (0, 0), as shown in Fig. 7b. Clearly, the location (0, 0) corresponds to a center point.

Chaotic solutions

Here, we study the existence of the chaotic dynamics in (30) by introducing a perturbed term. We conduct an examination of both two-dimensional and three-dimensional phase pictures for this particular system. We are considering the following dynamical system:

$$\begin{aligned} \begin{aligned}&\frac{dW(t)}{dt}=U(t), \\&\frac{dU(t)}{dt}=-{{\mu }_{1}}W(t)-{{\mu }_{2}}{{W(t)}^{3}}+\gamma \cos (\varepsilon t ). \\ \end{aligned} \end{aligned}$$

(34)

Alternatively, (34) can be articulated in the subsequent manner system.We are considering the following dynamical system:

$$\begin{aligned} \begin{aligned}&\frac{dW(t)}{dt}=U(t), \\&\frac{dU(t)}{dt}=-{{\mu }_{1}}W(t)-{{\mu }_{2}}{{W(t)}^{3}}+\gamma \cos (R(t)), \\&\frac{dR(t)}{dt}= \varepsilon ,\\ \end{aligned} \end{aligned}$$

(35)

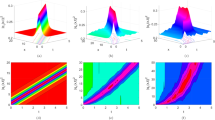
where $\gamma$ represents the outside force associated with the periodically perturbed part, and $\varepsilon$ denotes its frequency. The system (35) incorporates an exterior periodic force, distinguishing it from the dynamical system (30). We will present multiple graphical representations to elucidate the chaotic and quasi-periodic dynamical behavior of the planner system through the influence of the terms with perturbation and indeterminate parameters. These encompass three-dimensional and two-dimensional phase portrait plots, time series visualizations. The impact of the frequency and the external force of the perturbed term is analyzed, with all other physical characteristics of the system held constant. This study will explore how these factors impact the system (Fig. 8). The perturbation term in the planar dynamical system (35) is affected by $\gamma$ and $\varepsilon$. To maintain consistency, all other physical parameters in system (35) will remain fixed while we investigate how varying $\gamma$ and $\varepsilon$ influences the system.The perturbed system is illustrated in Fig. 9a–d, corresponding to the specific selection of physical parameters$:{{\mu }_{1}} \, =\, 1,\, {{\mu }_{2}}\, =\, -1,\,\,\gamma \, =\, 0.001,\, \varepsilon \, =\, \pi$, when $\kappa =1$, ${{\eta }_{1}}=-1.2$, ${{\eta }_{2}}=-2.1$, ${{\eta }_{3}}=1.1$, $w=-1$, and $s=4$, with the initial condition (0.05, 0.05, 0). The panel of Fig. 9a–d indicates that the perturbed dynamical system (35) demonstrates quasi-periodic patterns. Select the values of ${{\mu }_{1}}\, =\, 1$ instead of ${{\mu }_{1}}\, =\text { 0}\text {.1}$ while maintaining other settings.Quasi-periodic patterns are also observed, as depicted in Figures. Figure 10a–d, consistent with those in Fig. 9a–d. The time series plots (refer to Figs. 9a–d, 10a–d) validate these quasi-periodic wave patterns. maintaining the remaining parameters consistent with those in Fig. 10a–d, the perturbed dynamical system (35) exhibits an irregular pattern indicative of chaotic dynamics, indicating distinct characteristics of chaotic dynamics,as illustrated in Fig. 11a–d. The quasi-periodic pattern, as illustrated in Fig. 12a–d, is achieved in system (35) with the parameter values ${{\mu }_{1}}\, =\, 1,\, {{\mu }_{2}}\, =\, -1,\,\,\gamma \, =\, 0.4,\, \varepsilon \, =\, \pi$ , and the initial condition $(-0.075, -0.075, 0)$. The perturbed system (35) demonstrates quasi-periodic and chaotic behavior. It is noteworthy that the wave form exhibits a consistent pattern upon disregarding the perturbed term of system (35).

Sensitivity analysis for system

The objective of the subsection is to ascertain the system’s sensitivity that may influence a model’s performance based on its initial conditions. If the system experiences a minor alteration due to a slight modification in the original conditions, it is considered to have low sensitivity. If the system experiences a substantial alteration due to little changes in the original conditions, it is considered extremely sensitive. Consequently, we want to evaluate the sensitivity of system (30) by employing various three distinct initial circumstances.An extensive examination of systems (30) and (35) is presented in Figs. 13a,b, 14a,b, respectively, under three distinct initial conditions. Figure 13 illustrates the sensitivity of the system (30) under varying physical parameters. ${{\mu }_{1}}\, =\, 0.15,\, {{\mu }_{2}}\, =\text { -1}.5$, when $k=-2,{{\eta }_{1}}=-0.3,{{\eta }_{2}}=-0.6,{{\eta }_{3}}=-0.4,w=-1$,and $s=4$ , with beginning conditions shown as $(W, U) = (0.01, 0)$ in red, $(W, U) = (0.02, 0)$ in green, and $(W, U) = (0.03, 0)$ in blue. The panel of Fig. 13a,b illustrates that a minor alteration in the initial values results in a substantial variation in the model solution.Consequently, we conclude that the examined model has significant sensitivity. Additionally, Fig. 14 illustrates the sensitivity of system (35) with respect to various physical parameters: ${{\mu }_{1}}\, =\, 0.15,\, {{\mu }_{2}}\, =\text { -1}.5, \gamma =0.1 and \varepsilon =\pi$ where $k=-2,{{\eta }_{1}}=-0.3,{{\eta }_{2}}=-0.6,{{\eta }_{3}}=-0.4,w=-1$,and $s=4$ , for three distinct initial conditions: $(W, U, R) = (0.1, 0.1, 0)$ represented by the red line, $(W, U, R) = (0.2, 0.2, 0)$ depicted by the green line, and $(W, U, R) = (0.3, 0.3, 0)$ shown by the blue line. The panel of Fig. 14a,b reveals a significant alteration in the amplitude pattern of the waves, demonstrating the non-overlapping characteristics of the curves and underscoring the system’s sensitivity. The findings demonstrate that both systems exhibit significant sensitivity to beginning conditions, leading to chaotic behavior. The selection of beginning conditions is primarily reliant on trial and error, lacking a systematic approach for sensitivity analysis of the resultant dynamical system.

Fig. 13

Sensitivity analysis of the system (30) with physical parameters ${{\mu }_{1}}\, =\, 0.15,\, {{\mu }_{2}}\, =\text { -1}.5$ for various initial conditions: blue (0.03, 0), green (0.02, 0), and red (0.01, 0).

Fig. 14

Sensitivity analysis of the system (35) with physical parameters ${{\mu }_{1}}\, =\, 0.15,\, {{\mu }_{2}}\text { -1}.5, \gamma =0.1$ and $\varepsilon =\pi$ for various initial conditions.

Conclusion

This paper presented the construction of various optical soliton solutions and an analysis of chaotic behavior and bifurcations in the nonlinear conformable Schrödinger equation, which incorporates group velocity dispersion coefficients and second-order spatiotemporal terms. To construct various novel optical solutions for this form of the nonlinear Schrödinger equation with a conformable derivative, the new direct mapping method is utilized. The behavior of the obtained solutions is demonstrated through three-dimensional visualizations along with corresponding two-dimensional graphs. To gain a more comprehensive understanding of the system’s dynamics, bifurcation and chaos theories are applied. Chaotic solutions for the perturbed dynamical system are identified and illustrated using the provided graphs. In addition, we examined the extent of the current conformable system of equations by exploring how the conformable parameter and the time parameter influence different optical soliton solutions. The findings in this study emphasize the reliability and efficiency of the methods employed, demonstrating their applicability in solving a wide range of nonlinear systems with complex structures. The discussed Schrödinger model holds promise for applications in transmitting ultra-fast pulses through optical fibers. In the future, the present method can be used to study other types of nonlinear Schrödinger equation with integer and fractional orders.