Introduction

Determining and characterizing rock types is essential for every discipline and industry sector interested in earth sciences. The description of rock types is utilized at every stage, from the design studies for the operation of mine deposits to the fundamental processes applied for production (drilling, blasting, loading, and haulage). It is crucial and effective in determining the mining methods and equipment selection. The techniques to characterize the rock type are time-consuming and require unique expertise (geologists specializing in mineralogy and petrography). In some cases, the determination of rock type can also be inaccurate. However, it is possible to determine the rock type from the rock parameters (mechanical and physical properties) that have been analyzed for the design of mining methods by various statistical and computational methods.

Various statistical and computer science methods have been developed to perform deeper statistical analysis in recent years. Data mining is a scientific discipline that provides meaningful and usable information, especially from complex and large data. Data mining extends beyond classical statistics and uses algorithms to simplify and reveal hidden patterns and relationships within a data set1.

Researchers have studied extensively in the literature on predicting rock properties, especially those determined due to time-consuming and laborious experiments, using data mining techniques and classical statistical methods. Most studies focus on predicting rocks’ elastic modulus and strength parameters. It is reported that data mining methods have been successfully used to solve various problems in rock mechanics and outperform traditional empirical, mathematical, or statistical methods2,3. However, despite this, studies are limited because they require a specialization.

Martins and Miranda1 developed models for predicting the rock deformation modulus and the Rock Mass Rating (RMR) with data mining tools. Miranda et al.4 developed new, simple, and reliable data mining models to predict geomechanical parameters such as friction angle, cohesion, and deformability modulus using a geotechnical database of an underground structure constructed in granite rock formation. Martins et al.5 applied data mining techniques such as multiple regression, artificial neural networks, and support vector machines to predict the uniaxial compressive strength and deformation modulus of some Oporto granite rock characteristics. Ocak and Seker6 conducted a study on the prediction of modulus of elasticity from some intact rock properties by artificial neural networks. Aboutaleb et al.7 applied simple and multivariate regression, artificial neural network, and support vector regression to predict uniaxial compressive strength and static Young’s modulus of five different intact limestone rock samples. They found that the support vector regression model was preferable and advantageous. Gong et al.8 tried to predict the modulus of elasticity by data mining methods using mineralogical and pore characteristics of rocks. Erofeev et al.9 investigated the applicability of various machine-learning algorithms in predicting salt density, porosity, and permeability variations in salt rock. Roy and Singh10 constructed Young’s modulus and Poisson’s ratio prediction models by soft computing and regression analysis approaches using some geomechanical parameters, such as compressive strength, tensile strength, shear strength, and P-wave velocity as inputs. Khan et al.11 investigated thermal effects on some physical, chemical, and mechanical properties of marble. They also developed models using machine learning algorithms and multivariate regression to predict uniaxial compressive strength and static Young’s modulus using temperature, P-wave velocity, porosity, density, and dynamic Young’s modulus parameters. Abdi et al.12 proposed a model with tree-based techniques for predicting the elastic modulus of weak rock. By soft computing, Khajevand13 predicted the uniaxial compressive strength of some sedimentary rocks. Fang et al.14 applied some algorithms to predict sandstone rocks’ elastic modulus and uniaxial compressive strength. Khatti and Grover15 conducted to develop an optimal model to predict the uniaxial compressive strength of intact rock properties such as the area of the specimen, the mass of the specimen, the density of the specimen, P-wave velocity, and Young’s modulus.

Apart from the above studies on predicting rock properties by data mining, a few studies have tried to predict rock types with limited data. Zhou et al.16 proposed an adaptive unsupervised approach to predict rock types with an “Optimized Adjusted Penetration Rate” defined from drilling data. This approach minimized entropy and obtained satisfactory results for three types of rocks (shale, ore, and banded iron formation). Gonçalves et al.17 evaluated the classification of carbonate rocks using data mining algorithms using nuclear magnetic resonance (NMR) results. A total of 78 samples for six different carbonate rocks were used in this study and a successful classification rate of 97.4% was achieved. Houshmand et al.18 used different algorithms to classify five rock types from core samples based on P and S-wave velocities, Leeb hardness, and portable XRF results. Image analysis of the 35 m core used in the study was also used for rock type classification along with rock parameters. Among the machine learning algorithms, XGBoost showed the best performance, whereas the combination of images and rock properties gave a better final rock classification than either of them individually.

This study presents data mining implementations that will enable the most accurate determination of rock type using physical and mechanical properties. Unit volume weight (UVW), water absorption (WA), apparent porosity (AP), uniaxial compressive strength (UCS), Brazilian (indirect) tensile strength (TS), point load strength index (PL), modulus of elasticity (E), Shore hardness (SH) and Böhme surface abrasion strength (BSA) values of the rocks were selected as input parameters and the rock type (RT) as the output parameter was tried to predict. Hence, data mining methods have been demonstrated to determine rock types without a detailed mineralogical-petrographic analysis. Moreover, data mining methods can reliably and accurately predict the results of both expensive and time-consuming rock analysis studies. Determination of rock type from some rock properties can bypass many laboratory studies and provide rapid results. Data mining algorithms have been determined to give reliable results in such studies, and their usage in earth sciences should be widespread.

Research methodology

This research was carried out to investigate data mining models for the most accurate prediction of rock type from their physical and mechanical properties. For this purpose, the physical and mechanical properties of rock samples of different types were acquired from the author’s previous publications. Mineralogical and petrographic analyses of these rock samples were conducted, and rock types were clarified. The collected data were pre-processed. Then, input and output parameters were evaluated using appropriate data mining algorithms. The most suitable algorithms and models for rock type prediction were decided. Figure 1 shows the general methodology of the research.

Fig. 1
figure 1

General methodology of research.

Full size image

Data acquisition and computational approaches

Data acquisition

This study’s data set includes 92 samples representing three different rock types (sedimentary, metamorphic, and igneous). The samples used in the study are 40 of sedimentary origin, 41 of metamorphic origin, and 11 of igneous origin. Considering their origin, sedimentary samples are coded with “S”, metamorphic samples with “M” and igneous samples with “I”. Table 1 shows the sample codes by rock type.

Table 1 Sample codes by rock type.
Full size table

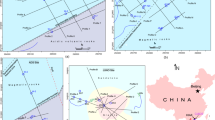
The study samples were from different regions of Türkiye. Figure 2 shows the sampling sites of the rock samples.

Fig. 2
figure 2

Sampling sites of the rock samples.

Full size image

Some physical and mechanical properties of these rock samples were determined. The laboratory studies were carried out by TS 699 19 standard and ISRM20 suggested methods. Some physical properties (unit volume weight [UVW], water absorption [WA], and apparent porosity [AP]) and mechanical properties (modulus of elasticity [E], uniaxial compressive strength [UCS], Brazilian (indirect) tensile strength [TS]), Shore hardness [SH], point load strength [PL], and Böhme surface abrasion strength [BSA]) were determined by the specified standards.

  1. a)

    Unit volume weight: The unit volume weight is one of the essential properties in the production of rocks and in determining their usage areas. In this experiment, the unit volume weight of rocks is determined to include the porosity structure. Experiments are performed with regular rock samples weighing at least 350 g, formed into cubes, rectangular prisms, or cylinders19.

  1. b)

    Water absorption: The water absorption test is a method for determining the water absorption of rocks by submerging them in water at atmospheric pressure. The 50 mm cube samples are first dried and allowed to rest at room temperature. Then they are kept in water until they are saturated. The percentage water absorption of the sample is calculated from the difference between dry and saturated weight19.

  1. c)

    Apparent porosity: The apparent porosity is the percentage ratio between the pore volume and the apparent volume of the sample. It is similar to the procedure in the water absorption test and a calculation is done volumetrically19.

  1. d)

    Uniaxial compression strength: The stress value at the failure of a material (rock) under the effect of uniaxial compressive stress is called uniaxial compressive strength. This test is mainly used for strength classification and characterization of intact rock. Intact core (cylindrical) samples with a diameter of at least 54 mm are used. The height-to-diameter ratio should be between 2.5 and 3 20.

  1. e)

    Brazilian (indirect) tensile strength: Tensile strength tests can be performed in two ways, direct and indirect. Indirect tensile strength is the strength of disk-shaped rock samples under diametrical loading. Samples are prepared in the form of disks with a height-diameter ratio greater than 0.5. The prepared samples are placed between the loading tables of the hydraulic press with side surfaces and loaded at a constant speed. As a result of the loading, the failure should occur between 15 and 30 s20.

  1. f)

    Point load strength: Point load strength is an index value that is used to indirectly determine other strength parameters such as uniaxial compressive and tensile strength and classify rocks according to their strength. In addition to cylindrical core specimens, block, and irregularly shaped specimens can also be used for this test. The ratio of length to diameter of core specimens should be greater than 1. Breaking should be between 10 and 60 s19.

  1. g)

    Modulus of elasticity: The modulus of elasticity is the ratio of the axial stress to the increase in axial unit deformation by loading. Therefore, to determine the modulus of elasticity, the strain under uniaxial loading conditions must be measured20. The modulus of elasticity is usually associated with the pre-peak portion of the entire stress-strain curve. The modulus of elasticity is the positive slope of the rising portion of this curve. In this study, the modulus of elasticity was calculated as the average slopes of the more or less straight-line portion of the axial stress-axial strain curve.

  1. h)

    Shore hardness: The Shore hardness test measures the relative hardness of rocks in terms of the material’s elasticity. The Shore hardness of rocks is determined according to ISRM20 suggested methods. The minimum test specimen volume of 80 cm3 is prepared for each rock in this test.

  1. i)

    Bohme abrasion rate: The Bohme surface abrasion test measures the amount of abrasion on the material surface through friction. These tests are carried out according to TSE19. The abrasive material consists mainly of Al2O3 (crystalline corundum) at different grain sizes fed between the rotating disc and sample. The dimensions of the test specimen were 71 × 71 × 71 mm. After the test, average volume loss is measured.

Table 2 shows all rock properties’ upper and lower limits according to rock types.

Table 2 Upper and lower limits for all rock properties according to rock types.
Full size table

Figure 3 shows the distribution of rock properties for each rock type.

Fig. 3
figure 3

The distribution of rock properties for each rock type.

Full size image

In addition, detailed mineralogical-petrographic analyses were carried out to determine the rock types of the samples used in the study. Rock types were determined with the assistance of thin-section studies. The origins of the rocks were classified as sedimentary, metamorphic, or igneous by mineralogical-petrographic studies.

Data selection and transformation

A basic statistical analysis of the data was carried out in this study phase. All of the physical and mechanical tests mentioned above were performed on the samples collected in periods separately. Therefore, data for some rock properties that can be used for rock type prediction in the study are missing. Some PL, E, and BSA data were found to need to be completed. Table 3 shows the general statistical characteristics of the data. Figure 4 gives the histogram of the variables.

Table 3 General statistical characteristics of the data.
Full size table

As seen in Table 3, data on some parameters (PL, E, and BSA) in the data set for data mining in the study are missing. These data were completed before the data mining applications. In the data completion process, the parameter with missing data was tried to be predicted by various data mining algorithms with other parameters with complete data. For example, missing PL values were predicted from UVW, WA, AP, UCS, TS, and SH values. E and BSA values with other missing data were not used to predict PL values. A similar procedure was followed for the other parameters with missing data. In addition, the target attribute (Rock Type) was not used in the data completion phase to avoid the possibility of overlapping.

Missing PL values were completed using the Sequential Minimal Optimization for Regression (SMOreg) algorithm. SMOreg implements the support vector machine for regression. Random Tree (RTree) algorithm was used to complete the missing E and BSA data. The RTree algorithm is a modern approach to supervised learning for categorical or continuous targets. The algorithm uses classification or regression trees to make predictions when applied to new observations. RTree classifies the data for constructing a tree considering randomly chosen attributes at each node. These algorithms produced the results with the highest correlation coefficient. Table 4 shows the results obtained in the data completion studies.

Fig. 4
figure 4

Histogram of the variables.

Full size image

Several algorithms were tested in the data completion process. The success of these algorithms was determined based on three metrics: Correlation coefficient (R), mean absolute error (MAE), and root mean square error (RMSE). The correlation coefficient (R) is a statistical metric that measures the strength and direction of correlation between variables. Mean absolute error (MAE) is the average of the errors between the actual and predicted values. The root mean square error (RMSE) represents the square root of the mean square differences between predicted and actual results. The algorithms with the highest correlation and the lowest errors were found, and the missing data were predicted.

Table 4 Statistical metrics of data completion studies.
Full size table

As a result of these processes, the data set required for the study was generated. A source file was prepared for the data mining algorithms to be applied for rock type prediction.

Data mining

At this study stage, data mining algorithms were applied to the data set prepared by completing the missing data in some attributes. The data mining implementations in this study were carried out with the widely accepted, open-source WEKA software, one of the most complete tools in data mining. Studies based on rock type prediction were carried out. In data mining studies, the rock type was predicted using a total of 9 variables (attributes) of rocks. ZeroR, J48 Decision Tree (J48), k-Nearest Neighbor (kNN), Naive Bayes (NB), Random Forest (RF), and Support Vector Machine (SVM) algorithms were used for this purpose. These algorithms were preferred to provide the best classification and prediction results for the dataset.

The data set is usually divided into two groups: training and test data when applying algorithms in data mining. The model’s performance built with training data is checked with test data. Different test methods can be used, such as percentage split and cross-validation. The cross-validation method divides the data set into k parts. k-1 parts are used to build the model, and the model’s performance is tested with the remaining part. This process is repeated k times. In each repetition, different training and test data are generated. In this study, the cross-validation method, the most widely used test method, was applied. The data set was divided into ten parts. In each repetition, nine parts were used as training data, and the remaining part was used as test data.

The first algorithm applied in the study is the ZeroR algorithm, considered a basic algorithm. ZeroR algorithm is the most straightforward data mining algorithm. It classifies all data into a single type with the most members. The success obtained after the algorithm application can be considered the lowest success level. Any algorithm that gives worse results can be regarded as unsuccessful. Although ZeroR lacks predictive capability, it helps establish a baseline performance as a benchmark for other classification methods.

The alternative algorithm was a decision tree in this study. A decision tree algorithm is an algorithm dividing the data into classes. Originally C4.5, the algorithm was later rewritten as J48 for open-source use. A decision tree is built from top to bottom from a root node and involves partitioning the data into subsets containing (homogeneous) instances with similar values. The decision tree builds classification or regression models as a tree structure21.

The other algorithm applied to the data set was the kNN algorithm22. This algorithm uses similarity functions. It is related to the proximity of the point to be classified to the k nearest neighbors. In general, the nearness is determined by the Euclidean distance. For k = 1, the sample is assigned to the class of its nearest neighbor. For k = 3, a new element is classified by taking the closest 3 of the previously classified elements. The selection of the optimal value for k is best done by first examining the data.

Another algorithm for this study was the NB algorithm. NB algorithm is an algorithm that depends on the probability of the outcome. It is based on calculating the probability of each attribute affecting the outcome. A calculation can be mentioned as the probability of occurrence of subclasses of more than one class multiplied by the class probability. It is based on Bayes theorem23.

RF algorithm was another alternative algorithm. It is one of the supervised classification algorithms. It is used in both regression and classification problems. The algorithm aims to increase the classification value during the classification process by generating more than one decision tree. It combines the outputs from randomly generated decision trees and uses them in classification and regression processes. How many decision trees will be used to create a random forest is essential. Generally, the user determines the number of trees by trial and error24.

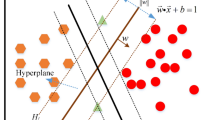
The last algorithm in this study was SVM25. The SVM algorithm was originally used to classify data and is one of the most influential and simple methods used in classification. The basis of this classification is to classify objects into two classes using some functions. For this process, two boundary lines (support vectors) are drawn close to each class and parallel to each other. Here, the support vectors with the largest interval between them, and these support vectors are brought closer to each other to produce a hyperplane. The aim is to determine the hyperplane that creates the most significant separation using iterative optimization.

Implementation of data mining algorithms

At this stage of the study, classification processes were performed using appropriate data mining algorithms in the data set. There are two main targets in this classification process. The first is to determine the algorithm that best represents all the data. The other is to assess the ability of the data mining algorithms to predict the desired parameter. It aims to increase the prediction ability’s success rate by applying various algorithms to the data set. The success rate is determined by the percentage of correctly classified data in the data set. No changes were made to the main settings of the algorithms in data mining applications. Considering only the success rate, some parameters were altered to obtain better results.

The first algorithm applied in modeling studies is the ZeroR algorithm. This algorithm produces a primary output in modeling studies. It is a crucial algorithm to evaluate other algorithms’ success and observe the increase in the correlation coefficient. The success of modeling studies in data mining can be measured by how far the success (correlation coefficient) of the ZeroR application is improved.

Other algorithms applied to the data set are J48 Decision Tree (J48), k-Nearest Neighbor (kNN), Naive Bayes (NB), Random Forest (RF), and Support Vector Machine (SVM) algorithms. In addition to the classification or prediction success, some statistics were used to determine the algorithm’s success. Kappa statistic, mean absolute error (MAE), and root mean square error (RMSE) values were used to evaluate the algorithm’s success. Table 5 shows the algorithms applied to the data set and the results obtained.

Table 5 Algorithms and success parameters used in data mining studies.
Full size table

As shown in Table 5, if the ZeroR algorithm results are considered the primary success, the results obtained from the other algorithms exceeded this success.

Performance evaluation of algorithms

In the performance evaluation of the algorithms, the confusion matrices were analyzed in the applications using cross-validation test methods. Figure 5 shows the confusion matrices obtained.

Fig. 5
figure 5

Confusion matrices of algorithms.

Full size image

In general, the confusion matrices show that the prediction ability of all algorithms except the ZeroR is acceptable for igneous and metamorphic rock types. In contrast, all the algorithms except SVM and RF for sedimentary rocks contain more errors. Consequently, SVM was the most successful prediction algorithm for all rock types. Subsequently, four different statistical metrics were evaluated to identify the performance of the data mining algorithms in the study. According to these metrics (R, Kappa statistic, MAE, and RMSE) given in Table 5, the SVM algorithm is the most successful in rock type prediction.

Results and evaluations

In this part of the study, the results of the algorithm applications were evaluated. The algorithm with the highest success rate (highest correlation coefficient, highest Kappa statistic, lowest error) was found in data mining applications for rock type prediction from physical and mechanical rock properties. According to the statistical metrics selected, the SVM algorithm was the most appropriate and successful for rock type prediction. According to the ZeroR application, which is considered the basis for the success rate, the prediction ability of the SVM algorithm is relatively high.

SVM is the most successful algorithm (R = 0.9565) in rock type prediction. With this algorithm, 88 out of 92 data were correctly predicted. There were only two incorrect predictions each for sedimentary and metamorphic rocks. All igneous rocks were predicted correctly. Figure 6 shows the success rate for the SVM algorithm in the actual and predicted rock type graph.

The performance of the data completion process was also evaluated in this part. Sensitivity analysis and AUC [area under the ROC (Receiver Operating Characteristic) curve] in the WEKA program was used for this evaluation. Sensitivity is the ratio of the number of correctly classified positive samples to the total number of positive samples. Receiver operating characteristic (ROC) analysis is a graphical approach used to analyze the performance of a classifier. The ROC curve is the true positive rate plotted against the false positive rate. The AUC measures the area under the entire ROC curve. These values range from 0 to 1. Rock types were predicted with the same algorithms and parameters as the data set before and after data completion. The sensitivity analysis and AUC values of the predictions are given in Table 6.

As seen in Table 6, data completion using SMOreg and RTree algorithms improved the performance of the algorithms (SVM and RF) used for rock type prediction, especially the AUC values.

Fig. 6
figure 6

Actual and predicted rock type for SVM.

Full size image
Table 6 Sensitivity and AUC values of the predictions before and after data completion.
Full size table

Conclusions

The prediction of rock type based on physical and mechanical properties using data mining algorithms was carried out in this study. A total of 92 rocks with different physical and mechanical properties were used in the prediction of the rock types by using data mining algorithms. Six different algorithms were used in this study.

Nine rock properties (UVW, WA, AP, UCS, TS, PL, E, SH, and BSA) were used to generate the dataset. Missing data for rock properties PL, E, and BSA were completed by data mining methods using other rock properties. SMOreg is the most appropriate algorithm for PL and RTree for E and BSA in data completion studies. The SMOreg algorithm succeeded at 0.902, while the RTree algorithm succeeded at 0.999 for both rock features. Sensitivity analysis and AUC values showed that data completion had a positive effect on the prediction of rock types.

The best algorithm for rock type prediction was SVM. The best result in the evaluation requires the correlation coefficient and Kappa statistic to be close to 1 and the error values to be close to 0. R, Kappa, MAE, and RMSE for the model developed with this algorithm were 0.9565, 0.9273, 0.0576, and 0.1725, respectively.

RF algorithm produced the closest results to the SVM algorithm. However, the correlation coefficient, Kappa statistic, and error values indicated that the SVM algorithm performed the best in rock type prediction.

This study showed that data mining methods can predict rock type from physical and mechanical properties. Rock type prediction can be reliable without labor-intensive mineralogical and petrographic analyses. This study was conducted on natural stones in general. Similar studies including different rock types and similar applications for larger data sets will contribute more to the literature.