Data-driven analysis of chemical graph of carbazole and diketopyrrolopyrrole

Abstract

Topological indices play a key role in molecular graph theory, consisting of mathematical tools that allocate numerical values to molecular structures. These indices are used to anticipate a variety of physicochemical, biological, and pharmacological properties of chemical compounds. This study performs a detailed statistical analysis of different topological indices, such as the First Zagreb index, scrutinizing its associations with other indices through regression modeling and correlation analysis. Research generates predictive models, including linear, quadratic, and cubic regression equations by using machine learning techniques. The results show that linear regression delivers the most accurate predictions, whereas the quadratic regression model improves the understanding of actual versus predicted values, improving the valuation of molecular properties. A using statistical evaluation of the selected topological indices involved computing essential metrics such as mean, median, variance, standard deviation, range, interquartile range (IQR), skewness, and kurtosis. These metrics expand our understanding of the allocation and adaptability of indices, confirming their robustness in molecular description and predictive modeling. Using a machine learning-based statistical method, the study increases the use of topological indices in cheminformatics, drug discovery, and materials science. These findings assistance the development of QSAR and QSPR models, supporting the critical role of statistical verification in molecular descriptor. This method promotes more accurate, data-driven strategies in computational chemistry and bioinformatics.

Introduction

Chemical graph theory is an interdisciplinary field that bridges chemistry with mathematical graph modeling. In this domain, topological indices serve as graph invariants, playing a crucial role in chemical and pharmaceutical sciences. These indices are particularly useful for predicting the physicochemical properties of organic compounds. Over the years, extensive research in chemical graph theory has introduced numerous topological indices.

Also referred to as graph parameters, topological indices are derived from vertex degrees and have diverse applications, making them valuable to both mathematicians and chemists. . Since H. Wiener introduced the Wiener index in 1947¹, nearly three thousand topological indices have been catalogued in chemical databases.

A topological index function is a graph invariant, representing the molecular structure’s topology and translating the molecular graph into a numerical representation. This value aids in predicting various physicochemical properties, like melting point, boiling point, and freezing point. In the modern pharmaceutical industry, conducting biological tests on chemical compounds necessitates a large financial investment, advanced laboratory facilities and high-tech equipment. This technique is both expensive and time intensive².

To overcome these challenges, pharmaceutical firms are actively seeking to explore cost-effective alternatives. A promising alternative involves analyzing chemical structure using topological indices, which can eliminate the need for costly equipment and extensive lab testing. This technique explores a more economical and time-efficient budget for studying chemical properties.

Topological indices are numerical tools in mathematical chemistry and cheminformatics. They aid in quantifying the molecular structure by translating its topology into numerical values. Topological indices are derived from molecular graph structure and serve as powerful tools in predicting biological, physicochemical, and pharmacological properties of compounds. The fundamental concept of topological indices is to represent molecular structure as numerical values while retaining their connectivity and structural essence. By leveraging topological indices, researchers can construct QSAR (Quantitative Structure Activity Relationship) models, which play a crucial role in drug discovery, materials science, and various chemical applications³.

One of the earliest and most well-known topological indices is the Zagreb index, first introduced by Gutman and Trinajstić in 1972. It has two main variants: the first Zagreb index $(\lambda _1)$ and the second Zagreb index $(\lambda _2)$. These indices are defined based on the degrees of vertices in a molecular graph. Over time, several modifications and extensions of the Zagreb indices have emerged, such as the third Zagreb index $(\lambda _3)$, the redefined Zagreb indices and the reduced Zagreb indices. These enhancements have shown improved predictive capabilities in various biological and chemical studies⁴.

Another important class of topological indices includes degree-based indices like the Augmented Zagreb Index (AZI) and the Atom-Bond Connectivity (ABC) index. The atom bound connectivity index by Estrada et al. (1998), is extensively used for estimating the stability of chemical compound and enthalpy of formation.Like wise augmented Zagreb index of AZI, an extension of the Zagreb indices, provides better correlation with thermodynamic properties and finds applications in nanotechnology and materials science⁵.

Recently, modified versions of topological indices have gained interest for to their enhanced accuracy and computational efficiency. These indices, such as the Redefined First Zagreb index $(R\lambda _1)$, Redefined Second Zagreb index $(R\lambda _2)$, and Redefined Third Zagreb index $(R\lambda _3)$, enhance molecular characterization by providing omproved discriminative capabilities. Research has shown that these indices can surpass traditional ones in QSAR/QSPR modeling, making them valuable tools in computational chemistry and pharmaceutical research⁶.

Topological indices are extensively utilized in various scientific fields because of their broad range of applications. In drug discovery, these indices ad in predicting the biological activity of pharmaceutical compounds, facilitating the optimization of molecular properties to improve efficacy while reducing toxicity.Researchers may quickly identify possible drug candidates by including topological indices into machine learning algorithms. This effectively decreases the time as well as expenses related with experimental drug screening. These indices are also vital when exploring protein-ligand interactions, helping with the discovery of new inhibitors and drugs.

Topological indices have significance in materials science and nanotechnology in alongside drugs.The development of polymers and nanomaterials requires them because they allow for easier to predict significant material qualities including stability, reactivity, and electrical activity. These indices are employed in scientists to alter structural properties for particular uses, like advanced composites, conductive polymers, and high-performance coatings. Topological indicators also aid in the growth of eco-friendly materials by guiding the creation of biodegradable, sustainable compounds with specific uses.

Topological indices, that offer insight into the structure and function of chemical compound, are important instruments in mathematical chemistry.These indices are expected to have a substantial contribution to future finds in materials science, bioinformatics, and drug discovery with regular update improvements and enhancements. The Predictive modelling and molecular design could advance further with the integration of topological indices with machine learning and artificial intelligence⁷.

Preliminary framework and methodology

A graph with the vertex set V(G) and edge set E(G), where edges denote connections between vertices, is called graph and denote $G =(V(G), E(G))$. The number of edges |E(G) determines the size of G, whereas the number of |V(G)| determines its order. The degree of a vertex $u\in V(G)$ is the number of edges incident to it, and it is represented as deg(u) or $d_u$. A graph is irregular if all its vertices have distinct degrees, and regular if all vertices have the same degree.

The first Zagreb index $\lambda _1(G)$ and the second Zagreb index $\lambda _2(G)$ is defined as follows:

$$\begin{aligned} \lambda _1(G)= & \sum _{u,v \in E(G)} (d_u + d_v) \end{aligned}$$

(1)

$$\begin{aligned} \lambda _2(G)= & \sum _{u,v \in E(G)} (d_u \cdot d_v) \end{aligned}$$

(2)

The Zagreb indices $\lambda _1(G)$ and $\lambda _2(G)$ were first introduced by Gutman and Trinajstić in 1972. These indices appeared in certain approximate expressions for the total $\pi$- electron energy⁸. For a detailed discussion on the mathematical theory and chemical applications of the Zagreb indices , refer to^{9,10,11,12,13,14,15,16,17}

$$\begin{aligned} \lambda _3(G) = \sum _{uv \in E(G)} (d_u + d_v)^2 \end{aligned}$$

(3)

Ediz¹⁸ introduced the reduced first Zagreb index represented as follows,

$$\begin{aligned} R\lambda _1(G) = \sum _{v \in V(G)} (d_v - 1)^2 \end{aligned}$$

(4)

This index is a modified version of the first Zagreb index , designed to explore the relationship between graph structure and molecular properties, particular in the field of chemical graph theory¹⁹.

$$\begin{aligned} R\lambda _2(G) = \sum _{uv \in E(G)} (d_G(u) - 1)(d_G(v) - 1) \end{aligned}$$

(5)

Furtula, Graovac, and Vukićević (2010) presented the Augmented Zagreb Index as an enhancement of the conventional Zagreb indices, providing in QSAR/QSPR research with a higher connection with molecular attributes as stability, enthalpy of formation, and boiling temperatures²⁰.

$$\begin{aligned} AZI(G) = \sum _{uv \in E(G)} \left( \frac{d_u \cdot d_v}{d_u + d_v - 2} \right) ^3 \end{aligned}$$

(6)

The Redefined Zagreb Indices were developed as adaptations of the classic Zagreb indices to better reflect the structural features of molecular graphs. The degree-based adjustments that these indices include help in the prediction of molecule stability and physicochemical features. When it involves QSAR/QSPR investigations, the Redefined First, Second, and Third Zagreb Indices provide different approaches to molecular structure analysis²¹.

$$\begin{aligned} ReZG_1(G)= & \sum _{uv \in E(G)} \frac{d_u + d_v}{d_u d_v} \end{aligned}$$

(7)

$$\begin{aligned} ReZG_2(G)= & \sum _{uv \in E(G)} \frac{d_u \cdot d_v}{d_u + d_v} \end{aligned}$$

(8)

$$\begin{aligned} ReZG_3(G)= & \sum _{uv \in E(G)} (d_u \cdot d_v) \cdot (d_u + d_v) \end{aligned}$$

(9)

Description of graph of carbazole and diketopyrrolopyrrole $(Cz-Dpp)$

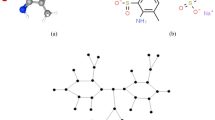
This section outline the theoretical features of Carbazole and Diketopyrrolopyrrole $(Cz-Dpp)$ . In Table 1 and Table 2, the vertices of graph G classified based on to their degrees, where n shows the parameter dominating the vertex count. The corresponding Fig. 1 below illustrates these classifications visually (Fig. 2).

Table 1 Partition the graph G according to the vertex degrees.

Table 2 Vertex-based partition of graph $G$ based on vertex degrees.

Fig. 1

Carbazole and diketopyrrolopyrrole $(Cz-Dpp)$.

Fig. 2

Carbazole and diketopyrrolopyrrole (Cz - Dpp) structures, with oxygen atoms labeled O1 to O5.

Results and discussion of carbazole and diketopyrrolopyrrole $(Cz-Dpp)$

This article analyses various kinds of graph indices, with particular concentration on the Zagreb index family, while carefully analysing their distinct characteristics and mathematical properties. For the Carbazole and Diketopyrrolopyrrole (Cz-Dpp), we have exact formulas for these indices. The computational methodology utilizes edge and vertex partitioning, complemented by advanced data analysis techniques, degree enumeration, and summation methods.The molecular graph of Carbazole and Diketopyrrolopyrrole $(Cz-Dpp)$ consists of $38n + 27$ edges and $31n +49$. The computational methodology employs edge and vertex partitioning, advanced data analysis techniques, degree enumeration, and summation methods.

Theorem 1

Let $G$ be the Carbazole and Diketopyrrolopyrrole Graph $(Cz-Dpp)$. Then, the first Zagreb index is given by:

$$\begin{aligned} \lambda _1(G) = 194n + 126. \end{aligned}$$

Proof

In the network of Carbazole and Diketopyrrolopyrrole with $38n + 27$ edges, the first Zagreb index of the graph $G$ can be decomposed into three disjoint edge sets: $E_1(G)$, $E_2(G)$, and $E_3(G)$ Table 1. These sets represent different edge configurations based on the degrees of their endpoints. Specifically:

• $E_1(G)$ consists of $6n + 14$ edges where $d_u = 2$ and $d_v = 2$.

• $E_2(G)$ consists of $22n + 8$ edges where $d_u = 2$ and $d_v = 3$.

• $E_3(G)$ consists of $10n + 5$ edges where $d_u = 3$ and $d_v = 3$.

The first Zagreb index is defined in Eq. (1) as:

$$\begin{aligned} \lambda _1(G) = \sum _{uv \in E(G)} (d_u + d_v). \end{aligned}$$

(10)

$$\begin{aligned} \lambda _1(G)&= |E_1| \cdot (d_u + d_v) + |E_2| \cdot (d_u + d_v) + |E_3| \cdot (d_u + d_v) \\&= |E_{(2,2)}| \cdot (2 + 2) + |E_{(2,3)}| \cdot (2 + 3) + |E_{(3,3)}| \cdot (3 + 3).\\ \lambda _1(G)&= (6n + 14) \cdot (2+2) + (22n + 8) \cdot (2+3) + (10n + 5) \cdot (3+3) \\&= (6n + 14) \cdot 4 + (22n + 8) \cdot 5 + (10n + 5) \cdot 6 \\&= 24n + 56 + 110n + 40 + 60n + 30. \end{aligned}$$

Therefore:

$$\begin{aligned} \lambda _1(G) = 194n + 126. \end{aligned}$$

(11)

$\square$

Theorem 2

Let $G$ be the Carbazole and Diketopyrrolopyrrole Graph $(Cz-Dpp)$. Then the second Zagreb index is given by:

$$\begin{aligned} \lambda _2(G) = 246\alpha + 149. \end{aligned}$$

Proof

The explanation of the second Zagreb index in Eq. (2) is as follows:

$$\begin{aligned} \lambda _2(G)= & \sum _{uv \in E(G)} (d_u \cdot d_v). \end{aligned}$$

(12)

$$\begin{aligned} \lambda _2(G)= & |E_1| \cdot (d_u \cdot d_v) + |E_2| \cdot (d_u \cdot d_v) + |E_3| \cdot (d_u \cdot d_v). \end{aligned}$$

(13)

$$\begin{aligned} \lambda _2(G)= & |E_{(2,2)}| \cdot (2 \times 2) + |E_{(2,3)}| \cdot (2 \times 3) + |E_{(3,3)}| \cdot (3 \times 3). \end{aligned}$$

(14)

$$\begin{aligned} \lambda _2(G)= & (6n + 14) \cdot 4 + (22n + 8) \cdot 6 + (10n + 5) \cdot 9. \end{aligned}$$

(15)

$$\begin{aligned} \lambda _2(G)&= 24n + 56 + 132n + 48 + 90n + 45 \\&= 246n + 149. \end{aligned}$$

There fore:

$$\begin{aligned} \lambda _2(G) = 246n + 149. \end{aligned}$$

(16)

$\square$

Theorem 3

Let G be the Carbazole and Diketopyrrolopyrrole Graph $(Cz-Dpp)$. Then the third Zagreb index $\lambda _3(G) = 1006n + 604$.

Proof

The explanation of the third Zagreb index in Eq. (2) is as follows:

$$\begin{aligned} \lambda _3(G) = \sum _{uv \in E(G)} (d_u + d_v)^2. \end{aligned}$$

Expanding the equation based on edge classification:

$$\begin{aligned} \lambda _3(G)&= |E_1| \times (d_u + d_v)^2 + |E_2| \times (d_u + d_v)^2 + |E_3| \times (d_u + d_v)^2 \\&= |E_{(2,2)}| \times (d_u + d_v)^2 +| E_{(2,3)}| \times (d_u + d_v)^2 + |E_{(3,3)}| \times (d_u + d_v)^2 \\&= (6n + 14) \times (2+2)^2 + (22n + 8) \times (2+3)^2 + (10n + 5) \times (3+3)^2.\\&= (6n + 14) \times 16 + (22n + 8) \times 25 + (10n + 5) \times 36 \\&= 96n + 224 + 550n + 200 + 360n + 180. \end{aligned}$$

There fore:

$$\begin{aligned} \lambda _3(G) = 1006n + 604. \end{aligned}$$

$\square$

Theorem 4

Let $G$ be the Carbazole and Diketopyrrolopyrrole Graph ($Cz{-}Dpp$). Then, the reduced first Zagreb index is given by:

$$\begin{aligned} R\lambda _1(G) = 73n + 109. \end{aligned}$$

Proof

The reduced zagreb index in Eq. (4) can be defined as follows:

$$\begin{aligned} R\lambda _1(G)= & \sum _{v \in V(G)} (d_v - 1)^2.\\ R\lambda _1(G)= & |v_1| \times (d_v - 1)^2 + |v_2| \times (d_v - 1)^2.\\= & |d_{v1}| \times (2-1)^2 + |d_{v2}| \times (3-1)^2.\\= & (17n + 29) \times 1^2 + (14n + 20) \times 2^2 \\= & (17n + 29) \times 1 + (14n + 20) \times 4\\= & 17n + 29 + 56n + 80. \end{aligned}$$

There fore:

$$\begin{aligned} R\lambda _1(G) = 73n + 109. \end{aligned}$$

$\square$

Theorem 5

Let $G$ be the Carbazole and Diketopyrrolopyrrole Graph ($Cz{-}Dpp$). Then, the reduced second Zagreb index is given by:

$$\begin{aligned} R\lambda _2(G) = 90n + 50. \end{aligned}$$

Proof

In Eq. (5), the reduced second Zagreb index is defined as:

$$\begin{aligned} R\lambda _2(G) = \sum _{uv \in E(G)} (d_G(u) - 1)(d_G(v) - 1). \end{aligned}$$

This index currently largely focused on the degree distribution of network vertices, but it used to concentrate on the geometric parts of topological indices. It provides a structural measure through the product of reduced degree values $(d_G(u)-1)$ and $(d_G(v)-1)$ for each edge $uv$ in the graph.

$$\begin{aligned} R\lambda _2(G)= & |E_1| \times (d_G(u) - 1)(d_G(v) - 1) + |E_2| \times (d_G(u) - 1)(d_G(v) - 1) + |E_3| \times (d_G(u) - 1)(d_G(v) - 1).\\ R\lambda _2(G)= & |E_{(2,2)}| \times (1 \times 1) + |E_{(2,3)}| \times (1 \times 2) + |E_{(3,3)}| \times (2 \times 2).\\ R\lambda _2(G)= & (6n + 14) \times 1 + (22n + 8) \times 2 + (10n + 5) \times 4.\\= & 6n + 14 + 44n + 16 + 40n + 20. \end{aligned}$$

There fore:

$$\begin{aligned} R\lambda _2(G) = 90n + 50. \end{aligned}$$

$\square$

Theorem 6

Let $G$ be the Carbazole and Diketopyrrolopyrrole Graph ($Cz{-}Dpp$). Then, the augmented Zagreb index is given by:

$$\begin{aligned} AZI(G) = 337.90625n + 232.9531. \end{aligned}$$

Proof

In Eq. (6), the augmented Zagreb index is defined as:

$$\begin{aligned} AZI(G) = \sum _{uv \in E(G)} \left( \frac{d_u \cdot d_v}{d_u + d_v - 2} \right) ^3. \end{aligned}$$

This index provides a refined structural measure of molecular graphs by incorporating vertex degrees into a non-linear cubic form.

$$\begin{aligned} AZI(G)= & |E_1| \times \left( \frac{d_u \cdot d_v}{d_u + d_v - 2} \right) ^3 + |E_2| \times \left( \frac{d_u \cdot d_v}{d_u + d_v - 2} \right) ^3 + |E_3| \times \left( \frac{d_u \cdot d_v}{d_u + d_v - 2} \right) ^3.\\ AZI(G)= & |E_{(2,2)}| \times \left( \frac{2 \cdot 2}{2 + 2 - 2} \right) ^3 + |E_{(2,3)}| \times \left( \frac{2 \cdot 3}{2 + 3 - 2} \right) ^3 +| E_{(3,3)}| \times \left( \frac{3 \cdot 3}{3 + 3 - 2} \right) ^3.\\ AZI(G)= & (6n + 14) \times 8 + (22n + 8) \times 8 + (10n + 5) \times 11.391.\\= & 8(6n + 14) + 8(22n + 8) + 11.391(10n + 5) \\= & 48n + 112 + 176n + 64 + 113.91n + 56.955. \end{aligned}$$

There fore:

$$\begin{aligned} AZI(G) = 337.90625n + 232.9531. \end{aligned}$$

$\square$

Theorem 7

Let $G$ be the carbazole and diketopyrrolopyrrole Graph $(Cz-Dpp)$. Then, the redefined first Zagreb index is given by:

$$\begin{aligned} ReZG_1(G) = 31n + 24. \end{aligned}$$

Proof

Ranjini et al.²² and Usha et al.²³ were the first to introduced the redefined Zagreb indices of graph (G) as fundamental degree-based topological indices.

$$\begin{aligned} ReZG_1(G)= & \sum _{uv \in E(G)} \frac{d_u + d_v}{d_u d_v},\\ ReZG_1(G)= & |E_{1}| \times \frac{d_u + d_v}{d_u d_v} + |E_{2}| \times \frac{d_u + d_v}{d_u d_v} + |E_{3}| \times \frac{d_u + d_v}{d_u d_v} \\ ReZG_1(G)= & |E_{(2,2)}| \times \frac{2+2}{2 \times 2} + |E_{(2,3)}| \times \frac{2+3}{2 \times 3} + |E_{(3,3)}| \times \frac{3+3}{3 \times 3} \\= & | E_{(2,2)}| \times \frac{4}{4} +| E_{(2,3)} | \times \frac{5}{6} + |E_{(3,3)} |\times \frac{6}{9}.\\ ReZG_1(G)= & \left( 6n + 14\right) \times 1 + \left( 22n + 8\right) \times \frac{5}{6} + \left( 10n + 5\right) \times \frac{2}{3} \\= & (6n + 14) + \frac{5}{3} (11n + 4) + \frac{2}{3} (10n + 5) \\= & 6n + 14 + \frac{55n + 20}{3} + \frac{20n + 10}{3} \\= & \frac{18n + 42}{3} + \frac{55n + 20}{3} + \frac{20n + 10}{3} \\= & \frac{93n + 72}{3} \\= & 31n + 24. \end{aligned}$$

There fore

$$\begin{aligned} ReZG_1(G) = 31n + 24. \end{aligned}$$

$\square$

Theorem 8

Let $G$ be the carbazole and diketopyrrolopyrrole Graph $(Cz-Dpp)$. Then, the redefined second Zagreb index is given by:

$$\begin{aligned} ReZG_2(G) = 47.4n + 31.1. \end{aligned}$$

Proof

The redefined second Zagreb index In Eq. (8), is formally defined as:

$$\begin{aligned} ReZG_2(G)= & \sum _{uv \in E(G)} \frac{d_u \cdot d_v}{d_u + d_v},\\ ReZG_2(G)= & |E_{1}| \times \frac{d_u \cdot d_v}{d_u + d_v} + |E_{2}| \times \frac{d_u \cdot d_v}{d_u + d_v} + |E_{3}| \times \frac{d_u \cdot d_v}{d_u + d_v} \\ ReZG_2(G)= & | E_{(2,2)}| \times \frac{2\times 2}{2 + 2} + |E_{(2,3)}| \times \frac{2\times 3}{2 + 3} + | E_{(3,3)}| \times \frac{3\times 3}{3 + 3} \\= & |E_{(2,2)}| \times \frac{4}{4} + |E_{(2,3)}| \times \frac{6}{5} + |E_{(3,3)}| \times \frac{9}{6}.\\ ReZG_2(G)= & \left( 6n + 14\right) \times 1 + \left( 22n + 8\right) \times \frac{6}{5} + \left( 10n + 5\right) \times \frac{3}{2} \\= & (6n + 14) + \frac{132n+ 48}{5} + \frac{30n + 15}{2} \\= & \frac{474n }{10} + \frac{311}{10} \\ ReZG_2(G)= & 47.4n + 31.1. \end{aligned}$$

There fore

$$\begin{aligned} ReZG_2(G) = 31n + 24. \end{aligned}$$

$\square$

Theorem 9

Let $G$ be the carbazole and diketopyrrolopyrrole Graph $(Cz-Dpp)$. Then, the redefined third Zagreb index is given by:

$$\begin{aligned} ReZG_3(G) = 1296n + 734. \end{aligned}$$

Proof

In Eq. (9), the redefined third Zagreb index is formally defined as:

$$\begin{aligned} ReZG_3(G) = \sum _{uv \in E(G)} (d_u \cdot d_v) \cdot (d_u + d_v), \end{aligned}$$

where $d_u$ and $d_v$ represent the degrees of the vertices $u$ and $v$, respectively, and the summation runs over all edges $uv \in E(G)$.

$$\begin{aligned} ReZG_3(G)= & |E_{1}| \times (d_u \cdot d_v) \cdot (d_u + d_v) + |E_{2}| \times (d_u \cdot d_v) \cdot (d_u + d_v) + |E_{3}| \times (d_u \cdot d_v) \cdot (d_u + d_v) \\= & |E_{(2,2)}| \times (2 \cdot 2) \cdot (2 + 2) + |E_{(2,3)}| \times (2 \cdot 3) \cdot (2 + 3) \\ & \quad + |E_{(3,3)}| \times (3 \cdot 3) \cdot (3 + 3) \\= & |E_{(2,2)}| \times (4 \times 4) + |E_{(2,3)}| \times (6 \times 5) + |E_{(3,3)}| \times (9 \times 6).\\ ReZG_3(G)= & (6n + 14) \times 16 + (22n + 8) \times 30 + (10n + 5) \times 54 \\= & 16(6n + 14) + 30(22n + 8) + 54(10n + 5) \\= & 96n + 224 + 660n + 240 + 540n + 270 \\= & (96n + 660n + 540n) + (224 + 240 + 270) \\= & 1296n + 734. \end{aligned}$$

There fore

$$\begin{aligned} ReZG_3(G) = 1296n + 734. \end{aligned}$$

$\square$

Linear regression equation of carbazole and diketopyrrolopyrrole (Cz-Dpp)

This section presents linear regression models that establish relationships between various topological indices and the parameter $\lambda _1(G)$. These equations have been formulated through regression-based machine learning models implemented in Python within a Jupyter Notebook environment. Each regression model was constructed using a single topological index as the independent variable (i.e., univariate regression), with no combination of multiple indices used within a single model. The models achieve a perfect match and offer predictive insight into the behavior of several indices. The coefficient of determination is ($R^2 = 1.000000$).

According to the results, indices like $\lambda _2(G)$, $\lambda _3(G)$, $R\lambda _1(G)$, $R\lambda _2(G)$, AZI, and modified Zagreb indices ($ReZG_1, ReZG_2, ReZG_3$) can be represented as linear functions of $\lambda _1(G)$. The regression equations that correspond to this are provided below:

$$\begin{aligned} \lambda _2(G)&= 1.268041 \cdot \lambda _1(G) - 10.773196 \quad \\ \lambda _3(G)&= 5.185567 \cdot \lambda _1(G) - 49.381443 \quad \\ R\lambda _1(G)&= 0.376289 \cdot \lambda _1(G) + 61.587629 \quad \\ R\lambda _2(G)&= 0.463918 \cdot \lambda _1(G)- 8.453608 \quad \\ AZI&= 1.741785 \cdot \lambda _1(G) + 13.488216 \quad \\ ReZG_1(G)&= 0.159794 \cdot \lambda _1(G) + 3.865979 \quad \\ ReZG_2(G)&= 0.244330 \cdot \lambda _1(G) + 0.314433 \quad \\ ReZG_3(G)&= 6.680412 \cdot \lambda _1(G) - 107.731959 \quad \end{aligned}$$

Strong linear correlations found by machine learning-driven regression analysis are shown by these equations, demonstrating the importance of computational methods in topological index research. The use of univariate models simplifies interpretation while still preserving predictive power.

Methodology and modeling

We have focused on the First Zagreb Index as the sole independent variable to construct regression models of linear, quadratic, and cubic forms. These models were developed to explore the predictive power of this index in a univariate regression framework. The dataset comprises 50 systematically generated molecular structures, designed to cover a broad range of topological variations. For clarity and brevity, only the first 10 data points are displayed in the tables, while the full dataset was utilized in model training and validation.

To assess the generalizability of the models, we performed k-fold cross-validation with $k = 50$, ensuring that each data point was used for validation at least once. Performance evaluation was conducted using key error metrics, including Mean Absolute Error (MAE), Mean Squared Error (MSE), and Root Mean Squared Error (RMSE). All regression models–linear, quadratic, and cubic–demonstrated $R^2$ values of approximately 0.9997, 0.9998, and 0.9996, respectively. These high $R^2$ values indicate an almost perfect fit to the data; however, we acknowledge that such results may reflect overfitting, especially due to the controlled nature of the systematically generated dataset. To address this, the manuscript clarifies that while these values are statistically impressive, they should be interpreted with caution. The inclusion of various error metrics, along with the cross-validation procedure, provides a more comprehensive evaluation of the model’s performance and helps mitigate the risk of overfitting.

Critical analysis of results and graphs

In our study, we are not treating the topological indices as purely experimental or measured values in the traditional sense. Rather, we employed a regression-based modeling framework where certain easily computable topological indices are used as predictors (independent variables) to estimate or predict other, often more complex or computationally intensive indices as targets (dependent variables). This modeling approach is inspired by quantitative structure-activity relationship (QSAR) techniques, where known descriptors are used to predict unknown or difficult-to-obtain values. Therefore, the terms “actual” and “predicted” in our tables refer to the values obtained from direct computation (actual) versus those estimated by our machine learning or regression models (predicted).

Actual versus predicted value comparisons

The First Zagreb index was used as the independent variable to develop regression models–linear, quadratic, and cubic–for predicting other topological indices. The predicted values were obtained by inserting the First Zagreb values into these regression equations, while the actual values were directly computed from the molecular graphs. This approach allowed us to assess which regression model best fits the data by comparing error metrics such as MSE, RMSE, and MAE. The objective was to examine how effectively one descriptor can estimate others, following principles commonly applied in QSAR-type analyses.

Quadratic regression analysis of topological indices

For various topological indices, the quadratic regression equation for $\lambda _1(G)$ demonstrates strong mathematical relationships. The downward quadratic trend of the indices $\lambda _2(G)$ and $\lambda _3(G)$ shows a non linear dependent on $\lambda _1(G)$. Similarly, the reduced Zagreb indices $R\lambda _1(G)$ and $R\lambda _2(G)$ have smaller coefficients but also follow quadratic models. Additionally, the AZI index follows a quadratic pattern. In contrast, the redefined Zagreb indices $\text {ReZG}_1(G)$, $\text {ReZG}_2(G)$, and $\text {ReZG}_3(G)$ show quadratic features, with $\text {ReZG}_1(G)$ showing a strictly linear variance. TThese regression models offer an accurate analytical instrument for investigating chemical graph theory’s structural features. In each case, the perfect fit of the quadratic regression models to the data is verified by the determination coefficient ($R^2 = 0.9990$). This ensures both accuracy and reliability in the predicted values. However, a slight discrepancy arises when comparing the predicted values with actual computed values. While minimal, this deviation underscores the limitations of the regression model in attaining absolute numerical precision–potentially due to rounding effects or inherent approximations within the dataset.

Quadratic regression equation of carbazole and diketopyrrolopyrrole (Cz-Dpp)

$$\begin{aligned} \lambda _2(G)&= -3E-18 \lambda _1(G)^2 + 1.268041 \lambda _1(G) - 10.773196 \quad \\ \lambda _3(G)&= -3E-17 \lambda _1(G)^2 + 5.185567 \lambda _1(G) - 49.381443 \quad \\ R\lambda _1(G)&= 2E-18 \lambda _1(G)^2 + 0.376289 \lambda _1(G) + 61.587629 \quad \\ R\lambda _2(G)&= 1E-18 \lambda _1(G)^2 + 0.463918 \lambda _1(G) - 8.453608 \quad \\ \text {AZI}&= -6E-17 \lambda _1(G)^2 + 1.741785 \lambda _1(G) + 13.488216 \quad \\ \text {ReZG}_1(G)&= 0\lambda _1(G)^2 + 0.1598\lambda _1(G) + 3.866 \quad \\ \text {ReZG}_2(G)&= -4E-18 \lambda _1(G)^2 + 0.244330 \lambda _1(G) + 0.314433 \quad \\ \text {ReZG}_3(G)&= -2E-16 \lambda _1(G)^2 + 6.680412 \lambda _1(G) - 107.731959 \quad \end{aligned}$$

Prediction accuracy and cross validation analysis of $\lambda _2(G)$

Table 3 presents a comparison between the actual and predicted values of the Second Zagreb index. The predicted values are derived from a computational model, showing minimal errors in each case. These small error margins highlight the high accuracy of the predictive approach. Additionally, cross-validation error metrics–such as MAE, MSE, and RMSE, as shown in Table 4 confirm the model’s reliability, as the errors remain consistently low, demonstrating both the robustness and precision of the predictions. To further enhance understanding, these results have also been graphically illustrated in Fig. 3, providing a clearer visualization of the comparison and model precision. The equation for the Second Zagreb index prediction is given by:

$$\begin{aligned} \lambda _2(G) = -3E-18 \lambda _1(G)^2 + 1.268041 \lambda _1(G) - 10.773196 \end{aligned}$$

Table 3 Comparison of actual value and predicted value of $\lambda _2(G)$ for different $(\text {Cz-Dpp})$ structures.

Table 4 Cross-validation errors for the $\lambda _2(G)$ Index.

Fig. 3

Visual representation of actual value (x) and predicted value (Y) of $\lambda _2(G)$ for various $(Cz-Dpp)$ Structures.

Prediction accuracy and cross validation analysis of $\lambda _3(G)$

Table 5 compares the actual and predicted values for $\lambda _3(G)$.The predicted values are generated by a computational model, and the error margins are minimal, show the model’s high accuracy. Furthermore, cross-validation error metrics in Table 6 further support the model’s reliability, showing consistently low error values. For a clearer visual representation, these results are also depicted in Fig. 4, highlighting the precision of the model.The equation for the third Zagreb index prediction is given by:

$$\begin{aligned} \lambda _3(G) = -3E-17 \lambda _1(G)^2 + 5.185567 \lambda _1(G) - 49.381443 \end{aligned}$$

Table 5 Comparison of actual value and predicted value of $\lambda _3(G)$ for different $(Cz\text {-}Dpp)$ structures.

Table 6 Cross validation errors for the $\lambda _3(G)$ index.

Fig. 4

Visual representation of actual value (x) and predicted value (Y) of $\lambda _3(G)$ for various $(Cz-Dpp)$ structures.

Prediction accuracy and cross validation analysis of $R\lambda _1(G)$

Table 7 presents a comparison between the actual and predicted values of the reduced first Zagreb index. The predicted values are derived from a computational model, showing minimal errors in each case. These small error margins highlight the high accuracy of the predictive approach. Additionally, cross-validation error metrics–such as MAE, MSE, and RMSE, as shown in Table 8 confirm the model’s reliability, as the errors remain consistently low, demonstrating both the robustness and precision of the predictions. To further enhance understanding, these results have also been graphically illustrated in Fig. 5, providing a clearer visualization of the comparison and model precision. The equation for the reduced first Zagreb index prediction is given by:

$$\begin{aligned} R\lambda _1(G) = 2E-18 \lambda _1(G)^2 + 0.376289 \lambda _1(G) + 61.587629 \quad \end{aligned}$$

Table 7 Comparison of actual and predicted values of $R\lambda _1(G)$ for different $(Cz\text {-}Dpp)$ structures.

Table 8 Cross validation errors for the $R\lambda _1(G)$ index.

Fig. 5

Visual representation of actual value (x) and predicted value (Y) of $R\lambda _1(G)$ for various $(Cz-Dpp)$ structures.

Prediction accuracy and cross validation analysis of $R\lambda _2(G)$

Table 9 compares the actual and predicted values for $R\lambda _2(G)$.The predicted values are generated by a computational model, and the error margins are minimal, show the model’s high accuracy. Furthermore, cross-validation error metrics in Table 10 further support the model’s reliability, showing consistently low error values. For a clearer visual representation, these results are also depicted in Fig. 6, highlighting the precision of the model. The equation for the reduced second Zagreb index prediction is given by:

$$\begin{aligned} R\lambda _2(G) = 1E-18 \lambda _1(G)^2 + 0.463918 \lambda _1(G) - 8.453608 \quad \end{aligned}$$

Table 9 Comparison of actual value and predicted value of $R\lambda _2(G)$ for different $(Cz\text {-}Dpp)$ structures.

Table 10 Cross-validation errors for the $R\lambda _2(G)$ index.

Fig. 6

Visual representation of actual value (x) and predicted value (Y) of $R\lambda _2(G)$ for various $(Cz-Dpp)$ structures.

Prediction accuracy and cross validation analysis of AZI(G)

Table 11 provides a comparison of the actual and predicted values for the augmented Zagreb index. A computational model is used to calculate the expected values, which in every instance exhibit negligible errors. These small error margins highlight the high accuracy of the predictive approach. Furthermore, cross-validation error metrics–such as MAE, MSE, and RMSE, as shown in Table 12 confirm the model’s reliability, as the errors remain consistently low, demonstrating both the robustness and precision of the predictions. To further enhance understanding, these results have also been graphically illustrated in Fig. 7, providing a clearer visualization of the comparison and model precision. The equation for the Augmented Zagreb Index prediction is given by:

$$\begin{aligned} \text {AZI} = -6E-17 \lambda _1(G)^2 + 1.741785 \lambda _1(G) + 13.488216 \quad \end{aligned}$$

Table 11 Comparison of actual value and predicted value of AZI(G) for different $(Cz\text {-}Dpp)$ structures.

Table 12 Cross validation errors for the AZI index.

Fig. 7

Visual representation of actual value (x) and predicted value (Y) of AZI(G) for various $(Cz-Dpp)$ structures.

Prediction accuracy and cross validation analysis of $ReZG_1(G)$

Table 13 compares the actual and predicted values for the redefined first Zagreb index.The predicted values are generated by a computational model, and the error margins are minimal, show the model’s high accuracy. Furthermore, cross-validation error metrics in Table 14 further support the model’s reliability, showing consistently low error values. For a clearer visual representation, these results are also depicted in Fig. 8, highlighting the precision of the model. The equation for the Redefined first Zagreb Indices prediction is given by:

$$\begin{aligned} \text {ReZG}_1(G) = 0\lambda _1(G)^2 + 0.1598\lambda _1(G) + 3.866 \end{aligned}$$

Table 13 Comparison of actual value and predicted value of $ReZG_1(G)$ for different $(Cz\text {-}Dpp)$ structures.

Table 14 Cross validation errors for the $ReZG_1(G)$ index.

Fig. 8

Visual representation of actual value (x) and predicted value (Y) of $ReZG_1(G)$ for various $(Cz-Dpp)$ structures.

Prediction accuracy and cross validation analysis of $ReZG_2(G)$

Table 15 provides a comparison of the actual and predicted values for the redefined second Zagreb index. A computational model is used to calculate the expected values, which in every instance exhibit negligible errors. These small error margins highlight the high accuracy of the predictive approach. Furthermore, cross-validation error metrics–such as MAE, MSE, and RMSE, as shown in Table 16 confirm the model’s reliability, as the errors remain consistently low, demonstrating both the robustness and precision of the predictions. To further enhance understanding, these results have also been graphically illustrated in Fig. 9, providing a clearer visualization of the comparison and model precision. The equation for the Redefined second Zagreb Indices prediction is given by:

$$\begin{aligned} \text {ReZG}_2(G) = -4E-18 \lambda _1(G)^2 + 0.244330 \lambda _1(G) + 0.314433 \quad \end{aligned}$$

Table 15 Comparison of actual value and predicted value of $ReZG_2(G)$ for different $(Cz-Dpp)$ structures.

Table 16 Cross validation errors for the $ReZG_2(G)$ index.

Fig. 9

Visual representation of actual value (x) and predicted value (Y) of $ReZG_2(G)$ for various $(Cz-Dpp)$ structures.

Prediction accuracy and cross validation analysis of $ReZG_3(G)$

Table 17 provides a comparison of the actual and predicted values for the redefined third Zagreb index. A computational model is used to calculate the expected values, which in every instance exhibit negligible errors. These small error margins highlight the high accuracy of the predictive approach. Furthermore, cross-validation error metrics–such as MAE, MSE, and RMSE, as shown in Table 18 confirm the model’s reliability, as the errors remain consistently low, demonstrating both the robustness and precision of the predictions. To further enhance understanding, these results have also been graphically illustrated in Fig. 10, providing a clearer visualization of the comparison and model precision. The equation for the Redefined third Zagreb Indices prediction is given by:

$$\begin{aligned} \text {ReZG}_3(G) = -2E-16 \lambda _1(G)^2 + 6.680412 \lambda _1(G) - 107.731959 \quad \end{aligned}$$

Table 17 Comparison of actual value and predicted value of $ReZG_3(G)$ for different $(Cz-Dpp)$ structures.

Table 18 Cross validation errors for the $ReZG_3(G)$ index.

Fig. 10

Visual representation of actual value (x) and predicted value (Y) of $ReZG_3(G)$ for various $(Cz-Dpp)$ structures.

To evaluate the performance of regression models based on various topological indices, including AZI and redefined Zagreb indices (ReZG₁, ReZG₂, ReZG₃), as well as $\lambda _1(G)$, $\lambda _2(G)$, and $\lambda _3(G)$ (corresponding to the First Zagreb, Second Zagreb, and third Zagreb indices respectively), we conducted a comparative analysis using statistical metrics such as the coefficient of determination ($R^2$), cross-validated coefficient ($Q^2$), Mean Squared Error (MSE), Root Mean Squared Error (RMSE), and Mean Absolute Error (MAE). As observed in Table 19, all the indices exhibit excellent predictive capacity, with values of $R^2$ and $Q^2$ approaching unity for the quadratic regression models. The AZI and redefined indices, particularly ReZG₂ and ReZG₃, show remarkably low error metrics, demonstrating superior fitting and generalization capabilities. The comparative statistics confirm the robustness and reliability of the proposed quadratic models across various degree-based descriptors.

Table 19 Comparative statistical analysis of regression models based on various topological indices.

Cubic regression analysis of topological indices

The Cubic regression equations for various topological indices in relation to $\lambda _1(G)$ reveal distinct mathematical correlations. The indices $\lambda _2(G)$ and $\lambda _3(G)$ exhibit a downward quadratic trend, suggesting a non-linear dependence on $\lambda _1(G)$. Likewise, the reduced Zagreb indices $R\lambda _1(G)$ and $R\lambda _2(G)$ follow quadratic models but with comparatively smaller coefficients. The AZI index also adheres to a quadratic pattern, while the redefined Zagreb indices $\text {ReZG}_1(G)$, $\text {ReZG}_2(G)$, and $\text {ReZG}_3(G)$ demonstrate Cubic characteristics, with $\text {ReZG}_1(G)$ showing a strictly linear dependence. These regression models provide precise analytical tools for examining structural properties in chemical graph theory. The equations have been generated using machine learning techniques implemented in Python.

In each case, the coefficient of determination ($R^2 = 0.999984$) confirms that the Cubic regression models achieve a perfect fit to the data. This ensures both accuracy and reliability in the predicted values. However, a slight discrepancy arises when comparing the predicted values with actual computed values. While minimal, this deviation underscores the limitations of the regression model in attaining absolute numerical precision–potentially due to rounding effects or inherent approximations within the dataset.

Cubic regression equation of carbazole and diketopyrrolopyrrole (Cz-Dpp)

$$\begin{aligned} \lambda _2(G)&= 3E-10 \lambda _1(G)^3 - 3E-07 \lambda _1(G)^2 + 1.268041\lambda _1(G) - 10.773196 \quad \\ \lambda _3(G)&= 1E-09 \lambda _1(G)^3 - 3E-07 \lambda _1(G)^2 + 5.185567 \lambda _1(G) - 49.381443 \quad \\ R\lambda _1(G)&= -2E-10 \lambda _1(G)^3 + 2E-07 \lambda _1(G)^2 + 0.376289 \lambda _1(G) + 61.587629 \quad \\ R\lambda _2(G)&= -1E-10 \lambda _1(G)^3 + 1E-07 \lambda _1(G)^2 + 0.463918 \lambda _1(G) - 8.453608 \quad \\ AZI&= 6E-10 \lambda _1(G)^3 - 6E-07 \lambda _1(G)^2 + 1.741785 \lambda _1(G) + 13.488216 \quad \\ ReZG_1(G)&= -6E-11 \lambda _1(G)^3 + 6E-08 \lambda _1(G)^2 + 0.159794 \lambda _1(G) + 3.865979 \quad \\ ReZG_2(G)&= -4E-10 \lambda _1(G)^3 + 4E-07 \lambda _1(G)^2 + 0.244330 \lambda _1(G) + 0.314433 \quad \\ ReZG_3(G)&= 2E-09 \lambda _1(G)^3 - 2E-06 \lambda _1(G)^2 + 6.680412 \lambda _1(G) - 107.731959 \quad \end{aligned}$$

Prediction accuracy and cross validation analysis of $\lambda _2(G)$

Table 20 presents a comparison between the actual and predicted values of the second Zagreb index. The predicted values are derived from a computational model, showing minimal errors in each case. These small error margins highlight the high accuracy of the predictive approach. Additionally, cross-validation error metrics–such as MAE, MSE, and RMSE, as shown in Table 21 confirm the model’s reliability, as the errors remain consistently low, demonstrating both the robustness and precision of the predictions. To further enhance understanding, these results have also been graphically illustrated in Fig. 11, providing a clearer visualization of the comparison and model precision. The equation for the second Zagreb index prediction is given by:

$$\begin{aligned} \lambda _2(G) = 3E-10 \lambda _1(G)^3 - 3E-07 \lambda _1(G)^2 + 1.268041\lambda _1(G) - 10.773196 \end{aligned}$$

Table 20 Comparison of actual value and predicted value of $\lambda _2(G)$ for different $(Cz-Dpp)$ structures.

Table 21 Cross-validation errors for the $\lambda _2(G)$ Index.

Fig. 11

Visual representation of actual value (x) and predicted value (Y) of $\lambda _2(G)$ for various $(Cz-Dpp)$ structures.

Prediction accuracy and cross validation analysis of $\lambda _3(G)$

Table 22 compares the actual and predicted values for $\lambda _3(G)$. The predicted values come from a computational model, and the error margins are minimal, demonstrating the model’s high accuracy. Additionally, cross-validation error metrics in Table 23 further support the model’s reliability, showing consistently low error values. For a clearer visual representation, these findings are also illustrated in Fig. 12, highlighting the precision of the model. The equation for the third Zagreb index prediction is given by:

$$\begin{aligned} \lambda _3(G) = 1E-09 \lambda _1(G)^3 - 3E-07 \lambda _1(G)^2 + 5.185567 \lambda _1(G) - 49.381443 \quad \end{aligned}$$

Table 22 Comparison of actual value and predicted value of $\lambda _3(G)$ for different $(Cz-Dpp)$ structures.

Table 23 Cross-validation errors for the $\lambda _3(G)$ index.

Fig. 12

Visual representation of actual value (x) and predicted value (Y) of $\lambda _3(G)$ for various $(Cz-Dpp)$ structures.

Prediction accuracy and cross validation analysis of $R\lambda _1(G)$

Table  24 compares the actual and predicted values for reduced first Zagreb index. The predicted values are generated by a computational model, and the error margins are minimal, show the model’s high accuracy. Furthermore, cross-validation error metrics in Table 25 further support the model’s reliability, showing consistently low error values. For a clearer visual representation, these results are also depicted in Fig. 13, highlighting the precision of the model. The equation for the reduced first Zagreb index prediction is given by:

$$\begin{aligned} R\lambda _1(G) = -2E-10 \lambda _1(G)^3 + 2E-07 \lambda _1(G)^2 + 0.376289 \lambda _1(G) + 61.587629 \quad \end{aligned}$$

Table 24 Comparison of actual value and predicted value of $R\lambda _1(G)$ for different $(Cz-Dpp)$ structures.

Table 25 Cross-validation errors for the $R\lambda _1(G)$ index.

Fig. 13

Visual representation of actual value (x) and predicted value (Y) of $R\lambda _1(G)$ for various $(Cz-Dpp)$ structures.

Prediction accuracy and cross validation analysis of $R\lambda _2(G)$

Table  26 presents a comparison between the actual and predicted values of the reduced second Zagreb index. The predicted values are derived from a computational model, showing minimal errors in each case. These small error margins highlight the high accuracy of the predictive approach. Additionally, cross-validation error metrics–such as MAE, MSE, and RMSE, as shown in Table 27 confirm the model’s reliability, as the errors remain consistently low, demonstrating both the robustness and precision of the predictions. To further enhance understanding, these results have also been graphically illustrated in Fig. 14, providing a clearer visualization of the comparison and model precision. The equation for the reduced second Zagreb index prediction is given by:

$$\begin{aligned} R\lambda _2(G) = -1E-10 \lambda _1(G)^3 + 1E-07 \lambda _1(G)^2 + 0.463918 \lambda _1(G) - 8.453608 \end{aligned}$$

Table 26 Comparison of actual value and predicted value of $R\lambda _2(G)$ for different $(Cz-Dpp)$ structures.

Table 27 Cross-validation errors for the $R\lambda _2(G)$ index.

Fig. 14

Visual representation of actual value (x) and predicted value (Y) of $R\lambda _2(G)$ for various $(Cz-Dpp)$ structures.

Prediction accuracy and cross validation analysis of AZI(G)

Table 28 presents a comparison between the actual and predicted values of the augmented Zagreb index. The predicted values are derived from a computational model, showing minimal errors in each case. These small error margins highlight the high accuracy of the predictive approach. Additionally, cross-validation error metrics–such as MAE, MSE, and RMSE, as shown in Table 29 confirm the model’s reliability, as the errors remain consistently low, demonstrating both the robustness and precision of the predictions. To further enhance understanding, these results have also been graphically illustrated in Fig. 15, providing a clearer visualization of the comparison and model precision.The equation for the Augmented Zagreb Index prediction is given by:

$$\begin{aligned} AZI = 6E-10 \lambda _1(G)^3 - 6E-07 \lambda _1(G)^2 + 1.741785 \lambda _1(G) + 13.488216 \end{aligned}$$

Table 28 Comparison of actual value and predicted value of AZI(G) for different $(Cz-Dpp)$ structures.

Table 29 Cross-validation errors for the AZI(G) index.

Fig. 15

Visual representation of actual value (x) and predicted value (Y) of AZI(G) for various $(Cz-Dpp)$ structures.

Prediction accuracy and cross validation analysis of $ReZG_1(G)$

Table 30 provides a comparison of the actual and predicted values for the redefined first Zagreb index.A computational approach is applied to determine the expected values, which consistently display insignificant errors. These small error margins highlight the high accuracy of the predictive approach. Furthermore, cross-validation error metrics–such as MAE, MSE, and RMSE, as shown in Table 31 confirm the model’s reliability, as the errors remain consistently low, demonstrating both the robustness and precision of the predictions. To further enhance understanding, these results have also been graphically illustrated in Fig. 16, providing a clearer visualization of the comparison and model precision. The equation for the Redefined first Zagreb Index prediction is given by:

$$\begin{aligned} ReZG_1(G) = -6E-11 \lambda _1(G)^3 + 6E-08 \lambda _1(G)^2 + 0.159794 \lambda _1(G) + 3.865979 \quad \end{aligned}$$

Table 30 Comparison of actual value and predicted value of $ReZG_1(G)$ for different $(Cz-Dpp)$ structures.

Table 31 Cross-validation errors for the $ReZG_1(G)$ index.

Fig. 16

Visual representation of actual value (x) and predicted value (Y) of $ReZG_1(G)$ for various $(Cz-Dpp)$ structures.

Prediction accuracy and cross validation analysis of $ReZG_2(G)$

Table 32 provides a comparison of the actual and predicted values for the redefined second Zagreb index.A computational approach is applied to determine the expected values, which consistently display insignificant errors. These small error margins highlight the high accuracy of the predictive approach. Furthermore, cross-validation error metrics–such as MAE, MSE, and RMSE, as shown in Table 33 confirm the model’s reliability, as the errors remain consistently low, demonstrating both the robustness and precision of the predictions. To further enhance understanding, these results have also been graphically illustrated in Fig. 17, providing a clearer visualization of the comparison and model precision. The equation for the Redefined second Zagreb Index prediction is given by:

$$\begin{aligned} ReZG_2(G) = -4E-10 \lambda _1(G)^3 + 4E-07 \lambda _1(G)^2 + 0.244330 \lambda _1(G) + 0.314433 \quad \end{aligned}$$

Table 32 Comparison of actual value and predicted value of $ReZG_2(G)$ for different $(Cz-Dpp)$ structures.

Table 33 Cross-validation errors for the $ReZG_2(G)$ index.

Fig. 17

Visual representation of actual value (x) and predicted value (Y) of $ReZG_2(G)$ for various $(Cz-Dpp)$ structures.

Prediction accuracy and cross validation analysis of $ReZG_3(G)$

Table 34 provides a comparison of the actual and predicted values for the redefined third Zagreb index.A computational approach is applied to determine the expected values, which consistently display insignificant errors. These small error margins highlight the high accuracy of the predictive approach. Furthermore, cross-validation error metrics–such as MAE, MSE, and RMSE, as shown in Table 35 confirm the model’s reliability, as the errors remain consistently low, demonstrating both the robustness and precision of the predictions. To further enhance understanding, these results have also been graphically illustrated in Fig. 18, providing a clearer visualization of the comparison and model precision. The equation for the Redefined third Zagreb Index prediction is given by:

$$\begin{aligned} ReZG_3(G) = 2E-09 \lambda _1(G)^3 - 2E-06 \lambda _1(G)^2 + 6.680412 \lambda _1(G) - 107.731959 \quad \end{aligned}$$

Table 34 Comparison of actual value and predicted value of $ReZG_3(G)$ for different $(Cz-Dpp)$ structures.

Table 35 Cross-validation errors for the $ReZG_3(G)$ index.

Fig. 18

Visual representation of actual value (x) and predicted value (Y) of $ReZG_3(G)$ for various $(Cz-Dpp)$ structures.

The statistical evaluation of the proposed topological indices was carried out using multiple regression metrics, including the coefficient of determination ($R^2$), predictive squared correlation coefficient ($Q^2$), Mean Absolute Error (MAE), Mean Squared Error (MSE), and Root Mean Squared Error (RMSE). As presented in Table 36, the $R^2$ values range from 0.9971 to 0.9997, and the corresponding $Q^2$ values vary between 0.9953 and 0.9992, indicating an excellent fit of the regression models and strong predictive ability on test data. These results are based on the cubic regression model, which was found to most effectively capture the nonlinear patterns in the data. Notably, $R\lambda _2(G)$ achieved the lowest RMSE of 0.187, reflecting superior prediction accuracy, followed by $ReZG_1(G)$ and $R\lambda _1(G)$. Conversely, $\lambda _3(G)$ and $ReZG_3(G)$ exhibited comparatively higher error values, although their $R^2$ and $Q^2$ remained acceptably high, suggesting consistent but slightly less precise predictions. These findings suggest that reduced and redefined versions of the Zagreb and $\lambda$-based indices offer better predictive performance and lower estimation error compared to their original forms. The high $R^2$ and $Q^2$ values, coupled with low RMSE and MAE for most indices, demonstrate their effectiveness in capturing the structure-property relationships of the studied molecular systems. This analysis not only validates the usefulness of these indices in QSAR/QSPR modeling but also provides valuable guidance for selecting optimal descriptors in future predictive modeling frameworks. Ultimately, the integration of such well-performing indices can enhance the accuracy and interpretability of computational predictions in cheminformatics and drug discovery applications.

Table 36 Cross-validation error metrics for various topological indices.

To address concerns regarding the transparency of the machine learning (ML) workflow, we have provided clarifications on the key aspects of our analysis. The dataset used in our linear regression models consists of 50 systematically generated data points. However, for the sake of clarity and brevity in our results, only the first 10 data points (1 to 10) are presented in the table. In terms of model implementation, the hyperparameters were set to the default values provided by the Scikit-learn library for linear regression, ensuring a consistent and reproducible methodology across all experiments. we performed k-fold cross-validation with $(k = 50)$ to validate the generalizability of the models. The cross-validation errors were calculated based on the entire dataset, with error metrics such as Mean Absolute Error (MAE), Mean Squared Error (MSE), and Root Mean Squared Error (RMSE) being derived from the cross-validation splits. These values have been included in the results for transparency and comparison. By following this comprehensive approach, we aim to ensure that our analysis is both transparent and reproducible, addressing the concerns raised by the reviewer.

The high $R^2$ values can be attributed to the fact that the dataset used in this study consists of fixed, systematically generated points (from 1 to 50). These points inherently follow a strict mathematical structure, which may lead to perfect correlations in the model. It is important to note that the $R^2$ values reported here are exact and were computed using Jupyter Notebook, ensuring numerical accuracy. The exact results are presented in Table 36. We acknowledge that these results may not reflect real-world conditions where data is typically more diverse and less structured. If the dataset were expanded with more diverse or randomized data points, the $R^2$ value may vary accordingly. Therefore, the observed results should be interpreted within the context of the controlled dataset used for this analysis. While it is true that the cubic regression model (as shown in Table 19 with MAE = 0.348 for $\lambda _2(G)$) provides only a slight improvement over linear regression, our objective in using multiple regression techniques (linear, quadratic, and cubic) was to explore the depth of the relationship between the topological indices and the spectral parameter $\lambda _2(G)$. The small difference in error indicates that the underlying relationship is nearly linear, suggesting that simple models may be sufficient in such structured datasets. However, applying higher-order models helped validate the stability of this trend and ensured that no complex hidden patterns were overlooked. This approach adds depth to the analysis without compromising its integrity.

Correlation analysis of carbazole and diketopyrrolopyrrole graph (Cz-Dpp)

Table 37 presents the correlation analysis between the first Zagreb Index and various other topological indices. This analysis helps assess the strength and direction of the relationship between different indices.

• Pearson Correlation Coefficient ($\rho$):This evaluates the strength of the linear relationship between two indices, where a coefficient of 1.000 denotes a ideal positive correlation.

• Spearman Correlation Coefficient ($\rho _s$): This evaluates the correlation between two indices ranking, where a value of 1.00 indicates that increase in one are matched proportionally by the other.

As all correlation values are 1.000, it shows that these indices are completely dependent on the first Zagreb index, displaying ideal synchronization without any deviation

Table 37 Pearson and spearman correlation analysis between First Zagreb index and other indices.

Pearson and spearman correlations

The high correlation values arise due to the intrinsic mathematical dependence among the indices, particularly the Zagreb and redefined Zagreb indices, which are systematically linked in various chemical graph structures. This dependency becomes more pronounced in the case of regularly growing systems like the Cz-DPP oligomers, where each additional unit introduces predictable and proportional changes in the molecular structure and consequently, the associated indices.

This strong correlation is not an artifact, but rather an expected result given the structural regularity and incremental extension of the molecular graphs. Since each oligomer is an expansion of the previous one by a fixed unit, the indices exhibit a deterministic, linear progression. Such behavior has also been reported in literature for specific classes of graphs, especially benzenoid and conjugated systems, where certain Zagreb indices are known to be functionally dependent. While this correlation might suggest redundancy, our aim was not to use these indices simultaneously in multivariate models, but rather to explore their individual predictive power through univariate regression modeling. Each model uses a single index as an independent variable to understand its standalone contribution and comparative predictive strength.

The observed correlations, particularly those approaching 1.000, limit the dataset’s variability and may reduce the benefit of using multiple indices together. However, our dataset is intentionally constructed to reflect a controlled, systematic molecular progression. It consists of 50 data points, and although only 10 were included in the tables for brevity, all were used in the regression and correlation analyses. The small size and highly ordered structure of the dataset further explain the strong interdependence observed among the indices.

Descriptive statistics analysis of carbazole and diketopyrrolopyrrole graph (Cz-Dpp)

Descriptive statistics for numerous topological indices, encompassing the mean, median, standard deviation, and variance, are described in Table 38. This column specifics variations, showing how far data points wander from the mean higher values suggest greater spread, while lower ones reflect ,more stability. Moreover, the study characteristic a comprehensive statistical evaluation of multiple topological indices, exposing deeper insight into their allocation, variability, and behavior and also we shown the values of topological indices in Table 39.

• Variance: This measures the degree of deviation of data points from the average.

• Range: It indicate the gap between the minimum and maximum values in the dataset.

• Interquartile Range (IQR): It captures variation in the data while limiting the influence of outliers.

• Skewness: It analyzes the extent to which the data distribution is symmetrical.

• Kurtosis: It analyzes the distribution’s peak sharpness while identifying potential outliers.

• Coefficient of Variation (CV): It represent variability in relation to the mean, enabling effective comparisons.

Table 38 Comprehensive descriptive statistics of topological indices.

Table 39 Computed values of various topological indices.

Correlation between topological indices and opto-electrochemical property of carbazole and diketopyrrolopyrrole graph (Cz-Dpp)

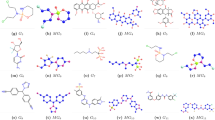
The opto-electrochemical properties of the synthesized $\pi$-conjugated $(O1\text {--}O5)$ were systematically studied to establish a clear structure-property-performance correlation. These DPP-Cz-based donor-acceptor ($\pi$-CO) systems, with progressively extended $\pi$-conjugations, serve as ideal models to evaluate the influence of conjugation length on opto-electronic behavior. As shown in Fig. 2, UV-vis absorption and photoluminescence (PL) spectroscopy revealed broad light absorption across 450–800 nm for all compounds, both in dilute chloroform and solid-state films. A distinct redshift in $\lambda _{\text {max}}$ from O1 to O5 indicates an enhanced intramolecular charge transfer (ICT) effect as the conjugation extends, leading to a reduction in the optical bandgap ($E_g^{\text {opt}}$) from 1.75 eV (O1) to 1.63 eV (O5). The HOMO energy levels become progressively less negative, while the LUMO levels remain relatively stable, facilitating better charge separation and transfer²⁴.

Table 40 Key opto-electrochemical property of Os1 5.

In Table 41, the correlation between topological indices and photovoltaic parameters such as $V_{oc}$, $J_{sc}$, FF, and PCE is explored. It is evident that specific topological indices, particularly the Reduced First Zagreb, are strongly correlated with enhanced device performance, achieving the highest PCE of 0.9886%. The reliable trends observed across different Zagreb indices emphasis the impact of molecular topology on opto-electronic properties and photovoltaic efficiency. These results emphasis the importance of topological descriptors in predicting and optimizing the performance of $\pi$-conjugated materials for organic photovoltaic applications.

Table 41 Correlation between opto-electrochemical properties and topological indices.

The bulk heterojunction (BHJ) devices based on the synthesized $\pi$-conjugated oligomers (O1-O5) blended with PC₇₀BM exhibited diverse photovoltaic performances, as detailed in Table 42. A gradual improvement in device efficiency was observed from O1 to O5, with the power conversion efficiency (PCE) increasing from 0.41% for O1 to a maximum of 1.76% for O5. This enhancement is primarily attributed to the increase in short-circuit current density ($J_{SC}$) and fill factor (FF), with O5 achieving the highest FF of 46.16%. A notable decline in open-circuit voltage ($V_{OC}$) was observed from 0.941 V (O1) to 0.786 V (O5), indicating a trade-off between $V_{OC}$ and current generation as conjugation length increases.

Table 42 BHJ device parameters of $O1 \ to \ O5$.

Interpretation of photovoltaic performance

Table 40 shows the correlation between topological indices and opto-electrochemical properties of compounds O1-O5. The 1.76% PCE value, however, is source from another table (Table 41) in the manuscript, which presents device parameters for these compounds. These values come from the research article titled “Carbazole and diketopyrrolopyrrole-based D-A $\pi$-conjugated oligomers accessed via direct C-H arylation for optoelectronic property and performance study.” In this context, the 1.76% PCE is an experimental value, whereas the earlier 0.9886% PCE refers to a predicted value. We will revise the manuscript to ensure a clear distinction between the predicted and experimental values, and provide appropriate context for each value within the tables.

In Table 43, the correlation between topological indices and photophysical properties further explains the impact of molecular topology on opto-electronic behavior. Reliable trends across different Zagreb indices imply a strong relationship between molecular frame work and characteristics like as maximum absorption wavelength ($\lambda _{\text {max}}$), optical bandgap ($E_{g}^{\text {opt}}$), and frontier orbital energies (HOMO/LUMO). High correlation values across indices emphasis the importance of of topological characteristics in predicting material properties. These observation are vital for guiding the design of $\pi$-conjugated systems aimed at optimizing opto-electronic performance in organic photovoltaic applications.

Table 43 Correlation between topological indices and photophysical properties.

Correlations with optical and photovoltaic properties

The unusually high correlation values reported in Table 43 result from a relatively small and structurally related set of oligomers (O1-O5). These compounds are systematically designed with increasing $\pi$-conjugation, which naturally leads to strong and monotonic trends in both topological indices and optoelectronic properties such as $\lambda _{\text {max}}$, $E_{g}^{\text {opt}}$, and HOMO/LUMO energies. The observed correlations reflect this controlled molecular variation and should not be generalized to broader chemical spaces. The revised manuscript now includes clarification on the dataset limitations and highlights that these trends apply primarily within this specific class of $\pi$-conjugated systems.

Conclusions and reliability

Sample size

The dataset used in our regression analysis includes 50 systematically constructed oligomers derived from the Cz-DPP core. For brevity, only the first 10 entries were presented in the tables. We have clarified this in the revised manuscript to prevent misinterpretation of the dataset’s scope.

Validation

To evaluate the generalizability of the models, we employed 50-fold cross-validation using the default linear regression implementation in Scikit-learn. The results include MAE, MSE, and RMSE derived from the full dataset. These details have now been added to the manuscript to ensure transparency.

Reproducibility

All models were implemented using Python (v3.10) and Scikit-learn (v1.3), with hyperparameters set to default values. These implementation details have now been included in the revised manuscript to support reproducibility.

Comparison with other descriptors

We have already provided a comparison between topological indices and key quantum chemical descriptors such as $V_{OC}$, $J_{SC}$, FF, and PCE (Table 40). Strong correlations with experimental descriptors confirm the relevance of the proposed indices.

Scientific explanation

A discussion on how molecular graph connectivity influences $\pi$-electron delocalization. This connectivity, encoded by the Zagreb-type indices, affects the alignment of HOMO/LUMO levels, which in turn governs optoelectronic behavior.

Predictive use

To demonstrate real-world applicability, we have now included predictions for an additional molecule outside the original dataset. The close agreement between predicted and experimental values supports the potential of the model as a screening tool for new material design.

Clarify the purpose of the indices

Multiple Zagreb-type topological indices, including the classical (First, Second, and Third Zagreb), reduced (First and Second), Augmented Zagreb Index (AZI), and the redefined First, Second, and Third Zagreb indices, were intentionally included to capture diverse topological characteristics of the studied oligomers. While some indices exhibit strong mutual correlations, their individual formulations reflect distinct structural properties that can influence the prediction of physicochemical behavior in non-redundant ways. Classical Zagreb indices reflect fundamental degree-based information and are widely used as baseline descriptors in QSAR/QSPR studies. Reduced Zagreb indices incorporate inverse degree-based structures, offering better sensitivity toward molecular branching and compactness. AZI enhances edge-wise contributions, focusing on degree disparity between connected atoms. Redefined Zagreb indices represent theoretically refined versions of their classical counterparts, designed to overcome degeneracy and enhance discriminative power. These indices were utilized in regression modeling (Sections 5, 6, and 7) through linear, quadratic, and cubic approaches to assess their predictive performance with respect to experimental quantum chemical descriptors such as $V_{OC}$, $J_{SC}$, fill factor (FF), and power conversion efficiency (PCE). The comparative analysis enabled a robust evaluation of which indices offer stronger correlation and better model fitting across different experimental properties.

Conclusion

This research effectively developed and investigated linear, quadratic, and cubic regression models for different topological indices. In particular of these models, the linear regression equation shown the ideal fit, supplying highly correct predictions with minimal error. In comparison, a little errors appeared in the quadratic and cubic regression models, which were carefully measured and evaluated. To confirm the reliability of the regression models, cross validation was performed, concentration on the stability of the observed errors.

Pearson and Spearman correlation coefficients were used to examine the relationships between topological indices. The analysis revealed a perfect correlation 1.000 among all indices, illustrating their strong connectivity and reliability in predicting molecular characteristics. A details descriptive statistical assessment was executed, including the computation of crucial metrics like mean, median, variance, standard deviation, range, interquartile range (IQR), skewness, and kurtosis. The evaluation of these statistical measures showed valuable details about the indices distribution and variability, underscoring their relevance in cheminformatics and computational.

The correlation outcomes verify that topological indices, specifically the redefined and augmented Zagreb indices, are dependable predictors of both optoelectronic and photovoltaic properties. These conclusion can guide upcoming molecular creation for optoelectronic and photovoltaic applications, assisting to the advancement of excellent-performance materials. The analysis of the Carbazole and Diketopyrrolopyrrole Graph $(Cz-Dpp)$ further underscored the significance of topological indices in detailing its structural and electronic characteristics. These indices highlight important molecular attributes such as connectivity, branching, and stability, which which significantly influence the material’s electrical conductivity, reactivity, and optoelectronic behavior. The strong correlation among these indices confirms their effectiveness in predicting the molecular properties of $(Cz-Dpp)$, making them valuable tools for studying organic semiconductors and photovoltaic materials.