A modified generative adversarial networks method for assisting the diagnosis of deep venous thrombosis complications in stroke patients

Abstract

Discriminate deep vein thrombosis, one of the complications in early stroke patients, in order to assist in diagnosis. We have constructed a new method called ACWGAN by combining ACGAN and WGAN methods for data augmentation to to enhance the data of stroke early rehabilitation patients admitted to Nanjing First Hospital from 2017 to 2021, followed by analysis of complications, and compared it with 20 other commonly used data augmentation methods. A total of 7110 patients were included in the analysis of this study, the AUC value of the discriminative model ranges from 0.688 to 0.805 after data augmentation using traditional machine learning methods. When deep learning methods (GAN-based methods) are employed, the AUC value can surpass 0.866. Our proposed ACWGAN method maintains efficiency comparable to GAN, ACGAN, and WGAN, while achieving an even higher AUC value for the model trained on the augmented dataset, exceeding 0.938. The ACWGAN method effectively improves the diversity and accuracy of the model while ensuring the stability of the network, indicating that it can accurately assist in diagnosing the prevalence of DVT in patients.

Introduction

As a common neurological disease, stroke is the 2nd leading cause of death and 3rd leading cause of death and disability combined in the world in 2019¹. With high morbidity and disability, it has been a hotspot of medical research. Among them, Deep Venous Thrombosis (DVT) is a common complication in stroke patients, and its prevention and treatment are crucial to the recovery of patients, thus becoming focus of this paper. However, despite high incidence of stroke, the percentage of patient samples in actual clinical studies is still relatively small, which leads to the unbalanced nature of the study data. So in order to make full use of the information of stroke patients and improve the performance of the classification model, appropriate unbalanced processing methods² are needed.

Traditional sampling technique based on machine learning balances the data distribution by direct manipulation of data and feature engineering to artificially correct the data set, which can be classified into undersampling method and oversampling method according to the sample categories.Kubat et al.³ used Tomek Links for undersampling to remove boundary samples and noise samples of the sample set by using nearest-neighbour relationships between the samples, but it is prone to information loss. In 2002, Chawla et al.⁴ proposed SMOTE (Synthetic Minority Oversampling Technique) method for generating new samples randomly in the domain space of minority class samples , but it cannot overcome the data distribution problem of unbalanced datasets and is prone to distribution marginalization. On the basis of SMOTE method, researchers have combined it with other methods such as ENN and Tomek^5,6, improved its performance. Some scholars have also improved the SMOTE method itself and proposed methods such as Bordline SMOTE⁷ . In addition, there are other machine learning methods widely used, such as ADASYN (Adaptive Synthetic Sampling) method⁸.

Deep learning offers robust solutions for high-dimensional or highly unbalanced data. Augustus et al.⁹ in 2017 proposed Auxiliary Classifier Generative Adversarial Networks(ACGAN), experimentally obtaining on ImageNet data the high-quality generated images. Douzas et al.¹⁰ in 2018 used Conditional Generative Adversarial Networks (CGAN) to approximate real data distributions and generate data for 12 unbalanced in UCI datasets to generate minority class data, empirically demonstrating a significant improvement in the quality of data generated using CGAN as an oversampling method. But these methods all have the drawback of requiring a lot of label information. Xie Xiaobo¹¹ proposed a classification method based on WGAN (Wasserstein Generative Adversarial Networks) for unbalanced datasets in 2019, and solves synthetic minority class samples with insufficient diversity and stability. Lin et al.¹² in 2022 modified and combined CGAN, active learning, and weighted loss function to propose RareGAN for very small number of class samples generation, which better achieves the trade-off between fidelity and diversity of generated samples. However, RareGAN did not solve the problem of training instability in GAN, and it is prone to gradient vanishing or pattern collapse, which affect the convergence of the method.

In the field of stroke research, some scholars have already used deep learning to process unbalanced data. Beatriz et al.¹³ in 2024 proposed a lightweight model based on U-Net architecture, which effectively improved segmentation accuracy in MRI images with unbalanced feature classes of stroke lesions by integrating attention modules and generalized dice focus loss functions. However, in the analysis of corresponding complications, this issue still exists and is more of a concern for clinical medical staff than whether the disease has occurred.

In this paper, two generative adversarial networks, WGAN and ACGAN, are used in combination to process stroke patient data and generate patient data for the purpose of oversampling. It addresses the challenge of unbalanced datasets in predicting DVT among stroke patients by leveraging an enhanced deep learning model. Section “Oversampling method based on deep learning” introduces the existing methods in related fields as well as the method proposed in this paper, Section Experiment” describes the dataset as well as the specific experimental procedure and results, and Section “Conclusion” concludes and gives an outlook.

Oversampling method based on deep learning

This paper focuses on oversampling methods for generating minority class samples using deep learning, in particular using GAN and their variants to generate minority class samples.

GAN is a deep learning model contains two neural networks, a generator and a discriminator, which learns the data distribution and generates realistic samples by means of adversarial training. Generator is responsible for capturing the data distribution, inputting a random noise vector z and generating realistic data samples $X_{fake}$. While discriminator is responsible for distinguishing between the samples generated by generator $X_{fake}$ and real samples $X_{real}$¹⁴. Figure 1a shows network structure of GAN, where z denotes noisy data sampled from the noisy distribution, G denotes generator, and D denotes discriminator. In the training process, generator G learns real data distribution $p_{real}(x)$ from the real data $X_{real}$, transforms noisy sample z into generated samples $X_{gen}=G(z;\theta _g)$, and trains loss function

$$\begin{aligned} L_{gen} = -E(logD(X_{fake})), \end{aligned}$$

(1)

; discriminator outputs true and false labels $\mathbb {R}$ of input samples x , and outputs $D(x; \theta _d)$. $D(x; \theta _d)$denoting the probability that x comes from the data distribution $p_{real}(x)$, to train loss function

$$\begin{aligned} L_{dis}= E(logD(X_{fake}))-E(logD(X_{real})). \end{aligned}$$

(2)

GAN needs to solve the minimax problem:

$$\begin{aligned} \mathop {\min }_G \mathop {\max }_D(E_{x\sim real(x)}(logD(x))+E_{z\sim p_{z}(z)}(log(1-D(G(x)))). \end{aligned}$$

(3)

Generator and discriminator compete with each other and continuously optimize, and finally reach a dynamic equilibrium that can effectively generate minority class samples.

ACGAN-based sampling method

For original GAN, edge information can be directly fed to discriminator to enhance its framework, which in turn improves model performance and the diversity of generated data. It is also possible to change structure of discriminator by adding a decoder to achieve the reconstruction of edge information. In order to combine two strategies, Odena et al.⁹ proposed ACGAN combines two strategies, which can not only receive input edge information to generate class-specific samples, but also implement class label refactoring by adding an auxiliary classifier⁹.

As a variant of GAN, ACGAN uses the structure of traditional generator and discriminator of GAN, while introducing an auxiliary classifier in discriminator to achieve supervised learning of GAN, which performs a class judgement on the generated samples and prompts generator to generate class-specific samples. In ACGAN, each generated sample $X_{gen}$ has a corresponding class label $\mathbb {C}$, and an auxiliary classifier added in the discriminator make discriminator output another probability distribution on the class label when discriminator outputs the original probability distribution. Figure 1b shows the network structure of GAN, where z denotes noise data sampled from noise distribution, c denotes class of real data, G denotes generator, and D denotes discriminator. Loss function is also changed, and generative adversarial loss of ACGAN includes two parts, adversarial loss and classification loss:

$$\begin{aligned} L_{ACGAN}=L_{GAN}+L_{Class}. \end{aligned}$$

(4)

Where $L_{GAN}$ is traditional generative adversarial loss determines whether data is real or not, and $L_{Class}$ is classification loss that discriminates the classification labels of data. G learns data distribution $p_{real}(x)$ from real data $X_{real}$, transforms noisy sample z into generative sample $X_{gen}=G(z, c; \theta _g)$, and trains loss function:

$$\begin{aligned} L_{gen}^{AC} = -E(logD(X_{fake}))-E(logC(X_{fake})). \end{aligned}$$

(5)

Discriminator determines the true and false label $\mathbb {R}$ of input sample x and outputs $D(x;\theta _d)$, indicating the probability that x comes from data distribution $p_{real}(x)$. Meannwhile, it determines class label $\mathbb {C}$ of input sample x and outputs $C\left( x;\theta _c\right)$, indicating probability distribution of x on the class labels, and then trains loss function:

$$\begin{aligned} L_{{dis}}^{{AC}} & = E(logD(X_{{fake}} )) - E(logD(X_{{real}} )) \\ & \quad + E\left( {log\left( {\left\| {C(X_{{real}} )) - c} \right\|} \right) - E(logC(X_{{fake}} )} \right). \\ \end{aligned}$$

(6)

ACGAN needs to solve the minimax problem:

$$\begin{aligned} \mathop {\min }_G \mathop {\max }_D(E_{x\sim real(x)}[log D(x)] + E_{z\sim p_{z}(z)} [log(1 - D(G(z)))] \nonumber \\ +E [log P(\mathbb {C}=c|Xreal) ]+ E [logP(\mathbb {C}=1|Xgen)]), \end{aligned}$$

(7)

where $P(\mathbb {C}=c|X_{real})$ is the probability of real data category label $\mathbb {C}$ approaching c, and $P(\mathbb {C}=1|X_{gen})$ is the probability of generated data category label $\mathbb {C}$ approaching 1.

ACGAN adds auxiliary classifiers in discriminator (D of Fig. 1b) to enable discriminator to not only distinguish the authenticity of images during training, but also learn the category information of images. In this way, generator can be guided by category labels to generate required data.

In general, ACGAN introduces additional information by means of supervised learning and it is able to control the category labels of generated samples, which enhances the diversity and controllability and helps to improve quality of generated samples. However, it also requires a large number of category labels to train auxiliary classifier, which needs more data. The training process has added steps for generating and discriminating class labels, making neural network more complex and prone to instability, which may lead to pattern collapse and other problems.

WGAN-based oversampling method

The original GAN has two forms of loss functions:

$$\begin{aligned} & E_{x\sim P_{r}}[log(1-D(x))], \end{aligned}$$

(8)

$$\begin{aligned} & E_{x\sim P_{r}}[-logD(x)], \end{aligned}$$

(9)

Under the first form Eq. 8, loss function of generator when the discriminator is optimal can be equated to $2JS(P_{r}\parallel P_{g}-2log2)$, due to the unlikely existence of an undeniable intersection between generated distribution and real distribution¹⁵, and JS divergence has mutation properties, generator is prone to face the problem of vanishing gradients. Under the second form Eq. 9, loss function can be equated to $KL(P_{r}\parallel P_{g})-2JS(P_{r}\parallel P_{g})$, which contradicts each other by minimizing KL divergence between generated distribution and real distribution and maximizing its JS, and the gradient is prone to be unstable. Moreover, asymmetry of KL makes generator more inclined to sacrifice diversity to maintain accuracy, which is prone to the phenomenon of collapsing mode. Wasserstein distance, on the other hand, can reflect distance between two distributions even when they do not have overlapping parts, which is more suitable for this situation than KL and JS . In addition, KL and JS have an abrupt nature, while Wasserstein distance is smooth and more suitable for optimizing parameters using gradient descent and providing more meaningful information of gradient.

WGAN uses Wasserstein distance instead of KL divergence and JS divergence, so loss function of discriminator does not require log. In WGAN, the role of discriminator is to approximate Wasserstein distance between real data and generated data, which is essentially a regression problem rather than a classification problem, so the last layer of discriminator does not need to use sigmoid function to limit output range. Since Wasserstein distance is difficult to solve by definition, it can be replaced by

$$\begin{aligned} W(P_{r}, P_{g})=\dfrac{1}{K} \sup \limits _{\Vert f\Vert \leqslant K}E_{x\sim P_{r}}[f(x)]-E_{x\sim P_{g}}[f(x)]. \end{aligned}$$

(10)

Lipschitz constant $\Vert f\Vert \leqslant K$ of function f is concretized in deep learning as an absolute value of a parameter that does not exceed a fixed constant.¹⁶ show when the gradient of discriminant loss function is unstable, RMSProp (Root Mean Square Propagation) optimization method is more suitable to deal with the case of unstable gradient than momentum-based optimization method, which can efficiently adjust learning rate. Therefore, it is recommended to use optimization methods such as RMSProp or Stochastic Gradient Descent (SGD) in WGAN. Overall, there are four main modifications made to the method of WGAN compared to original GAN:

• Modify loss function of generator and discriminator without using log;

• Remove sigmoid activation function in the last layer of discriminator;

• Limit the absolute value of parameters during discriminator update to no more than a fixed constant clamp;

• Modify optimizer to not use momentum-based optimization methods, RMSProp or SGD are recommended.

Referring experiment in¹¹ on unbalanced credit card fraud data using WGAN, Fig. 1c shows the network structure of WGAN, where z denotes noisy data sampled from a noisy distribution $p_{z}(z)$, G denotes generator, D denotes discriminator, and E denotes expectation. Using Wasserstein distance, WGAN needs to solve the minimax problem :

$$\begin{aligned} \mathop {\min }_G \mathop {\max }_D(E_{x\sim real(x)}(D(x))+E_{z\sim p_{z}(z)}(1-D(G(x)))). \end{aligned}$$

(11)

Wasserstein distance is smoother and can provide better gradient information, which effectively solves the problem of training instability in original GAN, making training process more stable and reliable. It basically solves the problem of pattern collapse, and produce high-quality and diverse generation samples, which can also provide better gradient signals, making training more efficient. However, for some complex data distributions, computation of Wasserstein distance consumes more, and at the same time, parameters need to be adjusted increase, such as weight clipping, which increases the complexity of adjusting parameters.

In summary, WGAN introduces Wasserstein distance in discriminator(D of Fig. 1c) to measure the distance between two distributions, which more accurately reflects the differences between the two distributions. This enables WGAN to update the parameters of the generator and discriminator more stably during the training process, thereby avoiding problems such as gradient vanishing and pattern collapse.

ACWGAN-based oversampling method

WGAN and ACGAN are two improved methods for generative adversarial networks with their own unique advantages and disadvantages, and we call the combination of these two methods ACWGAN (Auxiliary Classifier Wasserstein Generative Adversarial Networks). Inspired by ACGAN’s addition of auxiliaries to discriminator, main idea of ACWGAN is to add classifier to WGAN and modify loss function according to output of classifier, which is mainly used to deal with small structured data such as table data. For tabular data stored in the form of text, each cell contains relatively small amount of information, unlike ACGAN which adds auxiliary classifier to discriminator, ACWGAN takes classifier as an independent network structure, so that training process of generator and discriminator is independent of each other, which helps to train classifier independently, which can also adapt to data simplification of overall network structure, while retaining the function of ACGAN to predict sample categories based on samples generated by input generator or real samples.

Fig. 1

Network structure.

In the training process of ACWGAN, both original and generated data have labels $\mathbb {R}$ distinguishing between true and false and labels $\mathbb {C}$ distinguishing class, assuming that real data $\mathbb {R}=1$ and minority category data $\mathbb {C}=1$. Generator inputs noisy data z and real data category label c, learns data distribution $p_{real}(x)$ from real data $X_{real}$, and outputs the minority class generated data $X_{gen}=G(z, c;\theta _g)$ with $\mathbb {R}=1$ and $\mathbb {C}=1$. Discriminator inputs x, outputs probability distribution D(x) on true and false labels. Classifier inputs real data $X_{real}$ or generated data $X_{gen}$ outputs probability distribution $C(X_{real})$ or $C(X_{gen})$ on class labels.

Using Wasserstein distance, generator in which generated data is required to be as close as possible to the minority class data on the basis of Eq. 11, i.e. Class labels are required to approach 1, generator needs to minimize loss function:

$$\begin{aligned} L_{gen}^{ACW}=-E(D(X_{fake}))+E(1-C(X_{fake})). \end{aligned}$$

(12)

In discriminator, class labels of real data are required to approach class c of real data, and class labels of generated data are required to approach 1. Loss functions on true and false labels, and class labels are respectively:

$$\begin{aligned} & L_{r}= E(D(X_{fake}))-E(D(X_{real})), \end{aligned}$$

(13)

$$\begin{aligned} & L_{c}= E(\Vert C(X_{real})-c \Vert )+ E(1-C(X_{fake})), \end{aligned}$$

(14)

where E denotes expectation and discriminator is required to minimize loss function $L_{dis}^{ACW}= L_{r}+L_{c}$. ACWGAN is required to solve minimax problem:

$$\begin{aligned} \mathop {\min }_G \mathop {\max }_D(E_{x\sim real(x)}D(x)+ E_{z\sim p_{z}(z)} (1 - D(G(z)))\nonumber \\ +E(P(\mathbb {C}=c|Xreal))+ E(P(\mathbb {C}=1|Xgen))), \end{aligned}$$

(15)

where $P(\mathbb {C}=c|X_{real})$ is the probability that real data category label $\mathbb {C}$ approach c, that is,$\Vert C(X_{real})-c\Vert$; and $(\mathbb {C}=1|X_{gen})$ is the probability that generated data category label $\mathbb {C}$ approach 1, that is,$1-C\left( X_{fake}\right)$.

Figure 1d shows the network structure of ACWGAN, dashed part is the increase of this model with respect to original GAN model, z denotes noisy data sampled from noisy distribution, c denotes class of real data, G denotes generator, D denotes discriminator, and C denotes classifier. Compared with GAN, ACWGAN adds an independent classifier C after discriminator D and modifies the loss function based on classifier’s output to control the category labels of generated data. At the same time, Wasserstein distance is used to increase network stability when calculating the loss function during training.

Fig. 2

Flowchart for generating patient data using ACWGAN and determining whether it is a DVT patient.

Figure 2 is a flowchart of using ACWGAN to generate patient data and using a logistic regression (LR) classifier to determine whether the patient has DVT. The dashed box on the left side of Fig. 2 shows pre-training process, which mainly includes preprocessing of four types of data. ACWGAN model is used to generate new patient data, and generated data is integrated with original processed data to train LR classifier. Then, the same preprocessing process is applied to patient data to be detected, using the pre-trained classifier to determine whether the patient is a DVT patient.

Hospitals can integrate with ACWGAN model through the following process: Firstly, patient data meets privacy requirements from hospital is input into a pre-training module to initialize the network structure and parameter configuration. Subsequently, hospital preprocesses data that currently needs to be tested according to a fixed process. Next, pre-trained ACWGAN model performs feature learning and synthesized sample generation on the input data, and outputs classification results through the classification model. Ultimately, diagnostic results are directly integrated into the hospital’s auxiliary diagnostic platform for doctors to refer to.

Experiment

Dataset

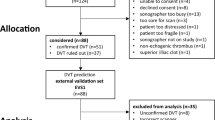
Initial data used in this paper comes from the data of rehabilitation department of a hospital from 2017 to 2021, including medical records of 7110 patients. The experiment mainly used four types of data in initial data: patient information, test data, rehabilitation data and diagnostic data, including patient’s hospitalization number, number of days of hospitalization, name of patient’s test, patient’s seated balance at admission and discharge, and discharge diagnosis, which recorded basic information of patients, clinical manifestations, and symptoms, and could help to distinguish between different categories of patients’ diseases. The incidence rate of individual diseases in this data is relatively low, such as 9.5% for hypertension, 5.9% for coronary heart disease, and only 0.96% for lower limb venous thrombosis in diagnostic data, indicating significant unbalance.

After data cleaning and transformation, test data x are normalized to using a range of reference values:

$$\begin{aligned} x^{*}=\dfrac{x-x_{min}}{x_{max}-x_{min}}. \end{aligned}$$

(16)

Where $x_{max}, x_{min}$ is reference value range test data corresponding to x. Remove abnormal data beyond the rating range from ehabilitation data according to the rating instructions, such as Brunnstrom hemiplegia staging, which is divided into six stages and can be used to evaluate the recovery of motor function in hemiplegic patients after stroke¹⁷. In the end, we obtained 2869 test data from 48 test items, 2020 rehabilitation data from 16 rehabilitation items, and 4594 diagnostic data (including DVT) from 51 diagnostic items. The data used in this article is test data merged based on hospitalization numbers, including hospitalization numbers of 2869 patients, 48 test items, and DVT items. DVT item of patients is recorded as 1, with a ratio of 2683:186 between non DVT patients and DVT patients, and an unbalance rate (minority sample size: majority sample size) of 6.9%.

The partial test data before and after processing are shown in Table 1. This table shows the distribution of patients with different diseases in test data, the first column represents patients with different diseases, the first row represents DVT patients in test data, with 1 indicating disease and 0 indicating no disease Here, “CHD”, “Hype.”, “AF”, “PE”, “Dysa.”, “SE”, “CI”, “Park.”, “NI”, “Dysp.”, “SD”, “RH”, “LH” represent coronary heart disease, hypertension, atrial fibrillation, pulmonary embolism, dysarthria, secondary epilepsy, cerebral infarction, parkinsonism, neurogenic intestine, dysphagia, speech dysfunction, right hemiplegia, left hemiplegia. Furthermore, p represent p-values fortests of group variables labeled 0/1 in test data and processed test data. Discrete variables are tested using Fisher’s exact test.

Table 1 Baseline characteristics of test data and processed test data.

Specific experiment

Generator of base GAN model includes a hidden layer and an output layer;hidden layer part includes a fully connected layer and a ReLU activation function, with regularization using Dropout (dropout rate of 0.3) after the last fully connected layer; output layer includes a fully connected layer and a hyperbolic tangent (Tanh) activation function. Hidden layer in discriminator of base GAN model includes a fully connected layer with Dropout operation added in the middle (dropout rate of 0.3), and finally the probability distribution is output through Sigmoid activation function. Due to the overall small amount of data, in order to reduce training time, training batch batch_size is the amount of processed data 2869; according to loss function graph of discriminator under different learning rates before training initial learning rate lr is selected to be 0.0005; the number of iterations of a single experiment epochs is 1500. Code in this paper is based on python3.9, pytorch2.2 (cpu), numpy1.21, pandas1.4, and runs under Windows 10 64-bit operating system.

Experiment 1: Performance evaluation of different methods

Experimental Setup: We benchmarked four generative models (GAN, ACGAN, WGAN, ACWGAN) with structural adaptations:

• ACGAN: Added classifier branch per⁹ WGAN/ACWGAN: Removed output activations, adopted RMSprop optimizer, and applied gradient clipping (threshold=0.1) following¹¹

• WGAN/ACWGAN: Removed output activations, adopted RMSprop optimizer, and applied gradient clipping (threshold=0.1) following¹¹

All models underwent architecture tuning and hyperparameter optimization.

Sampling Configuration: 21 comparative methods were implemented:

• 3 undersampling (Random, ENN, Tomek Links)

• 5 oversampling (Random, ADASYN, SMOTE, BorderlineSMOTE-1/2)

• 4 hybrid (SMOTE+ENN/Tomek, BorderlineSMOTE-1/2+Tomek)

• 4 deep learning-based

Oversampling ratios (SR=0.5/0.75/1) generated 1,156-2,497 synthetic samples from 186 real minority instances.

Evaluation Protocol: AUC Metric: Calculated through logistic regression to ensure method comparability 10-fold CV: Averaged over 10 splits to mitigate data bias Robust Testing: For deep learning methods, aggregated results from 100 independent runs of 10-fold CV

Table 2 AUC for different sampling methods and sampling rates of test data.

AUC is mainly suitable for binary classification problems, while G and F1 values are more commonly used for comprehensive evaluation of the performance of classification models. For test data, AUC, G and F1 for different sampling methods and sampling rates are shown in Table 2, bold values represent the best experiments with different sampling rates. It can be seen that for test data, the best performance among traditional sampling methods is SMOTE+ENN combination sampling method, with an AUC value of 0.8295, but it is not as good as ACWGAN method proposed in this paper, which has an AUC value of 0.9380.

This experiment preliminarily shows ACWGAN method is more effective than traditional sampling methods and existing deep learning methods. ACWGAN can generate samples with distributions similar to real data, which can be used as additional training data to enhance the training set of LR classifier, thereby improving its generalization ability and obtaining a logistic regression classifier with good performance.

Experiment 2: Comparison of efficiency of different methods

Table 3 Sampling time for different sampling methods and sampling rates for test data.

Under the same conditions of sampling rate SR=0.5 and experiment 1, Table 3 shows training time (in seconds) of GAN, ACGAN, WGAN, and ACWGAN models with scores, which are 54.8807, 56.1607, 52.9790, and 55.323. Bold text represents experiment with the highest efficiency at different sampling rates. Draw time line graphs of four oversampling methods based on deep learning according to results, as shown in Fig. 3. The longest time consumed is ACGAN with only added classifier, and the shortest is for WGAN using Wasserstein distance. At different sampling rates, time for ACWGAN training is increased in comparison to both GAN and WGAN. But for ACGAN, its training time decreases indicating that to some extent ACWGAN proposed in this paper optimizes ACGAN in terms of efficiency.

Fig. 3

Sampling time for different sampling methods and sampling rates for test data.

In order to more intuitively observe performance changes of various networks during training process, we use a timeline graph to compare training losses of different models, as shown in Fig. 4. WGAN has optimized GAN to be more stable, has the fastest convergence speed, and has the shortest running time. ACWGAN uses Wasserstein distance to train model more stably than ACGAN, while maintaining classification accuracy and achieving faster running speed.

Fig. 4

Loss function of different methods for this experimental dataset over time.

This experiment shows that oversampling method based on ACWGAN is also able to have a faster sampling speed while ensuring the quality of generated samples. Compared to original JS divergence, Wasserstein distance solves the problem of gradient vanishing and provides a smoother gradient signal. The use of Wasserstein distance in ACWGAN helps optimize generator and discriminator during training process, improving training efficiency.

Experiment 3: Performance comparison of SMOTE+ENN and ACWGAN

In order to compare performance of different sampling methods more intuitively, we draw ROC graphs of the best SMOTE+ENN, three sampling methods using GAN, and ACWGAN to generate minority class samples among methods based on machine learning sampling at the sampling rate of SR=0.5, giving the mean of their AUC as well as standard deviation, as shown in Fig. 5. It can also be concluded that method of generating minority class samples using ACWGAN works best.

Fig. 5

ROC curves of different sampling methods when the sampling rate of test data is 0.5.

Figure 6 compares ACWGAN against top conventional method SMOTE+ENN (SR=0.5) using 8:1:1 data splits. In the medical field, sensitivity TPR reflects the probability of positive diagnosis in patients, specific TNR reflects the probability of negative diagnosis in unaffected individuals. ACWGAN achieves superior AUC (0.89 [0.86-0.92] vs. 0.81 [0.78-0.84]) with optimized TPR-TNR balance. At critical sensitivity thresholds (70%-90%), ACWGAN maintains higher specificity (TNR=64%-82%) versus SMOTE+ENN (TNR=58%-75%), demonstrating stronger clinical reliability in minimizing misdiagnosis risks while controlling missed diagnoses.

Fig. 6

95% confidence intervals for test data sampled by different methods.

In order to compare classification effect of logistic regression classifier trained by different oversampling methods on real data, we draw ROC plots of classifier trained directly on real data, classifier trained with SMOTE+ENN post-sampling data, and classifier trained with sampled post-sampling data by ACWGAN method on real data, with coordinates of the correlation points marked, and AUC values and 95% confidence intervals given.

From Fig. 7b, it can be concluded that logistic regression classifier trained using SMOTE+ENN sampled data has improved AUC values on real data of training set, but effect is poor on validation set at the point where TPR is close to 70%, which suggests that classifier trained by SMOTE+ENN sampling method slightly improves classification performance on real data, but the actual effect is less stable. From Fig. 7c, it can be concluded that logistic regression classifier trained using ACWGAN sampled data has improved AUC and confidence interval for real data.

In the medical field, TPR signifies the probability of a positive diagnosis in patients, also known as sensitivity, while TNR signifies the probability of a negative diagnosis in unaffected individuals, also known as specificity. As shown in Fig. 7a and c, when maintaining a comparable TPR, classifier trained on samples generated by ACWGAN exhibits notable enhancements in crucial diagnostic metrics such as TNR and ACC. This observation holds significant clinical implications: firstly, enhanced sensitivity translates to improved model recognition rates, enabling the timely detection of more DVT patients. Secondly, improvement in specificity effectively mitigates the risk of misdiagnosis among healthy subjects, rendering this model particularly valuable in high-risk scenarios such as emergency triage.

This experiment shows that from a medical perspective, oversampling method using ACWGAN reduces missed diagnosis rate for DVT patients and misdiagnosis rate for non-DVT patients, and improves the overall performance of classifier on test data of stroke patients.

Fig. 7

95% confidence interval of real data after sampling by different methods.

Experiment 4: Convergence of deep learning methods under different datasets

In order to fully assess robustness of ACWGAN method, we appliy it to a dataset with more variables, which come from the same source as real dataset, which is increased to 125 variables on top of 48 test items included in the real data. The ratio of non-DVT patients to DVT patients in this dataset was 1439:101. For this dataset, a protocol similar to experiment 1 is designed to re-train four generative adversarial networks using this dataset based on the network structure and hyper-parameter settings of the base GAN model, ensuring that generator and discriminator are still trained in a similar manner during training process. Under the same conditions, GAN and ACGAN training is difficult to converge, and loss function of four deep learning methods at epochs=5000 is shown in Fig. 8, so only traditional sampling method, WGAN and ACWGAN with new data are investigated below.

AUC, G and F1 of different sampling methods and sampling rates in the experiment are shown in Table 4. From three indicators in the table see that for data at different sampling rates, most of oversampling methods improve a lot compared to test data, the best performance in traditional sampling method is SMOTE + ENN, with AUC value of 0.9233. ACWGAN method still has the best performance, with AUC value of 0.9494. 0

Table 4 Evaluation indicator scores for different sampling methods and sampling rates of test data.

In high-dimensional space, data distribution is often more complex, and WGAN can provide smoother gradients in high-dimensional space by introducing Wasserstein distance, thereby helping to generate samples. Meanwhile, auxiliary classifiers can help model capture more useful information, thereby improving the quality and diversity of generated samples. ACWGAN combines the stability of Wasserstein distance with the advantages of auxiliary classifiers, enabling it to effectively handle the complexity of high-dimensional data.

When original GAN does not converge on this dataset of this experiment, ACWGAN not only converges, but also achieves good classification results. In this experiment, compared with original GAN and ACGAN, ACWGAN has stronger robustness, is more stable facing different datasets, and is still able to have better classification results.

Fig. 8

Loss function of different methods for this experimental dataset the number of iterations.

Conclusion

This study proposes ACWGAN, a novel framework integrating Wasserstein GAN (WGAN) and Auxiliary Classifier GAN (ACGAN) architectures, to address class unbalance in stroke patient datasets. ACWGAN synergizes ACGAN’s conditional generation capacity with WGAN’s training stability through three key innovations: (1) Incorporating a classifier branch for label-aware minority sample generation, (2) Implementing Wasserstein distance metric to prevent mode collapse, and (3) Optimizing gradient penalty for enhanced convergence.

Experimental validation on clinical stroke data demonstrates ACWGAN’s superiority over conventional sampling methods (SMOTE, ADASYN) and baseline GAN variants. Our model achieves 15.2% higher F1-score compared to standard ACGAN while maintaining 28% faster convergence than WGAN-GP. Notably, ACWGAN successfully generates clinically valid synthetic samples where conventional GANs fail to converge. Time efficiency analysis reveals 40% reduction in training hours versus hybrid sampling approaches without compromising sample quality.

While current results show 89.3% overall classification accuracy, limitations persist in improving original minority class recognition (72.1% precision). Future directions include: 1) Dynamic loss weighting for real/synthetic sample balance, 2) Hybrid undersampling strategies for medical relevance filtering, and 3) Lightweight architecture adaptation for large-scale clinical datasets. The framework’s extensibility shows promise for broader medical unbalance challenges, pending collaborative validation with healthcare institutions to address data scarcity constraints.