Introduction

Soliton waves1,2, or self-reinforcing waves, maintain their shape and velocity even after interacting with other waves. These waves result from the nonlinear interactions of light with the medium it travels through. Solitons are highly valuable in optical fiber communication systems because they can transmit data over long distances with minimal distortion. Recent advancements3,4 have improved insights into the soliton theory within nonlinear fractional models, which incorporate fractional derivatives to capture anomalous transport and diffusion processes in complex media. Compared to classical approaches, fractional-order models describe long-range interactions and nonlocal dynamics more effectively. Furthermore, these models provide a better representation of memory-dependent processes, which are essential for accurately forecasting soliton propagation properties. Nonlinear fractional differential equations5,6 (NLFDEs) have recently become a focal point of interest in the research community. Traveling wave solutions derived from fractional nonlinear models are integral to various fields, including nonlinear optics7,8,9,10,11, optical fiber communications12,13,14,15,16,17,18,19, engineering20,21,22,23,24, and applied sciences25,26,27,28,29,30. Several researchers have proposed and examined different formulations for the fractional derivatives31,32,33,34,35,36. Khalil31 proposed the conformable derivative as a new formulation of fractional derivatives (FD). Later, Atangana and his collaborators investigated its fundamental properties, proving several theorems and introducing a refined definition known as the fractional beta-derivative32,33. This derivative preserves the essential characteristics of classical derivatives, addressing the limitations associated with other fractional derivatives such as the modified Jumarie Riemann-Liouville (JRL) derivative34, Caputo derivative35, and beta derivative36.

Soliton solutions37,38 within optical fiber models are essential for understanding the fundamental properties and behavior of signals. These solutions offer key insights into complex physical phenomena and have garnered increasing attention owing to their practical application in diverse real-world contexts39,40,41,42. Moreover, soliton solutions from both optical fiber models and related systems are significant across various scientific disciplines. Their importance arises from the intricate nature of nonlinear models, which consist of complex functions containing multiple variables and derivatives, thereby presenting considerable analytical challenges. Consequently, this field has become a focal point of extensive research efforts.

Recent research has introduced an array of effective strategies for examining soliton solutions in various nonlinear fractional models, particularly in the field of optical fiber communications. The latest methodologies include those of43,44,45,46,47,48,49. Collectively, these approaches have significantly enhanced the study of fractional-order models, broadening our insight into the intricate dynamics that characterize numerous real-world systems.

The NCLL model is widely utilized for investigating soliton dynamics in fiber-optic communication systems, allowing for the shaping and manipulation of soliton pulses within fibers. In addition, the optical soliton solutions obtained from this model provide a primary foundation for current telecommunication systems. Previous research has explored the NCLL model (1) using a range of techniques, including the Riccati and generalized Bernoulli sub-ODE methods as well as the generalized tanh method50. Other methods include the modified tanh technique51, the derivation of coupled amplitude-phase equations52, and the extended trial equation method53. Various additional approaches have also been employed, such as ansatz methods54, Lie symmetry techniques55, and the Laplace-Adomian decomposition method56. Other notable methods include the trial equation method57, MSE technique58, Adomian techniques59,60, simplest equation method61, new NEHF method62, and bifurcation analysis63.

While the NCLL model50 has been extensively analyzed using various methods, it has not yet been examined through the NGERF method and the NEHF technique, as far as we are aware. These methods represent recent advancements and are particularly relevant to a wide array of nonlinear evolution equations (NLEEs) and nonlinear models. Their flexibility and applicability have attracted significant research attention. Consequently, this study seeks to formulate extensive and generalized optical solitons related to the parameters of the NCLL model using NGERF and NEHF techniques. By selecting specific parameter values, we aim to uncover soliton solutions that have not been documented in previous studies. The accuracy of the derived solutions was validated by employing symbolic computation using Mathematica. In addition, we explore the physical implications of the NCLL model, focusing on its application in the propagation of ultrashort optical solitons for characterizing wave velocities within optical fibers. This analysis also aims to demonstrate wave dispersion in nonlinear media using optical fibers.

The remainder of this article is structured as follows. In the second section, we present the framework of the governing model. Section 3 outlines the algorithm for the beta derivative and the techniques utilized are described in section four. The fifth section focuses on the mathematical analysis of optical solutions. Furthermore, the sixth section provides graphical representations of the Mathematica simulations of the outcomes and concludes with a summary in the final section.

Framework of the NCLL model

The governing equation of the NCLL model is given by64

$$\begin{aligned} i ^{A}_0D^{\gamma }_t U+\zeta ^{A}_0D^{2\gamma }_x U+i\varpi (|U|^2) ^{A}_0D^{\gamma }_{x} U=0;\,\,\,0< \gamma \le 1, \end{aligned}$$
(1)

where U(x, t) represents the normalized envelope of the electric field and \(^{A}_0D^{\gamma }_t,~^{A}_0 D^{\gamma }_x,~^{A}_0 D^{2\gamma }_0\) denote the derivatives of U(x, t) in the context of the beta derivative. The parameter \(\zeta\) (appearing as a coefficient) indicates the dispersion in the group velocity, whereas \(\varpi\) is related to the Bohm potential, especially concerning propagating wave solutions linked to the quantum Hall effect behavior. The NCLL model is a recognized variant of the Schrödinger model (NS). It represents one of three derivative forms of NS64 and is frequently used to enhance our understanding of optical pulse propagation in single-mode fibers and soliton dynamics in fiber-optic communication systems.

Fractional beta derivative

The fractional beta derivative (FBD) is an extension of the established Riemann-Liouville (RL), Caputo, conformable, and modified Riemann (MRL) fractional derivatives. Its relevance has increased substantially owing to its effectiveness in modeling the behavior of various natural phenomena that are insufficiently described by integer-order derivatives. The FBD \(0 < \gamma \le 1\) for a function \(\mathcal {C}:( 0, \infty )\rightarrow \Re\) at \(t > 0\) is defined as follows32,33

$$\begin{aligned} D^\gamma (V(t))=\frac{d^\gamma (V(t))}{d t^\gamma }=\lim _{\epsilon \rightarrow \infty } \frac{V\left( t+\epsilon \left( t+\frac{1}{\Gamma (\gamma )}\right) ^{1-\gamma }\right) -V(t)}{\epsilon }; 0<\gamma \leqslant 1. \end{aligned}$$
(2)

The definition of the FBD outlines the following properties

$$\begin{array}{ll} (i) & D^\gamma (r V(t)+s P(t))=r D^\gamma (V(t))+s D^\gamma (P(t)),\forall r, s \in \mathbb {R}, \\ (ii) & D^\gamma (V(t) P(t)) =P(t) D^\gamma (V(t))+V(t) D^\gamma (P(t)), \\ (iii) & D^\gamma \left( \frac{V(t)}{P(t)}\right) =\frac{P(t) D^\gamma (V(t))-V(t) D^\gamma (P(t))}{P(t)^2}, \\ (iv) & D^\gamma (V(t)) =\left( t+\frac{1}{\Gamma (\gamma )}\right) ^{1-\gamma } \frac{d V(t)}{d t}, \\ (v) & D^\gamma ((V o P)(t)) =\left( t+\frac{1}{\Gamma (\gamma )}\right) ^{1-\gamma } P^{\prime }(t) V^{\prime }(P(t)), \\ (vi) & D^\gamma (b) =0, \text{ where } b \text{ is } \text{ a } \text{ constant. } \end{array}$$
(3)

FBD is a powerful tool for understanding the dynamics of complex systems involving non-integer-order derivatives. Its versatility in performing diverse mathematical and physical operations makes it highly effective in various fields of engineering and science.

Algorithmic implementation of the fractional beta derivative

In this section, we present an overview of the NGERF and NEHF methods, focusing on their application in investigating typical, practical, and more general traveling waves and optical solitons for the NCLL model (1).

Taking into account the general structure of the model

$$\begin{aligned} E(U, D_t^{\gamma }(U), D_x^{\gamma }(U), D_{xx}^{2\gamma }(U), D_{tt}^{2\gamma }(U), \ldots ) = 0, \end{aligned}$$
(4)

where E denotes a nonlinear function, and U(x, t) denotes the wave function. In order to transform the (4), the wave variable is defined in the following way

$$\begin{aligned} U(x,t)=W(\Lambda )e^{i\kappa (x,t)}, \end{aligned}$$
(5)

where the wave variable is defined as

$$\begin{aligned} \Lambda =\frac{1}{\gamma }\bigg (x+\frac{1}{\Gamma (\gamma )}\bigg )^{\gamma } -\frac{c}{\gamma }\bigg (t+\frac{1}{\Gamma (\gamma )}\bigg )^{\gamma }, \end{aligned}$$
(6)

and the phase component is given by

$$\begin{aligned} \kappa (x,t)=-\frac{k}{\gamma }\bigg (x+\frac{1}{\Gamma (\gamma )}\bigg )^{\gamma } +\frac{w}{\gamma }\bigg (t+\frac{1}{\Gamma (\gamma )}\bigg )^{\gamma }+\chi _0(\Lambda ), \end{aligned}$$
(7)

where w is defined as the frequency, \(\chi _0\) is referred to as a phase function depending on the variable \(\Lambda\), k signifies the wave number corresponding to the soliton, and c is the velocity of the wave. These components are employed to transform the model (4) into its nonlinear form as follows

$$\begin{aligned} H(W,W',W'',...)=0. \end{aligned}$$
(8)

In the expression above Eq (8), H is a polynomial function of \(W,\,\,W',\,\,W'',...,\) where \(W'(\Lambda )=\frac{dW}{d\Lambda }\).

Systematic algorithm for the generalized exponential rational function method

The primary steps of the proposed scheme are outlined as follows:

  • Step 1 The assumed solution to the ODE (8) is given as follows

    $$\begin{aligned} W(\Lambda )=c_0+\sum _{i=1}^{N}c_iK(\Lambda )^{i}+\sum _{i=1}^{N}d_iK(\Lambda )^{-i}. \end{aligned}$$
    (9)

    such that the function \(K(\Lambda )\) given by

    $$\begin{aligned} K(\Lambda )=\frac{\lambda _1e^{(\varrho _1\Lambda )}+\lambda _2e^{(\varrho _2\Lambda )}}{\lambda _3e^{(\varrho _3\Lambda )}+\lambda _4e^{(\varrho _4\Lambda )}}, \end{aligned}$$
    (10)

    where \(\lambda _n,~\varrho _n (1\le n \le 4)\) are constants that may be real or complex. The coefficients \(c_0,~c_i,~d_i~(1 \le {i} \le {N})\) are subsequently determined. Notably, the balancing principle can be employed to ascertain the positive integer N.

  • Step 2 Inserting Eq (9) into Eq (8) and collecting all terms, the left-hand side of Eq (8) is transformed into the polynomial equation \(P(\mathcal {F}_1,\mathcal {F}_2,\mathcal {F}_3,\mathcal {F}_4)=0\) in terms of \(\mathcal {F}_i=e^{\varrho _i\Lambda }\) for \(i=1,2,...,4\). Setting each coefficient of P to zero, we derive a set of algebraic equations for \(\lambda _n,\varrho _n~(1\le {n}\le {4})\) and \(c_0,c_1,d_1\) using Maple’s symbolic computation.

  • Step 3 The soliton structures of (1) can be acquired by finding the solution of the algebraic equations and then substituting the non-trivial structure in (9).

Algorithm of the new extended hyperbolic function method

The primary steps of the new EHFM are outlined in this section as follows

Form 1: We assume that the solution of Eq (8) can be expressed in the following form

$$\begin{aligned} W(\Lambda )=\sum _{i=0}^{N}g_i M^i(\Lambda ) \end{aligned}$$
(11)

where the coefficients \(g_i(i = (1,2,\cdots N))\) are constants to be determined later, and \(M(\Lambda )\) satisfies the following ODE

$$\begin{aligned} \frac{dM}{d\Lambda }=\sqrt{Q+RM^2},\,\,\,Q,\,\,R \in \textbf{R}. \end{aligned}$$
(12)

In Eq (11), to determine N, we balance the highest-order derivative with the highest power of the nonlinear term. Then, by solving the algebraic system, we obtain the following set of solutions:

Set 1: For the case of \(Q >0\) and \(R >0\),

$$\begin{aligned} M(\Lambda )=-\sqrt{\frac{Q}{R}}csch(\sqrt{Q}(\Lambda +\Lambda _0)). \end{aligned}$$
(13)

Set 2: For the case of \(Q <0\) and \(R >0\),

$$\begin{aligned} M(\Lambda )=\sqrt{-\frac{Q}{R}}\sec (\sqrt{-Q}(\Lambda +\Lambda _0)). \end{aligned}$$
(14)

Set 3: For the case of \(Q>0\) and \(R <0\),

$$\begin{aligned} M(\Lambda )=\sqrt{-\frac{Q}{R}}\text {sech}(\sqrt{Q}(\Lambda +\Lambda _0)). \end{aligned}$$
(15)

Set 4: For the case of \(Q<0\) and \(R >0\),

$$\begin{aligned} M(\Lambda )=\sqrt{-\frac{Q}{R}}\text {csc}(\sqrt{-Q}(\Lambda +\Lambda _0)). \end{aligned}$$
(16)

Set 5: For the case of \(Q >0\) and \(R =0\),

$$\begin{aligned} M(\Lambda )=\exp (\sqrt{Q}(\Lambda +\Lambda _0)). \end{aligned}$$
(17)

Set 6: For the case of \(Q<0\) and \(R =0\),

$$\begin{aligned} M(\Lambda )=\cos (\sqrt{-Q}(\Lambda +\Lambda _0))+i \text {sin}(\sqrt{-Q}(\Lambda +\Lambda _0)). \end{aligned}$$
(18)

Set 7: For the case of \(Q =0\) and \(R >0\),

$$\begin{aligned} M(\Lambda )=\pm \frac{1}{(\sqrt{R}(\Lambda +\Lambda _0))}. \end{aligned}$$
(19)

Set 8: For the case of \(Q =0\) and \(R <0\),

$$\begin{aligned} M(\Lambda )=\pm \frac{i}{(\sqrt{-R}(\Lambda +\Lambda _0))}. \end{aligned}$$
(20)

Form 2: Using a similar approach and following the same steps as before, we assume that the function \(M(\Lambda )\) satisfies the ODE in the following form

$$\begin{aligned} \frac{dM}{d\Lambda }=Q+RM^2,\,\,\,Q,\,R\in \textbf{R}. \end{aligned}$$
(21)

In this case, the following solutions can be pursued:

Set 1: For the case of \(QR >0\),

$$\begin{aligned} M(\Lambda )=\operatorname {sgn}(Q)\sqrt{\frac{Q}{R}}\tan (\sqrt{QR}(\Lambda +\Lambda _0)). \end{aligned}$$
(22)

Set 2: For the case of \(QR >0\),

$$\begin{aligned} M(\Lambda )=-\operatorname {sgn}(Q)\sqrt{\frac{Q}{R}}\cot (\sqrt{QR}(\Lambda +\Lambda _0)). \end{aligned}$$
(23)

Set 3: For the case of \(QR <0\),

$$\begin{aligned} M(\Lambda )=\operatorname {sgn}(Q)\sqrt{-\frac{Q}{R}}\tanh (\sqrt{-QR}(\Lambda +\Lambda _0)). \end{aligned}$$
(24)

Set 4: For the case of \(QR <0\),

$$\begin{aligned} M(\Lambda )=\operatorname {sgn}(Q)\sqrt{-\frac{Q}{R}}\coth (\sqrt{-QR}(\Lambda +\Lambda _0)). \end{aligned}$$
(25)

Set 5: For the case of \(Q=0\) and \(R<0\),

$$\begin{aligned} M(\Lambda )=-\frac{1}{(\sqrt{-R}(\Lambda +\Lambda _0))}. \end{aligned}$$
(26)

Set 6: For the case of \(Q =0\) and \(R>0\),

$$\begin{aligned} M(\Lambda )=(\sqrt{R}(\Lambda +\Lambda _0)), \end{aligned}$$
(27)

where in above cases \(\operatorname {sgn}\) is the well-known signum function, is defined as

$$\begin{aligned} \operatorname {sgn}(x) = {\left\{ \begin{array}{ll} 1, & \text {if } x > 0, \\ 0, & \text {if } x = 0, \\ -1, & \text {if } x < 0. \end{array}\right. } \end{aligned}$$

Mathematical formulation for the wave form solutions

The following section provides more extensive, functional, and illustrative optical soliton solutions for the NCLL model (1) using two robust, compatible, and efficient analytical methods. The model was reformulated into a nonlinear integer-order form by utilizing a complex wave transformation.

By implementing the wave transformation (5) and isolating the real and imaginary components, we arrive at the following formulation of the NCLL model (1)

$$\begin{aligned} -w W+c W \chi ^{\prime }_0+\zeta W^{\prime \prime }-\zeta W \chi ^{\prime 2}_0-\zeta k^2 W+2 \zeta k W \chi ^{\prime }_0-\varpi W^3 \chi ^{\prime }_0+\zeta k W^3=0, \end{aligned}$$
(28)

and

$$\begin{aligned} \zeta \left( W \chi ^{\prime \prime }_0+2 W^{\prime } \chi ^{\prime }_0\right) -c W^{\prime }-2 \zeta k W^{\prime }+\varpi W^2 \chi ^{\prime }_0=0, \end{aligned}$$
(29)

where \(W^{\prime }=\frac{d W}{d \Lambda }, W^{\prime \prime }=\frac{d^2 W}{d \Lambda ^2}, \chi ^{\prime }_0=\frac{d \chi _0}{d \Lambda }\) and \(\chi ^{\prime \prime }_0=\frac{d^2 \chi _0}{d \Lambda ^2}\). To solve the preceding equations, we employ the following transformation

$$\begin{aligned} \chi ^{\prime }_0=y_1 u^2+y_2, \end{aligned}$$
(30)

where \(y_1\) and \(y_2\) represent the nonlinear and constant chirp parameters, respectively, that must be determined. By substituting equation (30) into equation (29), we obtain two equations that determine the chirp parameters

$$\begin{aligned} y_1=-\frac{\varpi }{4 \zeta }, y_2=k+\frac{c}{2 \zeta }, \end{aligned}$$
(31)

Substituting equations (31) and (30) into equation (29) yields

$$\begin{aligned} W^{\prime \prime }+A_1 W+A_2 W^3+A_3 W^5=0, \end{aligned}$$
(32)

where \(A_1=\frac{c^2}{4 \zeta ^2}+\frac{c k}{\zeta }-\frac{w}{\zeta }, A_2=-\frac{\varpi c}{2 \zeta ^2}, A_3=\frac{3 \varpi ^2}{16 \zeta ^2}.\) Using the principle of homogeneous balancing, we find from equation (32) that \(N=\frac{1}{2}.\) When the balance number is non-integer, we can utilize a different transformation, such as

$$\begin{aligned} W=Y^\frac{1}{2}. \end{aligned}$$
(33)

Consequently, equation (32) transforms into

$$\begin{aligned} 4 A_1 Y^2+4 A_2 Y^3+4 A_3 Y^4+2 Y Y^{\prime \prime }-Y^{\prime 2}=0, \end{aligned}$$
(34)

where \(A_1=\frac{c^2}{4 \zeta ^2}+\frac{c k}{\zeta }-\frac{w}{\zeta }, A_2=-\frac{\varpi c}{2 \zeta ^2}, A_3=\frac{3 \varpi ^2}{16 \zeta ^2}\). The solutions of equation (34) combined with equation (33) allow us to obtain the standard and additional soliton solutions for the NCLL model (1).

Exploring multi-soliton solutions using NGERF

In this subsection, we derive various broad-spectrum general and fundamental soliton solutions for the NCLL model using the NGERF method. According to Eq (34), the balancing index is \(N=1\), which indicates that the optical solitons of (34) assume the following form

$$\begin{aligned} Y(\Lambda )=c_0+c_1 K(\Lambda )+\frac{d_1}{K(\Lambda )}, \end{aligned}$$
(35)

where \(c_0, c_1,~d_1\) are the parameters to be evaluated, such that \(c_1\ne 0\) or \(d_1\ne 0\). By adhering to Step 3 of the outlined approach, the following families and nontrivial structures for (1) can be derived.

Class 1:

$$\begin{aligned} \lambda _1=1,~\lambda _2=-1,~\lambda _3=1,~\lambda _4=1,~~~\varrho _1=1,~\varrho _2=-1,~\varrho _3=1,~\varrho _4=-1 \end{aligned}$$
$$\begin{aligned} K(\Lambda )=\frac{\sinh (\Lambda )}{\cosh (\Lambda )} \end{aligned}$$
(36)

Set 1.1

$$\begin{aligned} c=0,\,\,\,\zeta =w,\,\,\,c_0=0,\,\,\,c_1=\frac{2iw}{\varpi },\,\,\,d_1=-\frac{2i w}{\varpi }. \end{aligned}$$
(37)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{2iw}{\varpi }\left( \frac{\sinh (\Lambda )}{\cosh (\Lambda )}-\frac{\cosh (\Lambda )}{\sinh (\Lambda )}\right) . \end{aligned}$$
(38)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{1}(x,t)=\left( \frac{2iw}{\varpi }\left( \frac{\sinh (\Lambda )}{\cosh (\Lambda )}-\frac{\cosh (\Lambda )}{\sinh (\Lambda )}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(39)

For \(c = 0\) in the solution (39), reduces the wave variable \(\Lambda\)

$$\begin{aligned} \Lambda = \frac{1}{\gamma } \left( x + \frac{1}{\Gamma (\gamma )} \right) ^\gamma . \end{aligned}$$

This means that \(\Lambda\) depends only on the spatial variable \(x\) and is no longer coupled to the temporal variable \(t\). This suggests that the resulting solutions are static or stationary solutions that are entirely dependent on the spatial variable \(x\). These solutions include standing waves, spatially localized solitons, or stable waveforms that do not propagate or evolve in time. The absence of time dependence in \(\Lambda\) eliminates any possibility of dynamic wave propagation.

Set 1.2

$$\begin{aligned} c=\frac{w}{k},\,\,\,\zeta =\frac{iw}{2k},\,\,\,c_0=\frac{w}{k\varpi },\,\,\,c_1=0,\,\,\,d_1=\frac{w}{k\varpi }. \end{aligned}$$
(40)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{w}{k\varpi }\left( 1+\frac{\cosh (\Lambda )}{\sinh (\Lambda )}\right) \cdot \end{aligned}$$
(41)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{2}(x,t)=\left( \frac{w}{k\varpi }\left( 1+\frac{\cosh (\Lambda )}{\sinh (\Lambda )}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(42)

Set 1.3

$$\begin{aligned} c=\frac{4w}{4k-1},\,\,\,\zeta =\frac{w}{4k-1},\,\,\,c_0=\frac{4w}{\varpi (4k-1)},\,\,\,c_1=\frac{2iw}{\varpi (4k-1)},\,\,\,d_1=-\frac{2iw}{\varpi (4k-1)}. \end{aligned}$$
(43)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{2w}{\varpi (4k-1)}\left( 2+i\frac{\sinh (\Lambda )}{\cosh (\Lambda )}-i\frac{\cosh (\Lambda )}{\sinh (\Lambda )}\right) \cdot \end{aligned}$$
(44)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{3}(x,t)=\left( \frac{2w}{\varpi (4k-1)}\left( 2+i\frac{\sinh (\Lambda )}{\cosh (\Lambda )}-i\frac{\cosh (\Lambda )}{\sinh (\Lambda )}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(45)

Set 1.4

$$\begin{aligned} c=\frac{w}{k},\,\,\,\zeta =\frac{iw}{2k},\,\,\,c_0=\frac{w}{k\varpi },\,\,\,c_1=\frac{w}{k\varpi },\,\,\,d_1=0. \end{aligned}$$
(46)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{w}{k\varpi }\left( 1+\frac{\sinh (\Lambda )}{\cosh (\Lambda )}\right) \cdot \end{aligned}$$
(47)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{4}(x,t)=\left( \frac{w}{k\varpi }\left( 1+\frac{\sinh (\Lambda )}{\cosh (\Lambda )}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(48)

Set 1.5

$$\begin{aligned} c=\frac{w}{k},\,\,\,\zeta =\frac{iw}{4k},\,\,\,c_0=\frac{w}{k\varpi },\,\,\,c_1=\frac{w}{2k\varpi },\,\,\,d_1=\frac{w}{2k\varpi }. \end{aligned}$$
(49)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{w}{k\varpi }\left( 1+\frac{\sinh (\Lambda )}{2\cosh (\Lambda )}+\frac{\cosh (\Lambda )}{2\sinh (\Lambda )}\right) \cdot \end{aligned}$$
(50)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{5}(x,t)=\left( \frac{w}{k\varpi }\left( 1+\frac{\sinh (\Lambda )}{2\cosh (\Lambda )} +\frac{\cosh (\Lambda )}{2\sinh (\Lambda )}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(51)

Class 2:

$$\begin{aligned} \lambda _1=2+i,~\lambda _2=2-i,~\lambda _3=1,~\lambda _4=1,~~~\varrho _1=-i,~\varrho _2=i,~\varrho _3=-i,~\varrho _4=i \end{aligned}$$
$$\begin{aligned} W(\Lambda )=\frac{\sin (\Lambda )+2\cos (\Lambda )}{\cos (\Lambda )}\cdot \end{aligned}$$
(52)

Set 2.1

$$\begin{aligned} k=\frac{w}{c},\,\,\,\zeta =\frac{c}{2},\,\,\,c_0=\frac{(1+2i)c}{\varpi },\,\,\,c_1=0,\,\,\,d_1=-\frac{5ic}{\varpi }. \end{aligned}$$
(53)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{c}{\varpi }\left( 1+2i-\frac{i\cos (\Lambda )}{\sin (\Lambda )+2\cos (\Lambda )}\right) \cdot \end{aligned}$$
(54)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{6}(x,t)=\left( \frac{c}{\varpi }\left( 1+2i-\frac{i\cos (\Lambda )}{\sin (\Lambda )+2\cos (\Lambda )}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(55)

Set 2.2

$$\begin{aligned} k=\frac{5ic+4w}{4k},\,\,\,\zeta =\frac{ic}{4},\,\,\,c_0=\frac{2c}{\varpi },\,\,\,c_1=-\frac{c}{2\varpi },\,\,\,d_1=-\frac{c}{2\varpi }. \end{aligned}$$
(56)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{2c}{\varpi }\left( 1-\frac{\sin (\Lambda )+2\cos (\Lambda )}{4\cos (\Lambda )}-\frac{\cos (\Lambda )}{4(\sin (\Lambda )+2\cos (\Lambda ))}\right) \cdot \end{aligned}$$
(57)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{7}(x,t)=\left( \frac{2c}{\varpi }\left( 1-\frac{\sin (\Lambda )+2\cos (\Lambda )}{4\cos (\Lambda )}-\frac{\cos (\Lambda )}{4(\sin (\Lambda )+2\cos (\Lambda ))}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(58)

Set 2.3

$$\begin{aligned} k=\frac{w}{c},\,\,\,\zeta =\frac{c}{2},\,\,\,c_0=\frac{(1-2i)c}{\varpi },\,\,\,c_1=\frac{ic}{\varpi },\,\,\,d_1=0. \end{aligned}$$
(59)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{c}{\varpi }\left( 1-2i+i\frac{\sin (\Lambda )+2\cos (\Lambda )}{\cos (\Lambda )}\right) \cdot \end{aligned}$$
(60)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{8}(x,t)=\left( \frac{c}{\varpi }\left( 1-2i+i\frac{\sin (\Lambda )+2\cos (\Lambda )}{\cos (\Lambda )}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(61)

Set 2.4

$$\begin{aligned} k &= -\frac{2}{c(\sqrt{5}-1)(209\sqrt{5}-483)}\left(\frac{1}{4}I (836i(\sqrt{5}-1) \left(\frac{\sqrt{5}-1}{2} \right)w-548i (\sqrt{5}-1)w-2213 \left(\frac{\sqrt{5}-1}{2} \right)c \right. \\ & \quad +1326c ) ),\,\,\,\zeta =\frac{ic(\sqrt{5}-1)}{16},\,\,\,c_0=\frac{c(2\sqrt{5}-5)}{\varpi (\sqrt{5}-3)},\,\,\, c_1=\frac{c(\sqrt{5}-1)}{8\varpi },\,\,\,d_1=-\frac{5c(7\sqrt{5}-123)}{8\varpi (29\sqrt{5}+22)}. \end{aligned}$$
(62)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} \begin{aligned} Y(\Lambda )&=\frac{c(2\sqrt{5}-5)}{\varpi (\sqrt{5}-3)}+\frac{c(\sqrt{5}-1)}{8\varpi }\frac{\sin (\Lambda )+2\cos (\Lambda )}{\cos (\Lambda )}\\ & \quad - \frac{5c(7\sqrt{5}-123)}{8\varpi (29\sqrt{5}+22)}\frac{\cos (\Lambda )}{(\sin (\Lambda )+2\cos (\Lambda ))}\cdot \end{aligned} \end{aligned}$$
(63)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} \begin{aligned} U_{9}(x,t)&=\Bigg (\frac{c(2\sqrt{5}-5)}{\varpi (\sqrt{5}-3)}+\frac{c(\sqrt{5}-1)}{8\varpi }\frac{\sin (\Lambda )+2\cos (\Lambda )}{\cos (\Lambda )}\\ & \quad - \frac{5c(7\sqrt{5}-123)}{8\varpi (29\sqrt{5}+22)}\frac{\cos (\Lambda )}{(\sin (\Lambda )+2\cos (\Lambda ))}\Bigg )^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned} \end{aligned}$$
(64)

Class 3:

$$\begin{aligned} \lambda _1=i,~\lambda _2=-i,~\lambda _3=1,~\lambda _4=1,~~~\varrho _1=i,~\varrho _2=-i,~\varrho _3=i,~\varrho _4=-i \end{aligned}$$
$$\begin{aligned} W(\Lambda )=-\frac{\sin (\Lambda )}{\cos (\Lambda )}\cdot \end{aligned}$$
(65)

Set 3.1

$$\begin{aligned} c=\frac{w}{k},\,\,\,\zeta =\frac{w}{2k},\,\,\,c_0=\frac{w}{k\varpi },\,\,\,c_1=0,\,\,\,d_1=\frac{iw}{k\varpi }. \end{aligned}$$
(66)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{w}{k\varpi }\left( 1-i\frac{\cos (\Lambda )}{\sin (\Lambda )}\right) \cdot \end{aligned}$$
(67)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{10}(x,t)=\left( \frac{w}{k\varpi }\left( 1-i\frac{\cos (\Lambda )}{\sin (\Lambda )}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(68)

Set 3.2

$$\begin{aligned} c=\frac{w}{k},\,\,\,\zeta =-\frac{w}{2k},\,\,\,c_0=\frac{w}{k\varpi },\,\,\,c_1=\frac{iw}{k\varpi },\,\,\,d_1=0. \end{aligned}$$
(69)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{w}{k\varpi }\left( 1-i\frac{\sin (\Lambda )}{\cos (\Lambda )}\right) \cdot \end{aligned}$$
(70)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{11}(x,t)=\left( \frac{w}{k\varpi }\left( 1-i\frac{\sin (\Lambda )}{\cos (\Lambda )}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(71)

Set 3.3

$$\begin{aligned} c=\frac{w}{k},\,\,\,\zeta =\frac{w}{4k},\,\,\,c_0=\frac{w}{k\varpi },\,\,\,c_1=\frac{iw}{2k\varpi },\,\,\,d_1=-\frac{iw}{2k\varpi }. \end{aligned}$$
(72)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{w}{k\varpi }\left( 1-i\frac{\sin (\Lambda )}{2\cos (\Lambda )}+i\frac{\cos (\Lambda )}{2\sin (\Lambda )}\right) \cdot \end{aligned}$$
(73)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{12}(x,t)=\left( \frac{w}{k\varpi }\left( 1-i\frac{\sin (\Lambda )}{2\cos (\Lambda )}+i\frac{\cos (\Lambda )}{2\sin (\Lambda )}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(74)

Class 4:

$$\begin{aligned} \lambda _1=2,~\lambda _2=1,~\lambda _3=1,~\lambda _4=1,~~~\varrho _1=1,~\varrho _2=0,~\varrho _3=1,~\varrho _4=0 \end{aligned}$$
$$\begin{aligned} W(\Lambda )=\frac{2e^{\Lambda }+1}{e^{\Lambda }+1}\cdot \end{aligned}$$
(75)

Set 4.1

$$\begin{aligned} k=\frac{2ic+3w}{3c},\,\,\,\zeta =\frac{ic}{3},\,\,\,c_0=\frac{2c}{\varpi },\,\,\,c_1=-\frac{2c}{3\varpi },\,\,\,d_1=-\frac{4c}{3\varpi }. \end{aligned}$$
(76)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{2c}{3\varpi }\left( 3-\frac{2e^{\Lambda }+1}{e^{\Lambda }+1} -2\frac{e^{\Lambda }+1}{2e^{\Lambda }+1}\right) \cdot \end{aligned}$$
(77)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{13}(x,t)=\left( \frac{2c}{3\varpi }\left( 3-\frac{2e^{\Lambda }+1}{e^{\Lambda }+1} -2\frac{e^{\Lambda }+1}{2e^{\Lambda }+1}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}, \end{aligned}$$
(78)

Set 4.2

$$\begin{aligned} \begin{aligned} k&=-\frac{1}{c(4\sqrt{2}-3)(-17+12\sqrt{2})} \bigg (\frac{1}{4}i \bigg (276i \left(-\frac{3}{23}+\frac{4}{23}\sqrt{2} \right)(4\sqrt{2}-3)w- 2019 \left(-\frac{3}{23}+\frac{4}{23}\sqrt{2} \right)c\\& \quad -32i(4\sqrt{2}-3)w+33c\bigg )\bigg ),\,\,\, \zeta =\frac{ic(4\sqrt{2}-3)}{23},\,\,\,c_0=\frac{2c(-144+100\sqrt{2})}{23\varpi (4\sqrt{2}-6)},\,\,\, c_1=\frac{2c(-3+4\sqrt{2})}{23\varpi },\,\,\,\\d_1 & =\frac{4c(-3+4\sqrt{2})}{23\varpi )}. \end{aligned} \end{aligned}$$
(79)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{2c(-144+100\sqrt{2})}{23\varpi (4\sqrt{2}-6)}+\frac{2c(-3+4\sqrt{2})}{23\varpi }\frac{2e^{\Lambda }+1}{e^{\Lambda }+1} +\frac{4c(-3+4\sqrt{2})}{23\varpi )}\frac{e^{\Lambda }+1}{2e^{\Lambda }+1}, \end{aligned}$$
(80)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{14}(x,t)=\left( \frac{2c(-144+100\sqrt{2})}{23\varpi (4\sqrt{2}-6)}+\frac{2c(-3+4\sqrt{2})}{23\varpi }\frac{2e^{\Lambda }+1}{e^{\Lambda }+1} +\frac{4c(-3+4\sqrt{2})}{23\varpi )}\frac{e^{\Lambda }+1}{2e^{\Lambda }+1}\right) ^\frac{1}{2}\times e^{i\kappa (x,t)}, \end{aligned}$$
(81)

Set 4.3

$$\begin{aligned} k=\frac{w}{c},\,\,\,\zeta =ic,\,\,\,c_0=-\frac{2c}{\varpi },\,\,\,c_1=\frac{2c}{\varpi },\,\,\,d_1=0. \end{aligned}$$
(82)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{2c}{\varpi }\left( -1+\frac{2e^{\Lambda }+1}{e^{\Lambda }+1}\right) \cdot \end{aligned}$$
(83)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{15}(x,t)=\left( \frac{2c}{\varpi }\left( -1+\frac{2e^{\Lambda }+1}{e^{\Lambda }+1}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}, \end{aligned}$$
(84)

Class 5:

$$\begin{aligned} \lambda _1=1-i,~\lambda _2=1+i,~\lambda _3=1,~\lambda _4=1,~~~\varrho _1=-i,~\varrho _2=i,~\varrho _3=-i,~\varrho _4=0 \end{aligned}$$
$$\begin{aligned} W(\Lambda )=\frac{-\sin (\Lambda )+\cos (\Lambda )}{\cos (\Lambda )}\cdot \end{aligned}$$
(85)

Set 5.1

$$\begin{aligned} k=\frac{w}{c},\,\,\,\zeta =-\frac{c}{2},\,\,\,c_0=\frac{(1+i)c}{\varpi },\,\,\,c_1=0,\,\,\,d_1=-\frac{2ic}{\varpi }. \end{aligned}$$
(86)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{c}{\varpi }\left( 1+i-2i\frac{\cos (\Lambda )}{-\sin (\Lambda )+\cos (\Lambda )}\right) . \end{aligned}$$
(87)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{16}(x,t)=\left( \frac{c}{\varpi }\left( 1+i-2i\frac{\cos (\Lambda )}{-\sin (\Lambda )+\cos (\Lambda )}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(88)

Set 5.2

$$\begin{aligned} k=\frac{w}{c},\,\,\,\zeta =\frac{c}{2},\,\,\,c_0=\frac{(1-i)c}{\varpi },\,\,\,c_1=\frac{ic}{\varpi },\,\,\,d_1=0. \end{aligned}$$
(89)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{c}{\varpi }\left( 1-i+i\frac{-\sin (\Lambda )+\cos (\Lambda )}{\cos (\Lambda )}\right) \cdot \end{aligned}$$
(90)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{17}(x,t)=\left( \frac{c}{\varpi }\left( 1-i+i\frac{-\sin (\Lambda )+\cos (\Lambda )}{\cos (\Lambda )}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(91)

Set 5.3

$$\begin{aligned} k=\frac{ic+w}{c},\,\,\,\zeta =\frac{ic}{2},\,\,\,c_0=\frac{2c}{\varpi },\,\,\,c_1=-\frac{c}{\varpi },\,\,\,d_1=-\frac{c}{\varpi }. \end{aligned}$$
(92)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{2c}{\varpi }\left( 1-\frac{-\sin (\Lambda )+\cos (\Lambda )}{2\cos (\Lambda )}-\frac{\cos (\Lambda )}{-\sin (\Lambda )+\cos (\Lambda )}\right) \cdot \end{aligned}$$
(93)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{18}(x,t)=\left( \frac{2c}{\varpi }\left( 1-\frac{-\sin (\Lambda )+\cos (\Lambda )}{2\cos (\Lambda )}-\frac{\cos (\Lambda )}{-\sin (\Lambda )+\cos (\Lambda )}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(94)

Set 5.4

$$\begin{aligned} \begin{aligned} k&=-\frac{7}{c(2\sqrt{2}-1)(-401+298\sqrt{2})}\bigg (\frac{1}{14}i\bigg (2086i(-1+2\sqrt{2}) \left(-\frac{1}{7}+\frac{2}{7}\sqrt{2} \right)w- 504i(-1+2\sqrt{2})w\\ &\quad - 1707 \left(-\frac{1}{7}+\frac{2}{7}\sqrt{2} \right)r+493c\bigg)\bigg ),\,\,\, \zeta =\frac{ic(2\sqrt{2}-1)}{14},\,\,\,c_0=\frac{c(-88+50\sqrt{2})}{7\varpi (4\sqrt{2}-9)},\,\,\, c_1=\frac{c (-1+2\sqrt{2})}{7\varpi },\,\,\,\\ d_1 &=\frac{2c(-1+2\sqrt{2})}{7\varpi )}. \end{aligned} \end{aligned}$$
(95)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{c(-88+50\sqrt{2})}{7\varpi (4\sqrt{2}-9)}+\frac{c(-1+2\sqrt{2})}{7\varpi }\frac{-\sin (\Lambda )+\cos (\Lambda )}{\cos (\Lambda )} +\frac{2c(-1+2\sqrt{2})}{7\varpi )}\frac{\cos (\Lambda )}{-\sin (\Lambda )+\cos (\Lambda )}\cdot \end{aligned}$$
(96)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} \begin{aligned} U_{19}(x,t)&=\bigg (\frac{c(-88+50\sqrt{2})}{7\varpi (4\sqrt{2}-9)}+\frac{c(-1+2\sqrt{2})}{7\varpi }\frac{-\sin (\Lambda )+\cos (\Lambda )}{\cos (\Lambda )} +\frac{2c(-1+2\sqrt{2})}{7\varpi }\\ & \quad \frac{\cos (\Lambda )}{-\sin (\Lambda )+\cos (\Lambda )}\bigg )^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned} \end{aligned}$$
(97)

Class 6:

$$\begin{aligned} \lambda _1=2+i,~\lambda _2=2-i,~\lambda _3=1,~\lambda _4=1,~~~\varrho _1=-i,~\varrho _2=i,~\varrho _3=-i,~\varrho _4=i \end{aligned}$$
$$\begin{aligned} W(\Lambda )=\frac{\sin (\Lambda )-2\cos (\Lambda )}{\cos (\Lambda )}\cdot \end{aligned}$$
(98)

Set 6.1

$$\begin{aligned} k=\frac{w}{c},\,\,\,\zeta =\frac{c}{2},\,\,\,c_0=\frac{(1+2i)c}{\varpi },\,\,\,c_1=0,\,\,\,d_1=-\frac{5ic}{\varpi }. \end{aligned}$$
(99)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{c}{\varpi }\left( 1+2i-5i\frac{\cos (\Lambda )}{\sin (\Lambda )-2\cos (\Lambda )}\right) . \end{aligned}$$
(100)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{20}(x,t)=\left( \frac{c}{\varpi }\left( 1+2i-5i\frac{\cos (\Lambda )}{\sin (\Lambda )-2\cos (\Lambda )}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(101)

Set 6.2

$$\begin{aligned} k=\frac{5ir+4w}{c},\,\,\,\zeta =\frac{ic}{4},\,\,\,c_0=\frac{2c}{\varpi },\,\,\, c_1=\frac{c}{2\varpi },\,\,\,d_1=\frac{5c}{2\varpi }. \end{aligned}$$
(102)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{c}{2\varpi }\left( 4+\frac{\sin (\Lambda )-2\cos (\Lambda )}{\cos (\Lambda )} +5\frac{\cos (\Lambda )}{\sin (\Lambda )-2\cos (\Lambda )}\right) \cdot \end{aligned}$$
(103)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{21}(x,t)=\left( \frac{c}{2\varpi }\left( 4+\frac{\sin (\Lambda )-2\cos (\Lambda )}{\cos (\Lambda )} +5\frac{\cos (\Lambda )}{\sin (\Lambda )-2\cos (\Lambda )}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(104)

Set 6.3

$$\begin{aligned} k=\frac{w}{c},\,\,\,\zeta =-\frac{c}{2},\,\,\,c_0=\frac{(1+2i)c}{\varpi },\,\,\,c_1=\frac{ic}{\varpi },\,\,\,d_1=0. \end{aligned}$$
(105)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{c}{\varpi }\left( 1+2i+i\frac{\sin (\Lambda )-2\cos (\Lambda )}{\cos (\Lambda )}\right) \cdot \end{aligned}$$
(106)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{22}(x,t)=\left( \frac{c}{\varpi }\left( 1+2i+i\frac{\sin (\Lambda )-2\cos (\Lambda )}{\cos (\Lambda )}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(107)

Set 6.4

$$\begin{aligned} \begin{aligned} k&=-\frac{2}{c(\sqrt{5}+1)(483+209\sqrt{5})}\bigg (\frac{1}{4}i\bigg (836i(1+\sqrt{5})(\frac{1}{2}+\frac{1}{2}\sqrt{5})w- 548i(1+\sqrt{5})w\\ & \quad -2213 \left(\frac{1}{2}+\frac{1}{2}\sqrt{5} \right)c+1326r\bigg )\bigg ),\,\,\, \zeta =\frac{ic(2\sqrt{5}+5)}{16},\,\,\,c_0=\frac{c(2\sqrt{5}+5)}{\varpi (\sqrt{5}+3)},\,\,\, c_1=\frac{c(\sqrt{5}+1)}{8\varpi },\,\,\,\\ d_1 & =\frac{5c(123+7\sqrt{5})}{8\varpi (29\sqrt{5}-22)}. \end{aligned} \end{aligned}$$
(108)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\left( \frac{c(2\sqrt{5}+5)}{\varpi (\sqrt{5}+3)}+\frac{c(\sqrt{5}+1)}{8\varpi }\frac{\sin (\Lambda )-2\cos (\Lambda )}{\cos (\Lambda )} +\frac{5c(123+7\sqrt{5})}{8\varpi (29\sqrt{5}-22)}\frac{\cos (\Lambda )}{\sin (\Lambda )-2\cos (\Lambda )}\right) \cdot \end{aligned}$$
(109)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{23}(x,t)=\left( \frac{c(2\sqrt{5}+5)}{\varpi (\sqrt{5}+3)}+\frac{c(\sqrt{5}+1)}{8\varpi }\frac{\sin (\Lambda )-2\cos (\Lambda )}{\cos (\Lambda )} +\frac{5c(123+7\sqrt{5})}{8\varpi (29\sqrt{5}-22)}\frac{\cos (\Lambda )}{\sin (\Lambda )-2\cos (\Lambda )}\right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(110)

Class 7:

$$\begin{aligned} \lambda _1=1,~\lambda _2=2,~\lambda _3=1,~\lambda _4=1,~~~\varrho _1=1,~\varrho _2=0,~\varrho _3=1,~\varrho _4=0 \end{aligned}$$
$$\begin{aligned} W(\Lambda )=\frac{e^{\Lambda }+2}{e^{\Lambda }+1}\cdot \end{aligned}$$
(111)

Set 7.1

$$\begin{aligned} k=\frac{2ic+3w}{3c},\,\,\,\zeta =\frac{ic}{3},\,\,\,c_0=\frac{2c}{\varpi },\,\,\,c_1=-\frac{2c}{3\varpi },\,\,\,d_1=-\frac{4c}{3\varpi }. \end{aligned}$$
(112)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{2c}{3\varpi }\left( 3-\frac{e^{\Lambda }+2}{e^{\Lambda }+1}-2\frac{e^{\Lambda }+1}{e^{\Lambda }+2}\right) , \end{aligned}$$
(113)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{24}(x,t)=\left( \frac{2c}{3\varpi }\left( 3-\frac{e^{\Lambda }+2}{e^{\Lambda }+1}-2\frac{e^{\Lambda }+1}{e^{\Lambda }+2}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(114)

Set 7.2

$$\begin{aligned} \begin{aligned} k&=-\frac{1}{c(4\sqrt{2}-3)(-17+12\sqrt{2})}\bigg (\frac{1}{4}i\bigg (276i(-3+4\sqrt{2}) \left(-\frac{3}{23}+\frac{4}{23}\sqrt{2} \right)w- 32i(-3+4\sqrt{2})w\\ &\quad -2019 \left(-\frac{3}{23}+\frac{4}{23}\sqrt{2} \right)c+233c\bigg )\bigg ),\,\,\, \zeta =\frac{ic(4\sqrt{2}-3)}{23},\,\,\,c_0=\frac{2c(100\sqrt{2}-144)}{23\varpi (4\sqrt{2}-6)},\,\,\, c_1=\frac{2c(4\sqrt{2}-3)}{23\varpi },\,\,\,\\ d_1 & =\frac{4c(-3+4\sqrt{2})}{\varpi }. \end{aligned} \end{aligned}$$
(115)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{ic(4\sqrt{2}-3)}{23}+\frac{2c(100\sqrt{2}-144)}{23\varpi (4\sqrt{2}-6)}\frac{e^{\Lambda }+2}{e^{\Lambda }+1} +\frac{4c(-3+4\sqrt{2})}{\varpi }\frac{e^{\Lambda }+1}{e^{\Lambda }+2}, \end{aligned}$$
(116)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{25}(x,t)=\left( \frac{ic(4\sqrt{2}-3)}{23}+\frac{2c(100\sqrt{2}-144)}{23\varpi (4\sqrt{2}-6)}\frac{e^{\Lambda }+2}{e^{\Lambda }+1} +\frac{4c(-3+4\sqrt{2})}{\varpi }\frac{e^{\Lambda }+1}{e^{\Lambda }+2}\right) ^\frac{1}{2}\times e^{i\kappa (x,t)}, \end{aligned}$$
(117)

Set 7.3

$$\begin{aligned} k=\frac{w}{c},\,\,\,\zeta =ic,\,\,\,c_0=\frac{4c}{\varpi },\,\,\,c_1=0,\,\,\,d_1=-\frac{4c}{\varpi }. \end{aligned}$$
(118)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{4c}{\varpi }\left( 1-\frac{e^{\Lambda }+1}{e^{\Lambda }+2}\right) , \end{aligned}$$
(119)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{26}(x,t)=\left( \frac{4c}{\varpi }\left( 1-\frac{e^{\Lambda }+1}{e^{\Lambda }+2}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(120)

Set 7.4

$$\begin{aligned} k=\frac{w}{c},\,\,\,\zeta =ic,\,\,\,c_0=-\frac{2c}{\varpi },\,\,\,c_1=\frac{2c}{\varpi },\,\,\,d_1=0. \end{aligned}$$
(121)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{2c}{\varpi }\left( -1+\frac{e^{\Lambda }+2}{e^{\Lambda }+1}\right) . \end{aligned}$$
(122)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{27}(x,t)=\left( \frac{2c}{\varpi }\left( -1+\frac{e^{\Lambda }+2}{e^{\Lambda }+1}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(123)

Class 8:

$$\begin{aligned} \lambda _1=2,~\lambda _2=3,~\lambda _3=1,~\lambda _4=1,~~~\varrho _1=1,\varrho _2=0,~\varrho _3=1,~\varrho _4=0 \end{aligned}$$
$$\begin{aligned} W(\Lambda )=\frac{2e^{\Lambda }+3}{e^{\Lambda }+1}\cdot \end{aligned}$$
(124)

Set 8.1

$$\begin{aligned} c=2i\zeta ,\,\,\,w=2ki\zeta -2\zeta ,\,\,\,c_0=\frac{4i\zeta }{\varpi },\,\,\,c_1=-\frac{2i\zeta }{\varpi },\,\,\,d_1=\frac{4i\zeta }{\varpi }. \end{aligned}$$
(125)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{4i\zeta }{\varpi }\left( 1-\frac{2e^{\Lambda }+3}{2(e^{\Lambda }+1)}+\frac{e^{\Lambda }+1}{2e^{\Lambda }+3}\right) \cdot \end{aligned}$$
(126)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{28}(x,t)=\left( \frac{4i\zeta }{\varpi }\left( 1-\frac{2e^{\Lambda }+3}{2(e^{\Lambda }+1)}+\frac{e^{\Lambda }+1}{2e^{\Lambda }+3}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(127)

Set 8.2

$$\begin{aligned} c=-2\zeta ,\,\,\,w=-2k\zeta ,\,\,\,c_0=\frac{(-2+2i)\zeta }{\varpi },\,\,\,c_1=0,\,\,\,d_1=\frac{4i\zeta }{\varpi }. \end{aligned}$$
(128)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{2\kappa }{\varpi }\left( -1+i+2i\frac{e^{\Lambda }+1}{2e^{\Lambda }+3}\right) \cdot \end{aligned}$$
(129)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{29}(x,t)=\left( \frac{2\kappa }{\varpi }\left( -1+i+2i\frac{e^{\Lambda }+1}{2e^{\Lambda }+3}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(130)

Set 8.1

$$\begin{aligned} k=\frac{6ic+5w}{c},\,\,\,\zeta =\frac{ic}{5},\,\,\,c_0=\frac{2c}{\varpi },\,\,\, c_1=-\frac{2c}{5\varpi },\,\,\,d_1=-\frac{12c}{5\varpi }. \end{aligned}$$
(131)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{2c}{\varpi }\left( 1-\frac{2e^{\Lambda }+3}{5(e^{\Lambda }+1)} -\frac{6}{5}\frac{e^{\Lambda }+1}{2e^{\Lambda }+3}\right) \cdot \end{aligned}$$
(132)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{30}(x,t)=\left( \frac{2c}{\varpi }\left( 1-\frac{2e^{\Lambda }+3}{5(e^{\Lambda }+1)} -\frac{6}{5}\frac{e^{\Lambda }+1}{2e^{\Lambda }+3}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(133)

Set 8.2

$$\begin{aligned} \begin{aligned} y&=-\frac{1}{c(4\sqrt{6}-5)(-49+20\sqrt{6})}\bigg (\frac{1}{4}i\bigg (1420i(4\sqrt{6}-5) \left(-\frac{5}{71}+\frac{4}{71}\sqrt{6} \right)w- 96i(-5+4\sqrt{6})w\\ & \quad - 27365(-\frac{5}{71}+\frac{4}{71}\sqrt{6})r+1849c\bigg )\bigg ),\,\,\, \zeta =\frac{ic(4\sqrt{6}-5)}{71},\,\,\,c_0=\frac{2c(292\sqrt{6}-720)}{71\varpi (4\sqrt{6}-10)},\,\,\, c_1=\frac{2r(4\sqrt{6}-5)}{71\varpi },\,\,\,\\ d_1 & =\frac{12c(4\sqrt{6}-5)}{\varpi }. \end{aligned} \end{aligned}$$
(134)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{2c(292\sqrt{6}-720)}{71\varpi (4\sqrt{6}-10)} +\frac{2r(4\sqrt{6}-5)}{71\varpi }\frac{2e^{\Lambda }+3}{e^{\Lambda }+1}+ \frac{12c(4\sqrt{6}-5)}{\varpi }\frac{e^{\Lambda }+1}{2e^{\Lambda }+3}\cdot \end{aligned}$$
(135)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{31}(x,t)=\left( \frac{2c(292\sqrt{6}-720)}{71\varpi (4\sqrt{6}-10)}+\frac{2r(4\sqrt{6}-5)}{71\varpi }\frac{2e^{\Lambda }+3}{e^{\Lambda }+1}+ \frac{12c(4\sqrt{6}-5)}{\varpi }\frac{e^{\Lambda }+1}{2e^{\Lambda }+3}\right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(136)

Set 8.3

$$\begin{aligned} k=\frac{w}{c},\,\,\,\zeta =ic,\,\,\,c_0=\frac{6c}{\varpi },\,\,\,c_1=0,\,\,\,d_1=-\frac{12c}{\varpi }. \end{aligned}$$
(137)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{2c}{\varpi }\left( 1-6\frac{e^{\Lambda }+1}{2e^{\Lambda }+3}\right) \cdot \end{aligned}$$
(138)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{32}(x,t)=\left( \frac{2c}{\varpi }\left( 1-6\frac{e^{\Lambda }+1}{2e^{\Lambda }+3}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(139)

Set 8.4

$$\begin{aligned} k=\frac{w}{c},\,\,\,\zeta =ic,\,-ir,\,\,\,c_0=\frac{6c}{\varpi },\,\,\,c_1=-\frac{2c}{\varpi },\,\,\,d_1=0. \end{aligned}$$
(140)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{2c}{\varpi }\left( 3-\frac{2e^{\Lambda }+3}{(e^{\Lambda }+1)}\right) \cdot \end{aligned}$$
(141)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{33}(x,t)=\left( \frac{2c}{\varpi }\left( 3-\frac{2e^{\Lambda }+3}{(e^{\Lambda }+1)}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(142)

Class 9:

$$\begin{aligned} \lambda _1=1-i,~\lambda _2=-1-i,~\lambda _3=-1,~\lambda _4=1,~~~\varrho _1=i,~\varrho _2=-i,~\varrho _3=i,~\varrho _4=-i \end{aligned}$$
$$\begin{aligned} W(\Lambda )=\frac{-\sin (\Lambda )+\cos (\Lambda )}{\sin (\Lambda )}\cdot \end{aligned}$$
(143)

Set 9.1

$$\begin{aligned} c=2i\zeta ,\,\,\,w=2ik\zeta -2\zeta ,\,\,\,c_0=\frac{4i\zeta }{\varpi },\,\,\,c_1=\frac{2i\zeta }{\varpi },\,\,\,d_1=\frac{4i\zeta }{\varpi }. \end{aligned}$$
(144)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{4i\zeta }{\varpi }\left( 1+\frac{-\sin (\Lambda )+\cos (\Lambda )}{2\sin (\Lambda )}+\frac{\sin (\Lambda )}{-\sin (\Lambda )+\cos (\Lambda )}\right) \cdot \end{aligned}$$
(145)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{34}(x,t)=\left( \frac{4i\zeta }{\varpi }\left( 1+\frac{-\sin (\Lambda )+\cos (\Lambda )}{2\sin (\Lambda )}+\frac{\sin (\Lambda )}{-\sin (\Lambda )+\cos (\Lambda )}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(146)

Set 9.2

$$\begin{aligned} c=-2\zeta ,\,\,\,w=-2k\zeta ,\,\,\,c_0=\frac{(-2+2i)\zeta }{\varpi },\,\,\,c_1=0,\,\,\,d_1=\frac{4i\zeta }{\varpi }. \end{aligned}$$
(147)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{4i\zeta }{\varpi }\left( -1+i+2i\frac{\sin (\Lambda )}{-\sin (\Lambda )+\cos (\Lambda )}\right) \cdot \end{aligned}$$
(148)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{35}(x,t)=\left( \frac{4i\zeta }{\varpi }\left( -1+i+2i\frac{\sin (\Lambda )}{-\sin (\Lambda )+\cos (\Lambda )}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(149)

Class 10:

$$\begin{aligned} \lambda _1=-2-i,~\lambda _2=2-i,~\lambda _3=-1,~\lambda _4=1,~~~\varrho _1=i,~\varrho _2=-i,~\varrho _3=i,~\varrho _4=-i \end{aligned}$$
$$\begin{aligned} W(\Lambda )=\frac{\cos (\Lambda )+2\sin (\Lambda )}{\sin (\Lambda )}\cdot \end{aligned}$$
(150)

Set 10.1

$$\begin{aligned} c=-4i\zeta ,\,\,\,w=-4ik\zeta -5\zeta ,\,\,\,c_0=-\frac{8i\zeta }{\varpi },\,\,\,c_1=\frac{2i\zeta }{\varpi },\,\,\,d_1=\frac{10i\zeta }{\varpi }. \end{aligned}$$
(151)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{2i\zeta }{\varpi }\left( -4+\frac{\cos (\Lambda )+2\sin (\Lambda )}{\sin (\Lambda )}+5\frac{\sin (\Lambda )}{\cos (\Lambda )+2\sin (\Lambda )}\right) \cdot \end{aligned}$$
(152)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{36}(x,t)=\left( \frac{2i\zeta }{\varpi }\left( -4+\frac{\cos (\Lambda )+2\sin (\Lambda )}{\sin (\Lambda )}+5\frac{\sin (\Lambda )}{\cos (\Lambda )+2\sin (\Lambda )}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(153)

Set 10.2

$$\begin{aligned} c=-2\zeta ,\,\,\,w=-2k\zeta ,\,\,\,c_0=\frac{(-2-4i)\zeta }{\varpi },\,\,\,c_1=0,\,\,\,d_1=\frac{10i\zeta }{\varpi }. \end{aligned}$$
(154)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{2i\zeta }{\varpi }\left( -1-2i+5\frac{\sin (\Lambda )}{\cos (\Lambda )+2\sin (\Lambda )}\right) \cdot \end{aligned}$$
(155)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{37}(x,t)=\left( \frac{2i\zeta }{\varpi }\left( -1-2i+5\frac{\sin (\Lambda )}{\cos (\Lambda )+2\sin (\Lambda )}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(156)

Class 11:

$$\begin{aligned} \lambda _1=-1-i,~\lambda _2=1-i,~\lambda _3=-1,~\lambda _4=1,~~~\varrho _1=i,~\varrho _2=-i,~\varrho _3=i,~\varrho _4=-i \end{aligned}$$
$$\begin{aligned} W(\Lambda )=\frac{\sin (\Lambda )+\cos (\Lambda )}{\sin (\Lambda )}\cdot \end{aligned}$$
(157)

Set 11.1

$$\begin{aligned} c=-2i\zeta ,\,\,\,w=-2ik\zeta -2\zeta ,\,\,\,c_0=-\frac{4i\zeta }{\varpi },\,\,\,c_1=\frac{2i\zeta }{\varpi },\,\,\,d_1=\frac{4i\zeta }{\varpi }. \end{aligned}$$
(158)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{4i\zeta }{\varpi }\left( -1+\frac{\sin (\Lambda )+\cos (\Lambda )}{2\sin (\Lambda )}+\frac{\sin (\Lambda )}{\sin (\Lambda )+\cos (\Lambda )}\right) \cdot \end{aligned}$$
(159)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{38}(x,t)=\left( \frac{4i\zeta }{\varpi }\left( -1+\frac{\sin (\Lambda )+\cos (\Lambda )}{2\sin (\Lambda )}+\frac{\sin (\Lambda )}{\sin (\Lambda )+\cos (\Lambda )}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(160)

Set 11.2

$$\begin{aligned} c=-2\zeta ,\,\,\,w=-2k\zeta ,\,\,\,c_0=\frac{(-2-2i)\zeta }{\varpi },\,\,\,c_1=0,\,\,\,d_1=\frac{4i\zeta }{\varpi }. \end{aligned}$$
(161)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{2\zeta }{\varpi }\left( -1-i-2i\frac{\sin (\Lambda )}{\sin (\Lambda )+\cos (\Lambda )}\right) \cdot \end{aligned}$$
(162)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{39}(x,t)=\left( \frac{2\zeta }{\varpi }\left( -1-i-2i\frac{\sin (\Lambda )}{\sin (\Lambda )+\cos (\Lambda )}\right) \right) ^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned}$$
(163)

Class 12:

$$\begin{aligned} \lambda _1=1,~\lambda _2=0,~p=1,~\lambda _4=1,~~~\varrho _1=1,~\varrho _2=0,~\varrho _3=1,~\varrho _4=0 \end{aligned}$$
$$\begin{aligned} W(\Lambda )=\frac{e^{\Lambda }}{e^{\Lambda }+1}\cdot \end{aligned}$$
(164)

Set 12.1

$$\begin{aligned} c=\frac{w}{k},\,\,\,\zeta =\frac{iw}{k},\,\,\,c_0=0,\,\,\,c_1=\frac{2w}{k\varpi },\,\,\,d_1=0. \end{aligned}$$
(165)

By inserting values in Eq. (36), the solution for the governing ODE (34) as follows

$$\begin{aligned} Y(\Lambda )=\frac{2w}{k\varpi }\frac{e^{\Lambda }}{e^{\Lambda }+1}\cdot \end{aligned}$$
(166)

Therefore, the waveform solution for the NCLL model (1) encounters

$$\begin{aligned} U_{40}(x,t)=\left( \frac{2w}{k\varpi }\frac{e^{\Lambda }}{e^{\Lambda }+1}\right) ^\frac{1}{2}\times e^{i\kappa (x,t)}, \end{aligned}$$
(167)

Application of the new extended hyperbolic function method

Form 1: In this section, we apply the NEHF for the solutions of the NCLL model (1). For \(N = 1\), the solution (11) takes the form

$$\begin{aligned} Y(\Lambda )=g_0+g_1 M(\Lambda ), \end{aligned}$$
(168)

where \(g_0\) and \(g_1\) are the constants to be determined. By substituting (168) into (34) and equating the coefficients of each polynomial of \(M(\Lambda )\) to zero, we derive a set of algebraic equations involving \(g_0,\,\, g_1,\,\,\, Q,\) and R. Solving this set of equations yields

$$\begin{aligned} \begin{aligned} g_0&=\frac{4(2k\zeta +\sqrt{4k^2\zeta ^2-\zeta w})}{\varpi },\,\,\,c=8k\zeta +4\sqrt{4k^2\zeta ^2-\zeta w},\\ Q&=\frac{4(4\zeta (2k\zeta +\sqrt{4k^2\zeta ^2-\zeta w})-w)}{\zeta },\,\,\,g_1=\sqrt{-\frac{4R\zeta ^2}{\varpi ^2}}. \end{aligned} \end{aligned}$$
(169)

Class 13: For the case of \(Q>0\) and \(R >0\),

$$\begin{aligned} \begin{aligned} U_{41}(x,t)&=\bigg (\frac{4(2k\zeta +\sqrt{4k^2\zeta ^2-\zeta w})}{\varpi }-\sqrt{-\frac{16\zeta (4\zeta (2k\zeta +\sqrt{4k^2\zeta ^2-\zeta w})-w)}{\varpi ^2}}\\ & \quad \text {csch}\bigg (\sqrt{\frac{4(4\zeta (2k\zeta +\sqrt{4k^2\zeta ^2-\zeta w})-w)}{\zeta }}(\Lambda +\Lambda _0)\bigg )\bigg )^\frac{1}{2}\times e^{i\kappa (x,t)}. \end{aligned} \end{aligned}$$
(170)

Class 14: For the case of \(Q <0\) and \(R >0\),

$$\begin{aligned} \begin{aligned} U_{42}(x,t)&=\bigg (\frac{4(2k\zeta +\sqrt{4k^2\zeta ^2-\zeta w})}{\varpi }+\sqrt{\frac{16\zeta (4\zeta (2k\zeta +\sqrt{4k^2\zeta ^2-\zeta w})-w)}{\varpi ^2}}\\ & \quad \text {sec}\bigg (\sqrt{-\frac{4(4\zeta (2k\zeta +\sqrt{4k^2\zeta ^2-\zeta w})-w)}{\zeta }}(\Lambda +\Lambda _0)\bigg )\bigg )^\frac{1}{2}\times e^{i\kappa (x,t)}\cdot \end{aligned} \end{aligned}$$
(171)

Class 15: For the case of \(Q >0\) and \(R <0\),

$$\begin{aligned} \begin{aligned} U_{43}(x,t)&=\bigg (\frac{4(2k\zeta +\sqrt{4k^2\zeta ^2-\zeta w})}{\varpi }+\sqrt{\frac{16\zeta (4\zeta (2k\zeta +\sqrt{4k^2\zeta ^2-\zeta w})-w)}{\varpi ^2}}\\ & \quad \text {sech}\bigg (\sqrt{-\frac{4(4\zeta (2k\zeta +\sqrt{4k^2\zeta ^2-\zeta w})-w)}{\zeta }}(\Lambda +\Lambda _0)\bigg )\bigg )\bigg )^\frac{1}{2}\times e^{i\kappa (x,t)}\cdot \end{aligned} \end{aligned}$$
(172)

Class 16: For the case of \(Q<0\) and \(R <0\),

$$\begin{aligned} \begin{aligned} U_{44}(x,t)&=\bigg (\frac{4(2k\zeta +\sqrt{4k^2\zeta ^2-\zeta w})}{\varpi }+\sqrt{\frac{16\zeta (4\zeta (2k\zeta +\sqrt{4k^2\zeta ^2-\zeta w})-w)}{\varpi ^2}}\\ & \quad \text {csc}\bigg (\sqrt{-\frac{4(4\zeta (2k\zeta +\sqrt{4k^2\zeta ^2-\zeta w})-w)}{\zeta }}(\Lambda +\Lambda _0)\bigg )\bigg )^\frac{1}{2}\times e^{i\kappa (x,t)}\cdot \end{aligned} \end{aligned}$$
(173)

Class 17: For the case of \(Q=0\) and \(R >0\),

$$\begin{aligned} U_{45}(x,t)=\bigg (\frac{4(2k\zeta +\sqrt{4k^2\zeta ^2-\zeta w})}{\varpi }\pm \sqrt{-\frac{4\zeta ^2}{\varpi ^2}}(\Lambda +\Lambda _0)\bigg )^\frac{1}{2}\times e^{i\kappa (x,t)}\cdot \end{aligned}$$
(174)

Class 18: For the case of \(Q =0\) and \(R <0\),

$$\begin{aligned} U_{46}(x,t)=\bigg (\frac{4(2k\zeta +\sqrt{4k^2\zeta ^2-\zeta w})}{\varpi }\pm i\bigg (\sqrt{\frac{4\zeta ^2}{\varpi ^2}}(\Lambda +\Lambda _0)\bigg )\bigg )^\frac{1}{2}\times e^{i\kappa (x,t)}\cdot \end{aligned}$$
(175)

In a similar way, Form 2 provides following derived parameters;

$$\begin{aligned} g_0=\frac{w}{k\varpi },~~~\,\,\,c=\frac{w}{k},~~~ Q=-\frac{i w^2}{2k^2g_1\varpi \zeta },\,\,\,~~~g_1=\frac{2\kappa R}{i \varpi }. \end{aligned}$$
(176)

In a similar way, Form 2 provides following classes of solutions;

Class 19: For the case of \(QR >0\),

$$\begin{aligned} U_{47}(x,t)=\bigg (\frac{w}{k\varpi }+g_1\bigg (\operatorname {sgn}\bigg (-\frac{i w^2}{2k^2g_1\varpi \zeta }\bigg )\sqrt{-\frac{w^2}{k^2g_1^2\varpi ^2}} \tan \bigg (\sqrt{\frac{w^2}{4k^2\zeta ^2}}(\Lambda +\Lambda _0)\bigg )\bigg )\bigg )^\frac{1}{2}\times e^{i\kappa (x,t)}\cdot \end{aligned}$$
(177)

Class 20: For the case of \(QR >0\),

$$\begin{aligned} U_{48}(x,t)=\bigg (\frac{w}{k\varpi }+g_1\bigg (\operatorname {sgn}\bigg (-\frac{i w^2}{2k^2g_1\varpi \zeta }\bigg )\sqrt{-\frac{w^2}{k^2g_1^2\varpi ^2}} \cot \bigg (\sqrt{\frac{w^2}{4k^2\zeta ^2}}(\Lambda +\Lambda _0)\bigg )\bigg )\bigg )^\frac{1}{2}\times e^{i\kappa (x,t)}\cdot \end{aligned}$$
(178)

Class 21: For the case of \(QR <0\),

$$\begin{aligned} U_{49}(x,t)=\bigg (\frac{w}{k\varpi }+C_1\bigg (\operatorname {sgn}\bigg (-\frac{i w^2}{2k^2g_1\varpi \zeta }\bigg )\sqrt{\frac{w^2}{k^2g_1^2\varpi ^2}} \text {tanh}\bigg (\sqrt{-\frac{w^2}{4k^2\zeta ^2}}(\Lambda +\Lambda _0)\bigg )\bigg )\bigg )^\frac{1}{2}\times e^{i\kappa (x,t)}\cdot \end{aligned}$$
(179)

Class 22: For the case of \(QR <0\),

$$\begin{aligned} U_{50}(x,t)=\bigg (\frac{w}{k\varpi }+C_1\bigg (\operatorname {sgn}\bigg (-\frac{\iota w^2}{2k^2g_1\varpi \zeta }\bigg )\sqrt{\frac{w^2}{k^2g_1^2\varpi ^2}} \text {coth}\bigg (\sqrt{-\frac{w^2}{4k^2\zeta ^2}}(\Lambda +\Lambda _0)\bigg )\bigg )\bigg )^\frac{1}{2}\times e^{i\kappa (x,t)}\cdot \end{aligned}$$
(180)

Class 23: For the case of \(Q=0\) and \(R<0\),

$$\begin{aligned} U_{51}(x,t)=\bigg (\frac{w}{k\varpi }-g_1\sqrt{\frac{2\zeta }{i g_1\varpi }}(\Lambda +\Lambda _0)\bigg )^\frac{1}{2}\times e^{i\kappa (x,t)}\cdot \end{aligned}$$
(181)

Class 24: For the case of \(Q=0\) and \(R>0\),

$$\begin{aligned} U_{52}(x,t)=\bigg (\frac{w}{k\varpi }+g_1\sqrt{\frac{i g_1\varpi }{2\zeta }}(\Lambda +\Lambda _0)\bigg )^\frac{1}{2}\times e^{i\kappa (x,t)}\cdot \end{aligned}$$
(182)

In all cases \(\Lambda =\frac{1}{\gamma }\bigg (x+\frac{1}{\Gamma (\gamma )}\bigg )^{\gamma }-\frac{c}{\gamma }\bigg (t+\frac{1}{\Gamma (\gamma )}\bigg )^{\gamma },\) and \(\kappa (x,t)=-\frac{k}{\alpha }\bigg (x+\frac{1}{\Gamma (\gamma )}\bigg )^{\gamma }+\frac{w}{\gamma }\bigg (t+\frac{1}{\Gamma (\gamma )}\bigg )^{\gamma }+\chi _0(\Lambda ).\)

Interpretation of solutions in physical context

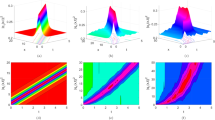
In this section, we analyze the physical relevance of the solutions derived for the NCLL model (1) using NGERF and NEHF techniques. Three-dimensional surface plots and two-dimensional plots illustrate the behavior of the solutions for specific parameter values within the appropriate ranges. The obtained solutions exhibit diverse structures, including bell-shaped solitons, singular solitons, compactons, singular periodic solitons, periodic solitons, kinks, and other solitonic profiles. For clarity, we present graphical representations of selected solutions, such as (1)–(12), while others are excluded. The potential applicability of these optical solutions was further examined using Mathematica software.

Figure 1 shows a singular bell-shaped soliton for parameter (fractional) values \(\gamma =0.6\), \(\gamma =0.8\), \(\gamma =1.0\). The 3D plots demonstrate how the soliton’s structure evolves with the parameter \(\gamma\) and time t variations. Keeping the model parameters fixed, the solution reveals distinct dynamical patterns for fractional values of \(\gamma\) ranging from 0.6 to 1.0 and time t spanning from 0 to 2.

Figure 2 shows a bell-shaped soliton for parameter (fractional) values \(\gamma =0.6\), \(\gamma =0.8\), \(\gamma =1.0\). The 3D plots demonstrate how the soliton’s structure evolves with parameter \(\gamma\) and time t variations. Keeping the model parameters fixed, the solution reveals distinct dynamical patterns for fractional values of \(\gamma\) ranging from 0.6 to 1.0 and time t spanning from 0 to 2.

Figures 3, 6, 7, 8, 9, and 12 show periodic solitons for the parameter (fractional) values \(\gamma =0.6\), \(\gamma =0.8\), \(\gamma =1.0\). The 3D plots demonstrate how the soliton’s structure evolves with parameter \(\gamma\) and time t variations. Keeping the model parameters fixed, the solution reveals distinct dynamical patterns for fractional values of \(\gamma\) ranging from 0.6 to 1.0 and time t spanning from 0 to 2.

Figures 4, 10, and 10 show singular soliton waves for the parameter (fractional) values \(\gamma =0.6\), \(\gamma =0.8\), \(\gamma =1.0\). The 3D plots demonstrate how the soliton’s structure evolves with parameter \(\gamma\) and time t variations. Keeping the model parameters fixed, the solution reveals distinct dynamical patterns for fractional values of \(\gamma\) ranging from 0.6 to 1.0 and time t spanning from 0 to 2.

Figures 5 and 11 show singular periodic solitons for the parameter (fractional) values \(\gamma =0.6\), \(\gamma =0.8\), \(\gamma =1.0\). The 3D plots demonstrate how the soliton’s structure evolves with parameter \(\gamma\) and time t variations. Keeping the model parameters fixed, the solution reveals distinct dynamical patterns for fractional values of \(\gamma\) ranging from 0.6 to 1.0 and time t spanning from 0 to 2.

Although singular solutions may not directly represent physically observable phenomena, they are important in mathematical modeling, particularly in nonlinear and fractional systems. These solutions help ensure the completeness of the analysis by revealing critical points or bifurcations that may signify transitions to different behaviors, such as soliton formation or instability. Singular solutions can also offer insight into boundary conditions or extreme parameter limits, describing behavior near singularities, such as blow-up points, which are important in understanding complex dynamics like shock waves or gravitational singularities. Moreover, in singular perturbation theory, these solutions aid in approximating the system’s behavior under certain conditions. In some cases, they help derive generalized solutions or distributional solutions, extending the class of possible solutions to include singular terms. Finally, singular solutions are useful in numerical simulations to test the robustness of computational methods, ensuring that extreme or degenerate behaviors are captured accurately. Thus, while they may not be physically realizable, singular solutions provide a comprehensive understanding of the system’s full behavior.

A graphical representation of the derived optical solitons for the NCLL model (1) shows the fundamental mechanism of the physical structure of the proposed model. This study identifies a variety of distinctive solitons that are of considerable importance for ultrashort optical solitons in parabolic law media. Furthermore, it underscores wave propagation in nonlinear media, offering an effective framework for modeling real-world phenomena, categorizing wave velocities, and other related aspects.

Fig. 1
figure 1

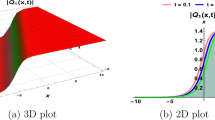
Graphical exploration of the behavior of NCLL model (1) by the solution \(|U_1(x,t)|\): (a) Two-dimensional dynamics at \(t=0,1,2\), (b) impact of fractional beta derivative for the values \(\gamma =0.6,~\gamma =0.8,\gamma =1.0\), (c) three-dimensional analysis for nature of the solution with parameters \(w=0.01,c=0.3,k=0.1,\varpi =0.3,\alpha =0.4\).

Full size image
Fig. 2
figure 2

Graphical exploration of the behavior of NCLL model (1) by the solution \(|U_2(x,t)|\): (a) Two-dimensional dynamics at \(t=0,1,2\), (b) impact of fractional beta derivative for the values \(\gamma =0.6,~\gamma =0.8,\gamma =1.0\), (c) three-dimensional analysis for nature of the solution with parameters \(w=0.01,c=0.3,k=0.1,\varpi =0.3,\alpha =0.4\).

Full size image
Fig. 3
figure 3

Graphical exploration of the behavior of NCLL model (1) by the solution \(|U_4(x,t)|\): (a) Two-dimensional dynamics at \(t=0,1,2\), (b) impact of fractional beta derivative for the values \(\gamma =0.6,~\gamma =0.8,\gamma =1.0\), (c) three-dimensional analysis for nature of the solution with parameters \(w=0.01,c=0.3,k=0.1,\varpi =0.3,\alpha =0.4\).

Full size image
Fig. 4
figure 4

Graphical exploration of the behavior of NCLL model (1) by the solution \(|U_6(x,t)|\): (a) Two-dimensional dynamics at \(t=0,1,2\), (b) impact of fractional beta derivative for the values \(\gamma =0.6,~\gamma =0.8,\gamma =1.0\), (c) three-dimensional analysis for nature of the solution with parameters \(w=0.01,c=0.3,k=0.1,\varpi =0.3,\alpha =0.4\).

Full size image
Fig. 5
figure 5

Graphical exploration of the behavior of NCLL model (1) by the solution \(|U_8(x,t)|\): (a) Two-dimensional dynamics at \(t=0,1,2\), (b) impact of fractional beta derivative for the values \(\gamma =0.6,~\gamma =0.8,\gamma =1.0\), (c) three-dimensional analysis for nature of the solution with parameters \(w=0.01,c=0.3,k=0.1,\varpi =0.3,\alpha =0.4\).

Full size image
Fig. 6
figure 6

Graphical exploration of the behavior of NCLL model (1) by the solution \(|U_{10}(x,t)|\): (a) Two-dimensional dynamics at \(t=0,1,2\), (b) impact of fractional beta derivative for the values \(\gamma =0.6,~\gamma =0.8,\gamma =1.0\), (c) three-dimensional analysis for nature of the solution with parameters \(w=0.01,c=0.3,k=0.1,\varpi =0.3,\alpha =0.4\).

Full size image
Fig. 7
figure 7

Graphical exploration of the behavior of NCLL model (1) by the solution \(|U_{11}(x,t)|\): (a) Two-dimensional dynamics at \(t=0,1,2\), (b) impact of fractional beta derivative for the values \(\gamma =0.6,~\gamma =0.8,\gamma =1.0\), (c) three-dimensional analysis for nature of the solution with parameters \(w=0.01,c=0.3,k=0.1,\varpi =0.3,\alpha =0.4\).

Full size image
Fig. 8
figure 8

Graphical exploration of the behavior of NCLL model (1) by the solution \(|U_{12}(x,t)|\): (a) Two-dimensional dynamics at \(t=0,1,2\), (b) impact of fractional beta derivative for the values \(\gamma =0.6,~\gamma =0.8,\gamma =1.0\), (c) three-dimensional analysis for nature of the solution with parameters \(w=0.01,c=0.3,k=0.1,\varpi =0.3,\alpha =0.4\).

Full size image
Fig. 9
figure 9

Graphical exploration of the behavior of NCLL model (1) by the solution \(|U_{40}(x,t)|\): (a) Two-dimensional dynamics at \(t=0,1,2\), (b) impact of fractional beta derivative for the values \(\gamma =0.6,~\gamma =0.8,\gamma =1.0\), (c) three-dimensional analysis for nature of the solution with parameters \(w=0.01,c=0.3,k=0.1,\varpi =0.3,\alpha =0.4\).

Full size image
Fig. 10
figure 10

Graphical exploration of the behavior of NCLL model (1) by the solution \(|U_{41}(x,t)|\): (a) Two-dimensional dynamics at \(t=0,1,2\), (b) impact of fractional beta derivative for the values \(\gamma =0.6,~\gamma =0.8,\gamma =1.0\), (c) three-dimensional analysis for nature of the solution with parameters \(w=0.01,c=0.3,k=0.1,\varpi =0.3,\alpha =0.4\).

Full size image
Fig. 11
figure 11

Graphical exploration of the behavior of NCLL model (1) by the solution \(|U_{42}(x,t)|\): (a) Two-dimensional dynamics at \(t=0,1,2\), (b) impact of fractional beta derivative for the values \(\gamma =0.6,~\gamma =0.8,\gamma =1.0\), (c) three-dimensional analysis for nature of the solution with parameters \(w=0.01,c=0.3,k=0.1,\varpi =0.3,\alpha =0.4\).

Full size image
Fig. 12
figure 12

Graphical exploration of the behavior of NCLL model (1) by the solution \(|U_{43}(x,t)|\): (a) Two-dimensional dynamics at \(t=0,1,2\), (b) impact of fractional beta derivative for the values \(\gamma =0.6,~\gamma =0.8,\gamma =1.0\), (c) three-dimensional analysis for nature of the solution with parameters \(w=0.01,c=0.3,k=0.1,\varpi =0.3,\alpha =0.4\).

Full size image

Discussion and the conclusions

The NCLL model (1), linked to the beta derivative, was analyzed using NGERF and NEHF techniques. The soliton solutions derived from this analysis are vital for examining nonlinear soliton interactions and for gaining insight into the underlying mechanisms of complex nonlinear physical phenomena. The solutions encompass hyperbolic, exponential, and trigonometric forms, along with their integrals, all of which are distinctive, compatible, and significant for the dynamics observed in optical fibers. These results contribute to the existing literature on the NCLL model (1) and provide new insights beyond those found in50,51,52,53,54,55,56,57,58,59,60,61,62,65.

Furthermore, Mathematica simulations reveal essential insights into optical solitons into the physical implications of the solutions for the model, which are critical for understanding its dynamic behaviors. The accuracy of the derived solutions was validated by substituting them back into the original model, thereby confirming their reliability. Finally, this research shows how the suggested methods can be applied to analyze the effectiveness of fiber-based communication systems in various associated models, generate valuable soliton solutions, and enhance the functionality of computer algebra systems.