Introduction

The rapid development of transportation infrastructure in western China has led to an increasing number of long and deep tunnels being constructed in areas with highly complex geological and geothermal conditions1,2. These regions are often characterized by intense tectonic activity, fractured strata, and elevated geothermal gradients. As a result, tunnel engineering in such environments faces severe technical challenges, particularly in ensuring the long-term performance and structural safety of tunnel linings3,4.

One of the most critical environmental factors affecting tunnel durability is high temperature. Driven by geothermal anomalies and heat accumulation in the surrounding rock mass, high temperatures introduce persistent thermal loading on tunnel linings throughout both the construction and operational phases. Previous studies have shown that elevated temperatures accelerate cement hydration and early-age strength development in concrete5. However, they also increase the risk of microcracking, shrinkage, and long-term degradation due to thermal stress and internal pore pressure. Over time, these effects contribute to reduced mechanical strength, increased porosity, and a higher likelihood of cracking and delamination in tunnel linings6. In parallel with the challenge of high temperature, many modern tunnels are constructed in hydrothermal environments where geothermal water interacts directly with tunnel structures7,8. Geothermal water typically contains high concentrations of aggressive ions, such as chloride (Cl⁻), sulfate (SO₄2−), and magnesium (Mg2⁺), which penetrate the concrete lining through diffusion and capillary action9,10. These ions chemically interact with cement hydration products, leading to the formation of expansive secondary products (e.g., ettringite, gypsum), pore structure disruption, and reinforcement corrosion. Over time, such processes cause substantial weakening of the concrete and pose serious risks to the structural integrity of the tunnel11,12,13.

Numerous studies have investigated the mechanical behavior of concrete when exposed to either high-temperature or corrosive environments14. In high geothermal settings, continuous heat transfer from the surrounding rock influences the concrete throughout its entire service life, beginning from the early hydration stage to long-term hardening. Compared to specimens cured under standard conditions, concrete exposed to elevated temperatures tends to exhibit reduced mechanical strength, a more porous internal structure, and a greater incidence of microcracks and micropores. Khatib et al.15 found that high-temperature curing significantly accelerates cement hydration and calcium silicate polymerization, increasing C–S–H gel nanoparticle size while densifying pore structure. However, it also elevates the risk of internal micro-cracks in concrete. Under low humidity, accelerated water evaporation further leads to a rebound increase in porosity at the later stage. Luo et al.16 demonstrated that elevated curing temperatures exert a positive influence on cement particle hydration, consequently modifying the microstructure and interstitial spaces. Julnipitawong et al.17 conducted a comparative analysis of early-age compressive strength development in concrete cured at 5 °C, 15 °C, 25 °C, and 35 °C, revealing that specimens maintained at 5 °C exhibited markedly reduced mechanical performance relative to those cured at higher temperatures (e.g., 25 °C). Lee et al.18 noted that concrete containing 30% slag powder cured at high temperature (30 °C) exhibited 12% higher 28-day strength than ordinary Portland concrete, but its 10-year strength increased by only 5%, which was significantly lower than the 22% increase observed in the normal-temperature curing group. Tran et al.19 demonstrated that early-stage high-temperature curing enhances the strength of fly ash-incorporated self-compacting concrete, while excessive fly ash dosage detrimentally influences its mechanical performance. Marulasiddappa et al.20 and Hui et al.21 found that when the initial curing temperature exceeds standard conditions, although the early-stage compressive strength temporarily increases, both the compressive strength and elastic modulus exhibit a significant reduction after a certain period. Cui et al.22 demonstrated that adhesive strength at the shotcrete-rock interface varied significantly under different high-temperature conditions, thereby influencing the mechanical performance of supporting structures. Therefore, high geothermal tunnels’ primary effect on concrete is the initial damage caused by high temperatures during the early curing stages. Additionally, concrete is a composite material made from aggregates, water, and cement, and inevitably contains pores formed during preparation. Aggressive ions, such as sulfates and chlorides, infiltrate concrete through capillary adsorption, diffusion, and infiltration, leading to damage23. In corrosive environments, these ions chemically interact with concrete’s hydration products, loosening its internal structure and promoting cracks, which can lead to reinforcement corrosion and overall structural failure24. Jia et al.25 reviewed the micro-mechanism of chloride-sulfate coupled corrosion, indicating that in high-concentration ionic environments, the chemical equilibrium of concrete pore solution is disrupted, triggering decomposition of hydration products and formation of secondary corrosion products, which ultimately leads to structural loosening and delamination spalling. Alava and Wang et al.26,27 revealed that chloride ion permeability in tensile regions of concrete was significantly greater compared to compressive zones, with increasing applied loads resulting in progressive deterioration of chloride ion corrosion resistance. Porosity and compactness are key indicators of concrete’s microstructure changes28. Dehwah et al.29 evaluated the corrosion resistance of self-compacting concrete containing various mineral admixtures using electrochemical testing and other methods, revealing that SCC exhibits superior chloride salt corrosion resistance. Changes in the concentration of corrosion solutions also alter the chemical reaction mechanisms; for example, sodium sulfate corrosion transitions from calcium alumina to gypsum, while magnesium sulfate corrosion becomes more aggressive with increasing solution concentration. Khan et al.30 reviewed chloride-induced reinforcement corrosion processes, including the effects of cement type, water-cement ratio, degree of hydration, and curing age. The environmental conditions, such as SO42−, Cl− concentration, temperature, humidity, and pH, also affect concretes susceptibility to corrosion31. Zhang et al.32 reported that temperature changes modify concrete porosity, which impacts permeability and ultimately corrosion levels.

Although considerable research has been conducted on the mechanical properties of concrete under either high-temperature or corrosive environments, most existing studies have examined these two factors in isolation. Due to the relatively limited number of tunnel engineering projects situated in extreme environments, the combined effects of high temperature and chemical corrosion have received far less attention. Hydrothermal high-temperature tunnels represent a unique and particularly harsh environment that differs significantly from conventional high rock temperature tunnels. In these settings, high-pressure geothermal water with a high content of aggressive ions (e.g., sulfate and chloride) infiltrates the tunnel through fractured rock masses, directly contacting the concrete lining. Under normal conditions, corrosion of concrete primarily results from the diffusion and penetration of ions, which disrupt the pore structure and initiate microcracking. However, elevated temperatures substantially alter the transport and reaction behavior of these ions. High temperatures accelerate water evaporation, promote ion migration due to concentration gradients, and enhance diffusion and reaction kinetics by increasing molecular activity. The result is a synergistic deterioration process that is far more severe than the effects of temperature or corrosion alone, and fundamentally different from marine or saline environments. This coupled deterioration mechanism—consisting of initial thermal damage followed by accelerated chemical attack—poses significant challenges for material performance in hydrothermal tunnel environments. As tunnel construction expands into high geothermal regions, the performance of concrete linings in such environments has become an urgent concern. However, there is currently a lack of systematic research on the multi-scale degradation behavior of concrete under these combined conditions, especially in relation to long-term structural safety and durability.

Therefore, this study aims to address this gap by conducting a comprehensive investigation into the mechanical degradation of concrete under coupled high-temperature and corrosion conditions, simulating the environment of hydrothermal tunnels. The specific objectives are:

  1. a.

    To experimentally investigate the mechanical response and deterioration characteristics of concrete under the simultaneous action of high temperature and corrosive ions, using a multi-scale simulation of the hydrothermal tunnel environment;

  2. b.

    To propose a novel constitutive damage model based on random damage theory, capturing macroscopic deterioration behaviors derived from microscopic mechanisms;

  3. c.

    To develop a discrete random damage model incorporating contact corrosion, aimed at analyzing damage evolution and performance degradation under thermal–chemical coupling.

The findings of this study are expected to provide valuable theoretical insights and technical support for the design and durability optimization of concrete materials used in hydrothermal tunnels.

Experiment design

Raw materials

The mix proportion of the test concrete was based on a tunnel located in a typical high-temperature and corrosive (HTC) environment. Following standard concrete mix design guidelines, ordinary Type 1 Portland cement was used as the binder in the tests. This cement has a strength grade of 42.5 MPa and a density of 3.0 g/cm3. The initial setting time of the cement was 65 min, with the final setting time not exceeding 550 min. The 3-day uniaxial compressive strength of the cement specimens was at least 22 MPa, and the 28-day uniaxial compressive strength was no less than 42.5 MPa. Additionally, the 28-day flexural strength of the cement specimens was not less than 6.5 MPa. For the experiment, the coarse aggregate was crushed gravel, with particle sizes ranging from 5 to 14 mm. The gravel had a crushing index of 5.5% and contained 1.6% needle-like particles. Haihe medium sand was chosen as the fine aggregate, with a mud content of 0.91%, a fineness modulus of 2.6, and particle sizes between 0.5 and 0.35 mm. The mud content of the sand was less than 1.5%.

Specimen preparation

This experiment was conducted by the method of indoor molded concrete blocks for testing the mechanical strength (as shown in Fig. 1). The testing samples for strength test were formed into cubes whose size was 100 mm*100 mm*100 mm, and every three specimens were selected as a group. The concrete specimens were prepared as shown in Table 1, and the cement mortar specimens were coated with release agent on the inner surface of the mold before the test. When mixing, cement and sand were mixed with a shovel until the color was uniform, then piled into a cone shape and mixed carefully with pure water until the basic uniformity. The mixing time was controlled within 5 min from the time of adding water. Fill the cement mortar mixture into the cement mortar test mold at one time and mold the specimen into shape using the manual inserting and pounding method. Ensure that the cement mortar can fill the test mold densely and avoid delamination of the over-vibrated cement mortar. Finally, scrape off the excess cement mortar on the test mold and smooth it out with a spatula, and then specimens were maintained after the initial setting of cement mortar.

Fig. 1
figure 1

Production of concrete specimens.

Full size image
Table 1 Concrete mix ratio.
Full size table

Test equipment

To investigate the macroscopic mechanical properties and microstructural characteristics of concrete, a series of experimental tests were performed on concrete specimens (see Fig. 2). The Topinduster electro-hydraulic servo universal testing machine was used for the mechanical tests, with a maximum axial force of 1000kN and a piston speed of up to 100 mm/min, with an accuracy of ± 0.5% for both displacement and speed. To achieve more uniform stress distribution, a rigid insert with a height-to-diameter ratio of 1.0 was placed between the specimen and the platen. The specimens were preloaded to reduce the effects of surface irregularities and the gap between the compression and loading surfaces. The hydraulic servo press system was used to apply a continuous and uniform load. A strain control mode was selected to maintain a constant strain rate at each stage, ensuring a complete stress–strain curve. The oil pump and electro-hydraulic servo valve, controlled by a PC-based servo controller, facilitated multi-channel closed-loop control for automatic loading, measurement, and data acquisition. The specimens were loaded until failure, and test data were collected for further analysis. Uniaxial compressive strength and elasticity modulus tests were conducted under different corrosion conditions. For microstructural observation, a scanning electron microscope (SEM) JSM-7800F was employed, with a scanning angle range from − 7° to 70°. The accelerating voltage and probe current were set between 0.5 and 30 kV and 10–12 to 10–8 A, respectively.

Fig. 2
figure 2

Equipment for test on concrete properties.

Full size image

Experimental procedures

Environment background

The high-temperature environment in high-geothermal tunnel caused by high water temperature is primarily caused by the deep circulation of groundwater. Additionally, the chemical composition of geothermal water is strongly influenced by its recharge sources and the surrounding rock conditions. Its formation and evolution are the result of multiple factors including the chemical composition of the aqueous medium, hydrochemical reactions, and sedimentary environments. Based on the investigation of the chemical composition of geothermal water in various regions, the predominant corrosive ions in areas of high geothermal activity are sulfate ions33,34. For instance, within the Longmen Mountain fault zone, the concentration of sulfate ions reaches 3829 mg/L. Thus, tunnels in high geothermal zones with geothermal water circulation often exhibit a unique environment subject to sulfate erosion.

Design of the experiment

The concrete material of initial support lining in high-geothermal tunnels is cured under variable temperature conditions according to previous research results2,14,21. Thus, conventional curing methods and constant high temperature curing are no longer applicable to accurately reflect the real conditions in hydrothermal high-geothermal tunnels. The high temperature curing is set at 40 °C (group B) and 60 °C (group C) with a humidity of 95%. During the first week there was a steady decrease in temperature, culminating on the seventh day at 28 °C, which is within the safety limits specified in the Code for the Design of Railway Tunnels (as shown in Fig. 32). Combined with the corrosive nature of the geothermal water in the study area and existing research results, the solution of 8% sodium sulfate was used as the corrosive medium of concrete35. Determine the total amount of water required in the tank based on the size of the tank and the amount of water required to submerge the concrete specimen. For each litre of water added to the tank, weigh 80 g of sodium sulphate powder. Stir the solution well until all the sodium sulphate is completely dissolved, ensuring a uniform concentration throughout the tank. The temperature of the water bath is set to 40 °C and 60 °C correspondingly. Based on the results of preliminary tests, replacing all the liquid in the tank every two weeks can maintain the concentration of corrosive ions at the required level under the designed temperature.

Fig. 3
figure 3

High temperature and corrosion environment for concrete.

Full size image

The tunnel lining concrete is subjected to a long cycle of damage due to sulphate erosion. In order to accelerate the erosion rate, most researchers have conducted experimental studies using wet cycle tests. The concrete specimens cured under high variable temperature were then placed in a water bath at the corresponding temperature for 12 h. After that, the specimens were taken out of the water bath box and dried naturally for 3 h, and then put into the drying oven with the corresponding temperature of the water bath for 6 h. Finally, the specimens were taken out of the oven and dried naturally for 3 h, and then put into the water bath again. At this point, one age of a complete wet and dry cycle is over. The age of concrete was set at 30 d, 45 d, 60 d, 90 d and 120 d. At the same time, the specimens under standard conditions of conservation (20 °C–95%) were used as a control group (group A). The specimens under different working conditions were used for the experimental study of macroscopic properties and microstructure of concrete, respectively. The duration of this indoor experimental study was greater than six months. Although the laboratory test conditions were not totally in accordance with the real environment, these curing methods would be sufficient to highlight the research emphasis in this work.

Experimental results and discussions

Mechanical characteristics of concrete

Stress–strain characteristics in compression

The general graph of the stress–strain curve was obtained on the basis of multiple sets of compressive tests as shown in Fig. 4, and the general pattern of curve variation was basically the same. Similar results had been obtained in the established studies. It can be divided into four deformation characteristics: elastic phase, plastic yield phase, post-peak phase and residual phase. The development of the curve indicated that the compressive stress first rose rapidly to a peak and then turned into a descending segment and decays from there to the residual strength. The first half of the curve was the linear elastic rise phase. The compressive stress first rises rapidly to a peak, then shifted to a descending segment and eventually decayed to the residual strength. This is mainly due to the gradual reduction of the interface gap as the specimen gradually contacts the bearing plate. The compressive stress increases linearly with the vertical strain, and the slope of the straight line remains essentially constant. Before reaching the peak of the curve, the internal microporosity of the concrete gradually expands and fine cracks begin to appear on the surface, accompanied by a slight cracking sound. Then, the curve shows a non-linear increase of compressive stress with the increase of compressive strain. As the compression test continued, the curve showed a decreasing trend. The vertical deformation rate of the specimen increased significantly and the specimen load capacity is obviously insufficient. As the normal stress continued to increase, the decreasing rate of stress slowed down, accompanied by an increasing number of cement mortar spalling, and finally the compressive stress was equal to the residual stress.

Fig. 4
figure 4

Characteristics of stress–strain curves of samples.

Full size image

It can be seen from the variation trend of characteristic points in stress–strain curve of concrete that although the deformation law of concrete was similar, the overall compressive performance of concrete decreases significantly with the increase of temperature and sulfate corrosion degree (see Fig. 5). In addition, the longer the corrosion time, the smaller the slope of the elastic segment curve. It indicated that the internal structure of concrete was loose and the rate of strength increase under pressure slows down significantly. Similar results were found with the change of temperature. Under the combined effect of two factors, concrete exhibited significant compressibility and friability. Two failure modes appeared in the test results. One was bevel shear failure. When peripheral concrete gradually peeled off, shear failure of the sample was obviously observed along the direction of 45° from the edge (M1). It often occured in concrete specimens which were less affected by coupling effect of thermal and corrosion. The other was the longitudinal breakdown failure, where the vertical penetration fracture was evident and fracture failure occurs (M2). It was more common under high temperature and long-term corrosion conditions.

Fig. 5
figure 5

Uniaxial compressive stress–strain curve of concrete under different condition.

Full size image

Strength and deformation properties

As shown in Fig. 6, the compressive strength of concrete already had a certain difference under different curing temperatures when the specimen was not affected by corrosion. The compressive strength and elasticity modulus of the specimens were decreasing with the extension of the corrosion time. Moreover, the higher the initial curing temperature, The greater the deterioration of the mechanical properties of concrete. The variation of compressive strength of samples at 20 °C and 40 °C was similar. At the early stage of corrosion (< 30d), the decrease in compressive strength was small. Then, the slope of the curve increased significantly from 30 to 90 d and the intensity decayed gradually after 90d. It showed a maximum decrease of 35.7% in their compressive strength. It was worth noting that initial corrosion did not cause distinct strength attenuation of concrete under 40 °C. The strength reduction caused by temperature difference reduced by 4.5% with the same corrosion time. However, there’s a much more significant reduction when the corrosion duration exceeded 45d compared to group A. From 45 to 90 d, the intensity deterioration of concrete increased by 7%. The strength curve of group C did not show the aforementioned trend. With the increase of corrosion time, the compressive strength of concrete decreased rapidly and maintained a relatively stable state of low strength after 60 days under the temperature of 60 °C. The maximum reduction in intensity was 68% under the coupling effect of high temperature and corrosion.

Fig. 6
figure 6

Change of concrete compressive strength under HTC conditions.

Full size image

As shown in Fig. 7, the modulus of elasticity showed a similar pattern of change with increasing corrosion time and temperature. When the temperature was from 20 to 40 °C, the elastic modulus decayed in the range of 3.9–45% under the corrosion effect for 90 days. The average slope of the elastic modulus curve from 30 to 60 d was 25–33%. The higher the temperature was, the faster the elastic modulus decays. It was consistent with the strength test results. When the corrosion time was 120d, the decay of elastic modulus due to high temperature reached by 36.8%.

Fig. 7
figure 7

Change of concrete elasticity modulus under HTC conditions.

Full size image

In order to further investigate the response of concrete elasticity modulus under sulphate attack conditions as influenced by temperature and corrosion time, the method of multivariate nonlinear regression analysis was chosen. The temperature and corrosion time were taken as two independent variables, and the modulus of concrete were taken as dependent variables, and the three-dimension curved surface describing the trend of elasticity modulus was obtained (see Fig. 8). The quantitative characterization of the concrete modulus of elasticity in a corrosion environment was defined by the following equation:

$$E = \frac{{33.09 - 0.215T - 0.001T^{2} - 0.086t}}{1 - 0.006T + 0.0013t}\left( {{\text{R}}^{{2}} = 0.{999}} \right)$$
(1)

where T is the initial curing temperature(°C); t is the cure age (d) and E is the modulus of elasticity (GPa). The R-square of the proposed model reach up to 0.932, which reflects a good correspondence between the actual and predicted data. The root mean square error (RMSE) is a statistical indicator that can be used to assess the difference between measured and predicted data. The estimated standard error is used to determine how well a model can describe the values of a data set. For this sample set, the RMSE of 1.598 and the standard error score of 1.615 are both quite low and represent well-organized data results. Therefore, these mathematical equations can be used as a quantitative description of the interaction between HTC conditions and elasticity modulus response of concrete.

Fig. 8
figure 8

Multiple regression surfaces of elasticity modulus.

Full size image

As for the elasticity modulus of concrete under HTC condition, the relative error between the experimental and theoretical results was less than 14.69%. Moreover, the overall relative error between calculation and experiment results ranged from 3.06 to 14.69%, revealing that the proposed calculation model can better meet the computational requirements for actual engineering tasks (less than 20%), as shown in Table 2.

Table 2 Prediction and verification of elastic modulus.
Full size table

Microstructural features

There were significant differences in the microscopic morphology of concrete under different temperature and corrosion duration (as shown in Fig. 9). The concrete specimens with higher curing temperature and longer corrosion time had more cracks inside and the overall structure was less dense, indicating that extensive corrosion damage had occurred inside the concrete.

Fig. 9
figure 9

Microstructure and corrosion product morphology of concrete specimens under HTC conditions.

Full size image

Take the scanning result of group B (40 °C) as an example. It can be seen that the overall structure of specimens was dense and less porous at the primal phase. Oriented aggregation of calcium at the edge of the pore structure, but the number of corrosion products is small. Corrosion ions had little influence on the internal structure of concrete when the corrosion time did not exceed 60 days. However, the internal hydration products of the specimen were reticulated and loose, with more pores when the corrosion time reached 120d. It indicated that with the increase of corrosion time, calcium alumina (needle and rod form) and gypsum (flake form) continue to grow inside the cracks and pores from the edges to the inside, continuously gathering and forming a network of cleavage. The interfacial transition zone also had more flaky calcium hydroxide crystals and was longer and wider in size. Corrosion products gradually produced expansion stress on inner wall of the pore, resulting in internal structural damage and cracking of concrete. Macroscopically, the concrete spalling and localized swelling damage were observed.

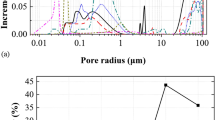
To analyze the development of pore and crack pattern, techniques of digital image processing were selected36. Figure 10 illustrated the results of SEM image (40 °C), processing and acquisition, including noise removal, multiple threshold segmentation, pore bridge, noisy particle elimination, and background extraction. It can be seen that the number of concrete pores increased gradually, and the structural completion became poorer from qualitative perspective. The statistical parameter such as average and corresponding standard deviation (SD) of pore area parameters with corrosion time were also presented in Fig. 11. It can be seen that the average porosity decreased from 128.4 to 82.7 and then increased rapidly to 471.7. The average porosity increased by a maximum of 4.7 times. This indicated that the internal pores of concrete were filled by corrosion products to a certain extent with the progress of corrosion in the early stage. But the internal pores of concrete will inevitably rise significantly under the action of long-term corrosion. One of the interesting things was that similar change occurred in the standard deviation. However, the maximum increase in standard deviation was 10.7 times. This reflected the transition from relatively uniform distribution of pores in concrete to through-cracks. The development of the pore area was polarized. It was further confirmed in Fig. 11. It showed the evolution of number and area of pore were larger than average value (227 pixels) with corrosion time. When the corrosion time increased from 30 to 60 days, the number of larger pores in the test block reduced by 76%, and then increased rapidly to 36 at 120d. The total pore area also increased significantly at 120d. The increase of pore area accompanied by the decrease of number means that the uniformity of pore decreases obviously and a large number of micropores in the concrete were gradually connecting to form some long cracks.

Fig. 10
figure 10

Statistical parameters of pore area under different conditions.

Full size image
Fig. 11
figure 11

Change in number of fractures and total pore area (compared to average).

Full size image

The variation of porosity of samples at different temperatures is similar, as shown in Fig. 12. It can be concluded that corrosion products will fill the internal pores of concrete to varying degrees with the increase of corrosion time. The concrete had few pores in initial state at 20 °C and 40 °C and the filling of corrosion products was at a lower level. Moreover, it was also difficult for the corrosion solution to get into the concrete inside and react quickly. However, the porosity of concrete decreased rapidly and the curve quickly turns to rise at 40 d with the increase of corrosion time at 60 °C. The inflection point of the curve appeared earlier than in both group A and B. The concrete porosity increased about 20 times when the corrosion duration was 120 d. The large number of pores and micro-cracks generated inside the concrete due to high temperature curing also provided a convenient channel for the entry of corrosion solutions. Thus, the microstructure characteristics of concrete do undergo special changes under the coupling effect of high temperature and corrosion.

Fig. 12
figure 12

Porosity distribution under coupling effect of high temperature and corrosion.

Full size image

Damage model of concrete under HTC condition

The above experimental results of microscopic and strength tests on concrete properties show that high temperatures and corrosion do cause damage to concrete microscopic units. The deteriorating effect of corrosion on the mechanical properties of concrete is exacerbated by excessive heat. With the development of internal defects, the macroscopic constitutive behavior of the material may change substantially. Therefore, a new constitutive model for thermal damage of concrete under the coupled effects of corrosion and high temperature must be able to reasonably reflect the preceding physical characteristics. Generally, the use of damage variables allows analysis of the extent of damage deterioration within a material or structure. When damage occurs in a material, it will manifest itself not only on the microscopic but also on the macroscopic level. The microscopic and macroscopic manifestations can be measured separately by different These parameters can be uniformly referred to as damage variables37,38.

The fine damage variables were obtained by Weibull function and using the fine damage micro-element probability distribution, so as to establish the damage constitutive model of concrete under HTC conditions. The probability density function of the micro-element material of concrete in terms of strength can be expressed as:

$$f(x) = \frac{{W_{1} }}{{W_{2} }}\left( {\frac{x}{{W_{2} }}} \right)^{{W_{1} - 1}} \exp \left( { - \left( {\frac{x}{{W_{2} }}} \right)^{{W_{1} }} } \right)$$
(2)

where W1 and W2 are the Weibull distribution parameters. Then the cumulative distribution probability can be expressed as:

$$f(x) = 1 - \exp \left( { - \left( {\frac{x}{{W_{2} }}} \right)^{{W_{1} }} } \right)$$
(3)

According to the damage mechanics of continuous media and using damage variables to characterize the development of damage inside the specimen, the stress–strain intrinsic structure relationship can be expressed as:

$$\sigma = E\varepsilon \left( {{1 - }D} \right)$$
(4)

where \(\sigma\) is the stress,\(\varepsilon\) is the strain, E is the initial modulus of elasticity, which can be obtained by Eq. 1. Assuming that for a total number of concrete microelements of corrosion duration n days is Gt and the number of microelements subjected to damage is G. The damage variable D can be expressed as:

$$D = \frac{{G_{{\text{t}}} }}{G}$$
(5)

Suppose the number of microcells destroyed in the interval \(\left[ {\varepsilon ,\varepsilon + ds} \right]\) is Gp(x), then:

$$G_{t} (\varepsilon ) = \int_{0}^{\varepsilon } {G(f} (x))dx = \left( {1 - \exp \left( { - \left( {\frac{\varepsilon }{{W_{2} }}} \right)^{{W_{1} }} } \right)} \right)G$$
(6)

Combining Eqs. 5 and 6 yields:

$$D = 1 - \exp \left( { - \left( {\frac{\varepsilon }{{W_{2} }}} \right)^{{W_{1} }} } \right)$$
(7)

When the value of D is 0, it means that the concrete is not attacked by chlorine salt; when the value of D is 1, it means that the concrete completely loses its compressive strength under the effect of corrosion damage of chlorine salt. Substitute Eq. 8 into Eq. 4:

$$\sigma = E\varepsilon \left( {{1 - }D} \right) = E\varepsilon \exp \left( { - \left( {\frac{\varepsilon }{{W_{2} }}} \right)^{{W_{1} }} } \right)$$
(8)

Derivative from the relationship between the coordinates corresponding to the peak stress point \((\varepsilon_{\max } ,\sigma_{\max } )\) and the slope of the curve shows:

$$W_{1} = - \frac{1}{{\ln \left( {\frac{{\sigma_{\max } }}{{E\varepsilon_{\max } }}} \right)}}\;W_{2} = \frac{{\varepsilon_{\max } }}{{\left( {\frac{1}{{W_{1} }}} \right)^{{\frac{1}{{W_{1} }}}} }}$$
(9)

The values of the parameters can be calculated by the above formulas and the results are shown in the following Table3:

Table 3 Parameters of concrete under HTC conditions.
Full size table

The relationship between the fitted parameters and the corrosion time and temperature can be obtained by regression analysis of the data.

$$W_{1} = 3.473T^{3} + 0.13T - 0.003T^{2} - 1.25T^{4} - 0.03{\text{t}} - 0.76\left( {{\text{R}}^{{2}} = 0.{913}} \right)$$
(10)
$$W_{2} = - 3.659T^{4} + 0.0001T^{3} - 0.095T^{2} + 0.38T - 0.057{\text{t}} - 1.57\left( {{\text{R}}^{{2}} = 0.{921}} \right)$$
(11)

The final principal equation for the compressive stress–strain of concrete under chloride ion attack conditions can be obtained by Substituting Eqs. 10 and 11 into Eq. 8. Moreover, it can be also seen that this mechanical model can characterize the change of concrete mechanical properties by environmental and time factors. In order to further improve the accuracy of model prediction, a linear correction term based on residual analysis was introduced. This term compensates for systematic deviations between the computed and experimental values, particularly under long-term high-temperature conditions. The correction term is expressed as:

$$\Delta \sigma_{{{\text{corr}}}} = 0.0031t + 0.8328$$
(12)

The final corrected peak stress can be calculated by:

$$\sigma = E\varepsilon \left( {{1 - }D} \right) = E\varepsilon \exp \left( { - \left( {\frac{\varepsilon }{{W_{2} }}} \right)^{{W_{1} }} } \right) + \Delta \sigma_{{{\text{corr}}}}$$
(13)

The calculations obtained by the novel constitutive model proposed in this paper allow to obtain the values of the parameters taken under HTC conditions, which leads to the standardized stress–strain relationship for concrete materials under hydrothermally corrosive environment. The comparison results of computation and test value are shown in Table 4. The error rate of the peak stress calculated by the model ranged from 0.88 to 19.81%, which was less than 20% overall and meets the accuracy requirements of engineering applications. From the comparison of the calculated results with the experimental results, it can be concluded that the calculated results of the model were in good agreement with the experimental results. It revealed that the proposed constitutive model can better reflect the compressive stress–strain relationship of concrete materials under hydrothermally corrosive environment.

Table 4 Fitting results of the corrosion damage model (peak stress).
Full size table

DEM simulation and numerical analysis

Findings from the earlier discussed microscopic concrete characteristics and macroscopic mechanical tests revealed substantial internal damage occurring in concrete within a highly corrosive high-temperature water environment. To delve deeper into understanding the microscopic mechanisms leading to concrete deterioration, crack initiation, expansion, and the subsequent decay of its macroscopic mechanical properties under HTC conditions, this study employed the Particle Flow Code (PFC 3D) utilizing the Discrete Element Method (DEM) technique.

Model establishment

The constitutive model in PFC is a fine-scale constitutive model for contact, which is very different from the macroscopic constitutive model of the material. Changes in the macroscopic physical properties of materials are often realized through the particle-to-particle contact model. Concrete is composed of different types of aggregates, which are bonded together by the cement paste. When concrete is subjected to high temperatures and corrosion by aqueous chemical solutions, the cementation between the cement paste particles will be weakened and destroyed, thus affecting the mechanical properties of concrete. Therefore, the microscopic fracture of concrete under HTC condition can be characterized by the breakage of contact bonds between particles and particles.

Linear Parallel Bond Model (LPBM), one of bond particle methods (BPMs) models are commonly used in PFC to characterize cementitious cements. It can be obtained from the operating mechanism of LPBM model (see Fig. 15) that the bonding elements in the model can be considered as a set of springs with constant normal and shear stiffnesses uniformly distributed over the contact surface and the central contact point. When relative motion occurs at the contact points, a force and a moment are generated in the contact, which act simultaneously on both contact elements. If either of these two maximum stresses exceeds its corresponding strength, the parallel bond breaks down and removes the bond along with its accompanying forces, moments and stiffnesses. As shown in Fig. 13, \({\overline{F} }_{n}\) is the normal component of the parallel bond force, \(\stackrel{-}{\overline{{F }_{s}}}\) is the tangential component of the parallel bond force and A was the contact cross-sectional area. \({\overline{M} }_{t}\) and \({\overline{M} }_{b}\) represented the torsional and bending moments to which the contact is subjected, \({\theta }_{t}\) and \({\theta }_{b}\) represent the torsional and bending quantities, and J and I represent the extreme moment of inertia and the moment of inertia, respectively. It can be seen that the parallel bond model degrades to a linear contact model when subjected to damage, thus reflecting the mechanical response of the cement under thermal-corrosion coupling effect. Therefore, the damage factor is introduced on the contact bond between ball-ball to establish the damage particle flow model of concrete in this paper through secondary development study on the LPBM model source code.

Fig. 13
figure 13

Destruction mode of the parallel bonding model.

Full size image

The study findings revealed internal damage in concrete samples exposed to HTC conditions, exhibiting varying degrees of intensity. Specifically, different sections of the specimen exhibited strength reduction following a discernible pattern. To account for this random intensity weakening in the numerical model, the simulation model adjusted the bond energy control parameters of the ball-ball particles, guided by the damage constitutive relationship of concrete obtained from the prior study. Using the Weibull model, a random damage factor between 0 and 1 was generated. The product of this factor and the conventional concrete mechanical parameters formed the initial parameters for the damaged specimen. This innovative modeling approach for concrete damage, termed the Discrete-Random Damage Model (DRDM). Figure 14 illustrates the entire generating process of DRDM.

Fig. 14
figure 14

Generation process for DRDM under hydrothermally corrosive environment.

Full size image

Micro-parameter selection and setting

Since the microscopic parameters in PFC do not correspond to the macroscopic parameters of the specimen, the damage parameters value W1 and W2 cannot be referred to Table 4 under HTC environments. We need to carry out the calibration of microscopic parameters of specimen under HTC condition based on the macroscopic Weibull theory model derived from the aforementioned test, while ensuring that the elastic modulus and Uniaxial compressive strength (UCS) are close to the test results. The main microscopic parameters of the LPBM model used in this paper are shown in Table7. The research results for LPBM-based simulation of mechanical behavior of concrete show that pb_kratio affects the Poisson’s ratio of macroscopic elastic deformation, and they are linearly related; pb_emod and emod are related to the macroscopic elastic modulus39. The pb_ten is related to the macroscopic tensile strength, while pb_coh represents the macroscopic compressive strength; the ratio of pb_ten and pb_coh both control the damage pattern of the model, and it is generally believed that the larger the ratio, the more the model tends to undergo shear damage. The smaller the ratio, the more the model tends to undergo brittle damage40. The damage of parallel bonding includes shear damage and tensile damage. Tensile damage occurs when the tensile force on the bond between the ball-ball exceeds pb_ten. Shear damage occurs when the shear force on the bond exceeds (pb_coh + σc × tan(pb_frci)). Therefore, in combination with the aforementioned DRDM modeling approach, the process of calibration of concrete deterioration parameters under HTC conditions is shown in Fig. 15 and Table 5.

Fig. 15
figure 15

Model parameter calibration process.

Full size image
Table 5 Main parameters in the parallel bonded contact model.
Full size table

In numerical tests, particle generation was based on DRDM and the shape of the model was rectangular with length × width = 100 mm × 100 mm. The specimens under different HTC conditions were subjected to uniaxial compression by numerical simulation. Due to the many test conditions, only 30 days, 60 days and 120 days of corrosion duration were selected here for the simulation study. The UCS and stress–strain curves of the DRDM samples were obtained and compared with laboratory tests. Finally, a two-dimensional model was used considering the specimen’s regular geometry and uniform boundary conditions. While 3D effects are simplified, the simulation results showed good agreement with experimental data, indicating the model’s validity for the intended analysis (as shown in Table 6 and Table 7).

Table 6 Comparison of calibration results.
Full size table
Table 7 Micromechanical properties for discrete element simulation.
Full size table

Simulation result analysis

Comparison of results by different modeling methods

To compare the simulation outcomes between the Discrete-Random Damage Model (P1) from this paper and conventional discrete element model (P2), the study focused on the conditions of 40 °C–60 d, examining distinct damage characteristics of specimens. Figure 16 illustrates clear differences in simulation results between the two methods. Both methods exhibited an "X" type damage in the morphology of macroscopic cracks. However, P2 displayed a more intact central area with a flat fracture surface containing fewer fine fragments, while P1 exhibited a rougher fracture surface, generating more fine fragments on the specimen’s surface. Macro debris statistics showed that the fragments followed the Weibull function, consistent with the experimental results of this paper and previous research41. Statistical analysis indicated 748 fragments for the P2 model and 868 fragments for the P1 model, representing a 13.8% increase compared to the conventional discrete element model. A greater distribution of fine fragments was observed, which can be attributed to the substantial non-uniformity of contact strength within the P1 model. This aligns more closely with the combined damage effects of high temperature and corrosion on concrete. The presence of numerous microscopic pores within discrete divisions of the sample compromised the specimen’s integrity, increasing the likelihood of linking to form macroscopic fractures in the damage zone under external loading. This intensified concrete fragmentation.

Fig. 16
figure 16

Statistical distribution of the fragment size when the specimen is damaged.

Full size image

From the perspective of microscopic crack development (see Fig. 17), the initial crack generation in P1 was apparently random and relatively uniformly distributed. In P2, fewer cracks were produced in the same state, and the cracks that penetrated were relatively concentrated. The comparison showed that the traditional model calibrated directly based on the mechanical response results cannot reflect the real microstructural characteristics of concrete under the coupling effect of high temperature corrosion. This was not conducive to further revealing the microscopic rupture evolution mechanism inside the concrete during the damage process. Therefore, the DRDM proposed in this paper based on the macroscopic intrinsic structure model of specimens under HTC conditions can be better used to study the performance evolution and strength prediction of lining materials under hydrothermally corrosive environment.

Fig. 17
figure 17

Microscopic crack evolution during compression damage of specimens.

Full size image

Features of fractures

The stress–strain curves of the specimens obtained from simulation tests under different working conditions and the acoustic emission results were shown in Fig. 18. It can be found that under a certain high temperature condition, the peak stress gradually decreased and the peak strain at final damage gradually increased as the age of corrosion rose. This was in good agreement with the indoor test results. The change in the acoustic emission curve showed that the longer the age of corrosion, the smaller the number of cracks per unit time. For example, under the condition of 20 °C, the maximum number of cracks broken per unit time was 187, 123 and 90 for specimens with an age of 30d, 60d and 120d, respectively. Similarly results can be found in the relationship between temperature and the number of cracks. For example, when the corrosion duration was 30 days, the number of cracks caused by an increase in temperature decreased from 187 to 148. Moreover, the combination of high temperature and long-term corrosion effects resulted in a 66.8% reduction in the maximum number of fractures per unit time, which indicated that the hydrothermally corrosive environment further exacerbated the internal damage to the specimens.

Fig. 18
figure 18

Analysis of acoustic emission results during compression of specimens under HTC conditions.

Full size image

Figure 19 showed the evolution of the total number of cracks with deformation of the specimen. The difference in the number of cracks due to temperature differences was greater at shorter ages of corrosion, but less when the age of corrosion was 120 days. The decrease in the number of cracks ranged from 13.8 to 9.3%. In the coupled hot corrosion environment, there was an overall downward trend in the total number of cracks, with a maximum reduction of 22.4%. However, the more severe the internal damage of the specimen, the greater the deformation required for its total number of cracks to reach a maximum under uniaxial compression. This is also consistent with the evolution of the macroscopic mechanical properties of the specimens in this paper and other research results42.

Fig. 19
figure 19

Statistics on the number of microscopic cracks during compression under HTC conditions.

Full size image

Failure pattern

It can be seen from Fig. 20 that the final damage pattern starts mainly with spalling on both sides and produced a dense band of X-shaped cracks when the specimen was damaged. As the corrosion duration increased, cracks tend to penetrate vertically. As the temperature increased, the formation and distribution of cracks became more or less similar under different conditions, but the area of crack spread became smaller and smaller. However, the formation of discrete cracks in the middle of the specimen increases significantly, especially when the temperature was 60 °C. The macroscopic damage diagram of the specimens showed that the degree of fragmentation at damage area deepened significantly with the increase of temperature and corrosion duration, and the number of medium-sized fragments decreased. This indicated that the degree of damage inside the specimen had been more serious at this time, and the overall damage of specimen was very likely to occur under external forces43. Interestingly, this is somewhat similar to the damage observed in the compression tests in Sect. "Microstructural features" of this paper.

Fig. 20
figure 20

Microscopic crack spreading diagram at the time of specimen damage under HTC conditions.

Full size image

It’s worth noting that the simulation method proposed in this paper is based on the basic assumption of uniform deterioration of concrete micro-units. It can only achieve a similar simulation of the mechanical properties of concrete and cannot interpret the real physicochemical corrosion process. The real sulfate degradation under high temperature conditions gradually from the surface, resulting in a spatial distribution of degradation. Therefore, the research results are somewhat different from reality, but the changes in the quantitative indicators of mechanics are informative.

Conclusions

This paper presented a study on the evolution of the performance of lining concrete materials under hydrothermally corrosive environment. Different tests on apparent, microscopic and mechanicalon of specimens were conducted to investigate the coupling effect of high temperature and corrosion damage on tunnel lining. Moreover, the quantitative computational model for the evolution of concrete properties and material constitute model were also presented and verified by novel discrete-random damage model proposed in this paper:

  1. (1)

    With increasing corrosion time and temperature, the mass loss rate of all specimens exhibited a two-stage trend: an initial decrease followed by a rapid increase. In the early stage of corrosion, sodium silicate solution temporarily filled the concrete pores, reducing mass loss. However, this compensating effect diminished over time. Prolonged exposure intensified the coupled effect of thermal and chemical corrosion. Compared to concrete under conventional conditions, high temperature increased the mass loss rate by up to 3.08 times at the same age.

  2. (2)

    SEM analysis revealed that higher curing temperatures and longer corrosion durations resulted in more internal cracking and reduced matrix density. Needle- and rod-like calcium aluminate and flake-like gypsum crystals were observed growing along crack paths and within pores, forming interconnected cleavage networks. Under the coupled effect of elevated temperature and corrosion, the average porosity increased by up to 4.7 times, and the standard deviation of pore distribution by up to 10.7 times. Pore development showed polarization, characterized by fewer but larger pores, indicating a significant reduction in pore uniformity and the progressive coalescence of microvoids into extended cracks.

  3. (3)

    Two failure modes were identified under hydrothermal corrosion (HTC) conditions during uniaxial compression tests. Longitudinal splitting failure became dominant at higher temperatures and longer corrosion duration. The concrete displayed increased brittleness and compressibility. Elevated temperatures notably aggravated the degradation of uniaxial compressive strength and elastic modulus, especially at 60 °C. The maximum strength reduction reached 68% under coupled conditions, and the elastic modulus decreased by 36.8% after 120 days of corrosion. The mechanical model developed in this study effectively captured the compressive stress–strain behavior of concrete in hydrothermally corrosive environments, with peak stress prediction errors ranging from 0.80 to 21.87% and relative elastic modulus errors within 14.69%.

  4. (4)

    A novel discrete random damage model (DRDM) based on contact strength discounting was proposed. Using the embedded FISH language, both linear and parallel-bond components at contact interfaces were simultaneously degraded according to a Weibull distribution. Simulation results showed a general decline in the total number of cracks, with a maximum reduction of 22.4%, and a 66.8% decrease in the peak fracture rate under HTC conditions. Crack fragmentation intensified in damaged zones as temperature and corrosion duration increased, indicating that the hydrothermal corrosive environment significantly exacerbated internal damage. These findings were consistent with the observed macroscopic mechanical deterioration, demonstrating that the DRDM realistically reflects the coupled effects of temperature and corrosion on concrete behavior.