Effect of geopolymer treatment on the ultimate bearing capacity of sabkha soil under axial loading

Abstract

Saline sabkha soils pose a major challenge for geotechnical engineering because of their low bearing capacity and high settlement potential. The purpose of this research was to evaluate the behavior of stabilized sabkha soil under axial stress after geopolymer treatment utilizing the mix and compact method. A comprehensive numerical analysis, validated by experimental results, was conducted to study the load–displacement behavior of sabkha soil in its natural and treated states. A parametric study using the finite element method was performed to examine the effects of the thickness and diameter of the geopolymer-treated soil layer on the ultimate bearing capacity (UBC). Response surface methodology and ANOVA were employed to develop and evaluate a predictive model for UBC as a function of the dimensionless ratios H_m/D_f and D_m/D_f. The results revealed that the geopolymer treatment significantly enhanced the load-bearing capacity of sabkha soil by increasing the thickness and diameter of the treated soil layer. However, a higher ratio of D_m/D_f than 2 adversely affected soil performance when the H_m/D_f ratio was less than 0.6. The study also demonstrated that geopolymer is a novel and environmentally friendly technique for stabilizing sabkha soils, as it utilizes waste materials (fly ash and mine tailings).

Introduction

Sabkha soil, which exhibits low shear strength and high compressibility, is widespread in the Kingdom of Saudi Arabia, where it supports a substantial and fast-growing area that hosts numerous large-scale petrochemical and other industrial projects. Sabkha soil poses inherent geotechnical difficulties, particularly near the surface, necessitating soil stabilization techniques to augment its bearing capacity and decrease settlement¹. The selection of a suitable stabilization technique is determined by a variety of factors, such as sabkha soil type, project specifications, improvement objectives, budget, and construction time frame^2,3. To improve the properties of weak sabkha soils, researchers have applied several stabilization and improvement methods, such as mechanical stabilization techniques (e.g., preloading, vibroflotation, stone columns, and dynamic compaction), chemical stabilization using additives (e.g., ordinary Portland cement (OPC), lime, or cement kiln dust [CKD]), and stabilization using geotextiles^{4,5,6,7,8,9,10}.

The use of additives, such as OPC, lime, or CKD, for chemical stabilization is a typical way of treating sabkha soil. This method improves the soil matrix’s stability by creating cementitious bonds that prevent its collapse when wet. However, this method has a high environmental cost, as OPC production accounts for 5–7% of all CO₂ emissions worldwide from industrial and energy sources^11,12. Therefore, there is an urgent need for environmentally friendly alternatives that can reduce the ecological footprint of soil stabilization. A potential alternative is the use of alkali-activated waste materials (also known as geopolymers) as a new technique for soil stabilization. Geopolymer is produced by activating aluminosilicate materials (e.g., fly ash [FA], glass waste, mine tailings [MTs], slag, and metakaolin) with alkaline activator solution. This technique eliminates the need for OPC and recycles waste materials that would otherwise be disposed of in landfills or open dumps. Geopolymer has been shown to have better cementing properties than OPC or lime, such as higher mechanical strength and durability in adverse conditions^{13,14,15,16,17}. Moreover, geopolymer can lower the CO₂ emissions and energy consumption associated with soil stabilization compared with OPC^18,19,20.

The behavior of superstructure loads transferred through sabkha deposits has been the subject of extensive research^1,8,21,22,23. Sabkha soil, which is the foundation material for many buildings, can be divided into two main categories: the soft sabkha layer and the dense sabkha base at great depths⁸. General principles for designing and building foundations within or on sabkha deposits are provided by the Saudi Building Code (SBC 2018)²⁴. These principles aim to avoid structural damage caused by differential settlement. They also require designers to consider the loss of strength of the surface crust of sabkha resulting from water infiltration, as well as the heterogeneity of compressibility properties within the site due to variations in layer thickness, relative density, and cementation degree. Furthermore, they demand that protective measures must be made to protect steel and concrete from corrosion induced by the high chloride and sulfate concentrations in sabkha soil and brine. Heavy structures on sabkha soil should have mat or deep foundations, as per the SBC, and light structures should have reinforced concrete strip foundations with suitable protective measures based on the groundwater level.

The use of artificially cemented soil layers as an economical alternative to deep foundations for enhancing the load-bearing capacity of shallow footings on weak soils has been explored by several researchers. Thomé et al.²⁵ developed a method for estimating the performance of shallow foundations founded on a cemented soil layer overlying a weakly bonded residual soil layer with a high void ratio. Their study, which consisted of field plate loading tests and simulations analysis, showed that the formation of artificially cemented layers directly beneath footings can effectively increase the bearing capacity and decrease settlement for light to moderate foundation stresses. Multiple regression analysis of the finite element method (FEM) simulations indicated that the key parameters affecting pressure–deformation behavior are the Young’s modulus of the weaker lower stratum, cohesion intercepts of the cemented upper layer and weaker lower stratum, and friction angle of the lower stratum. Moreover, they found that the load–settlement behavior becomes more rigid and robust as the treated layer thickness ($\:{H}_{m}$)-to-foundation diameter ($\:{D}_{f}$) ratio increases.

Foppa et al.²⁶ presented a novel methodology for assessing the bearing capacity of strip foundations resting on an artificially stabilized soil layer overlying weak foundation soil, accounting for its horizontal extension. Their method was verified by conducting tests on strip foundations placed on loose sandy soil and performing FEM analysis. Two different failure modes were detected. The loose sandy soil was penetrated by the artificially stabilized soil layer in the first mode, without any visible fracture. In the second mode, the stabilized soil layer broke after some initial displacement, revealing a cracks either near the edge or along the centerline of the footing, depending on the thickness of the stabilized layer. The study established that the determined tensile stress in the stabilized layer was influenced by the soil’s vertical reaction and the dimensionless parameter $\:\frac{{T}_{r}}{{H}_{m}}$, where $\:{T}_{r}$ is the horizontal distance between the footing’s edge and the stabilized layer’s edge, and $\:{H}_{m}$ is the thickness of the stabilized soil layer.

Consoli et al.²⁷ explored the behavior of plate load tests on two-layered soil systems composed of a stabilized soil layer over a compressible residual soil stratum. Their study analyzed the applied pressure–settlement behavior of tests by using circular steel plates on top of artificially cemented layers. The authors highlighted the importance of presenting test results as normalized pressure and settlement. They observed that in the field tests, the final failure mode invariably involves punching through the top layer. The authors established that the analytical model for the ultimate bearing capacity (UBC) of foundations on layered cohesive-frictional soils is fairly accurate up to a certain ratio of $\:\frac{{H}_{m}}{{D}_{f}}\:$ (i.e., $\:\frac{{H}_{m}}{{D}_{f}}\:$=1).

This study conducts a comprehensive investigation into the potential benefits of using the mix and compact method to enhance the geotechnical characteristics of sabkha soil and increase its bearing capacity. Numerical analyses were performed; using the FEM and validated/calibrated physical model tests on untreated and treated sabkha soil with geopolymer, incorporating different contents of FA and MT and different thicknesses and diameters of the treated layer. A statistical study was also conducted to evaluate the influence of altering the dimensions of the geopolymer-treated soil layer on the UBC. The results of these tests provide useful insights into the effectiveness of the mix and compact method in strengthening the geotechnical properties of sabkha soil.

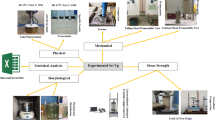
Experimental program

Material properties

Sabkha specimens have been sourced from the Ras-Al-Ghar site located in the Eastern Province of Saudi Arabia. To account for the geotechnical design implications of the deep portion of the soil layer, we removed the upper 0.3 m layer of subsoil before collecting the specimens. The water table was observed to be situated at a depth of 0.5 m underneath the surface, and the collected specimens exhibited a white color. Table 1 provides a comprehensive overview of the classification and physical features associated with saline sabkha soil.

Geopolymer synthesis involves the utilization of two distinct precursors, specifically copper MT and FA. The sample of MT was obtained from a copper mining location situated around 120 km towards southeast of Medina, Saudi Arabia. MT was acquired in the form of moist solids, which contained 29% natural water content. After the drying process in an oven at a controlled temperature of 105 ± 5 °C, the MT aggregates were subjected to crushing and sieving using a #10 sieve. This step was taken to prevent particle clustering and to ensure that all of the MT material was used.

FA class F imported from India as a raw material for producing geopolymers was also employed. Table 2 presents the chemical elements of sabkha soil, MT, and FA, as determined through XRF analyses. The elements alumina and silica were found to be the utmost prevalent in MT and FA, whereas calcium and silica were the dominant elements in sabkha soil. Nevertheless, the geopolymerization rate and pozzolanic efficiency of MT, FA, and sabkha soils exhibited an upward trend as the silica content increased.

Table 1 Sabkha soil classification and physical characteristics.

Table 2 XRF analysis of FA, MT, and Sabkha soil.

Preparation for the physical model test

In the case of geopolymer-treated sabkha soil prepared using the mix and compact method, the treated soil specimens were designed with a diameter of 100 mm—twice that of the foundation model—to ensure adequate stabilization. The thickness of the treated soil layer was varied as a ratio of the foundation diameter (D_f= 50 mm), with values of 0.2, 0.6, and 1, corresponding to thicknesses (H_m​) of 10 mm, 30 mm, and 50 mm, respectively. Two types of precursors, fly ash (FA) and metakaolin (MT), were utilized in proportions of 3%, 5%, and 10% of the dry soil weight. The proportions of FA and MT were set at 3%, 5%, and 10% as geopolymer precursors to systematically study the effect of this dosage on soil stabilization. This range was selected to identify an effective or optimal content by observing dose-response patterns, considering the specific reactivity and chemical nature of the FA and MT. These percentages also help achieve a balance between desired engineering performance, cost-effectiveness, and the environmental benefits of using these waste materials. Thus, the chosen percentages represent a practical range: 3% as a lower-bound initial response, 5% as an optimal intermediate level, and 10% as an upper-bound limit. This approach is consistent with common dosage ranges investigated in existing geopolymer soil stabilization literature^28,29,30.

For the preparation of cylindrical geopolymer-treated sabkha specimens, a three-part hollow vertically split mold and two steel O-rings were employed. The treated samples were formed within a 100-mm-diameter metal mold. The required quantities of dry materials (sabkha soil, and precursor) were precisely weighed and manually mixed for approximately 10 min to ensure uniform distribution. The alkaline activator solution, consisting of sodium silicate (SS) and sodium hydroxide (SH) in a 2:1 ratio, was prepared separately. A predetermined amount of this solution, based on the results of the standard Proctor compaction test, was added to the dry mixture and thoroughly blended until a homogeneous consistency was achieved. The resulting mixture was then placed into the mold in three equal layers, with each layer carefully leveled and statically compacted. Following compaction, the samples were immediately extruded and subjected to curing at ambient temperature (23 °C) for a minimum of seven days.

Numerical study

FEM is an efficient modeling technique for a variety of engineering problems. The objective of numerical analysis on loading experiments on untreated and treated sabkha with geopolymer is to validate experimental work and provide an alternative method for examining load transfer mechanisms under various conditions. Numerical analysis allows for high flexibility in modifying model parameters and inputs, enabling the examination of a broad range of potential outcomes. This work enables the analysis of soil behavior under a variety of conditions, which would be challenging to accomplish using a physical model. In addition, numerical analysis permits the observation of behavior in numerous kinds of situations, which is not possible during experimental work. In situations where instruments may be damaged during the pouring of concrete or the installation of strain gauges, numerical analysis can be applied to estimate values. In this study, a numerical investigation was conducted using the FEM through the comparison of data from small-scale physical model experiments with computed results of numerical analysis developed utilizing the finite element software PLAXIS 3D.

FEM involves dividing the domain of interest into a finite number of small subdomains or elements. The behavior of the system within each element is approximated using simple mathematical functions, and the equations governing the system are solved for each element. The solutions for all elements are then combined to obtain an approximate solution for the entire domain³¹.

Constitutive models and soil parameters

The hardening soil model (HS model)

The Hardening Soil (HS) model was employed to mimic the performance of the untreated sabkha soils. According to Schanz et al.³²the HS model is an advanced model that can be utilized to simulate the intricate behavior of a wide spectrum of soil types, encompassing both soft and stiff soils. Previous studies have utilized the Mohr–Coulomb (MC) model to simulate untreated sabkha soil because of its simplicity^21,33,34. Nonetheless, the model exhibits limitations that potentially result in soil behavior that differs from reality. The HS model is a sophisticated soil model that can produce soil response with strong reality in relation to non-linearity, inelasticity, and stress dependency. The HS model outperforms the MC model, as it uses a hyperbolic stress–strain curve rather than a bi-linear one and it can account for the stress level dependency. Even though Young’s modulus depends on the amount of stress in real soils, the MC model requires the user to choose a fixed value for this parameter. A significant limitation of the MC model is its assumption that the soil unloading–reloading stiffness modulus ($\:{E}_{ur}$) is identical to the soil loading stiffness ($\:{E}_{50}$). However, in reality, soils typically exhibit a much higher modulus under unloading–reloading conditions compared with loading conditions. The stiffness of unloading–reloading might be 2 to 5 times that of loading stiffness³⁵. When utilized to evaluate excavation problems, the MC model may over-predict soil heave in an unrealistic manner. Consequently, the stress levels present in the soil must be assessed, and this information can be utilized to derive appropriate stiffness values.

The stiffness values are established with respect to reference stress denoted as $\:{p}^{ref}$ to account for the influence of stress level on soil stiffness. The program utilizes a default value of $\:{p}^{ref}=100\frac{kN}{{m}^{2}}$. The equations used to calculate $\:{E}_{50}$, $\:{E}_{oed}$, and $\:{E}_{ur}$ are as follows:

$$\:{E}_{50}={E}_{50}^{ref}{\left(\frac{c\text{cos}\left(\phi\:\right)-{\sigma\:}_{3}^{{\prime\:}}\text{sin}\left(\phi\:\right)}{c\text{cos}\left(\phi\:\right)+{p}^{ref}\text{sin}\left(\phi\:\right)}\right)}^{m}$$

(1)

$$\:{E}_{oed}={E}_{oed}^{ref}{\left(\frac{c\text{cos}\left(\phi\:\right)-{\sigma\:}_{3}^{{\prime\:}}\text{sin}\left(\phi\:\right)}{c\text{cos}\left(\phi\:\right)+{p}^{ref}\text{sin}\left(\phi\:\right)}\right)}^{m}$$

(2)

$$\:{E}_{ur}={E}_{ur}^{ref}{\left(\frac{c\text{cos}\left(\phi\:\right)-{\sigma\:}_{3}^{{\prime\:}}\text{sin}\left(\phi\:\right)}{c\text{cos}\left(\phi\:\right)+{p}^{ref}\text{sin}\left(\phi\:\right)}\right)}^{m}$$

(3)

where $\:{E}_{50}^{ref}$, $\:{E}_{oed}^{ref}$, and $\:{E}_{ur}^{ref}$ are the secant stiffness in standard drained triaxial test, tangent stiffness for primary oedometer loading, and unloading/ reloading stiffness, respectively, corresponding to the reference confining pressure $\:{p}^{ref}$³⁶. The parameter $\:{\sigma\:}_{3}^{{\prime\:}}$ denotes the confining pressure employed throughout a triaxial test. The value of $\:m$ should be considered as 1.0 for soft clays, whereas it should be approximately 0.5 for sands and silts. Typically, the value exhibits variation within the interval of 0.5 to 1.0.

The default settings for average values of various soil types suggest that $\:{E}_{ur}$ is approximately equal to 3$\:{E}_{50}$, and $\:{E}_{oed}$ is approximately equal to $\:{E}_{50}$. However, soils that are either very soft or very stiff may yield different ratios of $\:\frac{{E}_{oed}}{{E}_{50}}$, which can be inputted by the user. Table 3 shows the values of parameters used in the HS model.

Table 3 Values of parameters used in HS model.

Hoek–Brown failure criterion (HB model)

The Hoek–Brown failure criterion (HB) is a relationship that has been derived empirically and is utilized to simulate the non-linear increase in the peak strength of isotropic rock with increasing confining stress. The mechanical response of rocks is distinct from that of soils, which exhibit greater stiffness and strength.

The use of the HB failure criterion for modeling geopolymer-treated sabkha soil is justified by the material’s transformation into a cemented, rock-like state after treatment. Although the HB criterion was originally developed for rock mechanics, it has been successfully adapted for cemented or stabilized soils that exhibit similar behavior^38,39,40,41.The geopolymer treatment significantly enhances the soil’s strength and stiffness, with the unconfined compressive strength (UCS) ranging from 5 MPa to 25 MPa, placing it within the classification of weak rock (ISRM). The qualitative differences between rock and untreated soil were carefully considered, particularly the development of strong cementitious bonds, stress-dependent behavior, and brittle failure modes in geopolymer-treated soil, which align well with the Hoek-Brown criterion’s ability to capture non-linear strength increases and brittle failure. The model parameters (e.g., $\:{m}_{i}$​, GSI, $\:{\sigma\:}_{ci}$) were derived from laboratory UCS tests on geopolymer-treated soil, ensuring accurate representation of its mechanical behavior. Furthermore, the model was calibrated and validated using experimental data, demonstrating excellent agreement between numerical simulations and physical test results. While soil-specific models (e.g., Mohr-Coulomb or HS) are typically used for untreated soils, the Hoek-Brown criterion was selected for its ability to better represent the treated soil’s rock-like properties and stress-dependent behavior.

The determination of Young’s modulus in rock samples can be achieved through axial compression tests. Nevertheless, Young’s modulus is primarily relevant to the intact rock material and must be decreased to acquire an accurate measure of the stiffness of the rock mass in its natural state. We assume that Young’s modulus of the rock mass ($\:{E}_{rm}$) remains constant for the specific rock layer under consideration. One of the proposed empirical correlations can be utilized to compute the stiffness of the rock mass, which can be determined using the rock quality criteria in the HB model⁴² as follows:

$$\:{E}_{rm}={E}_{i}\left(0.02+\frac{1-\frac{D}{2}}{1+{e}^{\left(\frac{60+15D-GSI}{11}\right)}}\right)$$

(4)

Where:

$\:{E}_{rm}$= in-situ rock mass modulus ($\:\frac{\text{k}\text{N}}{{\text{m}}^{2}}$).

$\:{E}_{i}$= intact rock modulus ($\:\frac{\text{k}\text{N}}{{\text{m}}^{2}}$).

D = disturbance factor.

GSI = Geological Strength Index.

The intact rock modulus ($\:{m}_{i}$), Poisson’s ratio ($\:\nu\:$), and unconfined compressive strength ($\:{\sigma\:}_{ci}$) values were derived from the outcomes of the laboratory-based UCS tests conducted on geopolymer-treated sabkha soil. The UCS of sabkha soil specimens treated with geopolymer was assessed following the procedures outlined in ASTM D2166. The specimens were subjected to axial loading at a constant displacement rate of 0.5 mm/min, enabling the generation of characteristic stress-strain relationships. Peak axial stress values obtained from these relationships were adopted as the representative UCS measurements for evaluating the mechanical behavior of the stabilized soil matrix. When a load was applied, vertical and horizontal strains in the geopolymer-treated sabkha soil samples were measured using strain gauges, as shown in Fig. 1. Thereafter, the Poisson’s ratio and Young’s modulus were calculated.

Fig. 1

Test setup for measurement of UCS, Young’s modulus and Poisson’s ratio; (a) full setup of the machine, (b) failure of the sample after UCS test.

$\:{m}_{i}$ is a model parameter that has an empirical relationship with the type of rock. GSI is a measurement used in geotechnical engineering to assess the strength and stability of rock masses. GSI is a rock mass categorization system that has been established in the field of engineering rock mechanics. Its purpose is to provide dependable input data regarding the characteristics of the rock mass that are necessary for numerical calculations or closed-form solutions when planning slopes, tunnels, or foundations in rock formations⁴³.

D is a parameter depending on the degree of rock disturbance caused by mechanical processes in tunnels, open excavations, or mines. These processes may include but are not limited to blasting, tunnel boring, machine-driven, or manual excavation⁴⁴. In the absence of any disruption, the value of D is zero, whereas the value of D is assigned as one in the case of significant disruption. A value of D = 0 was utilized for the purpose of modeling sabkha soil treated with geopolymer. Table 4 shows the parameters and their values used in the HB model.

Table 4 Values of parameters used in HB model.

Linear elastic model

The numerical model employed for the analysis of the circular foundation is a linear elastic model, which is a mathematical model that describes the behavior of solid materials under stress. This model is fundamentally rooted in Hooke’s Law of isotropic elasticity, which asserts that, at a material’s elastic limit, the strain in that material is precisely proportionate to the applied stress.

In the linear elastic model, two primary parameters are pivotal in characterizing the elastic behavior of a material: Young’s modulus (E), which quantifies the material’s inherent stiffness or resistance to elastic deformation under load; and Poisson’s ratio (ν), which measures the material’s propensity to contract or expand in directions orthogonal to the direction of compression or extension.

In this numerical model, the circular foundation is represented as a plate with a diameter and thickness measuring 50 and 30 mm, respectively. The material properties assigned to this foundation are reflective of those exhibited by aluminum, with a Poisson’s ratio of 0.3 and a Young’s modulus of 70 GPa³⁷. The values of the parameters employed to simulate the circular foundation in the linear elastic model are shown in Table 5.

Table 5 Values of parameters used in the linear elastic model to simulate the foundation.

FEM modeling considerations

Element type selection

Tetrahedral elements are one of the 3D elements, along with hexahedral and wedge elements. The first-order tetrahedral element has four nodes located at the ends of its six edges and four faces. The second-order tetrahedral element, also known as the quadratic tetrahedral element, has ten nodes: four at the ends of the edges and six at the midpoints of the edges. This ten-node tetrahedral element uses a complete quadratic function to interpolate the displacement field across the nodal values of the element. This element is available in the PLAXIS 3D program.

Soil-structure interfaces modeling

In the PLAXIS software, which employs the FEM, “Zero-thickness” interface elements may be utilized for modeling soil-structure interactions. On the soil adjacent to the interface, these elements apply a strength/stiffness reduction factor. The interface element’s key parameter is $\:{\text{R}}_{\text{i}\text{n}\text{t}\text{e}\text{r}}$, which represents the interface element’s strength as a ratio of the shear strength of the neighboring soil. In PLAXIS, $\:{\text{R}}_{\text{i}\text{n}\text{t}\text{e}\text{r}}$ ≤ 1.0 can be used to assign the interface properties, where a fully bonded interface corresponds to $\:{\text{R}}_{\text{i}\text{n}\text{t}\text{e}\text{r}}$ = 1.0 ⁴⁵. In this study, the interface elements were employed to model the interactions between untreated sabkha soil and geopolymer-treated sabkha soil, as well as the interaction between the geopolymer-treated sabkha soil and the foundation. For sabkha soil, $\:{\text{R}}_{\text{i}\text{n}\text{t}\text{e}\text{r}}$ values between 0.61 and 0.83 have been suggested by prior investigations²¹.

Load application

PLAXIS provides load-controlled and displacement-controlled options. Therefore, either a direct load or a prescribed displacement can be applied. A load-controlled approach was employed in the model to examine the performance of the loading test on the foundation. This approach involved the application of a concentrated load (point load) to the plate’s upper center. The applied load was executed in stages that were identical to those employed in the small-scale physical model.

Mesh size and refinement

The mesh in PLAXIS 3D was defined by utilizing two significant parameters, namely, the relative element size factor ($\:{r}_{e}$) and the average element size ($\:{L}_{e}$). The parameter r_e values for the predefined element has been assigned as follows: 2.0 for very coarse, 1.5 for coarse, 1.0 for medium, 0.7 for fine, and 0.5 for very fine. Similarly, the element size values allocated for the predefined element include 0.085 m for very coarse, 0.064 m for coarse, 0.043 m for medium, 0.030 m for fine, and 0.021 m for very fine.

In this study, a sensitivity analysis was conducted to determine the most appropriate element distribution mesh (i.e., very coarse, coarse, medium, fine, or very fine). As shown in Fig. 2, an inverse relationship was noted between the mesh size and the UBC. This relationship indicates that the solution becomes accurate as the mesh is refined. Nonetheless, there is a limit beyond which further refinement may not result in appreciable changes to the solution. In contrast to using a Very Fine mesh, using a Fine mesh type provides the optimal balance between accuracy and decreasing the time of running the model.

Fig. 2

Sensitivity analysis for the type of mesh.

Domain dimension

To mitigate the influence of boundary conditions on FEM outcomes, researchers proposed that the boundary distance for the model in a static analysis should be no less than five times the structure’s dimensions³⁷. Furthermore, Bhatia⁴⁶ suggested that the soil region’s dimensions should fall within a range of six to eight times the structure’s dimensions. Nonetheless, Alsanabani³⁷ performed a sensitivity analysis concerning domain size /foundation diameters of 2.5, 5, 7.5, 10, 12.5, and 15. For each domain, the foundation’s settlement due to static loading was assessed. The foundation was represented as a plate element possessing the linear elasticity of concrete material. On the basis of the relationship between the foundation’s settlement and the ratio of boundary domain to foundation diameter, the boundary effect becomes negligible once the boundary reaches a distance of five times the foundation’s diameter. Consequently, in this study, a model with dimensions equivalent to nine times those of the foundation model was employed. In PLAXIS 3D, it is important to mention that there are five distinct element sizes are as follows: very coarse, coarse, medium, fine, and very fine. During the meshing process, the diagonal distance is divided into a predetermined number of subdivisions. As a result, the size of fine and coarse elements varies for each domain.

Model calibration and validation

Untreated Sabkha soil model calibration

The process of calibrating the numerical model entailed multiple iterations of adjusting the soil and interface elements’ stiffness and strength properties within certain limits to enhance the alignment with the experimental response. The parameters listed in Table 3 were employed. Figure 3 shows the configuration of FEM for the untreated sabkha soil model and the system’s mesh. The determination of the modulus of elasticity $\:{E}_{50}$ for untreated sabkha soil was obtained from the triaxial testing results of sabkha soil, as reported by Alsanabani³⁷. $\:{E}_{rm}$ was set to $\:{3E}_{50}$ by default. With these values, a satisfactory agreement was achieved with the experimental test results, as shown in Fig. 4.

Fig. 3

FEM for untreated sabkha soil model; (a) dimensions of the model, (b) system’s mesh. Created using PLAXIS software (Version 22.02.00.1078). Available at: https://www.bentley.com/software/plaxis/.

Fig. 4

FEM for geopolymer treated sabkha soil using mix and compact method: (a) simulated model, (b) model showing interface elements. Created using PLAXIS software (Version 22.02.00.1078). Available at: https://www.bentley.com/software/plaxis/

Geopolymer treated Sabkha soil model calibration

To precisely simulate the behavior of geopolymer-treated soil, we implemented the initial parameters used for untreated sabkha soil to match those used for the model of untreated sabkha soil. Consequently, the treated soil layer was positioned on top of the untreated sabkha soil to replicate the physical model’s configuration.

Given the rock-like properties of the geopolymer-treated soil layer, the HB model was considered an appropriate approach for modeling the behavior of the treated sabkha soil (The UCS for weak rock ranges from 5 MPa to 25 MPa (ISRM))⁴⁷. In this framework, specific parameters were adjusted within permissible limits to accurately represent the treated soil and follow the actual outcomes of physical model loading experiments. These parameters consisted of GSI, $\:{R}_{inter}$, and $\:{m}_{i}$. Meanwhile, other parameters were kept constant and utilized in accordance with the outcomes of laboratory tests and previous studies. Figure 5 shows the configuration of FEM for geopolymer-treated sabkha soil using the mix and compact method.

Fig. 5

Load- displacement curves of untreated and geopolymer treated sabkha soil (mix and compact method) for experimental and FEM analysis.

The mechanical characteristics of treated sabkha soil with geopolymer, including modulus of elasticity, Poisson’s ratio, and UCS, were determined by analyzing the compression test results. Strain gauges were placed in the UCS samples to measure the Poisson’s ratio and modulus of elasticity. This procedure helped provide an accurate representation of the characteristics of the treated soil and enabled reliable comparison between physical and numerical investigations of models for both treated and untreated soil.

Model validation

The validation procedure for a numerical model simulation is crucial as it verifies the accuracy of the model’s representation of the real system. The ultimate objective of this procedure is to produce a FEM model that is accurate and trustworthy. The validity of the model was ascertained through a comparison of the load–settlement curves obtained from the physical model of geopolymer-treated sabkha soil with those derived from the FEM model under static loading conditions. Given that the load–settlement behavior is predominantly influenced by the dimensions and geometry of the geopolymer-treated soil layer, rather than the type and content of the precursor, the results were compared with the corresponding values obtained from the experiment tests based on the sabkha soil stabilized using 10% FA-based geopolymer.

In the development of the numerical model, ten-node tetrahedron elements were employed to mimic the untreated sabkha soil, the geopolymer-treated soil (mix and compact method), and the foundation. At the foundation–soil interfaces, interface elements were utilized, with their strength being equivalent to a percentage of the adjacent soil shear strength. The untreated sabkha soil model comprised a system of 19,723 elements and 30,432 nodes. By contrast, the number of elements for the geopolymer-treated sabkha soil model ranged from 19,805 to 21,627, and the number of nodes ranged from 30,582 to 33,858.

The PLAXIS program facilitated the execution of the FEM in phases to take into account the geostatic equilibrium, the construction sequence, and the incremental application of vertical loads. The loads were employed at a node located at the center of the foundation, commencing at 1 N and increasing in increments similar to the applied load in physical model testing until reaching a failure load. In Fig. 4, the load–displacement curves from the FEM models and the experimental models are compared. The data revealed a high degree of agreement between the two curves, indicating that the FEM model accurately simulated the load–displacement behavior of the system.

Parametric study

The aim of this parametric studies was to assess the influence of specific geometric parameters on the mechanical behavior of sabkha soil treated with geopolymer. A parametric study was executed utilizing the previously calibrated and verified FEM. The parameters under investigation included the precursor type, precursor content, and the thickness and diameter of the treated sabkha soil layer (H_m and D_m). Through systematic variation of these parameters, the study aimed to show their relative importance in influencing the UBC and load–settlement behavior of the soil. The findings of this analysis will provide valuable insights for practical applications and inform future research. Table 6 shows the parameters utilized in this study using the mix and compact method at different diameters and thicknesses.

Table 6 Parametric study using mix and compact method at different diameters and thicknesses.

Results and discussion

Effect of precursor type and content

Table 7 presents the results of a numerical analysis investigating the effect of precursor type (FA and MT) and precursor content (3%, 5%, and 10%) on the UBC of untreated and treated sabkha soil with geopolymer via the mix and compact method. Table 8 shows the improvement percentage of the treated sabkha soil with geopolymer using the mix and compact method compared with untreated soil. The findings indicated that the UBC of geopolymer-treated soil was similar for FA and MT at different precursor contents. However, a significant increase in bearing capacity was observed with increasing thickness of the treated layer. This behavior suggested that the thickness of the treated sabkha soil layer may have a greater impact on the UBC than the precursor content. As such, the geometry of the treated soil layer, including its diameter and thickness, appeared to be a key factor influencing changes in the UBC. Figure 6 shows the behavior of geopolymer-treated soil at failure in a 3D view. Figures 7 and 8 depict contour results for displacement behavior beneath the foundation at different thicknesses of the treated soil layer.

Fig. 6

Behavior of geopolymer treated sabkha soil at failure (mix and compact method). Created using PLAXIS software (Version 22.02.00.1078). Available at: https://www.bentley.com/software/plaxis/.

Fig. 7

Contour results for displacement behavior beneath the foundation in the case of untreated sabkha when the increment in the applied load reaches 50 N.

Fig. 8

Contour results for displacement behavior beneath foundation at different thicknesses of treated soil layer; (a) H_m=10 mm, at applied load = 191 N (b) H_m=30 mm, at applied load = 521.4 N, and ( c) H_m=50 mm, at applied load = 711 N.

Table 7 Numerical results of failure load and UBC of untreated and geopolymer treated Sabkha soil.

Table 8 Improvement percentage of the geopolymer treated Sabkha soil using mix and compact method compared to untreated soil.

Effect of thickness and diameter of geopolymer treated Sabkha soil

Figure 9 illustrates the relationship between the displacement ratio and the stress normalized by atmospheric pressure (p_a = 101.325 kPa) for treated sabkha soil with geopolymer subjected to varying layer thicknesses and diameters. The results revealed that displacement was decreased as the treated layer’s thickness increased, signifying that a thick geopolymer treatment layer contributed to enhanced stability and resistance to displacement. Moreover, the diameter of the treated soil layer played a significant role in governing displacement, with large diameters exhibiting low displacement ratios. This result suggested that a broad treated area provided an effective load distribution. However, when the H_m/D_f ratio is less than 0.6, increasing the D_m/D_f ratio beyond 2 has a detrimental effect on the soil’s performance.

Fig. 9

Displacement ratio versus pressure for geopolymer treated sabkha soil using a mix and compact method at different layer thicknesses and diameters.

Figure 10 further demonstrates the influence of stabilized soil layer thickness and diameter on the UBC. While the UBC generally improves with increasing thickness of the stabilized soil layer, the diameter of the stabilized soil layer also enhances the bearing capacity, particularly at high layer thicknesses. By contrast, when H_m/D_f is less than 0.6, the UBC decreases. This behavior may be attributed to the reduced effectiveness of the geopolymer treatment in thin layers. For D_m/D_f ratios greater than 2, tensile stress was initiated near the foundation’s edges, leading to treated layer failure and subsequent sudden displacements. This phenomenon could be mitigated by increasing the H_m/D_f ratio. For example, when H_m/D_f is 0.4, raising the D_m/D_f ratio from 2 to 2.5 reduces the UBC from 61.25 kPa to 42.03 kPa. By contrast, for an H_m/D_f ratio of 1, increasing D_m/D_f from 2 to 2.5 leads to a significant rise in the UBC, from 315.86 kPa to 446.28 kPa. This finding highlights the significance of optimizing the thickness and diameter of the treated soil for achieving the best performance in geopolymer-treated sabkha soil foundations.

Fig. 10

Ultimate bearing capacity of geopolymer treated sabkha soil using a mix and compact method at different thicknesses and diameters.

These results were consistent with those of prior research^26,27. Consoli et al.²⁷ conducted loading experiments on a layered soil structure composed of compressed soil, coal bottom ash, and carbide lime over deformable residual soil. They examined the load–settlement behavior of circular steel plates with diameters varying from 0.30 m to 0.60 m on an artificially stabilized soil layer with a thickness ranging from 0.15 m to 0.60 m. They observed that a thick layer of soil treatment or stabilization offers increased stability and deformation resistance. Foppa et al.²⁶ proposed a novel approach for determining the UBC of shallow strip foundation resting on a weak foundation soil with an artificially stabilized soil layer above it. The authors conducted experimental tests on strip footings placed on loose sandy soil layer and performed numerical analyses using the FEM. Their results revealed two distinct failure modes: in the first, the artificially stabilized soil penetrates the underlying loose sandy soil layer without any visible fissuring; in the second, following primary displacement of foundation, the stabilized layer fractures, exhibiting a fissure located either nearby the edge of the foundation or along the central axis, depending on the thickness of the stabilized soil layer. The maximum tensile stress within the stabilized soil layer was found to be dependent on the vertical reaction of the soil and the ratio of T_r to H_m, where T_r represents the lateral distance between the edge of the stabilized sabkha soil layer and the edge of the footing, and H_m denotes the thickness of the stabilized soil layer. However, the mentioned studies did not account for the complex interaction between the thickness and horizontal dimension (i.e., width or diameter) of the treated soil layer in influencing the load–displacement response and UBC.

Statistical analysis

Statistical analysis provides a robust set of instruments for examining data and drawing meaningful conclusions. Using statistical analysis for evaluating data facilitates a deep understanding of basic processes, permits the formulation of accurate predictions, enables the testing of hypotheses, quantifies uncertainty, and promotes data-driven decision-making. A nuanced comprehension of the effect of modified soil geometry on UBC can be developed by employing a comprehensive statistical analysis. Consequently, the response surface method (RSM) and ANOVA were employed. $\:\frac{{H}_{m}}{{D}_{f}}$ and $\:\frac{{D}_{m}}{{D}_{f}}$ were used as continuous factors in the case of geopolymer-treated soil using the mix and compact technique. The UBC was used as a response factor, and statistical models were developed accordingly. Using Minitab 2022, all statistical analyses were conducted.

Response surface method (RSM) analysis

The RSM is a technique that optimizes by using statistics to plan experiments, create a model for forecasting how predictor variables affect a response variable, and evaluate the impact of each predictor on the response. This approach is particularly well-suited for situations when there are many independent factors that affect the response variable⁴⁸. RSM analyses were performed in the current research to ascertain the impact of the key components (i.e., $\:\frac{{H}_{m}}{{D}_{f}}\:$and $\:\frac{{D}_{m}}{{D}_{f}}$) and how they interacted on the response variable, which was represented by UBC values.

The RSM equation for the treated soil using the mix and compact method is as follows:

$$\:UBC\:\left(kPa\right)={\beta\:}_{0}+{\beta\:}_{1}\left(\frac{{H}_{m}}{{D}_{f}}\right)+{\beta\:}_{2}\left(\frac{{D}_{m}}{{D}_{f}}\right)+{\beta\:}_{3}{\left(\frac{{H}_{m}}{{D}_{f}}\right)}^{2}+{\beta\:}_{4}{\left(\frac{{D}_{m}}{{D}_{f}}\right)}^{2}+{\beta\:}_{5}\left(\frac{{H}_{m}}{{D}_{f}}\right)\left(\frac{{D}_{m}}{{D}_{f}}\right)$$

(5)

Where $\:{\beta\:}_{0}$ is a constant, $\:{\beta\:}_{1}$, $\:{\beta\:}_{2}$, $\:{\beta\:}_{3}$, $\:{\beta\:}_{4}$, and $\:{\beta\:}_{5}$ are regression coefficients.

In this study, RSM analysis was employed to explore the effect of varying factors, including the thickness and diameter of the geopolymer-treated soil layer on the UBC using response surfaces and contour plots. A full RSM analysis was utilized to investigate the effects of primary components and their interactions. Figure 11 depicts the 3D response surface and contour plots for the UBC of treated soil versus two factors ($\:\frac{{H}_{m}}{{D}_{f}}$ and $\:\frac{{D}_{m}}{{D}_{f}}$,).

Fig. 11

3D response surface and contour plots for the relationship of UBC with $\:\frac{{H}_{m}}{{D}_{f}}$ and $\:\frac{{D}_{m}}{{D}_{f}}$ for geopolymer treated sabkha soil using mix and compact method. Created using Minitab software (Version 21.2). Available at: https://www.minitab.com.

The 3D surface and contour plots shown in Fig. 11 revealed a considerable change in the UBC when the thickness and diameter of the treated soil layer increased, indicating that both factors had a significant impact on responses. However, at low values of thickness, increasing the diameter of the treated soil layer did not result in a significant improvement in UBC, and vice versa. Additionally, the results demonstrated that increasing both factors led to an increase in UBC, illustrating the advantage of analyzing the interaction of both factors.

Table 9 presents the values of the regression coefficients obtained from the application of the RSM to the geopolymer-treated soil. The RSM model exhibited a high coefficient of determination ($\:{R}^{2})$ value of 98%, indicating a strong correlation between the observed and predicted values of the UBC. Thus, the RSM could be used as an accurate and reliable tool for predicting the UBC of geopolymer-treated soil.

Table 9 Summary of the values of regression coefficients for RSM in geopolymer treated soil layer.

Table 10 shows the ANOVA analysis for the RSM equation for geopolymer treatment using the mix and compact method. The table shows that the linear terms ($\:\frac{{H}_{m}}{{D}_{f}}$ and $\:\frac{{D}_{m}}{{D}_{f}}$) and their interaction term ($\:\left(\frac{{H}_{m}}{{D}_{f}}\right)\left(\frac{{D}_{m}}{{D}_{f}}\right)$) were significant predictors of the response variable, with p-values less than 0.001 indicating that they were statistically significant. The square terms ($\:{\left(\frac{{H}_{m}}{{D}_{f}}\right)}^{2}$ and $\:{\left(\frac{{D}_{m}}{{D}_{f}}\right)}^{2})$ were not significant predictors of the response variable, with p-values greater than 0.05 indicating that they were not statistically significant.

In summary, the results of ANOVA analysis indicated that for the geopolymer-treated soil using the mix and compact method, the linear terms were significant predictors of the UBC of the treated soil. Furthermore, the interaction term between ($\:\frac{{H}_{m}}{{D}_{f}}$ and $\:\frac{{D}_{m}}{{D}_{f}}$) emerged as a significant predictor of the UBC of the treated soil.

Table 10 ANOVA analysis for RSM.

Conclusions

Sabkha soils pose significant geotechnical challenges due to their low bearing capacity and high settlement potential. This study investigated the effectiveness of geopolymer treatment using the mix and compact method to enhance the load-bearing capacity of sabkha soil. A comprehensive approach combining experimental analysis and numerical modeling was employed to evaluate the soil’s behavior in both natural and treated conditions. The key findings are:

• Geopolymer treatment significantly improved the load–displacement behavior of sabkha soil, demonstrating its potential as an effective stabilization method.

• Increasing the thickness and diameter of the treated layer enhanced stability, but when the $\:\frac{{H}_{m}}{{D}_{f}}$ ratio was below 0.6, further increasing $\:\frac{{D}_{m}}{{D}_{f}}$ beyond 2 negatively impacted performance.

• A multiple linear regression model, developed using RSM, accurately predicted UBC with an R² value of 98%.

• ANOVA confirmed the significance of linear and interaction terms of $\:\frac{{H}_{m}}{{D}_{f}}\:$and $\:\frac{{D}_{m}}{{D}_{f}}$ in predicting UBC, while their quadratic terms were not influential.

This study contributes valuable insights into sustainable soil stabilization techniques, highlighting geopolymer treatment as an environmentally friendly solution that repurposes waste materials for geotechnical applications.