Introduction

With the advancement of China’s new urbanization, the scale of new rural construction and urban housing construction is expanding. Low-rise precast construction facilitates China’s residential industrialization1,2, while in northern Shaanxi mining areas, underground coal mining requires village relocation. Site-adaptive prefabricated rural housing not only aligns with national low-carbon transformation goals but also supports new urbanization strategies, demonstrating dual benefits in sustainable resource utilization and rural development. The reliability of the connection method between precast shear walls is the key to their integrity and seismic resistance3,4. Many domestic scholars have conducted in-depth research on precast shear wall structures. Zhu et al.5,6 conducted seismic performance tests on precast concrete shear wall structures and found that precast shear wall structures meet my country’s seismic fortification requirements. Through effective cast-in-place constraints, the overall performance of the wall panel structure can be improved. Qian et al.7,8,9 conducted quasi-static tests on precast shear walls with different connection methods, such as direct connection with sleeve grout anchors and indirect connection with hole-leaving grout anchors. The results showed that the failure mode of the precast wall specimens was the same as that of the cast-in-place wall specimens. Xue et al.10. A single-row bolt connection was used for shear wall reinforcement and a double-row sleeve grouting connection for edge member reinforcement. The mixed connection method demonstrated better seismic performance than cast-in-place specimens. Currently, precast buildings are mainly used in urban medium- and high-rise buildings, with less application in low-rise residential structures. Additionally, sleeve and grout anchor lap connections are more suited for medium- and high-rise buildings, though they involve high costs, significant on-site work, and complex construction11. Given the superstructure damage caused by underground mining in the northern Shaanxi mining area and the small scale of rural buildings, a new vertical distributed non-connected monolithic shear wall structure system (SGBL prefabricated shear wall) was proposed by selecting the farmhouse in Niutan Village of Bashe in Yulin as the research object. This system improves the traditional sleeve grouting connection to the extrusion grouting connection, significantly reducing material consumption and construction complexity, and has the advantages of energy conservation, efficiency improvement, and enhanced material utilization rate12,13,14. The hysteresis performance, deformation capacity, bearing capacity, and ductility of the system were analyzed through numerical simulation, providing a theoretical and technical basis for the application of SGBL structure in new rural residences in the northern Shaanxi mining area.

Brief introduction of the new SGBL assembled monolithic shear wall structure

New SGBL precast integral shear wall structure (SGBL precast shear wall structure). The wall is composed of a precast reinforced concrete wall and cast-in-place edge components. The precast wall panel is made of C30 concrete, with double-layer bidirectional steel mesh. Lap steel bars connected to the edge components are reserved on both sides. The wall edge components are post-cast C30 concrete with the same thickness as the precast wall panels15,16. In this paper, the low-rise SGBL precast integral shear wall structure takes a two-story residential building as an example. The upper and lower precast walls and floor slabs, and the precast wall panels and rectangular foundations are connected by M7.5 cement mortar, and the thickness of the mortar layer is 20 mm. The steel bar within the edge member extends through both the upper and lower sections. There are reinforcing ribs on the top of each precast wall, similar to the ring beam, which plays a role in enhancing the integrity and spatial rigidity of the house. Vertical force system: Prefabricated wall panels bear primary loads, while longitudinal reinforcement in cast-in-place edges provides secondary flexural capacity. Lateral force-bearing system: Cast-in-place boundary elements form plastic hinge energy dissipation zones, composite slabs act as rigid diaphragms to ensure deformation compatibility, and wall horizontal reinforcement anchored to boundaries creates shear-resistant interfaces. This rigidity-flexibility hybrid system optimizes balanced internal force redistribution.

The schematic diagram of the SGBL precast integral shear wall structure is shown in Fig. 1.

Fig. 1
figure 1

Schematic diagram of wall panel and structure layout.

Full size image

Material parameters and component dimensions

Concrete constitutive relationship model

In this study, the concrete damage plasticity (CDP) model constructed by the ABAQUS platform was used to numerically simulate concrete materials, mainly based on its universal ability to characterize the mechanical response of concrete under complex load paths (including monotone/cyclic load and dynamic/static load). It effectively captures the damage accumulation and stiffness degradation under cyclic loading, which is in good agreement with the concrete behavior observed experimentally17. By defining the tensile/compressive damage parameters of the SGBL prefabricated shear wall structure and incorporating stiffness degradation, its mechanical behavior is effectively analyzed18,19. The concrete plastic damage parameters are shown in Table 1.

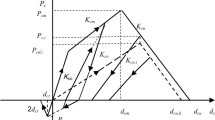
Table 1 Plastic damage parameters of concrete.
Full size table

Through the comparative analysis of literature20,21 and the “Code for Design of Concrete Structures (GB50010-2010), the constitutive relationship of concrete was verified. The uniaxial tensile/compressive stress–strain curve in GB50010-2010 is adopted as shown in Fig. 2. This curve has a strong empirical consistency with the construction practice in the northern Shaanxi region and is consistent with the regional material properties and construction tolerances in Chinese standards. The expression of the uniaxial tensile constitutive relation of concrete is as follows:

$$\sigma = (1 - d_{t} )E_{{\text{c}}} \varepsilon$$
(1)
$$d_{{\text{t}}} = \left\{ \begin{gathered} 1 - \rho_{t} \left[ {1.2 - 0.2x^{5} } \right] \, x \le 1 \, \hfill \\ 1 - \frac{{\rho_{t} }}{{\alpha_{t} (x - 1)^{1.7} + x}} \, x > 1 \, \hfill \\ \end{gathered} \right.$$
(2)
$$x = \frac{\varepsilon }{{\varepsilon_{t.r} }}$$
(3)
$$\varepsilon_{t.r} = f_{t.r}^{0.54} \times 65 \times 10^{ - 6}$$
(4)
$$\rho_{t} = \frac{{f_{t.r} }}{{E_{c} \varepsilon_{t.r} }}$$
(5)
$$\alpha_{t} = 0.312f_{t.r}^{2}$$
(6)
Fig. 2
figure 2

Uniaxial stress–strain curve of concrete.

Full size image

The constitutive relation of concrete under uniaxial compression is expressed as follows:

$$\sigma = (1 - d_{c} )E_{{\text{c}}} \varepsilon$$
(7)
$$d_{{\text{c}}} = \left\{ {\begin{array}{*{20}c} {1 - \frac{{\rho_{c} {\text{n }}}}{{n - 1 + x^{n} }}} & {x \le 1} \\ {1 - \frac{{\rho_{c} }}{{\alpha_{c} (x - 1)^{2} + x}}} & {x > 1} \\ \end{array} } \right.$$
(8)
$$\rho_{t} = \frac{{f_{c.r} }}{{E_{c} \varepsilon_{c.r} }}$$
(9)
$$n = \frac{{E_{c} \varepsilon_{c.r} }}{{E_{c} \varepsilon_{c.r} - f_{c.r} }}$$
(10)
$$x = \frac{\varepsilon }{{\varepsilon_{c.r} }}$$
(11)
$$\varepsilon_{c.r} = \left( {700 + 172\sqrt {f_{c} } } \right) \times 10^{ - 6}$$
(12)
$$\alpha_{c} = 0.157f_{c}^{0.785} - 0.905$$
(13)

where ft.r and fc.r are the representative values of concrete’s uniaxial tensile and compressive strengths, respectively. According to the Code for Design of Concrete Structures (GB50010-2010), Ec is the elastic modulus of concrete, and the other parameters are derived from Ec and ft.r (fc.r). Specifically, at and ac are the parameters for the reduced section in tensile and compressive constitutive analysis, εt.r and εc.r are the peak tensile and compressive strains and dt and dc represent the damage evolution parameters for uniaxial tensile and compressive loading, respectively.

Constitutive relationship model of steel bars

Reinforced concrete (RC) structural systems inherently manifest pinching phenomena in hysteretic load–displacement curves, attributable to synergistic interactions between steel–concrete bond-slip mechanisms and composite shear deformation kinematics. Contemporary research has quantitatively established that the cyclic plasticity behavior of reinforcing steel critically governs numerical simulation fidelity under reversed loading protocols22,23,24. To simulate this nonlinear hysteresis response more accurately, this study adopts the reinforcement circulation constitutive model25 as shown in Fig. 3, which is mathematically expressed as:

$$E_{{{\text{sr}}}} = \left\{ {\begin{array}{*{20}l} {E_{S} } \hfill & {(\beta < 1)} \hfill \\ {(1.05 - 0.05\beta )E_{S} } \hfill & {(1 \le \beta \le 4)} \hfill \\ {0.85E_{S} } \hfill & {(\beta \ge 4)} \hfill \\ \end{array} } \right.$$
(14)
$$\, \beta = \frac{{\varepsilon_{{\text{m}}} - \varepsilon_{0} }}{{\varepsilon_{{\text{y}}} }}$$
(15)
Fig. 3
figure 3

Constitutive model of steel bar hysteresis.

Full size image

The expression of the loading path of the rebar hysteresis model used in this paper is as follows:

$$\sigma = \gamma \left( {\overline{\varepsilon }^{3} - \overline{\varepsilon }^{2} } \right) + \sigma_{m} \overline{\varepsilon }\left( {1 - \alpha } \right) + \alpha \sigma_{m}$$
(16)
$$\gamma = E_{{{\text{sh}}}} \left( {\varepsilon_{m} - \varepsilon_{L} } \right) - (1 - \alpha )\sigma_{m}$$
(17)
$$\overline{\varepsilon } = \left( {\varepsilon - \varepsilon_{L} } \right)/(\varepsilon_{m} - \varepsilon_{L} )$$
(18)

where εL corresponds to the strain at point L, α is the hysteric energy consumption influence coefficient, and the expression is as follows.

$$\alpha = \left\{ {\begin{array}{*{20}l} {{0}{\text{.5}}} \hfill & {(\beta \le 1)} \hfill \\ {(20 - \beta )/38} \hfill & {(1 < \beta < 20)} \hfill \\ 0 \hfill & {(\beta \ge 20)} \hfill \\ \end{array} } \right.$$
(19)

Test model

Considering that the bays and depth of rural houses are relatively large and most of them are structures with a small shear span ratio, the shear span ratio (0.56/0.72/1.25) is taken as the research object. Also, since low-rise buildings are different from multi-story and high-rise buildings, a smaller axial compression ratio (0.05) is used to simulate the actual vertical load level of low-rise buildings. The paper designs five different SGBL prefabricated shear wall specimens (ZPQ-1 to ZPQ-5): ZPQ-2 is the baseline and ZPQ-4 is the opening. Wall panels (lengths 1800/3600/4800 mm, height 3020 mm, thickness 140/120 mm) incorporated cast-in-place edge members (300 × 140/120 mm section). All specimens used C30 concrete, M7.5 mortar (20 mm layer), with an axial compression ratio of 0.05, and foundation beams (600 × 300 mm). Key parameters are detailed in Table 2.

Table 2 Size parameters of specimens.
Full size table

The precast wall panels in the specimens are equipped with double-layer bidirectional steel bars of C6@250, and 2C12 reinforcement bars are arranged at the corners of the openings; the stirrups of the edge components are all C6@250, and the longitudinal bars are 6C10; the foundation beams are reinforced with C10@170 and 4C12. The stirrups are uniformly C6@250, while the longitudinal reinforcement consists of 6C10 bars.

Establishment of finite element model

1Boundary condition definition

  1. (1)

    Definition of contact between the mortar layer at the bottom of the precast wall.

In this paper, a 20 mm cement mortar mortar layer is set at the bottom of the precast shear wall. In the finite element analysis, the Coulomb friction model is used to simulate the contact relationship between the bottom of the precast wall and the mortar layer. The normal direction of the interface adopts hard contact to define the pressure and penetration relationship between the precast wall and the mortar layer. The tangential constitutive model adopts “penalty” friction contact, The critical stress (τcrit) is determined by the friction coefficient (μ) and the normal compressive stress (P), where τcrit = μP. The friction coefficient (μ) is set to 0.15, as shown in Fig. 4

Fig. 4
figure 4

Coulomb friction model.

Full size image
  1. (2)

    Definition of contact between precast wall and edge components.

The definition of the contact between precast wall panels and edge components is critical in the analysis of SGBL precast integral shear walls, which combine a precast central structure with cast-in-place edge components. This study employs the surface-based cohesive behavior model to model the interface between the new and old concrete26. This model simulates the contact properties between precast panels and cast-in-place elements, with the viscosity coefficient being determined through trial calculations. In defining the contact, a small sliding surface-to-surface contact approach is adopted. The cohesive model requires the selection of an appropriate viscosity coefficient to facilitate convergence in the calculations27,28. In this context, t0 represents the maximum shear stress, δ0 the corresponding displacement of the contact surface, and δf the limit displacement, as depicted in Fig. 5.

Fig. 5
figure 5

Surface-based cohesive behavior model.

Full size image
  1. (3)

    Definition of contact between the bottom of the ground beam model and the top of the plate wall loading.

To accurately simulate the boundary conditions of the bottom of the ground beam during the actual test, the ground beam is completely consolidated with the ground, that is, it is assumed that the ground beam model always maintains rigid contact without slip during the entire simulation process. A reference point is established at the top of the wall panel to couple with the top of the wall panel. To simulate the protection of the specimen by the out-of-plane anti-instability device, the reference point at the top of the specimen is constrained to prevent its rotation in the out-of-plane direction (U3 = 0) and rotation around the X and Y directions (UR1 = UR2 = 0).

The definition of the analysis phase

This study utilized ABAQUS/Standard to numerically analyze the SGBL prefabricated shear wall structure, harnessing its convergence algorithms to ensure simulation accuracy. The amplitude curve for the cyclic load is defined based on the displacement obtained from low-cycle repeated tests. Two distinct analysis steps are implemented to simulate the applied axial load and horizontal displacement load separately. In the first analysis step (Step 1), the axial load is converted to a uniform force and applied to the upper surface of the top connecting beam. In the second analysis step (Step 2), a horizontal displacement load is applied to the reference point at the top of the wall panel structure.

Since the hysteresis curve of the specimen takes a long time under low-cycle repeated loading, the increment size is set reasonably to ensure that the structural calculation can converge. The analysis step settings are shown in Table 3.

Table 3 Analysis step setting.
Full size table

Division of grid

Based on the deformation characteristics of precast concrete walls, this paper uses C3D8R units to simulate concrete in the model. This unit is a linear entity reduction integral of 8 nodes, and hourglass control is considered at the same time. The steel bars are simulated by two-node linear three-dimensional truss T3D2 units and 8-node hexahedral linear reduction integral units. The Mesh density of each component is shown in Table 4.

Table 4 Mesh density of each component.
Full size table

The finite element modeling approach utilized in this study adopts a modular strategy, with varying mesh refinements applied to different components of the structure. The specific mesh configurations are detailed in Fig. 6.

Fig. 6
figure 6

Schematic diagram of the mesh division of the specimen.

Full size image

Verification of finite element model

To further verify the reliability of finite element simulation, refer to Liu Kai et al.16. The seismic test of low-rise precast reinforced concrete horizontal mortar wall was carried out to investigate the seismic performance of the wall structure under low-cycle reciprocating loads and verify the load–displacement curves of the finite element model SW-1 and SW-2 specimens. As shown in Fig. 7, the curves are well-matched. The simulation value is slightly higher than the test value in the middle of loading, and the simulation value is lower than the experimental value in the later stage of loading. The yield stage and load drop stage of the simulation curve are consistent with the test results. The failure mode of the wall panel is consistent with the test results. However, since the bond-slip relationship of the steel bars in the concrete is not considered in the finite element calculation, the change process of the skeleton curve cannot be accurately simulated, resulting in a certain difference between the simulation results of the skeleton curve and the test.

Fig. 7
figure 7

Verification of the skeleton curve of a specimen.

Full size image

Results and discussion

Comparative analysis of hysteresis curves

Hysteresis curves serve as crucial indicators for evaluating structures’ seismic performance. A fuller hysteresis curve suggests greater plastic deformation and increased energy dissipation within the structure.

  1. (1)

    As depicted in Fig. 8a–e, the ZPQ-1 specimen exhibits a linear relationship between load and displacement at the onset of simulated loading. In this stage, the hysteresis loop area is minimal, and the curve is relatively narrow and elongated, indicating that the structure is operating within the elastic regime. As loading progresses, the specimen transitions into the elastic–plastic stage, resulting in a gradual increase in the fullness of the hysteresis curve. In contrast, the fullness of the curves of the other two groups of specimens gradually decreased. The curves were narrow and slender at the initial stage. Especially for the ZPQ-3 specimen, when the curve developed to the failure stage, it was in an inverted shape. The ZPQ-2 specimen as a whole was in a “bow shape”, indicating a strong deformation ability. The ZPQ-4 specimen showed a decrease in load-bearing capacity but an increase in deformation capacity. For the ZPQ-5 specimen with a smaller thickness, the overall trend remained consistent, but load-bearing capacity decreased.

    Fig. 8
    figure 8

    Load–displacement curves of specimens subjected to low-cycle repeated loads.

    Full size image
  2. (2)

    As the load level increases, the slope of the hysteresis curve decreases progressively, with a more pronounced trend. This behavior signifies a reduction in lateral stiffness and a deterioration in seismic performance. The degradation in structural stiffness is primarily attributed to the transition of the precast structure from the elastic stage to the elastoplastic stage. Additionally, as the load increases, cracks begin to form in the wall panel structure, leading to local concrete damage and further reduction in overall stiffness29.

By comparing the three groups of specimens with different shear-span ratios, the hysteresis curve of the ZPQ-1 specimen with a shear-span ratio of 1.25 is more full. This indicates better structural elasticity and stronger deformation performance. The ultimate displacements of the three groups of specimens all increased with the increase of the shear-span ratio, and the bearing capacity decreased with the increase of the shear-span ratio.

Comparative analysis of skeleton curves

The skeleton curve is the envelope trajectory of the peak load point in the hysteresis response. It aims to describe the equivalent monotonic mechanical behavior of the structure by simplifying the cyclic path.

  1. (1)

    As illustrated in Fig. 9a, the ZPQ-1 specimen demonstrated relatively stable behavior during the early and middle stages of loading. However, as loading progressed, the ascending portion of the curve gradually slowed, eventually reaching the peak bearing capacity. In contrast, the ZPQ-2 and ZPQ-3 specimens exhibited more rapid changes during the early and middle stages. The skeletal curves of these specimens did not show a significant downward trend. In the later stages of loading, the bearing capacity remained relatively high, indicating that the structure maintained a certain level of deformation capacity.

    Fig. 9
    figure 9

    Specimen skeleton curve.

    Full size image
  2. (2)

    As shown in Fig. 9b,c, compared to the ZPQ-5 specimen, the ZPQ-1 specimen exhibits a 10% increase in overall bearing capacity. However, the ZPQ-4 (opening specimen) shows a 14% decrease in bearing capacity relative to the BASE specimen, while its ultimate displacement increases by 47%. This is due to the opening in the shear wall, which reduces stiffness, increases horizontal displacement, and lowers ultimate bearing capacity30.

  3. (3)

    The comparison of the specimen skeleton curves reveals that the ZPQ-1 specimen exhibits more complete deformation but lower bearing capacity, with a smaller overall slope of the skeleton curve. As the shear span-to-depth ratio decreases, the specimen’s deformation capacity diminishes. In contrast, its ultimate bearing capacity significantly improves, with failure increasingly exhibiting brittle characteristics, Skeleton curves of three groups of specimens with a certain degree of decline, the late loading still maintains high bearing capacity, This load-transfer mechanism arises from the post-yielding synergism between steel reinforcement and concrete: While progressive failure mechanisms lead to material degradation and load resistance reduction, subsequent strain-hardening behavior of reinforcement introduces counteractive strength recovery through elastoplastic redistribution Furthermore, the implementation of controlled axial compression during advanced loading stages generates beneficial confinement effects, effectively stabilizing structural integrity while enhancing deformation capacity and failure resilience under cyclic demands.

Stiffness degradation

As the loading progresses, the plastic deformation gradually increases, and the stiffness of the specimen also degrades. In this paper, the secant stiffness specified in the “Code for Seismic Testing of Buildings” (JGJ/T101-2015) was used to characterize the stiffness degradation of each specimen.

Stiffness degradation K is expressed as: \(K_{{\text{i}}} = \frac{{\left| { + F_{i} } \right| + \left| { - F_{i} } \right|}}{{\left| { + \Delta_{i} } \right| + \left| { - \Delta_{i} } \right|}}\).

In the formula, + Fi denotes the peak load of the specimen during the i-th loading cycle under positive loading conditions, while − Fi represents the peak load under negative loading conditions. Similarly, + Xi and − Xi represent the corresponding displacements at the peak loads for the positive and negative loading conditions, respectively, during the i-th cycle.

The stiffness degradation curve of the specimen can be seen in Fig. 10a–c:

Fig. 10
figure 10

Secant stiffness degradation curve.

Full size image
  1. (1)

    The stiffness of the structure gradually decreases with the increase in the number of cycles, but the degradation rate of the stiffness is different. The initial stiffness of ZPQ-3 is about 479kN/mm, the initial stiffness of the ZPQ-2 specimen is about 364kN/mm, and the initial stiffness of the ZPQ-1 specimen is about 161kN/mm. This shows that the size affects the initial stiffness of the specimen. The longer the wall, the greater the initial stiffness.

  2. (2)

    The stiffness degradation trends of specimens with different shear span-to-depth ratios are roughly the same, but there are differences in their degradation speed and degree. The stiffness degradation rate of the ZPQ-3 specimen was the fastest, showing an obvious sudden drop stage. The residual stiffness in the later stage of loading was relatively high, about 80kN/mm; the stiffness degradation rate of the ZPQ-2 specimen was second, with a residual stiffness of about 32kN/mm; the stiffness degradation rate of the ZPQ-1 specimen was relatively slow, with a residual stiffness of about 12kN/mm. This shows that with the increase of the shear span-to-depth ratio, the stiffness degradation rate of the specimen slowed down, and the overall ductility performance of the specimen was improved.

  3. (3)

    Compared with the ZPQ-2 specimen, the initial stiffness of the ZPQ-4 (opening specimen) was lower, the stiffness degradation was more thorough, and the residual stiffness was smaller. The attenuation trends were roughly the same. The initial attenuation rate of ZPQ-2 was slightly greater than that of ZPQ-4 (opening specimen). The stiffness degradation was faster in the initial stage of loading, and it tended to be stable in the later stage. This was because after the specimen yielded, the new cracks gradually decreased and the steel bars yielded, resulting in the slowing down of stiffness degradation and stabilization.

  4. (4)

    The stiffness degradation trends of ZPQ-1 and ZPQ-5 are similar, with ZPQ-1 consistently showing slightly higher degradation values, resulting in a higher overall curve. This suggests that specimens with the same shear-span ratio but different thicknesses exhibit only minor differences in stiffness degradation rates, with the thicker specimen maintaining higher overall stiffness.

Bearing capacity and deformation capacity

Ductility refers to the deformation capacity of a structure or component from the point of maximum bearing capacity to yielding, or the point at which the bearing capacity is reached without a significant reduction. The ductility coefficient, μ, is defined as:μ = Δu/Δy.

where ∆u is the ultimate horizontal deformation and ∆y is the yield horizontal deformation.

Determining the ductility coefficient requires identifying key points of the structural system. The energy equivalence method typically defines the yield point and load. Here, Fu and Fy represent the ultimate and yield loads, respectively, ∆u represents the ultimate displacement, which is the displacement when the horizontal load drops to 0.80Fmax in the load–displacement skeleton curve. ∆y represents the yield displacement. and characteristic points are summarized in Table 5

Table 5 Bearing capacity and deformation capacity.
Full size table
  1. (1)

    For specimens with the same thickness but different shear span-to-depth ratios, the variations in both limit bearing capacity and deformation capacity are more pronounced. As the shear span-to-depth ratio decreases, the ductility coefficient of the specimen also decreases, resulting in a reduction in deformation capacity. Specifically, compared to the ZPQ-1 specimen, the ZPQ-3 specimen exhibits a 113% increase in yield load, a 34.6% decrease in yield displacement, a 129% increase in ultimate load, and a 69% decrease in ultimate displacement. Similarly, the yield load of the ZPQ-2 specimen increases by approximately 40.7%, while its yield displacement decreases by 18.5%, a 62% increase in ultimate load and a 37% decrease in ultimate displacement. These results indicate that as the shear span-to-depth ratio decreases, the bearing capacity of the wall panel structure increases, while both the yield displacement and ultimate displacement decrease accordingly.

  2. (2)

    With the same shear span-to-depth ratio, the ductility of the specimen with a smaller thickness is relatively higher. The yield load and ultimate load of ZPQ-1 are approximately 9% higher than those of ZPQ-5. The ductility coefficient of the ZPQ-4 specimens with holes is improved compared to the ZPQ-2 specimens. Specifically, the yield displacement increases by about 34%, and the ultimate displacement increases by approximately 49%. While thickness has a relatively small effect on the component’s ductility performance, the presence of openings in the specimen significantly enhances both its ductility and ultimate displacement.

Energy dissipation

The area of the hysteresis loop under horizontal cyclic loading reflects the energy dissipation capacity of the component, with a fuller loop indicating greater capacity. This capacity is typically quantified by the equivalent viscous damping coefficient he and the energy dissipation coefficient E, which are used to assess the structure’s energy dissipation performance.

As illustrated in Fig. 11a, the SGBL precast shear wall structure demonstrates a notable energy dissipation capacity. The trends of these three specimen groups are roughly similar. At the later stage of loading, the bonding coefficient of the ZPQ-1 specimen is stable at about 0.173, and the bonding coefficient of ZPQ-2 and ZPQ-3 specimens is maintained at about 0.162 and 0.151. For specimens with smaller thickness, the equivalent bonding damping coefficient of the ZPQ-5 specimen is slightly higher than that of the ZPQ-1 specimen. The bonding coefficient of ZPQ-4 specimens with openings is lower than that of ZPQ-2 specimens. Energy dissipation increases slowly in the early stage and more rapidly later. Overall, as the shear-span ratio decreases, energy dissipation performance weakens, with size and thickness having a minimal effect. The open-hole specimen shows weaker energy dissipation initially, which increases over time. The values of E and he in Table 6 reflect the same trend.

Fig. 11
figure 11

Comparison curve of energy dissipation capacity of the specimen.

Full size image
Table 6 Energy dissipation index.
Full size table
  1. (1)

    Elastic Stage Equivalent viscous damping coefficients increase rapidly with loading progression, demonstrating specimen-specific energy dissipation capacities: ZPQ-3 (highest early-stage energy dissipation) > ZPQ-2 > ZPQ-1 (slowest growth).

  2. (2)

    Elastoplastic Stage Post-yield concrete damage accumulation and crack propagation reduce energy dissipation by 21–28%. ZPQ-3 (minimum shear span-to-depth ratio) experiences the most severe degradation (23.7% decline) due to the damage intensifying and the impact being the most significant.

  3. (3)

    Plastic Stage Despite progressive stiffness degradation, plastic hinge formation and crack expansion activate secondary energy dissipation mechanisms. Maximum energy capacity emerges at limit states, with an 11.9%-20.9% enhancement compared to the elastoplastic phase.

The cumulative energy dissipation-displacement curve (Fig. 11b) shows that energy consumption gradually increases in the early stage and accelerates in the later stage. This is due to the transition of the prefabricated shear wall from the elastic stage to the plastic stage, where the wall’s stiffness continuously deteriorates, resulting in an increased energy dissipation capacity. Meanwhile, as the shear span-to-depth ratio increases, the cumulative energy dissipation rate accelerates. The ZPQ-2 specimen exhibits superior cumulative energy dissipation among the three specimens. The energy dissipation rate of the ZPQ-4 specimens with openings increases more gradually, ultimately reaching its maximum energy dissipation at the ultimate displacement. For the ZPQ-5 specimen with a smaller thickness, the energy dissipation rate aligns closely with that of the ZPQ-1 specimen, but the total cumulative energy dissipation remains consistently lower than that of the ZPQ-1 specimen.

Plastic damage analysis

The plastic damage analysis of concrete relies on the Concrete Damaged Plasticity (CDP) model, which integrates plasticity and damage mechanics to characterize concrete’s deformation and damage evolution under stress. The damage factor is implemented in ABAQUS to simulate phenomena such as tensile cracking and crushing, as shown in the plastic damage cloud diagram in Fig. 12.

Fig. 12
figure 12figure 12

Plastic damage cloud image.

Full size image
  1. (1)

    The concrete damage in specimen ZPQ-1, with a shear span-to-depth ratio of 1.25, is significant, with damage developing at the center of the prefabricated wall panel as load increases, indicating extensive crack propagation. For ZPQ-2 (shear span-to-depth ratio 0.72), the damaged area is smaller, with cracks primarily at the lower end of the edge component. ZPQ-3 (shear span-to-depth ratio 0.56) exhibits the least damage, with underdeveloped cracks. In the ZPQ-4 specimen with an opening, damage is concentrated at the upper part and sides of the opening, with cracks initially forming at the top. As loading progresses, tensile damage increases, leading to cracks along the sides of the opening, ultimately reducing the specimen’s seismic performance. The damaged areas of specimens ZPQ-5 and ZPQ-1 are similar, but the bottom damage in ZPQ-5 is more severe than in ZPQ-1.

  2. (2)

    The tensile and compressive damage cloud diagrams for the specimen groups show that stress is highest in the middle and lower regions of the edge components, while the central area of the precast wall panel experiences relatively lower stress. This indicates that the edge components play a key role in maintaining the structural integrity of the upper wall panel. A comparison of the simulation results across the groups reveals that, as the shear span-to-depth ratio decreases, the extent of damage in the specimen wall progressively decreases.

  3. (3)

    In the ZPQ-1 specimen, horizontal cracks dominate, with the most significant cracks occurring at the bottom of the precast wall panel. The crack length decreases with specimen height, exhibiting bending failure characteristics. In the ZPQ-2 specimen, horizontal cracks initially form, but as loading increases, they extend downward at about 45 degrees, transitioning from bending to shear failure. In the ZPQ-3 specimen, cracks are less pronounced, mainly forming obliquely downward. Crack propagation is limited in later loading stages, primarily occurring at the mortar interface, indicating the onset of shear failure.

Conclusion

This study uses finite element simulations to investigate the effects of parameters such as the shear span-to-depth ratio and specimen openings on the hysteresis behavior, deformation capacity, stiffness degradation, and energy dissipation of SGBL precast shear walls with a small shear span-to-depth ratio. The main conclusions are as follows:

  1. (1)

    As the shear span ratio increased from 0.56 to 1.25, the hysteretic loop fullness (improved by 16%) and ductility demonstrated positive correlations, while bearing capacity decreased by 53%. Wall thickness reduction to 120 mm caused minor peak load degradation (< 5%)—openings configuration induced 14% bearing capacity reduction with 12% ductility enhancement.

  2. (2)

    Under low-cycle loading, the prefabricated wall shows minimal damage, with energy dissipation concentrated in the edge components. Plastic deformation is mainly at the bottom and sides of the edges, while the upper panel remains largely undamaged. Openings create a ring-shaped stress concentration. The vertical seam remains uncracked, confirming the joint’s structural integrity.

  3. (3)

    The structure exhibits clear damage signs before failure while maintaining adequate bearing capacity. Additionally, further investigation into the shear span-to-depth ratio is needed to determine its optimal range and provide recommendations for component optimization.