Introduction

Brain-computer interface (BCI) systems enable direct interaction between the human brain and external devices, increasing their significance across various fields. BCIs have broad applications in assistive technology, rehabilitation, and healthcare. BCI systems based on electroencephalography (EEG) are widely used due to their non-invasive nature and ability to provide real-time insights into brain activity1. Progress of EEG signal is helpful for physicians for some illnesses’ cures like anxiety, epilepsy, learning and sleep disorders, and depression. In addition to its important role in applications of detection, the progress of EEG signal makes BCI systems development. BCI system gets and analyzes EEG signals for presenting straight integration as well as handling way from the brain of humans to computers/machines. The basic objectives include manipulating electrical brain signals as well as creating essential signals for controlling several external systems2. The interpretation of brain rhythms is central to the core focus of BCI systems.

These rhythms are micro-electrical activities occurring in our brains during various mental functions. The most practical and efficient non-invasive technique for recording brain rhythms is through electroencephalographic signals, commonly known as EEG. Decoding EEG signals has an essential role in different BCI fields like epileptic seizure detection, identification of emotion, movement imagery etc. EEG signals consist of five rhythmic waveforms: (a) delta (0.5–4 Hz), (b) theta (4–7 Hz), (c) alpha (7–13 Hz), (d) beta (13–25 Hz), and (e) gamma (25–50 Hz), which can be analyzed for target decoding3. EEG-based BCI systems face several technical challenges, including noise, time-variance, instability, high dimensionality, and susceptibility to external influences, such as ambient electromagnetic interference and muscle artifacts4. These factors limit the effectiveness of BCI devices in achieving accurate diagnostics for neurological conditions like epilepsy, as well as in real-time applications5]– [6. Additionally, certain shifts in EEG signals result from the integration or superposition of multiple shifts, which complicates the identification of consistent patterns and relationships across EEG signal bands. To enhance predictive capabilities, it is essential to regularly assess EEG signal trends and identify periodic shifts.

This paper introduces a novel approach for decoding MI-based EEG signals by leveraging a backpropagation neural network (BPNN) optimized using the Honey-Badger Algorithm (HBA)7 to effectively address existing challenges. BPNNs have been widely utilized in key areas such as prediction, control, data classification, optimization, and signal processing. However, the traditional gradient descent learning algorithm in BPNNs often leads to local optima in weight adjustments8. To overcome this limitation, the HBA algorithm enhances global convergence properties by utilizing its chaotic and ergodic behavior, providing an optimal solution for determining the weights and thresholds of the error backpropagation neural network. Additionally, the integration of chaotic disturbances9 further improves the model’s accuracy and convergence rate. This innovative approach combines the robust classification capabilities of BPNNs for MI EEG signals with the powerful search and optimization features of the HBA algorithm. As a preprocessing step, the Hilbert-Huang Transform (HHT)10 is employed to analyze non-linear and non-stationary EEG signals. HHT is particularly well-suited for EEG signal processing due to its adaptive signal analysis capabilities. Following this, the Permutation Conditional Mutual Information Common Spatial Pattern (PCMICSP)11 technique is applied to compute spatial features across different frequency bands. The method incorporates multi-frequency analysis by integrating spatial attributes across temporal and frequency domains. Feature extraction is enhanced through the integration of Common Spatial Pattern (CSP) and mutual Information theory. CSP improves classification precision, while MI estimates the linear and non-linear correlation in EEG signals, which is crucial for analyzing their non-stationary and non-linear nature. Furthermore, PCMI is utilized to diagnose the communication delay between brain regions, demonstrating robustness against EEG noise and preserving the intrinsic timing model, especially under conditions of strong coupling between channels.

PCMICSP has a progressive correction mechanism that dynamically adapts features based on signal changes. This makes the model more accurate in real-world conditions and across individuals. By making progressive corrections, PCMICSP helps the model avoid getting trapped in suboptimal states. As a result, the extracted features have better resolution. EEG has noisy data, and traditional CSP is sensitive to noise. By continuously correcting, PCMICSP can compensate for additional noise or small deviations in the data. Therefore, it has better real-world performance than conventional CSP, which directly transfers noise to the feature. By combining progressive correction, dynamic adaptation, and noise-robust feature extraction, PCMICSP overcomes the limitations of traditional CSP and provides better performance.

When compared to traditional wavelet-based approaches, HHT performs better time-frequency analysis on non-linear and non-stationary EEG signals, catching detailed patterns in motor imagery. The use of PCMICSP improves the feature extraction phase by utilizing mutual information between features, allowing motor imagery patterns to be distinguished more efficiently than traditional CSP or Filter-Bank CSP (FBCSP) techniques. Furthermore, the HBA optimizes the weights and thresholds of the BPNN more quickly than gradient-based optimization algorithms such as Adam, thanks to its global search capability and chaotic perturbation mechanism, which prevents local minima and promotes convergence. These enhancements result in higher classification accuracy, confirming the efficacy of our technique for EEG-based motor imagery tasks.

The structure of this paper is organized as follows: Section “Related work” deals related works conducted by various researchers, Section “Proposed method for MI classification” outlines the proposed methodology, Section “Experimental results” introduces the simulations performed to evaluate performance, and Section “Conclusion” concludes the study.

Related work

Classify MI from EEG signals has emerged as a challenging yet essential task in the field of BCI systems. The complexities of analyzing EEG data, including its non-linear and non-stationary characteristics, require innovative approaches that go beyond traditional methods. The dynamic nature of EEG signals, coupled with the need for real-time processing, calls for intelligent techniques capable of capturing subtle patterns associated with motor imagery.

In12 investigates EEG-based diagnosis with the BCI Competition III dataset. To reduce noise, a Laplacian filter is applied during preprocessing, and Principal Component Analysis (PCA) is utilized for feature extraction to improve essential mental features by lowering dimensionality. The classification is accomplished by a Deep Neural Network (DNN). The study is renowned for its non-invasiveness and ability to capture certain mental traits, although it has a long processing time and requires manual filtering.

In13 uses the DEAP dataset to diagnose emotional states. Preprocessing is done using the Common Spatial Pattern (CSP) approach, while feature extraction is carried out using the Continuous Wavelet Transform (CWT). A hybrid classification scheme is applied using Convolutional Neural Network (CNN), Bidirectional Long-Short-Term Memory (BiLSTM) network, and a multi-head self-attention technique. This method delivers proper accuracy and automatic feature extraction; however, it needs significant processing resources, making it difficult to execute in real time.

In14 examines the diagnosis of pain syndromes using data from 39 volunteers (34 men and 5 women). A band-pass filter is used for preprocessing, and temporal and frequency information are manually extracted. The classification is done by a Multi-Layer Perceptron Neural Network (MLPNN). While the method accurately diagnoses pain situations, it requires manually setting parameters, which restricts automation.

In15 uses a modified Whale Optimization Algorithm (WOA) to diagnose medical disorders based on ten medical datasets. No specific preprocessing or feature extraction procedures are provided, and classification is done with a Feedforward Neural Network (FNN). The study automates weight optimization; however, the convergence rate is slow.

In16 uses the Bonn EEG database to diagnose neurological illnesses. Z-score normalization is employed for preprocessing, and a CNN-LSTM model performs classification without the need for human feature extraction. While the method simplifies the procedure, it is data-intensive and requires huge datasets to perform optimally.

In17 diagnostic accuracy is improved utilizing the KITS EEG dataset. The Kruskal-Wallis test is used to identify features, whereas an Artificial Neural Network (ANN) is used for classification. Although feature selection enhances accuracy, the process is computationally expensive and complicated.

In18 focuses on detecting EEG problems in children by analyzing a dataset of their EEG signals. A moving average filter is used to preprocess data, and the Discrete Wavelet Transform (DWT) is used to extract features. A neural network is used to classify data. This strategy minimizes computing strain, but it requires huge datasets for accurate diagnosis.

In19 uses the CHB-MIT dataset to diagnose epileptic seizures. Preprocessing is the process of denoising signals and using filters to remove artifacts. A fully linked layer extracts features, and a Denoising Convolutional Autoencoder (DCAE) with BiLSTM is used to classify them. The model improves feature representation but is computationally demanding.

In20 uses LSTM for classification without feature extraction on the EEGMMIDB dataset. Preprocessing comprises signal cleaning and normalization. This strategy avoids the requirement for feature extraction but is largely reliant on the availability of high-quality data.

In21 uses the BCI Competition IV dataset to diagnose motor imagery tasks. Preprocessing is done using ResNet’s cross-layer connection, and features are retrieved using a CNN. The classification is done using BiLSTM. The approach achieves excellent precision but has difficulty with fading gradients.

In22 investigates motor imagery diagnosis with the EEG Motor Movement/Imagery Dataset. Preprocessing includes band-pass and notch filtering. Feature extraction methods such as common spatial pattern (CSP), wavelet transform, adaptive regression, and connectivity characteristics are used. Classification is carried out utilizing Riemannian geometric methods. While the approach offers a thorough evaluation, it necessitates deep topic knowledge.

In23 mental states are diagnosed based on data from 8 people (3 males and 5 females). Preprocessing steps include resampling at 250 Hz, filtering out artifacts, segmenting into a 3D matrix, and using ICA to isolate ocular components. The feature extraction is done with weighted time-domain features, and the classification is done with an SVM. The approach is accurate and fast, but it is restricted by the quantity of the dataset.

In24 uses the BCI Competition IV datasets (BCIC-IV-2a and BCIC-IV-2b) for diagnosis. Preprocessing entails signal segmentation and recombination. The features are pooled using variance and average pooling, shared self-attention, and a convolutional encoder. A CNN model with self-attention is used for classification. The method collects multimodal temporal information but is computationally demanding.

In25 uses power spectral density estimation for preprocessing in the BCI IV 2a and High Gamma datasets. Features are retrieved using the Multi-scale Spatio-Temporal Module (MS-STM), Multi-scale Temporal Module (MSTM), and PSD-Conv module. Classification is carried out using an attention-based MSFF-SENet. The method effectively combines Spatio-Temporal features, although it necessitates significant processing resources.

In26 uses the BCI Competition IV 2a dataset for multi-class classification. Standard EEG preprocessing techniques are used, and feature extraction is carried out with multi-scale residual blocks and squeeze-and-excitation attention. Classification employs a hybrid-attention network. This method extracts several features but is resource expensive.

In27 increases cross-subject decoding by utilizing three benchmark MI-EEG datasets. Preprocessing uses Gaussian weighting for spatial regularization, whereas feature extraction uses aligned EEG recorded characteristics along with domain adaptation. Regularized feature learning allows for good decoding, although subject-specific properties may be lost.

In28 uses the EEGMMIDB dataset to diagnose EEG-related illnesses. Preprocessing involves noise removal and normalization, and feature extraction is divided into disease-related, personal, and supplementary characteristics. Classification divides subjects into subject-related and non-subject-related random labels. While this is a suitable model for independent subjects, it requires further data for a thorough evaluation.

In29 performance on the EEGMMIDB dataset is assessed utilizing band-frequency filtering for preprocessing. Features are extracted via a fusion of several branches, and classification is done with different EEGNet models. The strategy simplifies model structure for a five-branch model but adds complexity to models with more branches.

In30, a portion of an electroencephalogram was retrieved and preprocessed. Second, the authors used a filter bank common spatial pattern (FBCSP) with one-vs-rest (OVR) technique to extract spatio-temporal-frequency information from numerous MI. Third, the F-score was used to optimise and choose these traits. Finally, the optimized features were supplied into the spiking neural network (SNN) for classification.

In31, to improve classification robustness, the authors combined brain functional connectivity (BFC) with one-versus-the-rest filter-bank common spatial pattern (OVR-FBCSP). The BFC features were extracted using the phase locking value (PLV), which represents the brain inter-regional interactions relevant to the MI, and the OVR-FBCSP was utilized to extract the spatial-frequency characteristics linked to the MI. These various attributes were then fed into the multi-kernel relevance vector machine (MK-RVM). The proposed method was evaluated using a dataset that included three motor imagery tasks (left hand MI, right hand MI, and feet MI).

In32, the authors propose a multiple patterns of motor imagery (MPMI) BCI approach that builds on the classic two patterns of motor imagery. The motor imagery BCI technique had been expanded to include various patterns: right-hand motor imagery, left-hand motor imagery, foot motor imagery, and both hands motor imagery, all of which resulted in turning right, turning left, acceleration, and deceleration for virtual automated vehicle control.

In33, investigates the use of an EEG and functional near-infrared spectroscopy (fNIRS) to improve the decoding performance of motor imagery tasks for BCI. The experiment required simultaneously measuring 64 channels of EEG signals and 20 channels of fNIRS data while performing a left-right hand MI task. The experiment required simultaneously measuring 64 channels of EEG signals and 20 channels of fNIRS data while performing a left-right hand MI task. The study used these two types of signals to investigate how feature fusion affected MI classification accuracy. To increase signal quality for further analysis, the EEG data were filtered into three bands (4–7 Hz, 8–13 Hz, and 14–30 Hz), and the fNIRS signals were filtered into 0.02–0.08 Hz. The CSP algorithm was used to extract features from EEG and fNIRS signals. This enabled the researchers to generate a fused signal containing both EEG and fNIRS components, which could then be processed with principal component analysis (PCA). Finally, the data was loaded into a support.

In34, the authors propose a cascade structure of dynamic graph convolutional and capsule networks for accurate decoding of motor imagery (MI)-based BCIs using EEG and fNIRS. The same network structure, but with various parameter settings, was used to extract features from these two modalities using temporal convolution, dynamic graph convolution, and capsule creation blocks. The temporal convolution block was used to learn temporal information, the dynamic graph convolution block for spatial features, and the capsule production block for creating principal capsules. The capsuled features will then be subjected to cross-attention before proceeding to a feature fusion block and a dynamic routing block, which is an iterative method aimed to learn the connection weights between primary and digit capsules.

Traditional optimization techniques, such as gradient descent, frequently exhibit local minima and sluggish convergence in complicated non-linear networks. To solve these constraints, metaheuristic optimizers have been investigated in EEG signal processing. Among these, the Honey Badger Algorithm (HBA) has lately demonstrated promising results because to its adaptive exploration-exploitation technique. In contrast to the usual CSP algorithm, our suggested PCMICSP technique optimizes the spatial filter selection process, resulting in superior discriminating of motor imagery tasks. Similar advances have been reported in recent studies that integrate filter-bank CSP with spiking neural networks30 or brain functional connectivity31. Furthermore, hybrid EEG-fNIRS approaches33,34 demonstrate the advantages of combining optimization and extra features for robust MI decoding.

Proposed method for MI classification

In recent years, BCI systems, which analyze electroencephalographic (EEG) brain signals to enable direct communication between the brain and external devices, have garnered significant attention. These systems have found critical applications in the medical and rehabilitation fields, particularly for improving the quality of life for individuals with mobility impairments. However, processing EEG data requires effective techniques capable of accurately interpreting the complex and non-linear patterns inherent in brain signals. The integration of advanced machine learning methods and intelligent optimization algorithms has led to substantial improvements in the precision of signal identification and classification. Despite this progress, challenges such as high noise levels, computational complexity, and the need for fine-tuned models persist, hindering the ability to achieve consistently high accuracy in signal decoding and prediction. This paper introduces an intelligent decoding framework for EEG signals, leveraging a BPNN optimized using the HBA algorithm. The proposed approach aims to enhance both the accuracy and efficiency of EEG signal processing. The following sections provide a detailed explanation of the proposed method.

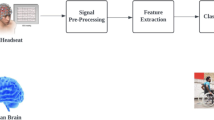
Block diagram illustrated the steps of the proposed EEG-based MI classification system is given in Fig. 1.

Fig. 1
figure 1

Block diagram the proposed EEG-based MI system.

Full size image

Preprocessing step of EEG data with HHT

For preprocessing EEG signals, the Hilbert-Huang Transform (HHT) was utilized9. HHT is an adaptive signal processing technique specifically suited for analyzing nonlinear and nonstationary signals. The process includes two main parts: Empirical Mode Decomposition (EMD) and the Hilbert Transform (HT). In the first part, EMD adaptively decomposes a complex signal into a series of Intrinsic Mode Functions (IMFs) based on the signal’s characteristics. This decomposition satisfies two key conditions: (1) the mean value of the local maxima and minima is zero, and (2) the difference between the number of extrema (sum of maxima and minima) and the number of zero-crossings does not exceed one. For a given signal x(t), EMD can be applied to decompose it into the following form:

$$\:x\left(t\right)=\sum\:_{i=1}^{k}{IMF}_{i}\left(t\right)+{r}_{k}\left(t\right).$$
(1)

Where is k intrinsic mode tasks, \(\:{r}_{k}\) is negligible signal residue that is basic signal subtraction remainder, \(\:{IMF}_{i}\left(t\right)\).

EEG data from subjects S001 to S005 in the EEG Motor Movement/Imagery Database (EEGMMIDB) were used. Each recording was segmented into windows of 128 samples (equivalent to 0.5 s at a 256 Hz sampling rate). No filtering beyond the decomposition method was applied.

Each EEG segment was decomposed using Hilbert-Huang Transform (HHT). The Empirical Mode Decomposition (EMD) was applied with K = 3 intrinsic mode functions (IMFs) retained per channel, capturing motor imagery-relevant frequencies (8–30 Hz).

Feature extraction step with PCMICSP

For feature extraction, we employ an effective strategy known as Permutation Conditional Mutual Information Common Space Pattern (PCMICSP)10. This technique involves utilizing total permutation conditional mutual information matrices for each channel, replacing the traditional mixed spatial covariance matrix used in the Common Space Pattern (CSP) algorithm. The eigenvalues and eigenvectors derived from this process are used to construct new spatial filters. Consequently, spatial features from different time and frequency domains are combined to generate a comprehensive 2D pixel map.

The CSP mechanism focuses on transforming the covariance matrices of two types of samples. It utilizes Principal Component Analysis (PCA) to identify components with the highest variance between the two sample types, thereby creating an optimal spatial filter. While this approach effectively targets spatial components with the greatest energy variance between the sample types, it is limited in its ability to capture nonlinear relationships within the EEG signal features across time series. PCMICSP computes PCMI between EEG channel pairs:

$$\:PCMI\left(X;Y|Z\right)=\sum\:_{x,y,z}\text{log}p(x,y,z)\left(\frac{p(x,y|z)}{p\left(x|z\right)p\left(y\right|z)}\right).$$
(2)

where p(x, y,z) is the joint probability distribution of the permuted signals.

After constructing the PCMI matrix, we apply CSP (Common Spatial Pattern) on the top-ranked channel pairs based on PCMI values to maximize the variance difference between the two MI classes (left vs. right hand).

Based on the PCMI matrix, top-ranked channels are selected, and CSP is applied to extract discriminative spatial patterns. Features are extracted from the IMFs obtained via HHT. Specifically, IMF1–IMF3 (corresponding to the 8–30 Hz band) are used. We retain K = 3 IMFs, focusing on motor-related rhythms based on prior research.

Feature selection in EEG-based MI system

In the proposed system, feature selection (Calculate Key characteristics) refers to the process of selecting the most informative characteristics from the retrieved EEG spatial data produced by PCMICSP. This step is critical to improving the efficiency and accuracy of the future classification task. Following feature extraction with PCMICSP, we will have a set of features that represent the spatial and temporal properties of EEG data. These features must be evaluated to discover which ones contribute most effectively to the classification process. This evaluation can be done using a variety of ways to determine feature importance. One way is to use mutual information, which quantifies how much knowledge a specific feature contributes about the class label. Features having a high MI are often regarded as more relevant since they provide more information about the categorization task. Another way is to look at the correlation between features. Removing highly correlated features reduces redundancy and improves feature diversity. Statistical techniques such as t-tests can also be used to assess the significance of features by comparing their variance or distribution across distinct class labels.

After determining the significance of each trait, the following step is to rank them according to their importance. This can be accomplished by assigning a score to each characteristic based on a metric such as MI or another selected criterion and then ranking them in descending order of relevance. Features are ranked according to their MI with the class labels:

$$\:MI(X;Y)=\sum\:_{x,y}\text{log}p(x,y)\left(\frac{p(x,y)}{p\left(x\right)p\left(y\right)}\right).$$
(3)

The top mmm features with the highest mutual information scores are selected. In our experiments, m is set to 20. The proposed pipeline is specifically adapted for MI EEG by emphasizing motor frequency bands, leveraging non-linear feature interactions (PCMI), and enhancing classifier training through HBA optimization. The final step in selecting critical characteristics is to choose the top-ranked features based on a predetermined criterion. This could involve selecting the top characteristics or those that meet or exceed a specific relevance threshold. Only the selected important features should proceed to the next stage, which involves optimizing the BPNN parameters with HBA. This ensures that the classification task is completed more effectively, resulting in higher accuracy and performance for the total EEG-based Motor Imagery system.

Optimizing BPNN with HBA

The Honey Badger Algorithm (HBA) was created mathematically to enhance search techniques for resolving optimization issues. It was inspired by the clever behavior of honey badgers in their quest for food. The two primary tactics used by this algorithm to control the search process are exploration and exploitation. The HBA method is a general-purpose heuristic search mechanism that finds extensive use in areas including robotics, image processing, and performance improvement11.

A feedforward neural network comprising two hidden layers with 20 and 10 neurons, respectively, was designed, employing sigmoid activation functions in each layer. The HBA algorithm is used to optimize the BPNN parameters. To optimize the network’s weights and biases, the HBA was utilized, configured with a population size of 20, a total of 200 iterations, and search space bounds set within the range of [-5, 5]. The following describes the procedures and essential elements of this optimization:

Particle definition (search variable definition)

In the HBA algorithm, each particle or individual in the population represents a set of BPNN parameters. These parameters include the weights and biases of different network layers that need to be optimized. Each parameter is confined within a predefined range, [ai, bi] ensuring appropriate bounds for the optimization process.

Initial population creation

A population of particles or solutions is produced in the first stage. Inverse learning is used to broaden the population’s diversity and move closer to the ideal answer. This approach creates inverse solutions for the original population, which are then added to the original population to help it contain more diverse and superior solutions.

The relationship of reverse learning is expressed in Eq. (4):

$$\:{X}_{i}^{{\prime\:}}=r\bullet\:(u+e)-{X}_{i}.$$
(4)

where \(\:{X}_{i}^{{\prime\:}}\) is the inverted value of the \(\:{X}_{i}\) position, \(\:{X}_{i}\) is the current position of each particle in the initial population, r refers to a random amount on [0,1], u and e are the upper and lower bounds of the search space, respectively.

It should be noted that Eq. (2) is used to create the inverse population and does not use randomness, but simply makes the initial population more diverse by calculating the inverse position of each particle relative to the search range.

Chaos algorithm

The algorithm leverages chaotic disturbances to navigate the search space effectively, enabling it to escape local optima and approach the global optimal points. The use of Chaos Disturbance is a critical step in the HBA, enhancing the stability and efficiency of the optimization algorithm. The ergodic nature of the chaos algorithm ensures thorough exploration of every local optimal space and facilitates escaping from those points. The sensitivity of chaotic dynamics allows individuals to diverge even when their fitness values are nearly identical. This approach not only preserves the best-performing individual but also maintains population diversity throughout the optimization process. Here, we apply Tent and Logistic mapping integration to create chaotic orders. The Tent mapping is applied for creating basic chaotic criteria amount, while the Logistic mapping is applied for chaotic disturbance. In order for the iteration to discover the best solution, the chaotic disturbance is then added to the initial ideal solution. Ultimately, the best answer serves as the starting weights and thresholds for the BPNN’s learning.

The Tent mapping refers to piecewise linear mapping which possesses good relation, sensitivity, and simplified structure performance to a basic amount. Classic Tent mapping is:

$$\:{x}_{n+1}=\left\{\begin{array}{c}\frac{1}{\mu\:}{x}_{n}.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:0\le\:{x}_{n}<\mu\:\\\:\frac{1}{\mu\:}\left(1-{x}_{n}\right)\:\:\:\:\mu\:\le\:{x}_{n}<1\end{array}\right..$$
(5)

Taking constant \(\:\mu\:\) = 0.5, here, the order achieved for various parameters possesses a unique density share. Classic Tent mapping refers to adjacent point segmentation with robust relevant attributes. Due to that digital accuracy is restricted in the progress of computation, achieving several inherent stable points from the basic amount after the finite iteration does not have meaning. Here, we apply the linear integration to prevent the lacks discussed before, the main state is:

$$\:{x}_{n+1}=\left\{\begin{array}{c}2{x}_{n}+psin\left(q{x}_{n}\right).\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}_{n}<0.5\\\:2\left(1-{x}_{n}\right)-psin\left(q{x}_{n}\right).\:\:\:\:\:\:{x}_{n}\ge\:0.5\end{array}\right.$$
(6)
$$\begin{array}{l}\:p = 2\pi \:n.\:n\varepsilon Z \cap \: \ne \:0\\0 \le \:\frac{2}{q}{\rm{arccos}}\left( { - \frac{2}{{pq}}} \right) + psin\left[ {{\rm{arccos}}( - \frac{2}{{pq}})} \right] \le \:1{\rm{l}}.\end{array}$$
(7)

Determining fitness function

In this step, the cost of each particle is evaluated based on the accuracy of the BPNN. The fitness value of each particle is defined based on the neural network error. If the network output is \(\:{T}_{i}\) and the expected output is \(\:{O}_{i}\), then the network error is calculated as the BP threshold of the network

$$\:Cost\:Function=\frac{1}{n}{\sum\:_{i=1}^{n}{({T}_{i}-{O}_{i})}^{2}}_{\:}.$$
(8)

Here, since the optimization problem is deductive, the inverse of the error is considered as the fitness measure:

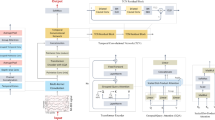
$$\:Fitness\:Function=\frac{1}{Cost\:Function}.$$
(9)

Also, the flowchart depicting the optimization process of the BPNN using the HBA algorithm is presented in Fig. 2.

Fig. 2
figure 2

The proposed flowchart for optimizing BPNN using HBA.

Full size image

Exploration and exploitation

The HBA algorithm operates in two key steps, exploration and exploitation, to perform optimization.

  • Exploration: This step aims to examine various regions of the search space, maintaining diversity and offer the potential for discovering global optimum.

  • Exploitation: In this step, the search focuses on specific space of the search space to refine solutions and converse toward a local and global optimum.

When one of the following circumstances is satisfied, the HBA algorithm terminates:

  • The predefined maximum number of iterations is reached.

  • Over a number of consecutive iterations, the fitness changes are negligible.

  • The neural network will achieve the required level of classification accuracy.

By taking these actions, the HBA algorithm may better optimize the BPNN parameters and classify EEG signals with more accuracy.

Classification of EEG-MI using BPNN-HBA

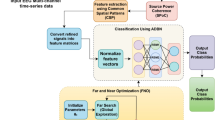
As previously noted, the BPNN is one of the most widely used and successful neural network architectures, employing a multi-layer learning mechanism based on backward error propagation. The core concept of the learning process involves two main stages: forward propagation of signals and backward propagation of errors. During forward propagation, input data is processed through the input layer and passed sequentially through hidden layers, ultimately reaching the output layer. If the actual output differs from the desired output, the backward propagation stage begins. In this stage, the error is propagated backward, layer by layer, along various pathways. Each layer’s error is distributed across its components proportionally, requiring an accurate calculation of error signals for each component. These error signals are used to adjust weights, ensuring gradual convergence toward the desired output. Furthermore, the pseudocode of the proposed EEG-based MI using BPNN optimized with the HBA algorithm is presented in Fig. 3.

Fig. 3
figure 3

Pseudocode of the proposed EEG-based motor imagery.

Full size image

Experimental results

This part presents a detailed experimental works analysis performed for our presented model. The computational complexity of the presented mechanism may vary depending on the size and features of the data set. Additionally, the parametric values may change dynamically according to the specific requirements of the data.

Dataset

This study used the EEG motor movement/imagery database (EEGMMIDB), publicly accessible via PhysioNet, as it aligns well the objectives of this study. Most significantly, this dataset includes a relatively large sample size of 109 subjects, making it more comprehensive compared to earlier BCI datasets. Every EEG signal in the EGMMIDB was captured consistently according to 14 distinct experimental blocks, the first two of which represent one-minute Rest with Eyes Open (REO) and Rest with Eyes Closed (REC) conditions, respectively35. The dataset, made by Grewin Schalk, and was gathered by applying a system of BCI 2000 EEG that records brain signals with 64 channels at the sampling rate of 160 Hz36. T0, T1, and T2 are the three codes assigned to each channel. T0 denotes the rest interval, T1 refers to left-hand movement for certain tasks and both fists in others. While T2 indicates the right-hand movement and both feet in others29. Figure 4 show a sample EEG signal from channel 1 of the EEGMMIDB dataset, illustrating the amplitude variation over time. The EEG motor imagery dataset for this investigation was obtained from the EGMMIDB database. It is made up of EEG recordings from five people who were undertaking motor imagery tasks (left- and right-hand movements). Each recording includes signals from 64 EEG channels, sampled at 128 time points each segment. In total, 5000 samples were collected and categorized based on the desired motor imaging task. The signals were preprocessed to remove artifacts before feature extraction, which focused on the sensorimotor rhythm (8–30 Hz) that is relevant to motor control tasks.

Fig. 4
figure 4

Sample EEG Signal from EEGMMIDB Dataset (Channel 1).

Full size image

This dataset design ensures enough heterogeneity across patients and trials to permit a thorough evaluation of the proposed method. In this work, we used a subject-dependent evaluation technique. The EEG data from the first five subjects in the EEGMMIDB dataset were pooled and randomly divided into training and testing groups. While this setup allows for an initial assessment of the proposed model’s learning capability, future work will try to test the system in a more rigorous subject-independent context, better reflecting real-world BCI applications.

Environment

The present study has been supported by many experimental assessments. Such assessment outcomes have been applied to provide our presented model accuracy also whole tests were performed in the platform of Matlab. The operating system applied is Windows 10 Pro with hardware configuration as RAM of 12.0 GB and an Intel processor. Some architectures were schemed for methods of ML, scheme, and optimization.

Details of the parameter

The various parameters used for the BPNN and HBA are outlined in Tables 1 and 2. These tables provide the parameter configurations for both the BPNN and the HBA optimization algorithm. Optimizing accuracy and efficiency during the processing and classification of EEG signals is the primary goal of these parameters. The modified parameters for the BPNN are detailed in Table 1. Key adjustments include the number of input and hidden layer neurons, the number of layers, the activation function, the number of iterations (epochs), and the mini batch size. These parameters enable the network to effectively learn and identify essential features from EEG signals, enhancing its classification capabilities. EEG data from patients S001 through S005 in the EEGMMIDB dataset were used. Each EEG recording was divided into 128 sample windows. Following HHT, feature extraction was carried out using PCMICSP with two permutations. The obtained features were normalized in the [0,1] range and fed into a backpropagation neural network with two hidden layers (20 and 10 neurons, respectively) using sigmoid activation. The network parameters were optimized with the HBA at a population size of 20 and 200 iterations. The weights’ lower and upper bounds were set to [-5, 5]. The subject-dependent protocol was employed for training and testing splits.

Table 1 Parameters applied for BPNN.
Full size table

The parameter settings for the HBA algorithm are presented in Table 2. These include factors such as the number of iterations and the population size, which significantly influence the convergence speed and the efficiency of the optimization process. Furthermore, the dataset has been divided for training and testing, and the model’s accuracy has been evaluated based on this split. These configurations ensure the robustness and reliability of the proposed approach.

Table 2 Parameters applied for HBA.
Full size table

Evaluation metrics

In general, the evaluation of classification problems is conducted using the confusion matrix, which provides the number of correctly and incorrectly classified instances. The performance of the proposed EEG-based MI BCI system is evaluated using metrics such as Precision, Sensitivity, Specificity, F-Measure, and Accuracy. These metrics are calculated based on True Positive (TP), True Negative (TN), False Positive (FP), and False Negative (FN) values derived from the confusion matrix.

Precision

assesses accurately grouped samples’ fraction between those grouped as positives.

$$\:Precision=\frac{TP}{TP+FP}.$$
(10)

Recall

accurately diagnosed certain positive models’ patterns/total number. The positive model shows the diagnosed seizure.

$$\:Sensitivity=\frac{TP}{TP+FN}.$$
(11)

Accuracy

accurately grouped patterns/Total Number.

$$\:Accuracy=\frac{TP+TN}{TP+FP+TN+FN}.$$
(12)

The precision and recall could be integrated for computing F-measure. The formula for computing the F-measure is provided in Eq. (13).

$$\:\mathbf{F}-\mathbf{m}\mathbf{e}\mathbf{a}\mathbf{s}\mathbf{u}\mathbf{r}\mathbf{e}=2\times\:\frac{\text{P}\text{r}\text{e}\text{c}\text{i}\text{s}\text{i}\text{o}\text{n}\times\:\text{R}\text{e}\text{c}\text{a}\text{l}\text{l}\:}{\text{P}\text{r}\text{e}\text{c}\text{i}\text{s}\text{i}\text{o}\text{n}+\text{R}\text{e}\text{c}\text{a}\text{l}\text{l}}.$$
(13)

Results and analysis

This section compares the proposed classifier against several preprocessing and feature extraction approaches utilizing 2-fold, 4-fold, and 10-fold cross-validation schemes. These tests are intended to examine the classifier’s efficiency and show the advantages of incorporating advanced approaches for EEG signal processing. Tables 3, 4 and 5 provide a full evaluation of different approaches and their impact on categorization accuracy. Finally, the proposed system’s results are compared to those of earlier studies that used the EEGMMIDB dataset to show its superiority and potential for EEG-based motor imaging tasks.

Table 3 compares the performance of several preprocessing and feature extraction approaches in the context of an EEG signal. The results reveal that the combination of Hilbert-Huang transform (HHT) preprocessing with PCMCISP feature extraction provides the greatest overall performance. This combination achieved higher Precision, Recall, Accuracy, and F-Measure values (90.5 ± 0.8, 90.5 ± 0.8, 90.7 ± 0.8, and 90.6 ± 0.8, respectively) than other combinations. On the contrary, the Band Pass Filter in combination with FFT produced the poorest results. This combination has 79.5 ± 1.2 precision, 78.8 ± 1.3 recall, 81.5 ± 1.4 overall accuracy, and 79.1 ± 1.4 F-Measure, which is lower than previous approaches. Among the pre-processing techniques, ANC has produced excellent results. The combination of ANC and PCMCISP resulted in accuracy and recall of 89.5 ± 0.9 and 89.3 ± 0.9, respectively. Overall accuracy and F-Measure were recorded as 89.4 ± 0.9 and 89.4 ± 0.9. This combination outperforms other strategies in terms of efficiency, as seen by these values. In various combinations, Wavelet Analysis and PCMCISP perform similarly to HHT, with Precision, Recall, Overall Accuracy, and F-Measure values of 90.2 ± 0.8, 90.0 ± 0.8, and 90.1 ± 0.8. 90.1 ± 0.8 was reported. This demonstrates that wavelet analysis is one of the most effective preprocessing approaches.

Table 4 show that the combination of HHT preprocessing and PCMCISP as feature extraction method outperforms all other combinations. This combination obtains Precision 93.0 ± 0.6, Recall 93.5 ± 0.6, Accuracy 93.5 ± 0.6, and F-Measure 93.4 ± 0.6, demonstrating high competence in signal analysis and classification. The EEG proves it. HHT’s superiority stems from its capacity to analyze non-stationary and non-linear signals and extract precise time-frequency information, whereas PCMCISP improves discriminating features by focusing on spatial patterns and optimizing channel selection. Other preprocessing approaches, such as wavelet analysis and adaptive denoising (ANC), perform well but fall short of the combined HHT and PCMCISP. PCMCISP outperforms other feature extraction methods in all combinations because it optimally recovers the spatial aspects of the signal and boosts the critical channels.

Table 5 compares the results of several preprocessing and feature extraction approaches when using BPNN for the EEGMMIDB dataset with 10-fold validation. The greatest performance was achieved using a combination of HHT preprocessing and PCMCISP feature extraction, with Precision 93.5 ± 0.3, Recall 93.8 ± 0.3, Accuracy 94.3 ± 0.3, and F-Measure 93.6 ± 0.3. These findings indicate that the combination of HHT and PCMCISP has a strong ability to accurately evaluate and classify EEG signals. The great performance of HHT is attributed to its ability to analyze non-stationary data and extract time-frequency information. Furthermore, PCMCISP improves key aspects by focusing on spatial feature extraction and channel selection optimization. Among other approaches, the combination of wavelet preprocessing and PCMCISP has performed well, although it is not as effective as HHT and PCMCISP. These findings highlight the necessity of selecting the optimal preprocessing and feature extraction methods to improve classifier performance.

The combined use of HHT as pre-processing and PCMCISP as feature extraction approach improves results due to their perfect compatibility with the complex and non-stationary character of EEG data. HHT is specifically intended for the analysis of non-linear and non-stationary signals. It uses Empirical Mode Decomposition (EMD) to break the signal into intrinsic components (IMFs) and then extracts correct time-frequency information using the Hilbert transform. This method maintains vital information by reducing noise and focusing on the signal’s local qualities. PCMCISP, on the other hand, optimizes extracted features by integrating CSP and channel spatter optimization approaches to produce high class discrimination. The synchronization of these two strategies allows PCMCISP to successfully handle the rich and detailed HHT information while reducing signal noise. As a result of this collaboration, high-quality and identifiable features are extracted, which improves the classification model’s performance and leads to higher precision, recall, and F-measure.

Table 3 Comparison of different preprocessing and feature extraction methods using the proposed BPNN on EGGMMIDB (2-fold cross validation).
Full size table
Table 4 Comparison of different preprocessing and feature extraction methods using the proposed BPNN on EGGMMIDB (4-fold cross validation).
Full size table
Table 5 Comparison of different preprocessing and feature extraction methods using the proposed BPNN on EGGMMIDB (10-fold cross validation).
Full size table

Figure 5 depicts the ROC curves of several feature extraction methods paired with HHT for binary classification of left- and right-hand motor imagery tasks. The classifiers employed the same optimized BPNN model to assess the efficacy of each feature extraction approach. The best model should have a TPR of 1 and an FPR of 0. The ROC curve in the figure compares the performance of various models on the EEGMMIDB dataset. The Area Under the Curve (AUC) score for each ROC curve indicates the model’s effectiveness. AUC scores near 1 suggest superior classifier performance.

The proposed ROC diagrams for various techniques clearly indicate each model’s ability in distinguishing positive and negative samples. The “HHT + PCMICSP” model has the best AUC of 0.96, and its ROC curve is very close to the upper and left corners of the graph, indicating that this model can detect positive samples with minimal errors (low FPR) and the highest true positive rate (high TPR). Other models, such as “HHT + PCA + CSP” and “HHT + STFT”, have high AUC and provide good performance, however they are slightly inferior to “HHT + PCMICSP”. In general, the ROC and AUC curves for each model clearly show the discriminating power and distinguishability of the features. The closer the AUC is near one. The highest AUC (0.94) was achieved using the HHT + PCMICSP combination, confirming the superiority of the proposed method in distinguishing between left and right motor imagery classes.

Fig. 5
figure 5

ROC curves of the proposed system.

Full size image

In this paper, the problem is represented as binary. In actuality, the model is intended to distinguish between motor imagery produced by the left and right hands. In actuality, the model is intended to distinguish between motor imagery produced by the left and right hands. The data comprises of EEG signals from the EEGMMIDB database, which are divided into two categories: left-hand and right-hand motions. Labels are specifically designed for the two signal types for this purpose, as noted in both the approach explanation and the figure caption.

For example, Fig. 5’s ROC curve description specifically states that the model evaluates its performance in identifying left- and right-hand movement images. The AUC (area under the ROC curve) was calculated using the trapezoidal method with 100 different criteria.

This procedure entails assessing the model at various prediction thresholds and computing the True Positive Rate (TPR) and False Positive Rate (FPR) for each one. After determining the threshold values, the trapezoidal method is used to calculate the area under the ROC curve.

Conclusion

The present paper is generated for proposing and developing several means that would finally be helpful to Medical Science for simply identifying a patient through detecting EEG signals with more sensitivity and accuracy in a short time. Present work concentrated on F-measure, accuracy, and sensitivity. Patients’ EEG signals contain usual brain death, and patients, are epileptic. So, we built 64 64-channel EEG signals including attribute signals provided as input to multiple BPNN and HBA mechanism patterns that provide better showing and testing with a short time, neurons’ number in the hidden layer, and mean square error. Such agents are in charge of proper outcomes. Such attributes’ associated agents were created. Such multiple patterns provide an increase in unfamiliar patients’ attributes and better detection decisions. A hybrid model of BPNN detects patient’s signals but does not optimize parameters. That illustrates that BPNN with HBA provides the best accuracy that provides better outcomes in comparison to other EEG signal models.