Introduction

In recent years, the limitations of satellite navigation systems have become increasingly apparent, posing a considerable threat to national economies and security. Consequently, the eLoran system has emerged as the preferred option for complementing and reinforcing satellite navigation systems owing to its robust anti-jamming capabilities and stable signal characteristics. Determining the propagation delays of long-wave signals from the transmitter to the receiver is essential to use long-wave signals for positioning and timing. However, this delay can be easily affected by meteorological conditions—such as temperature and humidity—along the propagation path, ground-based electrical parameters, and real-time factors—such as terrain—that hinder accurate predictions and affect the positioning and timing precision of long-wave systems. Moreover, real-time factors, such as meteorological and electrical parameters, cannot be accurately predicted by models; hence, their actual impact can only be analysed by measuring the long-wave propagation delays1,2,3. Although the influence of terrain undulation remains constant over time, it contributes to signal-propagation delays. Considering that these factors induce gradual changes within a specific spatial range, propagation theory suggests that these factors have a similar effect on long-wave propagation delays at neighbouring test points.

Consequently, this study analysed the variations in the long-wave propagation delay at each test point based on actual measurement results from several measurement points in neighbouring areas. The correlation of the data at each test point was meticulously analysed to validate differential positioning, which was then assessed for its feasibility in differential positioning analysis.

Methods

Long-wave propagation delay test

For the eLoran system, which primarily relies on ground-wave propagation for its positioning and timing functions, it is crucial to address three key errors that impact ground-wave propagation delays: the primary phase factor (PF), secondary phase factor (SF), and additional secondary phase factor (ASF)4,5,6. The ASF is the cumulative delay experienced by an eLoran signal propagating over land with varying earth conductivities. This correction is a time-varying parameter that changes with the season, temperature, humidity, and other climatic conditions. The PF is influenced by the great circle distance, whereas the ASF is affected by ground conductivity and relative permittivity.

To investigate the ASF characteristics of the eLoran system and its temporal and spatial correlation with the propagation path, we selected a straight-line path in Hubei Province for actual signal measurements and analyses. The experimental site was situated in the flat terrain of Wuhan, a transitional zone stretching from the southeastern hills of Hubei Province across the eastern edge of the Hanjiang Plain to lower elevations at the southern base of the Dabie Mountains. The test site was located approximately 50 m above sea level and was devoid of major elevation changes or natural shelters. We selected four test points that exhibited spatial correlations. The experiment was conducted in November 2022 under clear weather conditions with no precipitation, an average temperature of 25.6 °C, and relative humidity of 69.6% at a ground height of 2 m.

Figure 1 shows the spatial distribution of the sampling points used in this study. At these monitoring points, a magnetic antenna (H-field antenna) was set up to receive signals using an UrsaNav-UN152B receiver, as shown in Fig. 2. Additionally, we employed a high-precision global navigation satellite system (GNSS) receiver and used its output positioning data as the measurement reference.

Fig. 1
figure 1

Schematic of the propagation delay data-sampling points. ( Data source: National Earth System Science Data Center, National Science & Technology Infrastructure of China (http://www.geodata.cn). Mapping performed with ArcGIS 10.8.)

Full size image
Fig. 2
figure 2

Photographs of the test equipment. (a) eLoran receiver, and (b) Antenna and global navigation satellite system (GNSS) receiver.

Full size image

Theory: Long-wave propagation delay characteristics

In the eLoran system, a chain consists of one primary and two secondary stations. Within each chain, the primary and secondary stations form a station pair. By measuring the time difference between the signal arrivals at this station pair, a user can determine a hyperbolic position line relative to their current location. Within the coverage area of a chain, the primary and secondary stations can simultaneously generate two position lines, with their intersections defining the user’s navigation position.

For this test, the 8390 chain was used for positioning, focusing on three specific stations within this chain: 8390 M (the primary station located in Xuancheng), 8390X (the first subsidiary station, known as Raoping Station), and 8390Y (the second subsidiary station, known as Rongcheng station). The arrival time of the 8390-chain signal was used to calculate the ASF value.

During this study, eLoran signal measurements were conducted for over 1 h at each measurement point, with 1 h of valid data selected for subsequent correlation analysis. The receiver enabled direct measurements of the time of arrival (TOA) from one master and two slave stations of the 8390 chain to the current location. The TOA composition is expressed as follows7,

$$TOA=PF+SF+ASF$$
(1)

where PF represents the time taken by a signal to propagate through an infinite air medium from the transmitting to the receiving antenna, SF denotes the delay caused by the sea surface’s impact on signal propagation, and ASF accounts for delays specific to ground-based signal paths (i.e. variations in the time delay for long-wave ground-wave signals passing through land compared with the time delay for complete passing over seawater).

Here, the SF and ASF reflect the influence of the surface medium of the signal-propagation path (seawater or land surface cover) on the propagation delay and can be computed based on the phase of the ground-wave attenuation function8.

However, the ASF can be influenced by unpredictable propagation-related factors such as terrain, great circle distance, atmospheric refractive index, and climate9. Therefore, engineering applications often require actual measurements for time-delay correction.

In this test, the TOAs of the 8390-chain signals were used to calculate the ASF as follows10,

$$ASF=TO{A}_{\text{measurement}}-PF-SF$$
(2)

where TOAmeasurement denotes the arrival time measured at the receiver output. The PF and SF can be precisely calculated using a model based on the carrier location as the output of the GNSS receiver, as described in11.

In this study, ASF1 represents the ASF value corresponding to the arrival time difference between stations 8390 M (Xuancheng) and 8390X (Raoping), whereas ASF2 represents the ASF value for the arrival time difference between stations 8390 M and 8390Y (Rongcheng).

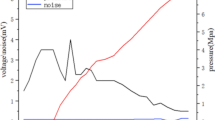
The test results from the measurement points were used to analyse the variation characteristics of long-wave propagation delays. As the test data contained random noise with no correlation between the noise components, the sampled data required filtering12. To retain effectively signal-change information during filtering and smoothing, the Savitzky–Golay filter was employed to process the sampled data in this study. Because of space constraints, only the results from test points P1 and P4 are presented, and their ASF distribution conforms to a Gaussian distribution.

Figure 3 shows the measured ASF-propagation delays at test points P1 and P4. By comparing the delays for all test points, it is evident that changes in the air-refractive index along the propagation path, which is influenced by factors such as temperature and humidity, ultimately affects parameters such as the ground equivalent dielectric constant, causing variations in the secondary delay of the long-wave signals measured by the receiver. These results demonstrate that the propagation path delay changes gradually across different locations, and similar propagation paths exhibit comparable delay trends. This observation suggests that a temporal and spatial correlation between the influencing factors affects the propagation path.

Fig. 3
figure 3

Propagation-delay test results at points (a) P1 and (b) P4.

Full size image

Results

Correlation represents a non-deterministic relationship, and the correlation coefficient serves as a measure of the degree of linear correlation between variables. Commonly used correlation coefficients include Pearson’s and Spearman’s. Although Pearson’s coefficient assesses the strength of linear relationships, Spearman’s coefficient is suitable for capturing non-linear relationships13.

In this study, the Spearman’s correlation coefficient was employed to analyse the correlation of the propagation delay. The Spearman’s correlation coefficient for two n-dimensional vectors x and y is expressed as

$$\rho_{S} = \frac{{\sum\limits_{i = 1}^{N} {\left( {R_{i} - \overline{R}} \right)\left( {S_{i} - \overline{S}} \right)} }}{{\sqrt {\sum\limits_{i = 1}^{N} {\left( {R_{i} - \overline{R}} \right)^{2} } } \sqrt {\sum\limits_{i = 1}^{N} {\left( {S_{i} - \overline{S}} \right)^{2} } } }} = 1 - \frac{{6\sum\limits_{i = 1}^{N} {d_{i}^{2} } }}{{N\left( {N^{2} - 1} \right)}}$$
(3)

where Ri and Si denote the ranks of observation i after sorting vectors x and y; \(\overline{R}\) \(\overline{S}\)and denote the average ranks of vectors x and y, N denotes the total number of observations i, and di = Ri-Si denotes the rank difference between two variables14.

The Spearman’s correlation coefficient (ρ) is a real number ranging from -1 to 1. When ρ > 0, the two variables are positively correlated, whereas when ρ < 0, they are negatively correlated. Larger values of ρ indicate stronger correlations between the variables. We categorized correlation strength based on Spearman’s correlation coefficient values. Specifically, ρ > 0.75 indicated strong correlation, values between 0.5 and 0.75 were classified as average correlation outcomes, and ρ ≤ 0.5 were deemed as weak outcomes. These thresholds were informed by standard statistical correlation benchmarks and helped guide our selection of effective reference points for differential correction.

Five points within the test area were selected to calculate the Spearman’s correlation coefficient and ρ-values and verified through a two-tailed significance test. Figure 4 illustrates the changing ASF correlations between the test sites in 2023.

Fig. 4
figure 4

Spearman’s correlation analysis results for (a) additional secondary factor 1 (ASF1) and (b) ASF2 in 2023.

Full size image

The colour depth and sizes of the graphs represent the magnitude of the correlation coefficient, with values displayed in the upper-right corner rounded to two significant figures. The mean signal-to-noise ratios (SNRs) for each station at the test points are listed in Table 1.

Figure 5 illustrates the distances from each test point to the stations, and the detailed distances are listed in Table 2. Notably, the test points towards the Xuancheng and Raoping stations predominantly follow land paths, whereas one-third of the test points towards the Rongcheng station traverse seawater paths (with two-thirds on land paths).

Fig. 5
figure 5

Schematic of the test points and existing stations. ( Data source: National Earth System Science Data Center, National Science & Technology Infrastructure of China (http://www.geodata.cn). Mapping performed with ArcGIS 10.8.)

Full size image
Table 1 Signal-to-noise ratios at the test points (dB).
Full size table

The correlation of ASF2 was higher than that of ASF1 for each test point along the linear path selected for the study. This discrepancy can be attributed to the differences in the propagation paths and varying distances from the stations to the test points. Specifically, for ASF1, the correlation between test point P1 and the others decreased as the distances to Xuancheng and Raoping decreased. Conversely, for ASF2, the correlation between test point P5 and the others increased as the distances to Xuancheng and Rongcheng decreased. Figure 4 illustrates that P1 and P3 exhibit weak correlations, as confirmed by the analysis of their SNRs. The results in Table 1 further indicate that external noise significantly impacted the signals originating from the Raoping and Rongcheng stations to the test point during testing, introducing interference in the eLoran signal. A correlation analysis of ASF1 and ASF2 revealed significant positive correlations at the 0.001 level between test points P2 and P4 as well as between test points P1 and P4. This indicates a strong correlation among neighbouring test points along the selected linear path, suggesting consistent ASF propagation-delay trends across space.

Table 2 Distances of test points from existing stations (km).
Full size table

To verify whether this correlation represents a fixed relationship, a secondary verification was conducted using the test results obtained in November 2022 from the same location, as depicted in Fig. 6. Although the test locations and antenna positions remained unchanged, the climatic conditions differed significantly. Specifically, the average air temperature in 2022 was 25.6 °C with a relative humidity of 49.3% at a height of 2 m above ground, whereas during the October 2023 test, the average air temperature was 14.6 °C with a relative humidity of 80.4% at the same height.

Fig. 6
figure 6

Spearman’s correlation analysis results for (a) ASF1 and (b) ASF2 in 2022.

Full size image

The correlation analysis using the Spearman method indicated that the correlation between the two tests were consistent with the overall trend, despite the minor differences observed at certain points. Specifically, for ASF1, the correlation between P1 and each test point decreased as the distance to Xuancheng Terrace decreased, whereas that between P5 and each test point increased as the distance to Xuancheng Terrace increased. Additionally, the strong correlation observed between P2 and P4 in 2023 persisted in 2022 suggesting that the ASF correlation was reproducible across the tests.

This consistency is attributed to the complex nature of signal propagation, where multiple paths influence the ground-wave signal as it travels from each station to the test point. The terrain undulation and atmospheric refraction index factors contribute to unpredictable propagation characteristics, potentially reducing system accuracy. In summary, correlation analyses of long-wave propagation delays in the eLoran system can help solidify the differential effects in critical areas, support the establishment of more accurate differential stations, provide early warnings for an enhanced eLoran system, and enhance the overall system integrity.

Discussion

Analysis of accurate long-wave ASF-propagation-delay measurements revealed that the ASF-propagation delay is not constant and fluctuates over time and space. However, within a certain range, meteorological conditions, Earth’s electrical conductivity, terrain undulation, and other factors exhibit similarities. Real-time changes in the propagation delay also demonstrated spatial and temporal correlations.

To enhance the positioning accuracy of the eLoran system, the real-time differential method was employed to mitigate fluctuations and noise effects on the propagation path. Therefore, we applied the differential method to correct the propagation delay of the eLoran system at different correlation test points to assess its impact on positioning performance.

The correlation results for ASF1 and ASF2 were synthesised using three pairs of test points categorised by correlation strength: better correlation (P2–P4), average correlation (P5–P4), and poor correlation (P3–P4) for differential correction. The 95% confidence intervals and scatter plots of positioning precisions are illustrated in Fig. 7.

Fig. 7
figure 7

P2, P5, and P3 test point correction value correction P4 test point comparison results: (a) P2–P4, (b) P5–P4, and (c) P3–P4.

Full size image

As shown in Fig. 7, the original positioning accuracy of the P4 test point was 400.36 m. Using the corrected values from the P2, P5, and P3 test points for differential correction, the positioning accuracy of P4 improved significantly. Specifically, employing direct differential correction based on the best correlation between P2 and P4 enhanced the positioning accuracy from 400.36 to 191.52 m. For P5 and P4 (with average correlation), direct differencing improved the accuracy from 400.36 to 257.98 m. However, for P3 and P4 (with poor correlation), the positioning accuracy did not improve and instead increased to 668.91 m. These findings underscore the non-constant nature of long-wave signal-propagation delays. Fluctuations in the test-point-propagation delays, used as differential correction factors, can be initially selected based on the ASF correlation strength. A higher correlation yields greater positioning accuracy improvement, whereas a poor correlation may worsen the positioning accuracy owing to insufficient corrections.

Conclusions

By accurately measuring the long-wave propagation delays in neighbouring areas and conducting correlation analyses of test points distributed along a linear path, a reference point can be selected, and its real-time propagation delay can be measured based on the change characteristics of the propagation delay. The fluctuations in the delay can be calculated as a differential correction factor that aids delay corrections in nearby areas. Correlation analysis serves as a preliminary guide for differential correction, effectively mitigating propagation-delay fluctuations over time and enhancing the positioning accuracy of the eLoran system. This approach theoretically reinforces the differential effects in critical areas, provides technical support for establishing more accurate differential stations, offers early warnings for eLoran system enhancement, and bolsters system integrity.