Introduction

The ship’s main propulsion motor is the electric motor that provides the primary propulsion power for the ship, either directly or through a gear transmission mechanism. In civilian electric propulsion ships, AC motors are more commonly used, while in some smaller tonnage ship electric propulsion systems, three-phase induction motors may be utilized. Larger inland passenger and cargo ships, as well as most sea vessels, typically use synchronous motors as the main propulsion motor. Permanent magnet synchronous motors are preferred in most electric propulsion ships due to their high power-density, low temperature rise, light weight, and large starting torque. The rapid development of permanent magnet materials in this century has significantly improved the performance, application fields, and technological innovation of permanent magnet synchronous motors, making them the motor of choice for electric propulsion ships1.

Controlling the torque and speed of a ship’s main propulsion motor is crucial. Inland vessels or those sailing in calm sea conditions need to focus on controlling the speed. On the other hand, in rough sea conditions with strong winds and waves, the main goal is to control the motor’s load (torque). Throughout the navigation process, ships must make a wide range of speed adjustments, from low or zero speed when approaching or leaving the dock, to full speed when sailing at sea, and even micro speed when passing through narrow waterways. Ship maneuvering commands mainly include heading commands (AHEAD and ASTERN) and speed commands (STOP, DEAD SLOW, first gear, second gear, and third gear). For ships with fixed pitch propellers, forward and reverse commands control the rotation of the main propulsion motor, namely clockwise and counterclockwise. In terms of the ship’s speed command, stopping and micro speed are typically considered the zero speed or low-speed zone of the main propulsion motor. The first, second, and third gears of the speed command correspond to the medium and high-speed zone of the main propulsion motor2. When a permanent magnet main propulsion motor operates in the medium and high-speed zone, its internal parameters like inductance and resistance fluctuate with changes in temperature, load, and other conditions. This can affect the waveform and phase of current and voltage, ultimately impacting the performance of the main propulsion motor and potentially influencing the safety of the ship’s navigation3. Moreover, issues with magnetic saturation and temperature rise during medium and high-speed operation can impact the performance of the main propulsion motor4. As a result, when the permanent magnet marine main propulsion motor operates at medium to high speeds, its control accuracy is limited and the complexity of the control algorithm increases. To address these challenges, it is essential to continuously optimize control algorithms, enhance sensor accuracy, and consider factors such as magnetic saturation and temperature rise. This requires the control system to monitor these parameter changes in real time and accurately, while also employing excellent control algorithms to ensure the system is robust and high-precision, allowing the propulsion motor to operate stably.

The main propulsion motors of medium to high-speed ships currently use advanced control strategies, including fuzzy control and deep learning5. There are limited control set model predictive current control (MPCC) methods, which represent an advanced control strategy that enables fast and accurate current control by directly selecting the optimal voltage vector. However, the traditional finite control set MPCC strategy is vulnerable to changes in parameters and external disturbances, which can lead to a decline in control performance6. In recent years, researchers have proposed an improved approach that integrates a sliding mode observer (SMO) to tackle this issue. Sliding mode observers are known for their strong robustness against variations in system parameters and external disturbances. By designing appropriate sliding surfaces and control laws, these observers can accurately estimate motor states, including position, speed, and current. Combining SMO with FCS-MPCC not only effectively mitigates the negative effects of parameter uncertainty but also enhances the steady-state accuracy and dynamic response speed of the system. This enhancement optimizes the control performance of the permanent magnet synchronous motor (PMSM) by real-time adjustments of the state variables in the current prediction model, making predictive control more precise. However, sliding mode control also has its drawbacks, such as difficulties in parameter selection, issues with jitter, and high hardware requirements.

The FCS-MPCC method offers several advantages; however, it also has relatively high computational complexity, particularly in applications involving multi-level inverters or high switching frequencies7. To address the computational burden while still achieving good control performance, researchers have introduced a simplified two-step model predictive control strategy. This approach significantly enhances computational efficiency, maintains high prediction accuracy, reduces the difficulty and cost of developing control systems, and facilitates broader industrial application. However, one drawback is that improper simplification of the model may lead to significant discrepancies between predicted results and the actual state, which can negatively impact control performance. In practical applications, it is essential to regularly calibrate system parameters or implement adaptive control strategies to address parameter variations. Additionally, limited computing resources may affect the real-time capabilities and accuracy of these control strategies.

These state-of-the-art strategies have yielded remarkable improvements in the maneuverability of the main propulsion motors. However, it’s essential to note that the main propulsion motor not only operates within the medium to high speed range, but also undergoes critical transition processes from low speed to medium to high speed, and vice versa. Hence, it’s crucial to thoroughly consider these transition issues when studying control strategies8. This comprehensive study delves into the main propulsion motor’s performance in the medium to high speed range, while also prioritizing the seamless execution of the two aforementioned transition processes.

Mathematical model

Modeling assumptions

In order to simplify mathematical equations and enable analysis, we make the following assumptions during the modeling process9.

  1. (1)

    The stator winding of the main propulsion motor is connected in a Y-shaped manner and symmetrically distributed, with a spatial separation of 120 degrees between them.

  2. (2)

    The permanent magnet on the rotor has zero conductivity, and both the main magnetic field and the armature magnetic field exhibit a sinusoidal distribution in the air gap. The damping effect of the permanent magnet is ignored.

  3. (3)

    We have disregarded Eddy current loss and hysteresis loss.

  4. (4)

    During stable motor operation, the back electromotive force follows a sinusoidal distribution, and armature reaction during commutation is disregarded.

State equation

  1. (1)

    The physical structure and coordination relationship The physical structure of the permanent magnet synchronous motor, as studied in this article, is shown in Fig. 1. In the figure, “NS” represents the magnetic pole of the rotor permanent magnet, and the corresponding excitation magnetic flux is denoted by the letter “\(\psi _{f}\).”. The “d-axis” of the “d-q” coordinate system aligns with the direction of the NS magnetic field lines and coincides with its axis. The angle between the “d-axis” of the “d-q” coordinate system and the “A-axis” of the stationary three-phase coordinate system is represented by the letter “\(\theta _{r}\) ”, and the mechanical speed of the rotor is represented by the letter “\(\omega _{r}\) ”. The “\({\alpha }\)-axis” in the “\({\alpha }\)-\({\beta }\)” coordinate system aligns with the “A-axis”.

Fig. 1
figure 1

Physical structure and coordinate relationship diagram.

Full size image

We construct the mathematical model outlined in this article based on the conventions of electric motors. This includes specifying that the positive direction of the current corresponds to the direction in which the current flows into the motor, and the positive direction of the voltage aligns with the positive direction of the current. Additionally, note that the direction of the back electromotive force is opposite to that of the current10.

  1. (2)

    Full-order state equation

  2. 1)

    Mathematical model in d-q coordinate system The mathematical model of the permanent magnet synchronous main propulsion motor in the d-q coordinate system can be obtained from Fig. 1.

    $$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{u_{1d}}}\\ {{u_{1q}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{R_1} + p{L_{1d}}}& { - \omega _e{L_{1q}}}\\ {\omega _e{L_{1d}}}& {{R_1} + p{L_{1q}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{i_{1d}}}\\ {{i_{1q}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0\\ {\omega _e{\psi _f}} \end{array}} \right] \end{aligned}$$
    (1)

    In Eq. (1), the letters \(\textit{u}_{1\textit{d}}\) and \(\textit{u}_{1\textit{q}}\) represent the components of the stator voltage on the d-q axis. The letter \(\textit{R}_{1}\) represents the resistance of the stator winding. The letter p represents the differential operator, d/dt. The letters \(\textit{L}_{1d}\) and \(\textit{L}_{1q}\) represent the components of stator inductance on the d-q axis. The letters \(\textit{i}_{1d }\)and \(\textit{i}_{1q}\) represent the components of stator current on the d-q axis. The letter \(\omega _{e}\) represents the rotor electrical angular velocity, and its relationship with the rotor mechanical speed \(\omega _{2}\) is described by \(\omega _{2}\)=\(\omega _{e}\)/p\(_{N}\), where the letter p\(_{N}\) represents the number of magnetic pole pairs.

  3. 2)

    Deduction of State Equation The mathematical model of the permanent magnet main propulsion motor in the \(\alpha\)-\(\beta\) coordinate system can be obtained from Eq. (1) as follows.

    $$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{u_{1\alpha }}}\\ {{u_{1\beta }}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{R_1} + p{L_{1d}}}& {{\omega _2}({L_{1d}} - {L_{1q}})}\\ { - {\omega _2}({L_{1d}} - {L_{1q}})}& {{R_1} + p{L_{1d}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{i_{1\alpha }}}\\ {{i_{1\beta }}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{e_{1\alpha }}}\\ {{e_{1\beta }}} \end{array}} \right] \end{aligned}$$
    (2)

In Eq. (2), the symbols \(\textit{u}_{1{\alpha }}\) and \(\textit{u}_{1{\beta }}\) represent the components of the stator voltage on the \({\alpha }\)-\({\beta }\) axis. The symbols \(\textit{ i}_{1{\alpha }}\) and \(\textit{i}_{1{\beta }}\) represent the components of the stator current on the \({\alpha }\)-\({\beta }\) axis. The symbols \(\textit{e}_{1{\alpha }}\) and \(\textit{e}_{1{\beta }}\) represent the components of the back electromotive force (EMF) on the stator along the \({\alpha }\)-\({\beta }\) axis.

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{e_{1\alpha }}}\\ {{e_{1\beta }}} \end{array}} \right] = [({L_{1d}} - {L_{1q}})({\omega _2}{i_{1d}} - p{i_{1q}}) + {\omega _2}{\psi _f}]\left[ {\begin{array}{*{20}{c}} { - \sin {\theta _r}}\\ {\cos {\theta _r}} \end{array}} \right] \end{aligned}$$
(3)

From Eq. (3), it is evident that the back electromotive forces \(\textit{e}_{1{\alpha }}\) and \(\textit{e}_{1{\beta }}\) contain a parameter \(\theta _{r}\) representing the position of the motor rotor.

The state equation for the current on the stator of the permanent magnet main propulsion motor can be derived from Eq. (2).

$$\begin{aligned} {L_{1d}}\left[ {\begin{array}{*{20}{c}} {p{i_{1\alpha }}}\\ {p{i_{1\beta }}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - {R_1}}& { - {\omega _2}({L_{1d}} - {L_{1q}})}\\ { - {\omega _2}({L_{1d}} - {L_{1q}})}& { - {R_1}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{i_{1\alpha }}}\\ {{i_{1\beta }}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{u_{1\alpha }} - {e_{1\alpha }}}\\ {{u_{1\beta }} - {e_{1\beta }}} \end{array}} \right] \end{aligned}$$
(4)

The main propulsion motor of the permanent magnet ship has a much greater mechanical inertia than electromagnetic inertia11. This means that within one PWM control cycle, we can assume that the mechanical speed (represented by the letter \(\omega _{2}\)) of the rotor is constant, which means.\(\frac{{d{\omega _2}}}{{dt}} = 0\) Therefore, we can use the following equation.

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {p{e_{1\alpha }}}\\ {p{e_{1\beta }}} \end{array}} \right] = {\omega _2}\left[ {\begin{array}{*{20}{c}} { - {e_{1\beta }}}\\ {{e_{1\alpha }}} \end{array}} \right] \end{aligned}$$
(5)

The full-order state equation of the permanent magnet ship’s main propulsion motor can be derived from Eqs. (4) and (5) as follows.

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {p{i_1}}\\ {p{e_1}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{M_{11}}}& {{M_{12}}}\\ 0& {{M_{22}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{i_1}}\\ {{e_1}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} { - {M_{12}}}\\ 0 \end{array}} \right] {u_1} \end{aligned}$$
(6)

In Eq. (6) \({i_1} = {[\begin{array}{*{20}{c}} {{i_{1\alpha }}}&{{i_{1\beta }}} \end{array}]^T}\),\({e_1} = {[\begin{array}{*{20}{c}} {{e_{1\alpha }}}&{{e_{1\beta }}} \end{array}]^T}\),\({u_1} = {[\begin{array}{*{20}{c}} {{u_{1\alpha }}}&{{u_{1\beta }}} \end{array}]^T}\), \({M_{11}} = [ - {R_1} \cdot {E_1} + {\omega _2}\) \(({L_{1d}} -{L_{1q}}) \cdot {E_2}]/{L_{1d}}\),\({M_{12}} = - {E_1}/{L_{1d}}\),\({M_{22}} ={\omega _2} \cdot {E_2}\),\({E_1} = \left[ {\begin{array}{*{20}{c}} 1& 0\\ 0& 1 \end{array}} \right]\).\({E_2} = \left[ {\begin{array}{*{20}{c}} 0& { - 1}\\ 1& 0 \end{array}} \right]\)

Control strategy

Algorithm description

The full-order sliding mode observer for the permanent magnet main propulsion motor, constructed from Eq. (6), is as follows.

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {p{{{\hat{i}}}_1}}\\ {p{{{\hat{e}}}_1}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{M_{11}}}& {{M_{12}}}\\ 0& {{M_{22}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{{{\hat{i}}}_1}}\\ {{{{\hat{e}}}_1}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} { - {M_{12}}}\\ 0 \end{array}} \right] {u_1} - \frac{1}{{{L_{1d}}}}D{\textrm{sgn}} (s) \end{aligned}$$
(7)

In Eq. (7), the symbol \(\wedge\) represents the observed value, and ,\({{\hat{i}}_1} = {[\begin{array}{*{20}{c}} {{{{\hat{i}}}_{1\alpha }}}&{{{{\hat{i}}}_{1\beta }}} \end{array}]^T}\),\({{\hat{e}}_1} = {[\begin{array}{*{20}{c}} {{{{\hat{e}}}_{1\alpha }}}&{{{{\hat{e}}}_{1\beta }}} \end{array}]^T}\).\(s = {\hat{i}} - i\) The symbol D represents the feedback gain matrix, and (\(D = {\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} a& 0& b& 0 \end{array}}\\ {\begin{array}{*{20}{c}} 0& a& 0& b \end{array}} \end{array}} \right] ^T}\)a and b are the sliding mode gains of the observer). Sgn() represents the sign function12, which is described as follows.

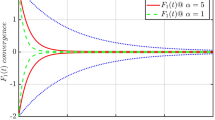
$$\begin{aligned} {\textrm{sgn}}(x) = \left\{ {\begin{array}{*{20}{c}} {1,x > 0}\\ {0,x = 0}\\ { - 1,x < 0} \end{array}} \right. \end{aligned}$$
(8)

In order to reduce the chattering problem caused by the discontinuity of the sgn() sign function, further improvements of the control strategy are necessary. This article utilizes the \(\gamma\)() function with a variable boundary layer.

$$\begin{aligned} \gamma (s) = \left\{ {\begin{array}{*{20}{c}} {{\textrm{sgn}} (s)(|s| \ge \Delta )}\\ {1 - \frac{2}{{1 + {e^{2\tau s}}}}(|s| < \Delta )} \end{array}} \right. \end{aligned}$$
(9)

In Eq. (9), \(\tau\)=\(\pi\)/\(\mu\), where \(\mu\) represents the thickness of the boundary layer. The boundary layer \(\gamma\)() function accelerates convergence speed and reduces chattering. Additionally, a new integral sliding mode function is designed in this paper to improve the stability and speed of the system13.

$$\begin{aligned} s = \left[ {\begin{array}{*{20}{c}} {{s_{1\alpha }}}\\ {{s_{1\beta }}} \end{array}} \right] \buildrel \Delta \over = \left[ {\begin{array}{*{20}{c}} {{{{\tilde{i}}}_{1\alpha }} + m{{{\textrm{sgn}} }^n}({{{\tilde{i}}}_{1\alpha }})}\\ {{{{\tilde{i}}}_{1\beta }} + m{{{\textrm{sgn}} }^n}({{{\tilde{i}}}_{1\beta }})} \end{array}} \right] \end{aligned}$$
(10)

In Eq. (10), the letters m and n represent constants, and n\(\in\)(0,R\(_{1}\)/L\(_{1}\)) \({\tilde{i}_{1\alpha }} = {{\hat{i}}_{1\alpha }} - {i_{1\alpha }}\).\({{\tilde{i}}_{1\beta }} = {{\hat{i}}_{1\beta }} - {i_{1\beta }}\)

By using Eq. (9) to improve Eq. (7), we can obtain the following equation.

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {p{{{\hat{i}}}_1}}\\ {p{{{\hat{e}}}_1}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{M_{11}}}& {{M_{12}}}\\ 0& {{{{\hat{M}}}_{22}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{{{\hat{i}}}_1}}\\ {{{{\hat{e}}}_1}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} { - {M_{12}}}\\ 0 \end{array}} \right] {u_1} - \frac{1}{{{L_{1d}}}}D\gamma (s) \end{aligned}$$
(11)

The expressions for the current error and back electromotive force error, obtained by subtracting Eq. (6) from Eq. (11), are as follows.

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {p{{{\tilde{i}}}_1}}\\ {p{{{\tilde{e}}}_1}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{M_{11}}}& {{M_{12}}}\\ 0& {{M_{22}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{{{\tilde{i}}}_1}}\\ {{{{\tilde{e}}}_1}} \end{array}} \right] + {{\tilde{M}}_{22}}\left[ {\begin{array}{*{20}{c}} 0\\ {{{{\hat{e}}}_1}} \end{array}} \right] - \frac{1}{{{L_{1d}}}}D\left[ {\begin{array}{*{20}{c}} {{\gamma _{1\alpha }}}\\ {{\gamma _{1\beta }}} \end{array}} \right] \end{aligned}$$
(12)

In Eq. (12), \({{\tilde{i}}_1} = {\left[ {\begin{array}{*{20}{c}} {{{{\tilde{i}}}_{1\alpha }}}&{{{{\tilde{i}}}_{1\beta }}} \end{array}} \right] ^T}\),\({{\tilde{e}}_1} = {\left[ {\begin{array}{*{20}{c}} {{{{\tilde{e}}}_{1\alpha }}}&{{{{\tilde{e}}}_{1\beta }}} \end{array}} \right] ^T}\),\({{\tilde{M}}_{22}} = {{\tilde{\omega }} _e}{E_2}\)The letter \({{\tilde{\omega }} _e}\)represents electrical angular velocity error.

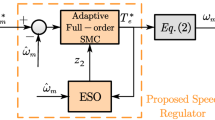
The corresponding structural diagram can be created from Eq. (11) as depicted in Fig. 2.

Fig. 2
figure 2

Block diagram of full order sliding mode control.

Full size image

Proof of stability

Define the current sliding surface and back electromotive force sliding surface as s\(_{1\textit{i}}\) and s\(_{1\textit{e}}\), respectively.

$$\begin{aligned} \left\{ {\begin{array}{*{20}{c}} {{s_{1i}} = \left[ {\begin{array}{*{20}{c}} {{s_{i\alpha }}}\\ {{s_{i\beta }}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{{\tilde{i}}}_{1\alpha }}}\\ {{{{\tilde{i}}}_{1\beta }}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{{\hat{i}}}_{1\alpha }} - {i_{1\alpha }}}\\ {{{{\hat{i}}}_{1\beta }} - {i_{1\beta }}} \end{array}} \right] }\\ {{s_{1e}} = \left[ {\begin{array}{*{20}{c}} {{s_{e\alpha }}}\\ {{s_{e\beta }}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{{\tilde{e}}}_{1\alpha }}}\\ {{{{\tilde{e}}}_{1\beta }}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{{\tilde{e}}}_{1\alpha }} - {e_{1\alpha }}}\\ {{{{\tilde{e}}}_{1\beta }} - {e_{1\beta }}} \end{array}} \right] } \end{array}} \right. \end{aligned}$$
(13)

To demonstrate stability, we construct a Lyapunov function \(V_{i}\) for current and a Lyapunov function \(V_{e}\) for back electromotive force14,15.

$$\begin{aligned} \left\{ {\begin{array}{*{20}{c}} {{V_i} = \frac{1}{2}(s_{i\alpha }^2 + s_{i\beta }^2)}\\ {{V_e} = \frac{1}{2}(s_{e\alpha }^2 + s_{e\beta }^2)} \end{array}} \right. \end{aligned}$$
(14)

In order to ensure system stability, it is necessary for both \({\dot{V}_i} < 0\)and \({\dot{V}_e} < 0\)to be met. First, we need to analyze the current Lyapunov function \(V_{i}\). We’ll take the derivative of \(V_{i}\) in Eq. (14) and substitute Eqs. (12) and (13) into the derived expression to obtain the following equation.

$$\begin{aligned} {\dot{V}_i}= & {\dot{s}_{i\alpha }}{s_{i\alpha }} + {\dot{s}_{i\beta }}{s_{i\beta }} = {{\dot{\tilde{i}}}_{1\alpha }}{\tilde{i}_{1\alpha }} + {{\dot{\tilde{i}}}_{1\beta }}{{\tilde{i}}_{1\beta }}\nonumber \\= & - \frac{{{R_1}}}{{{L_{1d}}}}(\tilde{i}_{1\alpha }^2 + \tilde{i}_{1\beta }^2) + \frac{1}{{{L_{1d}}}}{{\tilde{i}}_{1\alpha }}({e_{1\alpha }} - {\gamma _{1\alpha }} - {{\hat{e}}_{1\alpha }}) + \frac{1}{{{L_{1d}}}}{{\tilde{i}}_{1\beta }}({e_{1\beta }} - {\gamma _{1\beta }} - {{\hat{e}}_{1\beta }})\nonumber \\= & - \frac{{{R_1}}}{{{L_{1d}}}}\tilde{i}_{1\alpha }^2 + \frac{{{e_{1\alpha }} - {{\hat{e}}_{1\alpha }}}}{{{L_{1d}}}}{{\tilde{i}}_{1\alpha }} - \frac{1}{{{L_{1d}}}}|{{\tilde{i}}_{1\alpha }}| - \frac{{{R_1}}}{{{L_{1d}}}}\tilde{i}_{1\beta }^2 + \frac{{{e_{1\beta }} - {\hat{e}_{1\beta }}}}{{{L_{1d}}}}{{\tilde{i}}_{1\beta }} - \frac{1}{{{L_{1d}}}}|{{\tilde{i}}_{1\beta }}| \end{aligned}$$
(15)

According to Eq. (15), in order to ensure ,\({\dot{V}_i} < 0\) the sliding mode gain represented by the letter “a” is required to satisfy the following equation

$$\begin{aligned} a > \max \{ |{e_\alpha }|,|{e_\beta }|\} \end{aligned}$$
(16)

According to Eq. (15), while and ,\({{\tilde{i}}_{1\beta }} = 0\) The current observer has reached a stable state.

Similarly, the stability analysis of \(V_{e}\) is as follows.

$$\begin{aligned} \begin{array}{l} {{\dot{V}}_e} = {{\dot{s}}_{e\alpha }}{s_{e\alpha }} + {{\dot{s}}_{e\beta }}{s_{e\beta }} = {{\dot{\tilde{e}}}_{1\alpha }}{{{\tilde{e}}}_{1\alpha }} + {{\dot{\tilde{e}}}_{1\beta }}{{{\tilde{e}}}_{1\beta }}\\ = - b({\tilde{e}}_{1\alpha }^2 + {\tilde{e}}_{1\beta }^2) - {{{\tilde{\omega }} }_e}{{{\hat{e}}}_{1\beta }}{{{\tilde{e}}}_{1\alpha }} + {{{\tilde{\omega }} }_e}{{{\hat{e}}}_{1\alpha }}{{{\tilde{e}}}_{1\beta }} \end{array} \end{aligned}$$
(17)

In order to meet ,\({\dot{V}_e} < 0\) the sliding mode gain represented by the letter b is needed to satisfy the following equation.

$$\begin{aligned} b > \max \left\{ {\frac{{ - {{{\tilde{\omega }} }_e}{{{\hat{e}}}_{1\beta }}{{\tilde{e}}_{1\alpha }} + {{{\tilde{\omega }} }_e}{{{\hat{e}}}_{1\alpha }}{{{\tilde{e}}}_{1\beta }}}}{{{\tilde{e}}_{1\alpha }^2 + {\tilde{e}}_{1\beta }^2}}} \right\} \end{aligned}$$
(18)

When the gain values a and b satisfy Eqs. (16) and (18), the system enters the sliding surface from the starting state in a short time and reaches a stable state.

Design of phase Locked Loop

In Fig. 2, a phase-locked loop is introduced to prevent changes in the system bandwidth caused by fluctuations in the back electromotive force. This helps ensure more accurate information about the rotor speed and position16,17. To further improve the accuracy of the obtained information, a signal suppression unit is designed in this paper to suppress step disturbances during the process of acquiring rotor position information. The phase-locked loop consists of a Loop Filter, a Phase Calculator, and a Voltage Controlled Oscillator, as shown in Fig. 3.

Fig. 3
figure 3

Structure diagram of phase-locked loop.

Full size image

Simulation verification

In order to verify the feasibility of the control strategy designed in the previous section, the simulation software named Matlab/Simulink was used to build a simulation model of the corresponding control system in this paper. During the simulation process, the control object selected is a built-in synchronous motor, and its parameters are shown in Tab. 1.

Table 1 Simulation parameters.
Full size table

The operating conditions involve constant speed and variable load

When simulating this state with a constant speed of 750 rpm and an initial load torque of 0, a sudden load torque of 2 N.m is applied at 0.3 s, and the corresponding waveforms of parameter changes are shown below.

  1. (1)

    Speed waveform In the speed waveform of Fig. 4, there are two curves: PI+SMO and FSMO. The PI+SMO curve reflects the speed waveform of PI control combined with traditional sliding mode control, while the FSMO curve reflects the speed waveform under the improved full order sliding mode control studied in this paper. By comparing the two curves, it is evident that the improved full order sliding mode control (FSMO) is significantly better than the traditional sliding mode control with PI control. Particularly, during the starting process of the main propulsion motor, the FSMO control demonstrates better speed and a more sensitive response.

Fig. 4
figure 4

Speed waveform under constant speed and variable load.

Full size image

During the transition process of sudden load torque at 0.3 seconds, both control strategies exhibit nearly equal maximum dynamic deviation and overshoot. They can ultimately stabilize at the target speed of 750 revolutions per minute. However, the improved full-order sliding mode (FSMO) control demonstrates more sensitivity than the traditional sliding mode control based on proportional-integral (PI) after a sudden change in load torque.

  1. (2)

    Rotor position The rotor’s actual and observed positions under this operating condition are depicted in Fig. 5. The figure shows only a slight deviation between the observed and actual positions at the initial start-up moment. However, as the process progresses through starting, stabilizing, and changing load torque, the observed position of the rotor almost aligns with the actual position. The improved full-order sliding mode control proposed in this paper accurately observes the rotor’s position under this operating condition, demonstrating the usefulness and effectiveness of the control strategy designed in this paper.

Fig. 5
figure 5

Actual and observed positions of the rotor under constant speed and variable load.

Full size image
  1. (3)

    Current and torque The rotor current waveform and torque waveform under this operating condition are shown in Fig. 6 and Fig. 7, respectively. During the no-load starting process of the main propulsion motor, both the starting current and starting torque are relatively large. It takes about 0.03 seconds for the stator current and torque to reach a stable state. From the figures, it is evident that the time required for both physical quantities to reach stability from the starting point is almost the same.

Fig. 6
figure 6

Stator current waveform under constant speed variable load.

Full size image
Fig. 7
figure 7

Torque under constant speed and variable load.

Full size image

At 0.3 seconds into the simulation, the load on the main propulsion motor increases, causing a rise in stator current. This is consistent with the principle of converting electrical energy into mechanical energy in the motor. In other words, the increase in output power of the main propulsion motor is a result of the motor drawing more power from the grid.

  1. (4)

    Back electromotive force The back electromotive force (EMF) waveform under this operating condition is depicted in Fig. 8. Figure (a) shows the EMF waveform of the entire simulation process, while Figure (b) provides an enlarged view of the change in EMF when the load torque suddenly increases. When the main propulsion motor starts, the speed is low and has not yet reached stability, resulting in a relatively low back electromotive force. The time for the EMF to reach stability is consistent with the time required for the rotational speed to reach stability (Figure 4) and for the current to reach stability (Figure 6). Once the rotational speed stabilizes, the back electromotive force also stabilizes.

Fig. 8
figure 8

EMF under constant speed and variable load.

Full size image

In the moment at 0.3 seconds, when the load is suddenly applied, the back electromotive force in Fig. 8 (a) slightly decreases, consistent with the decrease in rotational speed shown in Fig. 4. Additionally, the transition time for the back electromotive force to reach a stable state after the decrease of rotational speed is about 0.06 seconds, as shown in Fig. 4. Examining Fig. 8 (b), it’s evident that during the sudden increase in load torque, the rotational speed decreases as in Fig. 4, and the back electromotive force also decreases. The back electromotive force remains consistent before and after the change in load torque, as the speed remains the same after the sudden increase in load torque stabilizes and before the increase in load torque. Looking at the waveform curve of the back electromotive force in Fig. 8, it is smooth with small harmonic components, indicating that the control strategy designed in this paper effectively suppresses chattering under constant speed and variable load conditions.

The operating conditions involve a constant load and variable speed

When simulating this state, with a given load torque of 2 N.m unchanged and an initial speed of 750 rpm, the speed increases to 1000 rpm at 0.3 seconds. The corresponding waveforms of parameter changes are shown below.

  1. (1)

    Speed waveform In the speed waveform curve shown in Fig. 9, there are two curves representing different control strategies. One curve, labeled as PI+SMO, reflects the speed waveform of PI control combined with traditional sliding mode control. The other curve, labeled as FSMO, reflects the speed waveform under the improved full order sliding mode control studied in this paper. The study finds that the improved full order sliding mode control (FSMO) is significantly superior to the traditional sliding mode control strategy based on PI control. Although both control strategies exhibit a maximum dynamic deviation of about 1055r/min and similar overshoot during the entire acceleration process, the FSMO strategy makes the system faster and more responsive in achieving the desired speed of 1000r/min.

Fig. 9
figure 9

Speed waveform under constant load and variable speed.

Full size image
  1. (2)

    Rotor position The actual and observed positions of the rotor under this operating condition are depicted in Fig. 10. It is evident from Fig. 10 that there is only a slight deviation between the observed position and the actual position at the initial start-up moment. The curve shows that during the acceleration process of the main propulsion motor, the observed position remains largely consistent with the actual position. The data from Fig. 10 indicates that the improved full-order sliding mode control proposed in this paper is beneficial and effective in handling sudden speed changes.

Figure 10
figure 10

Rotor Position under constant load and variable speed

Full size image
  1. (3)

    Current and torque The rotor current waveform and torque waveform under this operating condition are shown in Fig. 11 and Fig. 12, respectively. At 0.3 seconds, the main propulsion motor accelerates, causing an increase in stator current. After about 0.03 seconds, the stator current reaches a stable state, slightly increasing compared to before acceleration. The output torque of the main propulsion motor also increases at 0.3 seconds. After the torque increases, it stabilizes after about 0.03 seconds. The transition time of torque fluctuation in Fig. 12 is equivalent to the transition time of current fluctuation in Fig. 11. When the main propulsion motor accelerates, the stator current increases, which conforms to the principle of energy conversion in rotational motion. When the torque remains constant, the speed increases, and the input power increases. This means that the motor receives an increase in current from the power grid.

Fig. 11
figure 11

Current waveform under constant load and variable speed.

Full size image
Fig. 12
figure 12

Torque waveform under constant load and variable speed.

Full size image

The simulation is based on the premise that the load torque on the propeller remains constant. To increase the speed of the propeller, we need to enhance the output power of the motor. This increase in motor output power is achieved by boosting the input power from the grid, which, in turn, leads to an increase in the stator current of the motor. As the speed of the propeller increases, as illustrated in Fig. 11, the stator current also rises. This increase in current results in a corresponding rise in the output torque on the motor shaft, allowing the output torque (\(T_{e}\)) to exceed the load torque (\(T_{L}\)). Consequently, this surplus torque increases the speed of the propeller, as shown in Fig. 9. In Fig. 11, the current amplitude grows from 3.2 A to 10 A, while the associated output torque (Te) on the motor shaft rises from 3.2 N\(\cdot\)m to 10 N\(\cdot\)m. The relationship between stator current and motor output torque is approximately linear, as indicated by Eq. (19).

  1. (4)

    B

    $$\begin{aligned} {T_e} = \frac{3}{2}{p_N}{\psi _f}{i_{1q}} \end{aligned}$$
    (19)

    ack electromotive force.

In Fig. 13(a) at 0.3s, after the main propulsion motor accelerates, the back electromotive force increases. Before the acceleration, the amplitude of the back electromotive force is about 56V. After increasing the speed of the main propulsion motor, the back electromotive force changes and reaches a stable state after about 0.06 seconds, with an amplitude of about 75V at the stable state.

Fig. 13
figure 13

EMF under constant load and variable speed.

Full size image

In Eq. (3), for the surface-mounted permanent magnet synchronous motor, the inductance values are equal L1q=L1d. The back electromotive force (EMF) is related to the angular velocity \(\omega _{e}\) or the rotor speed \(\omega _{2}\), as well as the rotor position \(\theta\), as illustrated in Eq. (20).

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{e_{1\alpha }}}\\ {{e_{1\beta }}} \end{array}} \right] = {\omega _2}{\psi _f}\left[ {\begin{array}{*{20}{c}} { - \sin {\theta _r}}\\ {\cos {\theta _r}} \end{array}} \right] \end{aligned}$$
(20)

When the load remains constant and the propeller speed increases, the corresponding \(\omega\)\(_{2}\) on the motor shaft increases, and its back electromotive force increases from 56V to 75V. As shown in Fig. 9, when the rotational speed increases from 750rpm to 1000rpm, the increase in back electromotive force is approximately equal to the increase in rotational speed, which satisfies Eq. (21).

As sho

$$\begin{aligned} \frac{{75}}{{56}} \approx \frac{{1000}}{{750}} \end{aligned}$$
(21)

wn in Fig. 13, the waveform curve of the back electromotive force during the entire change process is smooth, and the harmonic components are small. This indicates that the improved full-order sliding mode control strategy designed in this paper has a significant effect on suppressing chattering under sudden speed changes.

Conclusion

In order to address the issue of chattering in traditional sliding mode control, a variable boundary layer function is employed to suppress chattering. Additionally, a new integral sliding mode function is designed to enhance system stability and speed. A phase-locked loop with a signal suppressor is utilized to ensure precise system observation in this study. Verification was carried out using simulation software, and the results demonstrate that the control strategy proposed in this paper is highly rational and effective.