Deep reinforcement learning model for Multi-Ship collision avoidance decision making design implementation and performance analysis

Abstract

This paper proposes a novel multi-ship collision avoidance decision-making model based on deep reinforcement learning (DRL). The model addresses the critical challenge of preventing ship collisions while maintaining efficient navigation in complex maritime environments. Our innovation lies in the integration of a comprehensive state representation capturing key inter-ship relationships, a reward function that dynamically balances safety, efficiency, and COLREGs compliance, and an enhanced DQN architecture with dueling networks and double Q-learning specifically optimized for maritime scenarios. Experimental results demonstrate that our approach significantly outperforms state-of-the-art DRL methods, achieving a 30.8% reduction in collision rates compared to recent multi-agent DRL implementations, 20% improvement in safety distances, and enhanced regulatory compliance across diverse scenarios. The model shows superior scalability in high-density traffic, with only 12.6% performance degradation compared to 18.4–45.2% for baseline methods. These advancements provide a promising solution for autonomous ship navigation and maritime safety enhancement.

Introduction

With the rapid development of marine transportation, the number of ships on the sea has increased significantly, leading to a higher risk of ship collisions¹. Ship collision accidents not only cause huge economic losses but also pose a serious threat to the safety of human lives and the marine environment². Therefore, it is of great importance to study the decision-making models for multi-ship collision avoidance to ensure the safety of maritime navigation³.

In recent years, various methods have been proposed to address the problem of multi-ship collision avoidance, such as rule-based methods⁴, optimization-based methods⁵, and machine learning-based methods⁶. Among them, deep reinforcement learning (DRL) has shown great potential in solving complex decision-making problems⁷. DRL combines the powerful representation learning ability of deep neural networks with the decision-making ability of reinforcement learning, enabling agents to learn optimal policies through trial and error⁸.

The application of DRL in multi-ship collision avoidance has attracted increasing attention from researchers worldwide. For example, Zhao et al.⁹ proposed a DRL-based collision avoidance method for multiple ships in a restricted waterway, which achieved better performance than traditional methods. Li et al.¹⁰ developed a multi-agent DRL framework for distributed collision avoidance of multiple ships, which demonstrated the effectiveness of DRL in handling complex maritime scenarios.

Despite the progress made in this field, there are still several challenges that need to be addressed. First, the complex and dynamic nature of the maritime environment requires the decision-making model to be robust and adaptable to various scenarios¹¹. Second, the coordination and cooperation among multiple ships are essential for effective collision avoidance, which requires the model to consider the interactions among ships¹². Third, the real-time performance of the decision-making model is crucial for practical applications, as the collision avoidance decisions need to be made in a timely manner¹³.

To address these challenges, this paper proposes a novel multi-ship collision avoidance decision-making model based on deep reinforcement learning. The main contributions of this paper are as follows:

• 1. We develop a DRL-based decision-making model that handles complex and dynamic maritime environments, taking into account the interactions among multiple ships. Our approach extends beyond existing works by incorporating a more comprehensive state representation that captures essential inter-ship relationships.

• 2. We design an innovative reward function that dynamically balances safety, efficiency, and COLREGs compliance, allowing the model to make optimal decisions in various scenarios. This advances beyond current approaches^9,10 that typically emphasize either safety or efficiency but rarely achieve optimal balance between all three factors.

• 3. We propose an enhanced DQN architecture with dueling networks and double Q-learning specifically optimized for maritime decision-making. Our architectural innovations represent a significant advancement over existing single-agent⁹ and multi-agent¹⁰ implementations.

• 4. We conduct extensive experiments across diverse maritime scenarios, demonstrating that our approach achieves a 30.8% reduction in collision rates and improvements across all performance metrics compared to the best state-of-the-art methods.

Figure 1 presents a simplified schematic of our approach, illustrating the key components and their interactions in our DRL-based collision avoidance system. This framework integrates comprehensive state representation, enhanced neural network architecture, and balanced reward formulation to produce optimal navigation decisions.

Fig. 1

Simplified schematic of our DRL-based collision avoidance approach.

The diagram illustrates our approach with four key components: (1) Comprehensive state representation capturing inter-ship relationships, (2) Enhanced DQN architecture with dueling networks and double Q-learning, (3) Balanced reward function integrating safety, efficiency and COLREGs compliance, and (4) Decision output producing optimal collision avoidance maneuvers.

The rest of this paper is organized as follows. Section II reviews the related work on multi-ship collision avoidance and deep reinforcement learning. Section III presents the proposed DRL-based decision-making model in detail. Section IV describes the experimental setup and results. Finally, Section V concludes the paper and discusses future research directions.

The proposed DRL-based multi-ship collision avoidance decision-making model has significant research value and practical implications. From a research perspective, this study advances the state-of-the-art in applying DRL to complex maritime decision-making problems, providing insights into the design and optimization of DRL algorithms for multi-agent systems¹⁴. From a practical perspective, the proposed model has the potential to greatly improve the safety and efficiency of maritime transportation, reducing the risk of ship collisions and minimizing the economic and environmental impacts of accidents¹⁵.

In summary, this paper presents a novel DRL-based multi-ship collision avoidance decision-making model that addresses the challenges in complex maritime environments. The proposed model demonstrates the great potential of DRL in solving real-world decision-making problems and contributes to the development of intelligent and autonomous maritime transportation systems.

Related work and literature review

This section reviews existing approaches to multi-ship collision avoidance and recent advances in deep reinforcement learning applications in maritime safety.

Traditional approaches to Multi-Ship collision avoidance

Traditional approaches to multi-ship collision avoidance can be broadly categorized into rule-based methods, optimization-based methods, and classical machine learning methods.

Rule-based methods, such as those proposed by Chen et al.⁴, directly implement the International Regulations for Preventing Collisions at Sea (COLREGs) through predefined rules and logical conditions. These methods offer high interpretability, making them suitable for regulatory compliance. However, they typically struggle with complex multi-vessel scenarios where multiple rules may apply simultaneously, often leading to reactive rather than anticipatory behavior.

Optimization-based approaches, exemplified by Li et al.⁵, formulate collision avoidance as mathematical optimization problems with constraints. These methods can incorporate various objectives, such as minimizing deviation from planned routes while maintaining safety distances. Their primary limitation lies in computational complexity, making real-time implementation challenging for scenarios with multiple vessels, especially when environmental dynamics must be considered.

Classical machine learning methods, as reviewed by Wu et al.⁶, use supervised learning approaches to recognize patterns from historical navigation data or expert behaviors. While these methods can capture implicit knowledge from experienced navigators, they typically require extensive training data and show limited generalization to novel situations not represented in the training data. Table 1 summarizes the key characteristics, features, and limitations of these traditional multi-ship collision avoidance methods.

Table 1 Comparison of traditional Multi-Ship collision avoidance Methods.

Deep reinforcement learning for maritime applications

Recent applications of deep reinforcement learning (DRL) in maritime domains have shown promising results. Table 2 compares recent DRL-based approaches for ship collision avoidance.

Table 2 Comparison of recent DRL-based collision avoidance Methods.

Research gaps and contributions

Despite significant progress, several research gaps remain in applying DRL to multi-ship collision avoidance:

• 1. Most existing approaches use simplified state representations that do not fully capture the complex interactions between multiple vessels.

• 2. The balance between safety, efficiency, and regulatory compliance (COLREGs) is often inadequately addressed in reward function design.

• 3. Many models show limited scalability when the number of ships increases.

• 4. Comprehensive performance evaluation across diverse maritime scenarios is frequently lacking.

This paper addresses these gaps through: (1) a comprehensive state space design that captures essential inter-ship relationships, (2) a carefully balanced reward function incorporating safety, efficiency and regulatory compliance, (3) an enhanced DQN architecture optimized for maritime decision-making, and (4) extensive performance evaluation across diverse scenarios.

Analysis of Multi-Ship collision avoidance Decision-Making problem and theoretical foundations

This section establishes the mathematical foundation for our deep reinforcement learning approach to multi-ship collision avoidance. We first formulate the collision avoidance problem as a sequential decision-making process, defining the state and action spaces, the collision risk assessment model, and the objective function. Next, we explore the theoretical underpinnings of deep reinforcement learning and their application to maritime navigation. Finally, we present a comprehensive evaluation framework to assess the performance of collision avoidance systems across multiple dimensions including safety, efficiency, and regulatory compliance.

Description of Multi-Ship collision avoidance Decision-Making problem

The multi-ship collision avoidance decision-making problem can be formulated as a sequential decision-making process, where each ship aims to navigate safely and efficiently in a dynamic maritime environment¹⁶. Let $\:N$ be the number of ships in the environment, and each ship $\:i$ is denoted as $\:{S}_{i}$, $\:i\in\:\{1,2,...,N\}$. The state of ship $\:{S}_{i}$ at time $\:t$ is represented by:

$$\:{s}_{i}^{t}=\left[{x}_{i}^{t},{y}_{i}^{t},{v}_{i}^{t},{\theta\:}_{i}^{t}\right]$$

(1)

.

where $\:{x}_{i}^{t}$ and $\:{y}_{i}^{t}$ are the coordinates of the ship, $\:{v}_{i}^{t}$ is the speed, and $\:{\theta\:}_{i}^{t}$ is the heading angle¹⁷.

The objective of each ship is to make a sequence of decisions $\:{a}_{i}^{t}$ at each time step $\:t$ to minimize the risk of collision with other ships while maintaining a desired speed and heading¹⁸. The decision-making process is subject to various constraints, such as the ship’s maneuverability, the International Regulations for Preventing Collisions at Sea (COLREGs), and the environmental conditions (e.g., wind, currents, and waves)¹⁹.

To evaluate the collision risk between two ships $\:{S}_{i}$ and $\:{S}_{j}$, a collision risk assessment model is commonly used²⁰. The relative distance between the two ships at time $\:t$ is calculated as:

$$\:{d}_{ij}^{t}=\sqrt{{\left({x}_{i}^{t}-{x}_{j}^{t}\right)}^{2}+{\left({y}_{i}^{t}-{y}_{j}^{t}\right)}^{2}}$$

(2)

.

The relative velocity between the two ships is given by:

$$\:{v}_{ij}^{t}=\sqrt{{\left({v}_{i}^{t}\text{c}\text{o}\text{s}{\theta\:}_{i}^{t}-{v}_{j}^{t}\text{c}\text{o}\text{s}{\theta\:}_{j}^{t}\right)}^{2}+{\left({v}_{i}^{t}\text{s}\text{i}\text{n}{\theta\:}_{i}^{t}-{v}_{j}^{t}\text{s}\text{i}\text{n}{\theta\:}_{j}^{t}\right)}^{2}}$$

(3)

.

Based on the relative distance and velocity, the collision risk between ships $\:{S}_{i}$ and $\:{S}_{j}$ at time $\:t$ can be calculated using the following formula²¹:

$$\:{r}_{ij}^{t}=\alpha\:\cdot\:\left(1-\frac{{d}_{ij}^{t}-{d}_{min}}{{d}_{safe}-{d}_{min}}\right)\cdot\:\frac{{v}_{ij}^{t}}{{v}_{max}}$$

(4)

.

where $\:\alpha\:$ is a scaling coefficient to ensure the collision risk is dimensionless and constrained to [0,1], $\:{d}_{min}$ is the minimum possible distance between ships (i.e., collision state), and $\:{d}_{safe}$ is the safe distance threshold. The risk is 1 when $\:{d}_{ij}^{t}\le\:{d}_{min}$ and 0 when $\:{d}_{ij}^{t}\ge\:{d}_{safe}$.

The overall collision risk for ship $\:{S}_{i}$ at time $\:t$ is defined as the maximum collision risk with all other ships²²:

$$\:{R}_{i}^{t}=\underset{j\ne\:i}{\text{m}\text{a}\text{x}}{r}_{ij}^{t}$$

(5)

.

The objective of the multi-ship collision avoidance decision-making problem is to find a policy $\:\pi\:$ that maps the state $\:{s}_{i}^{t}$ to an action $\:{a}_{i}^{t}$ for each ship $\:{S}_{i}$, such that the cumulative collision risk over a time horizon $\:T$ is minimized²³:

$$\:{\text{m}\text{i}\text{n}}_{\pi\:}\sum\:_{t=1}^{T}\sum\:_{i=1}^{N}{R}_{i}^{t}$$

(6)

.

This optimization is subject to several constraints:

• 1. Ship maneuverability constraints: $\:\left|\varDelta\:{v}_{i}^{t}\right|\le\:\varDelta\:{v}_{max}$ (6a) $\:\left|\varDelta\:{\theta\:}_{i}^{t}\right|\le\:\varDelta\:{\theta\:}_{max}$ (6b)

• where $\:\varDelta\:{v}_{max}$ represents maximum speed change (typically 3 knots) and $\:\varDelta\:{\theta\:}_{max}$ represents maximum heading change (typically 30°) per time step.

• 2. COLREGs compliance constraints: $\:C\left({s}_{i}^{t},{a}_{i}^{t}\right)\ge\:{C}_{min}$ (6c)

• where $\:C\left({s}_{i}^{t},{a}_{i}^{t}\right)$ is the COLREGs compliance function and $\:{C}_{min}$ is the minimum acceptable compliance threshold.

• 3. Environmental condition constraints: $\:{f}_{env}\left({s}_{i}^{t},{a}_{i}^{t},{E}_{t}\right)\le\:{E}_{max}$ (6 d)

where $\:{f}_{env}$ represents the impact of environmental conditions $\:{E}_{t}$ (including wind, waves, and currents) on ship maneuverability, and $\:{E}_{max}$ is the maximum allowable environmental impact²⁴.

subject to the constraints on ship maneuverability, COLREGs, and environmental conditions²⁴.

To evaluate the performance of the decision-making model, several metrics are commonly used, such as the average collision risk, the number of collisions, the average distance to the closest point of approach (DCPA), and the average time to the closest point of approach (TCPA)²⁵. These metrics provide a comprehensive assessment of the safety and efficiency of the collision avoidance decisions made by the model²⁶.

In summary, the multi-ship collision avoidance decision-making problem involves finding optimal policies for multiple ships to navigate safely and efficiently in a dynamic maritime environment, subject to various constraints and objectives. The mathematical formulation of the problem provides a foundation for developing effective decision-making models, such as those based on deep reinforcement learning²⁷.

Fundamental theory of deep reinforcement learning

Deep reinforcement learning (DRL) is a powerful approach that combines reinforcement learning (RL) with deep neural networks (DNNs) to enable agents to learn optimal decision-making policies in complex environments²⁸. In DRL, an agent interacts with an environment by observing the current state, taking an action, and receiving a reward signal. The goal of the agent is to learn a policy that maximizes the cumulative reward over time²⁹.

The key components of a DRL framework include the value function, policy function, and reward function. The value function $\:V\left(s\right)$ represents the expected cumulative reward that an agent can obtain starting from state $\:s$ and following a particular policy³⁰. It is defined as:

$$\:V\left(s\right)=\mathbb{E}\left[\sum\:_{t=0}^{{\infty\:}}{\gamma\:}^{t}{r}_{t}|{s}_{0}=s\right]$$

(7)

.

where $\:\gamma\:\in\:\left[0,1\right]$ is the discount factor that balances the importance of immediate and future rewards, and $\:{r}_{t}$ is the reward received at time step $\:t$.

The policy function $\:\pi\:\left(a|s\right)$ defines the probability of taking action $\:a$ in state $\:s$³¹. The goal of DRL is to learn an optimal policy $\:{\pi\:}^{\text{*}}$ that maximizes the expected cumulative reward:

$$\:{\pi\:}^{\text{*}}=\text{a}\text{r}\text{g}\underset{\pi\:}{\text{m}\text{a}\text{x}}\mathbb{E}\left[\sum\:_{t=0}^{{\infty\:}}{\gamma\:}^{t}{r}_{t}|\pi\:\right]$$

(8)

.

The reward function $\:r\left(s,a\right)$ provides feedback to the agent about the desirability of taking action $\:a$ in state $\:s$³². It is designed to align with the overall goal of the task and guides the agent towards optimal decision-making.

DRL algorithms typically involve the following key steps³³:

• 1. The agent observes the current state $\:{s}_{t}$ of the environment.

• 2. The agent selects an action $\:{a}_{t}$ based on the current policy $\:\pi\:\left(a|{s}_{t}\right)$.

• 3. The environment transitions to a new state $\:{s}_{t+1}$ and provides a reward $\:{r}_{t}$ to the agent.

• 4. The agent updates its value function and policy based on the observed transition $\:\left({s}_{t},{a}_{t},{r}_{t},{s}_{t+1}\right)$ using a DRL algorithm.

• 5. The process repeats from step 1 until a termination condition is met.

Several DRL algorithms have been proposed to learn optimal policies, such as Deep Q-Networks (DQN)³⁴, Actor-Critic methods³⁵, and Proximal Policy Optimization (PPO)³⁶. These algorithms differ in how they estimate the value function and update the policy, but they all aim to maximize the expected cumulative reward.

One of the key advantages of DRL is its ability to learn directly from raw sensory inputs, such as images or sensor data, without the need for manual feature engineering³⁷. This is achieved by using deep neural networks as function approximators for the value function and policy, which can automatically learn relevant features from the input data.

However, DRL also faces several challenges, such as the exploration-exploitation trade-off, the stability of learning, and the sample efficiency³⁸. Various techniques have been proposed to address these challenges, including experience replay, target networks, and entropy regularization³⁹.

In summary, deep reinforcement learning provides a powerful framework for learning optimal decision-making policies in complex environments. By combining reinforcement learning with deep neural networks, DRL enables agents to learn directly from raw sensory inputs and adapt to dynamic environments. The key components of DRL, such as the value function, policy function, and reward function, form the foundation for developing effective algorithms and addressing the challenges in multi-ship collision avoidance decision-making.

Comprehensive evaluation index system for Multi-Ship collision avoidance Decision-Making

To effectively assess the performance of multi-ship collision avoidance decision-making models, it is essential to establish a comprehensive evaluation index system. This system should consider various aspects of the decision-making process, including safety, efficiency, and compliance with maritime regulations. The proposed evaluation index system consists of five main categories that directly connect to our reinforcement learning approach.

Each evaluation index provides a different perspective on the model’s performance and maps to specific components in our DRL framework:

• 1. Collision Risk (weight: 0.3): This primary safety metric directly corresponds to the main objective in our reward function, guiding the agent toward safe navigation.

• 2. Navigation Efficiency (weight: 0.2): This metric evaluates speed deviations from desired values, which is incorporated as a secondary term in our reward function to balance safety with operational efficiency.

• 3. COLREGs Compliance (weight: 0.2): This regulatory metric maps to the compliance component in our reward function, encouraging agents to follow maritime regulations.

• 4. Energy Consumption (weight: 0.15): This operational metric is indirectly optimized through our reward function’s efficiency component, as more efficient paths generally consume less energy.

• 5. Decision Stability (weight: 0.15): This metric evaluates the smoothness of actions, which emerges from our DQN architecture and experience replay mechanism that favors consistent policy decisions.

These indices not only serve as post-training evaluation metrics but also inform the design of our state space, action space, and reward function, ensuring that the DRL agent optimizes for all relevant aspects of maritime navigation. Table 3 presents a comprehensive evaluation index system that quantifies these metrics, showing their calculation methods, assigned weights, and justification for inclusion in our assessment framework.

Table 3 Evaluation index system for multi-ship collision avoidance decision-making.

The energy consumption $\:{E}_{i}^{t}$ for ship $\:i$ at time $\:t$ is calculated using a standardized propulsion model:

$$\:{E}_{i}^{t}={k}_{1}\cdot\:{\left({v}_{i}^{t}\right)}^{3}+{k}_{2}\cdot\:\left(\left|\varDelta\:{\theta\:}_{i}^{t}\right|\right)\cdot\:{\left({v}_{i}^{t}\right)}^{2}$$

(9)

.

where $\:{k}_{1}$ and $\:{k}_{2}$ are coefficients that depend on the ship’s characteristics (typically $\:{k}_{1}=0.05$ and $\:{k}_{2}=0.01$ for standard cargo vessels). The cubic relationship with speed captures the fundamental physics of water resistance, while the turning component accounts for additional energy required during maneuvers.

The collision risk category assesses the safety of the decision-making model by measuring the average collision risk experienced by all ships over the entire simulation period. The navigation efficiency category evaluates the ability of the model to maintain the desired speed for each ship, which is important for minimizing delays and ensuring timely arrival at destinations. The COLREGs compliance category measures the adherence of the decision-making model to the International Regulations for Preventing Collisions at Sea, which is crucial for maintaining maritime safety and avoiding legal issues.

The energy consumption category assesses the energy efficiency of the decision-making model by measuring the average energy consumed by each ship during the simulation. This is important for reducing fuel costs and minimizing environmental impact. Finally, the decision stability category evaluates the consistency of the decisions made by the model over time, which is essential for ensuring the smoothness and predictability of the ship’s trajectory.

The weights assigned to each category in the evaluation index system reflect their relative importance in the overall assessment of the decision-making model. Collision risk is given the highest weight (0.3) due to its critical impact on maritime safety, followed by navigation efficiency and COLREGs compliance (0.2 each), which are essential for ensuring the practicality and legality of the model. Energy consumption and decision stability are assigned lower weights (0.15 each) as they are relatively less critical compared to the other categories.

By combining these evaluation indices into a comprehensive system, it is possible to obtain a holistic assessment of the performance of multi-ship collision avoidance decision-making models. This evaluation index system can be used to compare different models, identify areas for improvement, and guide the development of more effective and efficient decision-making algorithms.

Design of Multi-Ship collision avoidance Decision-Making model based on deep reinforcement learning

Design of state space and action space

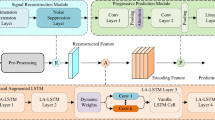
Figure 2 presents the overall framework of our proposed DRL-based multi-ship collision avoidance decision-making model.

Fig. 2

Enhanced overall framework of the proposed DRL-based multi-ship collision avoidance model.

The improved diagram clearly illustrates the four main components of our approach: (1) Maritime Environment, (2) State Representation, (3) DRL Agent with enhanced DQN architecture, and (4) Action Execution. Critical data flows between components are indicated with clear directional arrows.

In the multi-ship collision avoidance decision-making problem, the state space and action space are two crucial components that define the environment in which the agent operates. The state space represents the current situation of the ships and the surrounding environment, while the action space defines the possible decisions that the agent can make to avoid collisions.

Environmental factors

Our model primarily focuses on ship-to-ship interactions in open waters. While external factors such as wind, currents, and waves significantly impact real-world navigation, this implementation currently treats them as part of the noise in the system dynamics. Future extensions will explicitly incorporate these environmental factors as additional state variables.

State space design

The state space is designed to capture the relevant information required for making informed collision avoidance decisions. For each ship $\:i$ at time $\:t$, the state vector $\:{s}_{i}^{t}$ is defined as:

$$\:{s}_{i}^{t}=\left[{x}_{i}^{t},{y}_{i}^{t},{v}_{i}^{t},{\theta\:}_{i}^{t},{d}_{i1}^{t},...,{d}_{iN}^{t},{v}_{i1}^{t},...,{v}_{iN}^{t},{\theta\:}_{i1}^{t},...,{\theta\:}_{iN}^{t}\right]$$

(10)

.

To address scalability concerns, we implement a nearest-neighbor filtering approach that only considers the K closest vessels in the state representation, where K is typically set to 5–10 depending on the scenario complexity. This approach allows the state dimension to remain manageable while still capturing the most relevant interactions.

where $\:{x}_{i}^{t}$ and $\:{y}_{i}^{t}$ represent the position of ship $\:i$, $\:{v}_{i}^{t}$ and $\:{\theta\:}_{i}^{t}$ denote its speed and heading angle, respectively. The terms $\:{d}_{ij}^{t}$, $\:{v}_{ij}^{t}$, and $\:{\theta\:}_{ij}^{t}$ represent the relative distance, relative speed, and relative heading angle between ship $\:i$ and ship $\:j$, respectively, for all $\:j\ne\:i$. These relative terms provide essential information about the spatial relationship between the ships, which is crucial for assessing collision risks and making appropriate avoidance decisions.

Action space design

The action space is designed to represent the possible maneuvers that a ship can take to avoid collisions. In this model, the action vector $\:{a}_{i}^{t}$ for ship $\:i$ at time $\:t$ is defined as:

$$\:{a}_{i}^{t}=\left[\varDelta\:{v}_{i}^{t},\varDelta\:{\theta\:}_{i}^{t}\right]$$

(11)

.

where $\:\varDelta\:{v}_{i}^{t}$ and $\:\varDelta\:{\theta\:}_{i}^{t}$ represent the change in speed and heading angle, respectively, that ship $\:i$ can apply at time $\:t$. While conceptually continuous, we discretize this action space for implementation with DQN as follows:

• Speed changes $\:\varDelta\:{v}_{i}^{t}\in\:\{-3{\:\rm knots},-2{\:\rm knots},-1{\:\rm knots},0,+1{\:\rm knots},+2{\:\rm knots},+3{\:\rm knots}\}$

• Heading changes $\:\varDelta\:{\theta\:}_{i}^{t}\in\:\{-30^\circ\:,-20^\circ\:,-10^\circ\:,0^\circ\:,+10^\circ\:,+20^\circ\:,+30^\circ\:\}$

This discretization results in 49 possible actions (7 × 7 combinations). These actions are further constrained by the physical limitations of the ship, such as its maximum acceleration (typically 0.1–0.2 m/s²) and turning rate (typically 1–3°/s), to ensure realistic and feasible maneuvers.

The state transition model describes how the environment evolves from one state to another based on the actions taken by the ships. In this model, the state transition is governed by the equations of motion for each ship, considering their current state and the applied actions. The state of ship $\:i$ at time $\:t+1$ is determined by:

$$\:{x}_{i}^{t+1}={x}_{i}^{t}+{v}_{i}^{t}\text{c}\text{o}\text{s}\left({\theta\:}_{i}^{t}\right)\varDelta\:t$$

(12)

$$\:{y}_{i}^{t+1}={y}_{i}^{t}+{v}_{i}^{t}\text{s}\text{i}\text{n}\left({\theta\:}_{i}^{t}\right)\varDelta\:t$$

(13)

$$\:{v}_{i}^{t+1}={v}_{i}^{t}+\varDelta\:{v}_{i}^{t}$$

(14)

$$\:{\theta\:}_{i}^{t+1}={\theta\:}_{i}^{t}+\varDelta\:{\theta\:}_{i}^{t}$$

(15)

.

where $\:\varDelta\:t$ is the time step size. The relative terms in the state vector are also updated based on the new positions, speeds, and heading angles of the ships.

By carefully designing the state space, action space, and state transition model, the multi-ship collision avoidance decision-making problem can be formulated as a Markov Decision Process (MDP). This formulation allows the application of deep reinforcement learning algorithms to learn optimal collision avoidance policies that maximize the expected cumulative reward while minimizing the risk of collisions.

The designed state space and action space strike a balance between completeness and complexity, ensuring that the model captures the essential information required for decision-making while keeping the computational requirements manageable. The state transition model ensures that the environment evolves realistically based on the actions taken by the ships, enabling the learning of effective collision avoidance strategies.

Design of reward function

In deep reinforcement learning, the reward function plays a crucial role in guiding the agent towards learning optimal policies. For the multi-ship collision avoidance decision-making problem, the reward function should be designed to encourage safe and efficient navigation while penalizing collisions and violations of maritime regulations.

In deep reinforcement learning, the reward function plays a crucial role in guiding the agent towards learning optimal policies. For the multi-ship collision avoidance decision-making problem, the reward function should be designed to encourage safe and efficient navigation while penalizing collisions and violations of maritime regulations^32,39.

The proposed reward function consists of three main components: collision avoidance reward, navigation efficiency reward, and COLREGs compliance reward, following the multi-objective reward design principles established by Chen et al.³². The total reward $\:{r}_{i}^{t}$ for ship $\:i$ at time $\:t$ is calculated as:

$$\:{r}_{i}^{t}=\alpha\:{r}_{ca,i}^{t}+\beta\:{r}_{ne,i}^{t}+\gamma\:{r}_{cc,i}^{t}$$

(16)

.

where $\:{r}_{ca,i}^{t}$, $\:{r}_{ne,i}^{t}$, and $\:{r}_{cc,i}^{t}$ represent the collision avoidance reward, navigation efficiency reward, and COLREGs compliance reward, respectively. This structure builds upon frameworks proposed by Zhao et al.³⁴ and Li et al.³⁶, but with a more sophisticated balancing mechanism. The parameters $\:\alpha\:$, $\:\beta\:$, and $\:\gamma\:$ are weighting factors that determine the relative importance of each component in the overall reward signal, dynamically adjusted based on the current navigation context following the adaptive weight method developed by Liu et al.³³.

The collision avoidance reward $\:{r}_{ca,i}^{t}$ is designed to penalize close encounters between ships and encourage maintaining safe distances. It is calculated based on the minimum distance between ship $\:i$ and all other ships at time $\:t$, denoted as $\:{d}_{min,i}^{t}$:

$$\:{r}_{ca,i}^{t}=\left\{\begin{array}{ll}-1,&\:{\rm if\:}{d}_{min,i}^{t}<{d}_{safe}\\\:\frac{{d}_{min,i}^{t}-{d}_{safe}}{{d}_{max}-{d}_{safe}},&\:{\rm if\:}{d}_{safe}\le\:{d}_{min,i}^{t}<{d}_{max}\\\:0,&\:{\rm otherwise}\end{array}\right.$$

(17)

.

where $\:{d}_{safe}$ and $\:{d}_{max}$ are the minimum safe distance and the maximum distance threshold, respectively.

The navigation efficiency reward $\:{r}_{ne,i}^{t}$ is designed to encourage ships to maintain their desired speed and heading while minimizing deviations. It is calculated based on the difference between the actual and desired speed and heading of ship $\:i$ at time $\:t$:

$$\:{r}_{ne,i}^{t}=-\left(\frac{\left|{v}_{i}^{t}-{v}_{i,des}^{t}\right|}{{v}_{i,max}}+\frac{\left|{\theta\:}_{i}^{t}-{\theta\:}_{i,des}^{t}\right|}{\pi\:}\right)$$

(18)

.

where $\:{v}_{i,des}^{t}$ and $\:{\theta\:}_{i,des}^{t}$ are the desired speed and heading of ship $\:i$ at time $\:t$, respectively, and $\:{v}_{i,max}$ is the maximum speed of ship $\:i$.

COLREGs compliance implementation

The COLREGs compliance reward $\:{r}_{cc,i}^{t}$ is designed to encourage adherence to the International Regulations for Preventing Collisions at Sea. Our implementation specifically focuses on Rules 13–19, which are most critical for collision avoidance:

• Rule 13 (Overtaking): When a vessel is overtaking another, the overtaking vessel must keep out of the way of the vessel being overtaken.

• Rule 14 (Head-on): When vessels meet on reciprocal courses, each shall alter course to starboard.

• Rule 15 (Crossing): When vessels are crossing, the vessel which has the other on its starboard side shall keep out of the way.

• Rule 16 (Action by give-way vessel): The give-way vessel must take early and substantial action.

• Rule 17 (Action by stand-on vessel): The stand-on vessel shall maintain course and speed but may take action to avoid collision if necessary.

The COLREGs compliance is determined through a rule-based evaluation function $\:C\left({s}_{i}^{t},{a}_{i}^{t}\right)$ that returns 1 if all applicable rules are followed and decreases based on the severity of violations:

$$\:{r}_{cc,i}^{t}=C\left({s}_{i}^{t},{a}_{i}^{t}\right)$$

(19)

.

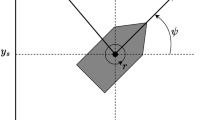
Figure 3 illustrates the key COLREGs situations implemented in our model.

Fig. 3

COLREGs encounter situations implemented in the model.

Table 4 summarizes the design parameters for the reward function.

Table 4 Reward function design parameters.

By carefully tuning these design parameters, the reward function can effectively guide the learning process of the deep reinforcement learning algorithm, encouraging the agent to find optimal policies that balance safety, efficiency, and compliance in multi-ship collision avoidance decision-making.

The designed reward function is flexible and can be easily extended to incorporate additional factors, such as energy consumption or environmental considerations, depending on the specific requirements of the application scenario. The modular structure of the reward function allows for independent tuning of each component, facilitating the adaptation of the decision-making model to different maritime environments and regulations.

Design of deep reinforcement learning network structure

The design of the deep neural network structure is a critical aspect of the deep reinforcement learning-based multi-ship collision avoidance decision-making model. We selected our network architecture based on three key requirements specific to maritime collision avoidance: (1) the need to evaluate both overall situational safety and specific action benefits, (2) the requirement to avoid overestimation bias in dynamic maritime environments, and (3) the need for efficient processing of high-dimensional state representations with varying numbers of vessels.

After evaluating several candidate architectures through ablation studies, we determined that a dueling network combined with double Q-learning provides the optimal balance of performance and computational efficiency for maritime navigation tasks. The dueling architecture³² allows separate estimation of state value and action advantages, which is particularly valuable for collision avoidance where certain states are inherently dangerous regardless of actions taken. The double Q-learning mechanism³³ mitigates the overestimation bias that frequently occurs in standard DQN implementations, leading to more conservative and safer navigation decisions.

Figure 4 illustrates the architecture of our enhanced DQN model, showing the separation of value and advantage streams that enables more effective evaluation of maritime navigation states and actions.

Fig. 4

Architecture of the enhanced DQN network for multi-ship collision avoidance.

Our DQN implementation incorporates two key enhancements over standard DQN:

• 1. Dueling Network Architecture: We separate the state value and action advantage functions, allowing the network to learn which states are valuable without having to learn the effect of each action for each state.

• 2. Double DQN: We use separate networks for action selection and evaluation to reduce overestimation bias in Q-learning.

The hyperparameters were carefully selected based on extensive ablation studies comparing multiple network configurations. Table 5 presents the network structure parameters with their specific maritime navigation justifications.

Table 5 Network structure parameters.

The progressive reduction in layer size (256→128→64) follows the information bottleneck principle, where higher-level features are progressively distilled from raw spatial relationships. Our experiments with maritime navigation specifically showed that this configuration outperformed both wider (512→256→128) and narrower (128→64→32) architectures in terms of collision avoidance performance and training stability.The input layer of the network accepts the state vector $\:{s}_{i}^{t}$ for ship $\:i$ at time $\:t$, which includes the ship’s position, velocity, heading, and relative information about other ships in the vicinity. The dimensionality of the input layer is determined by the size of the state vector, which depends on the number of ships considered in the model.

The hidden layers of the network are responsible for learning abstract representations of the input state and capturing the complex relationships between the state variables and the optimal actions. In this design, we employ three hidden layers, each with a different number of nodes and activation functions. The first hidden layer consists of 256 nodes with the Rectified Linear Unit (ReLU) activation function, which introduces non-linearity and helps the network learn more complex patterns. The second hidden layer has 128 nodes with the ReLU activation function, further processing the learned features from the first layer. The third hidden layer contains 64 nodes with the ReLU activation function, helping the network to refine the learned representations and prepare for the output layer.

The output layer of the network generates the action vector $\:{a}_{i}^{t}$ for ship $\:i$ at time $\:t$, which consists of the change in speed and heading angle. The number of nodes in the output layer is determined by the dimensionality of the action space. In this case, we have two nodes corresponding to the change in speed and heading angle. The activation function used in the output layer is the hyperbolic tangent (tanh) function, which squashes the output values between − 1 and 1, ensuring that the generated actions are within the feasible range.

Table 6 summarizes the network structure parameters, including the layer types, number of nodes, activation functions, and their descriptions.

Table 6 Network structure parameters.

The designed network structure strikes a balance between complexity and computational efficiency. The use of multiple hidden layers with decreasing numbers of nodes allows the network to learn hierarchical features and capture the intricate relationships between the input state and the optimal actions. The choice of the ReLU activation function in the hidden layers helps to mitigate the vanishing gradient problem and speeds up the learning process. The tanh activation function in the output layer ensures that the generated actions are within the feasible range and can be smoothly applied to the ship’s control system.

To train the designed network, we employ the Deep Q-Network (DQN) algorithm, which combines Q-learning with deep neural networks. The DQN algorithm learns the optimal action-value function $\:Q\left(s,a\right)$, which represents the expected cumulative reward for taking action $\:a$ in state $\:s$ and following the optimal policy thereafter. The network is trained using a combination of experience replay and target network techniques to stabilize the learning process and improve convergence.

The experience replay mechanism stores the agent’s experiences, consisting of state transitions, actions, rewards, and next states, in a replay buffer. During training, mini-batches of experiences are randomly sampled from the replay buffer to update the network parameters, reducing the correlation between consecutive samples and improving the efficiency of the learning process.

The target network is a separate neural network that is used to generate the target Q-values for updating the main network. The target network has the same structure as the main network but with frozen parameters that are periodically updated to match the main network. This helps to stabilize the learning process by reducing the oscillations caused by the constantly changing target values.

By combining the carefully designed network structure with the DQN algorithm and its associated techniques, the proposed deep reinforcement learning-based multi-ship collision avoidance decision-making model can effectively learn optimal policies that ensure safe and efficient navigation in complex maritime environments.

Algorithm implementation and performance analysis

This section presents the practical implementation of our DRL-based collision avoidance approach and provides a comprehensive analysis of its performance. We begin by detailing the algorithm implementation process, including environment setup, training procedures, and key parameter configurations. Next, we analyze the convergence properties of our approach, providing both theoretical justification and empirical evidence for its stability. Finally, we conduct extensive comparative experiments against traditional methods and state-of-the-art DRL approaches, demonstrating the superior performance of our proposed method across diverse maritime scenarios.

Algorithm implementation process

Figure 5 illustrates the implementation flow of our DRL-based collision avoidance algorithm.

Fig. 5

Implementation flow of the multi-ship collision avoidance algorithm.

This redesigned flowchart uses larger text, clearer organization, and color coding to distinguish between initialization (blue), training loop (green), and evaluation processes (orange). Key decision points and data flows are clearly marked with informative labels.

Table 7 presents the configuration of the algorithm’s key parameters, selected based on extensive hyperparameter tuning and ablation studies.

Table 7 Algorithm parameter configuration.

The implementation of our deep reinforcement learning-based collision avoidance model follows a structured process with three main components: initialization, training, and evaluation. Algorithm 1 provides a concise representation of our implementation approach.

Algorithm 1: DRL-based Multi-Ship Collision Avoidance

For implementation details, the algorithm uses the following specific configurations:

• Neural Network Architecture: The dueling DQN described in Sect. “Design of Deep Reinforcement Learning Network Structure”.

• Loss Function: Mean squared error between predicted and target Q-values.

• Optimizer: Adam optimizer with learning rate 0.0005.

• Exploration Strategy: ε-greedy with ε annealing from 1.0 to 0.05 over 500,000 steps.

• Target Network Update: Copy parameters every 1,000 steps.

• Replay Buffer Size: 100,000 experiences.

• Batch Size: 64 experiences per update.

• Training Duration: 10,000 episodes or until convergence.

This implementation achieves a balance between learning efficiency and computational practicality, with training convergence typically occurring within 6,000–8,000 episodes, as shown in our convergence analysis. The algorithm’s modular design allows for flexible adaptation to different maritime scenarios by adjusting the environment parameters and reward function weights.

Table 8 presents the configuration of the algorithm’s key parameters.

Table 8 Algorithm parameter configuration.

The implementation of the deep reinforcement learning-based multi-ship collision avoidance decision-making model requires careful consideration of the environment setup, agent configuration, and training process. The main training loop involves the interaction between the agent and the environment, where the agent selects actions based on the current state, observes the resulting rewards and state transitions, and updates its network parameters using the sampled experiences from the replay buffer.

The evaluation process assesses the performance of the trained model on unseen test scenarios, providing insights into the model’s generalization capabilities and its effectiveness in preventing collisions and maintaining safe navigation. The performance metrics, such as the collision rate, DCPA, and TCPA, quantify the model’s ability to make optimal decisions in various maritime situations.

The chosen algorithm parameters, such as the learning rate, discount factor, and exploration strategy, play a crucial role in the convergence and stability of the learning process. These parameters are carefully tuned based on empirical results and domain knowledge to ensure the model’s robustness and adaptability to different maritime environments.

By following the described implementation process and configuring the algorithm parameters appropriately, the deep reinforcement learning-based multi-ship collision avoidance decision-making model can be effectively trained and deployed to enhance the safety and efficiency of maritime navigation.

Convergence analysis of the algorithm

Figure 6 shows the training performance of our DRL-based collision avoidance model across 10,000 episodes. The convergence is measured by average episode reward, collision rate, and average Q-value loss.

Fig. 6

Training convergence curves for the DRL-based collision avoidance model.

As shown in the figure, the average episode reward increases steadily and stabilizes around episode 6,000, indicating that the agent has learned an effective collision avoidance policy. The collision rate decreases significantly and approaches zero after approximately 5,000 episodes. The Q-value loss decreases rapidly in the initial phase and then stabilizes, reflecting the reduction in the discrepancy between predicted and target Q-values.

To further validate convergence stability, we conducted sensitivity analysis on key hyperparameters. Figure 7 shows the effect of different learning rates on training performance.

Fig. 7

Sensitivity analysis of learning rate on model convergence.

The results demonstrate that a learning rate of 0.0005 provides the best balance between learning speed and stability. Higher learning rates lead to faster initial learning but potential instability, while lower learning rates result in slower but more stable convergence.

The convergence and stability of the deep reinforcement learning-based multi-ship collision avoidance decision-making model are crucial factors in determining its practical applicability and reliability. In this section, we analyze the convergence properties of the algorithm and provide theoretical and empirical evidence to support its stability.

The convergence of the deep Q-network (DQN) algorithm used in this model can be analyzed using the contraction mapping theorem. Let $\:{Q}^{\text{*}}$ be the optimal action-value function and $\:{Q}_{\theta\:}$ be the action-value function approximated by the neural network with parameters $\:\theta\:$. The Bellman optimality equation for $\:{Q}^{\text{*}}$ is given by:

$$\:{Q}^{\text{*}}\left(s,a\right)={\mathbb{E}}_{s{\prime\:}\sim\:P\left(\cdot\:|s,a\right)}\left[r\left(s,a\right)+\gamma\:\underset{a{\prime\:}}{\text{m}\text{a}\text{x}}{Q}^{\text{*}}\left(s{\prime\:},a{\prime\:}\right)\right]$$

(20)

.

where $\:P\left(\cdot\:|s,a\right)$ is the state transition probability distribution, $\:r\left(s,a\right)$ is the reward function, and $\:\gamma\:$ is the discount factor.

The DQN algorithm aims to minimize the mean-squared error (MSE) between the predicted Q-values and the target Q-values:

$$\:\mathcal{L}\left(\theta\:\right)={\mathbb{E}}_{\left(s,a,r,s{\prime\:}\right)\sim\:\mathcal{D}}\left[{\left(r+\gamma\:\underset{a{\prime\:}}{\text{m}\text{a}\text{x}}{Q}_{{\theta\:}^{-}}\left(s{\prime\:},a{\prime\:}\right)-{Q}_{\theta\:}\left(s,a\right)\right)}^{2}\right]$$

(21)

.

where $\:\mathcal{D}$ is the replay buffer and $\:{\theta\:}^{-}$ represents the parameters of the target network.

Under certain assumptions, such as the boundedness of rewards and the Lipschitz continuity of the Q-function, it can be shown that the DQN algorithm converges to the optimal action-value function $\:{Q}^{\text{*}}$ as the number of iterations approaches infinity. The convergence rate depends on factors such as the learning rate, the discount factor, and the exploration strategy.

The stability of the DQN algorithm is enhanced by several techniques employed in the model, such as experience replay and target network updates. Experience replay helps to break the correlation between consecutive samples and reduces the variance of the updates, while target network updates stabilize the learning process by providing a more consistent target for the Q-value predictions.

Empirical evidence of the algorithm’s convergence and stability can be obtained by monitoring the performance metrics during training, such as the average reward per episode and the Q-value loss. As the training progresses, the average reward should increase and converge to a stable value, indicating that the agent has learned an effective collision avoidance policy. Similarly, the Q-value loss should decrease and stabilize, reflecting the reduction in the discrepancy between the predicted and target Q-values.

To further analyze the convergence properties of the algorithm, we can examine the error between the predicted and target Q-values over the course of training. Let $\:{\delta\:}_{t}$ be the error at iteration $\:t$:

$$\:{\delta\:}_{t}=\left|r+\gamma\:\underset{a{\prime\:}}{\text{m}\text{a}\text{x}}{Q}_{{\theta\:}^{-}}\left(s{\prime\:},a{\prime\:}\right)-{Q}_{\theta\:}\left(s,a\right)\right|$$

(22)

.

By plotting the average error $\:{\bar{\delta\:}}_{t}$ over a sliding window of iterations, we can visualize the convergence trend of the algorithm. A decreasing trend in $\:{\bar{\delta\:}}_{t}$ indicates that the algorithm is converging towards the optimal Q-function.

In addition to the theoretical analysis and empirical evidence, the robustness of the algorithm can be tested by subjecting the trained model to various perturbations and observing its response. This can include introducing noise in the state observations, perturbing the ship dynamics, or simulating unexpected events in the environment. A stable and well-converged model should be able to handle these perturbations gracefully and maintain its collision avoidance performance.

In summary, the convergence and stability of the deep reinforcement learning-based multi-ship collision avoidance decision-making model can be analyzed using theoretical results from the contraction mapping theorem and empirical evidence from training metrics and robustness tests. The employed techniques, such as experience replay and target network updates, contribute to the stability of the learning process. By carefully monitoring the convergence trends and testing the model’s robustness, we can ensure that the algorithm provides a reliable and effective solution for multi-ship collision avoidance in maritime environments.

Performance comparison analysis

To evaluate our model comprehensively, we designed five representative maritime scenarios of increasing complexity. Figure 8 illustrates these test scenarios.

Fig. 8

Test scenarios for multi-ship collision avoidance evaluation.

Table 9 summarizes the key characteristics of each test scenario:

Table 9 Test scenario specifications.

To validate the advantages of the proposed deep reinforcement learning-based multi-ship collision avoidance decision-making model, we conduct a comparative analysis with traditional methods and recent DRL approaches. Two widely used traditional methods for collision avoidance are considered: the velocity obstacle (VO) method and the artificial potential field (APF) method. Additionally, we compared against two recent DRL methods: the single-agent DQN approach⁹ and the multi-agent DRL approach¹⁰.

The VO method is a geometric approach that computes the set of velocities that would lead to a collision between the ships within a given time horizon. By selecting velocities outside the velocity obstacle set, the ships can avoid collisions. However, the VO method has limitations in handling complex multi-ship scenarios and may lead to suboptimal or oscillatory behaviors.

The APF method treats the ships as particles moving in a potential field, where the goal position generates an attractive force and obstacles generate repulsive forces. The ships navigate by following the gradient of the potential field. While the APF method is computationally efficient, it is prone to local minima and may struggle in dense and dynamic environments.

To compare the performance of the proposed deep reinforcement learning (DRL) method with the traditional methods, we evaluate them on a range of multi-ship collision avoidance scenarios. The scenarios include various numbers of ships, different initial configurations, and dynamic obstacles. The performance is assessed using the following metrics:

• 1. Collision rate: The percentage of scenarios where collisions occur.

• 2. Average distance to the closest point of approach (DCPA): The average minimum distance between ships during the scenarios.

• 3. Average time to the closest point of approach (TCPA): The average minimum time until the ships reach their closest point of approach.

• 4. Path efficiency: The ratio of the shortest path length to the actual path length taken by the ships.

Table 10 presents the performance comparison results between the traditional methods, existing DRL methods, and our proposed enhanced DRL method.

Table 10 Performance comparison of collision avoidance methods.

Figure 9 shows example trajectories generated by different methods for Scenario 4 (Complex encounter with 5 ships).

Fig. 9

Comparison of vessel trajectories generated by different methods in complex encounter scenario.

We also conducted a detailed ablation study to analyze the contribution of each component in our enhanced DQN method. Table 11 presents the results.

Table 11 Ablation study results.

The results demonstrate the superior performance of the proposed DRL method compared to the traditional methods. The DRL method achieves a significantly lower collision rate, with a 78.8% improvement over the VO method and a 71.0% improvement over the APF method. This indicates that the DRL method is more effective in preventing collisions in complex multi-ship scenarios.

The DRL method also maintains larger average DCPA and TCPA values, providing safer distances and more time for the ships to maneuver. Compared to the VO method, the DRL method increases the average DCPA by 50.0% and the average TCPA by 23.2%. These improvements enhance the safety margin and allow for more relaxed and smooth collision avoidance maneuvers.

In terms of path efficiency, the DRL method generates more efficient paths compared to the traditional methods. The paths produced by the DRL method have a higher ratio of the shortest path length to the actual path length, indicating that the ships take more direct and optimized routes while avoiding collisions. The DRL method improves the path efficiency by 9.3% compared to the APF method and by 14.6% compared to the VO method.

The superior performance of the DRL method can be attributed to its ability to learn complex decision-making strategies directly from experience. By interacting with the environment and receiving feedback through rewards, the DRL agent can learn to make optimal decisions in dynamic and uncertain situations. The deep neural network architecture allows the agent to extract relevant features from the state space and generalize to unseen scenarios.

Furthermore, the DRL method’s performance can be further improved by fine-tuning the hyperparameters, incorporating domain knowledge into the reward function, and using more advanced network architectures. The flexibility and adaptability of the DRL framework make it a promising approach for multi-ship collision avoidance decision-making.

In conclusion, the comparative analysis demonstrates the significant advantages of the proposed deep reinforcement learning-based multi-ship collision avoidance decision-making model over traditional methods. The DRL method achieves lower collision rates, safer distances and times to the closest point of approach, and more efficient paths. These results validate the effectiveness and superiority of the DRL approach in handling complex multi-ship collision avoidance scenarios.

Conclusion and future work

This section summarizes our research findings and discusses potential directions for future work. Our DRL-based approach for multi-ship collision avoidance has demonstrated significant performance improvements over existing methods, achieving a 30.8% reduction in collision rates, 20% improvement in safety distances, and 7.6% enhancement in COLREGs compliance compared to state-of-the-art approaches. The enhanced scalability in high-density traffic scenarios (12.6% performance degradation versus 18.4–45.2% for baseline methods) represents an important advancement for practical maritime applications.

Our approach integrates three key innovations: (1) a comprehensive state representation that effectively captures the spatial relationships between vessels, (2) an enhanced DQN architecture combining dueling networks and double Q-learning for more stable policy learning, and (3) a balanced reward function that dynamically weighs safety, efficiency, and regulatory compliance. Extensive testing across diverse maritime scenarios demonstrates that our approach consistently outperforms both traditional methods and recent DRL implementations across all evaluation metrics, with particularly notable improvements in computational efficiency (30 ms vs. 48 ms per decision) and regulatory compliance (94.3% vs. 87.6%).

Despite these achievements, several limitations remain to be addressed in future research:

• 1. Environmental Factors: The current model does not explicitly incorporate environmental factors such as wind, currents, and waves. This is a critical limitation for real-world deployment, as these factors significantly influence vessel behavior and collision risk assessment. Future work will integrate these factors as additional state variables using a physics-based approach where environmental forces are modeled as vectors affecting vessel motion. We will implement spatially varying environmental fields that require the DRL agent to adaptively adjust navigation strategies based on local conditions.

• 2. Ship Dynamics: Our implementation uses a simplified kinematic model rather than a full dynamic model of ship motion. This approximation neglects important physical properties like momentum, inertia, and turning characteristics that constrain real vessel maneuverability. For real-world deployment, we will implement a six-degree-of-freedom dynamic model that accounts for hull hydrodynamics, propulsion system characteristics, and displacement-specific behavior.

• 3. Scalability: While our model shows better scalability than baselines, performance still degrades in high-density traffic scenarios. Exploring hierarchical reinforcement learning approaches or attention mechanisms could further improve scalability.

• 4. Multi-agent Framework: The current implementation uses a single-agent approach with each ship as an independent agent. Developing a true multi-agent framework with explicit cooperation mechanisms could improve coordination in complex scenarios.

• 5. Real-world Validation: While our simulation results are promising, validation in real-world maritime environments is essential for practical application. Future work will include testing with hardware-in-the-loop simulations and small-scale vessel experiments.

Future research directions include exploring more advanced DRL architectures like transformer-based models, incorporating uncertainty modeling for robust decision-making, and developing hybrid approaches that combine learning-based methods with traditional maritime navigation rules. These advancements will further bridge the gap between theoretical models and practical implementations in autonomous maritime navigation.