Air quality assessment in Beijing based on cloud model

Abstract

This research employs the cloud model method to assess the outdoor air quality in Beijing over the past ten years. The study establishes standard and evaluation clouds for major air pollutants and constructs a comprehensive evaluation cloud model for the Air Quality Index (AQI) using aggregation functions and cloud model attributes. A novel normal cloud similarity measurement method based on the second-order Fréchet distance is adopted to conduct annual assessments. The core findings indicate a significant improvement in Beijing’s air quality, with the AQI showing a continuous downward trend from moderate pollution in 2014 to mild pollution in 2023. Specific pollutants such as $PM_{10}$, $PM_{2.5}$, and $SO_2$ have shown marked reductions, transitioning from good or light pollution levels to excellent ratings. The cloud model method effectively captures the probabilistic nature of pollutant concentrations, providing a more nuanced and rigorous assessment compared to traditional methods. These results validate the effectiveness and precision of the cloud model approach, offering actionable insights for environmental management and policy development.

Introduction

Over the past few decades, China’s meteoric economic ascent and bustling urbanization have captured the world’s attention. However, this headlong rush towards development has not come without a price. The early stages of rapid industrialization have shouldered the environment with substantial burdens, particularly in the realm of air pollution. This issue not only highlights the adverse consequences lurking behind the facade of progress but also stands as a formidable barrier to the sustainable and robust growth of China’s socio-economic landscape¹.

Air quality degradation, particularly in densely populated urban areas, poses significant challenges. It directly impinges on the respiratory health of the populace and jeopardizes their overall well-being². Amidst this backdrop, the implementation of the Air Quality Index (AQI) system assumes paramount importance. This system is designed to demystify the intricacies of air quality through a standardized set of indicators, empowering the public to readily grasp the daily monitored levels of air pollutants and the potential health and environmental risks they entail^3,4.

A thorough evaluation of air quality necessitates a profound comprehension of the nature of principal air pollutants and their deleterious effects on health. Nitrogen dioxide ($NO_2$), sulfur dioxide ($SO_2$), ozone ($O_3$), inhalable particulate matter ($PM_{10}$), fine particulate matter ($PM_{2.5}$), and carbon monoxide (CO) are among the critical air pollutants identified by the World Health Organization in its Air Quality Guidelines. These pollutants have been scientifically linked to severe health hazards, including elevated risks of cardiovascular diseases, impaired respiratory and lung function, and even cognitive decline^{5,6,7,8,9,10,11,12}.

To thoroughly and scientifically assess current air quality, China has developed a simplified evaluation method for the Air Quality Index (AQI) called the lookup table method. This technique determines the index values of specific pollutants by directly referencing their breakpoint values and uses the highest value as the final AQI. This method is also adopted in the United States, the United Kingdom, and Europe. Additionally, the state of New South Wales in Australia employs a standardized method for calculating sub-indices, which is simpler than linear interpolation. This method standardizes monitoring data for each pollutant and visibility, with “standard” values for major pollutants defined by the National Environmental Protection Measures (NEPM). After deriving a set of standardized AQI values and comparing them across stations, the highest AQI value at each station is designated as the station AQI, and the highest station AQI in a region is used as the regional AQI¹³.

The scholarly community has also introduced a range of innovative methodologies, such as the Euclidean closeness method, applying EPA’s instruction method and the factor analysis-based Air Quality Index calculation method. These approaches enhance the theoretical framework for air quality assessment and furnish adaptable monitoring and evaluation tools for diverse countries and regions^{14,15,16,17,18}.

Current methods face limitations, particularly in addressing the inherent fuzziness and randomness of air quality data. To surmount these challenges, this paper presents an air quality evaluation technique founded on the cloud model. The cloud model, conceptualized by Academician Li Deyi, integrates probability theory and fuzzy mathematics to enable bidirectional conversion between qualitative concepts and quantitative data¹⁹.

The cloud model has demonstrated its unique applicability across various domains, including evolutionary computing, water quality assessment, fuzzy cluster analysis, safety evaluation and risk management^{20,21,22,23,24,25,26}. In the realm of air quality evaluation, the cloud model takes into account the randomness, fuzziness, and uncertainty inherent in air environmental quality assessments, offering a novel evaluation approach^{27,28,29,30,31}.

While cloud models have yielded significant insights in air quality assessments, the traditional methods for handling pollutants might neglect the interactions and cumulative effects among them. To more accurately reflect the state of air quality, we introduce an enhanced evaluation method that computes the comprehensive AQI cloud within the cloud model by aggregating pollutant data. This method not only considers the individual pollutant concentration levels but also synthesizes the interconnections and mutual impacts between various pollutants.

In this research, we undertook a thorough reevaluation of Beijing’s outdoor air quality over the past decade, utilizing advanced cloud modeling techniques. Initially, we established standard cloud models for various air pollution indices and the AQI. Subsequently, we created evaluation clouds from detailed air pollutant data to encapsulate the probability distribution characteristics of the actual air quality. Through the pollutant aggregation method, we integrated the evaluation clouds of various pollution indices to compute the comprehensive AQI evaluation cloud.

This paper conducts air quality rating based on the similarity of cloud models. By calculating the similarity between the evaluation cloud and the standard cloud, the pollution level to which the evaluation cloud belongs is determined. The higher the similarity between the evaluation cloud and the standard cloud, the greater the likelihood that it corresponds to the pollution level represented by that standard cloud. Existing cloud model similarity algorithms can be primarily categorized into three types³²: concept extension, numerical features, and characteristic curves. In the concept extension approach, Zhang et al.³³ proposed evaluating the similarity between two cloud models by calculating the extended average distance; Wang et al.³⁴ developed a fuzzy distance similarity method based on $\alpha$-cut (FDCM); and Dai et al.³⁵ introduced a method based on the contribution envelope area of cloud models (EACCM). In the numerical features approach, Zhang et al.³⁶ utilized the cosine angle similarity comparison method (LICM) to characterize similarity; Zhang et al.³⁷ proposed a multidimensional cloud model based on fuzzy similarity (MSCM). In the characteristic curves approach, Li et al.³⁸ proposed an area ratio algorithm based on expectation curves (ECM); Luo et al.³⁹ employed the maximum boundary of cloud models (MCM) for structural damage identification; and Lin⁴⁰ constructed similarities among five cloud concepts to reveal various similarities within uncertain concepts. Although these methods have their own contributions, they still have certain limitations. For example, the concept extension algorithm calculates similarity through random simulation, resulting in an increase in computational complexity; The numerical feature algorithm is insufficient in dealing with the intrinsic relationships between cloud model parameters; Although the characteristic curve algorithm can solve certain instability problems, it ignores some information about super entropy. This paper employs a normalized cloud similarity measurement approach, grounded in the second-order Fréchet distance,to quantify the similarity between the standard and evaluation clouds, thereby assessing the air quality level. The second-order Fréchet distance, a method commonly used to measure the similarity between curves, exhibits significant advantages in cloud model measurement. It not only accounts for differences in mean values but also incorporates the influence of variance, thereby enabling a more comprehensive capture of differences in the shape and probability distribution of cloud models.

In conclusion, the study delves into the decade-long trend of air quality fluctuations in Beijing, offering a scientific foundation and recommendations for the government to formulate environmental protection policies, aiming to foster the ongoing enhancement of environmental quality and the safeguarding of public health.

Research area and data

This section primarily introduces the geographical and climatic characteristics of the study area, Beijing, as well as its efforts in air quality management. It also provides a detailed description of the dataset used for the research and its processing methods. The dataset covers air quality data from multiple monitoring stations in Beijing from 2014 to 2023, including concentration records of six major pollutants. To address the issue of missing data, this study employs multiple imputation methods and validates the rationality of these methods through sensitivity analysis and statistical tests.

Overview of the study area

Beijing, a city steeped in history, is situated in the northern reaches of the North China Plain, encompassing an area of 16,410.54 square kilometers. The terrain slopes from a higher elevation in the northwest to a lower elevation in the southeast. The city’s geographical coordinates are $116^\circ 23^\prime 29^{\prime \prime }$ east longitude and $39^\circ 54^\prime 20^{\prime \prime }$ north latitude. Beijing experiences a warm temperate monsoon climate with semi-humid and semi-arid characteristics, marked by distinct seasonal variations. The summer is hot and rainy, while the winter is cold and dry, with spring and autumn being relatively brief.

As the capital of China, Beijing is not only a hub for political decision-making but also a pioneer in technological innovation. The city’s air quality concerns have, accordingly, garnered international attention. In a bid to enhance the well-being of its citizens, the Beijing Municipal Government has enacted a range of high-tech initiatives aimed at optimizing industrial structure, innovating transportation management, and fostering a green energy transformation.

Furthermore, Beijing is proactively engaging in regional environmental technology collaborations, working in tandem with neighboring areas to address the collective challenge of air pollution through joint prevention and control efforts. These endeavors not only contribute to a clearer sky and fresher air in Beijing but also make a significant impact on the global environmental protection, underscoring Beijing’s leadership in environmental stewardship.

Data introduction

This dataset is procured from the Environmental Meteorological Data Service Platform and encompasses meticulous records from 12 or 24 air quality monitoring stations across Beijing from 2014 to 2023. From 2014 to 2020, there were 12 monitoring stations, and the number increased to 24 from 2021 to 2023. The expansion involved adding 12 new stations, while the original 12 stations remained in their initial locations. Each station is responsible for monitoring the six types of pollutants. It includes daily atmospheric concentration data for six primary air pollution indicators–$SO_2$, $NO_2$, $PM_{10}$, CO, $O_3$, and $PM_{2.5}$. A thorough statistical analysis revealed that approximately 2% of the dataset’s values are absent. Table 1 provides a detailed description of the missing data situation.

Table 1 Summary of the percentage of missing data and its distribution across pollutants.The table shows the total data missing rates and the data missing rates for various pollutants from 2014 to 2023.

To address these missing values, we employed several data imputation methods, including linear interpolation, polynomial interpolation, and carrying forward the last observed non-missing value. We selected these methods due to their simplicity, efficiency in handling time-series data, and widespread acceptance in the field of environmental science.

We used each imputed dataset in the subsequent cloud model evaluation and compared the resulting annual AQI assessment outcomes. The analysis revealed that although there were minor differences in detail among the various imputation methods, their impact on the overall air quality assessment was negligible. This is likely because the trends in air quality indicators are relatively stable over long time series, and the absence of a single data point has a limited effect on the overall trend.

Furthermore, we performed statistical tests on the imputed datasets to ensure that the imputation did not introduce significant bias. The results of these statistical tests further confirmed the reasonableness of the imputation methods and the minimal impact they had on the assessment outcomes. Therefore, we ultimately chose to carry forward the last observed non-missing value for imputation as it provided a good balance between computational efficiency and the accuracy of the results.

To offer a holistic view of Beijing’s air quality situation, we further employed a comprehensive analysis technique: calculating the daily average concentrations of the six main pollution indicators at all 12 or 24 monitoring stations. This metric not only affords us a macroscopic perspective to assess the air quality in Beijing but also provides a scientific foundation for the formulation of corresponding environmental protection policies and measures.

Theory and method

This section provides a detailed introduction to the theoretical basis of cloud models and their application in air quality assessment. Cloud models achieve bidirectional mapping between qualitative concepts and quantitative data through three parameters: expected value Ex, En, and He. The forward cloud generator and backward cloud generator are used respectively to generate quantitative data from qualitative concepts and to infer qualitative concepts from quantitative data. The construction of evaluation cloud models and standard cloud models provides a scientific quantitative method for air quality assessment. Finally, the similarity measurement method based on the second-order Fréchet distance can effectively evaluate the similarity between the evaluation cloud model and the standard cloud model, thereby providing a basis for pollution level rating.

The cloud model, serves as a pioneering approach to bridge the gap between qualitative concepts and quantitative data within the realms of uncertainty and randomness. In the context of air quality assessment, this model demonstrates significant applicability due to its ability to encapsulate the stochastic and ambiguous nature of air quality data.

The cloud model effectively addresses the inherent randomness in air quality monitoring data by transforming quantitative data into probabilistic representations. By transforming quantitative data into qualitative cloud representations, it captures the variability and uncertainty associated with pollutant concentrations over time. Similarly, the model adeptly addresses fuzziness by allowing for the representation of imprecise data points within a probabilistic framework, thus providing a more comprehensive understanding of air quality trends.

Cloud model

This section introduces the basic concept of the cloud model and its core components. The cloud model describes the mapping between qualitative concepts and quantitative values through three key parameters: Ex, En, and He.

Definition 1

Let U be a quantitative domain represented by numerical values. If a random variable X belongs to U and is an instantiation of a qualitative concept A, then the membership degree $\mu$ of X to A is a random number with a stable tendency, and its distribution over U is referred to as a cloud. Each specific value of x in U is called a cloud droplet, denoted as $drop(x_i,\mu _i)$. If the membership degree $\mu$ of x to A satisfies $\mu (x) \in [0,1]$, then the distribution of $\mu (x)$ over U is called a normal cloud (or simply a cloud), and each specific value of $\mu (x)$ is called a cloud droplet. In this context, U is called the domain of discourse, A is called the qualitative concept, and X is called the instantiation of the qualitative concept.

If the random variable X follows a normal distribution with mean Ex and variance ${{{En}'}^{2}}$, and ${{{En}'}^{2}}$ follows a normal distribution with mean En and variance ${He}^2$, and the membership degree $\mu$ of X to concept A satisfies:

$$\begin{aligned} \mu (x)=\exp \left[ -\frac{(x-Ex)^{2}}{2\left( En^{\prime }\right) ^{2}}\right] . \end{aligned}$$

Then the distribution of X over domain U is referred to as a normal cloud (or Gaussian cloud). A normal cloud model is not a smooth curve but a scatter plot composed of numerous cloud droplets. Additionally, the probability density function of a cloud droplet X generated by the normal cloud model is given by⁴¹:

$$\begin{aligned} f(x)=\int _{-\infty }^{+\infty } \frac{1}{\sqrt{2 \pi {He}^{2}}}\exp {-\frac{(\sigma -E n)^{2}}{2 {He}^{2}}} \times \frac{1}{\sqrt{2 \pi \sigma ^{2}}} \exp {-\frac{(x-Ex)^{2}}{2 \sigma ^{2}}} d \sigma . \end{aligned}$$

Here, the expected value of X is Ex, and the variance is ${{En}^{2}}+{{He}^{2}}$, which characterizes the center position and the distribution width of the cloud model.

The numerical characteristics of the model are encapsulated in three fundamental parameters: Ex, En, and He. These quantitative traits form the bedrock of the cloud model, collectively delineating its shape and attributes. They serve as the digital foundation for the creation of virtual clouds, cloud computing, and cloud transformation processes. These three parameters ingeniously integrate fuzziness and randomness, enabling a bidirectional mapping and transformation between qualitative concepts and quantitative values. As such, the cloud model is frequently employed to symbolize $C=(Ex,En,He)$, and it can also be abbreviated as C(Ex, En, He).

Given the cloud model C(Ex, En, He), the outer envelope curve and the inner envelope curve are defined as ${y}_{O}$ and ${y}_{I}$:

$$\begin{aligned}&{{y}_{O}}={{e}^{-\frac{{{(x-Ex)}^{2}}}{2{{(En+3He)}^{2}}}}},\\&{{y}_{I}}={{e}^{-\frac{{{(x-Ex)}^{2}}}{2{{(En-3He)}^{2}}}}}. \end{aligned}$$

The inner and outer envelope curves are used to describe the range of uncertainty in the distribution of cloud droplets. The area between these two curves represents the main range of data distribution, which helps us understand the concentration trend and dispersion degree of the cloud droplets. Moreover, when $0< He < \frac{En}{3}$, 99.7% of the cloud droplets fall between the outer and inner envelope curves¹⁹.

Fig. 1

Cloud model for $O_3$ in 2023, where $Ex=109.12$, $En=58.08$, $He=6.35$.

As shown in Fig. 1, by using the cloud model of $O_3$ in 2023 as an example, we can gain a more intuitive understanding of the significance of these three numerical features¹⁹:

• 1. The Ex signifies the central position of the cloud model, indicating that the mean concentration of $O_3$ in 2023 is 109.12 $\upmu \mathrm {g/m}^3$.

• 2. The En characterizes the distribution width of cloud models and reflects the uncertainty of the concentration of $O_3$ distribution. A larger entropy value indicates a broader concentration range and a higher level of uncertainty. Conversely, a smaller entropy value suggests a more compact concentration distribution and a lower degree of uncertainty.

• 3. The He is a parameter that shapes the cloud model and defines the fuzzy boundaries of the cloud. In the context of the $O_3$ in 2023 cloud model, it can represent the ambiguity in defining the degree of pollution. For example, a higher super-entropy value results in a more indistinct boundary between air quality assessment grades, while a lower value leads to a clearer distinction.

• 4. The dashed lines on either side of the cloud $drop(x_i,\mu _i)$ represent the inner and outer envelope curves.

Cloud generator and algorithm

This section mainly introduces two key components of the cloud model: the Forward Cloud Generator and the Reverse Cloud Generator, and provides a detailed description of their functions and algorithms.The Clouds Generator, an indispensable component of cloud models, is classified into two distinct types: the forward cloud generator and the reverse cloud generator. These generators play a crucial role in handling the conversion between qualitative concepts and quantitative values.

Forward cloud generator

The Forward Cloud Generator, depicted in Fig. 2, is responsible for generating a predetermined number of cloud droplets based on three fundamental digital characteristics: the Ex, the En, and the He. This process serves to convert qualitative concepts into specific quantitative values by utilizing these numerical features, effectively generating cloud droplets. These droplets represent the distribution of qualitative concepts within the numerical domain, thereby laying a robust data foundation for quantitative analysis. The steps involved in the generation of a normal cloud are outlined in Algorithm 1.

Fig. 2

Illustration of the forward cloud generator process: inputting Ex, En, and He to obtain cloud droplets $drop(x_i,\mu _i)$.

Algorithm 1

Forward cloud generator algorithm.

Reverse cloud generator

In contrast to the Forward Cloud Generator, the Reverse Cloud Generator operates when the distribution of cloud droplets across various membership levels is already established, as illustrated in Fig. 3. It ascertains the three numerical features of the cloud model by examining these distributions. This process essentially reverses the transformation, converting quantitative values back into qualitative concepts, thereby enabling qualitative evaluation of the sample, the identification of patterns, and the understanding of trends within the data.

Fig. 3

Illustration of the reverse cloud generator process: inputting cloud droplets $drop(x_i,\mu _i)$ to obtain Ex, En, and He.

The inverse cloud generation algorithm employs cloud droplets $\{{{x}_{1}},{{x}_{2}},\ldots ,{{x}_{n}}\}$ to estimate the cloud value of the sample data. The formula used to calculate the cloud estimation value $C(\hat{Ex},\hat{En},\hat{He})$ for the sample data is represented as :

$$\begin{aligned} & \hat{Ex} = \frac{1}{n} \sum _{i=1}^{n} x_{i},\\ & \hat{En} = \sqrt{\frac{\pi }{2}} \times \frac{1}{n} \sum _{i=1}^{n}\left| x_{i}-\hat{Ex} \right| , \\ & \hat{He} = \sqrt{\left| \frac{1}{n-1} \sum _{i=1}^{n}\left( x_{i}-\hat{Ex}\right) ^{2}-{\hat{En}}^{2}\right| }. \end{aligned}$$

Construction of evaluation cloud model and standard cloud model

This section primarily discusses the construction of evaluation cloud models and standard cloud models and their application in air quality assessment. Cloud model theory provides an innovative tool for quantitatively addressing issues of uncertainty and ambiguity by integrating fuzziness and randomness.

The establishment of evaluation cloud models and standard cloud models forms the cornerstone of cloud model theory, offering an innovative tool for quantitatively addressing issues of uncertainty and ambiguity. The construction process of these models not only reflects a deep understanding of complex phenomena but also provides a scientific quantitative method for evaluation and policy-making.

Evaluating cloud models involves generating cloud models based on raw data using a reverse cloud generator. This method captures the evaluator’s subjective evaluation of a concept or object and converts it into a quantifiable set of values–cloud droplets. These droplets follow a specific probability distribution, forming evaluation clouds that reflect the statistical characteristics of pollutant concentrations, thereby transforming the evaluator’s subjective judgment into an objective numerical representation.

The standard cloud model corresponds to the evaluation cloud model. The standard cloud is generated by a forward cloud generator based on established evaluation criteria, defining the benchmark or ideal state of the evaluated object and providing a reference point for evaluation. The construction of the standard cloud model involves setting the values of Ex, En, and He, which collectively determine the shape and distribution of the standard cloud.

Once these two models are constructed, calculating the distance or difference between them becomes a crucial step. This calculation allows us to quantify the similarity or difference between the models and, consequently, determine the level to which the evaluation cloud belongs. In this study, this process was applied to the analysis of air pollutant values to determine and classify the level of air quality.

Construction of evaluation cloud

In the process of constructing an evaluation cloud model, we first defined an air quality index formula based on an aggregation function to quantify the comprehensive impact of various pollutants. The formula is expressed as:

$$\begin{aligned} I_{\rho }=\left( \sum _{k=1}^{K}\left( A Q I_{k}\right) ^{\rho }\right) ^{\frac{1}{\rho }}. \end{aligned}$$

Here, $\rho$ is a parameter greater than or equal to 1, and K represents the total number of pollutant types being considered. Each ${AQI}_k$ represents the air quality index for the k-th pollutant, calculated using the following formula:

$$\begin{aligned} A Q I_{k}=\frac{I_{H}-I_{L}}{C_{H}-C_{L}}\left( C_{k}-C_{L}\right) +I_{L}. \end{aligned}$$

In this formula, $C_k$ is the air quality concentration of k-th pollutant; $C_H$ is the concentration threshold higher than $C_k$; $C_L$ is the concentration threshold below $C_k$; $I_H$ is the AQI corresponding to $C_H$; $I_L$ is the AQI corresponding to $C_L$. By employing this formula, we can convert the concentration values of different pollutants into corresponding AQI values. Subsequently, we utilize the aggregation function $I_\rho$ to comprehensively evaluate air quality. The traditional AQI rating method involves converting the concentration values of different pollutants into corresponding AQI values and then selecting the maximum AQI value as the basis for the rating, without considering the other AQI values. In contrast, the method we propose not only takes into account the impact of individual pollutants but also allows us to adjust the $\rho$ value to strike a balance between the cumulative effect of pollutants and the single maximum impact based on the evaluation requirements.

In the realm of air quality assessment, the selection of $\rho$ values is pivotal in determining the aggregation method for pollution indicators. When $\rho$ equals 1, $I_\rho$ represents the straightforward sum of various pollutant index values, accounting for the cumulative effect of all pollutants. Conversely, when $\rho$ is set to infinity, $I_\rho$ is transformed into the maximum value among the various pollutant indicators, which with the calculation method of China’s Environmental Air Quality Index, which prioritizes the maximum impact of a single pollutant.

Studies by Zhang Feng et al.²⁷, Lin²⁸, Wang²⁹, and Zhao Jianping et al.³⁰ are founded upon this maximum value method to construct their evaluation cloud models. These investigations underscore the most severe impact that a single pollutant can have on air quality by setting $\rho$ to infinity.

To delve deeper into the influence of $\rho$ values on AQI, Ruggieri et al.⁴² conducted simulation studies. These studies not only assessed the impact of varying $\rho$ values on AQI but also validated the suitability and rationality of the $\rho =2$ choice in practical applications by comparing it with the daily mortality relative risk index proposed by Cairncross et al.⁴³. Building upon these scholarly findings, we have elected to utilize $I_2$ as the index for assessing air quality. This decision takes into account both the cumulative effect of pollutants and the potential maximum impact of a single pollutant, offering a more comprehensive and balanced perspective for the evaluation of air quality.

To derive the three numerical features necessary for evaluating cloud models, we have introduced Lemma 3.1 and Lemma 3.2. The Lemma 3.1 elucidates the rules for combining two independent normal cloud models, while Lemma 3.2 delineates the transformation rules for non-zero constant powers of normal cloud models.

Lemma 3.1

Consider two independent normal cloud models, $C_1$ and $C_2$, defined over a domain U. If $C_1$ is characterized by ${{Ex}_1},{{En}_1},{{He}_1}$, and $C_2$ is characterized by ${{Ex}_2},{{En}_2},{{He}_2}$, then the combined cloud model ${C_1}\pm {C_2}$ is represented by:

$$\begin{aligned} {C_1}\pm {C_2}= ({Ex}_1\pm {Ex}_2,\sqrt{{En}_1^{2}\pm {En}_2^{2}},\sqrt{{He}_1^{2}\pm {He}_2^{2}}). \end{aligned}$$

Lemma 3.2

Suppose there is a normal cloud $C_1$ defined over a domain U, and a non-zero constant $\alpha$. Then, the power of $C_1$ raised to the power of $\alpha$ is given by:

$$\begin{aligned} {C_1}^{\alpha }=({{Ex}_1}^{\alpha },\alpha {{Ex}_1}^{\alpha -1}{En_1},\alpha {{Ex}_1}^{\alpha -1}{He}_1). \end{aligned}$$

Let $C_k=({Ex}_k,{En}_k,{He}_k)$ denote the cloud model for the k-th pollutant. By applying Lemma 3.1 and Lemma 3.2, we can derive the three numerical features of the evaluation cloud for $I_\rho$, which are:

$$\begin{aligned}&\hat{E}{{x}_{I\rho }}={{(\sum \nolimits _{k=1}^{K}{Ex_{k}^{\rho }})}^{\frac{1}{\rho }}}\\&\hat{E}{{n}_{I\rho }}={{(\sum \nolimits _{k=1}^{K}{Ex_{k}^{\rho }})}^{\frac{1}{\rho }-1}}\sqrt{\sum \nolimits _{k=1}^{K}{{{(Ex_{k}^{\rho -1}E{{n}_{k}})}^{2}}}}\\&\hat{H}{{e}_{I\rho }}={{(\sum \nolimits _{k=1}^{K}{Ex_{k}^{\rho }})}^{\frac{1}{\rho }-1}}\sqrt{\sum \nolimits _{k=1}^{K}{{{( Ex_{k}^{\rho -1}H{{e}_{k}})}^{2}}}}. \end{aligned}$$

Among them, when $\rho = 2$, which are:

$$\begin{aligned}&\hat{E}x_{I_2} = \sqrt{\sum \nolimits _{k=1}^{K}Ex_{k}^{2}}, \end{aligned}$$

(1)

$$\begin{aligned}&\hat{E}n_{I_2} = \sqrt{\frac{\sum \nolimits _{k=1}^{K} Ex_{k}^{2}En_{k}^{2}}{\sum \nolimits _{k=1}^{K} Ex_{k}^{2}}}, \end{aligned}$$

(2)

$$\begin{aligned}&\hat{H}e_{I_2} = \sqrt{\frac{\sum \nolimits _{k=1}^{K} Ex_{k}^{2}He_{k}^{2} }{\sum \nolimits _{k=1}^{K} Ex_{k}^{2} }}. \end{aligned}$$

(3)

These expressions encapsulate the essential aspects of the evaluation cloud model for $I_2$, capturing the combined influence of the various pollutants on air quality. Therefore, we integrated cloud models of multiple pollutants to derive an evaluation cloud model that comprehensively reflects the air quality status. The cloud model for the k-th pollutant was estimated from the observation sample data using the reverse cloud approach.

Construction of standard cloud

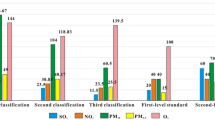
Building upon the technical specifications of China’s Environmental Air Quality Index and the grading standards for atmospheric environmental quality evaluation indicators⁴⁴, we have established a comprehensive quantitative framework, as detailed in Table 1. This framework categorizes AQI and various pollutants into five distinct pollution levels, each level associated with a specific quantification range, denoted as $[C_{min}^k,C_{max}^k)$, where $C_{min}^k$ and $C_{max}^k$ represent the lower and upper limits of quantification for the k-th indicator, respectively.

Table 2 Grade standards for atmospheric environmental quality indicators: a representation of pollutant concentration limits across diverse air quality levels.

To establish standard cloud models for the various pollution levels, we developed five one-dimensional standard clouds based on probability and consequence criteria⁴⁵. The numerical features of these standard clouds are determined by follow specific formulas, where r is a constant that can be adjusted according to the randomness of the data.

$$\begin{aligned} Ex=&\frac{1}{2}({{C}_{\max }}+{{C}_{\min }}),\\ En=&\frac{1}{6}({{C}_{\max }}-{{C}_{\min }}),\\ He=&r*En. \end{aligned}$$

In determining the numerical features of these standard clouds, we followed a configuration akin to that of Zhao Jianping et al.³⁰. With the exception of the CO cloud model, which is set with $r=0.01$, experiments have shown that the value of r does not affect the evaluation results. The value of $r = 0.01$ for CO is chosen because its concentration unit is relatively small. All other cloud models are assigned $r=0.1$. This configuration is designed to reflect the relative significance and uncertainty of the impact of various pollutants on air quality. The standard cloud assessment model’s numerical features, as presented in Table 2 of this paper, furnish us with a clear and methodical framework for evaluating and quantifying the pollution status of the atmospheric environment. Based on the AQI standard cloud digital features in Table 2, we utilized MATLAB programming to generate the standard cloud diagram, as depicted in Fig. 4.

Table 3 Numerical features of standard cloud models. This table shows the cloud model parameters for AQI and various pollutants at different pollution levels. Each pollution level (excellent, good, mild pollution, moderate pollution, severe pollution) has a set of parameters (Ex, En, He), representing Ex, En, and He, which describe the expected concentration, distribution width, and fuzzy boundary of pollutant concentrations at that level.

Fig. 4

AQI standard cloud diagram. From left to right, each cloud corresponds to an air quality rating of excellent, good, mild pollution, moderate pollution, and severe pollution.

Table 4 Numerical features of pollution index cloud model. This table displays the cloud model parameters for various pollutants from 2014 to 2023. Each set of parameters (Ex, En, He) describes the expected value, distribution width, and fuzzy boundary of pollutant concentrations for the corresponding year.

Similarity measurement between normal clouds

This section introduces a novel second-order Fréchet distance-based similarity measurement method for normal clouds, used to evaluate the similarity between the evaluation cloud model and the standard cloud model to determine pollution levels.

Evaluating the similarity between the evaluation cloud model and the standard cloud model is a critical step in ascertaining the level of pollution. While existing cloud model similarity measurement methods possess their distinct advantages, they may encounter certain limitations when dealing with precise quantitative calculations or analyses that rely on cloud model shape characteristics. These limitations can result in insufficient classification accuracy, diminished discrimination, and increased computational complexity, thereby impacting the precision of measurement outcomes. To address these challenges, this article introduces a novel normal cloud similarity measurement method that is based on the second-order Fréchet distance.

Definition 2

Let $\mu$ and v be probability measures defined on $R^n$. For any random variable $X\sim {\mu }$ and $Y\sim {v}$, the second-order Fréchet distance is defined as:

$$\begin{aligned} {{d}^{2}}(u,v)=inf E{{||X-Y||}^{2}}, \end{aligned}$$

where $||\cdot ||$ represents the Euclidean norm.

The second-order Fréchet distance is a method for quantifying the disparity between two probability distributions, characterized by key mathematical properties such as non-negativity, symmetry, and adherence to trigonometric inequalities. Specifically, when the random variables X and Y are drawn from the same distribution family and the family is closed under scaling and translation, the second-order Fréchet distance can be expressed as follows⁴⁶:

$$\begin{aligned} {{d}^{2}}(u,v)=({\mu }_X-{\mu }_Y)^{2}+({\sigma }_X-{\sigma }_Y)^{2}, \end{aligned}$$

where ${\mu }_X$ and ${\mu }_Y$ are the expectations of X and Y, respectively, and ${\sigma }_X$ and ${\sigma }_Y$ are their corresponding standard deviations.

As a mechanism for addressing uncertainty, cloud models exhibit closure under scale and displacement parameters. Within the cloud model framework, the expectation is represented by Ex, and the standard deviation is given by $(\sqrt{{En}^{2}+{He}^2})$. Given two cloud models $C_1=(Ex_1,En_1,He_1)$, and $C_2=(Ex_2,En_2,He_2)$, the second-order Fréchet distance between $C_1$ and $C_2$ can be expressed as:

$$\begin{aligned} {{d}^{2}}({{C}_{1}},{{C}_{2}}) = {{(E{{x}_{1}}-E{{x}_{2}})}^{2}} + {{\left( \sqrt{En_{1}^{2}+He_{1}^{2}}-\sqrt{En_{2}^{2}+He_{2}^{2}}\right) }^{2}}. \end{aligned}$$

This distance metric quantifies the structural similarity between two cloud models. A smaller value of $d^{2}(C_1,C_2)$ indicates a greater similarity in the probability distributions of $C_1$ and $C_2$. In essence, the aforementioned second-order Fréchet distance aligns with the distance metric proposed by Xu and Yang⁴⁷.

It is important to emphasize that the cloud similarity measurement based on the second-order Fréchet distance is a relative measure rather than an absolute one. We calculate the second-order Fréchet distance between the evaluation cloud and each of the all standard clouds corresponding to different pollution levels. The grade assigned to the evaluation cloud is determined by identifying which standard cloud has the smallest Fréchet distance to the evaluation cloud. In other words, the evaluation cloud is classified into the pollution level associated with the standard cloud that exhibits the highest similarity (i.e., the smallest Fréchet distance) to it.

Beijing air quality assessment

In this section, we endeavor to undertake a thorough reassessment of Beijing’s outdoor air quality spanning the past decade. The overarching objective of this research is to fabricate standard clouds and assessment clouds for a spectrum of air pollutants, thereby furnishing us with established standards for gauging air quality and the probability distributions of real-world observation data. Thereafter, we employed the set function approach to compute the evaluation cloud based on the $I_2$ index, which harmoniously incorporates the impacts of diverse pollutants to offer a more precise reflection of the prevailing air quality. Ultimately, we leveraged the concept of cloud similarity to compare the standard cloud against the evaluation cloud, thereby determining the annual air quality rating for Beijing.

In this paper, we systematically constructed cloud models to evaluate the air quality in Beijing, following these steps:

• 1. We employed a data imputation method to effectively fill in the missing values in the dataset, thereby ensuring the completeness and accuracy of the evaluation process.

• 2. We established five pollution levels for AQI and various pollutants based on the technical indicators of China’s Environmental Air Quality Index and the grading standards for atmospheric environmental quality evaluation indicators. The specific results are detailed in Table 2.

• 3. By utilizing the indicator approximation method, we developed standard cloud models for various pollutants and AQI. The detailed construction results of these models are summarized in Table 3.

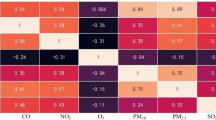
• 4. We constructed evaluation clouds for various pollutants using the reverse cloud generator, based on the actual pollutant monitoring data in Beijing. The relevant results are presented in Table 4. Taking the cloud chart of various pollutants in 2014 (Fig. 5) as an example, the smaller the distance between a pollutant’s cloud and a certain standard cloud of that pollutant in Table 3, the more the assessment level of the pollutant belongs to the level of that standard cloud.

• 5. We further obtained an evaluation cloud model based on the $I_2$ index, using the formula (1), (2) and (3). The results are detailed in Table 5.

• 6. Finally, annual pollutant and AQI ratings were derived using the second-order Fréchet distance, highlighting trends and improvements. The rating results are shown in Table 6.

Fig. 5

The cloud diagrams of various pollutants in 2014. The cloud diagrams allow for a preliminary estimation of the range of pollutant assessment grades.

Table 5 Numerical features of the evaluation cloud model. This table presents the numerical characteristics of the evaluation cloud model from 2014 to 2023. The evaluation cloud model is composed of three parameters: Ex, En, He. Each row in the table corresponds to a specific year, listing the three parameter values for that year, which reflect the average level, distribution breadth, and fuzziness of the air quality assessment for that year.

Table 6 Rating scale: 1=excellent grade, 2=good grade, 3=mild pollution grade, 4=moderate pollution grade.

Over the past decade from 2014 to 2023, Beijing has witnessed a remarkable improvement in its air quality. The AQI has consistently trended downward, transitioning from a moderate pollution level (Level 4) in 2014 to a mild pollution level (Level 3) by 2023, signifying a broad-based enhancement in overall air quality. Notably, the annual levels of CO, NO$_2$, and SO$_2$ have consistently maintained an excellent rating (Level 1), underscoring the effective control measures implemented for these pollutants.

The stability of O$_3$ at an annual good rating (Level 2) indicates the successful management of ozone pollution, with no discernible deterioration over the years. Moreover, the annual levels of inhalable particulate matter $PM_{10}$ and fine particulate matter $PM_{2.5}$ have notably declined from good or light pollution levels in 2014 to an excellent rating (Level 1) by 2023, indicating a significant reduction in the concentration of these key pollutants and their diminishing impact on air quality.

Data for 2016 and 2022 in particular highlight excellent ratings, suggesting notable air quality improvements during those years. The substantial decrease in the annual average concentration of $PM_{2.5}$ in Beijing from 89.5 ${\upmu }\mathrm{g/{m}}^3$ in 2013 to 32.0 ${\upmu }\mathrm{g/{m}}^3$ in 2023 is a testament to the significant strides made in $PM_{2.5}$ pollution control over the decade. Furthermore, the proportion of days with heavy and severe pollution has also significantly decreased from 15.9% in 2013, further corroborating the overall enhancement in Beijing’s air quality.

The consistently low pollution level of SO$_2$ can be attributed to stringent control measures on industrial emissions, particularly coal combustion, in recent years. The fluctuations in the pollution levels of NO$_2$, O$_3$, inhalable particulate matter $PM_{10}$, and fine particulate matter $PM_{2.5}$ across different years may be associated with changes in traffic emissions, industrial activities, and natural conditions such as wind speed, temperature, and humidity. These variations underscore the complexity of improving air quality, which necessitates multifaceted efforts and continuous monitoring.

To substantiate the efficacy of the cloud model in air quality assessment, we conducted a comparative analysis with traditional methods as shown in Fig. 6. Since the official data only provides daily AQI values and not annual AQI values, the traditional AQI rating results in this paper are determined by averaging the maximum daily AQI values annually and then assessed based on China’s technical specifications for atmospheric environmental quality evaluation. Our proposed $I_2$ method and the traditional AQI rating exhibit similar trends in results. However, our method imposes stricter criteria for pollution classification. The traditional AQI rating is mostly better than $I_2$ because it involves converting the concentration values of different pollutants into corresponding AQI values and then selecting the maximum AQI value as the basis for the rating, without considering the other AQI values. This approach may lead to an underestimation of pollution compared to our more rigorous $I_2$ method.

Fig. 6

The comparison between $I_2$ and traditional AQI.

Our cloud model not only provides a more nuanced representation of air quality by accounting for the probabilistic nature of pollutant concentrations but also offers a comprehensive framework that can integrate various pollutants’ effects synergistically. The results of our analysis indicate that the cloud model approach outperforms traditional methods across several key metrics.

This suggests that the cloud model is more adept at capturing the subtle variations and complexities in air quality data, which is critical for precise environmental monitoring and policy formulation. Regarding stability, the cloud model showed less variability in assessment outcomes over time, providing more consistent air quality evaluations. This is particularly important for long-term air quality management, as it allows for more reliable tracking of air quality trends and the effectiveness of pollution control measures.

Discussion and suggestions

This paper proposes an annual comprehensive evaluation method for air quality based on cloud models. The core findings of this study highlight a significant improvement in Beijing’s air quality over the past decade, with the AQI showing a continuous downward trend from moderate pollution in 2014 to mild pollution in 2023. Specific pollutants such as $PM_{10}$, $PM_{2.5}$, and SO$_2$ have shown marked reductions, transitioning from good or light pollution levels to excellent ratings. The cloud model method effectively captures the probabilistic nature of pollutant concentrations, providing a more nuanced and rigorous assessment compared to traditional methods. This method not only handles the inherent fuzziness and randomness in the data but also significantly improves evaluation accuracy through the introduction of a similarity measurement method based on the second-order Fréchet distance. The study provides a scientific basis for environmental management and policy-making by analyzing the ten-year trends of air quality in Beijing. The cloud model method is versatile and adaptable, making it suitable for air quality assessments in any city, regardless of its specific pollutant profiles or meteorological conditions. Future work should focus on integrating additional computational models and exploring the physical and chemical interactions between pollutants and other factors to further enhance the comprehensiveness and practical application value of the model.

Although the cloud model is effective, it faces limitations when dealing with sparse or unevenly distributed datasets. In situations with limited data, the model may fail to accurately represent the true distribution of air quality parameters, which could lead to biases in the evaluation results. Moreover, in areas with highly variable data distributions, the model might oversimplify the complexity of the data, thus compromising the precision of the assessment. In the process of evaluating the model, we only considered the impact of different He on the results, while failing to take Ex and En into account. At the same time, when constructing the comprehensive cloud model, we did not thoroughly explore the potential effects of different $\rho$ on the rating outcomes, limiting our analysis to the scenario where $\rho$ equals 2. Furthermore, this study does not link AQI to health impacts and only evaluates the AQI levels, which, to some extent, limits the comprehensiveness and practical application value of the model.

To tackle these challenges, we propose several strategies. Firstly, data augmentation through interpolation or simulation methods can enrich the dataset and enhance the model’s accuracy. Secondly, integrating other computational models, such as fuzzy logic or machine learning algorithms, can provide a more nuanced analysis of air quality data. Lastly, developing hybrid models that combine the cloud model with other statistical or machine learning techniques could offer a more robust framework for air quality assessment. Salcedo-Bosch et al.⁴⁸ developed a one-day-ahead air pollution forecasting model for Shanghai. This model integrates various meteorological variables, such as temperature, relative humidity, wind speed and direction and precipitation, and conducts an in-depth analysis of how these factors affect the concentrations of ${PM}_{10}$ and ${PM}_{2.5}$. Additionally, it incorporates aerosol optical depth at 550 nanometers and planetary boundary layer height, thereby significantly enhancing the model’s predictive accuracy. This study suggests that future research should further explore the physical and chemical interactions between pollutants and other factors⁴⁹, with the aim of improving the comprehensiveness and practical value of the model.

Building upon an in-depth analysis of Beijing’s outdoor air quality over the past decade, We have observed an overall improvement in Beijing’s air quality, particularly marked by significant achievements in the control of $PM_{10}$, $PM_{2.5}$, and SO$_2$. The rating for NO$_2$ has also improved from a 2 (good) in 2014 to a 1 (excellent) in 2023. However, the rating for O$_3$ has consistently remained at 2 (good), indicating that while ozone pollution control has been relatively stable, it still requires ongoing attention. Therefore, we propose the following three recommendations to enhance air quality management:

• 1. It is crucial to maintain the integrity of air quality monitoring data. We advocate adopting data filling techniques that carry forward the last observed non-missing value to address missing values and ensure the continuity and accuracy of the assessment. Additionally, the establishment of a real-time air quality monitoring and warning system is essential for timely capture and response to air quality changes. Moreover, the adoption of a multidimensional evaluation approach can better account for pollutant interactions, enhancing policy relevance.

• 2. Based on real-time evaluation results, the primary sources of pollution should be identified and controlled. From the evaluation results, it is evident that the primary pollutants are $PM_{10}$, $PM_{2.5}$, and O$_3$. Given the significant achievements in reducing $PM_{10}$ and $PM_{2.5}$ levels over the past decade, it is recommended to continue strengthening and optimizing existing control measures. This requires consistently enforcing strict industrial emission standards for heavy industries such as steel and cement. Additionally, promoting the use of advanced particulate filtration technologies in industrial processes and the transportation sector can further reduce emissions.

  Although O$_3$ levels have remained at a good level, ongoing attention is still necessary. O$_3$ is not directly emitted as a pollutant but is formed through photochemical reactions between nitrogen oxides (NOx) and volatile organic compounds (VOCs) under sunlight. Therefore, it is recommended to develop comprehensive strategies to control O$_3$ precursors, including NOx and VOCs.⁵⁰ This can be achieved by implementing stricter regulations on emissions from chemical and petrochemical industries and promoting the use of low-VOC products across various sectors. Continuous research and monitoring of ozone formation mechanisms can provide a basis for more effective control measures.

• 3. Raising public awareness and encouraging participation in environmental protection are equally important for improving air quality. We recommend enhancing environmental education and encouraging public involvement in monitoring and improving air quality activities. Additionally, technological innovation is pivotal for advancing air quality management. Encouraging interdisciplinary research and applying new technologies such as cloud computing, big data, and artificial intelligence to air quality monitoring and assessment can not only enhance the efficiency and accuracy of assessments but also provide a more robust scientific basis for policy making.

Beijing’s unique geographical location, characterized by its position in the North China Plain and its topography sloping from higher elevations in the northwest to lower in the southeast, plays a significant role in the distribution and dispersion of air pollutants. The city’s climate, marked by distinct seasonal variations with hot and rainy summers and cold, dry winters, also greatly influences air quality patterns. Industrial activities, particularly those related to coal combustion and vehicular emissions, contribute substantially to the pollution load, especially during periods of inversion when cold air traps pollutants close to the ground.

These factors combined make Beijing’s air quality assessment distinct. However, many of these characteristics are not exclusive to Beijing and can be found, to varying degrees, in other urban centers. For instance, other cities in the North China Plain also experience similar climatic conditions and topographical influences. Industrialization patterns, while specific to each city, often share common pollutants that can be similarly assessed using the cloud model.

When applying the cloud model to other cities, it is essential to consider the local context. For cities with different climatic conditions, such as those with maritime or continental climates, the model may need to account for the influence of weather systems on pollutant dispersion. Cities with different industrial profiles may require adjustments to the types of pollutants prioritized in the assessment.

To adapt the model, a comprehensive analysis of the local environment is necessary. This includes understanding the predominant pollution sources, the typical meteorological conditions, and the city’s specific topographical features. By tailoring the cloud model to these local characteristics, the assessment can be made more relevant and accurate.