Introduction

Small basins are of significant value of water resource management1,2,3agricultural irrigation4,5and disaster prevention and mitigation6,7,8. However, the lack of water monitoring data has substantially hindered the effective utilization of water resources and flood prevention efforts in these areas8,9. Researchers in related fields have conducted extensive studies and obtained valuable insights when designing flood calculations and runoff forecasts for small watersheds. Several studies10,11 have demonstrated a standardized the derivation of the design flood process for small data-scarce watersheds by calculating the design flood applying methods such as the unit hydrograph12,13,14 and reasoning formula methods15,16,17. In addition to calculations using results from hydrological manuals and other established sources, researchers have explored new models and methods to design flood calculations and runoff forecasts in these watersheds. Such as the unit hydrologic map theory18 and critical storm duration19. Other researchers have also focused on flood simulation and forecasting in small basins by constructing hydrological models, including HEC-HMS20,21, DHF22,23, GA-BP24and the double-hyper model25, which are crucial for addressing flood-related challenges in data-scarce watersheds.

Other researchers have also identified limitations in the above studies. In practical calculations, a watershed often consists of various terrains with significant variations across different areas26,27. Applying the same production and confluence parameters across these areas can lead to errors in design flood calculations. Xing28 calculated floods using two methods: considering the watershed as a whole and by dividing it into two types of terrain, mountainous and plain, and then superimposing the results. The latter method yielded more accurate results. Chu29 and Colby30 separately calculated flood for the mountainous and plain areas of the watershed, with the results showing significant difference between the two. Other researchers have incorporated different topography into basin flood calculation models, achieved better results than using the watershed as a whole [e.g.,31,32]. In recent years, to mitigate the influence of varying terrains on design flood calculations, researchers have focused on floods design in small watersheds with single terrains. Some researchers investigated flood modeling and forecasting in small watersheds in mountainous regions and achieved satisfactory results [e.g33,34,35,36,37]. Additionally, researchers have investigated the flood design for small watersheds on plains. Wang38 and Chen et al.39 enhanced the calculation accuracy of design floods in plains watersheds by utilizing existing data of developing corresponding models.

These researchers have recognized the limitations of using identical model parameters across different topographic regions and have explored method for calculating design floods in small watersheds with a single topographic [e.g.,40,41]. However, these approaches have limitations when applied to watersheds with composite topography, which constitute the majority of watersheds. Some researchers have attempted to overcome this limitation. Ge and Huang42 explored the adaptation of hydrological models for different types of watersheds. Xu et al.43 provided a detailed discussion of the design flood process of small watersheds in mixed zones, offering a valuable for related calculations. Zhou44 calculated a combination of flood flows in mountainous and plain areas within small watersheds. Other researchers have indirectly obtained the flood process in hilly and plain areas through evolutionary calculations using the dispatch downdraft process as input [e.g.,45,46,47]. The aforementioned research on flood differences across different topographic regions is noteworthy. However, in order to accurately model mountain and plain floods within a topographically composite watershed, it is essential to divide the entire flood event process into distinct mountain and plain floods, or even further subdivide these into more detailed sub-processes. This approach not only enhances the precision of flood simulations but also improves the adaptability and practical applicability of models under varying topographic conditions, thereby offering more reliable support for flood management and decision-making. Current research tends to focus predominantly on overall flood event simulations, with relatively limited attention given to the separate study of mountain and plain floods. Therefore, there is a need for further research in this area.

To address the challenge of distinguishing flood events across different terrain types48, which is often difficult in current flood calculations, this study proposes to solution through the development of a multi-layer hydrological process combination model (MHPCM). This model integrates all-natural hydrological processes, including precipitation, flow generation, flow confluence, and evolution. The combined model incorporates the runoff generation model, flow concentration model, evolution model, and optimization algorithm into an overarching framework. This framework allows for optimization and ensures the accurate determination of production and confluence model parameters for mountainous and plain regions. This approach enhances the scientific and theoretical foundations of flood division and simulation, fills the gap in flood event division methods for composite terrain areas, provides a scientific approach for division floods across various terrain regions, and offers more precise decision support for hydrological management, flood prevention, and control.

The main objectives of this work as follows:(I) MHPCM development: Sect. 2 develops the MHPCM for dividing different types of floods in different regions through the all-natural hydrological process of “precipitation - runoff generation - confluence - evolution.” (II) Application of MHPCM: Sect. 4 details the applicaton of the MHPCM in the study area, including the parameter calibration for the production and confluence model in mountainous and plain regions. The flood event division process is simulated for both regions and the results are evaluated. (III) Simulation results analysis: Sect. 5 analyzes the simulation results, explores their causes, and assesses the reasonableness of the model parameters used in the flood modeling. (IV) Conclusion and future research: Sect. 6 concludes with a summary, addresses key points, and suggests potential directions for future research on MHPCM. The MHPCM offers novel insights into flood division for terrain-complex watersheds, which is crucial for flood defense and the design of water conservancy projects in small watersheds.

Methodology

Flood characteristics vary significantly across different terrain regions, and the more detailed the terrain types division, the greater the complexity of the calculation. To simplify the calculation, this study focuses on a small binary watershed composed of mountainous and plain areas. This study provides a detailed explanation of the construction of the MHPCM.

Overview of the problem

In practice, failing to distinguish between mountain and plain floods may result in overly conservative flood control designs for mountain flood control facilities and water conservancy projects and overly lenient designs for plains. Not only does this increase construction costs, but it may also make it challenging to respond effectively to the threat of flooding, leading to disruptions in the water-building business and flood prevention. In addition, the scarcity of hydrological stations is an important reason for the lack of observed data for small- and medium-sized basins. The regionalized runoff production and confluence combined model developed in this study can address the issue of the absence of observed data in small watersheds to some extent. For the flood calculation of data-scarce small- and medium-sized watersheds, it is essential to determine the flow production and confluence model parameters for both mountainous and plain areas.

Modeling basics

Fig. 1
figure 1

Procedure for building and solving the MHPCM.

Full size image

The division of mountain and plain floods can be understood by considering the mountain and plain outlet sections of a topographically complex watershed as virtual hydrological stations and by calculating and determining their respective flood processes separately. Therefore, in the construction of the model, first, the areas with different topographies in the watershed must be divided based on the specification or hydrological regionalization44. Splitting an intact watershed can disrupt its integrity. However, in principle, it remains an intact catchment area with individual areas connected by the catchment model. Before constructing the model, it was necessary to determine the watershed characteristic parameters of the different sub-basins in the catchment area. Furthermore, collecting rainfall data from rainfall stations and measuring flood data from hydrological stations in the catchment area are the bases for calibrating production and confluence model parameters.

MHPCM

The MHPCM was proposed in response to these problems. The procedure for building and solving the MHPCM is shown in Fig. 1. The MHPCM can be used for areas with varying and contiguous terrains. For example, the front model can be applied with multiple back models. To facilitate understanding and calculation, this study divided the MHPCM into two layers: front and back, corresponding to mountainous and plain areas, respectively. The two layers of the model are as follows.

Foundational model

This study mainly emphasizes the research idea and work process of flood event division in different topographic, so the selection of hydrological model is replaceable. The Xin’anjiang model49,50 features a detailed structure, flexible parameterization, and relatively low data requirements. It is highly effective in simulating the complex hydrological processes within a watershed51 and has been widely applied and validated in fields such as watershed management52 and flood forecasting53,54. In this study, the basic model used was the Xin’anjiang model, and its flow routing module method is the Muskingum method, this combination is classical and research-validated. The model principle is shown in Fig. 2.

The Xin’anjiang model, as the foundation of the MHPCM, was utilized in both the front and back models. According to the application of the model, it is always subject to the constraints in Eqs. (1)-(5):

  1. (1)

    Soil water content should be non-negative:

$$\:WU,WL,WD\ge\:0$$
(1)

where \(\:WU\), \(\:WL\), and \(\:WD\) represent the upper, lower, and deep soil water content, respectively.

  1. (2)

    Constraints of model structural parameter:

$$\:KG+KI=0.7$$
(2)

where \(\:KG\) and \(\:KI\) are the outflow coefficients of the free-water reservoirs for the groundwater and loamy streams, respectively. This constraint can address the non-independence problem of parameters in water source division and prevent parameter correlation from negatively impacting the stability of the parameter optimization results.

Fig. 2
figure 2

Schematic of the Xin’anjiang model (The basic principle of the model is that precipitation is gathered in the outlet section of the watershed through surface runoff from impervious areas, intermediate flow from infiltration in permeable areas, and subsurface runoff, thus forming the runoff process. The meaning of each symbol is shown in the supplementary information.)

Full size image
  1. (3)

    Constraints of flow convergence velocity:

$$\:CG\ge\:CI\ge\:CS$$
(3)

where \(\:CG\), \(\:CI\), and \(\:CS\) are the confluence velocities of the slope, loam, and subsurface runoffs, respectively.

  1. (4)

    Constraints of flow convergence parameter:

$$\:2KE\cdot\:XE\le\:\varDelta\:t\le\:2KE-2KE\cdot\:XE$$
(4)

where \(\:KE\) and \(\:XE\) are the parameters of the Muskingum method, and \(\:\varDelta\:t\) is the computational time step.

  1. (5)

    Constraints of flow routing parameter:

$$\:{C}_{0}+{C}_{1}+{C}_{2}=1$$
(5)

where \(\:{C}_{0}\), \(\:{C}_{1}\), and \(\:{C}_{2}\) are Muskingum flow evolution coefficients, and \(\:{C}_{0}\in\:\left[0,1\right]\), \(\:{C}_{1}\in\:\left[0,1\right]\), \(\:{\text{C}}_{1}=1-{\text{C}}_{0}-{\text{C}}_{1}\in\:\left[0,1\right] .\)

The foundational model takes rainfall and evaporation process data within the region as inputs, and processes the inputs to obtain the simulated flood process at the outlet section.

Front level model

The main objective of the front-level model is to optimize the calibration parameters for production and confluence models in mountainous regions using hydrological data from an actual station in that region. Then, the results were applied to mountainous areas where flood division were necessary to obtain the flood process at the exit cross section of the mountainous region. This was also the input for the back-level model. The objective function of the front-level model is as follows:

  1. 1)

    Maximizing the NSE:

$$\:\text{m}\text{ax}\text{}f=\text{m}\text{a}\text{x}{\sum\:}_{i=1}^{n}{\sum\:}_{j=1}^{m}NS{E}_{i,j}=max{\sum\:}_{i=1}^{n}{\sum\:}_{j=1}^{m}(1-{\sum\:}_{t=1}^{T}({Q}_{i,j,R}^{t}-{Q}_{i,j,E}^{t}{)}^{2}/{\sum\:}_{t=1}^{T}({Q}_{i,j,R}^{t}-{{\bar Q}}_{i,j,R}{)}^{2})$$
(6)

where \(\:i\) represents the different small watersheds in the mountain, \(\:j\) represents the field floods of the different small watersheds, \(\:{Q}_{R}\) is the actual value, \(\:{Q}_{E}\) is the simulated value, \(\:{Q}^{t}\) is the value at a certain point in time, \(\:{\bar{Q}}_{R}\) is the average of the observed values, and T is the length of the field flood data.

The constraints of the front-level model involve accuracy requirements between the flood simulation process and the observed process. These mainly included the total flood volume, peak flow discharge, and peak time. The constraints are given by Eqs. (7)-(10).

  1. 2)

    The peak flow discharge, flood volumes, and present times of the simulated and observed flood processes do not exceed 20%:

$$\:{\delta\:}_{Q}^{\pm\:}\le\:0.2$$
(7)
$$\:{\delta\:}_{W}^{\pm\:}\le\:0.2$$
(8)
$$\:{\tau\:}^{\pm\:}\le\:0.3$$
(9)

where \(\:{\delta\:}_{Q}\) is the absolute value of the relative error between the simulated and observed values of the peak flow discharge, \(\:{\delta\:}_{W}\) is the absolute value of the relative error between the simulated and observed values of the flood volume, and \(\:\tau\:\) is the peak appearance time error between the simulated and observed processes.

  1. 3)

    Non-negative constraints: simulated runoff values are not negative:

$$\:{Q}_{E}\ge\:0$$
(10)

After determining the production and confluence model parameters in the mountainous region, the surface rainfall process was input into the front model to obtain the mountainous flood process.

Back level model

For the plain region model at the back level, the mountain flood process output from the front model was required as an input, in addition to the regional areal precipitation and evapotranspiration data. Both inputs were utilized in the plain area for production and confluence flow as were evolution calculations to ultimately obtain the flood simulation process of the outlet section in the plain area. The back model shares the same base as the front model. However, the objective function differs slightly because only one confluence area is present in the plain region. The objective function of the back-level model is to maximize the NSE.

$$\:\text{m}\text{ax}\text{}f=\text{m}\text{a}\text{x}{\sum\:}_{j=1}^{n}NS{E}_{j}=max{\sum\:}_{j=1}^{n}(1-{\sum\:}_{t=1}^{T}({Q}_{j,R}^{t}-{Q}_{j,E}^{t}{)}^{2}/{\sum\:}_{t=1}^{T}({Q}_{j,R}^{t}-{{\bar Q}}_{j,R}{)}^{2})$$
(11)

where \(\:j\) is the flood event at the composite topographic station. The constraints of the back model are the same as those of the base and front models and are not repeated here.

Model solution

Models in different topographic regions are interconnected based on runoff production and confluence mechanisms. However, the independence of the front and back models and the complexity of the parameters (including interval parameters and number of parameters) pose challenges in achieving an optimal solution for the combination models. To address this issue, this study introduces a method that combines front- and back-level models by “first combining and then evolving.” The output from the front model is first integrated with the flow generation process in the plains, followed by the calculation of the overall evolution to simulate the flood process across the entire region. The production and confluence flow parameters for different regions are optimally calibrated using a front-and-back model. Additionally, the flood processes in the mountainous and plain areas for each input field are divided. The Genetic Algorithm55,56,57 is an optimization method that simulates natural selection and genetic mechanisms58. It is a mature optimization technique widely applied to complex problems in various fields, including engineering59, artificial intelligence60and machine learning61, and we employs genetic algorithms in this study.

Application

Overview of the study region

Fig. 3
figure 3

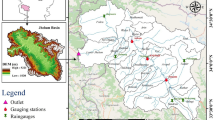
Overview of the study basin (The map is prepared in ArcGIS (Version 10.2.0.3348, URL: https://www.esri.com)).

Full size image

Xi’an, the capital of Shaanxi Province, China, is situated at the confluence of three distinct topographical regions: the Weihe Plain, the Loess Plateau, and the Qinling Mountains. The terrain south of the Wei River in Xi’an is characterized by higher elevations in the south and lower elevations in the north. With a clear boundary between the mountains and plains region at the northern foot of the Qinling Mountains, this creates two distinct natural landscapes. The southern mountainous area, located at the northern foothills of the Qinling Mountains, features fault-block tectonics with both northward and southward tilts. The is surrounded by numerous rivers and valleys, and is marked by short rivers and numerous rapids, making it particularly prone to flooding. In contrast, the Weihe Plain lies in the north is characterized by numerous rivers and consists of an impact or alluvial floodplain. The terrain is higher in the east and lower in the west.

Different topographies and geomorphologies have led to unique production and confluence zoning divisions in Xi’an. A notable feature is the independent separation of mountainous and plains areas. As a result, the catchment areas of the hydrological stations in the composite terrain area are divided into two parts, undermining the integrity of the watershed. Furthermore, the reduction in demarcation area has resulted in a lack of hydrological stations in mountainous and plain subareas, resulting in a lack of available observational data. Based on production and confluence partitioning result and related theories, it is essential to study the method of dividing floods into mountainous and plain areas sub-flood process and then calibrate the production and confluence parameters of each partition. Therefore, this study selects the Qinduzhen hydrological station, located in the northwest of Xi’an City, to explore the division method, which encompasses a watershed area of 566 km2. The area is split into mountainous and plain regions, separated by a delineation line. An overview of the study area is shown in Fig. 3.

Data collection

The data used in this study were partially sourced from the China Basic Geographic Information System, including information on the area, slope, and location of the studied watersheds, which served as foundational data for model construction. Additional data were obtained from hydrological statistical yearbooks, including a long series of flood data (1976–2020) from hydrological stations in Xi’an City, rainfall data from rainfall stations in the confluence area, and evaporation data. The methods for processing rainfall and flood data as flood events for model validation, the relevant methods are well established and are not repeated here.

Results

The combined model was solved using the aforementioned method to obtain the parameters, simulate the flood division results, and assess accuracy. The SWAT model62,63,64 with simplified parameters and conditions was used to simulate flooding in both mountainous and plains areas, serving as a comparison for the MHPCM model, to verify the reliability of the model.

Front level model

The surface rainfall processes of eighteen typical flood events (characterized by a single peak, strong rainfall-flood correspondence, prominent flood peaks, and substantial flood volumes) at mountain hydrologic station (Luolicun station) were selected as inputs for the front model. The first twelve flood events were used for calibration period, while the subsequent six flood events served as the validation period data. The simulation results for the calibration and validation periods are shown in Figs. 4 and 5, respectively.

Fig. 4
figure 4

Comparison of simulated and observed flood processes for the calibration period of the front model.

Full size image

According to the results of the front model of the MHPCM method, the NSE during the calibration period ranged from a maximum of 0.855 and a minimum of 0.567, with an average value of 0.764. In the validation period, the NSE ranged from 0.590 to 0.903, with an average value of 0.748. From the calculation results of the SWAT model, it can be seen that its simulation result is 0.585 at the calibration period. In contrast, the validation period has only 0.255 average value because of poor simulation and NSE negative value exists. The average flood error for the calibration period was 10.679%, while for the validation period, it was 7.544%, both below 11%. Based on relevant standard65, the model parameterization scheme was evaluated as Level B, indicating a usable level.

The optimized algorithm of the front model calibrated the parameters of the production and confluence model for the mountainous region, as demonstrated by the comparison between the simulated and observed flood processes during the calibration and validation periods. When the rainfall and flood volumes were small, the difference between the peak discharge of the simulated and observed flood processes was larger. Additionally, when the rainfall duration was relatively short, the error in the propagation time of flood peak of both was larger than that in floods with longer rainfall duration, although the model performed better in the simulation of the recession phase. The simulation results from the SWAT model demonstrate poor performance, particularly in cases with small peak flow values. However, it is able to capture the basic shape of most flood events. Overall, the front model of MHPCM exhibited good simulation performance, with minor errors between the simulation and the observed flood process in the selected region.

Fig. 5
figure 5

Comparison of simulated and observed flood processes for the validation period of the front model.

Full size image

Back level model

Fig. 6
figure 6

Comparison of simulated and observed flood processes for the calibration period of the back model.

Full size image

Eighteen typical flood events from the composite terrain stations were used for the back model (the typical flood event characteristics were the same as those of the front model). The surface rainfall process of each flood event was input into the front model to obtain the simulated mountain flood process of each flood. The back model was then constructed based on its underlying principle, using the mountain flood and surface rainfall process data from the plain area as inputs to derive the production and confluence model parameters and simulate the plain flood process. The first twelve flood events were used for calibration, while the last six events were used for validation. The comparison results between the simulated and observed data for the back model are shown in Figs. 6 and 7, respectively.

According to the results of back model, the NSE during the calibration period ranged from a maximum 0.841 to minimum of 0.628, with an average value of 0.737. In the validation period, the NSE ranged from 0.608 to 0.911, with an average value of 0.746. The SWAT model’s calculation results shown that its simulation result is 0.323 at the calibration period. In contrast, the validation period has only 0.423 average value because of same reason of the front model. The average flood errors for the calibration and validation periods were 13.398% and 11.349%, respectively. Although these errors were larger than those of the front model, they remained below 14%. Based on relevant standard65, the model parameterization scheme was evaluated as Level B, indicating a usable level. This indicates that the back model can effectively simulate the flood process in the plain region.

Fig. 7
figure 7

Comparison of simulated and observed flood processes for the validation period of the back model.

Full size image

The back model utilizes the same foundation as the front model, with the addition of simulated mountainous flood processes as inputs, alongside the base input data used in the production and confluence models. These inputs influence the simulation results of floods at topographically complex stations. As in the front model, precipitation affected the flood process simulation. This relationship also exists in the back model, albeit to a lesser extent. However, the underlying mechanism of this effect warrants further study and verification. Furthermore, the NSE and flood simulation errors of the back model were more substantial than those of the front model in MHPCM, and this is also true for the SWAT model.

Model parameters

Based on the front and back models constructed in Sect. 2, this study compares and analyzes several parameters (highlighted in Table 1) that are significantly influenced by the topographic features of the four computational modules of the base model (evapotranspiration module, runoff generation module, sub-source module, and confluence module) in the two regions. In the evapotranspiration module, the parameter KC decreases with increasing elevation. Its values are smaller in the mountainous region than in the plain region, which follows the general trend. In the runoff generation and sub-source module, the values of IM, B, and SM are smaller in mountainous areas. The results of model parameter calibration in this study are consistent with this pattern. In the confluence module, XE is larger in mountainous areas, while L is larger in plains. The calibrated parameters are also consistent with this rule.

Table 1 Comparison of model parameters between mountainous and plain regions.
Full size table

The parameters of the flow production and confluence model, which lack explicit laws, cannot be quantitatively analyzed due to additional influencing factors or the limited availability of relevant studies. Consequently, the remaining parameters can only be briefly analyzed here based on general principles. For the parameters, UM, WM, and EX, the mountain region is slightly larger than the plains region can be considered acceptable. The parameter LM is weakly these factors, in line with the base case. The parameter C primarily depends on the coverage area of deep-rooted plants. Since the soil cover is thicker in the plain, this value is larger in the plain areas. The parameters KG and CI , which reflect the permeability of deep soil, are generally larger in the plain than in the mountainous regions, and the calibrated parameters in this study are consistent with this pattern. The parameter CG is highly influenced by terrain and lithology, making it sensitive and difficult to accurately assess in either region. Finally, for EX, the general trend is that its value decreases as the channel slope decreases, and the calibrated parameters align with this trend.

In summary, the MHPCM effectively calibrates the runoff production and confluence model parameters in both mountainous and plain areas. Using the optimized models, the rainfall and evaporation processes of each sub-basin serve as inputs, enabling the simulation of flood processes within these sub-basins. This approach indirectly simulates and division the flood process in the mountainous and plain regions of the target basins, providing a scientific basis for development of related water conservation.

Discussion

This study extends the foundational model by applying a coupled multi-layer foundational modeling approach. Using the Qinduzhen basin in Xi’an City as a case study, the runoff production and confluence models for different topographic regions were optimized and calibrated. As a result, optimized simulation outcomes for mountainous and plain regions were obtained, along with the corresponding model parameters for each area. The comparison of observed floods with the simulation results during the determination process of the division model shows clear patterns in the simulation effects of different floods depending on the rainfall, flood volume, and flood morphology. This can be attributed to the difficulty in capturing the impact of rainfall on the flood process when rainfall is small and of short duration, which affects the performance of the evapotranspiration and runoff production models. In contrast, longer rainfall durations lead to the influence of subsequent precipitation on the flood process after the main peak, resulting in a degradation in the simulation of the recession section. Additionally, a simplified SWAT model was used to simulate flooding in the study area as a comparison to the MHPCM model. The simulation results indicate that, the performance of the SWAT model is suboptimal under the same data conditions. However, this result indirectly suggests that, in the case of limited hydrological data, the MHPCM model can effectively simulate division flood events in different topographic regions.

This study was conducted in a region at the intersection of different climatic zones, where rainfall in mountainous areas is more abundant than in plain regions, and vegetation cover has greater interception capacity. These factors contribute to variations in certain characteristics of the area. Some of the runoff production and confluence model parameters obtained from this optimization exhibit differences from the regular patterns in the mountainous and plain regions. Overall, the combined model provides a more accurate simulation of typical flood events in both mountainous and plain areas, facilitating the determination of more scientifically robust and reasonable parameters for the runoff production and confluence model in different terrain areas.

Although this study addresses the issue of the lack of methods for flood simulation division across different terrain areas to some extent and provides significant insights for a deeper understanding of the flood process and the optimization of flood management decisions, certain limitations remain. Specifically, the current model oversimplifies different terrain interactions and may neglect important dynamics such as lateral flows, groundwater-surface water exchange, and feedback mechanisms. To ensure the reliability of the proposed simulation division method, effective measures were taken, such as imposing stricter constraints on the model and utilizing observed data from similar mountainous stations for the calibration model parameters of the mountainous region. Future research should focus on validating the effectiveness of the MHPCM model in various regions, accumulating data will help improve the model. And may also explore factors such as the interaction mechanisms between mountainous and plain areas and parameter sensitivity analysis to further enhance the flood simulation division method.

Conclusions

This study proposes an MHPCM model that optimizes and calibrates production and confluence model parameters for mountainous and plain regions, addressing the challenge of differentiating floods in mountainous and plain regions by optimizes simulating the flood events processes. The key findings are summarized as follows:

  1. (i)

    Model Performance Evaluation: The MHPCM model showed a relatively high degree of accuracy in simulating flood events in mountainous and plains, with average NSE values of 0.756 and 0.742, respectively. In contrast, the simplified SWAT model underperformed in the same region, with average NSE values of 0.420 and 0.373, indicating its limited effectiveness in accurately predicting flood events under similar data conditions. However, this result indirectly suggests that, in the case of limited hydrological data, the MHPCM model can effectively simulate division flood events in different topographic regions.

  2. (ii)

    Model Application and Expansion: In the absence of observed data in mountainous regions, a pre-constructed mountainous region model can be employed for flood simulation. The resulting simulation outputs can serve as inputs for the pre-constructed plain region model, ultimately allowing for the simulation of flood processes at the outlet cross-section of the target basin. By comparing these results with observed data at the outlet cross-section, the model parameters for both the mountainous and plain regions can be optimized and calibrated simultaneously. The MHPCM model and its solution method can also be applied to the simulation of flood diversion processes in more complex terrain areas by adding the intermediate hierarchical model with the same connection principles.

  3. (iii)

    Future Model Improvements: The adaptability of the model could be further enhanced by incorporating different types of flood events, optimizing model parameters, or adding additional constraints. Furthermore, integrating the MHPCM model with other hydrological models and considering terrain interaction mechanisms could significantly improve its simulation and prediction performance.

The combined model developed in this study offers a partial solution to the issue of flood design calculations in composite watersheds, providing a straightforward and scientific method for estimating design floods in small data-scarce watersheds. However, the flooding process in different terrains is influenced by multiple factors, including rainfall, subsurface conditions, channel characteristics, etc. Simulating floods in diverse terrain types using hydrological models represents a key area for future research.