Introduction

The Meibomian glands (MGs), sebaceous glands located along the tarsal conjunctiva of the eyelids, play a crucial role in ocular health by producing meibum, a lipid essential for maintaining the stability of the tear film1. Dysfunction of these glands, collectively referred to as Meibomian gland dysfunction (MGD), is one of the leading causes of dry eye syndrome, a prevalent ocular condition that significantly impacts patients’ quality of life2. MGD is characterized by structural and functional abnormalities, including obstruction of the MG ducts and qualitative or quantitative changes in meibum secretion, leading to symptoms such as eye irritation, unstable tear film, and chronic ocular surface inflammation3,4. Accurate diagnosis and monitoring of MGD rely on evaluating both the functional and morphological characteristics of MGs. Despite its widespread occurrence, the proliferation of objective analysis methods has not yet led to standardized diagnostic criteria, complicating the clinical evaluation of MGD and necessitating innovative approaches to improve diagnostic accuracy5.

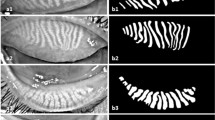
Meibography, a non-invasive imaging technique, provides detailed visualization of MG morphology6. By using infrared illumination of everted eyelids, meibography captures images of the MGs from which quantitative metrics, such as gland length, area, tortuosity, and dropout regions can be extracted to assess gland structure7. These features are clinically relevant, as they correlate with tear film stability and clinical markers like tear break-up time (TBUT) and lid margin scores8,9. To capture meibography images, several technologies are widely used, including the LipiView® II ocular surface interferometer (TearScience Inc., USA) and the EasyTear View-Plus® system (EasyTear, Italy). These devices differ in their technical specifications, such as resolution, imaging focus, and the degree of image post-processing, which can lead to variability in the appearance and characteristics of the captured images. In particular, LipiView II provides highly processed and enhanced images, while EasyTear View-Plus outputs raw, unprocessed images. This variability, illustrated in Fig. 1, presents challenges for the standardization and automation of meibography image analysis across different devices.

Figure 1
figure 1

Meibography images captured using different acquisition devices: (a) LipiView II ocular surface interferometer; (b) EasyTear View-Plus.

Full size image

Traditional meibography analysis heavily relies on manual interpretation, making it labor-intensive, subjective, and prone to significant interobserver variability10,11. This variability limits the reproducibility of findings and complicates their use in large-scale clinical studies. To address these challenges, automated and objective approaches have been proposed, ranging from rule-based algorithms to advanced artificial intelligence (AI) methods12,13. While AI-driven approaches, such as deep learning, have shown remarkable success in image classification and segmentation, their clinical applicability is limited by several factors, including the need for large labeled datasets, high computational demands, and, despite recent progress in interpretability, persistent challenges in achieving full transparency and clinical acceptance14,15. These challenges underscore the value of alternative methods that are not only automated but also interpretable, adaptable to diverse imaging systems, and computationally efficient, making them more feasible for widespread clinical adoption.

This study introduces a modular and adaptable algorithm for analyzing meibography images using piecewise linear regression to objectively quantify MG morphology. Designed to minimize user intervention, the algorithm is flexible enough to work across different imaging systems while enabling detailed morphometric analysis. This approach bridges the gap between traditional manual methods and fully automated techniques, offering an objective, reproducible, and clinically interpretable solution. The main contributions of this work are outlined below.

  • Development of a modular algorithm enabling automatic segmentation and extraction of gland- and image-level features, such as tortuosity, dropout area, and inter-gland distances.

  • Validation of the algorithm on 616 meibography images acquired from two different devices, demonstrating robustness and adaptability.

  • Demonstration of clinical utility through classification of images into Meiboscale grades using various machine learning (ML) models.

The remainder of this work is organized as follows. The Methods section describes the proposed modular algorithm, detailing the key steps for image preprocessing, MG identification, and morphological feature extraction. The Data Analysis section presents the dataset and experimental setup, including the validation methodology and the ML models employed. The Results section reports the algorithm’s performance, including its adaptability across imaging devices and its effectiveness in classifying Meiboscale grades. The Discussion section summarizes the contributions, explores clinical implications, and outlines future research directions. Finally, the Conclusion section provides a final synthesis of the study’s findings.

Methods

This section describes a modular algorithm for analyzing meibography images, designed to extract morphological features of MGs. The methodology consists of three stages: (1) Region of interest (ROI) selection, (2) identification and segmentation of MGs, and (3) extraction of morphological features. The proposed approach, presented in Section S1 of the Supplemental Material, was implemented in the R programming language16. The following subsections detail each stage of the methodology.

Image acquisition

The study utilized a dataset of 616 meibography images, comprising 310 images from the upper eyelids and 306 from the lower eyelids. These images were obtained using two different imaging devices: the LipiView® II Ocular Surface Interferometer (TearScience Inc., USA) and the EasyTear View-Plus® System (EasyTear, Italy). A subset of 310 images was obtained using the LipiView, which captured high-contrast infrared images at a resolution of 1280 \(\times\) 640 pixels, providing excellent quality for analysis. The remaining images were acquired with the EasyTear View-Plus, which produced images at a resolution of 742 \(\times\) 445 pixels but exhibited higher noise levels (see Fig. 1). To address the noise present in EasyTear images, a constant-time median filter17 was applied during preprocessing to reduce noise while preserving glandular features. Both types of images were saved in JPG format for consistency and ease of analysis.

Region of interest selection

The first step in the algorithm involves defining the ROI within the meibography images, corresponding to the area of the tarsal conjunctiva where the MGs are located. This step is implemented as a semi-automated process: the user manually selects five points along each eyelid border through a simple interactive interface, and the corresponding boundary curves are then automatically generated using interpolation. For the upper eyelid, the ROI was constructed as the region enclosed between two ellipses fitted from the user-selected points. For the lower eyelid, the upper boundary was defined similarly, while the lower boundary was replaced by a smoothing curve to better capture the distinct curvature of the region. Figure 2 illustrates the ROI selection process for both upper and lower eyelids.

Figure 2 illustrates the ROI selection process for both upper and lower eyelids.

Figure 2
figure 2

Illustration of the ROI selection process for the (a) upper and (b) lower eyelids. Dots indicate the user-selected points, and dashed lines represent the fitted curves. The ROI is defined as the overlapping region of these curves, shown as the non-blurred area.

Full size image

Identification and segmentation of Meibomian glands

Figure 3 illustrates the entire identification and segmentation process through a representative example. Although the example shows a relatively clean case, the pipeline is designed to adapt to a wide range of image qualities, including variations in resolution, noise levels, and glandular morphology. This multi-step process was designed to accurately delineate individual MGs within the ROI and consisted of three stages: image optimization, segmentation, and labeling with optional refinement.

Figure 3
figure 3

Illustration of the MG identification procedure. The algorithm includes optimization, filtering, morphological operations, and labeling steps to detect and delineate the MGs within the ROI.

Full size image

Image optimization

The first step, inspired by the approach proposed by Dai et al. (2021)18, focuses on enhancing visibility and standardizing image quality. Brightness and contrast levels were normalized using a standardization step to minimize variability between images and devices, ensuring consistent baseline conditions for subsequent analysis. Next, contrast limited adaptive histogram equalization (CLAHE) was applied to enhance local contrast, making glandular structures more discernible without overamplifying noise. To further optimize image intensity, gamma correction was applied, following the power-law expression, where the parameter \(\gamma\) represents the exponent. Device-specific \(\gamma\) values were used to account for differences in resolution and noise levels: a \(\gamma\) value of 5.00 was applied to LipiView images, while EasyTear images, which exhibited higher noise, required a lower \(\gamma\) value of 1.25.

Segmentation process

Following image optimization, the segmentation process was carried out to accurately delineate MGs within the ROI. This multi-step approach ensured robust segmentation across diverse imaging conditions and device outputs.

The process began with edge enhancement, where two Gaussian kernels were applied in parallel. The first kernel, with a large standard deviation of 30 pixels, effectively suppressed high-frequency spatial noise, while the second kernel, with a standard deviation of 2 pixels, highlighted intricate details and maintained sharp image features. This combination enabled precise detection of gland boundaries while preserving subtle glandular structures.

The enhanced image exhibited very low contrast, necessitating a binarization step. Adaptive thresholding with high sensitivity was employed, dynamically adjusting the threshold based on local pixel intensity. This approach ensured that even faint glandular structures were retained for further analysis.

Next, the segmented image underwent artifact filtering to remove non-glandular objects and improve accuracy. Small objects below a pixel size threshold were excluded (60 pixels for LipiView images and 25 pixels for EasyTear images), as these were unlikely to correspond to glands. Orientation filters were also applied, removing objects with angles outside the expected vertical alignment of MGs. Structures with orientation angles less than 40°or greater than 140°were filtered out. Additionally, an optional step was included to remove objects located in the nasal and temporal regions, which often exhibited imaging irregularities such as poor focus and insufficient illumination. This filtering approach aligns with techniques successfully demonstrated in previous works by Llorens-Quintana et al. (2019)19 and Xiao et al. (2021)20.

To refine the segmentation further, morphological operations were applied. Initial erosion using a 1 \(\times\) 3 pixel structural element was performed to expand the gaps between regions interconnected in branch-like configurations. This was followed by dilation using a vertically oriented 5-pixel-wide kernel to reinforce glandular boundaries. The size and shape of these structuring elements were empirically calibrated using a diverse subset of images to ensure that adjacent glands were effectively separated without fragmenting elongated or tortuous individual glands. This combination of operations helped preserve anatomical accuracy while preventing over-segmentation. In the rare cases where a gland was mistakenly divided or merged, the optional manual refinement step allowed the user to correct such artifacts. These precautions ensured that the segmented regions reflected the natural anatomy of the MGs with both robustness and flexibility.

Finally, the binary image was subjected to skeletonization using the Zhang-Suen thinning algorithm21. By retaining only the essential structural framework of the glands, skeletonization provided a foundation for accurately characterizing their shape and spatial arrangement.

Labeling and semi-manual refinement

To uniquely identify individual glands within the ROI, a watershed algorithm was employed22. This method treated the spatial structure of the binary image as a topographical map, interpreting changes in connectivity and contours as boundaries, enabling the differentiation of overlapping or adjacent glands. Each gland was assigned a distinct label, ensuring separation in regions where glandular structures were clustered.

To handle cases where automated labeling faced challenges, such as erroneously split glands, improperly merged glands, or missed regions, a semi-manual refinement step was integrated. This interactive feature allowed users to review the labeling output and make necessary adjustments to improve clinical relevance and anatomical accuracy. Specifically, users were able to: (1) separate glands that were incorrectly grouped under a single label; (2) combine regions that were mistakenly divided into multiple labels; and (3) manually include glands that were overlooked during the automated process.

This semi-manual refinement balanced efficiency with precision, providing clinicians or researchers control over the final labeled output. This combination of automated labeling and optional manual adjustment ensured that segmented and labeled glands reflected true anatomical structures, even in edge cases.

Extraction of gland morphological features

The final stage of the algorithm focuses on extracting and analyzing key morphological features of the MGs. This step is critical for objectively quantifying gland morphology and identifying clinically relevant patterns. The process involves modeling each gland using a piecewise linear regression framework and subsequently calculating both gland- and image-level metrics.

Modeling of Meibomian glands using piecewise linear regression

To accurately model the shape of each gland, a two-dimensional piecewise linear regression was applied to its corresponding skeleton in the skeletonized image. This approach segmented each gland into a series of linear components, effectively capturing local morphological variations. The process involved two key steps: preprocessing and spatial organization, followed by piecewise linear regression.

  1. 1.

    Preprocessing and spatial organization. Each image was first rotated by 90°to reorient the glands and prevent alignment along the vertical axis, thereby facilitating a more stable and accurate application of the regression model. The spatial coordinates (x, y) of pixels in the skeletonized gland region were extracted and organized into a structured matrix. Duplicate spatial observations, which could arise from overlapping or redundant points, were identified and removed to ensure a streamlined dataset.

    To impose a sequential order on the points based on their spatial proximity, the k-Nearest Neighbors (k-NN) algorithm23 was applied. This ordering step was critical for preparing the data for subsequent modeling stage. To improve computational efficiency, KD-trees24 were utilized in the k-NN implementation. By recursively dividing the space into hierarchical subsets along coordinate axes, KD-trees significantly expedited the search for nearest neighbors.

  2. 2.

    Piecewise linear regression. Each gland was represented as a union of linear segments, \(l_{k_g}\), defined by a linear regression function over intervals determined by breakpoints:

    $$\begin{aligned} l_{k_{g}} = \{(x,y): y=a_{k_g} + b_{k_g}x, x_{i(k_g)} \le x \le x_{i(k_g+1)}\}; k_g = 1, \dots , K_g \end{aligned}$$

    Here, \(a_{k_g}\) and \(b_{k_g}\) denote the intercept and slope parameters for the \(k-th\) segment, while \(x_{i(k_g)}\) and \(x_{i(k_g+1)}\) define the breakpoints delimiting each interval, with \(i(1) = 1< i(2)< \dots < i(K_g+1) = n_g\).

    Breakpoints were identified using a dynamic programming approach that optimized the fit by minimizing the variance of residuals within each segment. The recursion formula for identifying the optimal breakpoints was:

    $$\begin{aligned} S_{i(k_g+1)} = \max _{i(k_g) \le i(k_g+1)} \{ S_{i(k_g)} + E(i(k_g),i(k_g+1))\}, \end{aligned}$$

    where \(E(i(k_g),i(k_g+1))\) quantifies the goodness of fit for the segment between points \(i(k_g)\) and \(i(k_g+1)\). Specifically, this score function was defined as the negative variance of the residuals:

    $$\begin{aligned} E(i(k_g),i(k_g+1))= -\frac{1}{n_{k_g}-1} \left( \sum _{i=i(k_g)}^{i(k_g+1)} \left( y_i - \bar{y}\right) ^2 - \sum _{i=i(k_g)}^{i(k_g+1)} \left( \hat{y_i} - \bar{y}\right) ^2 \right) \end{aligned}$$

    In this equation, \(\hat{y_i}=\hat{a}_{k_g} + \hat{b}_{k_g}x_i\) represents the predicted value for the \(i-th\) data point within the segment, and \(\bar{y}\) is the mean of the observed y-values in the segment. The intercept and slope parameters were estimated using the least squares method, \(\hat{a}_{k_g}\) and \(\hat{b}_{k_g}\).

    The optimal segmentation was reconstructed through backtracing, starting from the last position \(i(K_g+1)=n_g\) and proceeding backward based on the position that maximized the score in each recursive step. Each gland \(MG_g\) was ultimately modeled with \(K_g\) segments and \(K_g +1\) breakpoints.

    The number of segments \(K_g\) was not fixed in advance, but selected automatically based on a penalized objective function. This criterion balances model accuracy and complexity by incorporating a penalty term that discourages over-segmentation. The strength of the penalty was estimated adaptively for each gland, based on the geometric variability of its contour. This strategy enables flexible modeling tailored to both simple and tortuous gland shapes. The segmentation procedure was implemented using the dpseg package in R25.

Figure 4 provides a visual representation of the modeling process, highlighting the utility of piecewise linear regression for capturing gland-specific morphological characteristics.

Figure 4
figure 4

Illustration of the MG modeling procedure. The figure depicts the step-by-step process for each MG, including 90-degree image rotation, removal of duplicated spatial coordinates, point organization using the k-NN algorithm, and application of two-dimensional piecewise linear regression to model gland morphology.

Full size image

Calculation of Meibomian gland metrics

The final step of the methodology involves calculating a comprehensive set of metrics to quantitatively characterize the morphology of MGs. These metrics are categorized into gland- and image-level features, enabling both detailed and global analyses of gland morphology.

  1. 1.

    Gland-level metrics. Gland-level metrics are derived for each individual MG to capture its structural and morphological characteristics. The length (L) of a gland is calculated as the sum of the pixel-wise lengths of all linear segments in its skeletonized representation, providing an overall measure of gland size.

    The orientation slope (m) is derived from the primary regression line obtained without segment differentiation and describes the inclination of the gland relative to its vertical alignment. This metric provides insights into potential structural deformations or misalignments that may result from pathological changes. Using the orientation slope, the shortening ratio (S) quantifies gland atrophy by measuring the proportion of the orientation line that remains unoccupied by gland pixels. For upper eyelid glands, this is assessed relative to the ROI’s lower boundary, while for lower eyelid glands, it is calculated from the ROI’s upper boundary.

    The area (A) of a gland is determined as the proportion of pixels within the labeled region of the binary image before skeletonization, reflecting the extent of the gland’s physical structure. The width (W) is computed as the median width along the gland’s central axis, measured perpendicular to the skeletonized representation, ensuring that the curvature of the gland is accounted for. Finally, the tortuosity (\(\tau\)) evaluates the irregularity of the gland’s shape by quantifying slope changes between consecutive linear segments, normalized to ensure comparability across glands of different sizes. A detailed explanation of the tortuosity calculation method is provided in Section S2 of the Supplemental Material.

    Figure 5a–d illustrates these gland-level metrics, including length, shortening ratio, width, and tortuosity, highlighting their relevance in understanding individual gland morphology.

  2. 2.

    Image-level metrics. Image-level metrics summarize the overall glandular morphology within the ROI, providing a broader perspective on gland health and organization. The dropout area (doa) represents the proportion of the ROI unoccupied by glands in the skeletonized image, computed as the fraction of the region enclosed between adjacent gland structures that is not covered by detected glands. This approach naturally reflects cases where severe degeneration of neighboring glands enlarges the dropout region, without affecting the robustness of the overall estimation. For upper eyelids, this is calculated relative to the lower boundary of the ROI (Fig. 5e), while for lower eyelids, it is referenced from the upper boundary (Fig. 5f). This orientation was chosen based on clinical evidence suggesting that MG dropout typically initiates at the distal end of the glands, toward the lower boundary in upper eyelids and the upper boundary in lower eyelids26,27.

    The spacing between glands (d) is another key metric, representing the median distance between adjacent glands within the ROI. This metric highlights disruptions in gland organization and density, which can be indicative of pathological changes such as MGD. An overall assessment of all glands identified in each meibography image was performed using the summary statistics outlined in Table 1. These statistics include measures of central tendency, variability, and other descriptors that provide a comprehensive evaluation of gland morphology within the image.

Figure 5
figure 5

Schematic illustration of selected MG metrics calculation. The figure shows: (a) Shortening ratio calculation for a MG in the upper eyelid; (b) Shortening ratio for a MG in the lower eyelid; (c) Measurement of gland width at three specific points along the central axis; (d) Quantification of slope changes to assess the tortuosity index, with an inset circle in the lower right corner illustrating the angle normalization process; (e) Identification of drop-out area (doa) in the upper eyelid; and (f) doa in the lower eyelid.

Full size image
Table 1 Summary statistics for the image-level evaluation of all MGs identified in each meibography image.
Full size table

Data analysis

Data description

The dataset consisted of 616 meibography images, obtained from patients at the Institute of Applied Ophthalmobiology (IOBA), University of Valladolid, Spain. These images were acquired as part of a clinical study approved by the Ethics Committee of the East Valladolid Health Area (Valladolid, Spain), adhering to the principles of the Declaration of Helsinki. Informed consent was obtained from all participants prior to image acquisition. To ensure patient privacy, all images were anonymized before analysis, and no personally identifiable information was retained. Data storage and processing complied with applicable data protection regulation, ensuring robust protection of patient information.

The dataset included 310 images from upper eyelids and 306 from lower eyelids, captured using two devices: LipiView® II Ocular Surface Interferometer and EasyTear View-Plus®.

All images were graded independently by a single experienced observer using the Pult five-grade Meiboscale28, which classifies gland loss severity into five levels (grades 0 to 4). Detailed information about the Pult Meiboscale is provided in the supplementary material (Supplementary Section S3).

Image classification

The classification process aimed to categorize meibography images into Meiboscale grades based on the 23 image-level metrics outlined in Table 1. To evaluate the ability of each metric to discriminate between the five Meiboscale grades, bootstrapped multiclass area under the receiver operating characteristics (ROC) curve (mAUC) values were computed using a multinomial logistic regression model29. This analysis assessed the separability of classes based on individual metrics, providing valuable insights into the most relevant features for classification. Metrics with higher mAUC values exhibited greater discriminatory power.

The dataset exhibited skewness and an imbalanced distribution of Meiboscale grades, with a notable scarcity of images in grades 3 and 4. This imbalance could bias the decision boundary of classifiers toward majority classes, potentially leading to suboptimal performance. To address this issue, classes with fewer than 15 images were collapsed: grades 3 and 4 were merged into a single category (\(\ge 3\)), improving class representation and consolidating severe gland loss into a clinically interpretable category. To further mitigate class imbalance, the Synthetic Minority Oversampling Technique (SMOTE)30 was applied. SMOTE generates synthetic samples for underrepresented classes through interpolation, balancing the dataset without duplicating samples.

A range of supervised ML algorithms were employed to classify the images into the adjusted four-grade system. Linear Discriminant Analysis (LDA) served as a baseline model, leveraging its capacity to maximize inter-class variance and identify linear boundaries. Generalized Linear Models with Regularization (GLMnet)31 extended this approach by incorporating L1 and L2 penalties to handle feature collinearity and reduce overfitting risks. To capture non-linear relationships, Support Vector Machines (SVM) with Gaussian kernels32 were employed, mapping features into higher-dimensional spaces to achieve more complex decision boundaries. Ensemble methods, including Random Forest (RF)33 and Extreme Gradient Boosting (XGBoost)34, combined decision trees to improve predictive power, with RF averaging predictions across multiple trees and XGBoost sequentially optimizing tree weights to minimize classification errors. Finally, k-Nearest Neighbors (k-NN) classified samples based on proximity to labeled data points in the feature space, making minimal assumptions about data distributions. Detailed descriptions of each algorithm and their hyperparameters are provided in the supplementary material (Supplementary Section S4). To identify the most influential features affecting the model’s predictions, we conducted a one-dimensional sensitivity analysis35. This approach evaluates the impact of each feature independently by perturbing its values and observing the corresponding changes in model predictions.

To ensure robust and unbiased performance assessment, a stratified 10-fold cross-validation approach was employed, with an 80/20 training/testing split in each fold. Stratified sampling preserved the proportional representation of Meiboscale grades in both training and test sets. To enhance reliability, this process was repeated five times, with each repetition using a different 20% subset as the test set. Classifier performance was evaluated using a comprehensive set of metrics, including accuracy, precision, recall, F1-score, and the area under the receiver operating characteristic curve (AUC). Global AUC was computed to summarize overall model performance, while grade-specific AUCs provided a more detailed understanding of how well each model distinguished between individual grades. Further details on the evaluation metrics and their computation are provided in the supplementary material (Supplementary Section S5).

Statistical analysis

The equality of Meiboscale score medians between images captured by the two devices was assessed using the Mann-Whitney U test, chosen for its robustness to non-normal distributions. Differences in image-level metrics among the five Meiboscale grades were evaluated using analysis of variance (ANOVA) with the F-test. A significance level of 0.05 was set for all statistical analyses. All analyses were conducted in R (version 4.3.3, The R Foundation, Vienna, Austria).

Results

A total of 616 meibography images were analyzed, equally distributed between the two imaging devices and between upper and lower eyelids. Table 2 presents the distribution of Meiboscale grades across devices for each eyelid. No significant differences in median Meiboscale scores were observed between devices (\(p > 0.05\) for both eyelids), as assessed by the Mann-Whitney U test.

Table 2 Distribution of Meiboscale grades by acquisition device.
Full size table

Discriminatory ability of individual image-level metrics

The mAUC analysis revealed significant associations between specific image-level metrics and Meiboscale grades. For upper eyelid images, metrics with mAUC \(> 0.8\), such as shortening ratio, dropout area, and total area occupied by the MGs (\(sum_A\)), demonstrated strong discriminatory capacity, suggesting their potential utility as biomarkers for glandular atrophy and dropout severity (Table 3). In contrast, dropout area was the strongest discriminator for lower eyelid images, with an mAUC of 0.77. Additionally, metrics such as the shortening ratio, the area occupied by glands, and the distance between adjacent glands, exhibited high discriminatory capabilities, with mAUC values above 0.7 (Table 4). Comparatively, the lower eyelid exhibited weaker discrimination across most features, except for gland width and inter-gland spacing. Notably, inter-gland spacing achieved higher mAUC values in the lower eyelid, reflecting its sensitivity to the distinct anatomical organization of MGs in this region.

Both eyelids exhibited a progressive reduction in gland count, length, and area with increasing grades, accompanied by increased variability in gland width and spacing. This increased variability underscores the morphological disorganization characteristic of severe Meiboscale grades. In the lower eyelid, orientation slope became notably more variable as the Meiboscale grade increased, further reflecting the structural disorganization associated with advanced gland dropout.

Table 3 Mean ± standard deviation (SD) for the evaluation statistics defined in Table 1, calculated for upper eyelid meibography images.
Full size table
Table 4 Mean ± standard deviation (SD) for the evaluation statistics defined in Table 1, calculated for lower eyelid meibography images.
Full size table

Classifiers training and evaluation

To classify meibography images into Meiboscale grades, various ML classifiers were trained and evaluated. In both the upper and lower eyelids, the highest Meiboscale grades (3 and 4) were merged into a single class (\(\ge 3\)) to address class imbalance. For the upper eyelid dataset, the 0-grade class was oversampled by 100% using SMOTE, resulting in a final class size of 42 images.

Table 5 Classification performance measures (in percentage, \(\%\)) for the multiclass classifier models.
Full size table

As summarized in Table 5, the RF classifier achieved the best overall performance for the upper eyelid across multiple metrics, including accuracy (\(79.33\%\)), recall (\(68.79\%\)), precision (\(68.59\%\)), and F1-score (\(65.61\%\)). RF also obtained the highest global AUC (\(81.16\%\)), indicating strong discriminatory power. For extreme grades, RF demonstrated high AUC values for both the 0-grade (\(89.74\%\)) and \(\ge\)3-grade (\(93\%\)). Other classifiers, such as SVM and XGBoost, performed competitively in specific areas, with SVM achieving the second-highest global AUC (\(74.84\%\)) and high performance in the \(\ge\)3-grade (\(91.84\%\)). XGBoost demonstrated balanced performance across all metrics but did not surpass RF in any category.

For the lower eyelid, classifier performance was generally weaker compared to the upper eyelid. RF again achieved the highest accuracy (\(69.6\%\)) and recall (\(49.18\%\)), demonstrating its robustness in correctly identifying positive cases. Nevertheless, SVM and GLMnet achieved higher global AUC values (\(70.56\%\) and \(70.32\%\), respectively). XGBoost outperformed other classifiers in identifying extreme cases, achieving the highest AUC for the \(\ge\)3-grade (\(90.9\%\)). Across classifiers, precision and F1-scores for the lower eyelid were moderate, reflecting the increased variability and anatomical differences in this region compared to the upper eyelid.

The importance of features was evaluated across classifiers and repetitions, as illustrated in Fig. 6. For the upper eyelid, the shortening ratio consistently emerged as the most influential metric across all classifiers, except for k-NN, which did not demonstrate a clear preference for any single feature. In contrast, for the lower eyelid, the dropout area (doa) was identified as the most critical metric by most classifiers, particularly GLMnet, RF, and SVM, reflecting its sensitivity to glandular atrophy in this region. Although the shortening ratio also held importance for the lower eyelid, its influence was less pronounced compared to the upper eyelid. These results underscore the clinical relevance of both metrics, especially in advanced cases of gland loss, where their discriminatory power is critical for accurate grading of MGD.

Figure 6
figure 6

Average normalized importance of the variables for each classifier, evaluated across five repetitions.

Full size image

Discussion

The proposed modular algorithm provides a flexible and interpretable framework for meibography analysis, ensuring adaptability across different imaging systems. This method allows for direct clinical interpretation of key morphological metrics, making it particularly valuable for ophthalmologists and optometrists. Validation across 616 images from two distinct imaging devices demonstrated the robustness of the algorithm, achieving consistent performance across varied image qualities. The classification of MG morphological features into Meiboscale grades further emphasized the clinical relevance of the extracted metrics.

Algorithmic insights

Recent years have seen an increasing number of objective methods for quantifying MG morphology, including approaches focusing on detailed grading systems36,37,38 and morphometric parameters such as gland length, width, tortuosity, dropout area, and density8,19,20,39,40. Several recent studies have leveraged deep learning techniques for segmentation and classification12,13,41,42,43,44. While these methods may achieve higher segmentation accuracy under controlled conditions, their adoption in clinical practice remains limited due to challenges such as interpretability, reliance on large annotated datasets, and high computational demands14,15,45.

Our methodology intentionally diverges from end-to-end deep learning pipelines by prioritizing modularity, interpretability, and robustness in data-limited settings. Rather than competing directly with deep learning architectures, our pipeline can be integrated into hybrid frameworks, for instance as a feature extractor or validation layer. The proposed metrics can serve both as interpretable inputs for explainable AI models and as benchmarks for assessing the reliability and clinical interpretability of black-box predictions14,46,47. In this way, the method bridges the gap between fully manual and fully automated strategies, supporting both transparency and practical deployment in clinical settings.

It is also important to note that while our dataset is sufficiently large for classical image-level analysis, it lacks the pixel-level annotations and grade distribution needed to train or validate deep learning models, particularly those relying on instance-level segmentation. This limitation precludes a formal numerical comparison with such approaches. However, it reinforces the motivation for developing a modular, interpretable pipeline that is more aligned with the constraints and needs of clinical settings.

In the specific context of MG analysis, the proposed method offers several advantages over AI-based approaches in terms of transparency, clinical adaptability, and resource efficiency. Our pipeline provides full visibility of each processing step, operates on standard computing equipment, and allows expert interaction when needed, making it especially well suited for routine clinical workflows and deployment in data-constrained environments. The interpretability is crucial in medical diagnostics, as clinicians require clear, explainable outputs to understand how decisions are derived, ensuring trust and compliance with medical standards14. Moreover, this approach is well-suited for ophthalmic imaging, where annotated datasets are often scarce. Deep learning models typically require extensive labeled data, which may not always be feasible due to clinical constraints15. In contrast, the proposed methodology remains robust and reliable even with smaller datasets, making it a valuable tool in data-limited settings.

Additionally, the computational efficiency of the algorithm makes it well-suited for clinical applications. Manual analysis of meibography images often requires 10–15 min per image, depending on observer expertise and the complexity of the image38. Although deep learning-based methods are faster, typically requiring slightly over 1 second per image for image segmentation and morphometric parameter evaluation on high-performance hardware43, these methods often involve additional preprocessing steps and a reliance on computationally demanding GPUs. Such requirements can pose barriers in resource-limited settings. Processing a single image with our proposed methodology, including semi-automated ROI selection, takes approximately 18 seconds on standard consumer-grade computers. Once the ROI is defined, the fully automated steps of MG identification, segmentation, and morphological feature extraction are completed in 8 seconds, making it feasible for routine use without requiring high-performance hardware.

Although the pipeline emphasizes automation and efficiency, certain steps, such as ROI identification and gland labeling, allow for optional manual refinement. This design choice reflects the intended use of the tool as a support system for ophthalmologists and optometrists, balancing automated analysis with the flexibility needed to accommodate clinical judgment in real-world settings.

Metric development

Gland-level metrics provide detailed insights into individual gland morphology, while image-level metrics offer a broader perspective on overall glandular health. Morphometric parameters such as gland length, width, and tortuosity have been widely recognized as critical markers for assessing MGD severity. However, definitions of these metrics often vary across studies and methodologies, complicating direct comparisons between datasets and limiting reproducibility. A detailed review of these metrics can be found in Swiderska et al. (2022)48.

A key innovation of this study is the use of piecewise linear regression to capture detailed MG morphology. Our method enhances the precision of traditional metrics by segmenting the gland structure into discrete linear components, enabling robust, translation- and rotation-independent analyses44,49. This approach ensures consistent quantification across datasets with varying imaging conditions, enhancing reproducibility.

For example, tortuosity, a well-established marker of gland health, is quantified by evaluating slope changes between linear segments, penalizing shorter glands and providing reliable comparisons across spatial orientations49. Similarly, the piecewise skeleton improves gland width measurements by accounting for curvature, which is often overlooked in other approaches13,20. The proposed refinements improve the diagnostic utility of meibography-based assessments and align with clinically relevant markers of MGD.

Classification performance

The image-level metrics derived from the proposed methodology, particularly the shortening ratio and dropout area, demonstrated strong classification performance according to the Meiboscale grading system27,44,46.

Performance was consistently higher for upper eyelid images across all classifiers. This is expected, as upper eyelid meibography generally provides a more complete view of the glands, which tend to be longer, less obscured by anatomical structures, and better defined than those in the lower eyelid50,51,52. Additionally, lower eyelid images often suffer from increased curvature, reduced contrast, and motion artifacts, which can degrade the quality of feature extraction and classification. These factors likely contributed to the weaker performance observed in this subset. In general, upper eyelids exhibit more pronounced glandular features and stronger correlations with clinical signs than lower eyelids, aligning with prior studies53,54.

The shortening ratio emerged as the most important feature in the upper eyelid, reflecting its sensitivity to glandular shortening, a hallmark of severe MGD55. Conversely, dropout area was the dominant metric for the lower eyelid, aligning with the higher prevalence of gland dropout in this region56.

Despite an imbalance in Meiboscale grades within the dataset, particularly the underrepresentation of severe cases, the classification models achieved promising performance. For upper eyelid images, the RF classifier consistently outperformed other models, achieving high accuracy, recall, and discriminatory power across all grades. For lower eyelids, while classifier performance was generally weaker due to increased variability in gland morphology50, ensemble methods like RF and XGBoost performed well, particularly in detecting advanced gland dropout. The ability to achieve robust classification with relatively simple models, such as RF, highlights the practical applicability of the approach in diverse clinical settings, from small clinics to large-scale research studies.

While some features showed lower discriminative power, they still contribute to a more comprehensive morphological characterization of the glands, capturing aspects such as intra-image variability, spatial distribution, and subtle anatomical differences. Nevertheless, we acknowledge that simplified models using only the most informative features could improve classification performance and enhance interpretability in certain contexts. Importantly, the modular nature of our pipeline supports this flexibility, allowing users to include, exclude, or prioritize features depending on clinical needs, data availability, or performance requirements.

It is important to emphasize that the Meiboscale grades were not used as ground truth labels for training or clinical decision-making. Rather, they served as an external reference to validate whether the extracted morphological features aligned with widely accepted visual grading criteria. Our primary aim was not to optimize classification performance, but to demonstrate that objective, quantitative descriptors, such as gland shortening, dropout, and tortuosity, vary consistently with increasing Meiboscale grades. Indeed, a key motivation of our work is to move beyond subjective visual assessment by offering a reproducible and interpretable alternative that supports more consistent evaluations of MG morphology in clinical and research settings.

Clinical relevance and translational potential

The extracted morphological metrics, such as shortening ratio, dropout area, gland tortuosity, and width, are closely aligned with the visual cues that clinicians use when evaluating MG morphology27,28,46. In routine clinical practice, ophthalmologists and optometrists visually assess the extent of gland dropout, gland shortening relative to the tarsal height, and patterns of gland distortion or tortuosity to infer the severity and progression of MGD. These features effectively translate qualitative expert assessments into objective, reproducible descriptors. For example, dropout area reflects gland loss typically assessed visually by observing regions of absent or atrophic glands, while increased tortuosity and shortening are recognized as early morphological changes preceding gland atrophy53.

By formalizing these features mathematically, the proposed method improves consistency across clinicians and supports objective grading, reducing subjectivity in diagnosis. The extracted metrics complement existing scales such as the Meiboscale by offering granular insight into morphological progression, enabling earlier detection, longitudinal monitoring, and standardized documentation of disease severity.

In clinical research, these metrics also provide standardized endpoints for interventional trials or comparative studies26,57. Their modular and interpretable nature makes them particularly well suited to translational applications where traceability, auditability, and user confidence are essential. In addition, the low computational demands and flexibility of the proposed pipeline facilitate its potential integration into clinical workflows, either as a standalone evaluation tool or as part of larger diagnostic systems. Importantly, the modular structure of the method allows for straightforward adaptation to images from different acquisition systems, despite variability in appearance due to differences in post-processing levels. This adaptability further enhances the method’s applicability across diverse clinical environments and research settings.

Limitations and future work

While this study underscores the robustness and adaptability of the proposed algorithm, several limitations warrant discussion and guide future research directions.

The dataset exhibited an underrepresentation of severe Meiboscale grades, likely reflecting their lower prevalence in the general population54. This imbalance may limit the generalizability of the classification models, particularly for extreme cases. Leveraging techniques such as targeted recruitment or augmentation strategies could address this limitation, ensuring that models are robust and clinically applicable even for rare presentations of advanced MGD.

Although the proposed methodology requires minimal manual intervention during ROI selection, this step introduces a potential source of variability. Automating ROI selection using existing solutions19 or developing in-house algorithms could reduce subjectivity and improve reproducibility in large-scale applications. However, manual intervention offers distinct advantages in clinical scenarios, ensuring that the specialist visually inspects the image. This review allows for the detection of potential issues, such as subtle glandular features or variations in image quality, which automated methods might overlook. In such cases, limited subjectivity may actually improve practical applicability by increasing adaptability to patient-specific characteristics.

To quantify this potential source of variability, we conducted an inter-observer reproducibility analysis. Using a balanced subset of 38 images, spanning devices, eyelids, and Meiboscale grades, we compared the morphological features extracted by two independent observers following the standard 5-point ROI protocol. Agreement was assessed using intra-class correlation coefficients (ICCs) and mean absolute differences (MADs). The results showed excellent reproducibility for clinically relevant metrics such as gland count (ICC = 0.94), median width (ICC = 0.91), and total gland area (ICC = 0.89). Although dispersion-based metrics (e.g., CVs) yielded slightly lower ICCs, overall agreement was high. This robustness is supported by the geometric regularization introduced by fitting ellipses or smoothing curves through a small number of user-defined points. Full results are reported in Section S6 of the Supplementary Material.

The algorithm demonstrated adaptability across two imaging devices, but further validation across a broader range of systems is needed to confirm its robustness. Although the current dataset includes images from both EasyTearView and LipiFlow, all data were collected in a single clinical center, limiting the evaluation of generalizability to other environments or imaging conditions. Extending the validation to include multi-center datasets and additional devices with varying resolutions, noise levels, and operational characteristics would further confirm the robustness and clinical applicability of the methodology.

Although the same pipeline was applied to both upper and lower eyelid images, classification performance was consistently higher in upper eyelid cases. This is expected, as upper eyelid meibography generally provides a clearer and more complete view of the glands. While a unified framework enhances usability and deployment, future iterations of the algorithm may benefit from tailored preprocessing or segmentation strategies for lower eyelids.

Future work should explore integrating additional clinical parameters, such as tear film stability, lid margin scores, and patient-reported symptoms, to provide a more comprehensive assessment of MGD. Combining morphological metrics with functional and symptomatic data could provide a more comprehensive understanding of MGD, enabling better disease staging and personalized treatment strategies. This multimodal approach could bridge the gap between morphological analysis and clinical decision-making.

Finally, while the focus of this study was on a modular, interpretable algorithm, future work could explore its integration with AI-based methods. For example, deep learning techniques could automate certain stages, such as ROI selection or gland segmentation, where large annotated datasets are available. Conversely, the proposed metrics could serve as interpretable inputs or validation tools for AI models, enhancing their reliability and clinical relevance. These hybrid approaches could combine the strengths of both methodologies, ensuring scalability, adaptability, and clinical impact.

Conclusion

This study presents a modular, interpretable, and adaptable approach for automated meibography analysis. The proposed algorithm successfully extracts clinically relevant morphological features while maintaining a balance between automation and manual oversight. By leveraging a structured feature extraction pipeline, the method enables robust and reproducible assessments of MG morphology, providing a potential tool for standardizing MGD diagnosis.

Future developments should explore full automation of the ROI selection process and integration with deep learning techniques to enhance classification accuracy while maintaining interpretability. Additionally, validating this approach in diverse clinical settings will be essential for ensuring its reliability and usability in routine practice. Ultimately, this method has the potential to support ophthalmologists and optometrists by providing a consistent, objective, and scalable solution for meibography-based diagnostics.