Introduction

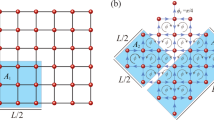
The topic of QPT in nuclei has attracted the attention of many researchers for several decades1,2,3. One of the models for studying QPT with a rich phase structure is IBM-2. In this model, the s- and d-bosons generate a six-dimensional space are described by the \(U_{\pi }(6)\otimes U_{\nu }(6)\) algebra3,5. The parametric space corresponding to the Hamiltonian IBM-2 in the consistent-Q formalism is three-dimensional and has a geometrically pyramidal structure, known as the Casten pyramid. As shown in Fig. 1, the dynamical symmetries are located at the vertices and center of the base of the Casten pyramid6. The symmetries of IBM-2 are similar to the symmetries in IBM-1. It is clear that, every boson with an integer spin can be created by coupling two fermions. In the framework of IBM-2, if the coupled fermions are protons (or neutrons), we call the resulting boson, protonic-boson (or neutronic-boson). These bosons are used to create new symmetries. In addition to the \(SU_{\pi \nu }(3)\) and \(\overline{SU_{\pi \nu }(3)}\), IBM-2 allows the construction of the other dynamical symmetries such as \(SU^{*}_{\pi \nu }(3)\) and \(\overline{SU^{*}_{\pi \nu }(3)}\) by exchanging protonic- and neutronic-bosons7,8. The dynamical symmetries of \(SU_{\pi \nu }(3)\) and \(SU^{*}_{\pi \nu }(3)\) describe prolate deformed nuclei, and the limits of \(\overline{SU_{\pi \nu }(3)}\) and \(\overline{SU^{*}_{\pi \nu }(3)}\) describe oblate deformed nuclei. Iachello and Caprio studied the Casten pyramid in the IBM-2 by analyzing the energy surfaces in 2005. They investigated the QPT between some of the limits such as: \(SU_{\pi \nu }(3)\), \(U_{\pi \nu }(5)\), \(SU^{*}_{\pi \nu }(3)\), and \(O_{\pi \nu }(6)\)9. In 2014, Ramos et al. investigated critical points and QPT using catastrophe theory within the framework of the semi-classical approximation IBM-210. A complete description of the QPT in the semi-classical approximation of IBM and IBFM (interacting boson-fermion model) is provided in Refs.11,12,13,14,15.

Fig. 1
figure 1

Symmetrical limits and their coordinates according to the control parameters \(\eta\) , \(\chi _{\pi }\), and \(\chi _{\nu }\) in the Casten pyramid.

Full size image

In addition to energy surfaces, there are several observables, such as the two-neutron separation energy, \({R_{{4 / 2}}}\), etc., for studying the QPT in nuclei16,17,18,19,20. One of the observables that has recently attracted the attention of some researchers is von Neumann entropy, also known as entanglement entropy21,22,23,24. In general, entanglement entropy in nuclear systems includes entanglement between nucleon subsystems and the entanglement between quantum states or modes25,26,27,28,29. Recently, this observable has been used to investigate the QPT in the IBM-1, IBFM-1, and IBM-2 using affine SU(1,1) Lie algebra and Schmidt decomposition. The results showed that the entanglement entropy is sensitive to the QPT, and it shows the QPT well in isotope chains28,29.

In this manuscript, a new theoretical technique for tracking and quantitatively studying the QPT within the framework of IBM-2 is introduced using the entanglement entropy. To investigate QPT in various pathes of the Casten pyramid, the energy surfaces and the entanglement entropy are obtained. The entanglement entropy is calculated in the framework of semi-classical approximation IBM-2 using coherent state formalism and Schmidt decomposition. In examining entanglement entropy, we investigate the entanglement between protonic- and neutronic-bosons, as well as between s and d bosons.

This manuscript is organized as follows. In “Entanglement entropy in the semi-classical approximation of IBM-2” section, the entanglement entropy in the semi-classical approximation of IBM-2 is obtained. “Results” section, is devoted to the analysis of results, and the conclusion is given in “Conclusions” section.

Entanglement entropy in the semi-classical approximation of IBM-2

The phase structure in IBM-2 is more complex than in IBM-1. The parametric space in IBM-2, unlike in IBM-1, is three-dimensional, with the axes: \(\eta\), \(\chi _{\pi }\), and \(\chi _{\nu }\). As shown in Fig. 1, the phase diagram is pyramidal and is referred to as the Casten pyramid. The pyramid’s base is square, with one symmetry limit at each apex of the pyramid and its center of the base. The coordinates of these limits are shown in Fig. 19,10. According to the given coordinates, the QPT occurs as a result of changes in the values of these parameters. In this manuscript, the physical system is described by the IBM-2 Hamiltonian, and the tool used to investigate the QPT is the entanglement entropy.

This section consists of two subsections. In the first subsection, we introduce the IBM-2 Hamiltonian using consistent-Q formalism and the energy surface in the semi-classical approximation. The second subsection emphasizes the calculation of entanglement entropy using the Schmidt decomposition of states within the semi-classical framework.

Semi-classical approximation of IBM-2

The properties of collective states in nuclei relate to their geometric structure. From this perspective, the geometric description of IBM-2 is significant due to its theoretical and experimental aspects. The study of IBM-2’s geometric properties in the semi-classical approximation is more convenient. In this approximation, the energy surface (E) is derived as a function of shape variables using the boson coherent state (\({\left| {{\text {BCOS}}} \right\rangle }\)) formalism. The energy surface is defined as follows4

$$\begin{aligned} E = \frac{{\left\langle {{\text {BCOS}}} \right| {{\hat{H}}_{IBM - 2}}\left| {{\text {BCOS}}} \right\rangle }}{{\left\langle {{{\text {BCOS}}}} \mathrel {\left| \right. } {{{\text {BCOS}}}} \right\rangle }}, \end{aligned}$$
(1)

where \(\hat{H}_{IBM - 2}\) is

$$\begin{aligned} {\hat{H}_{IBM - 2}} = {\hat{H}_\nu } + {\hat{H}_\pi } + {\hat{V}_{\pi \nu }}. \end{aligned}$$
(2)

Here, \({\hat{H}_\pi }\), \({\hat{H}_\nu }\), and \(\hat{V}_{\pi \nu }\) represent the protonic-bosons Hamiltonian, the neutronic-bosons Hamiltonian, and the interacting potential operator between neutronic- and protonic-bosons, respectively. The Hamiltonian for each type of boson (i.e., \({\hat{H}_\rho }\), \(\rho =\pi ,\nu\)) and the interacting potential in terms of creation (\(b_{\rho ,l}^\dag\) ) and annihilation (\({\tilde{b}_{\rho ,l}}\) ) boson operators are given as follows4

$$\begin{aligned} \begin{aligned}&{{\hat{H}}_\rho } = E_0^{\left( \rho \right) } + \sum \limits _l {\alpha _l^{\left( \rho \right) }\left( {b_{\rho ,l}^\dag \cdot {{\tilde{b}}_{\rho ,l}}} \right) } + \sum \limits _{L,{l_1},{l_2},{l_3},{l_4}} {\beta _L^{\left( \rho \right) }} \left[ {{{\left[ {b_{\rho ,{l_1}}^\dag \times b_{\rho ,{l_2}}^\dag } \right] }^{\left( L \right) }} \times {{\left[ {{{\tilde{b}}_{\rho ,{l_3}}} \times {{\tilde{b}}_{\rho ,{l_4}}}} \right] }^{\left( L \right) }}} \right] _0^{\left( 0 \right) } + {\text {O}}\left( {{\text {3 - body}}} \right) \\&\quad {{\hat{V}}_{\pi \nu }} = \sum \limits _{L,{l_1},{l_2},{l_3},{l_4}} {{\gamma _L}\left[ {{{\left[ {b_{\pi ,{l_1}}^\dag \times {{\tilde{b}}_{\pi ,{l_2}}}} \right] }^{\left( L \right) }} \times {{\left[ {b_{\nu ,{l_3}}^\dag \times {{\tilde{b}}_{\nu ,{l_4}}}} \right] }^{\left( L \right) }}} \right] _0^{\left( 0 \right) } + {\text {O}}\left( {{\text {3 - body}}} \right) } \end{aligned}. \end{aligned}$$
(3)

In Eq. (3), \(\alpha _l^{\left( \rho \right) }\), \({\gamma _L}\) and \(\beta _L^{\left( \rho \right) }\) are constant coefficients. Here, the Hamiltonian has been written in terms of constant expressions \(E_0^{\left( \rho \right) }\), one-body, two-body, and higher-order expressions (\({\text {O}}\left( {{\text {3 - body}}} \right)\) ), respectively. In practice, contributions from 3-body and higher-order terms are not considered. Thus, within the framework of IBM-2, by considering the s- and d-bosons while omitting the 3-body and higher-order contributions, one can obtain4

$$\begin{aligned} {{\hat{H}}_\rho }& = E_0^{\left( \rho \right) } + \alpha _s^{\left( \rho \right) }\left( {s_\rho ^\dag \cdot {{\tilde{s}}_\rho }} \right) + \alpha _d^{\left( \rho \right) }\left( {d_\rho ^\dag \cdot {{\tilde{d}}_\rho }} \right) + \sum \limits _{L = 0,2,4} {\beta _L^{\left( \rho \right) }\sqrt{2L + 1} } \left[ {{{\left[ {d_\rho ^\dag \times d_\rho ^\dag } \right] }^{\left( L \right) }} \times {{\left[ {{{\tilde{d}}_\rho } \times {{\tilde{d}}_\rho }} \right] }^{\left( L \right) }}} \right] _0^{\left( 0 \right) } \\&\quad {\text { + }}\beta _1^{\left( \rho \right) }\left[ {{{\left[ {d_\rho ^\dag \times d_\rho ^\dag } \right] }^{\left( 2 \right) }} \times {{\left[ {{{\tilde{d}}_\rho } \times {{\tilde{s}}_\rho }} \right] }^{\left( 2 \right) }} + {{\left[ {d_\rho ^\dag \times s_\rho ^\dag } \right] }^{\left( 2 \right) }} \times {{\left[ {{{\tilde{d}}_\rho } \times {{\tilde{d}}_\rho }} \right] }^{\left( 2 \right) }}} \right] _0^{\left( 0 \right) } \\&\quad {\text { + }}\beta _3^{\left( \rho \right) }\left[ {{{\left[ {d_\rho ^\dag \times d_\rho ^\dag } \right] }^{\left( 0 \right) }} \times {{\left[ {{{\tilde{s}}_\rho } \times {{\tilde{s}}_\rho }} \right] }^{\left( 0 \right) }} + {{\left[ {s_\rho ^\dag \times s_\rho ^\dag } \right] }^{\left( 0 \right) }} \times {{\left[ {{{\tilde{d}}_\rho } \times {{\tilde{d}}_\rho }} \right] }^{\left( 0 \right) }}} \right] _0^{\left( 0 \right) } \\&\quad {\text { + }}\beta _5^{\left( \rho \right) }\left[ {{{\left[ {d_\rho ^\dag \times s_\rho ^\dag } \right] }^{\left( 2 \right) }} \times {{\left[ {{{\tilde{d}}_\rho } \times {{\tilde{s}}_\rho }} \right] }^{\left( 2 \right) }}} \right] _0^{\left( 0 \right) }{\text { + }}\beta _6^{\left( \rho \right) }\left[ {{{\left[ {s_\rho ^\dag \times s_\rho ^\dag } \right] }^{\left( 0 \right) }} \times {{\left[ {{{\tilde{s}}_\rho } \times {{\tilde{s}}_\rho }} \right] }^{\left( 0 \right) }}} \right] _0^{\left( 0 \right) } \\ {{\hat{V}}_{\pi \nu }} &= \sum \limits _{L = 0,1,2,3,4} {{\gamma _L}} \left[ {{{\left[ {d_\pi ^\dag \times {{\tilde{d}}_\pi }} \right] }^{\left( L \right) }} \times {{\left[ {d_\nu ^\dag \times {{\tilde{d}}_\nu }} \right] }^{\left( L \right) }}} \right] _0^{\left( 0 \right) } + {\gamma _5}\left[ {{{\left[ {s_\pi ^\dag \times {{\tilde{s}}_\pi }} \right] }^{\left( 0 \right) }} \times {{\left[ {s_\nu ^\dag \times {{\tilde{s}}_\nu }} \right] }^{\left( 0 \right) }}} \right] _0^{\left( 0 \right) } \\&\quad + {\gamma _6}\left[ {{{\left[ {s_\pi ^\dag \times {{\tilde{s}}_\pi }} \right] }^{\left( 0 \right) }} \times {{\left[ {d_\nu ^\dag \times {{\tilde{d}}_\nu }} \right] }^{\left( 0 \right) }}} \right] _0^{\left( 0 \right) } + {\gamma _7}\left[ {{{\left[ {d_\pi ^\dag \times {{\tilde{d}}_\pi }} \right] }^{\left( 0 \right) }} \times {{\left[ {s_\nu ^\dag \times {{\tilde{s}}_\nu }} \right] }^{\left( 0 \right) }}} \right] _0^{\left( 0 \right) } \\&\quad + {\gamma _8}\left[ {{{\left[ {d_\pi ^\dag \times {{\tilde{s}}_\pi } + s_\pi ^\dag \times {{\tilde{d}}_\pi }} \right] }^{\left( 2 \right) }} \times {{\left[ {d_\nu ^\dag \times {{\tilde{s}}_\nu } + s_\nu ^\dag \times {{\tilde{d}}_\nu }} \right] }^{\left( 2 \right) }}} \right] _0^{\left( 0 \right) } \\&\quad + {\gamma _9}\left[ {{{\left[ {d_\pi ^\dag \times {{\tilde{s}}_\pi } - s_\pi ^\dag \times {{\tilde{d}}_\pi }} \right] }^{\left( 2 \right) }} \times {{\left[ {d_\nu ^\dag \times {{\tilde{s}}_\nu } - s_\nu ^\dag \times {{\tilde{d}}_\nu }} \right] }^{\left( 2 \right) }}} \right] _0^{\left( 0 \right) } \\&\quad + {\gamma _{10}}\left[ {{{\left[ {d_\pi ^\dag \times {{\tilde{d}}_\pi }} \right] }^{\left( 2 \right) }} \times {{\left[ {d_\nu ^\dag \times {{\tilde{s}}_\nu } + s_\nu ^\dag \times {{\tilde{d}}_\nu }} \right] }^{\left( 2 \right) }}} \right] _0^{\left( 0 \right) } + {\gamma _{11}}\left[ {{{\left[ {d_\pi ^\dag \times {{\tilde{s}}_\pi } + s_\pi ^\dag \times {{\tilde{d}}_\pi }} \right] }^{\left( 2 \right) }} \times {{\left[ {d_\nu ^\dag \times {{\tilde{d}}_\nu }} \right] }^{\left( 2 \right) }}} \right] _0^{\left( 0 \right) } \end{aligned} \ $$
(4)

The IBM-2 Hamiltonian contains many terms that are applied in phenomenological studies. However, to investigate QPT in nuclei, only a few of the terms in Eq. (4) are important. Therefore, by taking into account the d-boson number operator (\({\hat{n}_{d\rho }}\)), Majorana operator (\({\hat{M}_{\pi \nu }}\)), and quadrupole-quadrupole interaction (\(\hat{Q}_\mu ^{\left( {{\chi _\pi },{\chi _\nu }} \right) }.\hat{Q}_\mu ^{\left( {{\chi _\pi },{\chi _\nu }} \right) }\)) while neglecting the residual terms, one can derive consistent-Q formalism as follows9

$$\begin{aligned} {\hat{H}_{IBM - 2}} = \eta \left( {{{\hat{n}}_{d\pi }} + {{\hat{n}}_{d\nu }}} \right) - \frac{{1 - \eta }}{N}\hat{Q}_\rho ^{\left( {{\chi _\pi },{\chi _\nu }} \right) }.\hat{Q}_\rho ^{\left( {{\chi _\pi },{\chi _\nu }} \right) } + \lambda {\hat{M}_{\pi \nu }}, \end{aligned}$$
(5)

where

$$\begin{aligned} \begin{aligned}&{{\hat{M}}_{\pi \nu }} = {\left[ {s_\nu ^\dag \times d_\pi ^\dag - s_\pi ^\dag \times d_\nu ^\dag } \right] ^{\left( 2 \right) }} \cdot {\left[ {{{\tilde{s}}_\nu } \times {{\tilde{d}}_\pi } - {{\tilde{s}}_\pi } \times {{\tilde{d}}_\nu }} \right] ^{\left( 2 \right) }} - 2\sum \limits _{k = 1,3} {{{\left[ {d_\nu ^\dag \times d_\pi ^\dag } \right] }^{\left( k \right) }} \cdot {{\left[ {{{\tilde{d}}_\nu } \times {{\tilde{d}}_\pi }} \right] }^{\left( k \right) }}} \\&\quad \hat{Q}_\mu ^{\left( {{\chi _\pi },{\chi _\nu }} \right) } = {\left( {\hat{Q}_\pi ^{{\chi _\pi }} + \hat{Q}_\nu ^{{\chi _\nu }}} \right) _\mu } \\&\quad \hat{Q}_\mu ^{{\chi _\rho }} = \left[ {d_\rho ^\dag \tilde{s} + s_\rho ^\dag {{\tilde{d}}_\rho }} \right] _\mu ^{\left( 2 \right) } + {\chi _\rho }\left[ {d_\rho ^\dag {{\tilde{d}}_\rho }} \right] _\mu ^{\left( 2 \right) } \\&\quad {{\hat{n}}_{d\rho }} = \sum \limits _\mu {d_{\rho \mu }^\dag {d_{\rho \mu }}}. \end{aligned} \end{aligned}$$
(6)

The Majorana term represents the symmetry energy of the protonic- and neutronic-bosons in-phase. By ignoring the Majorana term, the essential dynamical symmetry features of the Hamiltonian are still preserved9. Thus, the consistent-Q Hamiltonian of the IBM-2 is written as6,9,10

$$\begin{aligned} {\hat{H}_{IBM - 2}}\left( {\eta ,\chi } \right) = \eta \left( {{{\hat{n}}_{d\pi }} + {{\hat{n}}_{d\nu }}} \right) - \frac{{1 - \eta }}{N}\hat{Q}_\rho ^{\left( {{\chi _\pi },{\chi _\nu }} \right) }.\hat{Q}_\rho ^{\left( {{\chi _\pi },{\chi _\nu }} \right) }, \end{aligned}$$
(7)

where \(0 \le \eta \le 1\) and \(- {{\sqrt{7} }/ 2} \le {\chi _\rho } \le {{\sqrt{7} } / {2,\;\rho = \pi ,\nu }}\) are real parameters.

Using the coherent states formalism, expressed as a boson condensate, one can establish a connection between IBM-2 and potential energy surfaces, QPTs, and the geometric shapes of the nucleus3,9. So, the boson coherent state is given as follows

$$\begin{aligned} {\left| {{\text {BCOS}}} \right\rangle }:=|N_{\pi }, N_{\nu },\beta _{\pi },\beta _{\nu }, \gamma _{\pi },\gamma _{\nu }\rangle =|\psi _{\beta _{\pi },\beta _{\nu }, \gamma _{\pi },\gamma _{\nu }}(N_{\pi }, N_{\nu })\rangle =\theta _{\pi \nu } (B^{\dagger }_{\pi })^{N_{\pi }}(B^{\dagger }_{\nu })^{N_{\nu }}|0\rangle . \end{aligned}$$
(8)

Here, \(N_{\pi }\) and \(N_{\nu }\) represent the total numbers of valence protonic-bosons and neutronic-bosons, respectively. Also, the parameters of \(\beta _{\pi },\beta _{\nu }, \gamma _{\pi }\), and \(\gamma _{\nu }\) are the intrinsic shape variables relating to the degrees of freedom of protons and neutrons. The normalization factor \(\theta _{\pi \nu }\) is defined as3,9

$$\begin{aligned} \begin{aligned}&\theta _{\pi \nu }=\theta _{\pi }\theta _{\nu } \\ &\theta _{\pi }=\frac{1}{\sqrt{ N_{\pi }!(1+\beta ^{2}_{\pi })^{N_{\pi }}}}, \quad \quad \theta _{\nu }=\frac{1}{\sqrt{ N_{\nu }!(1+\beta ^{2}_{\nu })^{N_{\nu }}}}. \end{aligned} \end{aligned}$$
(9)

In Eq. (8), \(B^{\dagger }_{\pi }\) and \(B^{\dagger }_{\nu }\) are the creation operators of protonic- and neutronic-boson coherent states, respectively. These operators are defined in terms of boson creation operators (i.e., \(s^{\dagger }_{\pi }\), \(s^{\dagger }_{\nu }\), \(d^{\dagger }_{\pi }\), and \(d^{\dagger }_{\nu }\)) as follows

$$\begin{aligned} \begin{aligned}&B^{\dagger }_{\pi }=s^{\dagger }_{\pi }+\beta _{\pi } (cos\gamma _{\pi } d^{\dagger }_{\pi 0}+\frac{sin\gamma _{\pi }}{\sqrt{2}}(d^{\dagger }_{\pi 2}+d^{\dagger }_{\pi -2}))=\alpha _{s}^{\pi } s^{\dagger }_{\pi }+\alpha _{d_{0}}^{\pi }d^{\dagger }_{\pi 0}+\alpha _{d_{2}}^{\pi }d^{\dagger }_{\pi 2}+\alpha _{d_{-2}}^{\pi }d^{\dagger }_{\pi -2} \\ &B^{\dagger }_{\nu }=s^{\dagger }_{\nu }+\beta _{\nu } (cos\gamma _{\nu } d^{\dagger }_{\nu 0}+\frac{sin\gamma _{\nu }}{\sqrt{2}}(d^{\dagger }_{\nu 2}+d^{\dagger }_{\nu -2}))=\alpha _{s}^{\nu } s^{\dagger }_{\nu }+\alpha _{d_{0}}^{\nu }d^{\dagger }_{\nu 0}+\alpha _{d_{2}}^{\nu }d^{\dagger }_{\nu 2}+\alpha _{d_{-2}}^{\nu }d^{\dagger }_{\nu -2}, \end{aligned} \end{aligned}$$
(10)

where, the \(\alpha\)’s coefficients in Eq (10) are

$$\begin{aligned} \begin{aligned} \alpha _s^\rho = 1,\quad \alpha _{{d_0}}^\rho = {\beta _\rho }\sin {\gamma _\rho },\quad \alpha _{{d_2}}^\rho = \alpha _{{d_{ - 2}}}^\rho = {\beta _\rho }\frac{{\sin {\gamma _\rho }}}{{\sqrt{2} }},\quad \quad \quad \rho : = \pi ,\nu . \end{aligned} \end{aligned}$$
(11)

By minimizing the energy surface function (Eq. (1)), the equilibrium shape of nuclei corresponding to the IBM-2 Hamiltonian is determined. Therefore, one can express

$$\begin{aligned} \begin{array}{l} E = \langle {N_\pi },{\alpha _\pi },{N_\nu },{\alpha _\nu }|\hat{H}\left| {{N_\pi },{\alpha _\pi },{N_\nu },{\alpha _\nu }} \right\rangle \\ \quad = \eta \left\{ {\left\langle {{{\hat{n}}_{d\pi }}} \right\rangle + \left\langle {{{\hat{n}}_{d\nu }}} \right\rangle } \right\} + \frac{{\eta - 1}}{N}\left\{ {2\left\langle {\hat{Q}_\nu ^{{\chi _\nu }} \cdot \hat{Q}_\pi ^{{\chi _\pi }}} \right\rangle + \left\langle {\hat{Q}_\pi ^{{\chi _\pi }} \cdot \hat{Q}_\pi ^{{\chi _\pi }}} \right\rangle + \left\langle {\hat{Q}_\nu ^{{\chi _\nu }} \cdot \hat{Q}_\nu ^{{\chi _\nu }}} \right\rangle } \right\} . \end{array}\ \end{aligned}$$
(12)

The expectation value of each term in Eq. (12) is given as follows

$$\begin{aligned} \begin{array}{l} \left\langle {{{\hat{n}}_{d\rho }}} \right\rangle = \frac{{{N_\rho }\beta _\rho ^2}}{{1 + \beta _\rho ^2}}\\ \left\langle {\hat{Q}_\rho ^{{\chi _\rho }} \cdot \hat{Q}_\rho ^{{\chi _\rho }}} \right\rangle = \frac{{{N_\rho }}}{{1 + \beta _\rho ^2}}\left( {5 + \left( {1 + \chi _\rho ^2} \right) \beta _\rho ^2} \right) \\ \quad \quad \qquad \qquad \mathrm{{ + }}\frac{{{N_\rho }\left( {{N_\rho } - 1} \right) }}{{{{\left( {1 + \beta _\rho ^2} \right) }^2}}}\left[ {4\beta _\rho ^2 - 4\sqrt{\frac{2}{7}} {\chi _\rho }\beta _\rho ^3\cos \left( {3{\gamma _\rho }} \right) + \frac{2}{7}\chi _\rho ^2\beta _\rho ^4} \right] \\ \left\langle {\hat{Q}_\nu ^{{\chi _\nu }} \cdot \hat{Q}_\pi ^{{\chi _\pi }}} \right\rangle = \frac{{2{N_\pi }{N_\nu }{\beta _\pi }{\beta _\nu }}}{{7\left( {1 + \beta _\pi ^2} \right) \left( {1 + \beta _\nu ^2} \right) }}\left[ {14\cos \left( {{\gamma _\pi } - {\gamma _\nu }} \right) } \right. + {\chi _\nu }{\chi _\pi }{\beta _\pi }{\beta _\nu }\cos \left( {2{\gamma _\pi } - 2{\gamma _\nu }} \right) \\ \quad \quad \qquad \qquad \left. {\mathrm{{ + }}\sqrt{14} \left\{ {{\chi _\pi }{\beta _\pi }\cos \left( {2{\gamma _\pi } + {\gamma _\nu }} \right) + {\chi _\nu }{\beta _\nu }\cos \left( {{\gamma _\pi } + 2{\gamma _\nu }} \right) } \right\} } \right. \end{array} \end{aligned}$$
(13)

By substituting Eq. (13) into Eq. (12), the energy surface as a function of shape variables and parameters is derived and simplified to9

$$\begin{aligned} \begin{array}{l} E = \left\{ {\eta \frac{{{N_\pi }\beta _\pi ^2}}{{1 + \beta _\pi ^2}} + \frac{{\eta - 1}}{N}\left\{ {\frac{{{N_\pi }}}{{1 + \beta _\pi ^2}}\left( {5 + \left( {1 + \chi _\pi ^2} \right) \beta _\pi ^2} \right) \mathrm{{ + }}\frac{{{N_\pi }\left( {{N_\pi } - 1} \right) }}{{{{\left( {1 + \beta _\pi ^2} \right) }^2}}}\left[ {4\beta _\pi ^2 - 4\sqrt{\frac{2}{7}} {\chi _\pi }\beta _\pi ^3\cos \left( {3{\gamma _\pi }} \right) + \frac{2}{7}\chi _\pi ^2\beta _\pi ^4} \right] } \right\} } \right\} \\ \qquad \mathrm{{ + }}\left\{ {\eta \frac{{{N_\nu }\beta _\nu ^2}}{{1 + \beta _\nu ^2}} + \frac{{\eta - 1}}{N}\left\{ {\frac{{{N_\nu }}}{{1 + \beta _\nu ^2}}\left( {5 + \left( {1 + \chi _\nu ^2} \right) \beta _\nu ^2} \right) \mathrm{{ + }}\frac{{{N_\nu }\left( {{N_\nu } - 1} \right) }}{{{{\left( {1 + \beta _\nu ^2} \right) }^2}}}\left[ {4\beta _\nu ^2 - 4\sqrt{\frac{2}{7}} {\chi _\nu }\beta _\nu ^3\cos \left( {3{\gamma _\nu }} \right) + \frac{2}{7}\chi _\nu ^2\beta _\nu ^4} \right] } \right\} } \right\} \\ \qquad \; + \frac{{4{N_\pi }{N_\nu }{\beta _\pi }{\beta _\nu }\left( {\eta - 1} \right) }}{{7N\left( {1 + \beta _\pi ^2} \right) \left( {1 + \beta _\nu ^2} \right) }}\left[ {14\cos \left( {{\gamma _\pi } - {\gamma _\nu }} \right) } \right. + {\chi _\nu }{\chi _\pi }{\beta _\pi }{\beta _\nu }\cos \left( {2{\gamma _\pi } - 2{\gamma _\nu }} \right) \\ \qquad \mathrm{ }\left. {\mathrm{{ + }}\sqrt{14} \left\{ {{\chi _\pi }{\beta _\pi }\cos \left( {2{\gamma _\pi } + {\gamma _\nu }} \right) + {\chi _\nu }{\beta _\nu }\cos \left( {{\gamma _\pi } + 2{\gamma _\nu }} \right) } \right\} } \right] . \end{array}\ \end{aligned}$$
(14)

Equation (14) is a non-linear function of four variables and three parameters. It is practically impossible to find the extremum points of this function analytically because at least the first derivative leads to complex nonlinear equations, which currently cannot be obtained except by numerical methods.

Entanglement entropy

In examining the entanglement entropy in the semi-classical approximation of the IBM-2, two states are considered:

  1. (i)

    Entanglement entropy between protonic- and neutronic-bosons The coherent state in IBM-2 is expressed as a product of protonic-bosons and neutronic-bosons. So, there is no entanglement between them.

  2. (ii)

    Entanglement entropy between s and d bosons

To calculate the entanglement entropy between s and d bosons in IBM-2, the entanglement entropies between s and d protonic-bosons, and between s and d neutronic-bosons are separately obtained. The total entanglement entropy equals the sum of them.

According to Eq. (8), the boson coherent state for each type of boson is

$$\begin{aligned} \left| {{\psi _{{\beta _\rho },{\gamma _\rho }}}\left( {{N_\rho }} \right) } \right\rangle = {\theta _\rho }{\left( {B_\rho ^\dag } \right) ^{{N_\rho }}}\left| 0 \right\rangle = {\theta _\rho }{\left( {\alpha _s^\rho s_\rho ^\dag + \alpha _{{d_0}}^\rho d_{\rho 0}^\dag + \alpha _{{d_2}}^\rho d_{\rho 2}^\dag + \alpha _{{d_{ - 2}}}^\rho d_{\rho - 2}^\dag } \right) ^{{N_\rho }}}\left| 0 \right\rangle ,\quad \rho : = \pi ,\nu . \end{aligned}$$
(15)

By generalizing the binomial relation to a multinomial, one can express it as follows30

$$\begin{aligned} {\left( {{a_1} + {a_2} + \cdots + {a_r}} \right) ^N} = \sum \limits _{{l_1},{l_2},...,{l_r} = 0}^N {\frac{{N!}}{{{l_1}!{l_2}! \cdots {l_r}!}}} a_1^{{l_1}}a_2^{{l_2}} \cdots a_r^{{l_r}},\quad {l_1} + {l_2} + \cdots + {l_r} = N. \end{aligned}$$
(16)

Using Eq. (16), we have

$$\begin{aligned} \left| {{\psi _{{\beta _\rho },{\gamma _\rho }}}\left( {{N_\rho }} \right) } \right\rangle = {\theta _\rho }\sum \limits _{l_1^\rho ,l_2^\rho ,l_3^\rho ,l_4^\rho = 0}^{{N_\rho }} {\frac{{{N_\rho }!}}{{l_1^\rho !l_2^\rho !l_3^\rho !l_4^\rho !}}} \alpha _s^{l_1^\rho }\alpha _{{d_0}}^{l_1^\rho }\alpha _{{d_2}}^{l_1^\rho }\alpha _{{d_{ - 2}}}^{l_1^\rho }{\left( {s_\rho ^\dag } \right) ^{l_1^\rho }}{\left( {d_{\rho 0}^\dag } \right) ^{l_2^\rho }}{\left( {d_{\rho 2}^\dag } \right) ^{l_3^\rho }}{\left( {d_{\rho - 2}^\dag } \right) ^{l_4^\rho }}\left| 0 \right\rangle . \end{aligned}$$
(17)

Equation (17) must satisfy the relation of \(l_1^\rho + l_2^\rho + l_3^\rho + l_4^\rho = {N_\rho }\). Additionally, the vacuum ket is the tensor product of the vacuum kets of each boson creation operator, so that one can write

$$\begin{aligned} \left| 0 \right\rangle \equiv \left| {0,0,0,0} \right\rangle = {\left| 0 \right\rangle _s} \otimes {\left| 0 \right\rangle _{{d_0}}} \otimes {\left| 0 \right\rangle _{{d_2}}} \otimes {\left| 0 \right\rangle _{{d_{ - 2}}}}. \end{aligned}$$
(18)

By applying each operator (e.g., \(d_{\rho - 2}^\dag\)) to the vacuum ket, one can obtain

$$\begin{aligned} \left| 0 \right\rangle _s \otimes {\left| 0 \right\rangle _{{d_0}}} \otimes {\left| 0 \right\rangle _{{d_2}}} \otimes {\left| {l_4^\rho } \right\rangle _{{d_{ - 2}}}} = \frac{{{{\left( {d_{\rho - 2}^\dag } \right) }^{l_4^\rho }}}}{{\sqrt{l_4^\rho !} }}\left| 0 \right\rangle . \end{aligned}$$
(19)

It can be easily demonstrated

$$\begin{aligned} \left| {{\psi _{{\beta _\rho },{\gamma _\rho }}}\left( {{N_\rho }} \right) } \right\rangle = {\theta _\rho }\sum \limits _{l_1^\rho ,l_2^\rho ,l_3^\rho ,l_4^\rho = 0}^{{N_\rho }} {\frac{{{N_\rho }!}}{{\sqrt{l_1^\rho !l_2^\rho !l_3^\rho !l_4^\rho !} }}} \alpha _s^{l_1^\rho }\alpha _{{d_0}}^{l_1^\rho }\alpha _{{d_2}}^{l_1^\rho }\alpha _{{d_{ - 2}}}^{l_1^\rho }{\delta _{l_1^\rho + l_2^\rho + l_3^\rho + l_4^\rho ,{N_\rho }}}{\left| {l_1^\rho } \right\rangle _s} \otimes {\left| {l_2^\rho } \right\rangle _{{d_0}}} \otimes {\left| {l_3^\rho } \right\rangle _{{d_2}}} \otimes {\left| {l_4^\rho } \right\rangle _{{d_{ - 2}}}}. \end{aligned}$$
(20)

In Eq. (20), the Kronecker delta function imposes the conservation condition for the number of bosons. Therefore, the general form of the neutronic- or protonic-boson coherent state, as presented by the Schmidt decomposition in the IBM-2, is written

$$\begin{aligned} \begin{aligned}&|\psi _{\beta _{\rho },\gamma _{\rho }}(N_{\rho })\rangle = \sum _{l_{1}^{\rho },l_{2}^{\rho },l_{3}^{\rho },l_{4}^{\rho }}{\delta _{N_{\rho },l_{1}^{\rho }+l_{2}^{\rho } +l_{3}^{\rho }+l_{4}^{\rho }}\eta _{l_{1}^{\rho },l_{2}^{\rho } ,l_{3}^{\rho },l_{4}^{\rho }}|l_{1}^{\rho }\rangle _{s} \otimes |l_{2}^{\rho }\rangle _{d_{0}} \otimes |l_{3}^{\rho }\rangle _{d_{2}} \otimes |l_{4}^{\rho }\rangle _{d_{-2}}}, \qquad \rho = \pi , \nu \\ &\eta _{l_{1}^{\rho },l_{2}^{\rho } ,l_{3}^{\rho },l_{4}^{\rho }}=\theta _{\rho } \frac{N_{\rho }!}{\sqrt{{l_{1}^{\rho }!l_{2}^{\rho }!l_{3}^{\rho }!l_{4}^{\rho }!}}}\alpha _{s}^{l_{1}^{\rho }}\alpha _{d_{0}}^{l_{2}^{\rho }}\alpha _{d_{2}}^{l_{3}^{\rho }}\alpha _{d_{-2}}^{l_{4}^{\rho }}. \end{aligned} \end{aligned}$$
(21)

The Schmidt decomposition Eq. (21) is

$$\begin{aligned} \begin{aligned}&|\psi _{\beta _{\rho },\gamma _{\rho }}(N_{\rho })\rangle = \sum _{l_{1}^{\rho }=0}^{N_{\rho }}\lambda _{l_{1}^{\rho }}|l_{1}^{\rho }\rangle _{s} \otimes |\varphi \rangle _{d,N_{\rho }-l_{1}^{\rho }} \\ &|\varphi {\rangle _{d,{N_\rho } - l_1^\rho }}: = \frac{1}{{{\lambda _{l_1^\rho }}}}\sum \limits _{l_2^\rho ,l_3^\rho ,l_4^\rho } {{\delta _{{N_\rho },l_1^\rho + l_2^\rho + l_3^\rho + l_4^\rho }}{\eta _{l_1^\rho ,l_2^\rho ,l_3^\rho ,l_4^\rho }}|l_2^\rho {\rangle _{{d_0}}} \otimes |l_3^\rho {\rangle _{{d_2}}} \otimes |l_4^\rho {\rangle _{{d_{ - 2}}}}}, \end{aligned} \end{aligned}$$
(22)

with the following Schmidt numbers

$$\begin{aligned} \lambda _{l_{1}^{\rho }}=\sqrt{\sum _{l_{2}^{\rho },l_{3}^{\rho },l_{4}^{\rho }}{\delta _{N_{\rho }-l_{1}^{\rho },l_{2}^{\rho } +l_{3}^{\rho }+l_{4}^{\rho }}}\eta _{l_{1}^{\rho },l_{2}^{\rho } ,l_{3}^{\rho },l_{4}^{\rho }}^{2}}. \end{aligned}$$
(23)

One can obtain

$$\begin{aligned} \lambda _{l_1^\rho }^2 = \theta _\rho ^2\frac{{{{\left( {{N_\rho }!} \right) }^2}}}{{l_1^\rho !({N_\rho } - l_1^\rho )!}}{(\beta _\rho ^2)^{{N_\rho } - l_1^\rho }}. \end{aligned}$$
(24)

By reducing the bases of each part of a bipartite system, one can obtain the ’reduced density matrix’. Here, the reduction has been done over the d-bosons. Therefore, the ’reduced density matrix of s-bosons’ (\(\Gamma _s^{\left( \rho \right) }\)) is given as follows

$$\begin{aligned} \Gamma _s^{\left( \rho \right) } = T{r_d}\left| {{\psi _{{\beta _\rho },{\gamma _\rho }}}\left( {{N_\rho }} \right) } \right\rangle \left\langle {{\psi _{{\beta _\rho },{\gamma _\rho }}}\left( {{N_\rho }} \right) } \right| = \sum \limits _{l_1^\rho = 0}^{{N_\rho }} {\lambda _{l_1^\rho }^2{{\left| {l_1^\rho } \right\rangle }_s}{{\left\langle {l_1^\rho } \right| }_s}}. \end{aligned}$$
(25)

The entanglement entropy for the protonic- or neutronic-bosons is equal to

$$\begin{aligned} S_{\rho }(\Gamma _s^{\rho })=-\sum _{l_{1}^{\rho }}^{N_{\rho }}{\lambda _{l_{1}^{\rho }}^{2}} log(\lambda _{l_{1}^{\rho }}^{2}). \end{aligned}$$
(26)

So, the total entanglement entropy (\(S_{\pi \nu }(\Gamma _s^{\left( {\pi \nu } \right) })\)) in the semi-classical approximation of IBM-2 is written as

$$\begin{aligned} S_{\pi \nu }(\Gamma _s^{\left( {\pi \nu } \right) }) = \sum \limits _{\rho = \pi ,\nu } {S_{\rho }(\Gamma _s^{\left( \rho \right) })} = - \sum \limits _{\rho = \pi ,\nu } {\sum \limits _{l_1^\rho = 0}^{{N_\rho }} {\lambda _{l_1^\rho }^2} log(\lambda _{l_1^\rho }^2)}. \end{aligned}$$
(27)

Results

In this section, the energy surfaces and entanglement entropies have been calculated and analyzed in the framework of the semi-classical approximation IBM-2. All critical points in the previous pathes of Castan Pyramid (Fig. 1) have been considered. These pathes are divided into two groups based on their common properties, which are:

A. The connected pathes to the \({U_{\pi \nu }}\left( 5\right)\) limit.

B. Pathes of \(S{U_{\pi \nu }}\left( 3 \right) \leftrightarrow {O_{\pi \nu }}\left( 6 \right) \leftrightarrow \overline{S{U_{\pi \nu }}\left( 3 \right) }\) and \(SU_{\pi \nu }^*\left( 3 \right) \leftrightarrow {O_{\pi \nu }}\left( 6 \right) \leftrightarrow \overline{SU_{\pi \nu }^*\left( 3 \right) }\).

Each group of these pathes is examined in detail in a separate subsection discussed below.

The connected pathes to the \({U_{\pi \nu }}\left( 5\right)\) limit

According to Fig. 1, the connected pathes to the \(U_{\pi \nu }(5)\) limit and the parametric equations of \(\eta\), \(\chi _{\pi }\), and \(\chi _{\nu }\) in terms of t are presented in Table 1.

Table 1 Parametric equations of the connected lines to the \(U_{\pi \nu }(5)\) limit in the interval of \(0 \le t \le 1\).
Full size table

The energy surfaces of each path are shown in Fig. 2.

Fig. 2
figure 2

Contours of energy surface in the pathes of (I) \({U_{\pi \nu }}\left( 5 \right) \leftrightarrow {O_{\pi \nu }}\left( 6 \right)\), (II) \({U_{\pi \nu }}\left( 5 \right) \leftrightarrow S{U_{\pi \nu }}\left( 3 \right)\), (III) \({U_{\pi \nu }}\left( 5 \right) \leftrightarrow \overline{S{U_{\pi \nu }}\left( 3 \right) }\), (IV) \({U_{\pi \nu }}\left( 5 \right) \leftrightarrow SU_{\pi \nu }^*\left( 3 \right)\), and (V) \({U_{\pi \nu }}\left( 5 \right) \leftrightarrow \overline{SU_{\pi \nu }^*\left( 3 \right) }\) for \(N= 50\).

Full size image

In all the subplots in Fig. 2, the changes of extremum points per path follow the same pattern. Thus, for \(0 \le \eta < {\eta _c}\) the relative minima in the subplots converge. They join at \(\eta =\eta _{c}\) and form a flat minimum in \(\beta _{\pi }=\beta _{\nu }=0\). This is the critical point from \(U_{\pi \nu }(5)\) to all connected limits. The interval of \(0 \le \eta < {\eta _c}\) is known as the spinodal region for \({U_{\pi \nu }}\left( 5 \right) \leftrightarrow S{U_{\pi \nu }}\left( 3 \right)\) and \({U_{\pi \nu }}\left( 5 \right) \leftrightarrow SU_{\pi \nu }^*\left( 3 \right)\). In contrast, this interval for the pathes of \({U_{\pi \nu }}\left( 5 \right) \leftrightarrow \overline{S{U_{\pi \nu }}\left( 3 \right) }\) and \({U_{\pi \nu }}\left( 5 \right) \leftrightarrow \overline{SU_{\pi \nu }^*\left( 3 \right) }\) is referred to as the anti-spinodal region. Increasing the value of \(\eta\) from \(\eta _{c}\) to 1, reduces the width of the single global minimum point. However, the position of the global minimum remains unchanged. The values of deformation parameters in the global minimum at \({\eta _c} \le \eta \le 1\) are \(\beta _{\pi }=0\) and \(\beta _{\nu }=0\). Thus, the spherical region occurs at the \({\eta _c} \le \eta \le 1\). As shown in Fig. 2, the critical point for \(N=10, 50,\) and 100 is \(\eta _{c} \approx 0.8\) (or \(t \approx 0.2\)).

The entanglement entropy also confirms the critical point in the transition to \(U_{\pi \nu }(5)\) limit. The entanglement entropy versus \(\eta\) for pathes connected to \(U_{\pi \nu }(5)\) for \(N=10, 50\), and 100 are shown in the Fig. 3. In Fig. 3, the blue curves illustrate the transition from \(O_{\pi \nu }(6)\) to \(U_{\pi \nu }(5)\), and the red curves represent other pathes connected to \(U_{\pi \nu }(5)\). Numerical calculations show that the entanglement entropy versus \(\eta\) for each number of bosons in the pathes of \(S{U_{\pi \nu }}\left( 3 \right)\), \(\overline{S{U_{\pi \nu }}\left( 3 \right) }\), \(SU_{\pi \nu }^*\left( 3 \right)\), and \(\overline{SU_{\pi \nu }^*\left( 3 \right) }\) connected to \(U_{\pi \nu }(5)\) are exactly equal to each other. The difference in the entanglement entropy values in the pathes of II, III, IV, and V with I is evident in Fig. 3a–c. Additionally, Similar to IBM-1, in IBM-2 the transition from \(U_{\pi \nu }(5)\) to \(O_{\pi \nu }(6)\) is the second-order transition, whereas the transitions from \(U_{\pi \nu }(5)\) to the \(S{U_{\pi \nu }}\left( 3 \right)\), \(\overline{S{U_{\pi \nu }}\left( 3 \right) }\), \(SU_{\pi \nu }^*\left( 3 \right)\), and \(\overline{SU_{\pi \nu }^*\left( 3 \right) }\) are first-order. It seems that the observed differences in the entropy values in these Figures are related to their transition order. In all the pathes, for \(\eta =0\) and \(N \gg 1\), the maximum entanglement entropy occurs in the \({O_{\pi \nu }}\left( 6 \right)\), \(S{U_{\pi \nu }}\left( 3 \right)\), \(\overline{S{U_{\pi \nu }}\left( 3 \right) }\),\(SU_{\pi \nu }^*\left( 3 \right)\), and \(\overline{SU_{\pi \nu }^*\left( 3 \right) }\), respectively (see Fig. 3). According to Fig. 3, in the interval of \(0 \le \eta \le 0.65\), the entanglement entropy value remains nearly constant. In the region of \(0.65 \le \eta \le 0.8\), the values decrease suddenly, reaching zero at \(\eta \approx 0.8\). In the interval of \(0.8 \le \eta \le 1\), the value of entanglement entropy is zero. So, there is no entanglement between s protonic- and neutronic- bosons, and d protonic- and neutronic- bosons. This region is the same as the spherical region.

Pathes of \(S{U_{\pi \nu }}\left( 3 \right) \leftrightarrow {O_{\pi \nu }}\left( 6 \right) \leftrightarrow \overline{S{U_{\pi \nu }}\left( 3 \right) }\) and \(SU_{\pi \nu }^*\left( 3 \right) \leftrightarrow {O_{\pi \nu }}\left( 6 \right) \leftrightarrow \overline{SU_{\pi \nu }^*\left( 3 \right) }\)

The values of parameters \(\eta\), \(\chi _{\pi }\), and \(\chi _{\nu }\) in pathes \(S{U_{\pi \nu }}\left( 3 \right) \leftrightarrow {O_{\pi \nu }}\left( 6 \right) \leftrightarrow \overline{S{U_{\pi \nu }}\left( 3 \right) }\) and \(SU_{\pi \nu }^*\left( 3 \right) \leftrightarrow {O_{\pi \nu }}\left( 6 \right) \leftrightarrow \overline{SU_{\pi \nu }^*\left( 3 \right) }\) are \(\left( { - 1.33 \le {\chi _\pi } \le 1.33,\;{\chi _\pi } = {\chi _\nu },\;\eta = 0} \right)\) and \(\left( { - 1.33 \le {\chi _\pi } \le 1.33,\;{\chi _\pi } = -{\chi _\nu },\;\eta = 0} \right)\), respectively. As shown in Fig. 4, the energy surfaces in the \(SU_{\pi \nu }\left( 3 \right)\) limit have two minimums and two maximums in front of each other. By changing the values χπ of \(\chi _{\pi }\), the points of maximums converge and disappear at \(\chi _{\pi }=\chi _{\nu }=0\), resulting in two identical minima forming at their initial positions (see Fig. 4b). This point is the same critical point in the transition from \(SU_{\pi \nu }\left( 3 \right)\) to \(\overline{SU_{\pi \nu }\left( 3 \right) }\), and its coordinates correspond to the \({O_{\pi \nu }}\left( 6 \right)\) limit. By comparing Fig. 4a with Fig. 4c, one can conclude that the extremum points in the \(SU_{\pi \nu }\left( 3 \right)\) limit are mirror images of the extremum points in the \(\overline{SU_{\pi \nu }\left( 3 \right) }\) limit. The entanglement entropy versus \(\chi _{\pi }\) in this path is shown in Fig. 5 for \(N=10, 50,\) and 100. As shown in Fig. 5, increasing the number of bosons results in a decrease in the depth of the minimum point; consequently, at \(N \gg 1\), the minimum point transforms into the absolute maximum. The coordinate of this point is (0, 0, 0), which corresponds to the \({O_{\pi \nu }}\left( 6 \right)\) limit. This result perfectly agrees with the critical point predicted by the energy surfaces (Fig. 4b).

The energy surfaces and entanglement entropies related to the path of \(SU_{\pi \nu }^*\left( 3 \right) \leftrightarrow {O_{\pi \nu }}\left( 6 \right) \leftrightarrow \overline{SU_{\pi \nu }^*\left( 3 \right) }\) for \(N=10, 50,\) and 100 are presented in Figs. 6 and 7. According to Fig. 6a, there are two minimum points and one maximum point in the \(SU_{\pi \nu }^*\left( 3 \right)\) limit. As \(\chi _{\pi }\) changes from − 1.33 to near zero, the position of the maximum point changes, unlike the points of minimum. At the point (0, 0, 0), the point of maximum disappears completely, while two minima remain (see Fig. 6b). By increasing \(\chi _{\pi }\) from 0 to 1.33, the point of maximum appears completely symmetrically on the opposite side again (see Fig. 6c). Here, similar to the previous path, the extremum points in the \(SU_{\pi \nu }^*\left( 3 \right)\) and \(\overline{SU_{\pi \nu }^*\left( 3 \right) }\) limits are mirror images of each other, and the critical point in this path is (0, 0, 0), which corresponds to the \({O_{\pi \nu }}\left( 6 \right)\) limit. Numerical calculations demonstrate that the behavior of entanglement entropy along this path is completely similar to the path of \(SU_{\pi \nu }\left( 3 \right)\) to \(\overline{SU_{\pi \nu }\left( 3 \right) }\). The results are shown in Fig. 7. It can be easily demonstrated that for \(N \gg 1\), the maximum entropy value occurs at the \({O_{\pi \nu }}\left( 6 \right)\) limit, which aligns perfectly with the critical point derived from the analysis of energy surfaces. These results and the previous findings illustrate that the entanglement entropy is not only a suitable observable for investigating the QPT, but its critical points can also be determined for transitions between symmetrical limits.

Fig. 3
figure 3

Entanglement entropy versus \(\eta\) and in the pathes of \({U_{\pi \nu }}\left( 5 \right) \leftrightarrow {O_{\pi \nu }}\left( 6 \right)\) (blue lines), \({U_{\pi \nu }}\left( 5 \right) \leftrightarrow S{U_{\pi \nu }}\left( 3 \right)\), \({U_{\pi \nu }}\left( 5 \right) \leftrightarrow \overline{S{U_{\pi \nu }}\left( 3 \right) }\), \({U_{\pi \nu }}\left( 5 \right) \leftrightarrow SU_{\pi \nu }^*\left( 3 \right)\), and \({U_{\pi \nu }}\left( 5 \right) \leftrightarrow \overline{SU_{\pi \nu }^*\left( 3 \right) }\) (red lines) for \(N=10, 50, 100\).

Full size image
Fig. 4
figure 4

Energy surface in the path of \(S{U_{\pi \nu }}\left( 3 \right) \leftrightarrow {O_{\pi \nu }}\left( 6 \right) \leftrightarrow \overline{S{U_{\pi \nu }}\left( 3 \right) }\) for \(N= 50\).

Full size image
Fig. 5
figure 5

Entanglement entropy versus \(\chi _{\pi }\) (or \(\chi _{\nu }\)) and in the path from \(S{U_{\pi \nu }}\left( 3 \right) \leftrightarrow {O_{\pi \nu }}\left( 6 \right) \leftrightarrow \overline{S{U_{\pi \nu }}\left( 3 \right) }\) for \(N_{B}=10, 50,100\).

Full size image
Fig. 6
figure 6

Energy surface in the path of \(SU_{\pi \nu }^*\left( 3 \right) \leftrightarrow {O_{\pi \nu }}\left( 6 \right) \leftrightarrow \overline{SU_{\pi \nu }^*\left( 3 \right) }\) for \(N= 50\).

Full size image
Fig. 7
figure 7

Entanglement entropy versus \(\chi _{\pi }\) and in the path of \(SU_{\pi \nu }^*\left( 3 \right) \leftrightarrow {O_{\pi \nu }}\left( 6 \right) \leftrightarrow \overline{SU_{\pi \nu }^*\left( 3 \right) }\) for \(N_{B}=10, 50,100\).

Full size image

Conclusions

Entanglement entropy is a novel observable for studying QPT in nuclei that has recently garnered significant attention . To achieve this, the entanglement entropy within the semi-classical approximation IBM-2 framework was calculated. The parametric space in this model is three-dimensional, and geometrically, the pathes in the parametric space have been described within the framework of the Casten pyramid. Based on common characteristics, particularly the presence of critical points, the pathes in the Casten pyramid were divided into two groups. These groups are: the connected pathes to the \({U_{\pi \nu }}(5)\) limit and the connected pathes to the \(O_{\pi \nu } (6)\) limit. In each group, the energy surfaces and entanglement entropy of the correspondence pathes were calculated and analyzed. The results indicated that entanglement entropy is sensitive to the QPT and effectively describes the critical points. The numerical analysis of energy surfaces also fully confirms the results of entanglement entropy.