A graph-based computational approach for modeling physicochemical properties in drug design

Abstract

The efficacy and effectiveness of antibiotics and neuropathic drugs are essentially guided by their physicochemical properties governing stability, bioavailability, and therapeutic activity. This work utilises mathematical modelling and quantitative structure-property relationship (QSPR) analysis for predicting important physicochemical properties such as boiling point, enthalpy of vaporisation, flash point, and molar refraction of chosen antibiotics and neuropathic drugs. Modified degree-based topological indices are utilised as molecular descriptors for correlations between physicochemical functionality and molecular structure. Linear and quadratic forms are various forms of regression models employed for improved predictions. The findings exhibit excellent performance of quadratic models across all but one property compared to linear models, highlighted by significant statistical markers like high $R^{2}$ values and low error margins. These results highlight the potential use of topological descriptors in combination with sound mathematical frameworks for drug optimisation and early-stage screening.

Introduction

Over recent years, QSPR modeling has been established as a highly viable technique in pharmaceutical chemistry for its potential in predicting major physicochemical properties from molecular structure directly¹. This predictive property is important for accelerating drug discovery since early evaluation of molecular performance can be conducted without requiring long-term laboratory experiments². Boiling points, enthalpy for vaporization, flash points, and molar refraction are particularly significant due to their impact on influential pharmaceutical parameters such as stability, availability, and formulation safety³. Such considerations are particularly significant when developing antibiotics, where therapeutic efficacy is highly dependent upon molecular traits. A QSPR model provides standardized means for connecting molecular descriptors and such properties, making the rationale-based lead optimization and drugs design possible⁴. For an elaborate review of QSPR methods applied to drug molecules, see⁵. Kumar and Das⁶ compared Generalized Quadratic (GQ) and Quadratic Generalized (QG) indices as molecular descriptors. Their work shows how these indices are effective in modeling structural aspects pertinent for quantum chemical properties. The analysis indicates that these two descriptors hold potential for improved predictive modeling for QSPR research work.

Here, important physicochemical traits are studied for a group of drugs of pharmacological interest, such as Norfloxacin, Ciprofloxacin, Gemifloxacin, Chlorpyrifos, Dimethoate, Phorate, Monocrotophos, Thiram, Azoxystrobin, Atrazine, Chlorothalonil, and Warfarin. Most of these drugs, which are either antibiotics or structurally analogous bioactive molecules, are extensively employed for various therapeutic and agricultural applications and share diverse and pertinent physicochemical requirements⁷. For example, vaporization enthalpy informs about the amount of energy needed for phase boundary transitions, which has direct bearing on drug formulation and storage functions. In a similar vein, data for boiling points for drugs such as Norfloxacin and doxycycline are important for gauging thermal stability for various temperature and pressure conditions⁸. Kumar and Das⁹ explored the structural sensitivity and chemical applicability of numerous newly developed degree-based topological indices. Their analysis proved how these indices react under different structural changes in molecules. The analysis reaffirmed their potential applicability in QSPR/QSAR modeling by proving effective for correlation with important chemical parameters. In turn, molar refraction is a gauge of the polarizability of a molecule and has predictive value for drug biological environment interactions, whereas flash point measurements are important for determining flammability and for proper handling of volatile drugs¹⁰.

The present research utilizes degree-based topological indices, which are mathematical descriptors of molecular structure^11,12. In graph theory, vertex degree noted $\widehat{\lambda }_{a}$ refers to the number of connected edges linking a given vertex a¹³. Degree-based topological indices are highly effective for predicting physicochemical, thermodynamic, and biological characteristics because they capture essential structural information such as molecular branching and network connectivity¹⁴. Kumar and Das¹⁵ compared the performance of Nirmala and Sombor indices in detail, i.e., comparing their applicability, degeneracy, and smoothness. This work compared how each index functions in differentiating between molecular structures. The results underscore the efficacy and limitations of these two indices and offer insights into their possible use for modeling molecules using graphs. Within QSAR and QSPR analysis, degree-based topological indices constitute an important subdomain because vertex degree-based information allows for high correlation between molecular structure and experimentally tangible properties or bioactivities¹⁶.

Jacob and Clement¹⁷ elucidated the structural complexity of zeolite EDI through the application of topological entropy and proved the efficacy of the model to predict the interaction of molecules inside zeolite structures. The method introduced a new quantitative means to interpret host-guest behavior in porous compounds. Gayathri, Santiago, and Govardhan¹⁸ investigated hexagonal fractals via the application of topological indices and the use of fractal dimensions to describe structure-property relationships. Their work showed the capability of the aforementioned mathematical measures to predict the behavior of molecules and predict material properties. Peter et al.¹⁹ created a predictive model of interaction energies between molecules through the application of topological and spectral entropies of zeolite AWW. The article stressed the significance of descriptors of the entropic kind to predict the interaction of molecules inside porous compounds. Shenoy et al.²⁰ carried out statistical analysis of the application of Revan topological indices to drug compounds for the treatment of tuberculosis. Their analysis showed the promise of the indices to analyze and discriminate molecular structures for application to pharmaceutical research. Jacob et al.²¹ carried out network topology and entropy analysis of tetragonal farneseite zeolites in order to study their structural complexity. Their research emphasized the use of measures of entropy to identify complex topological properties of the zeolite structures.

The application of topological indices as structural descriptors has a history dating back a long time in predicting molecular properties. The first contribution was made by Wiener²², who proved that paraffin boiling points could be well estimated through topological indices, setting a precursor to the relationship between molecular structure and thermodynamic property. This was further developed upon by Gutman and Trinajstic²³ when the first Zagreb indices were introduced degree-based topological indices that have been an integral part in investigating the electronic aspect of molecules thereafter. This framework was expanded upon later by Kulli²⁴ when he introduced reverse Zagreb indices that capture reverse vertex degrees and present additional structural insights. Further building upon this was done by Khabyah et al.²⁵, who applied reverse degree-based indices toward extracting knowledge about coronene structures. Being symmetric, two-dimensional, and highly conjugated in nature, coronene is a perfect system for studying molecular symmetry and stability using topological analysis. For this work, a diversity of modified degree based topological indices are applied toward capturing the antibiotic and related molecules’ molecular structure. The indices are capable of encoding essential structural features size, branching, and connectivity effectively, enabling quantitative correlation between architectural building blocks and physicochemical behavior²⁶.

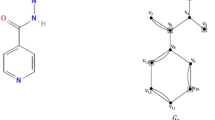
Quantitative Structure-Property Relationship (QSPR) models have been widely developed for predicting chemical and physical properties of pharmacologically active compounds, illustrated by comparison analysis between regression models depicted in Figs. 1, 2, 3, and 4. Amongst these studied compounds, Norfloxacin, a synthetic fluoroquinolone antibiotic, is extensively utilized in clinical practice for treating urinary tract infection (UTI), prostatitis, and various gastrointestinal infections caused by susceptible bacteria. Norfloxacin inhibits bacterial DNA gyrase and ultimately causes cell division and DNA replication inhibition, which leads ultimately to cell death in bacteria. This drug is mainly effective in gram-negative organisms like Escherichia coli and Klebsiella pneumoniae and is administered orally. Nevertheless, in clinical use, its activity is sometimes hindered because of side effects like nausea, dizziness, and uncommon but serious tendon issues, particularly in elderly patients. Norfloxacin is contraindicated in infancy and pregnant individuals because of possible adverse cartilage and joint development effects, as depicted in Fig. 1a (source: http://www.chemspider.com).

Ciprofloxacin Ciprofloxacin is a fluoroquinolone antibiotic agent that exerts broad-spectrum efficacy against bacterial infections, including respiratory, urinary, gastrointestinal, and skin infections. This agent exerts its antibacterial effects by inhibiting bacterial DNA gyrase and topoisomerase IV, enzymes critical for DNA replication in bacteria^27,28. This triggers the death of bacterial cells. Side effects may include nausea, diarrhea, and photosensitivity, risk of tendon ruptures, particularly in the elderly. Because of these possible adverse effects, it is usually avoided in children as well as pregnant women see Fig. 1b.

Gemifloxacin Gemifloxacin is a fluoroquinolone antimicrobial agent indicated for respiratory tract infections, including acute bacterial exacerbation’s of chronic bronchitis and mild to moderate forms of community-acquired pneumonia^29,30. The drug exerts its antibacterial activity by inhibiting DNA gyrase and topoisomerase IV-bacterial enzymes critical for DNA replication. The common side effects include rash, diarrhea, and nausea, while serious ones might include tendonitis and tendon rupture. This is a cautious prescription that should not be dispensed to children or pregnant women see Fig. 1c.

Fig. 1

(a) Norfloxacin     (b) Ciprofloxacin    (c) Gemifloxacin.

Chlorpyrifos Chlorpyrifos is not an antibiotic but an organophosphate pesticide in common use for the control of insect pests both in agriculture and residentially. It works through the inhibition of acetyl cholinesterase enzyme action in insects, an action which causes overstimulation of the nervous system and eventually death^31,32. It is due to these reasons that it has been restricted or banned in many countries, with studies linking exposures to developmental and neurological problems. see Fig. 2a.

Dimethoate It is not an antibiotic; it is an organophosphate insecticide, widely used in agriculture to control a wide range of pests on crops. It works by inhibiting acetyl cholinesterase, an enzyme essential for insect nerve function, thus disrupting their nervous system and eventually killing them^33,34. While effectively applied for pest control, dimethoate had raised health and environmental concerns because of its toxicity, affecting not only non-target species, including beneficial insects, but also humans upon exposure. Due to its associated risks, certain countries restrict its use; recommended guidelines on safety are advised upon application to reduce the impact on the environment and human health see Fig. 2b .

Phorate Phorate is a highly toxic organophosphate insecticide and acaricide. It is not an antibiotic, and its application is only for the safety of crops such as corn, potatoes, and cotton. Phorate acts through the inhibition of acetyl cholinesterase, an enzyme critical to the normal functioning of the nervous system; the insects are then paralyzed and dead^35,36. Phorate is extremely toxic and, therefore, particularly dangerous to humans, wild animals, and the environment through exposure. Because of this, its use has been seriously circumscribed when this insecticide is used, and certain countries have banned it. Recommended safety precautions during handling and application are rigorous see Fig. 2c.

Fig. 2

(a) Chlorpyrifos     (b) Dimethoate    (c) Phorate.

Monocrotophos Monocrotophos is not an antibiotic, but it contains a highly toxic organophosphorus insecticide used in large-scale control of various pests in a variety of crops such as cotton, rice, and sugar cane. It acts through the inhibition of acetyl cholinesterase that overstimulates the nervous system and eventually leads to paralysis and death in insects. Monocrotophos is highly toxic, and exposure has a severe threat to human beings, birds, and aquatic life^37,38. For this reason, several countries have banned or restricted the use of the chemical, due to which only a High degree of care can be afforded to those areas where the use of the chemical is not prohibited for agricultural purposes see Fig. 3a.

Thiram Thiram is not an antibiotic. It is a chemical type of fungicide, and it finds wide application in agriculture to prevent fungal infections in crops such as fruits, vegetables, and ornamental plants. This effect is through the inhibition of spore germination of fungi, thus protecting the plants from diseases such as blight, rust, and mold^39,40. It is injurious to health if inhaled and ingested and can cause irritation to the skin of human beings too. As it is hazardous to the environment, its use has some prescription on the basis of which it has to be handled and applied see Fig. 3b.

Azoxystrobin In fact, it is not an antibiotic but a broad-spectrum fungicide. It finds wide application in agriculture for the protection of various crops against very different fungal diseases such as blight, rust, and powdery mildew. The mode of action consists of the inhibition of mitochondrial respiration in fungi, which halts the growth of fungal cells and stops the proliferation of the infection^41,42. This product is taken to be generally safe while being used in the prescribed manner; however, it does have a potential threat to the environment, particularly aquatic life, and should be carried out very carefully near water systems to minimize ecological damage see Fig. 3c.

Fig. 3

(a) Monocrotophos     (b) Thiram    (c) Azoxystrobin.

Atrazine Atrazine is not an antibiotic, but it is one of the most widely used herbicides in the world. It is applied for the control of broadleaf and grassy weeds in a number of crops, including corn, sugarcane, and sorghum^43,44. A chemical kill of plants, it inhibits photosynthesis in plants, thus causing death to the weeds and increasing crop yields. Due to the possible influence of the chemical on fauna and suspected endocrine-disrupting activity, its use is either limited or prohibited in some countries, while it remains one of the most widely used herbicides in other countries see Fig. 4a.

Chlorothalonil Chlorothalonil is not an antibiotic. It is a broad-spectrum fungicide. It finds wide application in agriculture and horticulture for the protection of crops such as peanuts, potatoes, tomatoes, and turf grass against fungal diseases like mold, blight, and leaf spot. Where chlorothalonil is effective, there is also a risk to the environment, aquatic organisms in particular, and irritation in man in the case of exposure⁴⁵. Its use is thus regulated in many regions with specific view to minimizing ecological impacts, and safety measures are advised during application with a view to reducing health risks see Fig. 4b.

Warfarin Warfarin is not an antibiotic; it is an anticoagulant or blood thinner used to prevent and treat blood clots that form in the veins of the legs, in the lungs, and with atrial fibrillation. Warfarin requires close monitoring since its efficacy depends on dietary factors, concurrent medications, and patient variables. Blood sampling is frequent to maintain it within a narrow window of safety and efficacy⁴⁶. Adverse effects include bleeding complications, which may well require a patient to be advised about diet and the use of medications cautiously to avoid undesirable interactions see Fig. 4c.

Fig. 4

(a) Atrazine     (b) Chlorothalonil    (c) Warfarin.

Degree based topological indices

In this section, we provide the initial literature review for topological indices.

Gutman and Polansky introduced the first and second Zagreb index⁴⁷ as:

$$M_{1}(G) = \sum \limits _{ab \in E(G)} (\widehat{\lambda }_a + \widehat{\lambda }_b),\,\,\ M_{2}(G) = \sum \limits _{ab \in E(G)} (\widehat{\lambda }_a \times \widehat{\lambda }_b)$$

Martinez-Martinez et al.⁴⁸ defined the Harmonic index as follows:

$$H(G) = \sum \limits _{ab \in E(G)} \frac{2}{(\widehat{\lambda }_a + \widehat{\lambda }_b)}$$

The forgotten index was introduced by Furtula and Gutman⁴⁹ as:

$$F(G) = \sum \limits _{ab \in E(G)} [(\widehat{\lambda }_a)^2 + (\widehat{\lambda }_b)^2]$$

The Shilpa-Shanmukha Index was defined by Zhao et al.⁵⁰ as follows:

$$SS(G) = \sum \limits _{ab \in E(G)} \sqrt{\frac{\widehat{\lambda }_a \times \widehat{\lambda }_b}{\widehat{\lambda }_a + \widehat{\lambda }_b}}$$

The atom bond connectivity index was introduced by Estrada et al.⁵¹ as:

$$ABC(G) = \sum \limits _{ab \in E(G)} \sqrt{\frac{\widehat{\lambda }_a + \widehat{\lambda }_b - 2}{\widehat{\lambda }_a \times \widehat{\lambda }_b}}$$

The Randic index was defined by Randic et al.⁵²as:

$$RI(G) = \sum \limits _{ab \in E(G)} \frac{1}{\widehat{\lambda }_a \times \widehat{\lambda }_b}$$

The sum connectivity index and the geometric arithmetic index was defined by Vukicevic et al.⁵³ as:

$$SC(G) = \sum \limits _{ab \in E(G)} \frac{1}{\widehat{\lambda }_a + \widehat{\lambda }_b},\,\,\ GA(G) = \sum \limits _{ab \in E(G)} \frac{2\sqrt{\widehat{\lambda }_a \times \widehat{\lambda }_b}}{\widehat{\lambda }_a + \widehat{\lambda }_b}$$

The Hyper Zagreb Index was introduced by Rajasekharaiah et al.⁵⁴ as:

$$HZ(G) = \sum \limits _{ab \in E(G)} (\widehat{\lambda }_a+\widehat{\lambda }_b)^2$$

Main results

In this section, we presented antibiotic drug molecules’ degree-based bond partitions, see Table 1. Moreover using this edge partition for all antibiotic drugs, we have computed degree-based topological indices.

Table 1 Degree-based bond partitions of antibiotic drug molecules.

For the drug molecule Norfloxacin $\left( G_1\right)$, By using first and second Zagreb index and edge partition of $G_1$.

$$\begin{aligned} M_{1}(G)= & \sum \limits _{ab \in E(G)} (\widehat{\lambda }_a + \widehat{\lambda }_b)\\ M_{1}(G_1)= & (1+2)(2)+(1+3)(5)+(2+2)(3)+(2+3)(8)+(3+3)(7)=120 \\ M_{2}(G)= & \sum \limits _{ab \in E(G)} (\widehat{\lambda }_a + \widehat{\lambda }_b)\\ M_{1}(G_1)= & (1 \times 2)(2)+(1\times 3)(5)+(2\times 2)(3)+(2\times 3)(8)+(3\times 3)(7)=142\\ \end{aligned}$$

By using Harmonic index and edge partition of $G_1$

$$\begin{aligned} H(G)= & \sum \limits _{ab \in E(G)} \frac{2}{(\widehat{\lambda }_a + \widehat{\lambda }_b)}\\ H(G_1)= & \frac{2}{({1}+ {2})}{(2)}+\frac{2}{({1}+ {3})}{(5)}+\frac{2}{({2}+ {2})}{(3)}+\frac{2}{({2}+ {3})}{(8)}+\frac{2}{({3}+ {3})}{(7)} =10.87 \\ \end{aligned}$$

By using forgotten index and edge partition of $G_1$

$$\begin{aligned} F(G)= & \sum \limits _{ab \in E(G)} [(\widehat{\lambda }_a)^2 + (\widehat{\lambda }_b)^2]\\ F(G_1)= & (1^{2}+2^{2})(2)+(1^{2}+3^{2})(5)+(2^{2}+2^{2})(3)+(2^{2}+3^{2})(8)+(3^{2}+3^{2})(7)=314 \end{aligned}$$

By using Shilpa-Shanmukha Index and edge partition of $G_1$

$$\begin{aligned} SS(G)= & \sum \limits _{ab \in E(G)} \sqrt{\frac{\widehat{\lambda }_a \times \widehat{\lambda }_b}{\widehat{\lambda }_a + \widehat{\lambda }_b}}\\ SS(G_1)= & \sqrt{\frac{1\times 2}{(1+ 2)}}(2)+\sqrt{\frac{1\times 3}{(1 + 3)}}(5)+\sqrt{\frac{2\times 2}{(2 + 2)}}(3)+\sqrt{\frac{2\times 3}{(2 + 3)}}(8)+\sqrt{\frac{3\times 3}{(3 + 3)}}(7)=26.30 \end{aligned}$$

By using atom bond connectivity index and edge partition of $G_1$

$$\begin{aligned} ABC(G)= & \sum \limits _{ab \in E(G)} \sqrt{\frac{\widehat{\lambda }_a + \widehat{\lambda }_b - 2}{\widehat{\lambda }_a \times \widehat{\lambda }_b}}\\ ABC(G_1)= & \sqrt{\frac{1+2-2}{(1 \times 2)}}(2)+\sqrt{\frac{1+3-2}{(1 \times 3)}}(5)+\sqrt{\frac{2+2-2}{(2 \times 2)}}(3)+\sqrt{\frac{2+3-2}{(2 \times 3)}}(8)+\sqrt{\frac{3+3-2}{(3\times 3)}}(7)=17.94\\ \end{aligned}$$

By using Randic index and edge partition of $G_1$

$$\begin{aligned} RI(G)= & \sum \limits _{ab \in E(G)} \frac{1}{\widehat{\lambda }_a \times \widehat{\lambda }_b}\\ RI(G_1)= & \left( \frac{1}{1 \times 2}\right) (2)+\left( \frac{1}{1 \times 3}\right) (5)+\left( \frac{1}{2 \times 2}\right) (3)+\left( \frac{1}{2 \times 3}\right) (8)+\left( \frac{1}{3 \times 3}\right) (7)=11.40\\ \end{aligned}$$

By using sum connectivity index and edge partition of $G_1$

$$\begin{aligned} SC(G)= & \sum \limits _{ab \in E(G)} \frac{1}{\widehat{\lambda }_a + \widehat{\lambda }_b}\\ SC(G_1)= & \left( \frac{1}{1+2}\right) (2)+\left( \frac{1}{1+3}\right) (5)+\left( \frac{1}{2+2}\right) (3)+\left( \frac{1}{2+3}\right) (8)+\left( \frac{1}{3+3}\right) (7)=11.59\\ \end{aligned}$$

By using geometric arithmetic index and edge partition of $G_1$

$$\begin{aligned} GA(G)= & \sum \limits _{ab \in E(G)} \frac{2\sqrt{\widehat{\lambda }_a \times \widehat{\lambda }_b}}{\widehat{\lambda }_a + \widehat{\lambda }_b}\\ GA(G_1)= & \frac{2\sqrt{1 \times 2}}{(1+2)}(2)+\frac{2\sqrt{1 \times 3}}{(1+3)}(5)+\frac{2\sqrt{2 \times 2}}{(2+2)}(3)+\frac{2\sqrt{2 \times 3}}{(2+3)}(8)+\frac{2\sqrt{3 \times 3}}{(3+3)}(7)=24.05\\ \end{aligned}$$

By using Hyper Zagreb Index and edge partition of $G_1$

$$\begin{aligned} HZ(G)= & \sum \limits _{ab \in E(G)} (\widehat{\lambda }_a+\widehat{\lambda }_b)^2\\ HZ(G)= & (1+2)^2(2)+(1+3)^2(5)+(2+2)^2(3)+(2+3)^2(8)+(3+3)^2(7)=598 \end{aligned}$$

Similarly, in accordance with what was described above, this computation process was applied to all of the entire dataset, and the calculated values correspondingly for all 12 antibiotic drugs. The ERC’s governing instruments are compiled with Table 2.

Table 2 Degree based topological indices for antibiotics drug molecules.

Exploring topological indices and physicochemical properties via regression models

Quantitative Structure-property Relationship (QSPR) models allow for predictions of a compound’s various physical and chemical properties solely from its molecular structure⁵⁵. Quantitative Structure-Activity Relationship (QSAR) models provide a mathematical approach for investigating complex interdependencies between a molecule’s structure and its physicochemical or biochemical activities⁵⁶. Topological descriptors are particularly significant in QSPR investigations, as they contain useful connections with a variety of physicochemical properties pertinent to drugs employed for treating various medical conditions⁵⁷. Both linear and quadratic regression models were employed in this study for analyzing antibiotic drugs’ physicochemical properties. The experimental property values for these antibiotics are given in Table 3.

Table 3 Antibiotics’ physicochemical characteristics.

Table 4 Statistical parameters and regression models for ${M_1(G)}$.

Table 4 comparison between linear and quadratic regression models against various physicochemical properties prediction based on the model $M_1(G)$. Quadratic models generally outperform the linear one with a higher value of $R^2$ and lower SE: properties like BP, ENP, and HAC provide the best fitting with the quadratic model with $R^2 = 0.962$. The quadratic model for HAC is the most accurate in predicting the property with $(R = 0.980)$, $(F = 115.763)$. Both models perform badly for molar volume and MV since $R^2 \le 0.7$. Overall, a quadratic model provides the best predictions for most properties in this dataset. The graphical prediction is shown in Fig. 5.

Fig. 5

Comparison of fits of models for HAC prediction based on $M_1(G)$.

Table 5 Statistical parameters and regression models for ${M_2(G)}$.

Table 5 compares the performance of linear and quadratic regression models for the prediction of physicochemical properties using $M_2 (G)$. A quadratic model tends to make better predictions, higher $R^2$ values and lower standard errors (SE). For properties like boiling point (BP), enthalpy of vaporization (ENP), and heavy atom count (HAC), quadratic models show excellent performance, with . The best prediction is observed for BP, with $R^2 = 0.957$ and high statistical significance $p<10^{-6}$. The flash point (FP) and molar refraction (MR) are also well described by quadratic models. Molar volume (MV) yields poorer correlations, with $R^2< 0.7$ In general, both models normally fit below 0.7, while the quadratic models are the best for most of the properties. The graphical prediction is shown in Fig. 6.

Fig. 6

Comparison of fits of models for BP prediction based on $M_2(G)$.

Table 6 Statistical parameters and regression models for H(G).

Table 6 presents a comparison of linear versus quadratic regression models against each other for the prediction of physicochemical properties using H(G). The quadratic model gives better performance with considerably high values of $R^2$ and lower values of standard error (SE) in the case of most of the properties. The boiling point and heavy atom count are best fitted by quadratic models with $R^2 = 0.917$ and $R^2 =0.972$, respectively, with high statistical significance $p< 10^{-5}$. Quadratic equations also provide very good predictions for properties such as molar refraction and polarization. The opposite holds for the enthalpy of vaporization, ENP; both have fair correlations, $R^2 =0.831$. Globally, quadratic models are the best predictors for the data. The graphical explanation of the comparison is shown in Fig. 7.

Fig. 7

Comparison of fits of models for HAC prediction based on H(G).

Table 7 Statistical parameters and regression models for F(G).

This Table 7 collects some statistical parameters and also the regression model in the different properties as functions of F(G). Each property is modeled by a linear and quadratic model. The best model between these two is the one that realizes higher $R^2$ and the lowest p-values. For the most important properties, the quadratic model resulted in better fitted (higher R and $R^2$), indicating a nonlinear relation. Properties like BP, ENP, MR, POL, and Com give good $( R^2 )$ values greater than 0.9 for a quadratic model, indicating that the predictive accuracy is fairly good. The P-values of such models are also very low, hence statistically significant. In the scatter plot of highlighted properties, the quadratic model comes out to be the best for many properties, something as HAC. The graphical explanation of the comparison is shown in Fig. 8.

Fig. 8

Comparison of fits of models for HAC prediction based on F(G).

Table 8 Statistical parameters and regression models for SS(G).

The Table 8 below shows the statistical parameters and regression models for different properties as functions of SS(G), for which both linear and quadratic models have been fitted, considering that the best fit always correlates with higher $R^2$ values with lowerp-values. Most of the properties have a better fit, as by $R^2$ values closer to 1, with quadratic models like BP, FP, POL, and MW. On the other hand, for properties such as HIAC, ENP, and MR, the quadratic model is highly predictive with large p-values, indicating thereby how appropriate this approach is. In general, the quadratic models do better for this data set. The graphical comparison is shown in Fig. 9.

Fig. 9

Comparison of fits of models for HAC prediction based on SS(G).

Table 9 Statistical parameters and regression models for ABC.

Table 9 above shows, for a number of properties, regression models as functions of the ABC index. In general, quadratic models are better fits, as measured by the higher p-value. The quadratic model for BP has an $R^2=0.947$ with a $p=1.68 \times 10^{-6}$, where as the quadratic model for ENP has an $R^2=0.863$ with a $p=1.82\times 10^{-5}$. The quadratic model systematically demonstrates an outstanding fit for HIAC with $R^2=0.960$ and $p=5.25\times 10^{-7}$; hence, it was the best model for this property. Most of the other properties, such as FP, POL, and MW, also presented high $R^2$ values in their respective quadratic models, confirming their accuracy and suitability. The graphical comparison is shown in Fig. 10.

Fig. 10

Comparison of fits of models for HAC prediction based on ABC(G).

Table 10 Statistical parameters and regression models for RI(G).

The Table 10 below depicts the quality of fit tests utilizing linear and quadratic regression models for several properties with RI(G). From the rather higher values, it is obvious that in most cases the quadratic model fits best. Most importantly, the best fit is manifested by HAC with $R^2=0.948$, followed by BP with $R^2=0.920$, and POL with $R^2=0.868$. The results point to how well the quadratic model fits to catch nonlinear relationships and thus serves as the best predictive model across the data. The graphical comparison is shown in Fig. 11.

Fig. 11

Comparison of fits of models for HAC prediction based on RI(G).

Table 11 Statistical parameters and regression models for SC(G).

The Table 11 shows quadratic regression models fitting best for most properties of SS(G), as evidenced by high values of $R^2$. The best fittings are for HAC, with $R^2= 0.957$, MW, with $R^2= 0.977$, and BP, with $R^2= 0.984$. This suggests that the quadratic model does a better job of capturing nonlinear trends in the data than the linear model. The graphical comparison is shown in Fig. 12.

Fig. 12

Comparison of fits of models for HAC prediction based on SC(G).

Table 12 Statistical parameters and regression models for GA(G).

Table 12 presents the regression models together with their statistical parameters for different properties versus GA(G). Most of the properties were tested both for linear and quadratic models, and the Table 12 gives values of the equation, correlation coefficient R, determination coefficient $R^2$, standard error $S_E$, and p-values. Quadratic models generally exhibit better $R^2$ values compared to linear models, hence a better fit of the model. For example, the quadratic model for HAC has a high value of $R^2=0.978$, compared to $R^2=0.897$ for the linear model. All the models have very low values of p, hence they are statistically significant. Notably, properties such as ENP and POL also exhibit excellent fits with $R^2$ values surpassing 0.9. The graphical comparison is shown in Fig. 13.

Fig. 13

Comparison of fits of models for HAC prediction based on GA(G).

Table 13 Statistical parameters and regression models for HZ(G).

Table 13 gives statistical parameters and regression models of different properties concerning relation HZ(G). Quadratic models generally provide higher values $R^2$ than linear models, which express better fittings. For example, a quadratic model of the HAC property yields an $R^2$ of 0.951 against that of the linear model, 0.917, indicating that the performance is better. The computed values in all the models were much less, indicating that they are statistically significant. In general, the quadratic models provide a much better explanation for the properties with much higher $R^2$ values for most properties and smaller standard errors. In other words, the quadratic models can normally explain property HZ(G) more effectively. The graphical comparison is shown in Fig. 14.

Fig. 14

Comparison of fits of models for HAC prediction based on HZ(G).

Comparison of actual and prediction values of drugs properties

Table 14 compares the predicted boiling point, enthalpy of vaporization and Flash point from various models linear and quadratic of different types of drug molecules to real values. In each case, the quadratic model provided the closest yield on boiling point and enthalpy of vaporization to real values, especially for complex drug molecules . This means that the quadratic model handles the representation of drug molecular complexity better than the other models. The graphical comparison is shown in Fig. 15.

Table 14 Comparison of actual values against predictions for Boiling Point, Enthalpy of Vapourization and Flash point.

Fig. 15

(a) Comparison of actual and predicted values for BP, (b) Comparison of actual and predicted values for ENV, (c) Comparison of actual and predicted values for FP.

Table 15 Comparison of actual values against predictions for Molar refractivity, Polarizability, and Molar weight.

The Table 15 below shows the comparison of the predicted and experimental values of Molar refractivity, Polarizability and Molar weight of various drug molecules using different models: linear, and quadratic. The quadratic model generally shows closer alignment with the actual values of both properties, especially for the most complex molecules. This trend in general points toward the better performance of the quadratic model in correct property prediction, although some deviations remain, more precisely concerning molar refraction. The graphical comparison is shown in Fig. 16.

Fig. 16

(a) Comparison of actual and predicted values for Molar refractivity,    (b) Comparison of actual and predicted values for Polarizability,    (c) Comparison of actual and predicted values for Molar weight.

Table 16 Comparison of actual values against predictions for Heavy atom count, Complexity and Molar volume.

Table 16 shows that, overall, the quadratic model gives the closest predictions to real values in respect to polarization and molar weight for different drug molecules. While the model generally predicts polarization very well for most drugs considered, significant deviations become apparent for Abamectin, which documents the limitations of the model for some compounds. The linear and logarithmic models tend to underestimate polarization, especially if high values are considered. This is so true, especially for molar weight, since all models’ results keep close to the actual values, therefore indicating simpler predictive needs versus polarization. Lastly, according to both properties in this dataset, the quadratic model gives more accurate results. The graphical comparison is shown in Fig. 17.

Fig. 17

(a) Comparison of actual and predicted values for Heavy atom count,    (b) Comparison of actual and predicted values for Complexity,    (c) Comparison of actual and predicted values for Molar volume.

Conclusion

Our study presents a systematic QSPR analysis of antibiotic drugs, utilizing degree-based topological indices to predict critical physicochemical properties. The findings highlight the effectiveness of reverse degree-based indices in capturing molecular structural attributes and their correlation with drug characteristics. The application of regression models, particularly quadratic models, demonstrates high predictive accuracy, indicating the potential for structural tailoring in drug development. Future research can extend this approach to a broader range of pharmaceuticals, incorporating machine learning techniques for enhanced predictive performance. These findings highlight the application of the use of QSPR models as a valuable drug development aid that enables scientists to design the required drug candidates at an early development phase. This computational approach not only saves the effort and the cost of laboratory screening but also provides a superior insight into the molecular factors affecting the behavior of the drug.

Future work

For applied drug discovery purposes, merging bioactivity information (QSAR) into QSPR descriptors has the potential for producing multifaceted predictive models enabling lead optimization early in drug development. Further, affiliating these topological descriptors with ADMET (absorption, distribution, metabolism, excretion, and toxicity) traits would lead to a comprehensive predictive system, enhancing new drug candidates’ pharmacokinetic profiling. Finally, building an automation pipeline or an analogous software package using this methodology would help medicinal chemists screen drug-like molecules virtually in high-throughput, speeding up drug development.