Optimization of MXene-based aqueous ionic liquids for solar systems using conventional and AI-based techniques

Abstract

MXene-based aqueous ionic liquids hold significant promise for enhancing heat transfer in solar energy systems. However, their full potential remains underexplored, particularly concerning the simultaneous optimization of key thermophysical properties such as thermal conductivity (TC), dynamic viscosity (DV), and specific heat capacity (SHC). This study employs an integrated data-driven approach to optimize MXene-based aqueous ionic liquids by varying system temperature and MXene mass fraction (MF). Response surface methodology (RSM) is used for predictive modeling, while enhanced hill climbing (EHC), non-dominated sorting genetic algorithm II (NSGA-II), and the multi-objective generalized normal distribution optimizer (MOGNDO) are applied for multi-objective optimization. Weighted decision-making tools, including the desirability function and the MARCOS method, refine the selection of optimal solutions. The cubic RSM models effectively captured the relationships between input variables and responses, facilitating accurate optimization. MOGNDO demonstrated broader solution diversity and more comprehensive Pareto front coverage compared to NSGA-II. Optimal thermophysical performance was observed at 50 °C with MF ranging from 0.00188 to 0.2%. Predicted optimal values include TC up to 0.797 W/m K, DV between 2.028 and 2.157 mPa s, and SHC ranging from 2.192 to 2.503 J/g K. The proposed methodology offers a reliable and scalable strategy for optimizing MXene-based nanofluids, contributing to improved thermo-hydraulic performance in solar systems. These findings support the advancement of renewable energy solutions and provide a robust framework applicable to broader engineering optimization problems.

Introduction

Heat transfer enhancement (HTE) techniques uniquely improve the system’s efficiency in various technological applications. These techniques can be classified into active and passive. Active methods require external power sources to HTE¹. Conversely, passive methods enhance the heat transfer rate by modifying thermofluidic systems through the integration of inserts², fins^3,4, nanomaterials⁵, or rough surfaces⁶. In recent years, industries have embraced nanofluids as a new class of heat transfer fluids due to advancements in nanotechnology-based HTE techniques. Nanofluids result from dispersing various metal⁷, metal oxide⁸, and carbon-based⁹ nanomaterials in traditional fluids. Nanofluids exhibit superior thermal properties and have the potential to replace conventional fluids in various applications, such as HVAC, renewable energy, heat exchangers and energy storage^10,11. Nanofluids, with enhanced thermal conductivity (TC) and specific heat capacity (SHC), significantly improve the efficiency of solar energy systems¹². By incorporating novel nanoparticles, they facilitate superior thermal performance, leading to increased energy absorption, storage, and transfer¹³. This enhancement contributes to more efficient photovoltaic, thermal, and hybrid solar technologies, promoting renewable energy adoption¹⁴.

Building on this progress, the growing importance of nanomaterials has spurred extensive research aimed at identifying highly efficient materials tailored to specific applications. The emergence of 2D nano-sized materials, such as transition metal oxides/dichalcogenides, boron nitrides, and graphene-based materials revolutionized the field of nanotechnology^15,16. Mxene is a promising 2D nanomaterial comprising a few atomic layers of transition metal carbides or nitrides. It has unique characteristics, such as a 2D lamellar structure, metal-like conductivity, high density, and fast ion intercalation, making it suitable for various applications, including energy production and storage^17,18. MXene-based nanofluids have been studied for their potential use as industrial coolants, solar thermal collectors, and photovoltaic/thermal (PV/T) panels¹⁹. Kadirgama et al.²⁰ investigated MXene-based nanofluids, highlighting MXene’s hydrophilic nature and potential for highly efficient solar applications. Sreekumar et al.²¹ performed a numerical study on PV/T solar systems with water/MXene nanofluid, showing increased thermal and electrical efficiency. Aslfattahi et al.²² analyzed the thermal performance of a solar dish collector with MXene nanomaterials added to soybean oil, observing improved thermal efficiency for the nanofluid compared to the pure fluid.

Building on such developments, recent studies have shown that MXene-based nanofluids can significantly enhance TC, photo-thermal conversion (PTC) performance, and overall energy conversion efficiency^23,24. Rubbi et al.²⁵ conducted experiments using Therminol55 oil mixed with MXene (Ti₃C₂) and CuO nanomaterials to enhance the performance of PV/T solar systems. They observed significant improvements in the system’s PTC and TC when MXene nanomaterials were present. In a direct absorption solar collector application, Wang et al.²⁶ utilized an MXene/water nanofluid, achieving higher PTC efficiency than a graphene-based nanofluid. MXene-based nanofluids have also demonstrated excellent stability, low dynamic viscosity (DV), and superior light absorption capacity²⁷. In some studies, it was observed that the DV of nanofluids remained almost constant with the addition of MXene²⁸. However, other studies reported a significant decrease in DV when MXene was added to nanofluids²⁹. Also, MXene was found to improve the dispersion stability of nanofluids, which could contribute to the decrease in DV²⁵. Bao et al.³⁰ examined Ti₃C₂T_x MXene/EG nanofluid, noting increased TC and excellent stability compared to graphene and MWCNT nanofluids. Mao et al.¹⁹ measured the TC of MXene-based nanofluids with water and EG, reporting notable improvements while experiencing slight changes in DV. Also, Jin et al.²⁹ measured the DV and TC of water-based fluids containing mono (graphene) and hybrid (graphene/MXene) nanomaterials. Graphene-based nanofluid increased TC by 65.34% and DV by 70.69%, while adding MXene to the nanofluid had little impact on TC but reduced DV.

The insights from the reviewed experimental studies highlight the importance of developing precise models for predicting the TPPs of nanofluids, which can significantly reduce the cost and time required for extensive laboratory testing³¹. The application of response surface methodology (RSM) as a powerful statistical-based approach in modeling and optimizing the TPPs of nanofluids has gained significant attention in recent years. In contrast, the emergence of artificial intelligence (AI) and machine learning (ML) algorithms has arisen as a strong competitor to traditional statistical methods, offering alternative approaches for development and improvement in various fields^32,33. Machine learning models such as ANFIS have demonstrated high predictive accuracy in modeling complex nonlinear systems, making them effective tools for estimating physical properties in engineering and energy applications³⁴. Researchers have employed both RSM and ML techniques to predict the TPPs of various nanofluids. Table 1 illustrates the details of the recent investigations on this issue. The findings from Table 1 indicate that ML techniques such as GPR, ANFIS, and ANN tend to produce complex models with high accuracy levels. Conversely, RSM models, despite their straightforwardness, provide satisfactory precision. RSM offers low-complexity models that can rival the accuracy achieved by ANN, presenting an advantage in applications where computational cost and simplicity are paramount. This emphasizes the potential benefits of utilizing RSM models in diverse real-world scenarios. The RSM method is employed for regression modeling in this study due to these advantages.

Table 1 Comparison of ML and RSM approaches in predicting TPPs of nanofluids.

In addition to the separate application of ML and RSM for modeling TPPs, recent research has focused on optimizing TPPs using a two-objective approach, maximizing TC while minimizing DV. Various studies, such as those conducted by Danish et al.⁴³ and Esfe et al.⁴⁴, utilized RSM to identify the optimal TPP values for water-based nanofluids. Maqsood et al.⁴⁵ optimized MWCNT-based nanofluids employing ANN and RSM techniques. Esfe and Tilebon⁴⁶ used RSM and NSGA-II to optimize TPPs in an oil-MWCNT/Al₂O₃ nanofluid. Said et al.⁴⁷ employed fuzzy logic and PSO to model and optimize TPPs in water/EG mixtures containing TiO₂ and Al₂O₃ nano-sized materials. Amani et al.⁴⁸ applied multiple techniques, including ANN, GA, and decision-making, to achieve optimal TPP values in nanofluids. Esfe et al.⁴⁹ combined RSM, ANN, GA, and PSO to optimize TPPs in water-based nanofluids comprising CuO, Al₂O₃, SiO₂, and ZnO nanomaterials.

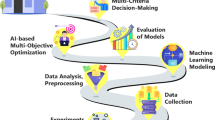
Reviewed studies clearly show that the performance of solar energy systems depends significantly on the thermophysical properties of the working fluids used for heat transfer. However, there is a lack of comprehensive strategies specifically tailored to optimize these properties in MXene-based aqueous ionic liquids. While prior research has broadly explored nanofluids, no studies have applied integrated data-driven modeling, optimization, and decision-making approaches to this emerging class of materials. This study addresses that gap by optimizing three key thermophysical properties (TC, DV, and SHC) to enhance the performance of MXene-based aqueous ionic liquids in solar energy systems. The study strategically examines two independent variables: the MXene mass fraction and the system temperature, providing a focused approach to achieving optimal performance. A key innovation of this research lies in the development of a dual-framework optimization strategy that considers traditional heuristic and advanced metaheuristic algorithms with data-driven modeling and decision-making, an approach not previously applied to MXene-based aqueous ionic liquids. The study introduces a hybrid methodology by integrating response surface methodology with enhanced hill climbing (EHC) for low-cost heuristic optimization, and the novel multi-objective generalized normal distribution optimization (MOGNDO) algorithm for high-accuracy metaheuristic optimization. Uniquely, the outputs from EHC are refined using the desirability function, while MOGNDO’s Pareto-optimal solutions are evaluated using the MARCOS multi-criteria decision-making technique. This dual-path strategy allows for a trade-off between computational efficiency and solution accuracy. This is the first comprehensive implementation of a multi-layered optimization and decision-making framework specifically applied to enhance MXene-based nanofluids. This integrated methodology offers a scalable, accurate, and systematic approach to improving the thermo-hydraulic performance of solar energy systems, filling a significant gap in the current literature. The methodological flowchart, encompassing data analysis, RSM modeling, multi-objective optimization, and decision-making, is summarized in Fig. 1, highlighting the study’s structured and innovative strategy.

Fig. 1

Flowchart of the proposed methodology in the present research from data analysis to the decision-making.

Data

The laboratory data from Das et al.⁵⁰ are used to implement the proposed hybrid approach based on RSM. The aim of Das et al. was to enhance the performance of aqueous ionic liquid used in a hybrid PV/T solar system by dispersing MXene (Ti₃C₂) nanomaterials at three different mass fractions: 0.05 wt%, 0.1 wt%, and 0.2 wt%. Various TPPs were measured, and for the present study, TC, DV, and SHC were specifically selected due to their significant importance in optimizing solar-based energy systems. Additionally, the properties were measured across various temperature ranges. For the current research, the modeling and optimization process focused on the common temperature range of 25 to 50 °C. Tables 2 and 3 present the characteristics of the independent and dependent variables, respectively, derived from the extracted data. In order to gain a deeper understanding of the data, various variables are plotted using the violin plot in Fig. 2. The data are normalized within the range of − 1 to 1 to facilitate better comparison utilizing the following relationship:

Table 2 Characteristics of independent variables (mass fraction and temperature).

Table 3 Characteristics of dependent variables (TC, DV, and SHC).

Fig. 2

The violin plots of the independent and dependent variables.

$${x}_{norm}=\frac{x-{x}_{min}}{{x}_{max}-{x}_{min}}\times 2-1$$

(1)

Violin plots visualize probability density functions of random variables using sample data. They combine nonparametric estimates with other summary information, enabling comparison of distributions across variables. Advantages include showcasing distinct peaks, positions, and relative amplitudes, preserving raw data for meta-analysis, representing different designs in one graph, and providing a compact and informative visualization of sample distribution⁵¹.

Besides the data distribution, the relationship between different variables can provide insight into how sensitive the objectives are to the inputs. The Pearson correlation coefficient (PCC) is a statistical metric that quantifies the linear correlation between two variables⁵². With values ranging from − 1 to 1, the coefficient indicates the strength and direction of the linear relationship: 1 represents a perfect positive linear relationship, − 1 indicates a perfect negative linear relationship, and 0 suggests no linear relationship. The PCC is calculated as follows⁵³:

$$PCC=\frac{\sum_{i=1}^{N}\left({X}_{i}-\overline{X }\right)\left({Y}_{i}-\overline{Y }\right)}{\sqrt{\sum_{i=1}^{N}{\left({X}_{i}-\overline{X }\right)}^{2}\sum_{i=1}^{N}{\left({Y}_{i}-\overline{Y }\right)}^{2}}}$$

(2)

where $N$ is number of data points, ${X}_{i}$ and ${Y}_{i}$ denote the specific values of the variables $X$ and $Y$, and $\overline{X }$ and $\overline{Y }$ are their respective average values.

Figure 3 presents PCC matrix plots for different TPPs. The results reveal a significant positive correlation (PCC = 0.84) between thermal conductivity and MXene nanoparticle concentration, while TC shows a weaker correlation (PCC = 0.41) with temperature. In contrast, dynamic viscosity exhibits a strong negative correlation (PCC = − 0.93) with temperature, indicating the profound impact of temperature on MXene-based nanofluid’s dynamic viscosity. Interestingly, the mass fraction of MXene nanoparticles shows a low influence (PCC = 0.27) on dynamic viscosity. Similar to TC, specific heat capacity demonstrates a strong linear dependence (PCC = 0.94) on mass fraction, while its temperature dependence is comparatively weaker than other TPPs. It is important to acknowledge that the relationship between TPPs and input variables may not always follow a linear pattern. In such cases, the weak correlation observed between certain input variables and TPPs should not be overlooked or underestimated. Non-linear relationships can have significant implications and should be carefully considered in the analysis and interpretation of the data.

Fig. 3

PCC diagrams for (a) TC, (b) DV, and (c) SHC.

RSM modeling

Response surface methodology, a statistical and mathematical technique used in experimental design and analysis, aims to elucidate and optimize the intricate relationship between a response variable and its corresponding input factors⁵⁴. By generating mathematical models, RSM effectively enables the comprehension and interpretation of the system. Moreover, this methodology aids in identifying the most optimal combination of input factors while simultaneously allowing for the assessment of their interactions and overall influence on the response variable. RSM plays a pivotal role in enhancing our understanding of complex systems and facilitating informed decision-making processes.

In a hypothetical situation, the association between the various system responses, denoted as ${y}_{i}$, and the input vector $x$, which consists of elements ${x}_{1},{x}_{2},\dots$, and ${x}_{n}$, is elucidated through a sophisticated function that is denoted as $f$:

$${y}_{i}=f\left({x}_{i1},{x}_{i2},\dots {x}_{in}\right) (i=\text{1,2},\dots ,M)$$

(3)

The primary objective of RSM is to obtain a derived function ($\widehat{f}$), that minimizes the difference or gap between the system responses (${y}_{i}$) and the anticipated responses (${\widehat{y}}_{i}$):

$${\widehat{y}}_{i}=\widehat{f}\left({x}_{i1},{x}_{i2},\dots {x}_{in}\right) (i=\text{1,2},\dots ,M)$$

(4)

$$\sum_{i=1}^{M}{\left[{\widehat{y}}_{i}-{y}_{i}\right]}^{2} \stackrel{ }{\to } min$$

(5)

To attain the utmost conceivable precision in the estimation of $\widehat{f}$, the RSM considers several mathematical models, including but not limited to linear, two-factor interaction (2FI), quadratic, cubic, quartic, etc. These models incorporate an exhaustive spectrum of forms that can encapsulate and effectively characterize the intricate relationship between the input and target variables. The coefficients for the RSM models were estimated using the least squares method, which minimizes the sum of squared errors between predicted and observed values, thereby ensuring statistical robustness and model reliability.

The RSM employs rigorous statistical validation techniques to prevent overfitting and strengthen the model’s generalization ability for novel datasets. Overfitting arises when a model is overly adapted to the training data, leading to diminished predictive performance on unfamiliar scenarios. For this purpose, predicted R² is used. Unlike traditional R², which assesses how well a model explains the variability within its training data, predicted R² specifically evaluates the model’s predictive accuracy for new, unseen data. This metric is derived using Leave-One-Out Cross-Validation (LOOCV), a method that rigorously tests the model’s performance by sequentially excluding each data point and predicting its value. In LOOCV, each observation is individually excluded from the dataset, and the model is developed using the remaining data. The excluded data point is then predicted, and the associated prediction error is determined. This process is systematically repeated for every observation, offering a thorough evaluation of the model’s predictive accuracy. Moreover, RSM uses Analysis of Variance (ANOVA) to mitigate the risk of overfitting by applying statistical criteria like p-values to assess the significance of model terms. When models contain numerous terms, they are more prone to overfitting, as they may unintentionally model random noise instead of true underlying patterns. In the context of ANOVA, p-values act as indicators to detect variables that could lead to overfitting. A variable with a high p-value is deemed statistically insignificant, suggesting it likely represents random noise instead of a meaningful association. Eliminating such irrelevant variables refines the RSM model, improving its robustness against overfitting and enhancing both predictive accuracy and generalization capability.

Thermal conductivity

According to Table 4, the accuracy analysis of RSM in developing thermal conductivity predictive models suggests that the cubic model is the most suitable form based on the available data. The quartic model could not be fully processed due to the limited data points and includes terms that do not correctly describe the model. For the proposed model, the R², adjusted R², and predicted R² are 0.9967, 0.9945, and 0.9832, respectively, indicating the validity and precision of this model. It should be noted that the adjusted R² considers the influence of coefficients on the model. The proposed cubic model and its coefficients are presented in Eq. 6 and Table 5.

Table 4 Accuracy of models developed by RSM in predicting TC.

Table 5 Coefficients of TC predictive model.

$$TC={\alpha }_{0}+{\alpha }_{1}T+{\alpha }_{2}MF+{\alpha }_{3}TMF+{\alpha }_{4}{T}^{2}+{\alpha }_{5}{MF}^{2}+{\alpha }_{6}{T}^{2}MF+{\alpha }_{7}T{MF}^{2}+{\alpha }_{8}{T}^{3}+{\alpha }_{9}{MF}^{3}$$

(6)

The analysis of the variance of the TC predictive model is presented in Table 6. According to the table, the A, B, AB, B², A²B, AB², B³ terms have a P-value less than 0.05, which indicates their statistical significance. Also, term A³ shows a P-value beyond 0.1, which indicates its lack of importance and influence. The F-value of the model is equal to 464.80, which shows a high precision for the proposed model. In addition, Adeq Precision, which is the signal-to-noise proportion, has a value far beyond the standard value for the proposed model (67.299 >  > 4). All the examined criteria confirm the reliability of the suggested model.

Table 6 ANOVA of TC predictive model.

A detailed comparison of the predicted values obtained from the RSM-based model with the actual data is crucial for deeply understanding its performance. For this purpose, Fig. 4 presents three visual representations: regression graph, violin plot, and margin of deviation (MOD) diagram. The MOD presents the relative error (RE) of outputs. Based on Fig. 4a, all points touch a part of the Y = X line, indicating an acceptable match between the predictions and the observations. Figure 4b compares the model outputs’ probability density function (PDF) with that of observations. As can be seen, there is generally a satisfactory compatibility between the two functions, but in some areas, a slight difference is visible. Figure 4c shows the RE of the outputs in the range of − 1.95% to 1.76%. According to the figure, four data points have an error higher than 1%. Also, only three points show errors larger than − 1%. While the proposed model demonstrates a satisfactory balance between overestimating and underestimating observations, a quantitative analysis reveals that more data points fall below MOD = 0. This indicates a tendency of the model to overestimate the observations.

Fig. 4

Details of the TC model developed by RSM: (a) regression plot, (b) violin diagram, (c) MOD graph, and (d) TC contour in terms of T and MF.

A visual representation in three dimensions is depicted in Fig. 4d, illustrating the influence of T and MXene MF on the thermal conductivity using the proposed RSM-based model. The figure clearly demonstrates that as the temperature increases, the TC also rises. This phenomenon can be attributed to the fact that higher temperatures augment the TC of fluids due to an escalation in molecular motion and collision frequency. As the temperature increases, the kinetic energy of fluid molecules also rises. This leads to more frequent and energetic collisions between the molecules. Consequently, this heightened molecular activity facilitates thermal energy transfer, ultimately resulting in a higher thermal conductivity. Additionally, the TC is enhanced with a growth in the MF of MXene nanomaterials. Indeed, the augmentation of the MF of nanoparticles within a fluid bolsters thermal conductivity through the promotion of particle–particle interactions, the improvement of particle dispersion, and the amplification of phonon transport facilitated by the higher surface-to-volume percentage of nano-sized materials.

Dynamic viscosity

Based on the accuracy analysis of RSM conducted on developing dynamic viscosity predictive models, Table 7 suggests that the cubic model is the most suitable considering the available data. It is noted that the quartic model could not be fully processed due to limited data points, and it includes terms that do not accurately describe the model. The proposed model demonstrates high validity, as indicated by the R², adjusted R², and predicted R² values of 0.9985, 0.9976, and 0.9935, respectively. These values signify the strong performance and precision of the proposed cubic model in predicting DV. The model’s formulation and the corresponding coefficient values are presented in Eq. 7 and Table 8.

Table 7 Accuracy of models developed by RSM in predicting DV.

Table 8 Coefficients of DV predictive model.

$$DV={\beta }_{0}+{\beta }_{1}T+{\beta }_{2}MF+{\beta }_{3}TMF+{\beta }_{4}{T}^{2}+{\beta }_{5}{MF}^{2}+{\beta }_{6}{T}^{2}MF+{\beta }_{7}T{MF}^{2}+{\beta }_{8}{T}^{3}+{\beta }_{9}{MF}^{3}$$

(7)

The analysis of the variance of the model predicting the dynamic viscosity is displayed in Table 9, showcasing a comprehensive evaluation of the various terms and their statistical significance. The table reveals that terms such as A, AB, A², B², AB², and B³ possess a P-value that falls below the threshold of 0.05, thus denoting their notable statistical significance. Conversely, the P-value associated with terms B, A²B, and A³ surpasses the threshold of 0.1, indicating their lack of importance and leverage within the model. Regarding the model’s precision, the F-value stands at an impressive 1061.17, illustrating the model’s ability to yield highly accurate predictions. Furthermore, the Adeq Precision, which measures the adequacy of the model, greatly exceeds the standard value for the proposed model, with a value of 107.556 compared to the benchmark of 4. Consequently, all the assessed criteria unequivocally affirm the soundness and validity of the suggested model.

Table 9 ANOVA of DV predictive model.

Figure 5 shows various graphs for evaluating the viscosity prediction model. Delving into the details of Fig. 5a, it becomes evident that all data points intersect with a portion of the Y = X line, indicating a satisfactory correspondence between the predicted values and the actual measurements. Furthermore, Fig. 5b shows a commendable level of compatibility between the PDFs. However, it is worth noting that a slight disparity is discernible in certain regions. Figure 5c visually depicts the relative error of the outputs within a specific range of -0.68% to 0.97%. A close analysis of the figure reveals that three data points exceed the error threshold of 0.5%. Similarly, another three points show errors that exceed the threshold of − 0.5%. The data point that generates an RE of 0.97% stands out as it imposes a greater degree of discrepancy on the model than the remaining data points. Furthermore, from a quantitative perspective, it is observed that the majority of the data points are positioned above the MOD = 0 line, signifying that the model consistently underestimates the observations. However, it is worth noting that except for four highly underestimated data points, most are situated close to the MOD = 0 line. Consequently, this proximity leads to a comparatively minor error in the estimation process.

Fig. 5

Details of the DV model developed by RSM: (a) regression plot, (b) violin diagram, (c) MOD graph, and (d) DV contour in terms of T and MF.

A three-dimensional visual representation is presented in Fig. 5d, illustrating the effect of temperature and MXene concentration on the DV utilizing the proposed RSM-based model. The figure unequivocally demonstrates that an escalation in temperature is inversely proportional to the DV. Indeed, as the temperature rises, the molecular motion becomes increasingly vigorous, resulting in a reduction in the strength of intermolecular interactions and the subsequent reduction of internal friction. Consequently, this phenomenon culminates in a decrement of dynamic viscosity. Conversely, the augmentation of the mass fraction yields an increase in dynamic viscosity, albeit its impact is less potent than that of temperature. The elevation of nanoparticle mass fraction within nanofluids engenders a rise in dynamic viscosity due to various contributing factors. Notably, nanoparticles possess a larger surface area when contrasted with the base fluid, which subsequently induces augmented interactions and friction between particles, thereby increasing viscosity. Furthermore, the existence of nanoparticles hinders the movement of the fluid, leading to heightened resistance and consequently leading to a comprehensive rise in viscosity.

Specific heat capacity

Based on the analysis conducted on the RSM in developing predictive models for specific heat capacity, the findings presented in Table 10 suggest that the cubic model emerges as the most suitable choice considering the characteristics and quantity of available data. The proposed model showcases a remarkable level of validity, evident from the impressive values obtained for R², adjusted R², and predicted R², which stand at 0.9997, 0.9995, and 0.9983, respectively. These values testify to the exceptional performance and accuracy exhibited by the proposed cubic model in predicting SHC. To comprehensively understand the model, its formulation and the corresponding coefficient values have been presented in Eq. 8 and Table 11.

Table 10 Accuracy of models developed by RSM in predicting SHC.

Table 11 Coefficients of SHC predictive model.

$$SHC={\gamma }_{0}+{\gamma }_{1}T+{\gamma }_{2}MF+{\gamma }_{3}TMF+{\gamma }_{4}{T}^{2}+{\gamma }_{5}{MF}^{2}+{\gamma }_{6}{T}^{2}MF+{\gamma }_{7}T{MF}^{2}+{\gamma }_{8}{T}^{3}+{\gamma }_{9}{MF}^{3}$$

(8)

The variance analysis of the model that predicts the specific heat capacity can be observed in Table 12, which provides a comprehensive evaluation of the different terms in the model and their statistical significance. The information presented in the table sheds light on the importance of various terms, such as A, B, AB, A², B², AB², A³, B³, as these terms exhibit a P-value below the critical threshold of 0.05. This indicates that these terms have a noteworthy statistical significance in the model. On the other hand, just one term, A²B, has a P-value that exceeds the threshold of 0.1, suggesting its lack of importance within the model. When considering the precision of the model, it is worth noting that the F-value is an impressive 5035.16. This high F-value highlights the model’s ability to generate highly accurate predictions. With a value of 231.856, in contrast to the benchmark of 4, the Adeq Precision further reinforces the reliability and validity of the suggested model. Therefore, based on the assessment of these criteria, it is unequivocally evident that the suggested model is sound and valid.

Table 12 ANOVA of SHC predictive model.

Figure 6 provides a comprehensive analysis of the data points in terms of accuracy. Figure 6a provides evidence of a flawless correspondence between the experimental and predicted data. This perfect alignment between the two data sets is visually apparent and strengthens the reliability of the SHC predictions made by RSM. Additionally, Fig. 6b showcases a remarkable resemblance between the PDFs of the observed data and the predicted data. The level of accuracy achieved in this similarity surpasses that observed in the previous two models that were investigated. Figure 6c exhibits the RE of the outputs within the range spanning from 0.159 to 0.131%. This particular range unveils a remarkable level of performance displayed by the suggested RSM model. The proposed model showcases an exceptional equilibrium between overestimating and underestimating observations, accentuating its efficacy. A meticulous quantitative analysis further underscores that precisely 50% of the data points lay beneath the MOD = 0, while the remaining 50% are positioned above this reference line. The findings above shed light on the noteworthy capabilities of the suggested RSM model.

Fig. 6

Details of the SHC model developed by RSM: (a) regression plot, (b) violin diagram, (c) MOD graph, and (d) SHC contour in terms of T and MF.

A three-dimensional visual representation is presented in Fig. 6d illustrating the influence of temperature and MXene MF on the SHC. The figure reveals that raising the temperature and MXene concentration raises SHC. However, the effect of the MF is more significant. The influence of nanoparticle MF in nanofluids on the specific heat capacity cannot be understated. As the MF rises, the SHC of nanofluids also exhibits an upward trend. This phenomenon can be predominantly attributed to nanoparticles, bolstering the fluid’s heat transfer mechanisms. The enlarged surface area of the nanoparticles facilitates enhanced interaction with the surrounding fluid, resulting in augmented heat absorption and retention. Moreover, nanoparticles can serve as conductive pathways, thereby ameliorating convective heat transfer and substantially contributing to the overall augmentation of SHC.

Heuristic optimization

EHC and desirability function

Optimizing the TPPs of MXene-based nanofluid is made possible by employing a numerical heuristic technique that operates on the hill-climbing approach. To elaborate further, the hill-climbing approach, a widely adopted methodology in optimization, can be succinctly summarized in a sequence of seven steps⁵⁵:

• 1. Considering an initial solution

• 2. Evaluating the current solution with the objective function

• 3. Generating neighboring solutions by applying minor changes to the current solution

• 4. Choosing the neighbor that has the best improvement over the current solution

• 5. Checking the stop condition (maximum repetition or reaching a limit)

• 6. Updating the current solution with the selected neighbor

• 7. Returning to step 2 and repeating the steps until the stopping condition is satisfied

It is of utmost significance to acknowledge that the hill-climbing technique is classified as a local search algorithm. Thus, it is content with becoming trapped in the local optimum and is not guaranteed to reach the global optimum. In order to surmount this predicament, apart from the designated points that are regarded as the initial solution, a collection of random points is also examined. This significantly improves the efficiency of the algorithm, leading to the development of a new approach known as the enhanced hill climbing technique.

For the EHC algorithm, an adaptive local search mechanism was applied. Initial solutions were generated by perturbing each decision variable within ± 5% of its current value using a uniform random distribution. This strategy maintained population diversity while enhancing convergence reliability. The penalty parameter in the penalized objective function was set to 10, a value adopted based on preliminary sensitivity analysis. This choice provided a stable balance between constraint handling and solution quality in the multi-objective framework.

To enable multi-objective optimization with the EHC technique, the desirability method proposed by Myers et al.⁵⁶ is employed. The desirability function (DF) acts as an objective function that assesses and merges multiple objectives. The DF assigns a ranking between one and zero to the values of each optimal point, with values closer to one indicating more favorable conditions for achieving all objectives simultaneously. The DF incorporates the geometric mean of different objectives and can be expressed as follows:

$$DF={\left({d}_{1}\cdot {d}_{2}\cdot \dots \cdot {d}_{n}\right)}^\frac{1}{n}={\left(\prod_{i=1}^{n}{d}_{i}\right)}^\frac{1}{n}$$

(9)

The variable “n” signifies the count of objectives. It is imperative to emphasize that should any objectives deviate from their desirable range, the overall function will result in zero, indicating an unsuccessful optimization.

The weight or importance factor of the objectives varies based on specific design conditions, differing considerably from one problem to another, and assists the designer in making informed decisions. In the present study, weights are assigned to each objective, resulting in a modification of Eq. 9 as follows:

$$DF={\left({d}_{1}^{{w}_{1}}\cdot {d}_{2}^{{w}_{2}}\cdot \dots \cdot {d}_{n}^{{w}_{n}}\right)}^{\frac{1}{\sum {w}_{i}}}={\left(\prod_{i=1}^{n}{d}_{i}^{{w}_{i}}\right)}^{\frac{1}{\sum {w}_{i}}}$$

(10)

The hybrid EHC/Desirability technique was independently implemented by the authors in the MATLAB environment (R2024a), following the theoretical formulations provided in the literature.

Results

As shown in Table 13, combining the EHC technique with the desirability function yields four optimal design scenarios with varying objective weights. In all cases, the maximum operating temperature is identified as 50 °C, and the optimal mass fraction of MXene nanoparticles consistently lies near the upper concentration limit.

• Scenario 1 (Equal importance: W_TC = W_DV = W_SHC = 1): Optimal MF is 0.197%.

• Scenario 2 (Thermal conductivity prioritized: W_TC = 3): Similar optimal MF to Scenario 1.

• Scenario 3 (Dynamic viscosity prioritized: W_DV = 3): Slightly lower optimal MF at 0.195%.

• Scenario 4 (Specific heat capacity prioritized: W_SHC = 3): Maximum MF of 0.2% is required for optimal performance.

Table 13 The proposed optimal points for various importance coefficients based on EHC and desirability function.

Additionally, optimal MF values were examined under varying temperatures. Figure 7 presents these temperature-dependent trends across all scenarios:

• In Scenario 1, MF increases sharply from ~ 0.06% at 25 °C to 0.161% at ~ 25.07 °C, gradually rising until it stabilizes at 0.2% between 32 and 47 °C, then slightly drops to 0.197% at 50 °C.

• In Scenario 2, MF starts higher at 0.163%, increases to ~ 0.182%, and finally reaches 0.197%.

• In Scenario 3, MF begins as low as 0.029–0.039% at low temperatures, rises steadily, and stabilizes around 0.183–0.195% at higher temperatures.

• In Scenario 4, MF rapidly climbs to 0.196% by 26.1 °C and remains fixed at 0.2% thereafter.

Fig. 7

Optimum MF values in various temperatures for different scenarios.

Discussion

The observed trends emphasize the complex interplay between thermal conductivity, dynamic viscosity, and specific heat capacity as influenced by both MF and temperature. One notable behavior is the slight decline in optimal MF after 0.16%, particularly evident in Scenario 1. This can be attributed to interfacial saturation and aggregation effects of MXene nanoparticles. Beyond a critical concentration, additional nanoparticles may lead to agglomeration, reducing the effective surface area for heat transfer and impeding thermal transport pathways. This saturation behavior is well-documented in nanofluid studies, where increasing particle concentration enhances TC up to a threshold, after which thermal conductivity plateaus or slightly decreases due to reduced Brownian motion and enhanced clustering.

Moreover, increased MF beyond this threshold can disproportionately increase viscosity, negatively impacting fluid mobility and system efficiency. The desirability function, in balancing multiple objectives, identifies this trade-off, hence slightly lowering the optimal MF at the highest temperatures despite a favorable trend at moderate ones.

In scenarios emphasizing SHC (Scenario 4), the model pushes for maximum concentration (0.2%) throughout, as SHC benefits consistently from higher nanoparticle presence. Conversely, prioritizing DV (Scenario 3) naturally constrains MF due to viscosity-related penalties at higher concentrations.

Metaheuristic optimization

Traditional multi-objective optimization methods often fall short in identifying a single definitive solution due to the conflicting influences. To overcome this issue, the Pareto front methodology provides a powerful alternative, enabling a thorough analysis of the solution space and revealing a spectrum of optimal trade-offs. Unlike conventional approaches that aim for a singular best result, the Pareto front strategy generates a diverse array of solutions, each offering a unique compromise among the objectives. This research utilizes the novel multi-objective generalized normal distribution optimization (MOGNDO) algorithm to accurately determine these Pareto optimal points. To evaluate the effectiveness of MOGNDO, the widely regarded non-dominated sorting genetic algorithm II (NSGA-II) is employed as a benchmark. NSGA-II, an evolutionary algorithm, improves a population of solutions through iterative processes such as selection, crossover, and mutation⁵⁷. It prioritizes solutions based on non-domination and utilizes crowding distance to preserve solution diversity. The parameter settings used for NSGA-II are a population size of 200, 500 generations, a crossover rate of 0.8, a mutation rate of 0.1, and a Pareto fraction of 0.5. These values were selected based on preliminary sensitivity analyses aimed at achieving an optimal balance between convergence speed and exploration capability. NSGA-II, widely recognized for its robustness and efficiency, is extensively applied in scenarios requiring balanced solutions among conflicting objectives, demonstrating reliable results in various studies such as^58,59,60. For a deeper understanding of this algorithm, readers are directed to the primary references^61,62. The NSGA-II and MOGNDO techniques were independently implemented by the authors in the MATLAB environment (R2024a), based on the theoretical formulations presented in the literature.

Multi-objective generalized normal distribution optimization

The generalized normal distribution optimization (GNDO) algorithm, introduced by Zhang et al.⁶³, is a metaheuristic method designed to solve optimization problems by balancing exploration and exploitation through various strategies. The GNDO algorithm employs a population-based search approach, typically involving three main stages. Initially, the algorithm generates a random population of candidate solutions, which are distributed across the search space. These solutions then move towards the optimal solution using specific search and refinement strategies. Eventually, the population converges near the best-found solution.

The GNDO approach uses the concept of normal distributions to describe the positions of solutions. At the beginning of the search, the average position of the solutions is distant from the best position, and there is significant variation in the solution positions. As the algorithm progresses, this gap narrows, and the variance in positions decreases, leading to convergence towards the optimal solution. GNDO’s structure is straightforward, with information-sharing mechanisms that combine local exploitation and global exploration. Exploitation relies on a generalized normal distribution model, guided by the current average and optimal positions. In contrast, exploration involves selecting three random individuals to ensure a broad search of the solution space. The algorithm starts with a randomly generated population using:

$$\begin{array}{c}{x}_{i,j}^{t}={l}_{j}+\left({u}_{j}-{l}_{j}\right)\times {\lambda }_{5}\end{array}$$

(11)

where $i$ and $j$ represent the indices of the population and design variables, respectively, ${l}_{j}$ and ${u}_{j}$ are the lower and upper bounds of the design variables, and ${\lambda }_{5}$ is a random number between 0 and 1. During the exploration phase, GNDO employs a global search strategy using a combination of local and global learning terms. The exploration equation is:

$$\begin{array}{*{20}c} {v_{i}^{t} = x_{i}^{t} + \underbrace {{\beta \times \left( {\left| {\lambda_{3} } \right| \times v_{1} } \right)}}_{{\text{Local learning term }}} + \underbrace {{\left( {1 - \beta } \right) \times \left( {\left| {\lambda_{4} } \right| \times v_{2} } \right)}}_{{\text{Global learning term }}}} \\ \end{array}$$

(12)

where $\beta$ is a random coefficient, and ${v}_{1}$ and ${v}_{2}$ are trail vectors defined by the relative positions of randomly selected individuals. This dual strategy allows the algorithm to balance between local exploitation and global exploration. Random variables ${\lambda }_{3}$ and ${\lambda }_{4}$ follow a normal distribution, broadening the search space. Exploitation in GNDO focuses on refining solutions near the best candidates using a generalized normal distribution model. The exploitation equation is:

$$\begin{array}{c}{v}_{i}^{t}={\mu }_{i}+{\delta }_{i}\times \eta , i=\text{1,2},3,\dots ,N\end{array}$$

(13)

where ${\mu }_{i}$ is the generalized mean position, ${\delta }_{i}$ is the standard deviation, and $\eta$ is a penalty factor influenced by random variables. This approach fine-tunes the solutions around the best current findings to enhance convergence accuracy. A selection mechanism ensures that the better solutions are preserved for the next generation, defined by:

$$\begin{array}{c}{x}_{i}^{t+1}=\left\{\begin{array}{cc}{v}_{i}^{t},& \text{ if }f({\text{v}}_{i}^{t})<f\left({x}_{i}^{t}\right)\\ {x}_{i}^{t},& \text{ otherwise }\end{array}\right.\end{array}$$

(14)

The MOGNDO extends GNDO to handle multi-objective optimization problems⁶⁴. It incorporates two additional components: an archive mechanism and a leader selection strategy. The archive mechanism is designed to store non-dominated Pareto-optimal solutions found during the search process. It uses an archive controller to manage the inclusion of new solutions and a grid-based approach to maintain diversity among archived solutions. The controller discards dominated solutions while retaining or adding non-dominated ones to the archive. If the archive is full, a crowding mechanism is employed to remove the most crowded solutions, ensuring a balanced distribution of Pareto solutions. The leader selection strategy helps identify the best solutions from the archive to guide the search process. This approach uses grid-based selection to ensure diversity and balance in exploring the Pareto front. MOGNDO combines the exploration and exploitation mechanisms of GNDO with the multi-objective components to efficiently navigate the trade-offs between different objectives, delivering a well-distributed set of optimal solutions.

Pareto fronts

Figure 8 presents the Pareto optimal points obtained using the MOGNDO algorithm and the NSGA-II for optimizing the thermal conductivity, dynamic viscosity, and specific heat capacity of the MXene-based aqueous ionic liquid for solar systems. Figure 8a, b, and c respectively illustrate the relationships between TC and DV, TC and SHC, and DV and SHC. In all subplots, the Pareto fronts generated by both algorithms align closely, demonstrating a strong agreement between the solutions. However, a deeper analysis reveals that the MOGNDO algorithm offers superior performance in several aspects. Firstly, MOGNDO demonstrates enhanced coverage of the optimization space. This broader coverage is critical for providing decision-makers with a wider range of trade-off solutions, especially when balancing multiple objectives. Secondly, the uniform distribution of MOGNDO’s solutions indicates better diversity maintenance compared to NSGA-II, which shows slight gaps and density inconsistencies in some regions of the Pareto front. The ability of MOGNDO to maintain a consistent spread is advantageous in multi-objective optimization, as it avoids premature convergence and enhances robustness. Furthermore, MOGNDO’s search mechanism, influenced by the generalized normal distribution model, appears to facilitate both exploration and exploitation effectively, contributing to its improved convergence behavior. Overall, while both algorithms provide high-quality solutions, MOGNDO not only matches the Pareto front obtained by NSGA-II but also offers better space coverage and greater reliability in finding optimal solutions. Figure 9 presents a three-dimensional representation of the Pareto front developed by the MOGNDO algorithm.

Fig. 8

Pareto optimal points generated through the implementation of the MOGNDO and NSGA-II optimization algorithms.

Fig. 9

Three-dimensional visualization of the Pareto front produced by the MOGNDO approach.

Figure 10 illustrates the alteration of optimal input variables (mass fraction of MXene and temperature) across the Pareto optimal points for various objectives. Figure 10a, b, and c depict the relationships between optimum MF and T with respect to TC, DV, and SHC, respectively. Based on the figures, the temperature remains constant at 50°C for all Pareto optimal points, emphasizing that the optimization primarily targeted variations in the mass fraction of MXene (MF) to fine-tune the thermophysical properties. The MF values span from as low as 0.00188 to a maximum of 0.2%, indicating a broad range over which adjustments can be made. This variability suggests that different trade-offs between various TPPs can be strategically managed by modifying the MXene concentration, allowing for tailored optimization based on specific application needs. The TC values range from approximately 0.579 to 0.797 W/m K. The lowest TC values are associated with MF values near zero, whereas the highest TC values are observed when MF is close to 0.16%. Figure 10a shows a prominent increase in TC with the rise in MF, reaching a peak around 0.8 W/m K at approximately 0.16%. Beyond this concentration, TC decreases with further increases in MF. This trend can be attributed to the agglomeration of MXene nanoparticles at higher concentrations, which may hinder heat transfer efficiency due to increased viscosity and particle clustering. On the other hand, DV varies from 2.028 to 2.157 mPa s across the Pareto points. It exhibits a slight increase with rising MF values. Higher concentrations of MXene contribute to increased particle–particle interactions and hindered molecular motion, resulting in greater viscosity. This is a critical consideration since excessive viscosity can impact fluid flow performance and reduce the efficiency of heat transfer applications. Aslo, SHC values range from 2.192 to 2.503 J/g K. An increasing trend in SHC is observed with higher MF values. This suggests that higher MXene concentrations lead to improved energy storage capacity within the ionic liquid. While this is advantageous for solar thermal systems, excessive increases in SHC should be balanced against changes in viscosity and thermal conductivity to ensure optimal heat transfer performance.

Fig. 10

Optimal input values associated with Pareto-optimal points based on the MOGNDO approach.

Based on the information from Fig. 10, it can be concluded that in the low MF regime (MF < 0.05), TC remains below 0.65, indicating poor heat conduction capability, while DV is at its lowest values, facilitating better fluid flow, and SHC is also on the lower side, limiting heat storage capacity. The moderate MF regime (0.05% < MF < 0.15%) sees TC increase significantly to around 0.7–0.75, while DV also rises but remains within acceptable limits, and SHC improves, providing a better balance between thermal conduction and energy storage. In the high MF regime (MF > 0.15%), TC reaches its highest values (~ 0.79–0.797), making it ideal for applications requiring high thermal conduction, but DV also peaks, potentially causing flow challenges, while SHC is maximized, enhancing heat storage potential. These findings highlight the necessity of selecting an appropriate MF range based on specific application requirements to balance thermal conductivity, viscosity, and heat capacity effectively.

Multi-criteria decision-making

The Pareto front derived in the previous section encapsulates a set of optimal solutions within the objective function domain, where no single solution outperforms the others within this set. However, as mentioned, different areas on the Pareto front reflect the strengths and weaknesses of different objectives. In other words, shifting between optimal points does not lead to simultaneous enhancements across all objective functions; rather, improving one criterion comes at the cost of another. Thus, selecting a specific solution from the Pareto front inherently alters the prioritization of competing objectives. Given the complexity of this selection process, multi-criteria decision-making methods are crucial for identifying a scenario-specific design point. In this research, the MARCOS (Measurement Alternatives and Ranking according to Compromise Solution) methodology is utilized to effectively navigate this challenge.

MARCOS approach

The MARCOS approach is a sophisticated multi-criteria decision-making framework designed to assess various alternatives by analyzing their relative proximity to both optimal and least desirable reference points⁶⁵. By establishing a comparative relationship between each alternative and these benchmark solutions, the method computes utility values that aid in systematically ranking the options. The core concept underlying MARCOS is that the most optimal choice is the one that exhibits the smallest deviation from the ideal solution while simultaneously being positioned farthest from the least favorable alternative. This methodology is implemented through a structured procedural framework, which unfolds in the following steps⁶⁵:

Step 1 The initial phase of the decision-making process involves constructing a decision matrix that encompasses n evaluation criteria and m potential alternatives. In cases where the decision is made collaboratively, multiple experts (r) provide assessments for each alternative based on the defined criteria. These individual evaluations are then systematically consolidated into a unified group decision matrix to ensure a comprehensive representation of expert opinions.

Step 2 At this stage, the initial decision matrix is extended to incorporate both the optimal (AI) and least favorable (AAI) solutions, forming an augmented decision matrix:

$$X=\begin{array}{c}AAI{C}_{1}\\ {C}_{2}\\ {A}_{1}\\ {A}_{2}\\ \cdots \\ {A}_{m}\\ AI\end{array}\left[\begin{array}{cccc}{x}_{aa1}& {x}_{aa2}& \dots & {x}_{\text{aan }}\\ {x}_{11}& {x}_{12}& \dots & {x}_{1n}\\ {x}_{21}& {x}_{22}& \dots & {x}_{2n}\\ \dots & \dots & \dots & \dots \\ {x}_{m1}& {x}_{22}& \dots & {x}_{mn}\\ {x}_{ai1}& {x}_{ai2}& \cdots & {x}_{\text{ain}}\end{array}\right]$$

(15)

Here, the anti-ideal solution (AAI) corresponds to the alternative with the least favorable performance across all evaluation criteria, while the ideal solution (AI) represents the alternative that performs optimally. These reference points are determined based on the nature of the criteria, distinguishing between benefit-oriented (B) and cost-oriented (C) factors, as defined by the following mathematical expressions:

$$AAI=\underset{i}{min} {x}_{ij}\,if\,j\in B\,and\,\underset{i}{max} {x}_{ij}\,if\,j\in C$$

(16)

$$AI=\underset{i}{max} {x}_{ij}\,if\,j\in B\,and\,\underset{i}{min} {x}_{ij}\,if\,j\in C$$

(17)

Step 3 In order to facilitate a fair comparison among alternatives, the decision matrix undergoes a normalization process using the following expressions:

$$n_{ij} = \frac{{x_{ai} }}{{x_{ij} }} \;if\;j \in C$$

(18)

$$n_{ij} = \frac{{x_{ij} }}{{x_{ai} }}\; if\;j \in B$$

(19)

Here, ${x}_{ij}$ and ${x}_{ai}$ are elements extracted from the extended decision matrix X. This normalization ensures that all criteria, regardless of their units or scales, are transformed into a standardized format for objective evaluation.

Step 4 The weighted decision matrix $V={\left[{v}_{ij}\right]}_{m\times n}$ is derived by multiplying the normalized matrix with the corresponding weight coefficients ${w}_{j}$:

$${v}_{ij}={n}_{ij}\times {w}_{j}$$

(20)

Step 5 The degree of utility for each alternative is calculated in relation to both the ideal and anti-ideal solutions through the following equations:

$${K}_{i}^{-}=\frac{{S}_{i}}{{S}_{aai}}$$

(21)

$${K}_{i}^{+}=\frac{{S}_{i}}{{S}_{ai}}$$

(22)

Here, ${S}_{i}$ represents the total sum of the elements within the weighted decision matrix:

$${S}_{i}=\sum_{i=1}^{n} {v}_{ij}$$

(23)

Step 6 The utility function measures the trade-off between the ideal and anti-ideal solutions, and is calculated using the following formula:

$$f\left({K}_{i}\right)=\frac{{K}_{i}^{+}+{K}_{i}^{-}}{1+\frac{1-f\left({K}_{i}^{+}\right)}{f\left({K}_{i}^{+}\right)}+\frac{1-f\left({K}_{i}^{-}\right)}{f\left({K}_{i}^{-}\right)}};$$

(24)

where:

$$f\left({K}_{i}^{-}\right)=\frac{{K}_{i}^{+}}{{K}_{i}^{+}+{K}_{i}^{-}}$$

(25)

$$f\left({K}_{i}^{+}\right)=\frac{{K}_{i}^{-}}{{K}_{i}^{+}+{K}_{i}^{-}}$$

(26)

Step 7 In the final step, the alternatives are ordered according to their utility values. The alternative with the highest utility value is considered the most preferred, as it represents the best compromise between closeness to the ideal solution and remoteness from the anti-ideal reference.

The MARCOS method is a recent approach with significant potential, though not widely utilized. It provides a structured framework for decision-making by combining expert assessments, mathematical normalization techniques, and utility function analysis to generate a logical ranking of alternatives in intricate multi-criteria decision-making scenarios.

Design points

Table 14 shows decision-making for design points considering the varying objective weights and the number of criteria. Also, Fig. 11 presents a visual representation of the most favorable design points associated with Scenarios A to J along the Pareto front. Based on Table 14 and Fig. 11, scenarios A, B, and C represent one-criteria decision-making, where a single objective is prioritized while others are ignored. According to Table 14, the different scenarios considering a single goal are as follows:

• Scenario A (TC Maximization, W_TC = 1, W_DV = 0, W_SHC = 0): The decision aims to maximize thermal conductivity, leading to the selection of a design point with MF = 0.16% and T = 50 °C. This results in TC = 0.7969 W/m K, which is the highest among the available choices. However, the trade-off includes increased viscosity (DV = 2.1470 mPa s) and a moderate SHC (2.4183 J/g K), which may impact overall system efficiency.

• Scenario B (DV Minimization, W_TC = 0, W_DV = 1, W_SHC = 0): Here, the lowest dynamic viscosity is prioritized, leading to the selection of MF = 0% and T = 50 °C. This results in DV = 2.0284 mPa s, which enhances fluid flow characteristics but compromises TC (0.5790 W/m K) and SHC (2.1922 J/g K), potentially affecting thermal efficiency.

• Scenario C (SHC Maximization, W_TC = 0, W_DV = 0, W_SHC = 1): The objective is to maximize SHC, leading to MF = 0.2% and T = 50 °C. This selection ensures the highest SHC (2.5035 J/g·K) while maintaining a balanced TC (0.7702 W/m K) and a relatively higher viscosity (DV = 2.1573 mPa s).

Table 14 Decision-making for design points considering the varying objective weights and the number of criteria.

Fig. 11

Graphical depiction of the chosen design points associated with Scenarios A–J along the Pareto front.

Scenarios D, E, and F incorporate two criteria, allowing for more balanced trade-offs:

• Scenario D (TC and DV Consideration, W_TC = 1, W_DV = 1, W_SHC = 0): This selection results in MF = 0.158%, which provides a high TC (0.7969 W/m K) and relatively low DV (2.1466 mPa s). However, the SHC is slightly compromised (2.4147 J/g K).

• Scenario E (TC and SHC Consideration, W_TC = 1, W_DV = 0, W_SHC = 1): With MF = 0.18%, this scenario balances high TC (0.7901 W/m K) and SHC (2.4530 J/g K), while the viscosity is relatively higher (DV = 2.1506 mPa s).

• Scenario F (DV and SHC Consideration, W_TC = 0, W_DV = 1, W_SHC = 1): The decision focuses on achieving a balance between viscosity and heat capacity, selecting MF = 0.2%. This results in the highest SHC (2.5035 J/g K) while maintaining a manageable DV (2.1573 mPa s).

Scenarios G, H, I, and J incorporate all three objective functions with different weight distributions.

• Scenario G (Equal Weights, W_TC = 1, W_DV = 1, W_SHC = 1): This selection (MF = 0.175%) ensures a balanced trade-off with TC = 0.7931 W/m K, DV = 2.1494 mPa s, and SHC = 2.4428 J/g K, offering a well-rounded solution.

• Scenario H (Higher TC Emphasis, W_TC = 3, W_DV = 1, W_SHC = 1): By emphasizing TC, the chosen design (MF = 0.165%) optimizes thermal conductivity (0.7965 W/m K) while keeping DV (2.1476 mPa s) and SHC (2.4250 J/g K) within acceptable ranges.

• Scenario I (Higher DV Emphasis, W_TC = 1, W_DV = 3, W_SHC = 1): The selection (MF = 0.169%) prioritizes reducing viscosity while maintaining a balance, resulting in TC = 0.7955 W/m K, DV = 2.1483 mPa s, and SHC = 2.4320 J/g K.

• Scenario J (Higher SHC Emphasis, W_TC = 1, W_DV = 1, W_SHC = 3): The highest SHC (2.5035 J/g K) is achieved with MF = 0.2%, while TC (0.7702 W/m K) remains moderately high and DV (2.1573 mPa s) is acceptable.

The real-world users of each scenario vary based on their operational needs and system priorities. In single-criteria decision-making, Scenario A (TC Maximization) is ideal for thermal management applications, such as heat exchangers and solar collectors, where maximizing thermal conductivity enhances efficiency. Scenario B (DV Minimization) benefits industries dealing with fluid transport, such as cooling systems in microelectronics, where lower viscosity reduces energy consumption in pumping. Scenario C (SHC Maximization) is useful for thermal energy storage applications, where maximizing heat capacity is essential for efficient energy retention. In two-criteria decision-making, Scenario D (TC and DV) is applicable in HVAC systems where high thermal conductivity and lower viscosity improve heat transfer efficiency. Scenario E (TC and SHC) benefits solar thermal storage, where both properties enhance heat absorption and retention. Scenario F (DV and SHC) is relevant for advanced lubricants and heat transfer fluids. In three-criteria decision-making, Scenario G (Balanced Weights) applies to multifunctional heat transfer fluids, Scenario H (Higher TC) supports industrial heating systems, Scenario I (Lower DV) aids in fuel efficiency, and Scenario J (Higher SHC) benefits phase change materials for energy storage. Each scenario addresses specific industry needs, ensuring optimal material selection based on application demands.

Conclusion

Summary of contributions

This study introduces an integrated optimization framework tailored to improve the thermophysical properties of MXene–based nanofluids for enhanced solar energy efficiency. By optimizing thermal conductivity, viscosity, and specific heat capacity through advanced data-driven modeling and multi-objective algorithms, the proposed method supports the development of high-performance heat transfer fluids. The results offer valuable insights into tailoring MXene–based nanofluid compositions and operating conditions, directly contributing to improved thermal management and overall efficiency in solar energy systems.

Key modeling and optimization results

RSM modeling revealed the high accuracy and robustness of the developed models, with cubic models demonstrating exceptional predictive capabilities for TC, DV, and SHC. The R² values for these models were consistently above 0.99, indicating high model precision and validity. In comparison to NSGA-II, MOGNDO provided broader coverage of the optimization space and a more uniform distribution of Pareto optimal points, enhancing solution diversity and avoiding premature convergence. The MOGNDO pareto points showed that the temperature remained constant at 50°C, while the mass fraction of MXene varied from 0.00188 to 0.2%. TC ranged from 0.579 to 0.797 W/m K, with the highest values around 0.16 wt% MF. DV ranged from 2.028 to 2.157 mPa s, showing a slight increase with MF. SHC ranged from 2.192 to 2.503 J/g K, increasing with MF, indicating enhanced energy storage capacity. Also, the MARCOS decision-making method evaluated scenarios with varying objective weights. In single-objective scenarios, maximizing TC required MF = 0.16%, minimizing DV required MF = 0%, and maximizing SHC required MF = 0.2%. Two-objective scenarios demonstrated balanced trade-offs between TC, DV, and SHC. In multi-objective scenarios, an equal weight scenario (Scenario G) with MF = 0.175% achieved a balanced performance (TC = 0.7931 W/m K, DV = 2.1494 mPa s, SHC = 2.4428 J/g K).

Implications for solar energy systems

These findings have meaningful implications for solar energy technologies. By offering a systematic and scalable optimization framework, this study facilitates the design of nanofluids that support improved thermal regulation and energy storage in solar collectors, PVT systems, and other renewable energy applications. Enhanced thermophysical properties translate to increased solar-to-thermal conversion efficiency, contributing to the broader goals of sustainability, energy conservation, and decarbonization.

Limitations and future directions

Beyond the application-specific results, this study contributes methodologically by combining heuristic and metaheuristic techniques with multi-criteria decision-making. This hybrid framework can be adapted to other complex, multi-variable engineering problems. However, several limitations were identified. The scope of experimental data constrained the complexity of RSM models, particularly for higher-order interactions. Additionally, results are specific to the tested MXene-based aqueous ionic liquid, which may limit generalizability. Further fine-tuning or hybridization of the employed algorithms could also enhance convergence speed and solution precision. Future research should focus on expanding the experimental dataset to improve model robustness and explore the potential of hybrid optimization algorithms to further enhance performance. Additionally, investigating the effects of other operational parameters, such as flow dynamics and heat transfer coefficients in real-world solar systems, would provide valuable insights for practical applications. Extending the methodology to other emerging nanomaterials could also broaden the applicability of the proposed framework. Ultimately, this study sets a foundation for advancing the design and implementation of high-performance nanofluids in solar energy systems, contributing to the broader goals of sustainability and energy efficiency.