Utilizing unified progressive hybrid censored data in parametric inference under accelerated life tests

Abstract

Progressive-stress accelerated life testing (PSALT) is a specialized experimental method that evaluates the longevity of a product under continuously fluctuating stress levels. Due to the constraints of testing equipment and expenses, the lifetime data collected by PSALT are typically censored. This paper introduces the PSALT model that utilizes Type-II unified progressive hybrid censoring to address this data characteristic, specifically when the lifespan of test units follows a truncated Cauchy power exponential (TCPE) distribution. The distribution’s scale parameter follows the inverse power law, and the cumulative exposure model is relevant for the effects of differing stress levels. The estimation methods for the TCPE parameters and the acceleration factor are examined, including maximum likelihood and Bayesian estimation techniques. Bayesian estimates are generated using the Markov chain Monte Carlo technique based on symmetric and asymmetric loss functions. The highest posterior density intervals are assessed, as well as asymptotic confidence intervals. A simulation study is conducted to evaluate the efficacy of the proposed point and interval estimators. Ultimately, a real data set is applied to the TCPE distribution, and the proposed estimators are assessed.

Introduction

Scientific and technological advancements have resulted in the development of intricate and highly durable products, including lamp LEDs, computers, and silicone seals. Product quality is contingent upon reliability; consequently, manufacturers allocate substantial resources to testing, design, and other initiatives that guarantee consistent functionality. The ideal scenario would entail an abundance of life-testing data. However, a challenge arises with highly reliable products, as their extended lifespans frequently result in very few or even zero failures within a reasonable testing period under normal operating conditions.

Accelerated life tests (ALTs) have become a critical process that enables researchers to describe the life characteristics of products (systems or components), causing them to fail more rapidly than the normal operating condition. Higher stress loadings in ALT can be applied in various ways, with the three most common being constant-stress, step-stress, and progressive-stress. Nelson¹ and Meeker and Escobar² provided further information about ALTs. In constant-stress ALT, the products are tested under a constant stress level until the test terminates. Test termination can be determined based on the requirements, such as by establishing a threshold for the number of failures or by establishing a time limit for the test. Several authors investigated constant stress ALTs, for example, see Hassan³, Hassan and Al-Ghamdi⁴, Lin et al.⁵, Shi et al.⁶, Hassan et al.⁷, Ling⁸, Nassar and Alam⁹, Wang et al.¹⁰, Yousef et al.¹¹, and Alomani et al.¹².

Step-stress ALT products with increasing stress levels step by step by fixing the stress change criteria, which can be either the stress changing time or the number of failures. Several authors, including Ling and Hu¹³, Klemenc and Nagode¹⁴, Alam and Ahmed¹⁵, Chen et al.¹⁶, Yousef et al.¹⁷, and Hassan et al.¹⁸ have considered the study of step-stress ALT. In a progressive-stress ALT (PSALT), the amount of stress placed on the test product gradually increases over time. A ramp test is an ALT with linearly increasing stress. Starr and Endicolt¹⁹ evaluated capacitors using the ramp method. Solomon et al.²⁰ and Chan²¹ applied the ramp test to insulations and integrated circuits, respectively. For PSALT, see^{22,23,24,25,26}.

Predicting remaining useful life (RUL) for products or systems is usually the ultimate aim of such life-testing and dependability analysis. Recent studies, for example, investigate RUL prediction using sophisticated stochastic process models for multivariate and dependent degradation data²⁷ or for systems displaying multi-phase degradation²⁸. Moreover, data-driven solutions including federated learning with adaptive sampling are under development for challenging uses including aircraft engine RUL prediction²⁹.

Censoring is widely used in life and reliability tests, as it is a result of the constraints of time and budget. Two of the most frequently employed censoring schemes are Type-I and Type-II. The hybrid censored scheme is a combination of the Type-I censored scheme and the Type-II censored scheme. The Type-I hybrid censoring and Type-II hybrid censoring schemes were also proposed by Epstein^30,31. It is a more advanced type of censoring that combines Type-I and Type-II censoring, where the experiment will be terminated at $min(Z_{m:n}, \tau )$. Merging the Type-II progressive censoring and hybrid censoring schemes produce the so called progressive hybrid censoring scheme (PHCS), which allows us to remove the reliable units at any time, and the experiment ends at $min(Z_{m:n}, \tau )$, see Kundu and Joarder³² and Childs et al.³³. However, the PHCS has the drawback of not being applicable when only a few failures are likely to occur before time $\tau$. Cho et al.³⁴ proposed a Type-I generalized PHCS, while Lee et al.³⁵ proposed a Type-II generalized PHCS. While generalized PHCS outperform Type-I and Type-II PHCS, they do have significant drawbacks. To address some of the shortcomings of these schemes, Górny and Cramer³⁶ developed Type-II unified UPHCS (Type-II UPHCS), a general type of generalized PHCS. The lifetime experiment will be completed under Type-II UPHCS with a minimum of k number of unit failures, which ensures that the statistical inference is carried out more effectively. The UHCS has been studied for a variety of lifetime distributions, as demonstrated by the research of Jeon and Kang³⁷, Shahrastani and Makhdoom³⁸, and Lone and Panahi³⁹.

Suppose n identical items are put to the test in a life test. One way to characterize the Type-II UPHCS is as follows: Let integer $k,m\in {1,2,...,n}$ and $\tau _{1}, \tau _{2} \in (0,\infty )$ be prefixed such that $\tau _{1}<\tau _{2}$ and $k<m$ with $R=(R_{1}, R_{2},..., R_{m})$ is also prefixed integers satisfying $n=m+R_{1}+R_{2}+...+R_{m}$. When the first unit fails, $R_{1}$ is randomly removed from the remaining units. In the event of a second failure $R_{2}$, the remaining units are removed and so on. Experiment termination occurs at $min \{max(Z_{m:m:n},\tau _{1}),\tau _{2}\}$ if the $k^{th}$ failure occurs prior to time $\tau _{1}$. In the event that the $k^{th}$ failure occurs between $\tau _{1}$ and $\tau _{2}$, the experiment is terminated at $min(Z_{m:m:n}, \tau _{2})$, and if the $k^{th}$ failure occurs after $\tau _{2}$, the experiment is terminated at $Z_{k:n}$. Through this censoring methodology, we can ensure that the experiment will conclude within a maximum duration of $\tau _{2}$, with a minimum of k failures; otherwise, we can assure precisely k failures. Let $C_{1}$ and $C_{2}$ represent the numbers of observed failures by time $\tau _{1}$ and $\tau _{2}$, respectively. Furthermore, $c_{1}$ and $c_{2}$ represent the observed values of $C_{1}$ and $C_{2}$, respectively.

We have one of the following types of observations under the Type-II UPHCS described above: the experiment ends at $min \{max(Z_{m:m:n},\tau _{1}),\tau _{2}\}$ if the $k^{th}$ failure occurs before time $\tau _{1}$. In that case, we have the first three subcases in Table 1. The experiment will terminate at $min \{max(Z_{k:m:n},\tau _{2}),Z_{m:m:n}\}$ if time $\tau _{1}$ occurs before the $k^{th}$. The remaining three subcases are listed in Table 1. As a result, the six scenarios outlined in Table 1 are encountered within the Type-II UPHCS framework. Furthermore, Figure 1 illustrates the Type-II UPHCS mechanism.

Table 1 Circumstances in which a test administered under Type-II UPHCS will be concluded.

Figure 1

Schematic diagram of the Type-II UPHCS.

If $\textbf{Z}$ is a Type-II UPHCS from a distribution with the probability density function (PDF) f(z) and the cumulative distribution function (CDF) F(z), then the likelihood function based on the Type-II UPHCS can be written as

$$\begin{aligned} L(\textbf{Z})=\left\{ \begin{array}{l} \left[ \prod _{i=1}^{c_{1}}\sum _{j=1}^{m}(\Re _{j}+1)\right] \prod _{i=1}^{c_{1}}f(z_{i,m,n})[\bar{F}(z_{i,m,n})]^{\Re _{i}}[\bar{F}(\tau _{1})]^{\Re _{t_{1}}},\quad \quad \text {in Case I}\\ \left[ \prod _{i=1}^{m}\sum _{j=1}^{m}(\Re _{j}+1)\right] \prod _{i=1}^{m}f(z_{i,m,n})[\bar{F}(z_{i,m,n})]^{\Re _{i}},\qquad \qquad \qquad \text {in Case II}\\ \left[ \prod _{i=1}^{c_{2}}\sum _{j=1}^{m}(\Re _{j}+1)\right] \prod _{i=1}^{c_{2}}f(z_{i,m,n})[\bar{F}(z_{i,m,n})]^{\Re _{i}}[\bar{F}(\tau _{2})]^{\Re _{t_{2}}},\quad \quad \text {in Case III}\\ \left[ \prod _{i=1}^{k}\sum _{j=1}^{m}(\Re _{j}+1)\right] \prod _{i=1}^{k}f(z_{i,m,n})[\bar{F}(z_{i,m,n})]^{\Re _{i}},\qquad \qquad \qquad \text {in Case IV}\\ \left[ \prod _{i=1}^{m}\sum _{j=1}^{m}(\Re _{j}+1)\right] \prod _{i=1}^{m}f(z_{i,m,n})[\bar{F}(z_{i,m,n})]^{\Re _{i}},\qquad \qquad \qquad \text {in Case V}\\ \left[ \prod _{i=1}^{c_{2}}\sum _{j=1}^{m}(\Re _{j}+1)\right] \prod _{i=1}^{c_{2}}f(z_{i,m,n})[\bar{F}(z_{i,m,n})]^{\Re _{i}}[\bar{F}(\tau _{2})]^{\Re _{t_{2}}},\quad \quad \text {in Case VI} \end{array} \right. \end{aligned}$$

Thus, these scenarios may be amalgamated to yield the following:

$$\begin{aligned} L(\textbf{Z})= \left[ \prod _{i=1}^{c^{*}}\sum _{j=1}^{m}(\Re _{j}+1)\right] \prod _{i=1}^{c^{*}}f(z_{i,m,n})[\bar{F}(z_{i,m,n})]^{\Re _{i}}[\bar{F}(\tau _{1})]^{\Re _{t_{1}}}[\bar{F}(\tau _{2})]^{\Re _{t_{2}}}. \end{aligned}$$

(1)

where

$$\begin{aligned} \bar{F}&=1-F,\\ \Re _{t_{1}}&=n-c_{1}-\sum _{j=1}^{m-1}\Re _{j}, \quad \text {is the number of surviving units that are eliminated at} \tau _{1},\\ \Re _{t_{2}}&=n-c_{2}-\sum _{j=1}^{c_{2}}\Re _{j}, \quad \text {is the number of surviving units that are eliminated at} \tau _{2}. \end{aligned}$$

The motivation for employing UPHCS stems from its flexibility and efficiency in handling real-life constraints in life-testing experiments. Unlike Type-I censoring (fixed time) or Type-II censoring (fixed number of failures), UPHCS incorporates both a minimum number of failures (k) and dual time limits ($\tau _1, \tau _2$), allowing experiments to terminate early without sacrificing statistical information.

Moreover, UPHCS enhances the classical PHCS by enabling better control over test duration and ensuring sufficient failure data, even when failure events are sparse. It also supports progressive removals, allowing units to be withdrawn at specific failure times, thereby improving resource efficiency.

To highlight its advantage, we compare UPHCS with other schemes in Table 2.

Table 2 Comparison of censoring schemes.

Furthermore, we conducted a simulation comparing the performance of UPHCS with PHCS and Type-II schemes under the same sample size and censoring proportion. The results, summarized in “Simulation study”, show that UPHCS consistently achieves lower bias and mean squared error (MSE) in parameter estimation. This demonstrates the practical and statistical superiority of UPHCS in accelerated life testing experiments.

The novelty of this paper is that there is no previous study related to truncated Cauchy power exponential (TCPE) distribution under PSALT with Type-II UPHCS. Our goal is to investigate the estimation problem using the classical and Bayesian approaches. The Markov chain Monte Carlo (MCMC) method is employed to obtain Bayesian estimates under distinct loss functions. This paper employs a real-world data analysis to illustrate the practical application of the proposed methods. Additionally, a simulation study is conducted to gauge the efficacy of a variety of estimators with an emphasis on bias, MSE for point estimation, and length for confidence intervals. All of these contributions collectively enhance the methodological tools for the analysis of intricate reliability data using ALTs.

The remainder of this paper is organized as follows. The model description and its assumption are given in “Model description and test assumption”. The maximum likelihood estimates (MLEs) are evaluated in “Maximum likelihood estimation”. The Bayes estimates are developed using MCMC technique in “Bayesian analysis”. The highest posterior density (HPD) interval, asymptotic confidence interval (ACI), and Bootstrap confidence interval (BCI) are created in “Interval estimation”. A Monte Carlo simulation is carried out in “Simulation study” to examine how well the suggested methods work. In “An application”, a real data set is analyzed as an example of the discussed methods. In “Summary and conclusion”, some final observations are summarized.

Model description and test assumption

In this section, an overview of the model under consideration is provided. Also, PSALT model is constructed according to the assumptions outlined in the second subsection.

Truncated cauchy power exponential distribution

The truncated Cauchy power-G (TCP-G) family was designed to be rich and contain many new distributions that may be interesting from a statistical perspective (with different supports, numbers of parameters, properties, etc). Here, we concentrate on one defined member of the TCP-G family using the exponential distribution as the baseline. It is referred to as the TCPE distribution for the purposes of this study.

Recently, Aldahlan et al.⁴⁰ proposed a new class of distributions called the TCP-G class. It is an extension of the Cauchy distribution. The CDF, PDF, and hazard rate function (HR), respectively, are defined as:

$$\begin{aligned} \left. \begin{aligned} F(z;\lambda , \theta )&=\frac{4}{\pi }\arctan \left[ G(z;\theta )^{\lambda } \right] , z, \theta \in \textbf{R}, \lambda >0,\\ f(z;\lambda , \theta )&=\frac{4\lambda }{\pi }\frac{ g(z;\theta ) G(z;\theta )^{\lambda -1} }{1+G(z;\theta )^{2\lambda }},\\ H(z;\lambda , \theta )&=\frac{4\lambda }{\pi }\frac{g(z;\theta ) G(z;\theta )^{\lambda -1}}{[1+G(z;\theta )^{2\lambda }][1-\frac{4}{\pi }\arctan (G(z;\theta )^{\lambda })]}, \end{aligned}\right\} \end{aligned}$$

(2)

where $G(z;\theta )$ and $g(z;\theta )$ are the CDF and PDF of a baseline continuous distribution with $\theta$ as parameter vector and $\lambda$ is a shape parameter, respectively.

The CDF and PDF of the exponential distribution are defined by $G(z;\theta )=1-e^{-\theta z}, z> 0$ and $g(z;\theta )=\theta e^{-\theta z}$. Therefore, by substituting this CDF, PDF, and HR into (2), the CDF, PDF, and HR of TCPE($\lambda , \theta$) can be defined as

$$\begin{aligned} \left. \begin{aligned} F(z;\lambda , \theta )&=\frac{4}{\pi }\arctan \left[ ( 1-e^{-\theta z})^{\lambda } \right] ,\ z> 0, \lambda ,\theta >0,\\ f(z;\lambda , \theta )&=\frac{4\lambda \theta }{\pi }\frac{e^{-\theta z}(1-e^{-\theta z})^{\lambda -1}}{1+(1-e^{-\theta z})^{2\lambda }}, \end{aligned}\right\} \end{aligned}$$

(3)

and

$$\begin{aligned} H(z;\lambda , \theta )&=\frac{4\lambda \theta }{\pi }\frac{e^{-\theta z}(1-e^{-\theta z})^{\lambda -1}}{[1+(1-e^{-\theta z})^{2\lambda }]\left[ 1-\frac{4}{ \pi }\arctan [(1-e^{-\theta z})^{\lambda }]\right] }, z, \lambda ,\theta >0. \end{aligned}$$

(4)

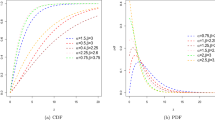
where $\lambda$ and $\theta$ are shape and scale parameters, respectively. Figure 2 presents the PDF and HR plots of the TCPE distribution. The PDF of the TCPE distribution can take different shapes, including several asymmetric shapes, unimodal, and reversed J-shaped. The HRF can be increasing, decreasing, or constant.

Figure 2

Graph of PDF (left panel) and hazard function (right panel) for different values of $\lambda$ and $\theta$.

Data structure and assumptions

The effect of stress changes from one stress level to another is formed by using a linear cumulative exposure model, for more details, see Nelson⁴¹. When the applied stress V is a function of time, $V = V(z)$, and affects the scale parameter $\theta$ of the underlying distribution, then $\theta$ becomes a function of time, $\theta (z) = \theta (V(z))$.

A test unit’s CDF under progressive stress V(z) can be expressed as

$$\begin{aligned} Q(z)=F(\Delta z), \end{aligned}$$

(5)

where the linear cumulative exposure model is;

$$\begin{aligned} \Delta z=\int _{0}^{z} \frac{dx}{\theta (V(x))}. \end{aligned}$$

(6)

For estimation under PSALT based on TCPE distribution, we make the following assumptions.

• (1) Under normal operating conditions, a unit’s lifetime is provided by TCPE distribution.

• (2) With two parameters, $\eta$ and $\zeta$, the parameter $\theta$ follows the inverse power law. This implies that $\theta (z)=\frac{1}{\eta [V(z)]^{\zeta }}$, where $\eta > 0$ and $\zeta > 0$ are parameters to be estimated.

• (3) The progressive stress V(z) has a direct relationship with time and a constant rate $s$, i.e., $V(z)=sz, s >0$.

• (4) The n items to be tested are split into $\hbar (\ge 2)$ groups during the testing process. The progressive stress is applied to each group, which contains $n_{u}$ items. In light of this, when $u = 1,..., \hbar$, $V_{u}(z)=s_{u}z, \qquad 0< s_{1}<...<s_{\hbar }$.

• (5) The failure mechanisms of a unit are the same regardless of the stress level $V_{u}, u=1,...,\hbar$.

• (6) The statistically independent random variables $Z_{u,1}, Z_{u,2},..., Z_{u,n_{u}}$ denote the $n_{u}$ failure times in group u for $u = 1,..., \hbar$.

By applying Assumptions 2 and 4, the cumulative exposure model (6) can be reformulated as follows:

$$\begin{aligned} \Delta z= \frac{\eta [s_{u}]^{\zeta }z^{\zeta +1}}{(\zeta +1)}. \end{aligned}$$

(7)

The CDF (5) of TCPE distribution under progressive-stress $V_{u}(z)$, is given by

$$\begin{aligned} Q_{u}(z)=\frac{4}{\pi }\arctan \left[ \bigg (1-e^{-\frac{\eta s_{u}^{\zeta }z^{\zeta +1}}{(\zeta +1)}}\bigg )^{\lambda }\right] ,\ \qquad z>0, \lambda ,\eta ,\zeta >0, \end{aligned}$$

(8)

and the corresponding PDF is given by

$$\begin{aligned} q_{u}(z)=\frac{4}{\pi }\lambda \eta s_{u}^{\zeta }z^{\zeta }e^{-\frac{\eta s_{u}^{\zeta }z^{\zeta +1}}{(\zeta +1)}}\frac{\bigg (1-e^{-\frac{\eta s_{u}^{\zeta }z^{\zeta +1}}{(\zeta +1)}}\bigg )^{\lambda -1}}{1+\bigg (1-e^{-\frac{\eta s_{u}^{\zeta }z^{\zeta +1}}{(\zeta +1)}}\bigg ) ^{2\lambda }},\ \qquad z>0, \lambda ,\eta ,\zeta >0. \end{aligned}$$

(9)

Maximum likelihood estimation

This section discusses the MLE of the parameters $\zeta , \eta ,$ and $\lambda$ under PSALT when the data are Type-II UPHCS. Let $\underline{Y} = (y_{1,c^{*},n},...,y_{uv,c^{*},n})$ under the stress level $V_{u}(z), u=1,...,\hbar$ denotes the Type-II UPHCS of size $c^{*}$ from a sample of size n drawn from a TCPE($\lambda , \theta$). Upon substituting (8) and (9) in (1), the likelihood function of the set of parameters $\vartheta =( \eta , \zeta , \lambda )$ can be expressed as:

$$\begin{aligned} L(\vartheta |\underline{\text {Y}})&=\prod _{u=1}^{\hbar }\left[ \prod _{v=1}^{c^{*}}\sum _{w=1}^{m_{u}}(\tilde{R}_{w}+1)\right] \prod _{v=1}^{c^{*}}\frac{\lambda \eta }{4 \pi } s_{u}^{\zeta }y_{uv}^{\zeta }e^{-\frac{\eta s_{u}^{\zeta }y_{uv}^{\zeta +1}}{(\zeta +1)}}\frac{\bigg (1-e^{-\frac{\eta s_{u}^{\zeta }y_{uv}^{\zeta +1}}{(\zeta +1)}}\bigg )^{\lambda -1}}{1+\bigg (1-e^{-\frac{\eta s_{u}^{\zeta }y_{uv}^{\zeta +1}}{(\zeta +1)}}\bigg )^{2\lambda }}\nonumber \\&\times \bigg (1-\frac{4}{\pi }\arctan \left[ \bigg (1-e^{-\frac{\eta s_{u}^{\zeta }y_{uv}^{\zeta +1}}{(\zeta +1)}}\bigg )^{\lambda }\right] \bigg )^{\tilde{R}_{v}}\bigg (1-\frac{4}{\pi }\arctan \left[ \bigg (1-e^{-\frac{\eta s_{u}^{\zeta }\tau _{1}^{\zeta +1}}{(\zeta +1)}}\bigg )^{\lambda }\right] \bigg )^{\tilde{R}_{t_{1}}}\nonumber \\&\times \bigg (1-\frac{4}{\pi }\arctan \left[ \bigg (1-e^{-\frac{\eta s_{u}^{\zeta }\tau _{2}^{\zeta +1}}{(\zeta +1)}}\bigg )^{\lambda }\right] \bigg )^{\tilde{R}_{t_{2}}}. \end{aligned}$$

(10)

We replace $y_{uv,c{*},n}$ by $y_{uv}$ for simplicity of notation. Hence, we can rewrite (10) as follows:

$$\begin{aligned} L_{\vartheta |\underline{\text {Y}}}(\vartheta |\underline{\text {Y}})&=\prod _{u=1}^{\hbar }\left[ \prod _{v=1}^{c^{*}}\sum _{w=1}^{m_{u}}(\tilde{R}_{w}+1)\right] \prod _{v=1}^{c^{*}}\frac{\lambda \eta }{4 \pi } s_{u}^{\zeta }y_{uv}^{\zeta }e^{-\delta (y_{uv})}\frac{[\Upsilon (y_{uv})]^{\lambda -1}}{1+[\Upsilon (y_{uv})]^{2\lambda }}[\psi (y_{uv})]^{\tilde{R}_{v}}\nonumber \\&\times [\psi (\tau _{1})]^{\tilde{R}_{t_{1}}}[\psi (\tau _{2})]^{\tilde{R}_{t_{2}}}, \end{aligned}$$

(11)

where

$$\begin{aligned} \left. \begin{aligned} \delta (y_{uv})&=\frac{\eta s_{u}^{\zeta }y_{uv}^{\zeta +1}}{(\zeta +1)}, \\ \Upsilon (y_{uv})&=\bigg (1-e^{-\delta (y_{uv})}\bigg ), \\ \psi (y_{uv})&=\bigg (1-\frac{4}{\pi }\arctan [\Upsilon (y_{uv})]^{\lambda }\bigg ), \end{aligned}\right\} \end{aligned}$$

(12)

and $\psi (\tau _{1})$ is the same as in (12) with $y_{uv}=\tau _{1}$. Similarly for $\psi (\tau _{2})$.

Then, the log-likelihood function can be written as

$$\begin{aligned} l_{\vartheta |\underline{\text {Y}}}(\vartheta |\underline{\text {Y}})&\propto \bigg (\ln \eta + \ln \lambda \bigg ) \sum _{u=1}^{\hbar }c^{*}+ \zeta [ \sum _{u=1}^{\hbar } c^{*}\ln s_{u}+ \sum _{u=1}^{\hbar }\sum _{v=1}^{c^{*}} \ln y_{uv}]-\sum _{u=1}^{\hbar }\sum _{v=1}^{c^{*}}\delta (y_{uv})\nonumber \\&+(\lambda -1)\sum _{u=1}^{\hbar }\sum _{v=1}^{c^{*}}\ln \Upsilon (y_{uv})-\sum _{u=1}^{\hbar }\sum _{v=1}^{c^{*}}\ln [1+[\Upsilon (y_{uv})]^{2\lambda }] +\sum _{u=1}^{\hbar }\sum _{v=1}^{c^{*}}\tilde{R}_{v}\ln \bigg (\psi (y_{uv})\bigg )\nonumber \\&+\tilde{R}_{t_{1}}\ln \bigg (\psi (\tau _{1})\bigg ) +\tilde{R}_{t_{2}}\ln \bigg (\psi (\tau _{2})\bigg ). \end{aligned}$$

(13)

The log-likelihood equations for the parameters $\eta , \zeta$ and $\lambda$ are, respectively, given by

$$\begin{aligned} \left. \begin{aligned} \frac{\partial L}{\partial \eta }&=\frac{1}{\eta }[\sum _{u=1}^{\hbar }c^{*}-\sum _{u=1}^{\hbar }\sum _{v=1}^{c^{*}}\delta (y_{uv})]+\sum _{u=1}^{\hbar }\sum _{v=1}^{c^{*}}\psi _{1}(y_{uv})[(\lambda -1)-\omega (y_{uv})]\\&-\tilde{R}_{v}\psi _{2}(y_{uv})-\tilde{R}_{t_{1}}\psi _{2}(\tau _{1})-\tilde{R}_{t_{2}}\psi _{2}(\tau _{2}),\\ \frac{\partial L}{\partial \zeta }&=\sum _{u=1}^{\hbar }c^{*}\ln s_{u}+\sum _{u=1}^{\hbar }\sum _{v=1}^{c^{*}}\bigg (\ln y_{uv}-\phi (y_{uv})\bigg )+\sum _{u=1}^{\hbar }\sum _{v=1}^{c^{*}}\psi ^{*}_{1}(y_{uv})[(\lambda -1)-\omega (y_{uv})]\\&-\tilde{R}_{v}\psi ^{*}_{2}(y_{uv})-\tilde{R}_{t_{1}}\psi ^{*}_{2}(\tau _{1})-\tilde{R}_{t_{2}}\psi ^{*}_{2}(\tau _{2}),\\ \frac{\partial L}{\partial \lambda }&=\frac{1}{\lambda }\sum _{u=1}^{p}c^{*}+\sum _{u=1}^{p}\sum _{v=1}^{c^{*}}\ln \Upsilon (y_{uv})[1-\frac{\omega (y_{uv})}{\lambda }]-\tilde{R}_{v}\psi _{3}(y_{uv})-\tilde{R}_{t_{1}}\psi _{3}(\tau _{1})-\tilde{R}_{t_{2}}\psi _{3}(\tau _{2}), \end{aligned}\right\} \end{aligned}$$

(14)

where

$$\begin{aligned} \left. \begin{aligned} \phi (y_{uv})&=\frac{\delta (y_{uv})}{\zeta +1}\left[ (\zeta +1)\ln s_{u}y_{uv}-1\right] ,\\ \psi _{1}(y_{uv})&=\frac{\delta (y_{uv})}{\eta \Upsilon (y_{uv})}e^{-\delta (y_{uv})},\qquad \psi ^{*}_{1}(y_{uv})=\frac{\phi (y_{uv})}{\eta \Upsilon (y_{uv})}e^{-\delta (y_{uv})},\\ \omega (y_{uv})&=\frac{2\lambda [\Upsilon (y_{uv})]^{2\lambda }}{1+[\Upsilon (y_{uv})]^{2\lambda }},\qquad \psi _{2}(y_{uv})=\frac{2}{\pi }\frac{\omega (y_{uv})\psi _{1}(y_{uv})}{\Upsilon (y_{uv})\psi (y_{uv})},\\ \psi ^{*}_{2}(y_{uv})&=\frac{2}{\pi }\frac{\omega (y_{uv})\psi ^{*}_{1}(y_{uv})}{\Upsilon (y_{uv})\psi (y_{uv})},\qquad \psi _{3}(y_{uv})=\frac{2}{\pi }\frac{\omega (y_{uv})\ln \Upsilon (y_{uv})}{\Upsilon (y_{uv})\psi (y_{uv})},\\ \end{aligned}\right\} \end{aligned}$$

(15)

and $\psi _{2}(\tau _{1}), \psi ^{*}_{2}(\tau _{1}), \psi _{3}(\tau _{1})$ are the same as in (15) with $y_{uv}=\tau _{1}$. Similarly for $\psi _{2}(\tau _{2}), \psi ^{*}_{2}(\tau _{2})$ and $\psi _{3}(\tau _{2})$. Since the likelihood equations of $\eta , \zeta ,$ and $\lambda$ are nonlinear and solving them analytically is difficult, some numerical techniques such as the Newton–Raphson method can be used to obtain the MLEs of the distribution parameters $\eta , \zeta ,$ and $\lambda$, namely $\hat{\eta }, \hat{\zeta },$ and $\hat{\lambda }$.

Bayesian analysis

In this section, Bayesian analysis is considered with different prior and posterior distributions.

Prior and posterior distribution

To precede the Bayesian analysis, prior distributions for each unknown parameter must be taken into consideration. Here, in order to make the Bayesian analysis comparable with the likelihood-based analysis formed in “Maximum likelihood estimation”, we assume that the three parameters $\eta , \zeta ,$ and $\lambda$ have gamma prior, thus

$$\begin{aligned} \pi (\eta )&\propto \eta ^{\alpha _{1}-1}e^{-\frac{\eta }{\beta _{1}}},\qquad \eta>0, \alpha _{1},\beta _{1}>0,\\ \pi (\zeta )&\propto \zeta ^{\alpha _{2}-1}e^{-\frac{\zeta }{\beta _{2}}},\qquad \zeta>0, \alpha _{2},\beta _{2}>0,\\ \pi (\lambda )&\propto \lambda ^{\alpha _{3}-1}e^{-\frac{\lambda }{\beta _{3}}},\qquad \lambda>0, \alpha _{3},\beta _{3}>0. \end{aligned}$$

Assuming that the parameters $\eta , \zeta$, and $\lambda$ are independent, the joint prior PDF is given by

$$\begin{aligned} \pi (\eta ,\zeta ,\lambda )&\propto \eta ^{\alpha _{1}-1} \zeta ^{\alpha _{2}-1} \lambda ^{\alpha _{3}-1} e^{-(\frac{\eta }{\beta _{1}}+\frac{\zeta }{\beta _{2}}+\frac{\lambda }{\beta _{3}})},\qquad \eta>0, \zeta>0, \lambda >0. \end{aligned}$$

(16)

Together with the likelihood function in (11), by using the Bayesian theorem, the joint posterior density of $\eta , \zeta$, and $\lambda$ can be written as follows

$$\begin{aligned} \pi (\vartheta |\underline{\text {Y}})&\propto L(\vartheta |\underline{\text {Y}}) \pi (\eta ,\zeta ,\lambda )\nonumber \\&\propto \eta ^{\alpha _{1}-1+\sum _{u=1}^{\hbar }c^{*}}\zeta ^{\alpha _{2}-1}\lambda ^{\alpha _{3}-1+\sum _{u=1}^{\hbar }c^{*}} e^{-(\frac{\eta }{\beta _{1}}+\frac{\zeta }{\beta _{2}}+\frac{\lambda }{\beta _{3}})}\prod _{u=1}^{\hbar }\prod _{v=1}^{c^{*}}s_{u}^{\zeta }y_{uv}^{\zeta }e^{-\delta (y_{uv})}\frac{[\Upsilon (y_{uv})]^{\lambda -1}}{1+[\Upsilon (y_{uv})]^{2\lambda }}\nonumber \\&\times [\psi (y_{uv})]^{\tilde{R}_{v}} [\psi (\tau _{1})]^{\tilde{R}_{t_{1}}}[\psi (\tau _{2})]^{\tilde{R}_{t_{2}}}. \end{aligned}$$

(17)

Symmetric and asymmetric loss functions

Two different types of loss functions for Bayesian estimation are examined in this study. The initial one is the squared error loss function (SELF), a symmetric function that values both overestimation and underestimation equally when estimating parameters. The second option is the linear exponential loss function (LLF), which is asymmetric and provides various weights according to overestimation and underestimation.

The Bayes estimate of the function of parameters $D=D(\vartheta )$ based on SELF is given by

$$\begin{aligned} \tilde{D}_{SELF}=\int _{\vartheta } D \pi (\vartheta )\quad d\vartheta . \end{aligned}$$

(18)

The Bayes estimate under LLF of D is given by

$$\begin{aligned} \tilde{D}_{LLF}=\frac{-1}{\nu }\log \bigg [\int _{\vartheta } e^{-\nu D} \pi (\vartheta )\quad d\vartheta \bigg ], \end{aligned}$$

(19)

where $\nu \ne 0$ is the shape parameter of the LLF.

It should be noted that the Bayes estimates of D in (18) and (19) are analogous to a ratio of two multiple integrals that cannot be reduced analytically. In this regard, using an approximation technique to calculate requested estimates is recommended, as discussed in the following subsection.

MCMC method

Here, the MCMC method is employed to generate samples from the posterior distribution and then compute the Bayes estimates of D under PSALT. The conditional posterior distributions of $\eta , \zeta$, and $\lambda$ are derived using the joint posterior density function in (17).

$$\begin{aligned} \pi (\eta |\zeta ,\lambda ,\underline{\text {Y}})&\propto \eta ^{\alpha _{1}-1+\sum _{u=1}^{\hbar }c^{*}}e^{-\eta /\beta _{1}}\prod _{u=1}^{\hbar }\prod _{v=1}^{c^{*}}e^{-\delta (y_{uv})}\frac{[\Upsilon (y_{uv})]^{\lambda -1}}{1+[\Upsilon (y_{uv})]^{2\lambda }}[\psi (y_{uv})]^{\tilde{R}_{v}}[\psi (\tau _{1})]^{\tilde{R}_{t_{1}}}[\psi (\tau _{2})]^{\tilde{R}_{t_{2}}},\nonumber \\ \pi (\zeta |\eta ,\lambda ,\underline{\text {Y}})&\propto \zeta ^{\alpha _{2}-1}e^{-\zeta /\beta _{2}}\prod _{u=1}^{\hbar }\prod _{v=1}^{c^{*}}s_{u}^{\zeta }y_{uv}^{\zeta }e^{-\delta (y_{uv})}\frac{[\Upsilon (y_{uv})]^{\lambda -1}}{1+[\Upsilon (y_{uv})]^{2\lambda }}[\psi (y_{uv})]^{\tilde{R}_{v}}[\psi (\tau _{1})]^{\tilde{R}_{t_{1}}}[\psi (\tau _{2})]^{\tilde{R}_{t_{2}}},\nonumber \\ \pi (\lambda |\eta ,\zeta ,\underline{\text {Y}})&\propto \lambda ^{\alpha _{3}-1+\sum _{u=1}^{\hbar }c^{*}}e^{-\lambda /\beta _{3}}\prod _{u=1}^{\hbar }\prod _{v=1}^{c^{*}}\frac{[\Upsilon (y_{uv})]^{\lambda -1}}{1+[\Upsilon (y_{uv})]^{2\lambda }}[\psi (y_{uv})]^{\tilde{R}_{v}}[\psi (\tau _{1})]^{\tilde{R}_{t_{1}}}[\psi (\tau _{2})]^{\tilde{R}_{t_{2}}}.\nonumber \\ \end{aligned}$$

(20)

Since the conditional posterior distributions of the parameters $\eta ,\zeta$, and $\lambda$ are not reducible into the forms of some well-known distributions, we use Metropolis–Hastings algorithm, see Upadhyay and Gupta⁴². To evaluate Bayes estimates of $D=D(\lambda , \eta , \zeta )$ under SELF and LLF, the following procedure is utilized.

• (1) Assign some initial values for $\eta ,\zeta$ and $\lambda$.

• (2) Set $j=1$.

• (3) Generate $\eta \sim N(\eta _{j},\sigma _{11}), \zeta \sim N(\zeta _{j},\sigma _{22})$ and $\lambda \sim N(\lambda _{j},\sigma _{33})$ where $\sigma$ denotes the variance-covariance matrix.

• (4) Calculate

  $$\begin{aligned} T_{j}=\frac{\pi ( \eta _{j}, \zeta _{j}, \lambda _{j} |\underline{\text {Y}})}{\pi ( \eta _{j-1}, \zeta _{j-1},\lambda _{j-1}|\underline{\text {Y}})}. \end{aligned}$$

• (5) Accept $( \eta _{j}, \zeta _{j},\lambda _{j})$ with probability $min(1,T_{j})$.

• (6) Repeat steps (3) to (5) $\mathbb {M}$ times to obtain $\mathbb {M}$ number of samples for the parameters $(\eta , \zeta , \lambda )$.

• (7) Compute the Bayes estimates under SELF and LLF of $\eta ,\zeta ,$ and $\lambda$, using (18), (19) as

  $$\begin{aligned} \left. \begin{aligned} \tilde{\eta }_{SELF}&=\frac{1}{\mathbb {\acute{M}}}\sum _{j=1}^{\mathbb {\acute{M}}}\eta _{j},\\ \tilde{\zeta }_{SELF}&=\frac{1}{\mathbb {\acute{M}}}\sum _{j=1}^{\mathbb {\acute{M}}}\zeta _{j},\\ \tilde{\lambda }_{SELF}&=\frac{1}{\mathbb {\acute{M}}}\sum _{j=1}^{\mathbb {\acute{M}}}\lambda _{j}. \end{aligned}\right\} \qquad \left. \begin{aligned} \tilde{\eta }_{LLF}&=\frac{-1}{\nu }\log \bigg [\frac{1}{\mathbb {\acute{M}}}\sum _{j=1}^{\mathbb {\acute{M}}}e^{-\nu \eta _{j}}],\\ \tilde{\zeta }_{LLF}&=\frac{-1}{\nu }\log \bigg [\frac{1}{\mathbb {\acute{M}}}\sum _{j=1}^{\mathbb {\acute{M}}}e^{-\nu \zeta _{j}}],\\ \tilde{\lambda }_{LLF}&=\frac{-1}{\nu }\log \bigg [\frac{1}{\mathbb {\acute{M}}}\sum _{j=1}^{\mathbb {\acute{M}}}e^{-\nu \lambda _{j}}]. \end{aligned}\right\} \end{aligned}$$

  (21)

  where $\mathbb {\acute{M}}=\mathbb {M}-M_{0}$ and $M_{0}$ is also known as burn-in sample.

Interval estimation

In this section, we construct ACIs using MLE’s normality property, the BCIs, and HPD credible intervals for the parameters $\eta , \zeta$, and $\lambda$.

Approximate confidence intervals

Since the MLEs of the unknown parameters, cannot be derived in a closed form, it is difficult to calculate the exact distribution of the MLEs. As a result, the exact CIs of the parameters cannot be obtained. Hence, the ACI for the parameters $\lambda , \eta$, and $\zeta$ are developed based on large sample approximation.

The ACIs of $\vartheta =( \eta , \zeta , \lambda )$ based on the observed Fisher information matrix can be computed in accordance with the asymptotic normality results of the MLEs. The observed information matrix, which can be obtained by deriving the unknown parameters of the log-likelihood function, can be applied to approximate the asymptotical variance-covariance of the MLEs.

$$\begin{aligned} I(\hat{\vartheta })=\bigg (\frac{\partial ^{2} L}{\partial \vartheta _{i}\vartheta _{j}}\bigg ). \end{aligned}$$

(22)

Then the approximate asymptotic variance-covariance matrix is

$$\begin{aligned} Cov(\hat{\vartheta })=I^{-1}(\hat{\vartheta }). \end{aligned}$$

(23)

The MLEs of parameters approximately follow the multivariate normal distribution with mean $\vartheta$ and variance-covariance matrix $Cov(\hat{\vartheta })$, namely $\hat{\vartheta }\sim N(\vartheta , Cov(\hat{\vartheta }))$. Therefore, for arbitrary $0<\epsilon <1$, the $100(1-\epsilon )\%$ ACIs of the unknown parameters can be expressed as follows:

$$\begin{aligned} \bigg (\hat{\vartheta }-\rho _{\frac{\epsilon }{2}}\sqrt{V(\hat{\vartheta })}, \hat{\vartheta }+\rho _{\frac{\epsilon }{2}}\sqrt{V(\hat{\vartheta })}\bigg ), \end{aligned}$$

(24)

where $V(\hat{\vartheta })$ is the asymptotic variance of ${\hat{\vartheta }}$, $\rho _{\frac{\epsilon }{2}}$ is the $(1-\epsilon )$ quantile of the standard normal distribution N(0, 1).

Bootstrap confidence intervals

A resampling technique for statistical inference is the bootstrap. Confidence interval estimation uses frequently (see Efron⁴³ for more details). In this part, we create confidence intervals for the unknown parameters $\eta , \zeta ,$ and $\lambda$ using the parametric bootstrap approach. We presented the percentile bootstrap (BP) and bootstrap-T (BT) CI parametric bootstrap approaches.

Percentile bootstrap CI

• 1. Compute the MLE of PSALT for parameters of TCPE distribution.

• 2. Generate a bootstrap samples using $\eta ,\zeta$ and $\lambda$ to obtain the bootstrap estimate of $\eta$ say $\hat{\eta }^{*b}$ , $\zeta$ say $\hat{\zeta }^{*b}$ and $\lambda$ say $\hat{\lambda }^{*b}$ using the bootstrap sample.

• 3. Repeat step (2) $\mathcal {B}$ times to have $(\hat{\eta }^{*b(1)},\hat{\eta }^{*b(2)},\ldots ,\hat{\eta }^{*b(\mathcal {B})}), (\hat{\zeta }^{*b(1)},\hat{\zeta }^{*b(2)},\ldots \hat{\zeta }^{*b(\mathcal {B})})$ and

  $(\hat{\lambda } ^{*b(1)},\hat{\lambda }^{*b(2)},\ldots ,\hat{\lambda }^{*b(\mathcal {B})})$.

• 4. Arrange all values of $\hat{\eta }^{*b}, \hat{\zeta }^{*b}$ and $\hat{\lambda }^{*b}$ obtained in step 3 in an ascending order as $(\hat{\eta }^{*b[1]},\hat{\eta }^{*b[2]},\ldots ,\hat{\eta }^{*b([\mathcal {B}])}), (\hat{\zeta }^{*b[1]},\hat{\zeta }^{*b[2]},\ldots \hat{\zeta }^{*b[\mathcal {B}]})$ and $(\hat{\lambda } ^{*b[1]},\hat{\lambda }^{*b[2]},\ldots ,\hat{\lambda }^{*b[\mathcal {B}]})$.

• 5. Two sided $100(1 - \epsilon )\%$ BP confidence intervals for the unknown parameters $\eta ,\zeta ,\lambda$ are given by $[\hat{\eta }^{*b([\mathcal {B}\frac{\epsilon }{2}])},\hat{\eta }^{*b([\mathcal {B}(1-\frac{\epsilon }{2})])}], [\hat{\zeta }^{*b([\mathcal {B}\frac{\epsilon }{2}])}, \hat{\zeta }^{*b([\mathcal {B}(1-\frac{\epsilon }{2})])}]$ and $[\hat{\lambda }^{*b([\mathcal {B}\frac{\epsilon }{2}])},\hat{\lambda }^{*b([\mathcal {B}(1-\frac{\epsilon }{2})])}]$.

Bootstrap-T CI

• 1. Same as the steps (1,2) in BP.

• 2. Compute the t-statistic of $\vartheta$ as $T_{k}=\frac{\hat{\vartheta }^{*b}-\hat{\vartheta }}{\sqrt{V(\hat{\vartheta }^{*b})}}$ where $V(\hat{\vartheta }^{*b})$ is asymptotic variances of $\hat{\vartheta }^b$ and it can be obtained using the Fisher information matrix.

• 3. Repeat steps 2-3 $\mathcal {B}$ times and obtain $(T_{k}^{(1)}, T_{k}^{(2)}, \ldots , T_{k}^{(\mathcal {B})})$.

• 4. Arrange the values obtained in step 3 in an ascending order as $(T_{k}^{[1]}, T_{k}^{[2]}, \ldots , T_{k}^{[\mathcal {B}]})$.

• 5. A two side $100(1 - \epsilon )\%$ BT confidence intervals for the unknown parameters $\eta ,\zeta ,$ and $\lambda$ are given by $[\hat{\eta }+ T_k^{[\mathcal {B}\frac{\epsilon }{2}]}\sqrt{V(\hat{\eta })},\hat{\eta }+ \sqrt{V(\hat{\eta })} T_k^{[\mathcal {B}(1-\frac{\epsilon }{2})]}]$, $[\hat{\zeta }+ T_k^{[\mathcal {B}\frac{\epsilon }{2}]}\sqrt{V(\hat{\zeta })},\hat{\zeta }+ \sqrt{V(\hat{\zeta })} T_k^{[\mathcal {B}(1-\frac{\epsilon }{2})]}]$ and $[\hat{\lambda }+ T_k^{[\mathcal {B}\frac{\epsilon }{2}]}\sqrt{V(\hat{\lambda })},\hat{\lambda }+ \sqrt{V(\hat{\lambda })} T_k^{[\mathcal {B}(1-\frac{\epsilon }{2})]}]$.

Highest posterior density credible interval

The 95% HPD credible interval represents the range within which the true parameter value lies with 95% probability, based on the posterior distribution. Unlike equal-tailed intervals, the HPD interval is the shortest interval that contains the most probable values of the parameter, making it particularly informative for skewed or multimodal distributions. We compute the HPD interval using the posterior samples generated via MCMC methods. To compute the Bayesian HPD credible intervals of any function of $\vartheta$, set the credible level to $100(1-\epsilon )\%$ and apply the MCMC method described in “MCMC method” based on its point estimation. The following are the specific steps:

• (1) To get $\mathbb {M}$ groups of samples, repeat Steps (1)-(6) of the MCMC method sampling in “MCMC method”.

• (2) Arrange $\vartheta _{[j]}$, as $\eta _{[1]}, \eta _{[2]},...,\eta _{[\mathbb {\acute{M}}]},\zeta _{[1]},\zeta _{[2]},...,\zeta _{[\mathbb {\acute{M}}]}$ and $\lambda _{[1]},\lambda _{[2]},...,\lambda _{[\mathbb {\acute{M}}]}$, where $\mathbb {\acute{M}}$ denotes the length of the generated simulation.

• (3) The $100(1-\epsilon )\%$ HPD credible interval of $\vartheta$ are acquired as:

  $$\begin{aligned} \big (\vartheta _{[\mathbb {\acute{M}}\frac{\epsilon }{2}]}, \vartheta _{[\mathbb {\acute{M}}(1-\frac{\epsilon }{2})]} \big ). \end{aligned}$$

  For more details on HPD intervals, see Chen and Shao⁴⁴, El-Saeed⁴⁵, and Kruschke⁴⁶.

Simulation study

A simulation analysis is considered in this section to compare the effectiveness of the traditional maximum likelihood and Bayesian estimation techniques under various schemes of Type-II UPHCS. The statistical program R-package was used to carry out extensive computations. To generate samples under Type-II UPHCS, different values of r, k, $\tau _1$, and $\tau _2$ have been determined as illustrated in the steps below:

• The parameter values $(\lambda , \zeta , \eta )$ in this simulation are ($\lambda =0.7, \zeta =1.4, \eta =1.6$), ($\lambda =0.7, \zeta =1.4, \eta =0.5$), ($\lambda =0.7, \zeta =0.4, \eta =0.5$) and ($\lambda =2, \zeta =1.4, \eta =2.5$), and sample sizes $n_1=50$, $n_2=40$, $n_3=30$, and $n_4=20$ ($\hbar =4$) are taken into consideration.

• Generate four samples from a uniform distribution (0, 1).

• Generate TCPE samples by using the inverse of CDF, but this inverse hasn’t existed in mathematical form. So the iterative algorithm has been used by ’uniroot’ function in R-packages. Return four samples have TCPE distribution.

• Select censoring size $m_u$; $u=1,\dots ,\hbar$ by using relative censoring size r as 0.6, and 0.8, where $m_u=r\times n_u$, and $k_u=\frac{m_u}{2}$.

• Select the censoring scheme removal as:

  Scheme 1: $R_{m_u}=n_u-m_u$, and $R_w=0~; w=1:m_u-1$ where $u=1,\dots ,\hbar$.

  Scheme 2: $R_{1_u}=n_u-m_u$, and $R_w=0~; w=2:m_u$ where $u=1,\dots ,\hbar$.

  Scheme 3: $R_{1_u}=\frac{n_u-m_u}{2}$, $R_{m_u}=\frac{n_u-m_u}{2}$ and $R_w=0~; w=2:m_u-1$ where $u=1,\dots ,\hbar$.

• The algorithm technique in²⁶ has produced a Type-II PC from TCPE distribution with a size of $n_u$ and a censoring size of $m_u$.

• If the generated Type-II PC data is $(z_{1,m_u,n_u}, z_{2,m_u,n_u}, \dots , z_{m_u,m_u,n_u}),$ then $z_{m_u,m_u},n_u <\tau _1$, we set $R_{m_u} = 0$ and use the transformation which was suggested by Ng et al.⁴⁷.

• Now, we have $m_u$ observation as Type-II PC data as the following

  $(z_{1,m_u,n_u}, z_{2,m_u,n_u}, \dots , z_{m_u,m_u,n_u}, z_{m_u+1,n_u},\dots , z_{m_u+R{m_u},n_u})$. Then, as stated in “Model description and test assumption”, we determined the experiment’s end time and the matching Type-II UPHC data that were observed.

For the point estimate, we calculated the MSE and estimated bias for MLE and the Bayesian estimates of $\lambda , \zeta ,$ and $\eta$, using the gamma informative prior under SELF, LLF (with $\nu =-0.5$), and LLF (with $\nu =0.5$). Using 5,000 simulations, we also create the length of ACIs (LAICs), length of Bootstrap-P CIs (LBPCI), length of Bootstrap-T CIs (LBTCI), coverage probabilities (CP), and Bayesian credible ranges for $\lambda , \zeta$ and $\eta$ for 95% CIs. We can use the estimate and variance-covariance matrix of the MLE approach to get appropriate and superior values for the independent joint prior’s hyper-parameters. The estimated hyper-parameters can be calculated as follows by equating the mean and variance of gamma priors as the following equations:

$$\begin{aligned} \alpha _j= & \frac{\left[ \frac{1}{I} \sum _{i=1}^{I} \hat{\vartheta }^j_i\right] ^2 }{\frac{1}{B-1} \sum _{i=1}^{I} \left[ \hat{\vartheta }^j_i - \frac{1}{I} \sum _{i=1}^{I} \hat{\vartheta }^j_i\right] ^2 },~j=1,2,3,\\ \beta _j= & \frac{\frac{1}{I} \sum _{i=1}^{I} \hat{\vartheta }^j_i }{\frac{1}{B-1} \sum _{i=1}^{I} \left[ \hat{\vartheta }^j_i - \frac{1}{I} \sum _{i=1}^{I} \hat{\vartheta }^j_i\right] ^2 },~j=1,2,3, \end{aligned}$$

where, I is the number of iteration and $\hat{\vartheta }^1=\hat{\lambda }$, $\hat{\vartheta }^2=\hat{\zeta }$, and $\hat{\vartheta }^3=\hat{\eta }$ .

Classical estimators can be assessed numerically by using an appropriate iterative approach, such as the Nelder-Mead (N-M) method, but they cannot be derived in explicit form. One can use the R statistical programming language software by creating the “maxLik” package, which uses the N-M approach of maximisation in the maximum likelihood computations, developed by Henningsen and Toomet⁴⁸, to calculate the desired MLE of $\lambda , \zeta ,$ and $\eta$ for any given data set. We simulated 12,000 MCMC samples and disregarded the first 2000 iterations as burn-in to obtain the Bayes point estimates along with their HPD interval estimates of the same unknown parameters using the “coda” tools of the R programming language.

The following comments can be concluded based on Tables 3, 4, 5 and 6:

Table 3 illustrates that the MLE of the parameter $\lambda$ demonstrates a substantial negative bias, particularly at the higher censoring rate ($r = 0.8$). This bias is significantly mitigated by Bayesian estimators. The limitations of relying on asymptotic approximations in this scenario are underscored by the poor coverage provided by ACI, particularly for parameter $\lambda$, as indicated by scheme 1. Additionally, scheme 3 generates less bias than schemes 1 and 2. Furthermore, LLF performs well when censoring is low and performs poorly when censoring is high. Consequently, this may suggest that the LLF will perform poorly on smaller datasets where censoring will increase.

Table 4 indicates that the performance of MLE for $\eta$ is significantly subpar, with a high MSE, particularly when $r=0.8$. Significant enhancements in MSE are provided by the Bayesian approach. Additionally, the coverage probabilities of both bootstrap methods are nearly 95% . The decision between BP and PT is arbitrary due to the similar interval lengths and coverage rates. It is important to note that the coverage rates of HPDs in the table for a variety of scenarios are less than 90%. This suggests that HPDs provide subpar estimates in this dataset.

Table 5 summarizes that scheme 3 exhibits a reasonable MSE and outperforms schemes 1 and 2. Schemes 1 and 2 are generally more biased than scheme 3. Across all schemes, Bootstrap confidence intervals maintain acceptable performance. In contrast to the SELF, LLF with $\nu <0$ and $\nu >0$ exhibit superior bias performance. The coverage and bias of all estimators are reasonable.

Table 6 illustrates that the asymptotic assumptions are less reliable for this parameter due to the higher MSE for $\eta$ under MLE. In terms of improved performance, Bayesian methods offer substantial improvements in terms of reduced bias and MSE. Scheme 1 expands the credible ranges of HPD. Scheme 3 demonstrates an unacceptable low coverage rate and a substantial MSE. It is important to note that the loss function selection had a minimal impact on the tested values. This may imply that any loss function can be reasonably applied.

Across all tables, the censoring rate increases the bias and MSE for all estimators and potentially degrades the coverage probabilities of ACIs across all tables. Consequently, it is necessary to consider the censoring rate. Changes in the censoring level are less sensitive to the Bayesian estimates, which increases their resilience. More specifically, MLEs are comparable in situations where censoring is low ($<=30\%$), but they are not comparable when censoring levels are high ($>=50\%$). Estimates that are calculated using Bayesian estimators are more reliable. The loss function selection has a moderate effect, as LLF may occasionally decrease MSE but may potentially impact coverage. It is contingent upon the specific application and the parameter value that is the subject of the practical implications. Generally, the HPD credible intervals are shorter than the ACIs; however, this is not always present. The reliability of the HPD intervals (as determined by coverage) should be meticulously evaluated. In order to reduce bias, employ LLF with $\nu =-0.5$ to achieve low censoring. In the event of high censorship, SELF is the superior option for robustness.

Table 3 MLE and Bayesian for TCPE parameters based on Type-II UPHCS: $\lambda =0.7, \zeta =1.4, \eta =1.6$.

Table 4 MLE and Bayesian for TCPE parameters based on Type-II UPHCS: $\lambda =0.7, \zeta =1.4, \eta =0.5$.

Table 5 MLE and Bayesian for TCPE parameters based on Type-II UPHCS: $\lambda =0.7, \zeta =0.4, \eta =0.5$.

Table 6 MLE and Bayesian for TCPE parameters based on Type-II UPHCS: $\lambda =2, \zeta =1.4, \eta =2.5$.

An application

Now, using an actual data set analysed in⁴⁹ and⁵⁰, our aim is to illustrate the point and interval estimation techniques mentioned in this paper. The information shows the failure times (in hours) of electrolytic capacitors placed under two sets of Type-II UPHCS and having a size of 32 volts and 22 microfarads. 30 units make up each testing group. The following are the failure times (in hours):

First group ($s_1 = 5.0417$): “7.21, 10.24, 10.26, 10.37, 10.51, 10.56, 11.25, 11.28, 11.29, 11.35, 12.23, 12.25, 12.36, 12.57, 13.03, 13.04, 13.05, 13.27, 13.46, 13.49, 14.23, 14.45, 15.00, 15.43, 15.47, 16.55, 17.07, 17.21, 17.23, 18.49”.

Second group ($s_2 = 5.833$): “7.36, 7.55, 7.57, 8.00, 8.23, 8.46, 9.02, 9.03, 9.04, 9.22, 9.32, 9.34, 9.49, 10.28, 10.53, 11.33, 11.34, 11.54, 12.16, 12.53, 12.55, 13.20, 14.06, 14.21, 14.21, 14.21, 16.24, 16.41, 17.53, 21.26”.

Figure 3 discussed box plots, total time on test (TTT), hazard rates, and strip plots for each data set. The box plot and the strip chart were used to explain the data and ensure that there are no outliers and to see whether the data tends to the right or left side. Through these graphics, we notice that there are no outliers and that the data tends to the right side.

Figure 3

Different graph measures of data set for each group.

Before continuing, it is determined whether the TCPE distribution with CDF (8) is appropriate for fitting the aforementioned data using the statistical test of Kolmogorov-Smirnov (K-S) and its corresponding P-value for each group. The aforementioned information and CDF (8) can be used to demonstrate that the TCPE parameter estimates in Table 7 maximize the likelihood function of parameters. The MLEs of parameters and their standard error (SE) are calculated. Also, measures values of Akaike information criterion (AIC), the consistent AIC (CAIC), Bayesian IC (BIC), and Hannan-Quinn IC (HQIC). Table 7 provides the K-S, Cramér–von Mises (CVM), Anderson–Darling (AD) test statistics, and the P-value are provided. By the result in Table 7, we note that data are fitted for this model where P-values are larger than 0.05. Also, these results are better than the results presented in⁵⁰ for the Rayleigh and Weibull distributions.

Table 7 MLE with SE value and different measures of fitting.

Figure 4

Profile likelihood for TCPE based on PSALT for $t_1$.

Figure 5

Profile likelihood for TCPE based on PSALT for $t_2$.

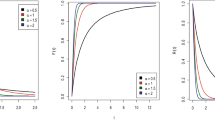
The profile likelihood plots in Figures. 4 and 5 clearly demonstrate that the MLEs are unique and correspond to the highest values of the likelihood function, confirming the presence of well-defined peaks for each parameter. The TCPE distribution fits the data better than the Weibull distribution (see⁵⁰), as indicated by the P-value for the corresponding TCPE distribution being higher than that calculated for Weibull distribution. Additionally, Figure. 6 shows that the TCPE distribution fits these data rather well.

Figure 6

PDF, CDF, and PP estimated for TCPE distribution.

Point estimates of the parameters based on the Type-II UPHCS introduced from the provided real data sets have been derived and summarized in Table 9 using data selected of Type-II UPHCS as obtained in Table 8.

Table 8 Data based on Type-II UPHCS with different schemes.

Table 9 Data based on Type-II UPHCS with different schemes.

By results in Table 9, we note that scheme 2 has smaller values of ACI, CACI, BIC, and HQIC.

Summary and conclusion

In many different sectors, accelerated life testing has been used to rapidly collect failure time data for test units in a significantly shorter period than testing under typical operating circumstances. A PSALT under Type-II UPHC is taken into consideration in this article when the lifetime of test units follows TCPE distribution. The scale parameter of the distribution follows the inverse power law, and the cumulative exposure model accounts for the effect of fluctuating stress. Using Type-II UPHC, the maximum likelihood estimates are compared with the Bayesian estimates of the unknown parameters based on symmetric and asymmetric loss functions via MCMC technique. We also provide some interval estimators of the unknown parameters including asymptotic intervals, bootstrap intervals, and highest posterior density intervals. Simulations are used to compare the accuracy of the maximum likelihood estimates with the Bayesian estimates. Also, to evaluate the effectiveness of the proposed confidence intervals for various parameter values and sample sizes. Analysis to real data has been examined.