Adaptive VSS-EWMA control chart for monitoring the process dispersion

Abstract

Effectively monitoring process dispersion is critical in ensuring high-quality production in various industrial sectors. This study presents an innovative approach by developing a Dynamic Exponentially Weighted Moving Average (EWMA) control chart with a Variable Sample Size (VSS) to monitor process dispersion. The proposed method enhances the detection capability of small shifts in the coefficient of variation (CV) by adjusting the sample size based on the observed process behavior. Extensive Monte Carlo simulations demonstrate the superior performance of the VSS-EWMA chart over traditional Fixed Sample Size (FSS) EWMA charts, highlighting its robustness in identifying process variability. The practical application of the proposed control chart is validated through empirical data, showing significant improvements in process stability and product quality. This research advances statistical process control by providing a more responsive and efficient real-time quality monitoring and improvement tool.

Introduction

Statistical Process Control (SPC) is a basic approach in industrial engineering that improves the quality and speed of manufacturing processes. Starting in the 1920s, SPC employed statistical methods to differentiate between random and assignable variations to take appropriate control actions. It, therefore, signifies that SPC, upon its application, reduces cost and wastage and increases the efficiency and effectiveness of operations and knowledge-based decisions. The steps involved are: (i) defining critical processes, (ii) data gathering, (iii) determining the proper control charts, (iv) setting up control limits, and (v) processing and analyzing data consistently. Implemented across automotive, pharmaceutical, and food industries, SPC is used to verify quality, compliance with requirements, and performance improvement in manufacturing processes.

The exponentially weighted moving average (EWMA) chart by Roberts¹ aims at controlling the process mean. At the same time, Page² presented a cumulative sum (CUSUM) chart for controlling the variation in the process mean. More specifically, monitoring the variation in the process dispersion is useful in the practical applications of process improvement since a higher dispersion is likely to decline the process quality. In contrast, a reduced dispersion will enhance the capability and productivity of the process. Sarwar et al.³ introduced an adaptive control chart based on the EWMA statistic to monitor irregular variations in the mean of a two-parameter Weibull distribution, utilizing Hasting’s approximation for normalization. The chart’s effectiveness was evaluated using a real dataset to illustrate its design and application procedures. Alduais and Khan⁴ introduced the Rayleigh EWMA (REWMA) control chart, enhancing detection capabilities over the traditional VSQR chart. Monte Carlo simulations and simulated and real-life data applications show significant improvements and sensitivity to small shifts in the Rayleigh distribution’s scaling parameter. Castagliola et al.⁵ offered an adaptive Shewhart chart for monitoring the CV utilizing the VSS strategy. The methodology introduces a 3-parameter logarithmic transformation, derives performance formulas, provides optimal parameter tables, and compares the chart with other control charts illustrated by real data from a casting process. Noor-ul-Amin and Riaz⁶ proposed an exponentially weighted moving CV chart based on three parametric lognormal transformations implemented under ranked set sampling. Monte Carlo simulations show that the proposed chart efficiently detects shifts compared to existing CV charts, with an example demonstrating its implementation on real data. Riaz et al.⁷ introduced two adaptive control charts for detecting shifts in the process mean vector, incorporating PCA for dimensionality reduction and adaptive methods like Huber and Bi-square functions. A multivariate CUSUM-PCA chart is designed, and its statistics are used as input in a classical EWMA chart. Monte Carlo simulations assess performance through RL characteristics, showing superiority over existing methods. A real-life wind turbine process example demonstrates its practical benefits. Liu et al.⁸ proposed an EWMA control chart for quality control in asphalt mixture production, considering multiple sources of variation. The EWMA-ϕ chart, optimized through an exhaustive search, outperforms traditional EWMA and CUSUM charts in detecting process shifts, especially for small offsets, demonstrating superior timeliness and broader applicability in QC. Tran et al.⁹ explore the impact of measurement error (ME) on Run Rules control charts monitoring squared CV. They enhanced CV monitoring using two one-sided Run Rules charts for CV squared, showing improved shift detection. Simulations highlight the negative effects of precision and accuracy errors on chart performance, with the limited effectiveness of multiple measurements per item in reducing these effects. Abbas et al.¹⁰ propose two nonparametric adaptive EWMA charts, NPHAEWMA-SN and NPHAEWMA-SR, for detecting unknown process shifts. They offer robust performance under non-normal distributions like heavy-tailed and contaminated normal. The charts are validated using simulated data and an industrial case from piston ring manufacturing. Abbas et al.¹¹ introduce a nonparametric adaptive CUSUM signed-rank (NPACUSUM-SR) chart for monitoring median shifts in processes. Monte Carlo simulations and RL profiles show superior steady-state performance under various distributions. Its effectiveness is validated through a real-world manufacturing application. Zhang et al.¹² introduced a modified EWMA chart to enhance sensitivity, building on the work of Castagliola et al. (2011). Statistical properties are detailed with tables, demonstrating superior ARL performance compared to competitors. Real-world manufacturing data illustrates its effective application. W.L. et al.¹³ introduced efficient run-sum charts (RS-γ) for identifying CV with optimized algorithms minimizing ARL for deterministic shifts. They expected ARL over a shift domain, demonstrating superior effectiveness compared to Shewhart-γ, Run-rules-γ, and EWMA-γ charts across various shift scenarios, validated with real casting process data. Muhammad et al.¹⁴ introduced a novel VSS EWMA chart for monitoring squared CV, presenting derived formulas for ARL, ASS, and EARL alongside an optimization algorithm. It demonstrates superior performance over five existing CV charts, validated with an industrial implementation across various scenarios. Noor-ul-Amin et al.¹⁵ introduced a blended control chart monitoring process mean and CV concurrently, enhancing sensitivity by integrating an auxiliary variable and utilizing EWMA and log transformation for distribution normalization. Performance comparisons based on ARLs and SDRLs highlight advantages over existing methods, supported by empirical evidence from real-life data. Nguyen¹⁶ introduced the VSI SH-γ² control chart for monitoring squared CV, resolving ARL bias using two one-sided charts. It corrects a previous study formula and examines the impact of measurement errors through numerical simulations. The findings reveal the negative effects of precision and accuracy errors on chart performance. A mitigation strategy is proposed to enhance the accuracy and reliability of the VSI SH-γ² chart. Thong Nguyen et al.¹⁷ explored a VSI Shewhart control chart for monitoring multivariate CV, where sampling intervals vary based on previous CV values to enhance shift detection. A comparison with the fixed sampling interval Shewhart chart highlights the superiority of the VSI method. Numerical results confirm its improved performance in detecting process shifts. Finally, a real-data example demonstrates its practical applicability. Saghir et al.¹⁸ introduced a modified EWMA control chart for monitoring process variance. It generalizes existing charts as special cases and determines necessary coefficients for various sample sizes and smoothing constants. Performance evaluation shows superiority in early shift detection compared to other control charts, with real-life data demonstrating its effectiveness. Riaz and Noor-ul-Amin¹⁹ propose an online monitoring technique based on lognormal transformation under RSS for monitoring the process mean and CV with the EWMA statistic. This methodology shows that, relative to simple random sampling, RSS improves surveillance efficiency concerning identifying shifts in mean, CV, and concurrently while minimizing the negative impact on the implementation of the monitoring plan. Haq and Khoo²⁰ introduced the AEWMA chart for monitoring CV and multivariate CV (MCV) in normally distributed processes, showing through Monte Carlo simulations that AEWMA CV outperforms optimal EWMA and CUSUM CV charts in identifying moderate-to-large CV shifts. AEWMA MCV also outperforms Shewhart MCV charts, which are validated with real dataset implementations. Khaw et al.²¹ introduced a CV chart using VSSI to enhance the detection of small to moderate CV shifts, measured by average time to signal (ATS) and expected average time to signal (EATS). The VSSI CV chart, designed with a Markov chain approach, outperforms existing CV charts. Castagliola et al.⁵ introduced an adaptive Shewhart chart with variable sample size to monitor the CV, proposing a 3-parameter logarithmic transformation for CV and deriving formulas for performance metrics like ARL and sample size. Optimal chart parameters and comparisons with other charts are provided, and a real casting process example illustrates its application. Amdouni et al.²² present an adaptive Shewhart chart with a VSS strategy to monitor CV for short production runs and develop the formula for ARL of truncated form. This involves comparing this chart with the Fixed Sampling Rate Shewhart chart and using real data to explain further.

This paper introduces an innovative VSS-based EWMA control chart to monitor CVs and significantly enhance sensitivity to small process shifts. Unlike traditional EWMA charts, the proposed VEWMA chart dynamically adjusts sample sizes based on observed process variations, ensuring a more responsive and adaptive monitoring mechanism. This advancement strengthens the statistical power of shift detection and optimizes resource utilization by intelligently allocating sample sizes. Furthermore, this study enriches the existing control chart architecture by integrating a novel adaptive sampling framework, which refines process stability assessment and improves detection accuracy across diverse industrial applications. The proposed approach demonstrates superior performance over fixed-sample EWMA charts through rigorous Monte Carlo simulations and real-world validation, marking a significant step forward in modern statistical process control. This is done through theoretical and practical comparisons of the suggested approach with the others and numerous Monte Carlo experiments that show a higher sensitivity of the new method to small shifts. However, based on the above results, this study reveals that the proposed VEWMA chart detects the variance shift quicker than the EWMA chart with FSS. On this basis, the present research continues to enhance control charting approaches in the modern context of quality management, offering further tools for stabilizing processes and improving the quality of the end products in various industries.

Design of the proposed control chart

The variable of interest Y, has a mean $\:{\mu\:}_{Y}$ and a variance $\:{\sigma\:}_{Y}^{2}$. It follows a normal distribution, represented as $\:Y \sim N\left({{\mu\:}_{Y},\sigma\:}_{Y}^{2}\right)$. For times t ≥ 1, the production units $\:\left\{{Y}_{t}\right\}$ are normally distributed in sequence. With the mean $\:{\mu\:}_{Y}$ and standard deviation $\:{\sigma\:}_{Y}$ being fixed, the coefficient of variation $\:{\gamma\:}_{{Y}_{t}}\:$ is computed as $\:{\gamma\:}_{{Y}_{t}}=\frac{{\sigma\:}_{{Y}_{t}}}{{\mu\:}_{{Y}_{t}}}.$ This suggests that although the parameters $\:{\mu\:}_{{Y}_{t}}$ and $\:{\sigma\:}_{{Y}_{t}}$ vary individually within each group, the ratio $\:{\gamma\:}_{{Y}_{t}}$ is expected to remain constant over time t for a process that is in control. Thus, the monitoring of the in-control process $\:{\gamma\:}_{{Y}_{t}}$ is based on $\:{\gamma\:}_{{Y}_{t=0}}$, using a sample of size n drawn through simple random sampling. For times $\:t>{t}_{0}$, the sequence of Y values is $\:\left\{{Y}_{t}\right\}$, representing random observation units $\:\left\{{Y}_{1t},{Y}_{2t},\dots\:,{Y}_{nt}\right\}$. Here, $\:{Y}_{it}$ denotes the i-th observation in the sample for i = 1, 2,…,n at time t. The sequence CV observations for the production $\:\left\{{Y}_{t}\right\}$ are computed utilizing the corresponding mean $\:\stackrel{-}{{Y}_{t}}=\sum\:_{i=1}^{n}{Y}_{it}/n$ and the standard deviations$\:\:{S}_{t}=\sqrt{{\sum\:}_{i=1}^{n}{\left({Y}_{it}-\stackrel{-}{{Y}_{t}}\right)}^{2}/(n-1)}$. As $\:\left\{{\widehat{\gamma\:}}_{t}=\frac{{S}_{t}}{\stackrel{-}{{Y}_{t}}}\right\}$, is the respective sequence of the random variables of the time domain $\:t>1,$ the sample estimate $\:{\widehat{\gamma\:}}_{t}$, defined within the range $\:(0,\infty\:)$, represent the sequenced CV observation. The non-central t-distribution for (n-1) degrees of freedom is followed by $\:\left\{\frac{\sqrt{n}}{{\widehat{\gamma\:}}_{t}}\right\}$ with the non-centrality parameter becoming $\:\frac{\sqrt{n}}{{\gamma\:}_{t}}.\:$

In this context, the non-central F distribution is characterized by $\:\frac{n}{{{\widehat{\gamma\:}}_{t}}^{2}}$ with degrees of freedom (1, n − 1) and the non-centrality parameter $\:\frac{n}{{\gamma\:}_{t}^{2}}$. Thus as $\:\frac{n}{{{\widehat{\gamma\:}}_{t}}^{2}}\:\sim\:F(\:1,\:\:n-1,\:\frac{n}{{\gamma\:}_{t}^{2}}\:)$. The statistic follows a normal distribution and the cumulative distribution function (CDF) transformation for the corresponding non-central $\:{F}_{F}\:$ distribution is represented as $\:{F}_{F}$, resulting in a uniformly distributed random variable, given by:

$$\:{F}_{F}(\frac{n}{{{\widehat{\gamma\:}}_{t}}^{2}};1,n-1,\frac{n}{{\gamma\:}_{t}^{2}}\:)\:\sim\:U(\:0,\:1).$$

(1)

Additionally, the inverse CDF transformation of this uniform variable into a standard normal random variable is

$$\:{Y}_{t}^{*}={{\Phi\:}}^{-1}\left({F}_{F}\left(\frac{n}{{{\widehat{\gamma\:}}_{t}}^{2}};1,n-1,\frac{n}{{\gamma\:}_{t}^{2}}\:\right)\right)\:\sim\:U(\:\mu\:=0,\sigma\:=\:1),$$

(2)

where $\:{{\Phi\:}}^{-1}\left(.\right)$ represents the inverse CDF of the standard normal distribution.

Now, $\:{Y}_{t}^{*}\sim N\left(\text{0,1}\right)$ indicates that the statistic $\:{Y}_{t}^{*}$ follows a standard normal distribution after the applied transformations. To create a CV chart, document the run length (RL) values while identifying variations in the process CV.

The basic CV chart method assumes that the shift size $\:{\varvec{\delta\:}}_{t}$ at time t is $\:{\varvec{\delta\:}}_{t}=E\left({Y}_{t}^{*}\right)$ with $\:{\:\varvec{\delta\:}}_{t}=0,$ representing an in-control state for $\:t\le\:{t}_{0}$. When the process shifts and indicates an out-of-control state, the shift becomes $\:{\varvec{\delta\:}}_{t}\ne\:0$ for $\:t>{t}_{0}$, and the CV shift state changes $\:{\gamma\:}_{y=1}{\ne\:\:\gamma\:}_{y=0}$. When the process shifts from in-control to out-of-control, it results in a change in both the process variability and the statistic $\:{Y}_{t}^{*}$. After normalization, the sequence of $\:{Y}_{t}^{*}$ values is represented as $\:\left\{{Y}_{t}^{*}\right\}$. The computed CV value in the presence of a shift δ is determined using an unbiased estimator, originally introduced by Jiang et al.²³. The methodology involves estimating the shift from the sample values at time t. Consequently, the shift δ is estimated using the EWMA statistic as follows:

$${Z_i}=\psi {Y_i}+\left( {1 - \psi } \right){Z_{i - 1}}$$

(3)

$$\:ni\:=\:f\left(\right|Zi-1\left|\right).$$

(4)

Therefore, a linear relationship exists between Z and n_i, and since the sample size must be an integer, an integer linear function proposed by Amirhossein et al.²⁴ is used.

$$\:{\text{n}}_{\text{i}}=\left[\right(\frac{n2\:-\:n1}{{\text{U}\text{C}\text{L}}_{\text{i}-1}\:-\:\mu\:}\left)\right|{\text{Z}}_{\text{i}-1}|+({\text{n}}_{1}-\frac{n2\:-\:n1}{{\text{U}\text{C}\text{L}}_{\text{i}-1}\:-\:\mu\:}\times\:\:\mu\:\left)\right].$$

(5)

The sample size function in Eq. (5) dynamically adjusts the sample size at each time point based on the value of the EWMA statistic. This approach is a central feature of Variable Sample Size (VSS) control charts, improving sensitivity to process shifts while controlling sampling cost.

Where n_i is a positive integer ranging between n₁ and n₂. Due to the variable nature of the sample size, the control limits of this chart will adjust accordingly. Therefore, by substituting Eq. (4), the upper and lower control limits can be expressed as follows.:

$$LC{L_i}=\mu - L\sigma \sqrt {\frac{\psi }{{{n_i}\left( {2 - \psi } \right)}}\left( {1 - \left( {1 - {{\left( {1 - \psi } \right)}^{2i}}} \right)} \right)}$$

(6)

$$UC{L_i}=\mu +L\sigma \sqrt {\frac{\psi }{{{n_i}\left( {2 - \psi } \right)}}\left( {1 - \left( {1 - {{\left( {1 - \psi } \right)}^{2i}}} \right)} \right)} .$$

(7)

The detailed steps for the mathematical development of the control chart are discussed in Appendix 1, which is given as a supplementary file. A comprehensive Monte Carlo simulation study was conducted to evaluate the performance of the proposed CV Chart. The primary objective is to assess the efficiency of the chart in detecting shifts in the process CV while adapting the sample size dynamically. The following steps are given to describe the simulation steps:

• 1. Initialize parameters

  • i. Set the in-control Average Run Length (ARL₀​) to 370.

  • ii. Determine the control limit hhh corresponding to ARL₀.

  • iii. Fix parameters γ₀, and λ and determine the control limits at Phase I.

• 2. Compute the VEWMA CV statistic

  • i. Use different parametric combinations, as reported in the tables.

  • i. Introduce process shifts for Phase II out-of-control performance evaluation.

  • ii. Generate the sample of size n_i determined from the equ (5) by following the design given in this section and compute the plotting statistic.

• 3. Control chart decision

  • i. Evaluate the proposed control chart statistic given in (3) with the control limits.

  • ii. Classify the process as out-of-control and record the RL if the plotting statistic is beyond the control limits.

• 4. Summarize results

  • i. Iterate the procedure for 50,000 replications to compute RL values.

  • ii. Store RL values for different at different shifts​.

  • iv. Average the RL values for all the replications and compute the ARL and SDRL for each scenario. The same are reported in the tables.

Comparative study

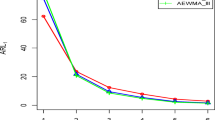
This section evaluates the performance of the proposed EWMA control chart for monitoring the process CV using ARL and SDRL values. In Statistical Process Control (SPC), various simulation techniques like integral equations, Markov chains, and Monte Carlo (MC) simulations are employed. Among these techniques, MC simulation is most widely used due to its ability to customize, acceptable computational performance, and suitability when modeling process dynamics and distributions. Due to this, it is one of the most used techniques to approximate control chart performance in SPC research. Tables 1, 2, 3 and 4 summarizes the RL characteristics resulting from MC simulations where various predicted shifts in the monitored process are described. Thus, both tables contain analyzed data obtained from 100,000 replications per iteration, which allows for assessing the effectiveness of the control chart in terms of statistical validity. The MC study proves that the suggested VEWMA CV control chart can detect the different shift sizes and their direction and, as such, the information about its robustness and efficiency. Evaluations based on large simulation data are more robust. Thus, the results are useful for practitioners who may wish to apply this control chart to a real-life scenario. For instance, Table 1 proves that the recommended VEWMA chart is more efficient than the FEWMA charts, i.e., $\psi$= 0.10, n₁ = 5, and n₂ = 10 with δ = 0.75 and δ = 1.05, the run length results for the VEWMA chart are 9.60 (4.98) and 136.72 (132.06), respectively. In contrast, for the FEWMA chart, the ARL and SDRL are 15. 00 (9.75) and 165. 38 (166. 01), thus implying that the VEWMA chart can monitor the process shift more promptly and accurately. Similarly, Table 4 presents the Run Length (RL) outcomes for the recommended and existing control charts with $\psi$= 0.15, n₁ = 3, and n₂ = 6 for shift magnitudes δ = 0.75 and δ = 1.05. The ARL and SDRL for the proposed control chart are 20.01 (13.54) and 202.74 (200.16), respectively. The ARL and SDRL for the existing EWMA chart are 43.98 (37.80) and 235.02 (237.23), respectively. This demonstrates the superior effectiveness of the proposed VEWMA chart in detecting out-of-control signals compared to the existing control chart. The significantly lower ARL and SDRL values for the VEWMA chart indicate its heightened sensitivity and quicker response to shifts in the monitored process. In other words, the VEWMA chart can identify deviations from the desired process state more rapidly and reliably, making it a superior tool for maintaining process control and ensuring quality. The comparison reveals that the suggested VEWMA chart consistently outperforms its counterparts, with calculated ARL values demonstrating its superiority. Using the VEWMA in industrial processes yields benefits because the method helps detect shifts in time. However, based on the simulation study, it is also understood that the proposed chart’s effectiveness worsens as the value of the smoothing constant increases. Figures 1, 2, 3 and 4 collectively confirm that the VEWMA control chart is a superior alternative to the traditional FEWMA chart for monitoring process dispersion. By adapting sample sizes dynamically, it detects shifts more quickly and consistently, reducing the likelihood of false alarms while maintaining high sensitivity to process variations. These findings demonstrate that the VEWMA chart is advantageous in modern industrial settings where early shift detection is crucial for maintaining product quality and process efficiency. Table 5 shows a sensitivity analysis of the suggested chart under varying shifts, and λ values offer critical insights into its effectiveness across diverse process conditions. The results reveal notable ARL and SDRL fluctuations with shift magnitude changes and $\psi$, highlighting the chart’s responsiveness and adaptability. For analyzing $\delta$ =0.25, the VEWMA scheme consistently reveals lower ARL values than FEWMA across all $\psi$ values, underscoring VEWMA’s heightened sensitivity to minor process variations. This increased sensitivity is crucial for early detection, permitting prompt corrective measures and enhancing overall process stability. The SDRL values remain relatively low for VEWMA, signifying greater consistency in detection times. As the magnitude increases, the run length values decrease accordingly, sparkly faster detection of significant shifts. For instance, at a $\delta$= 1.50, the ARL for VEWMA drops to 7.01 ($\psi$= 0.10), while FEWMA records a higher ARL of 9.42. This trend reaffirms VEWMA’s superior sensitivity, particularly for moderate to large shifts, making it a more efficient tool for rapidly monitoring process deviations. As $\psi$ increases, the ARL values rise slightly, indicating a trade-off between quicker detection and mitigating false alarms. Higher λ values lead to smoother detection but may delay the identification of smaller shifts. In scenarios where the process remains in control, the ARL values stabilize around 370, aligning with theoretical expectations under stable conditions. This behavior confirms the robustness of the control chart, ensuring minimal false alarms when the process is stable. Additionally, the SDRL values remain consistent, further validating the chart’s reliability. Table 6 for the VEWMA control chart consistently demonstrates superior performance in faster shift detection, particularly for small to moderate shifts, compared to the FCUSUM chart across different configurations of smoothing constants and sample sizes. For instance, at a small shift of δ = 0.25, the VEWMA chart achieves an ARL of 2.57 (SDRL = 0.54) with sample sizes n₁ = 3 and n₂ = 6, and an ARL of 1.98 (SDRL = 0.19) for n₁ = 5 and n₂ = 10. In comparison, the FCUSUM with n = 3 and K = 0.30 has an ARL of 5.41 (SDRL = 0.86), indicating slower detection. Even with more optimal FCUSUM settings (K = 0.50), the ARL values remain higher than VEWMA’s. This trend persists across all other shift levels. At δ = 0.50, VEWMA shows ARLs of 4.99 and 3.17 for the two sample configurations, while FCUSUM ranges from 5.35 to 10.54. The performance gap becomes more pronounced at moderate shifts such as δ = 0.75 and δ = 0.90, where VEWMA significantly outperforms FCUSUM in ARL and lower variability (SDRL), which is crucial for consistent performance. For example, at δ = 0.90, VEWMA (n₁ = 5, n₂ = 10) reports an ARL of 54.65 (SDRL = 47.01), compared to FCUSUM’s best ARL of 90.46 (SDRL = 76.68), showing nearly double the delay in signal detection. Importantly, even at large shifts (e.g., δ = 1.25 or 2.0), VEWMA retains its advantage with quicker detection times and lower ARL values than FCUSUM, while both maintain a nominal ARL of approximately 370 under in-control conditions (δ = 1.0), confirming their statistical comparability under stable process behavior. This comparison confirms that VEWMA, with its dynamic sample size mechanism, provides a more agile and efficient approach for detecting process variability than FCUSUM, especially when early detection of small or moderate shifts is critical. The comprehensive sensitivity analysis highlights the proposed control chart’s ability to swiftly detect smaller shifts under the VEWMA scheme while maintaining robustness in stable conditions. The flexibility across varying $\psi$ values balances sensitivity and stability, making the chart a valuable tool for diverse process monitoring applications. These findings reinforce the chart’s practicality in enhancing process control by providing timely signals for corrective actions and minimizing disruptions due to false alarms.

Table 1 Control charts for n₁ = 5, n₂ = 10, $\psi$= 0.10.

Table 2 Control charts for n₁ = 5, n₂ = 10, $\psi$= 0.15.

Table 3 Control charts for n₁ = 3, n₂ = 6, $\psi$= 0.10.

Table 4 Control charts for n₁ = 3, n₂ = 6, $\psi$= 0.15.

Fig. 1

Increased and decreased shift comparison for ψ = 0.10 with n₁ = 5 and n₂ = 10.

Fig. 2

Increased and decreased shift comparison for ψ = 0.15 with n₁ = 5 and n₂ = 10.

Fig. 3

Increased and decreased shift comparison for $\psi$= 0.10 with ${n_1}=3$and ${n_2}=6$.

Fig. 4

Increased and decreased shift comparison for ψ = 0.10 with n₁ = 3 and n₂ = 6.

Table 5 Sensitivity analysis of the proposed control chart at ARL₀ ≈ 370 using n₁ = 3 and n₂ = 6.

Table 6 Comparison of the proposed control chart with CUSUM chart at ARL₀ ≈ 370.

Main findings

The following are the main findings of the study:

• Based on the results presented in Tables 1, 2, 3 and 4, it can be concluded that the smoothing parameter $\psi$ significantly impacts the ARL and SDRL values and the algorithms’ performance in both the in-control and the out-of-control conditions. $\psi$ variations significantly impact a system’s ARL and SDRL values, with lower $\psi$ values giving shorter processing time and more consistent fault detection, specifically in identifying process shifts. As shown above, $\psi$ significantly influences the efficiency and reliability of the monitoring system. Therefore, setting the ideal $\psi$ value that suits the process needs to minimize false positives/negatives, response time, etc.

• With a constant δ value, the ARL generally increases as $\psi$ increases and decreases as $\psi$ decreases. For instance, in Tables 1 and 2, when δ = 0.90 and ARL₀ = 370, the ARL is 54.65 for $\psi$= 0.10 and 69.42 for $\psi$= 0.15, with ₁ = 5 and ₂ = 10. Similarly, Tables 3 and 4 indicate that when δ = 0.90 and ARL₀ = 370, the ARL values are 103.70 for $\psi$= 0.10 and 133.52 for $\psi$= 0.15, with ₁ = 3 and ₂ = 6. This trend demonstrates that some datasets are more sensitive to changes in $\psi$ values affecting ARLs, showing a direct relationship between the two factors.

• With variable sample sizes and fixed values of δ, the ARL values typically increase as the sample sizes decrease. For instance, in Tables 1 and 2 with δ = 0.50 and sample sizes ₁ = 5 and ₂ = 10, the ARL values are 3.17 for $\psi$= 0.10 and 3.25 for $\psi$= 0.15. Therefore, when the sample sizes are reduced to n1 = 3 and n2 = 6, the ARL is seen in Tables 3 and 4 to be 4. 99 for $\psi$= 0. 10 and 5. 14 for $\psi$= 0. 15. This pattern underlines that the lower the sample size, the larger the ARL value, thus the slower the detection of process shift. The rise of ARL with decreased sample size stresses the need to maintain adequate sample size in monitoring since the sensitivity and responsiveness of the monitoring system are directly dependent on the sample size chosen to monitor the process being monitored.

• Tables 1, 2, 3 and 4 consistently demonstrate that as the parameter δ increases, the RL percentiles decrease across various scenarios. For instance, in Table 4 with an in-control ARL of 370 and δ values of 0.50, 1.05, and 1.50, the corresponding percentiles (P₀₅, P₁₀, P₂₅, P₅₀, P₇₅, P₉₀, P₉₅) for $\psi$= 0.20 decrease as follows: (3, 3, 4, 5, 6, 8, 8), (11, 22, 58, 139, 288, 465, 603), and (2, 2, 4, 6, 9, 14, 17). In the decomposition presented in Tables 1, 2, 3 and 4, it is seen that as increases, RL percentiles decrease. This shows that as increases, run lengths for finding process changes are smaller, proving the enhanced sensitivity and response time of the control charts in these cases. It is necessary to comprehend this relationship to improve the monitoring system’s effectiveness, which in turn allows for the early identification of out-of-control conditions across various operational contexts.

• Selecting a smaller $\psi$ value increases the chart’s ability to identify early trends closely and be more sensitive to current data, allowing for quicker recognition of small variations from the process variance. This capability supports swift corrective measures, enhancing overall process control efficiency.

Real-life data applications

This article applies the proposed VEWMA chart to data from the hard-bake process in semiconductor production, following Montgomery²⁵. The dataset comprises 35 samples containing 5 wafers, totaling 175 Flow Width measurements in microns collected hourly. The normality of the dataset, consisting of 175 Flow Width measurements in microns from the hard-bake process in semiconductor production, was evaluated using the Shapiro–Wilk test. The test yielded a statistic of 0.9521 with a p-value of 0.0658. Since the p-value exceeds the standard significance level of 0.05, we fail to reject the null hypothesis that the data follows a normal distribution. Phase-I includes the first 20 samples (100 observations), representing a controlled process, while Phase-II consists of the remaining 20 samples, simulating an out-of-control process scenario. Phase-I establishes baseline statistics for the VEWMA chart under normal conditions, while Phase-II introduces intentional process deviations to assess the chart’s effectiveness in detecting anomalies.

We aim to evaluate the VEWMA chart’s performance in real-world semiconductor manufacturing, focusing on its ability to monitor and control Flow Width parameters and ensure prompt corrective actions to maintain high-quality production standards.

Fig. 5

FEWMA control chart for fixed sample size with $\lambda =0.25$and ${n_1}=5$.

Fig. 6

Proposed CV control chart for variable sample size with $\lambda =0.25$, ${n_1}=5$and ${n_2}=10$.

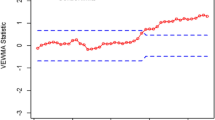
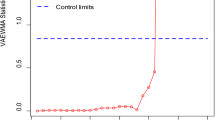
The plotted statistical data of both the recommended VEWMA chart and the existing FEWMA chart (Figs. 5 and 6) reveals significant system variations, encompassing upward and downward trends. Both control charts on the initial 20 samples demonstrated stable control, which means the constant productive activity t ≤ t₀. However, applying the new methods in Phase II where the first 20 shifted samples were introduced, enabled both charts to immediately depict the impacts of δ on the shape of the process variability in terms of the changes in the trend directions. The suggested VEWMA CV chart indicated that the process is out of control on the 21st sample. However, the conventional FEWMA CV chart revealed that the process was out of control on the 27th sample. Therefore, it validates that implementing the VEWMA dispersion chart can work for observing changes in δ quickly and can be applied to various industries. It is crucial to give an instantaneous response toward the variations in the process, enhancing the overall process control and quality measures in other sectors such as semiconductors, etc.

Conclusion

The importance of control charts has risen considerably since they have become more effective at promptly indicating a shift in the process. These charts are more sensitive than the Shewhart and EWMA, mean, and dispersion monitors charts, especially when small and moderate values of δ are evident, as shown above. Their design is deliberately developed to promptly distinguish variations in process performance within allowed tolerances, which are significant for some industries as deviations could mean a lot of difference, e.g., pharmaceutical industries, automobile manufacturing, food industry, packaging, and automation. An innovative VSS EWMA CV chart called VEWMA was created to complement the existing monitoring methods. It is designed to monitor changes in terms of the specified δ intervals at a high frequency, especially regarding the magnitude of change. It promptly alerts when needed, making it superior to the FEWMA CV chart. The performance of the VEWMA chart is verified through the use of Monte Carlo simulations and results desired run-length profiles to show that it comes out with improved results more frequently. As the critical analysis of the findings reveals, the VEWMA chart outperforms the existing FEWMA chart for all considered values, indicating the plan’s efficiency for scenarios with small, moderate, and significant changes. Thus, it can be concluded that the VEWMA chart improves the efficiency of monitoring change in process dispersion compared to the conventional methods. As a valuable tool in clinical trials, disease prediction, and assessing the efficacy of various treatments, it provides insights that could be useful in decision-making processes and enhance understanding of trends found in medical data.

Limitations and future recommendations

This study assumes a normal distribution for process observations, limiting its applicability to real-world scenarios where data often exhibit non-normal characteristics. It focuses on univariate process monitoring, while many industrial applications require multivariate control. The AEWMA chart’s effectiveness depends on fixed parameter selection, which may not be optimal across varying process conditions. Although Monte Carlo simulations demonstrate strong performance, real-world validation is limited, and the impact of measurement errors is not considered, affecting practical reliability. Future research should extend AEWMA to multivariate and non-normal processes, integrate hybrid control strategies like variable sampling intervals, and leverage machine learning for real-time parameter optimization. Additionally, addressing measurement errors and exploring applications in advanced manufacturing and innovative factory environments would enhance its robustness and industrial relevance.